승객 탈출 시간 계산을 위한 Simplified Evacuation Analysis 자동화
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The International Maritime Organization (IMO) mandates that evacuation analysis must be performed at the design stage to ensure the safety of passengers aboard ships. Therefore, ship designers are required to conduct this evacuation analysis during the ship design process. Evacuation analysis begins with creating an escape diagram that outlines the routes from each cabin to the designated assembly stations based on the designed plans. Subsequently, necessary parameters for escape analysis are measured and recorded, and the analysis is conducted using an Excel-based program. This process is manual and time-consuming. Additionally, due to the frequent design changes characteristic of passenger ships, this process must be repeated multiple times. Hence, this study proposes a method to automate this analysis process. The proposed method in this study starts with a preprocessing step to extract key components from 2D drawings. Following this, it distinguishes spaces such as cabins, corridors, and doors within the processed drawings. Using the identified spaces, it then searches for the shortest evacuation routes from each cabin to the assembly station. Based on the identified routes, the method automatically performs the simplified evacuation analysis as prescribed by IMO regulations. Applying the algorithm for automated escape analysis to Ro-Pax vessels demonstrated that the analysis time per ship, which previously took about 15 days, can be reduced to less than 10 minutes.
Keywords:
Passenger evacuation, Simplified evacuation analysis, Automation키워드:
승객 탈출, 단순 탈출 해석, 자동화1. 서 론
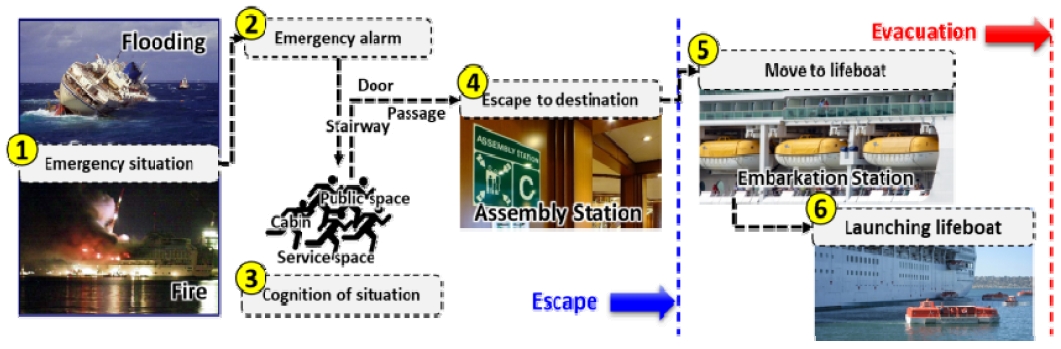
IMO(국제해사기구)는 승객의 안전을 위해 승객 탈출에 관한 규정을 재정하여 적용하고 있다. 1912년 Titanic호 참사를 기점으로 승객의 안전을 위한 SOLAS(Safety of Life At Sea) 규정이 재정되어 발효 중이며, Estonia호 참사 등 다양한 해난사고에 의해 추가적인 규정들이 재정되어 발효 중이다. 이 중, 승객 탈출 해석(evacuation analysis)은 화재, 선박 침몰 또는 기타 사고 상황에서 승객들의 안전한 대피와 탈출을 보장하기 위한 규칙과 지침을 제시하고 있다. IMO의 승객 탈출 해석은 1999년에 최초로 도입되었다 (IMO, 1999). 그리고 여러 번의 개정 과정을 거쳐 현재는 2016년 재정된 규정을 적용하고 있다 (IMO, 2016). 해당 규정은 MSC.1-Circ.1533 (IMO, 2016)으로, 승객 안전을 위해 여객선의 설계에서 두 가지 사항을 고려하도록 규정하고 있다. 첫 번째는 여객선 설계 과정 중, 문과 계단의 폭이 승객 탈출 규정 (IMO, 2002)을 만족하는지 평가하는 과정이다. 그리고 두 번째는 승객 탈출 총 소요 시간이 요구 규정 (IMO, 2016)을 만족하는지 평가하는 것이다. 승객 탈출 소요 시간을 계산하기 위해서는 승객의 비상 탈출 과정을 알 필요가 있다. 선박에서 침수나 화재 등에 의해 승객이 선박에서 탈출해야 할 상황이 발생하면 비상 알람이 울린다. 이후 승객들은 비상상황임을 인지하고, 승객들이 위치하는 다양한 장소에서 지정 장소로 대피한다. 이때, 지정 장소를 assembly station이라 하며, 여기까지의 과정을 대피(escape)로 규정하고 있다. 그리고 지정 장소부터 선원의 지시하에 구난정 탑승을 위한 탑승 장소로 이동한다. 탑승 장소는 embarkation station이라 칭한다. 탑승 장소에서 승객들은 차례대로 구난정에 탑승하고 구난정을 진수시켜 선박에서 벗어난다.
이와 같이 승객이 선박에서 완전히 벗어나는 과정까지를 탈출(evacuation)로 규정하고 있다. 이를 도식화하여 표현하면 Fig. 1과 같다.
또한, IMO는 식 (1)과 식 (2)를 이용해 승객의 총 탈출 시간을 규정하고 있다. 식 (1)과 식 (2)에서 R은 비상 상황에서의 승객의 반응 시간(response duration)이며, T는 승객의 총 이동 시간(total travel duration)이다. 그리고 E는 구난정에 탑승하는 시간(embarkation duration)이며, L은 진수 시간(launching duration)이다. 마지막으로 n은 허용 탈출 시간이다. E + L은 30분을 초과하지 않아야 하며, 식 (1)과 같이 허용 탈출 시간에는 승객의 반응시간과 이동 시간이 포함된다. 식 (1), (2)에 포함된 모든 기호는 분 [min]단위를 사용한다.
| (1) |
| (2) |
MSC/Circ.1533 (IMO, 2016) 보고서에서는 총 두 가지 방법으로 승객 탈출 소요 시간을 계산하는 방법을 제시하고 있다. 첫 번째는 simplified evacuation analysis(SEA) 방법이며, 두 번째는 advanced evacuation analysis(AEA)이다.
SEA 방법의 경우, 승객의 이동을 유체의 흐름으로 표현하여, 각 격실에서 해당 흐름이 합쳐지고 빠져나가는 시간을 계산하는 방식으로 탈출 시간을 계산한다. 따라서, 단시간 내에 빠르게 계산 가능하다는 장점이 있지만, 실제 사람의 움직임 특성이나 심리를 고려하지 못한다는 단점이 있다. 반면, AEA 방법의 경우 승객 개개인의 특성을 반영하여 실제 남녀노소 및 선원과 승객을 구분한 개인들이 실제로 객실 내에서 대피하는 시간을 계산한다. 따라서, 복잡하지만 실제와 유사한 대피 상황을 재현하고 어느 부분에서 병목현상이 일어나는지 쉽게 파악할 수 있는 장점이 있다. AEA 방법을 이용해 승객의 탈출 시간을 계산하는 여러 가지 방법이 최근 연구들에서 제시되고 있으며, 이를 상용화한 프로그램도 출시되기 시작하였다. Ha et al. (2012)은 개인의 행동 모델을 속도 기반 모델로 가정하고 대피 경로를 그리드 기반으로 추정하는 방법을 제안한 바 있다. 해당 연구에서는 승객들의 집단행동에 관한 다양한 고려사항을 추가하였다. 또한 Kim et al. (2019)도 속도 기반 모델로 개인의 행동을 표현하고, 그리드 대신 벡터(vector)기반으로 탐색을 수행하는 방법을 제안하였다. 해당 연구에서는 사고 시 선박의 기울어짐을 고려하였다는 특징이 있다. 상용 프로그램으로는 Maritime Exodus, Evi, IMEX 등의 프로그램이 승객의 탈출 해석을 위해 개발되어 판매되고 있으며, 상용 프로그램에서는 속도 기반 모델과 다르게 가속도 기반 모델을 사용하는 프로그램도 존재한다.
IMO에서도 AEA를 이용하여 승객의 탈출 해석을 수행하는 것을 추천하고 있으나, 아직 규정화되지는 않았다. 하지만, SEA의 경우 반드시 수행하여 선급의 검토를 받게 되어있다. 따라서, SEA를 통한 승객 탈출 시간을 검토할 뿐 AEA를 실선에 적용하지 않는다. 본 연구에서는 현업에 적용이 가능한 SEA를 자동화하는 방안에 대해 제안하고, 그 효용성을 검토하였다.
2. SEA를 이용한 승객 탈출 해석 과정
현업에서는 승객들이 탑승하는 선박에 대하여 선급의 도면 승인을 받기 위해 반드시 SEA를 이용해 승객 탈출 시간을 계산하고, 계산된 탈출 시간이 식 (1)의 허용 탈출 시간을 만족함을 보여야 한다. 현재 실제 현업에서 SEA를 이용해 승객의 탈출 시간을 해석하는 과정은 다음과 같다.
2.1 선실 2D 도면으로부터 escape diagram 작성
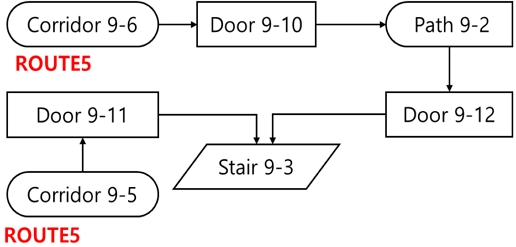
Escape diagram이란 승객이 각자의 위치에서 어떠한 경로로 대피를 수행하는지 작성한 논리 도표를 의미한다. Escape diagram의 작성은 선실의 2D 도면으로부터 설계자가 승객이 위치하는 각 선실로부터 지정 장소까지 대피하는 경로를 산정하여 도표로 작성된다. Fig. 2는 escape diagram의 예시를 표현한 것이다.
Escape diagram은 전문 설계자에 의해 수작업으로 작성되며, 선실의 설계가 변경되면 escape diagram이 변경될 소지가 있다. 따라서, 기본설계, 상세설계를 진행하며 여러 번의 선실 배치 변경이 일어나며 이에 따른 escape diagram의 수정이 필요하고 이 과정에서 작업자의 시수가 많이 소모된다.
2.2 Escape diagram의 경로 계산을 위한 2D 도면의 제원 측정
SEA를 수행하기 위해서는 2.1절에서 산정된 escape diagram으로부터 각 대피 경로 계산을 위한 도면의 정확한 제원 측정이 필요하다. 여기에서 제원이란 선실에서 복도까지의 거리 복도에서 복도 합류지점까지의 거리 합류지점에서 데크 내 계단까지의 거리 등을 포함한다.
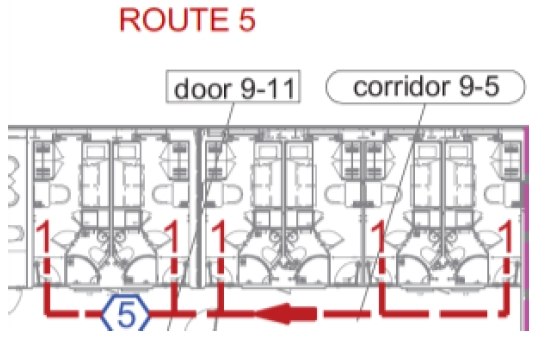
Fig. 3은 2D 도면에서 대피 경로 산정을 위한 제원 추출의 예시를 표현한 그림으로 각 선실 내에서 복도까지의 경로 및 대피 경로의 방향을 2D 도면 내에 표기한 것이다. 그림에서 ‘ROUTE 5’라고 표기된 빨간 글씨는 현재 데크에서 다섯 번째 탈출 경로를 의미하는 것으로 도면에서는 파란색 육각형의 5에 해당하는 경로로 표현된다.
2.3 측정된 제원과 escape diagram을 이용한 SEA 수행
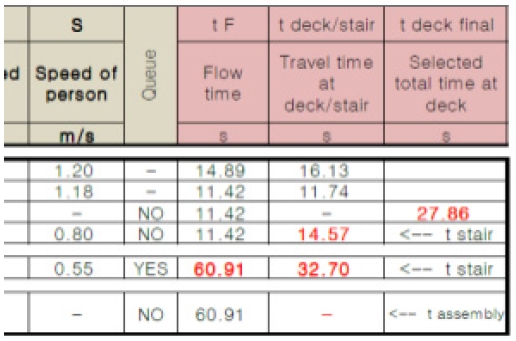
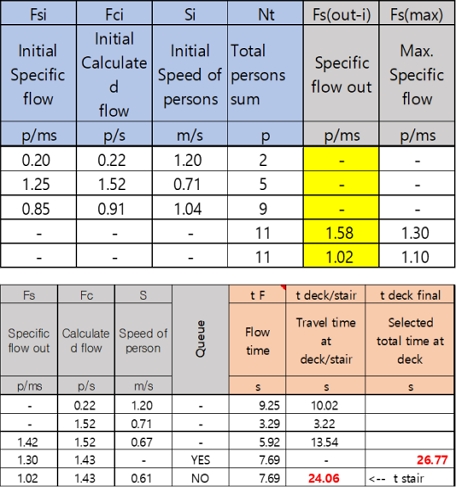
설계된 선실 도면 내에서 escape diagram과 SEA 수행을 위해 필요한 제원을 모두 수집하면 이를 excel 기반의 프로그램에 입력하여 SEA를 수행한다. SEA를 이용해 탈출 해석을 수행하기 위해서는 대피 경로의 밀도를 계산하는 것으로부터 시작해 최종 탈출 시간 T를 구하는 것까지 많은 단계를 거친다. 위의 모든 과정은 현업에서 excel 기반의 프로그램으로 수행되지만, 수행을 위해 필요한 기입 과정 및 중간 계산 과정들은 설계자가 매번 개별로 수행해야 해 시수가 많이 소모된다. Fig. 4는 excel 기반의 프로그램으로 대피 시간 T를 구하는 계산 과정 일부를 표현한 것이다.
앞서 설명한 바와 같이 SEA를 이용해 탈출 해석을 수행하기 위해서는 escape diagram을 구성하는 것부터 실제 계산까지 많은 과정이 소요된다. 또한 최근 선박이 대형화됨에 따라 여객선에서 수많은 데크가 존재하고 매 데크마다 승객이 위치할 가능성이 있는 모든 구역에 대하여 동일한 과정을 반복하여야 하기에 일반적으로 숙달된 설계자의 경우에도 한 척의 선박에 대해 SEA를 수행하기 위해서는 십수일 이상의 시간이 소요된다. 탈출 해석을 수행하는 호선마다 크기가 다르기에 SEA를 수행하는 작업시간을 상이할 수 있다. 다만, 본 연구에서 참고한 길이 약 130m의 Ro-Pax 호선에서는 SEA를 수행하는데 약 보름 정도의 시일이 소요되는 것으로 확인하였다.
기본설계 이후 상세설계 과정에서 수많은 선실 배치 변경이 이루어지며, 매번 동일한 작업을 반복해야 한다. 물론 변경 시에는 일부만 재계산을 수행하지만, 변경 내용이 많을 경우 escape diagram이 변경될 소지가 있고, 이 경우 설계자의 착오 혹은 실수로 인해 결과가 달라질 수 있다.
따라서, 본 연구에서는 SEA 수행 과정을 자동화하여 2D 도면에서 곧바로 대피 시간 T를 계산하는 과정을 제안하고자 한다.
3. SEA 자동화 알고리즘
1, 2장에서 설명한 바와 같이 승객이 탑승하는 선박은 승객들이 반드시 허용 탈출 시간 이내에 탈출할 수 있도록 설계되어야 한다. 이를 위해 설계 단계에서 SEA를 이용한 탈출 해석을 반드시 수행하여야 하며, 현재 현업에서는 전문 설계자들이 이를 수작업으로 수행하고 있다. 다만, 해당 작업에는 대피 경로 산정, 제원 측정을 동반하기에 오랜 시간이 소요되고, 또한 설계 변경 시 작업을 수차례 반복해야 하는 어려움이 있다. 따라서, 본 연구에서는 이를 자동화하는 알고리즘을 제안하였다.
SEA를 자동화하는 과정은 제작된 2D 도면을 단순화하는 것으로부터 시작한다. 따라서, 도면의 전처리 과정이 필요하다. 도면 내에서 경로 선정에 필요 없는 불필요한 요소들을 제거하고, 단순화하는 작업이 필요하다. 두 번째로 도면 내의 선들로 이루어진 공간을 인식하는 작업이다. 공간 인식을 통해 승객들이 위치하는 객실인지 혹은 복도인지 혹은 지정 장소인지 구분하는 알고리즘을 제안하였다. 세 번째로 각 객실에서 지정 장소까지의 대피 경로 산정이 필요하다. 이 경우 대표적으로는 최단 경로를 찾는 알고리즘 등을 활용할 수 있다. 마지막으로 모든 경로를 이용하여 SEA를 수행하여 승객 탈출 시간을 도출한다. 본 장에서는 위에 설명한 총 네 단계의 SEA 자동화 알고리즘을 상세히 설명한다.
3.1 도면 전처리
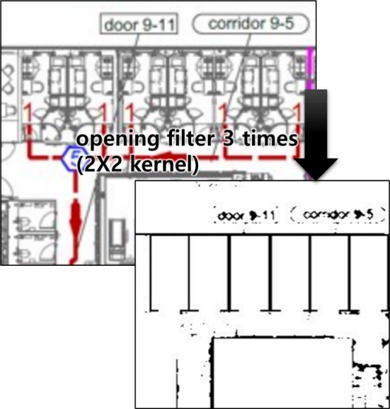
SEA를 수행하기 위해서는 escape diagram과 도면의 제원을 측정하는 일이 우선된다. 이 두 작업을 진행하는 이유는 도면 내 객실에서 승객이 대피하는 경로를 찾기 위함이다. 따라서, 설계 전문가가 수행하는 위 과정을 자동화 하기 위해서는 우선 도면의 전처리가 필요하다. 도면의 전처리를 통해서 도면에서 필요 없는 요소를 제거하고 승객이 거주하는 방, 복도 등에 대한 공간을 구분할 수 있는 주요 선만을 남길 수 있다. 통상 이러한 전처리를 위해서는 dilation 필터와 erosion 필터를 조합한 opening 필터 혹은 closing 필터의 적용이 가능하다 (Serra, 1982). 다만, opening 혹은 closing 필터 중 어떤 것을 사용할 것인지와 몇 회 사용하는지 그리고 kernel 함수의 크기는 어떻게 선정할 것인지 등은 적용하는 대상에 따라 달라질 수 있다. 본 연구에서는 여러 가지 필터의 테스트를 통해 2X2 kernel을 사용한 opening 필터를 총 3회 적용하는 것이 가장 효율적인 것으로 확인하였다. Fig. 5는 선박의 도면에 앞서 설명한 opening 필터를 적용한 예시를 나타낸 것이다. 도면에서 필요 없는 선들은 제거되었으며, 추후 공간 인식에 필요한 외곽선만 남은 것을 확인할 수 있다.
3.2 도면 내 선을 이용한 공간 인식
도면 내 선을 이용한 공간 인식을 통해, 해당 공간이 객실인지 혹은 복도인지 구분할 수 있다. 공간 인식을 위해서는 우선 선만으로 이루어진 도면에서 어떤 부분이 닫힌 영역인지 확인할 필요가 있다. 이를 위해서 우선 3.1절에서 간소화된 도면을 이용한 코너의 인식이 필요하다. 코너의 인식이 필요한 이유는 코너를 이용해 해당 공간의 꺾인 부분을 인식할 수 있기 때문이다. 본 연구에서는 도면의 코너 인식을 위해서 Harris 코너 인식 방법(Harris and Stephens, 1988)을 사용하였다. Harris 코너 인식 방법이란 픽셀(pixel)로 이루어진 디지털 이미지의 특징을 이용해 픽셀값의 차이를 이용해 코너를 검출하는 방법이다. 식 (3)은 Harris 코너 검출 방법에 사용되는 함수 E를 계산하는 방법을 나타낸다.
| (3) |
식 (3)에서 E함수는 평균 밝기 값의 변화량을 나타낸다. w는 윈도우 내부의 평균 픽셀값을 계산하는 과정을 의미하며, u, v는 픽셀 위치 변화를 의미한다. x, y는 이미지 속 픽셀의 위치를 의미하며, 마지막으로 I는 이미지 밝기 값을 의미한다. 따라서, 식 (3)을 이용해 E값의 변화가 거의 없을 경우 변화가 없는 일반적인 이미지 영역을 의미하며, E값이 작을 경우 모서리(edge)를 의미한다. 그리고 E값이 특정 임계값(threshold)을 넘을 경우 코너로 판단한다.
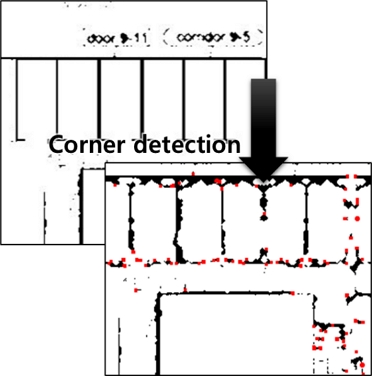
이와 같이 모든 도면 내에서 코너 노드를 판단하며, 중복된 노드의 생성을 막기 위해 특정 거리 이내의 노드들을 하나로 합쳐 중복된 노드를 제거하면 도면 내에서 모든 코너 지점을 판단할 수 있다. Fig. 6은 Harris 코너 인식 방법을 이용해 도면 내의 코너를 인식한 결과를 나타낸 것이다.
인식된 코너 노드들을 이용해 공간을 인식하는 방법이 필요하다. 본 연구에서는 총 3가지의 공간으로 도면을 인식하였다. 첫 번째는 승객들이 기거할 수 있는 공간인 선실(room)이며, 두 번째는 승객들이 대피할 수 있는 공간인 복도(corridor) 그리고 세 번째는 선실에서 복도로 나아갈 수 있는 문(door)이다. 공간의 구분을 위해서 코너로 판단된 인접 노드들을 잇는 가상의 선을 그은뒤 해당 가상의 선의 4면이 모두 닫힌 경우 선실로 구분하였다. 그리고 노드와 노드 사이의 거리가 IMO 규정에서 판단하는 문의 거리 이상일 경우 문으로 간주하였다. 그리고 위의 두 공간으로 모두 구분하고 난 남은 공간을 모두 복도로 간주하였다. Fig. 7은 방과 복도를 구분한 도면을 색깔로 표기한 것이다. 문은 도면은 선분 성분으로 도면에 표기하기가 어려움으로 메모리상에 리스트 형태로 저장하였다.
도면의 모든 영역을 세 영역으로 구분하고 나면, 승객들이 기거하는 공간으로부터 지정 장소까지의 경로를 선정해야 한다. 물론 이 과정에서 지정 장소는 별도로 지정해야 하며, 자동으로 지정 장소의 구분이 불가능하다.
3.3 대피 경로 탐색
앞선 절에서 진행된 도면의 전처리 그리고 도면 내 공간 인식을 수행하고 난 뒤, 수행된 결과를 이용해 대피 경로를 선정해야 한다. 대피 경로를 산정하기 위해서는 다양한 경로 탐색 방법들을 사용할 수 있다. 다만, 일반적으로 도면 내에서 대피 경로를 복잡한 경로 탐색 문제에 비해 상대적으로 단순하며, 빠른 실행 속도를 우선으로 하기에 복잡한 알고리즘보다는 단순하고 처리 속도가 빠른 알고리즘이 더 유리하다. 본 연구에서는 일반적인 경로 탐색에 많이 활용되는 A*알고리즘 (Delling et al., 2009)을 활용하였다.
A*알고리즘은 Dijkstra’s 알고리즘 (Prim, 1957)에서 탐색 속도를 개선한 방법으로 그래프 탐색 방법을 개선한 것이다. A*알고리즘을 이용해 경로를 탐색하는 방법은 다음과 같다.
- (1) 시작 위치로부터 이동 가능한 위치를 open 리스트에 저장한다. 그리고 closed 리스트에 시작 위치를 저장한다.
- (2) open 리스트에 포함된 위치까지 이동하는 비용(F = G + H)을 계산한다. 비용에서 G 값은 해당 위치까지 실제로 이동한 비용을 나타내는 것이며, 일반적으로 해당 위치까지의 거리를 사용한다. 그리고 H값은 휴리스틱 비용으로 해당 위치에서 목적 위치까지의 추정 비용을 의미한다. 일반적으로 휴리스틱 비용은 해당 위치에서 목적 위치까지의 유클리디안 거리를 사용한다.
- (3) (2)에서 검색된 위치 중, 목적 위치가 포함되었는지 확인한다. 목적 위치가 있을 경우, 탐색을 종료하고 경로를 반환한다. 목적 위치가 없을 경우, (4)로 넘어간다.
- (4) open 리스트에서 F 값이 가장 작은 위치를 현재 위치로 선정하고, (2)부터 다시 수행한다.
- (5) 위 (2)부터 (4)까지의 과정을 반복하여 open 리스트에 요소가 없거나, (3)에서 목적 위치에 도달하면 탐색을 중단한다.
A*알고리즘을 진행하기 위해서는 위치라는 개념을 도면상에서 정의할 필요가 있다. 일반적으로 정사각 그리드를 위치로 정의하는 경우가 많다. 본 연구에서는 앞서 처리된 도면을 가로세로 0.4m로 구분하여 그리드를 제작하였다. 0.4m로 구분한 이유는 IMO/MSC Circ. 1238 (IMO, 2007)에 따르면 평균 승객의 속도를 0.8m/s로 지정하고 있고, 0.5초를 하나의 스텝으로 구분하면 0.4m로 그리드 사이즈를 산정하는 것이 합리적이라는 판단하에, 해당 사이즈로 지정하였다 (Ha et al., 2012).
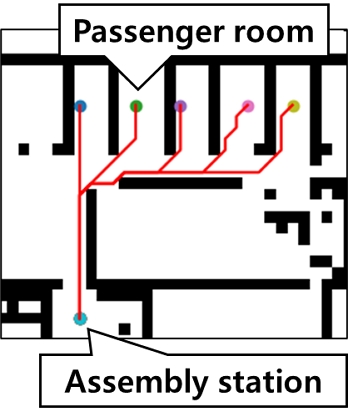
승객들의 선실 중앙 지점을 매 출발 위치로 지정하였으며, 해당 위치로부터 가장 가까운 지정 장소까지의 경로를 산출하였다. 데크 내에 통상 수 많은 선실들이 존재하기에 여러 번의 경로 탐색 과정을 거쳐야 하지만, A*알고리즘을 이용하면 한 번의 경로 탐색 과정이 ms단위 내에 계산되기에, 전체 경로 탐색 과정은 수초 이내로 매우 짧은 시간 내에 수행할 수 있다. Fig. 8은 선실로부터 지정 장소까지 A*알고리즘을 활용해 최단 경로를 찾은 결과를 나타낸다.
Fig. 8의 결과를 확인하면 경로 탐색을 위한 그리드가 직교로 생성되어 있어, 꺾인 경로가 존재한다. 따라서, 실제 승객이 이동하는 경로와는 상이하다. 다만, 해당 경로는 2.1절에서 설명한 escape diagram을 선정하기 위한 것으로 SEA에서는 승객들이 각 선실로부터 어떠한 구역을 따라 이동하는지에 대한 정보만을 필요로 한다. 따라서, 현재 수준의 경로만으로도 해당 정보를 얻기에 충분한 것으로 판단하였다.
3.4 대피 경로를 이용한 SEA 자동화
3.3절까지 수행된 결과를 이용하면, 2.1 절에서 설명한 escape diagram과 동일한 정보를 획득할 수 있으며, 이를 이용하여 SEA 자동화를 진행할 수 있다. 본 절에서는 SEA를 자동화하는 과정에 대해 설명한다. 우선, 단순화된 탈출 해석 방법인 SEA에서 가정하는 일반적인 사항은 아래와 같다.
- ⓐ 연기 및 유독성 화재는 승객/승무원의 탈출에 영향을 미치지 않는 것으로 간주.
- ⓑ 선박의 운동과 피해는 고려되지 않음.
모든 승객과 승무원은 동시에 대피를 시작하며, 서로를 방해하지 않음. - ⓒ 초기 보행 속도는 사람의 밀도에 따라 달라지며, 흐름이 대피 경로 방향으로만 흐르고 추월이 없음.
- ⓓ 역류는 역류 보정 계수에 의해 고려됨.
- ⓔ 단순화는 보정 계수와 안전 계수로 고려됨.
IMO의 규정에 따라 SEA를 위해 필요한 매개변수 및 표는 다음과 같다.
- 매개변수 종류 및 의미
- ⓐ 복도, 계단, 문의 폭 (clear width, Wc)[m]
- ⓑ 복도 및 계단 이동 거리 (L)[m]
- ⓒ 대피 경로의 넓이 (A = L × Wc)[m2]
- ⓓ 대피 승객 인원수 (N)[p]
- ⓔ 대피 경로의 승객 밀도 (D = A/N)[m2/p]
- ⓕ 대피 승객의 이동 속도 (S)[m/s]
- ⓖ 유동 인구의 유량 (Fs)[p/ms]
- ⓗ 계산된 유동 인구 유량 (Fc = Fs × Wc)[p/s]
- ⓘ 유동의 지속 시간 (tf = N/Fc)[s]
- ⓙ 대피 경로에서 도착 지점의 Fc(in)i[p/s]
대피 경로에서 출발 지점의 Fc(out)j[p/s] - ⓙ 이상적인 조건에서의 최대 이동 시간 (ti)[s]
계단에서 지정 장소까지의 이동 시간 (ts)[s]
데크의 가장 먼 지점으로부터 계단까지의 이동 시간 (td)[s]
계단 끝에서 다음 계단까지의 이동 시간 (ta)[s] - ⓚ 전체 대피 시간 (T)[s]
- 표 종류 및 의미
- ⓐ 시설 유형에 따른 초기 승객 밀도, 유량 및 속도 (IMO, 2016)
- ⓑ 시설 유형에 따른 최대 승객 밀도 (IMO, 2016)
- ⓒ 시설 유형에 따른 승객 유량 및 이동 속도 (IMO, 2016)
IMO에서 제공하는 도표 3가지를 이용하여 시설 유형, 초기 승객 밀도를 바탕으로 주어진 고정값을 이용하거나 선형 보간법을 통해서 Fs, Fc, S값을 구할 수 있다. 위 정보들을 이용해 SEA를 수행하는 과정은 다음과 같다.
- ⓐ 각 데크의 주요 대피 경로의 밀도(D)를 계산하고, 각 문을 사용하는 대피자 수는 문의 폭에 비례하는 것으로 가정한다.
- ⓑ 복도 및 문에 대한 유량 Fc를 대피 경로의 계단이 지정된 방향으로 계산한다.
- ⓒ 합류 지점에 도달하면 식 (4)를 이용해 Fc를 구한다. 이 때, 두 개 이상의 경로가 합류지점에서 분기되는 경우 각 경로의 유량 Fc는 분기된 복도의 폭에 비례하는 것으로 계산한다.
- ⓓ 각 데크에 대해 위의 절차를 반복하여 계산된 유량 Fc와 속도 S의 값이 각각 할당되어 대피 경로 상 다른 데크로 이동하는 계산으로 들어가는 것으로 판단한다.
- ⓔ tf는 대피 경로 중 가장 긴 시간으로 선정한다.
- ⓕ td는 데크 내 계단까지 가장 먼 지점으로부터의 이동 시간으로 선정한다.
- ⓖ ts는 해당 데크와 지정 장소를 연결하는 모든 계단의 이동 시간을 합한 값으로 선정한다.
- ⓗ ta는 데크 내 계단 끝에서 다음 계단까지의 이동 시간으로 선정한다.
- ⓘ 식 (5)를 이용하여 이상적인 조건에서 최대 이동 시간인 ti를 계산한다.
- ⓙ 모든 대피 경로에 대한 계산이 완료되면 식 (6)을 이용하여 승객 대피 시간 T를 계산하며, T는 ti 중 가장 높은 값으로 선정한다.
| (4) |
| (5) |
| (6) |
식 (6)에서 γ는 보정계수, δ는 역류보정계수를 의미한다. 위의 총 10단계 과정을 통해서 계산된 T가 식 (1)에서 사용되며, 이를 승객 탈출 시간이 IMO에서 정한 규정에 만족하는지 판단할 수 있다.
4. Ro-Pax 선종에의 적용
Ro-Pax(Roll-On/Roll-Off Passenger) 선박은 승객과 화물을 함께 운송할 수 있는 화물, 승객 겸용 운반선을 의미한다. 로로 시스템은 선박 끝에 설치한 받침대를 통해 화물트럭이 화물과 함께 그대로 배에 올라 항구에 도착한 후 최종 목적지까지 그대로 운송하는 물류 방식을 의미한다. 본 연구에서 제안한 SEA 자동화 방법을 Ro-Pax 선종에 적용하여 그 효과를 확인하였다.
적용 호선의 주요 제원은 LOA(length overall) 약 130m, 폭 약 25m, 흘수 약 5.5m의 선박으로 총 승객 약 900명이 탑승하는 선박이다. 해당 선박에 대해 통상 승객이 각자의 선실에 위치하는 저녁 시간 대피하는 것을 기준으로 탈출 시간을 해석하였다.
해당 선박에는 총 승객이 거주하는 총 3개의 데크가 존재하며, 각 데크의 승객이 최하층 데크에 존재하는 지정 장소로 이동하는 시간을 해석하였다. 그리고 이를 실제 현업에서 수행한 excel 기반 프로그램과 해석 시간 및 결과와 비교하였다.
Fig. 9 는 실제 설계자가 해석한 SEA의 결과 excel 프로그램의 일부를 표기한 것이다. 도면을 통해 사람이 실제로 선정한 escape diagram을 이용해 대피 경로를 선정하고, 이를 기반으로 사람이 수작업으로 관련 매개변수를 수집하여 작성한 결과이다. 해석 결과 승객의 총 이동 시간 T는 14분으로 계산되었다. IMO 규정에서 제공하고 있는 저녁시간의 반응시간 R은 10분, 구난정 탑승시간과 진수 시간을 합친 E + L은 총 30분으로 위 계산될 결과들을 식 (1)에 대입하면 총 탈출 시간은 49.99분으로 계산된다. IMO 규정에서 여객선은 총 60분 이내로 탈출 허용 시간을 제한하고 있기에, 계산된 탈출 시간을 규정을 만족하는 것으로 확인되었다.
본 연구에서 제안한 방법을 이용해 총 3개의 데크에 SEA 자동화를 수행한 결과는 Table 1과 같다. 모든 도면에 대해 3장에서 설명한 도면 전처리, 도면 내 공간 인식, 대피 경로를 탐색한 후 선정된 대피 경로에 대하여 자동으로 SEA를 실행한 결과를 표기하였다. 총 3개의 데크의 모든 경로에 대해 SEA를 수행하여 대피 시간 계산에 필요한 tf, td, ts, ta를 계산하였다. 그리고 식 (5)를 와 앞서 계산된 값을 이용해 모든 경로에 대한 ti를 계산하였다. 식 (6)과 계산된 ti값을 이용하면 승객의 이동 시간 T를 계산할 수 있다. T를 계산할 때는 계산된 ti중 가장 높은 값인 2번 데크의 경로 3, 4를 이용하였다. 저녁시간 케이스에 대해 승객 탈출 시간을 계산하였음으로, 이때 식 (6)에 적용되는 보정계수와 역류보정 계수는 IMO 규정에 따라 각각 2와 0.3으로 적용하였다. 앞서 설명한 대로, 반응시간, 구난정 탑승시간, 진수시간을 적용하여 최종 탈출 시간을 계산하면, 전체 탈출 시간은 47.01분으로 계산된다. 이는 역시 여객선 탈출 허용 시간인 60분 이내를 만족한다.
다만, 앞서 수작업으로 설계자가 해석한 결과와 약 3분가량 차이가 발생한다. 이는 실제 작업자가 생성한 escape diagram의 경우, 승객의 편의성을 고려하고 있기 때문이다. SEA 방법 자체에서는 승객의 편의성을 고려할 수 없지만, escape diagram을 만드는 단계에서 이를 간접적으로 고려한다. 예를 들면, 더 먼 경로로 돌아가더라도 붐비지 않고 폭이 넓은 통로로 이동하는 등의 방식으로 diagram을 작성하는 것이다. 따라서, 현업 설계자가 선정한 경로는 대피할 때의 편의성까지 고려하기 때문에 본 연구에서 생성한 최단 경로와 대피 경로가 일부 다른 부분이 존재한다. 따라서, 수작업으로 계산된 경로가 해석 시 더 보수적인 결과를 산출하는 것으로 확인할 수 있다.
Table 2는 현업에서 SEA를 수행하는 시간과 본 연구에서 제안한 방법을 이용해 SEA를 수행하는 방법의 작업시간을 비교한 것이다. 현업 설계자와의 인터뷰를 통해 작업시간을 추산한 결과 데크 하나당 약 5일간의 작업시간이 소요되며, 3개의 데크가 있는 호선의 경우 약 보름의 작업시간이 소요되는 것으로 확인하였다. 하지만 본 연구에서 제안한 방법으로 해석을 수행할 경우 데크당 약 2분 정도로 매우 빠르게 해석 수행이 가능하다.
5. 결론 및 향후 연구계획
본 연구에서는 기존 여객선에 적용 중이던 SEA를 자동화하는 연구를 수행하였다. 기존의 SEA는 설계 도면으로부터 escape diagram을 생성하고, 필요한 매개변수를 측정한 뒤, excel 기반의 프로그램에 직접 매개변수들을 기입하여 탈출 시간을 계산하였다. 본 연구에서는 이미지 필터링 방법을 이용해 설계된 도면을 단순화하였다. 그리고 Harris 코너 인식 방법을 이용하여 도면에서 코너들을 인식하고 이를 선분으로 연결하여 생성되는 도형들의 형태에 따라 구분하여 선실, 복도, 문으로 도면의 공간을 구분하였다. 이후 구분된 공간에서 지정 장소까지 A* 방법을 이용해 대피 경로를 도출하였으며, 도출된 경로를 SEA 계산을 위한 입력자료로 활용하였다. 또한, SEA를 자동화하여 전체 승객의 대피 시간을 계산하였다.
현업의 경우 일반적으로 설계 변경이 다수 발생하기에, 이와 같은 해석을 수차례 수행하여야 한다. 물론 설계 변경 시 수행되는 탈출 해석의 경우 초기 설계 시 수행하는 탈출 해석보다는 현저히 작업시간을 줄일 수 있으니, 여전히 해당 업무는 높은 시수를 필요로 한다. 따라서, 본 연구에서 제안한 방법을 이용하면 반복 작업의 시수를 절감하고, 설계자의 오류를 줄일 수 있을 것으로 예상한다.
본 연구에서 제안한 방법은 일부 구분이 어려운 선실에 대해서는 공간 파악이 어렵거나, 도면에서 선실의 형상이 일반적이지 않을 경우 공간을 수작업으로 할당해야 하는 어려움이 있다. 또한, 현업에서 작성한 escape diagram의 경우 승객의 밀도와 편의를 고려하여 대피 경로가 조금 더 멀더라도 사람이 생각하는 일반적인 경로로 선정하는 것에 비해, 본 연구에서는 최단 경로만을 고려하였다. 따라서, 승객의 심리나 편의성을 고려할 필요가 있다.
본 연구에서는 현재 IMO에서 규정한 대로 반드시 수행해야 하는 SEA 자동화에 집중하고 있다. 하지만, 앞서 설명한 대로 해당 방법은 승객의 이동을 유량으로 고려하기에 실제 탈출 시간과는 상이하다. 따라서, 앞으로는 승객 개개인의 특성을 고려할 수 있는 AEA가 유효할 것으로 판단하고 있으며, 이에 따라 본 연구를 확장할 방안을 개발해야 할 것으로 예상한다.
Acknowledgments
본 연구는 울산대학교와 2024년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 지자체-대학 협력기반 지역혁신 사업의 결과임을 밝히며, 이에 감사드립니다(2021RIS-003).
References
-
Delling, D., Sanders, P., Schultes, D. and Wagner, D., 2009. Engineering Route Planning Algorithms. Springer.
[https://doi.org/10.1007/978-3-642-02094-0_7]

-
Ha, S., Ku, N.K., Roh, M.I. and Lee, K.Y., 2012. Cell-based evacuation simulation considering human behavior in a passenger ship. Ocean Engineering, 53, pp.138-152.
[https://doi.org/10.1016/j.oceaneng.2012.05.019]

-
Harris, C. and Stephens, M., 1988. A combind corner and edge detector. Proceedings of the Alvey Vision Conference 1988, Manchester, United Kingdom, September 1988.
[https://doi.org/10.5244/C.2.23]

- IMO, 1999. Interim guidelines for a simplified evacuation analysis on RO-RO passenger ships. MSC/Circ.909.
- IMO, 2002. Interim guidelines for evacuation analysis for new and existing passenger ships. MSC/Circ.1033.
- IMO, 2007. Guidelines for evacuation analysis for new and existing passenger ships. MSC/Circ.1238.
- IMO, 2016. Revised guidelines for evacuation analysis for new and existing passenger ships. MSC/Circ.1533.
-
Kim, H., Roh, M.I. and Han, S,, 2019. Passenger evacuation simulation considering the heeling angle change during sinking. International Journal of Naval Architecture and Ocean Engineering, 11(1), pp.329-343.
[https://doi.org/10.1016/j.ijnaoe.2018.06.007]

-
Prim, R., 1957. Shortest connection networks and some generalizations. Bell System Technical Journal, 36(6), pp.1389-1401.
[https://doi.org/10.1002/j.1538-7305.1957.tb01515.x]

- Serra, J., 1982. Image analysis and mathematical morphology. Academic Press, Inc.