부가저항 모형시험 결과와 실해역 운항 자료를 이용한 VLCC의 연료 소모량 모델 개발
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Data-driven model for estimating fuel oil consumption in seaways is suggested using the model test results and operation data. The data-driven model requires the forecasted wind speed, direction, and the desired ship speed as inputs to predict the engine speed, power, and fuel oil consumption. The structure of the data-driven model is based on the deterministic model of added power of a similar vessel of which model test results in the calm water and head seas are accessible. For a given wind speed, the wind resistance and added resistance in irregular waves presented by Pierson-Moskowitz spectrum are computed to be applied to the propulsion performance prediction. The deterministic model takes a cubic approximation between the wind speed and engine speed. The model is tuned by actual operation data in seaways with various wind direction groups. The shaft power and fuel oil consumption estimation are added to the model to be validated with the operation data. The prediction model is validated with the operation data to confirm that the estimation of the engine speed is the most significant uncertainty source.
Keywords:
Added power, 1978 ITTC performance prediction method, Carbon intensity index키워드:
부가 동력, 1978 ITTC 성능추정법, 탄소 집약도 지수1. 서 론
탄소집약도지수(carbon intensity indicator, CII)는 국제해사기구를 통해 강제되는 선박 탄소 배출량의 규제사항으로, 선박의 실제 연간 연료소모량과 운항거리를 바탕으로 환경 영향을 평가하게 된다. 선박의 운항에 있어 CII를 고려한 최적 항로를 선정해야 하며, 이를 위해 예보된 해상환경과 목표한 선속에서 CII를 추정하기 위한 기술의 개발이 선행되어야 한다.
CII는 주기관의 연료소모량에 큰 영향을 받는데, 연료소모량은 직접 계측되거나 주기관의 출력, 회전수를 이용해 추정할 수 있다. 이러한 실선 운항 해석에 대해 과거에는 국제표준화기구(International Organization for Standardization, ISO)에서 만든 ISO15016 선속-동력 시운전 해석법 (ISO, 2015)에 근거하여 접근하였다. 이 해석법에서는 바람, 파도, 수온, 조류, 조종 중 방향타 작동의 영향을 다룬다. 같은 방식의 시운전의 해석 절차에 대한 내용은 국제수조회의(International Towing Tank Conference, ITTC)에서도 제안한 바 있다 (ITTC, 2022). Seo et al. (2019)는 ISO15016 해석법의 불확실성을 연료소모량 이전의 전달동력의 관점에서 추산하였고, 해상환경의 영향을 제외하면 축 동력의 계측이 불확실성의 주요한 원인임을 확인하였다. Kim et al. (2021a)의 연구에서는 Seo et al. (2019)의 불확실성 해석 기법을 실선 시운전 결과에 적용하였다. Kim and Roh (2020)은 ISO15016 방법에 기반한 연료 소모량의 추정 모델을 제안하고 이를 운항 데이터로부터 얻은 데이터 기반 모델과 비교하였다. 비교 결과, 실제 운항에서는 풍하중의 영향이 시운전 상황과 큰 차이가 있기 때문에 연료 소모량의 정확한 추정에 한계가 있음을 지적하였다.
ISO15016 해석법에서 다루는 바람의 영향은 파랑 중 부가저항과 부가동력 문제로 볼 수 있다. 파랑 중 부가저항은 대개 규칙파의 파장에 대한 저항 증가에 대한 전달함수를 구한 뒤 파 스펙트럼을 조합해 불규칙파 중 저항 증가를 해석하는 방식으로 접근하는 연구가 모형시험과 수치해석을 통해 수행되었다 (Yang et al., 2013; Seo et al., 2014; Park et al., 2015; Yang et al., 2015; Seo and Park, 2017; Yu et al., 2017; Kim et al., 2018; Lee et al., 2022a). 그리고 선체 자체의 저항 증가에 더하여, 자항 요소의 변화를 고려한 부가동력에 대한 연구가 수행되기도 하였다 (Lee et al., 2019; Seo et al., 2020; Kim et al., 2021b; Lee et al., 2022b; Sanada et al., 2022).
앞의 연구와 같이 부가동력 문제를 결정론적 모델로 접근하는데 있어서는 실해역 해상상태의 올바른 식별이나 모델링에서 고려하지 않은 다른 물리적 현상의 영향 등이 한계로 작용한다. 결정론적 모델의 개발에 대한 추가적인 어려움으로, 실선의 운항 자료에서는 부가저항의 크기나 반류비, 추력감소비와 같은 자항 요소를 직접 알 수 없으므로 모델의 해석 중간과정에 대한 검증이 불가하다는 문제도 있다.
실제 운항 데이터로부터 연료 소모량이나 동력 모델을 개발하기 위한 연구에서는 외란의 영향을 물리적으로 설명하기보다는 데이터 기반의 모델링으로 접근하여, 데이터의 전처리와 모델의 검증의 관점에서 연구가 주로 수행되었다. 연료소모량 관련 변수와 해상환경 변수의 관계를 모델링하는 방법에 대해, Shaw and Lin (2021)은 물리적 이해 없이 구성하는 데이터 기반 모델, 저항추진 성능에 대한 자료를 바탕으로 한 결정론적 모델과 이 둘을 조합한 방식의 하이브리드 모델로 구분하였다. 이들은 시스템 모델링 관점에서는 각각 블랙박스(black box), 화이트박스(white box), 그레이박스(grey box) 접근법으로 이해될 수 있는데, 앞에서 소개한 ISO15016 기반 방법이 물리적 모델에 기반한 화이트 박스 접근법인데 반해 실선 운항 데이터에 기반한 모델링은 블랙박스나 그레이박스 접근법으로 볼 수 있다.
실운항 데이터 기반 모델의 개발에 대해서는 Trodden et al. (2015)는 정속 항주 상태의 연료소모량을 실운항 자료로부터 얻어내기 위해 정속 운항 구간 데이터의 추출 방안을 연속된 데이터의 개수와 허용 변화량의 관점에서 제안했다. Lee et al. (2021a)의 연구에서는 데이터 전처리와 인공신경망을 이용해 선박의 동력을 추정하였다. 이들을 절충한 하이브리드 모델의 개발을 위해서는 파랑 중 부가저항에 대한 물리적 모델을 얻고, 이 모델의 구성에 기반하여 실선의 동력이나 연료소모량의 모델을 개발한다. Mittendorf et al. (2023)은 다양한 컨테이너 운반선의 운항 데이터와 물리적 모델로부터 유의파고에 따른 부가저항을 추정한 결과를 보였다.
위의 연구 내용을 고려하여 해상환경 중 CII의 추정에 대한 방향을 제안하자면, 결정론적 모델을 통해 주요한 변수간의 관계를 정의하고, 이를 실운항 자료를 이용해 수정보완하는 하이브리드 모델이 현실적인 것으로 생각된다. 물론 각 변수들은 적절한 전처리를 통해 선형성을 최대한 확보하여 모델의 구성을 간단하게 하며, 해석 중간 과정을 사용자가 이해할 수 있는 물리량으로 제공해야 할 것이다.
본 연구에서는 주기관의 상태 자료 중 다른 변수와 상관관계가 가장 큰 추진기의 회전수를 중심으로 해상환경의 영향을 해석하는 방안을 제안하였다. 추진기의 슬립(slip)과 전진비(advance ratio)의 개념에 착안해 모형시험 결과로부터 선속-기관 회전수 관계에 해상환경이 미치는 영향의 모델을 개발하고, 이를 실운항 정보와 연계하여 연료소모량을 추정하는 모델을 개발하였다.
본 논문은 다음과 같이 구성된다. 2장은 연구 대상 선박과 실운항 자료를 소개하였다. 3장에서는 풍속-기관 회전수 관계의 결정론적 모델 개발 과정을 보였다. 4장은 결정론적 모델의 구조를 이용한 데이터 기반 모델 개발과 그 정확도의 평가 결과를 보였다. 5장은 본 연구의 결론이다.
2. 모델링의 기본 구성
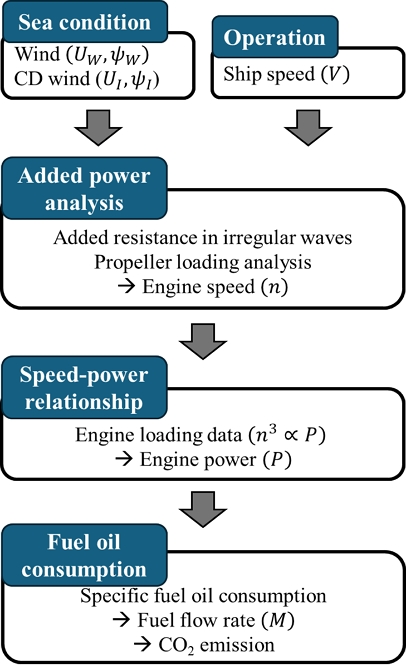
본 연구에서 개발하고자 하는 데이터 기반 모델링은 운항 중 예보된 해상상태 변수에 따른 연료소모량(M)의 추정 모델이다. Fig. 1에 본 연구에서 개발하고자 하는 모델링의 기본 구성을 소개하였다.
모델링의 입력은 해상상태 변수와 선속(V)이며, 이에 대한 연료소모량을 출력하도록 한다. 그리고 입출력 사이에서는 부가저항, 기관 회전수(n), 기관동력(engine power, P)과 같은 중간 변수들이 얻어질 것이다. 본 연구에서는 입출력에 대한 모델링 구성에서 더 나아가 중간변수들의 데이터 기반 모델링의 물리적 타당성을 검토하였다. 그리고 Lee et al. (2024a)에서 제안한 내용을 바탕으로 변수 간 선형성을 확보하기 위한 방안을 적용하였다.
Table 1은 본 연구의 대상인 320K급 원유운반선(very large crude oil carrier, VLCC)의 운항 자료 변수와 그 값이다. 1척의 VLCC에 대해 총 1년 6개월간 수집된 운항데이터를 활용하였다. 이 중 본 연구의 데이터 기반 모델링에 사용된 운항 조건은 CII 추정에서 가장 불리한 영역인 연료로 중유(heavy fuel oil, HFO)만을 사용, 설계 흘수, 설계 선속 근처 영역으로 선정하였다. 선속이 증가하면 CII는 불리해지므로 연료 소모량의 추정은 저속영역보다는 설계속도 근처인 12knots 이상에 집중하였다. 이렇게 선정된 자료는 총 36,465개로, 25일 분량의 운항 데이터이다.
실운항 자료에서 해상환경과 관련한 변수는 선박에서 직접 계측되거나 기상예보에서 제공된다. 본 연구에서 사용된 자료는 선상에서 직접 계측된 바람, 기상정보(climate data, CD)에서 제공된 바람, 파도(wave), 너울(swell)의 정보가 제공된다. 본 연구에서는 이 중 바람에 대한 풍속과 풍향정보를 이용하였다. 선체에서 직접 계측된 풍속은 UW, CD에서 얻은 풍속은 UI로 나타냈다. 선체에서 바람을 맞는 방향과 선체가 향하는 방향 사이의 각도인 입사각은 ψW, ψI로 표시하였다. 이러한 해상환경 변수로부터 V/n로 대표되는 추진기의 하중 조건의 관계를 구하였다. 그 내용은 3장에서 상세히 다뤘다.
MAN (2023)에서는 기관 회전수와 기관 동력(P)의 관계를 P∝n3의 3차식으로 근사하였는데, 본 연구에서도 이를 참고하였다. 동력은 축동력(shaft power, PS)을 사용할수도 있고 기관 운용 중 입력되는 연속최대출력(maximum continuous rating, MCR, PMCR)에 대한 부하 비율(P/PMCR)을 이용할 수도 있다. Fig. 2는 실운항 자료에서 확인된 n과 동력 관련 변수의 관계로, 그 관계식은 식 (1)-(3)과 같다.
| (1) |
| (2) |
| (3) |
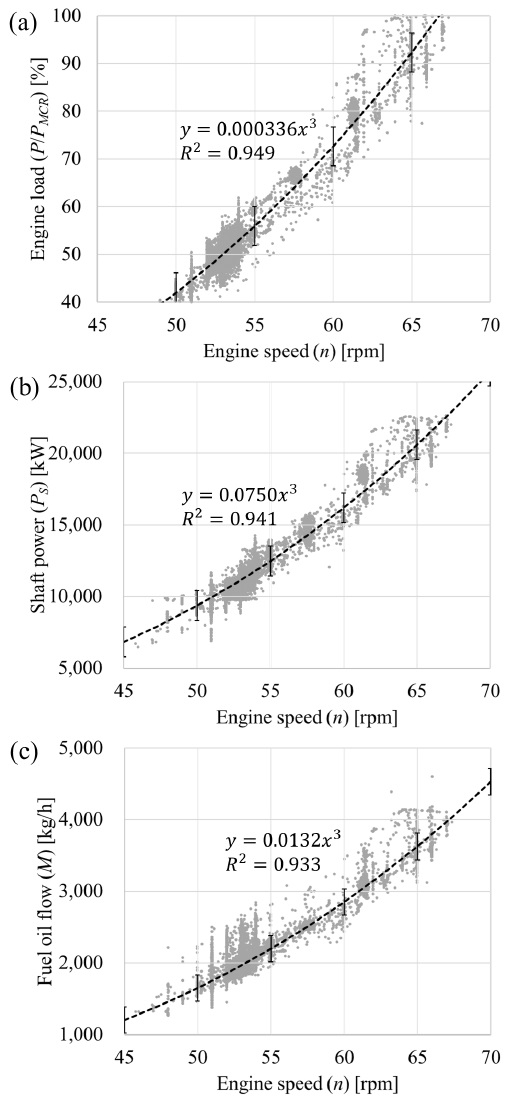
Correlation between engine speed (n) and engine power parameters: (a) engine load (P/PMCR), (b) shaft power (PS), and (c) fuel oil flow rate (M). Error bars indicates 95% confidence interval.
기관 동력에 대해 단위 동력 당 연료소비량(specific fuel oil consumption, SFOC)을 이용하면 운항 중 연료 소비량을 구할 수 있다. SFOC는 기관 제작사에서 제공하는 값을 쓸 수 있는데 이는 n에 대해 소폭 변화함이 알려져 있다 (MAN, 2023). 그리고 M에 HFO의 탄소지수(carbon factor, C)인 3.1144를 곱하면 운항 중 이산화탄소 배출량을 구할 수 있다. 다른 연료를 사용했다면 이에 맞는 C를 적용해야 한다.
위의 내용을 감안하면 이산화탄소 배출량이나 연료소모량은 P와 마찬가지로 n3에 비례할 것으로 예상된다. Fig. 2(c)에 나타낸 n과 M의 관계에서 이를 확인할 수 있다. 다만 M의 결정계수(R2)는 다른 변수보다 감소하였는데, 이는 SFOC가 기관 회전수에 따라 달라지는 점과 연료 유량 계측의 불확실성이 반영된 탓으로 생각된다.
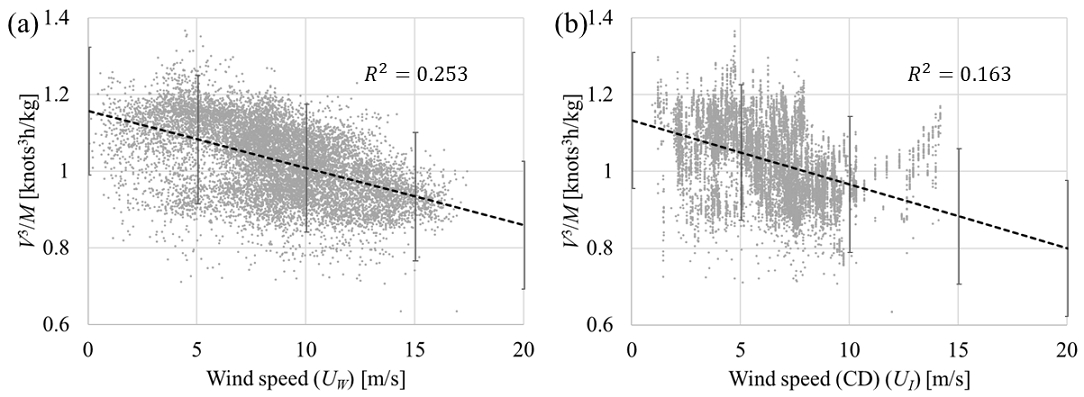
실해역 운항 시 추진기 하중에 따라 V3∝n3, P, M의 비례관계를 정의하는 비례상수가 달라질 것으로 보았다. 즉, V3/M의 값이 달라질 것이다. 이에 해상환경의 영향의 해석이 용이한 맞바람 조건(-22.5° < ψW, ψI < 22.5°)에서 풍속에 따른 V3/M의 변화를 정리하여 Fig. 3에 나타내었다. 풍속의 증가에 따라 V3/M가 감소하는 경향이 잘 나타났다. 이는 거친 해상환경에서 같은 선속을 내기 위해 기관 동력이 더 요구되면서 연료 소모량이 증가함을 의미한다.
3. 부가동력 모델
3.1 물리적 모델의 구성
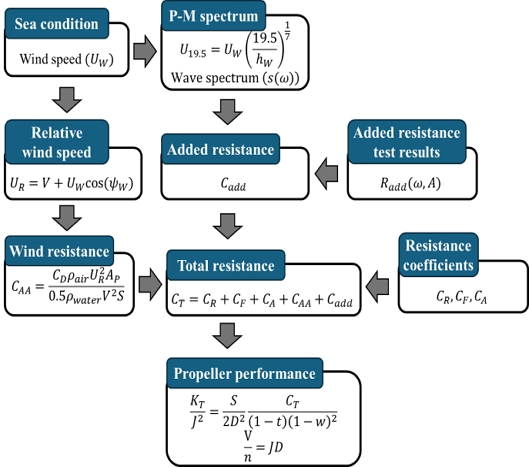
데이터 기반 모델링의 구성에서 풍속과 V에 따른 n의 추정 단계를 이해하기 위해 유사한 선형의 실험 결과를 이용해 결정론적 부가동력 모델을 먼저 개발했다. Fig. 4에 부가동력 해석을 위한 물리적 모델의 구성을 나타냈다. 주어진 해상환경 변수로부터 풍하중과 파도로 인한 부가저항을 우선 계산한다. 1978 ITTC 성능추정법 (ITTC, 2021)에서 제안된 저항 추정식에 해상환경으로 인한 저항 성분을 추가한 식 (4)를 이용해 선체의 전저항계수(CT)를 계산하였다. CR, CF는 각각 잉여저항계수, ITTC 1957 모형-실선 상관곡선에 따른 마찰저항계수이다. CA는 1978 ITTC 성능추정법에서 제안한 표면거칠기의 보정과 모형선-실선 상관관계의 수정계수를 더한 값이다.
| (4) |
1978 ITTC에서 성능추정법의 공기저항계수(CAA)는 정속 항주 중 선속으로 인한 공기저항만을 다루나, 본 연구에서는 풍속 영향을 추가하였다. 풍하중은 선체의 전면 투영면적(AP)을 이용해 식 (5)와 같이 계산한다.
| (5) |
여기서 ρ, S는 각각 유체의 밀도와 선박의 침수면적이고, CD는 항력계수로 0.5를 적용한다. V+UWcos(ψW)가 0보다 작다면 바람은 추가적인 추력으로 해석된다.
파도로 인한 부가저항을 해석하기 위해서는 주어진 해상환경 변수로부터 파 스펙트럼을 구한다. 그리고 규칙파에서 수행한 파장 별 부가저항 시험 결과인 2차 전달함수(quadratic transfer function, QTF)를 이용해 해당 해상환경과 주어진 V에서 파도로 인한 부가저항의 스펙트럼을 얻어 부가저항계수(Cadd)를 계산해낸다.
풍속에 따른 파 스펙트럼은 Pierson-Moskowitz(P-M)스펙트럼이 가장 기본적이다. 19.5m 높이에서 계측된 풍속 U19.5를 적용했을 때, 완전히 발달된 파 스펙트럼은 식 (6)과 같이 나타낸다.
| (6) |
여기서 g는 중력가속도, ω는 파의 각진동수이다. UW와 U19.5의 관계는 경계층 이론을 적용하여 식 (7)과 같이 계산할 수 있다. 여기서 hW는 풍속계의 장착 높이이다.
| (7) |
실해역에서는 P-M스펙트럼에서 가정한 바와 달리 시공간적으로 파가 완전히 발달될 여유가 없으므로 Bretschneider나 JONSWAP 스펙트럼을 사용한다. 항로의 다양한 실해역 특성을 반영한 상세한 스펙트럼의 적용은 후속 연구에서 다루도록 하고, 본 연구에서는 P-M 스펙트럼을 적용하여 얻은 결과의 추세를 데이터 기반 모델의 결과와 비교하였다. 부가저항의 계산 과정은 뒤의 대상선박의 사례에서 자세히 다뤘다.
식 (4)의 CT를 구한 다음, 식 (8)을 이용해 구한 KT/J2에 대응하는 n을 실선 스케일의 추진기 단독성능곡선으로부터 구하여 V/n을 얻는다. 여기서 KT, J, t, w는 각각 추력계수, 전진비(J = (1 - w)V/nD), 추력감소비, 반류비이다.
| (8) |
3.2 공개 선형의 적용
물리적 모델링 과정을 300K VLCC의 공개선형인 KVLCC2의 실험 결과에 적용하였다. 실선의 부가동력 해석에 사용된 자료는 축척비 1/58 모형선의 저항, 자항, 추진기 단독시험자료와 (Hino et al., 2005) 축척비 1/177.8 모형선의 규칙파 중 부가저항 시험 자료이다 (Lee et al., 2021b). 이를 이용해 실선 스케일의 맞바람 조건에서 U19.5에 따른 V/n을 추정하였다. Table 2와 3은 각각 대상 선형의 실선 스케일의 주요 요목과 저항, 자항 요소이다. KVLCC2는 상부구조물이 설계되지 않았으므로 풍하중 계산을 위한 AP는 실제 운항 중인 VLCC의 값을 대신 적용하였다.
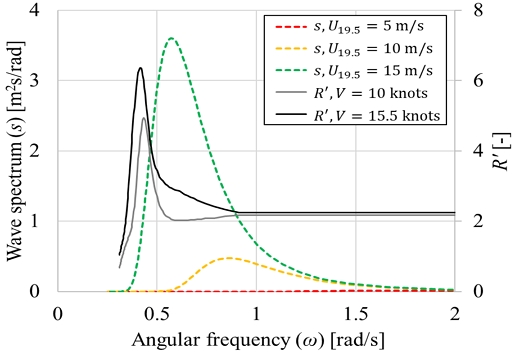
U19.5 = 5, 10, 15m/s 조건에서 구한 Pierson-Moskowitz 스펙트럼의 분포와 Lee et al. (2021b)의 V = 10, 15.5knots 조건의 실험에서 구한 부가저항의 QTF(R'(ω)) 결과를 Fig. 5에 나타냈다. R'(ω)는 식 (9)를 통해 계산하였다.
| (9) |
Fig. 5의 s(ω), R'(ω)결과로부터 식 (10)을 통해 Cadd를 계산할 수 있다.
| (10) |
Fig. 6은 U19.5와 V가 주어졌을 때 CT의 변화이다. UW = 10m/s를 넘어가면서 CT가 급격히 증가하면서 선속에 따른 CT 차이가 벌어졌다. 이는 실제 저항 크기의 변화보다는 저항계수 계산식에서 분모의 V가 줄어드는 영향으로 파악되었다. U19.5 = 0m/s의 정수 중 조건에서는 V에 따른 CT의 변화가 잘 나타나지 않았다.
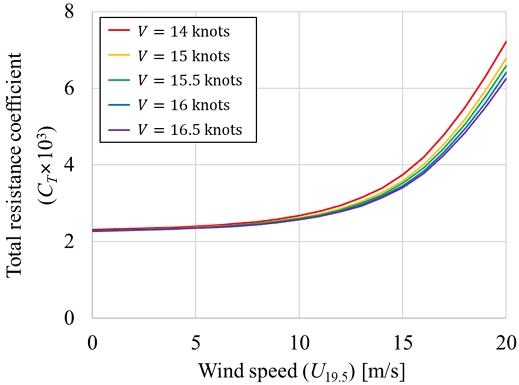
Total resistance coefficient (CT) of KVLCC2 with respect to wind speed (U19.5) variation in headwind
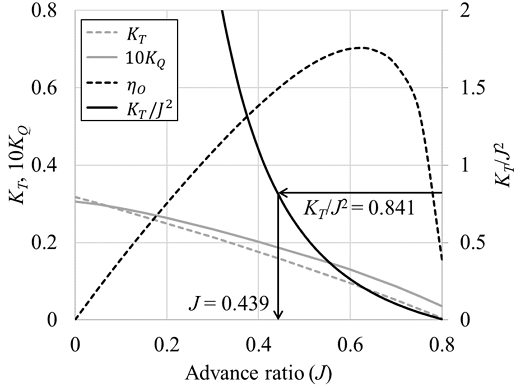
식 (8)을 통해 CT에서 KT/J2를 얻는다. w, t와 같은 자항요소는 정수 중 자항시험의 값에 1978 ITTC 성능추정법에서 제안된 실선 확장법을 통해 구하였다. Saettone et al.(2021)의 실험 연구에서 큰 파경사각 조건을 제외하면 자항 요소의 변화는 파랑의 영향을 거의 받지 않음을 보인 바 있으므로, 본 연구에서도 자항 요소의 파랑 중 변화는 고려하지 않았다. Fig. 7은 KVLCC2 선형의 실선 스케일 추진기 단독성능곡선에서 정수 중 15.5knots 조건에 대응하는 추진기의 전진비를 찾는 과정이다. 식 (8)과 Table 3의 값을 통해 구한 15.5knots 조건의 KT/J2는 0.841이고, 이에 대응하는 J는 0.439이다. 이 과정을 통해 V/n = 0.202 knots/RPM를 얻었다.
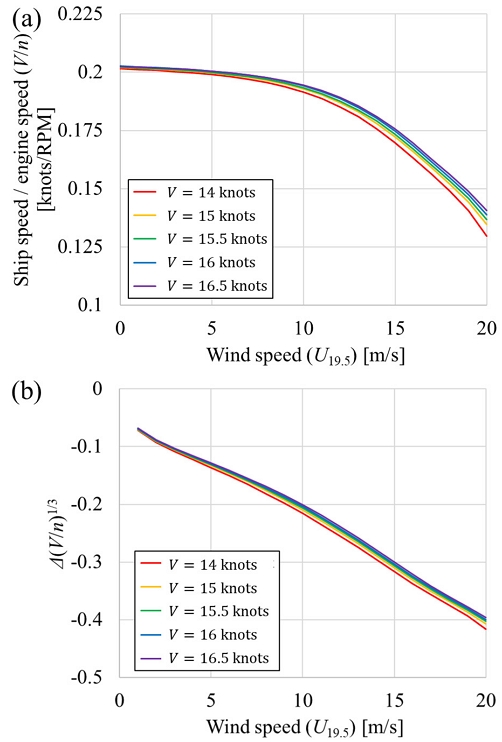
실해역에서 풍하중이나 부가저항이 발생하면 KT/J2이 증가하여 이에 대응하는 J는 감소한다. 이에 V/n도 감소할 것으로 보아, U19.5에 따른 V/n의 변화를 구했다. Fig. 8(a)는 그 결과이다. U19.5과 V/n의 관계를 다항식으로 근사하기 위해 U19.5과 Δ(V/n)1/3을 비교하여 Fig. 8(b)에 나타냈다. Δ(V/n)1/3은 정수 중의 (V/n)1/3과 비교했을 때 맞바람 조건의 U19.5로 인한 Δ(V/n)1/3의 변화량을 의미한다. 이를 통해 기관 회전수의 변화에 대한 풍속의 영향은 에 비례하여 표현할 수 있음을 확인하였다.
KVLCC2의 맞바람 중 와 V에 따른 n의 추정 모델을 식 (11)에 나타냈다. 식 (11)의 분모 전체에서 V의 변화의 영향은 U19.5에 비하면 무시할만한 수준으로 보인다. 따라서 식 (11)의 분모의 V를 Table 3에서 보인 KVLCC2의 설계속도 영역의 중간값인 15.25 knots로 고정하여 식 (12)와 같이 U19.5에 따른 V/n만을 비교할 수 있게 하였다.
| (11) |
| (12) |
4. 실운항 자료의 반영
4.1 실운항 자료와 비교
실운항 자료에서 선수파, 맞바람 영역에서 기록된 V/n을 식 (12)의 결정론적 모델 결과와 비교하였다. 식 (4)를 이용한 U19.5의 계산에서 hW = 45m이다. Fig. 9에 결정론적 모델과 대상선형의 결과를 나타내었다. 데이터 기반 모델링과 물리적 모델링의 대상 선박과 추진기 특성이 다르기 때문에 V/n을 직접 비교할 수는 없었다. 대신 두 선박의 V/n을 (V/n)calm에 대한 비율로 무차원화하여 비교하였다.
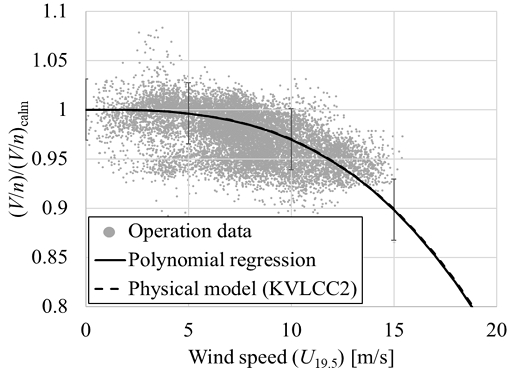
Comparison of V/n with respect to U19.5 by onboard measurement of operation data, polynomial regression, and deterministic physics-based model. Error bars indicates 95% confidence interval.
식 (12)의 구조를 따라 식 (13)을 제안하고, 실운항 자료를 가장 잘 추총하는 α, β를 구했다. (V/n)calm를 의미하는 β = 0.245를 얻었다. 이는 앞에서 보인 KVLCC2의 0.202보다 큰 값으로, 같은 선속을 달성하기 위한 기관 회전수가 실운항 VLCC의 경우 더 낮음을 의미한다. 이는 추진기 회전수를 낮추고 지름을 키워 추진 효율을 높이는 선박 설계 경향을 잘 반영한다.
| (13) |
최소자승법 대신 이상치에 대해 더 강건한 최소절대편차법(least absolute deviation method)을 적용해 α = -7.23을 얻었다. 특이하게도 대상 선박의 데이터에서 구한 3차 근사식이 KVLCC2의 물리적 모델과도 거의 차이가 없었다. 하지만 KVLCC2의 경우에서 운항 해역의 특성이 무시된 P-M 스펙트럼을 가정하고 실제 VLCC와 저항추진 특성에 차이가 있었으므로, 두 선박의 데이터의 일치는 여러 불확실성 요소의 결합으로 나타난 우연성이 작용한 것으로 생각된다.
4.2 입사각 영향 분석
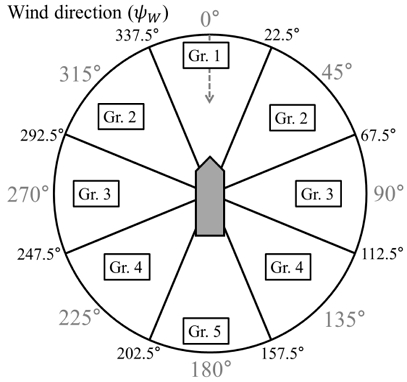
맞바람 조건에서 확인된 UW과 V/n의 3차식 관계를 다양한 ψW 조건으로 확장했다. Fig. 10에서 보인 대로 ψW을 5개의 영역으로 나누어 각 영역별로 3차식의 계수를 구했다. 4.1장에서 해석한 맞바람 조건은 1번 영역이며 5번은 뒷바람 조건이다.
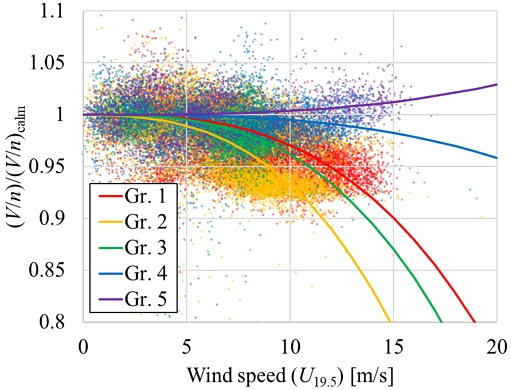
Fig. 11은 ψW 영역별로 얻어진 U19.5, V/n의 분포와 최소절대편차법을 통해 구한 3차 근사식이다. 그 계수와 3차항을 이용한 근사의 정확도는 Table 4에 나타내었다. 파도로 인한 부가저항은 ψW에 대한 영향을 덜 받을 것으로 보았고, 맞바람에서 뒷바람으로 진행함에 따라 공기저항은 줄어들기 때문에 전반적으로 α의 크기는 꾸준히 감소할 것으로 기대하였다.

Coefficients and absolute deviation of cubic regression model for added power analysis with respect to ψW
1번 영역에 비해 2번, 3번 영역의 α의 크기가 증가하여 선수사파나 횡파로 발달할 수 있는 풍향에서 부가저항이 더 큰 경향을 보였다. 이는 다양한 입사각에서 부가저항 해석을 수행한 Lee et al. (2024b)의 연구 내용을 통해 설명할 수 있다. 해당 연구에서는 선수사파 중에는 선수파에 비해 부가저항의 공진주파수가 증가하는 경향을 보고한 바 있다. 이를 Fig. 5와 연계하자면 부가저항의 QTF가 2, 3번 영역에서는 더 높은 주파수 쪽으로 이동하여 주어진 파 스펙트럼과 겹치는 영역이 증가하기 때문에 부가저항 또한 증가할 것이라 볼 수 있다. 비슷한 현상이 Uharek and Cura-Hochbaum (2018)의 단파장 중 부가저항 결과와 Mittendorf et al. (2023)의 연구에서도 보고되었으므로, 해상환경에 따른 부가동력이나 연료소모량 모델링에서는 선수사파에서의 부가저항 증가를 정확히 다뤄야 할 것으로 보인다. 추가로, 횡파조건인 3번 영역은 1번 영역에 비해 방향타의 작동 소요가 더 많을 것이므로 추가적인 저항의 증가가 반영된 것으로 보인다.
4, 5번 영역에서는 기대한대로 UW에 따른 V/n의 변화가 줄어들었기 때문에 뒷바람의 영향으로 추가적인 추력의 영향을 확인할 수 있었다. 그리고 어느 정도 뒷바람을 받는 4번 영역에서는 UW의 증가에서 V/n의 감소가 나타났으므로 해상환경에서는 풍향의 영향보다는 모든 방향에 걸친 파도로 인한 부가저항이 더 지배적인 것으로 판단된다.
4.3 연료 소모량 모델 검증
4.2장에서 구한 해상환경에 따른 부가동력 모델을 2장 내용과 연계해 연료소모량 추정 모델으로 확장하였다. 추정 모델에서는 실제 계측 풍속과 풍향인 UW, ψW를 사용할 수 없으므로 기상정보의 UI, ψI를 대신 사용하였다. 실운항 정보에서 UW와 UI의 상호상관도는 0.741였다. 그리고 기상정보의 풍속 계측 기준높이는 10m임을 이용해 U19.5를 구했다. 이렇게 준비된 실운항 자료로 식 (13)을 구성하는 α, β를 구했다. 그 결과는 Table 5와 같다. UW를 이용할때보다 α의 크기가 커졌는데, 이는 Fig. 3에서도 확인할 수 있듯 전반적으로 UW이 UI보다 크게 얻어졌기 때문이다.

Coefficients and absolute deviation of cubic regression model for added power analysis with respect to ψI
Fig. 2(a)에서 기관 출력은 n3에 비례함을 확인하였으므로, Table 5의 계수를 이용해 구한 n으로부터 P/PMCR를 추정할 수 있다. 이렇게 UW, UI에 대해 얻은 P/PMCR의 추정값과 실운항 자료를 비교하였다. Fig. 12(a)는 그 결과로, 모델링의 정확도(AP)를 식 (14)와 같이 정의하여 나타냈다. 이는 절대편차의 평균에 대해 실운항 자료의 95% 영역 범위인 ±2σ로 나눈 값이다. 세로축의 추정값에서 40% 이하의 P/PMCR값이 나타나지 않은 것은 비교 대상 데이터가 12knots 이상의 선속만을 취했으므로 동력 추정의 하한선이 발생하였기 때문이다.
| (14) |
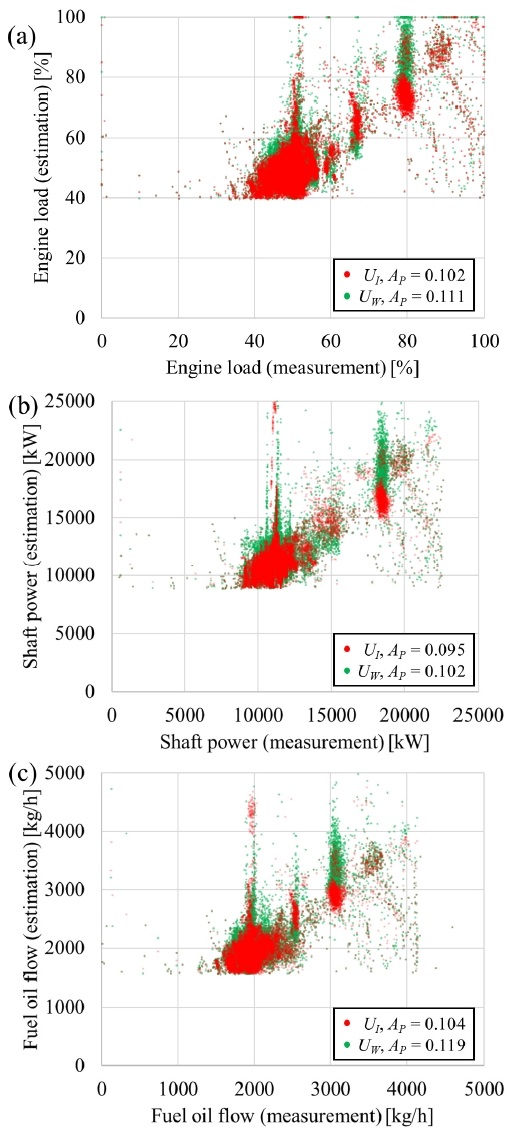
Comparison of data-driven model using UI and UW: (a) engine load (P/PMCR), (b) shaft power (PS), and (c) fuel oil flow rate (M).
UW를 이용한 모델에서 국부적으로 나타난 동력 관련 변수가 증가하는 경향이 UI에서는 줄어들었다. 이는 선상에서 계측된 UW은 마스트와의 간섭이나 계측 시스템 자체의 정확도 한계로 인해 UI에 비해 일관성이 부족한 결과를 내기 때문으로 보인다. 따라서 UI를 데이터 기반 모델의 입력으로 활용하는 것이 더 나은 방법으로 생각되며, 이는 예측 모델의 목적에도 부합한다.
n에서 Fig. 2의 관계를 이용해 PS, M을 추정한 결과를 각각 Fig. 12(b), (c)에 나타냈다. 정확도는 앞의 P/PMCR과 큰 차이는 없었으므로, P/PMCR, PS, M의 순차적인 추정 과정에서 오차의 전파는 별 영향이 없는 것으로 판단되었다. 각 변수의 정확도는 10% 내외로 얻어졌다. 따라서 3장에서 다룬 해상환경 변수에 따른 V/n 추정 모델이 그 이후의 과정에 비해 연료 소모량 추정에 더 큰 영향을 주는 것으로 생각된다.
5. 결 론
선박의 실해역 운항 중 연료소모량의 추정을 위해 풍속과 풍향 조건을 입력으로 갖는 데이터 기반 모델을 개발하였다. 모델의 개발 과정을 통해 다음의 사항을 확인하였다.
공개 선형인 KVLCC2의 실험 자료를 이용해 맞바람 중 부가동력 해석 모델을 개발하였다. 이 모델에서 부가동력으로 인한 선속의 감소 정도는 풍하중과 파도 중 부가저항의 비선형적인 계산 과정에도 불구하고 풍속의 세제곱에 비례하는 것을 확인하였다.
KVLCC2의 맞바람 조건에서 구한 부가동력 모델을 실운항 자료의 풍향 별로 보정하였다. 맞바람 영역에서는 완전한 맞바람보다는 옆바람 성분이 발생할 때 부가동력이 증가하여 선속이 감소하는 경향이 얻어졌다. 뒷바람에서는 정수 중 조건보다 높은 선속이 나타나기도 했다. 이러한 물리적 특성을 반영해 3차항의 계수를 풍향별로 구할 수 있었다.
추진기의 회전수, 기관동력, 연료소모량의 관계를 적용해 연료소모량 예측 모델을 개발했고, 이를 실운항 자료와 비교하였다. 추정 모델의 불확실성은 대부분 해상환경 변수에서 회전수를 추정하는 과정에서 얻어졌으며, 축동력이나 연료 유량의 계측의 불확실성의 영향은 그보다 작은 것으로 보인다.
본 연구에서 개발된 모델에 대해 실해역의 파랑 스펙트럼을 적용하거나 대상선박의 저항추진 요소를 이용해 데이터 기반 모델을 개선하여 그 신뢰도를 더 높일 수 있을 것이다. 모델의 구성이 간단하므로 운항데이터가 많지 않거나, 혹은 정수 중 모형시험 결과만 있는 신조 선박에 대해서도 운항 전에 CII 관점에서 최적항로를 선정하는데 활용될 수 있을 것으로 기대된다.
Acknowledgments
본 연구는 2024년 삼성중공업의 재원으로 충남대학교에서 수행된 ‘자율운항시스템 핵심 기술 개발’과제 및 2024년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임(P0017006, 2024년 산업혁신인재성장지원사업).
References
- Hino, T., 2005. Proceedings of CFD Workshop Tokyo 2005. National Maritime Research Institute, Tokyo, Japan.
- ISO, 2015. Ships and Marine Technology – Guidelines for the assessment of speed and power performance by analysis of speed trial data. ISO 15016:2015, Geneva, Switzerland.
- ITTC, 2021. 1978 ITTC performance prediction method. ITTC-Recommended Procedures and Guidelines, 7.5-02-03-01.4, ITTC, Zurich, Switzerland.
- ITTC, 2022. Preparation, conduct and analysis of speed/power trials. ITTC-Recommended Procedures and Guidelines, 7.5-04-01-01.1, ITTC, Zurich, Switzerland.
-
Kim, Y.-C., Kim, Y., Kim, J. and Kim, K.-S., 2018. Added resistance and 2DOF motion analysis of KVLCC2 in regular head waves using dynamic overset scheme. Journal of the Society of Naval Architects of Korea, 55(5), pp.385-393.
[https://doi.org/10.3744/SNAK.2018.55.5.385]

-
Kim, K.-S. and Roh, M.-I., 2020. ISO 15016:2015-based method for estimating the fuel oil consumption of a ship. Journal of Marine Science and Engineering, 8, Article No. 791.
[https://doi.org/10.3390/jmse8100791]

-
Kim, H., Lee, J.-H., Jang, J.-H., Ahn, H.-S., Kang, D.-Y. and Byeon, S.-S., 2021a. Study on the speed-power characteristics through a speed trial of a large container vessel during a commercial voyage part 1, Journal of the Society of Naval Architects of Korea, 58(6), pp.366-374.
[https://doi.org/10.3744/SNAK.2021.58.6.366]

-
Kim, D.-H., Sanada, Y., Sadat-Hosseini, H. and Stern, F., 2021b. URANS simulations for a free-running container ship: part 2. added power. Journal of hydrodynamics, 33(3), pp.448-467.
[https://doi.org/10.1007/s42241-021-0053-5]

-
Lee, C.-M., Seo, J.-H., Yu, J.-W., Choi, J.-E. and Lee, I., 2019. Comparative study of prediction methods of power increase and propulsive performances in regular head short waves of KVLCC2 using CFD. International Journal of Naval Architecture and Ocean Engineering, 11, pp.883-898.
[https://doi.org/10.1016/j.ijnaoe.2019.02.001]

-
Lee, J.-B., Roh, M.-I. and Kim, K.-S., 2021a. Prediction of ship power based on variation in deep feed-forward neural network. International Journal of Naval Architecture and Ocean Engineering, 13, pp.641-649.
[https://doi.org/10.1016/j.ijnaoe.2021.08.001]

-
Lee, S.-H., Paik, K.-J., Hwang, H.-S., Eom, M.-J. and Kim, S.-H., 2021b. A study on ship performance in waves using a RANS solver, part 1: comparison of power prediction methods in regular waves. Ocean Engineering, 227, Article No. 108900.
[https://doi.org/10.1016/j.oceaneng.2021.108900]

-
Lee, S.-H., Paik, K.-J. and Lee, J.-H., 2022a. A study on ship performance in waves using a RANS solver, part 2: comparison of added resistance performance in various regular and irregular waves. Ocean Engineering, 263, Article No. 112174.
[https://doi.org/10.1016/j.oceaneng.2022.112174]

-
Lee, S.-H., Paik, K,-J., Cho, J.-H., Kim, G.-H., Kim, H.-S. and Kim, S.-H., 2022b. A numerical study on self-propulsion performance in regular waves and power prediction in irregular waves. International Journal of Naval Architecture and Ocean Engineering, 14, Article No. 100454.
[https://doi.org/10.1016/j.ijnaoe.2022.100454]

-
Lee, S., Seo, J., Kim, D.-H., Han, S., Kim, K., Chung, S. and Yoo, B., 2024a. Reduced order modeling of marine engine status by principal component analysis. Journal of the Society of Naval Architects of Korea, 61(1), pp.8-18.
[https://doi.org/10.3744/SNAK.2024.61.1.8]

-
Lee, S.-H., Kim, C., Paik, K.-J., Kim, H. and Chun, J., 2024b. A numerical study of added resistance performance and hydrodynamics of KCS hull in oblique regular waves and estimation of resistance in short-crested irregular waves through spectral method. International Journal of Naval Architecture and Ocean Engineering, Vol. 16, Article No. 100563.
[https://doi.org/10.1016/j.ijnaoe.2023.100563]

- MAN, 2023. Basic Principles of Ship Propulsion. MAN Energy Solutions, Copenhagen, Denmark.
-
Mittendorf, M., Nielson, U.D., Bingham, H.B. and Dietz, J., 2023. Assessment of added resistance estimates based on monitoring data from a fleet of container vessels. Ocean Engineering, 272, Article No. 113892.
[https://doi.org/10.1016/j.oceaneng.2023.113892]

-
Park, D.-M., Lee, J. and Kim, Y., 2015. Uncertainty analysis for added resistance experiment of KVLCC2 ship. Ocean Engineering, 95, pp.14-156.
[https://doi.org/10.1016/j.oceaneng.2014.12.007]

-
Saettone, S., Taskar, B., Steen, S. and Andersen, P., 2021. Experimental measurements of propulsive factors in following and head waves. Applied Ocean Research, 111, Article No. 102639.
[https://doi.org/10.1016/j.apor.2021.102639]

-
Sanada, Y., Kim, D.-H., Sadat-Hosseini, H., Stern, F., Hossain, M.A., Wu, P.-C., Toda, Y., Otzen, J., Simonsen, C., Abdel-Maksoud, M., Scharf, M. and Grigoropoulos, G., 2022. Assessment of EFD and CFD capability for KRISO Container Ship added power in head and oblique waves. Ocean Engineering, 243, Article No. 110224.
[https://doi.org/10.1016/j.oceaneng.2021.110224]

-
Seo, M.-G., Yang, K.-K., Park, D.-M. and Kim, Y., 2014. Numerical analysis of added resistance on ships in short waves, Ocean Engineering, 87, pp.97-110.
[https://doi.org/10.1016/j.oceaneng.2014.05.011]

-
Seo, S. and Park, S., 2017. Numerical simulations of added resistance and motions of KCS in regular head waves. Journal of the Society of Naval Architects of Korea, 54(2), pp.132-142.
[https://doi.org/10.3744/SNAK.2017.54.2.132]

-
Seo, D.-W., Kim, M.-S. and Kim, S.-Y., 2019. Uncertainty analysis for speed and power performance in sea trial using Monte Carlo simulation. Journal of the Society of Naval Architects of Korea, 56(3), pp.242-250.
[https://doi.org/10.3744/SNAK.2019.56.3.242]

-
Seo, J.-H., Lee, C.-M., Yu, J.-W., Choi, J.-E. and Lee, I., 2020. Power increase and propulsive characteristics in regular head waves of KVLCC2 using model tests. Ocean Engineering, 216, Article no. 108058.
[https://doi.org/10.1016/j.oceaneng.2020.108058]

-
Shaw, H.-J. and Lin, C.-K., 2021. Marine big data analysis of ships for the energy efficiency changes of the hull and maintenance evaluation based on the ISO 19030 standard. Ocean Engineering, 232, Article No. 108953.
[https://doi.org/10.1016/j.oceaneng.2021.108953]

-
Trodden, D.G., Murphy, A.J., Pazouki, K. and Sargeant, J., 2015. Fuel usage data analysis for efficient shipping operations. Ocean Engineering, 11, pp.75-84.
[https://doi.org/10.1016/j.oceaneng.2015.09.028]

-
Uharek, S. and Cura-Hochbaum, A., 2018. The influence of inertial effects on the mean forces and moments on a ship sailing in oblique waves Part B: numerical prediction using an RANS code. Ocean Engineering, 165, pp.264-276.
[https://doi.org/10.1016/j.oceaneng.2018.07.002]

-
Yang, K.-K., Lee, J.-H., Nam, B.-W. and Kim, Y., 2013. Analysis of added resistance using a Cartesian-grid-based computational method. Journal of the Society of Naval Architects of Korea, 50(2), pp.79-87.
[https://doi.org/10.3744/SNAK.2013.50.2.79]

-
Yang, K.-K., Seo, M.-G. and Kim, Y., 2015. Analysis of added resistance in short waves. Journal of the Society of Naval Architecture of Korea, 52(4), pp.338-348.
[https://doi.org/10.3744/SNAK.2015.52.4.338]

-
Yu, J.-W., Lee, C.-M., Choi, J.-E. and Lee, I., 2017. Effect of ship motions on added resistance in regular head waves of KVLCC2. Ocean Engineering, 146, pp.375-387.
[https://doi.org/10.1016/j.oceaneng.2017.09.019]