함정의 전자기파 산란자 분포를 고려한 레이더 호밍 대함미사일 피격 위치 추정 프로그램 개발
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The susceptibility of warships denotes the hit probability by anti-ship missiles in a hostile environment. The distribution characteristics of the hit location directly influence the vulnerability. This paper proposes a simulation method to determine the hit location of radar-homing anti-ship missiles by their approach direction. The method uses high-frequency analysis theory to calculate electromagnetic scatterers and determines the equivalent scattering center position corresponding to the hit location. The proposed method was implemented to an in-house software called SCTracer/RCS, which follows the process: importing numerical analysis model, defining calculation condition, calculating electromagnetic wave scattering centers, storing to database, calling scattering center data, estimating equivalent scattering center, and analyzing hit-point distribution. To validate the feasibility and practical applicability of this software, the hit-point distribution is examined for a 90-meter-class virtual warship.
Keywords:
Warship, Survivability, Susceptibility, Anti-ship missile, Equivalent scattering center키워드:
함정, 생존성, 피격성, 대함미사일, 등가산란중심1. 서 론
세계적인 안보 환경 변화와 해상 무기체계의 획기적인 발전으로 인해 현대 해양의 전장 환경은 다양한 복잡성을 갖게 되었으며, 이러한 어려움을 극복하기 위해 함정의 설계과정에서 생존성 향상을 위한 기술 적용은 일반화 되었다 (Yoon et al., 2017). 함정의 생존성은 적대적 전장 환경하에서 고유의 기능을 유지한 상태로 임무를 수행할 수 있는 능력을 의미하며, 피격성, 취약성, 회복성 등으로 분류하여 평가한다. 함정의 생존성을 높이기 위해서는 피격성과 취약성은 낮추고 회복성은 높여야 한다 (Choi et al., 2020). 함정의 생존성 중 피격성은 적의 탐지 센서나 위협 무기에 노출되어 피격당할 확률을 뜻하며, 함정의 피탐지 성능과 대함전 방어체계 성능을 나타내는 척도로 사용된다. 현대의 함정은 피탐지 확률을 낮추기 위해 레이더 반사 면적(RCS, Rader Cross Section), 적외선(IR, Infra-Red), 수중 방사 소음(URN, Underwater Radiated Noise) 등에 대한 신호 관리 체계를 마련하고 있으며, 이를 위해 함정의 획득 단계별 신호 추정과 요구 성능 만족에 노력을 기하고 있다.
함정의 전체 RCS 신호는 함정에 분포하는 전자기파 산란자들의 RCS 크기와 위상에 따라 결정된다. 또한 레이더 호밍 미사일의 접근 방향과 거리는, 함정 전체 RCS 크기와 위상뿐 아니라 등가산란중심의 위치를 변화시켜 대함미사일의 피격점을 변화시키는 요인이 된다. 대함미사일의 접근 방향과 거리에 따른 피격점 변화는 대상 함정의 구획별 피격확률을 변화시키며, 궁극적으로는 취약성에 직접적인 영향을 미치게 된다. 따라서 대함미사일에 의한 피격시나리오에 따른 피격성 평가와 그에 따른 취약성을 연계 평가하는 기술의 확보가 필요하다.
Kim et al. (2005a, 2005b)은 RCS 해석을 위해 적응 삼각형 빔 방법을 적용한 OPM(Object Precision Method) 기반 프로그램을 개발하고, 복합 구조물 및 실물 크기의 코르벳(corvette) 함정에 대한 검증 해석을 수행하였다. Kim et al. (2014)은 산란자의 분포를 모의하기 위해 함정의 RCS 신호와 면적에 대한 확률밀도함수를 고려해 함정의 피격성을 평가하였다. Lee et al. (2023)은 함정으로 다가오는 위협에 대해 함정에 설치된 대공방어 시스템들의 효과도를 활용해 피격성 추정에 대한 연구를 수행하였다. Jang et al. (2014)은 물리광학법과 기하광학법을 연계한 고주파수 해석 기법의 해석 코드를 개발하고, 이를 비행체 형상에 대해 적용한 바 있다. 그럼에도 불구하고 이러한 방법들은 현실적인 산란중심 분포 특성을 고려한 취약성 평가에 한계가 있다.
본 연구에서는 피격성과 취약성을 연계 평가하기 위한 기초연구로, 레이더 호밍 대함미사일이 함정으로 접근할 때 접근 방향에 따른 함정의 전자기파 산란자 분포를 해석하고 그에 따른 등가 산란 중심의 위치를 추정하는 수치해석 방법을 제시하였다. 전자기파 산란자 분포 산정은 고주파수 해석 기법을 적용하였으며, 산정된 산란자 분포를 이용해 피격점에 해당하는 등가 산란중심 방법을 제안하였다. 제안된 방법을 기반으로 등가산란중심 및 분포 특성을 해석하기 위한 소프트웨어를 개발하였으며, 이의 타당성 검토를 위해 가상의 90m급 코르벳 함정에 대한 수치 해석을 수행하고 그 결과를 검토한다.
2. 등가 산란중심 해석
2.1 고주파수 레이더 반사면적 해석
RCS 해석을 위한 수치해석기법에는 모멘트법(method of moment), 경계요소법(boundary element method), 유한차분법(finite element method), 유한 차분 시간영역 해석법(finite difference time domain) 등의 저주파수 해석이론과 기하광학법(geometric optics), 물리광학법(physical optics), 기하광학 회절이론(geometric theory of diffraction), 물리/기하광학 혼합 방법 등의 고주파수 해석 이론이 있다 (Knott et al. 1990).
함정과 같이 크기가 크고 복잡한 형상을 갖는 대형 복합구조물의 경우 고주파수 해석 이론에 기반한 수치해석기법이 적합하며, 실무적으로는 효율적인 가시면과 은면(hidden surface) 산정기법으로 기하광학 이론을, 최종 반사면에 대해 물리광학방법을 적용하는 물리광학/기하광학 혼합방법이 실무적으로 활용되고 있다 (Wang et al., 1997). 물리광학/기하광학 혼합 방법은 가시면과 은면의 처리 방식에 따라 IPM(Image Precision Method)과 OPM으로 분류할 수 있다. IPM에서는 전자기파 면을 무수히 많은 광선들(rays)로 분할하고 각각을 하나의 화소로 간주하며, OPM에서는 표적면을 구성하는 평면 요소의 모양을 따라 전자기파 빔을 형성하고 이를 추적한다.
2.2 레이더 반사면적 해석
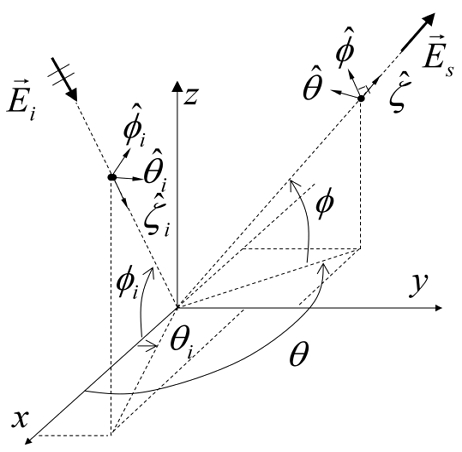
Fig. 1은 구면좌표계에서 원점에 위치한 표적에 대한 전자기파의 입사와 산란을 나타낸 것이다. 이때 와 는 전자기파의 입사와 산란 전기장 벡터를, 와 는 전기장과 자기장의 편파벡터를 나타낸다. 또한, , 는 전자기파의 입사와 산란 방향벡터이며, θi와 ϕi, θ, ϕ 는 이에 대응하는 구면 좌표이다.
표적의 RCS는 전자기파의 편파성분을 고려해 RCS 행렬 [σ]로 정의하며, 식 (1)과 같다.
| (1) |
여기서, σuv(u, v = θ, ϕ)는 uv편파 복소 RCS이며, 이에 대응하는 산란행렬요소 Suv로부터 산정한다. |•|은 복소수의 크기를 의미한다.
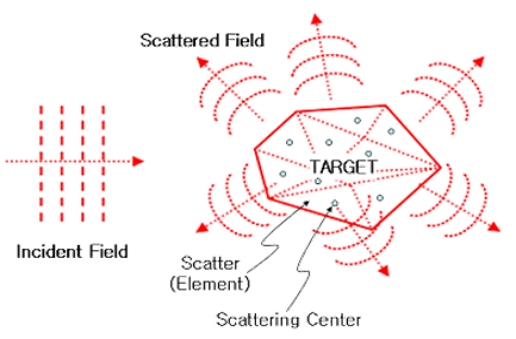
고주파수 이론에 기반한 RCS 해석기법에서는 Fig. 2에 보인 바와 같이 표적을 유한개의 산란자(scatter)의 조합이며, 각각의 산란자에 대응하는 산란 중심(scattering center)은 전체 RCS에 독립적으로 기여하는 것으로 간주한다.
각 산라자에 대한 등가 산란중심의 RCS σuv는 식 (2)와 같이 전자기파의 산란 특성에 따라 단일반사성분과 다중반사성분으로 구분하고 고주파수 해석이론인 물리광학법과 물리광학/기하광학 혼합법을 각각 적용하여 산정한다 (Kim et al., 2012).
| (2) |
여기서, N은 표적 전체를 조합하는 산란자의 개수이며, 단일반사 산란자 개수 Ns, 다중 반사 산란자 개수 Nm의 합이다. 및 는 각각 단일 반사와 다중 반사의 산란 행렬 요소를 나타낸다.
2.3 산란중심 분포 산정
표적의 RCS를 계산할 때, 식 (2)에 적용된 산란 중심들의 RCS뿐 아니라 위치 정보를 조합해 전체 표적에 대한 등가 산란중심을 산정한다. 따라서 각각의 산란 중심의 산란 특성에 따른 효율적인 산란 중심 위치 산정이 요구된다.
본 연구에서는 표적을 평면 삼각형 산란자로 모델링하고, 단일반사에 대해서는 산란자의 면적 중심을 산란 중심 위치로, 다중반사에 대해서는 수정된 가상면 개념을 도입하여 산정한다.
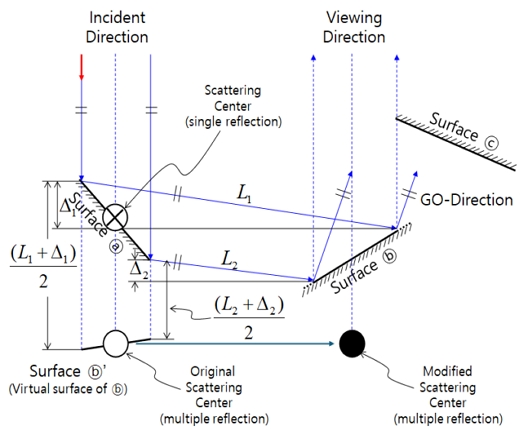
Fig. 3은 산란 중심 위치 산정 개념을 도식화한 것이다. 3개의 표적면에 전자기파가 입사한다고 가정하면, 표적면 ⓐ에 입사한 전자기파 에너지는 반사 후 표적면 ⓑ에 유기되며, 이는 다시 표적면 ⓒ에 의해 가려지지 않는 에너지만 레이더로 돌아간다.
단일반사에 의한 RCS를 계산하기 위해 표적면 ⓐ에 대해 물리광학법을 적용하였으며, 다중반사에 의한 RCS를 계산하기 위해 표적면에 입사해 다중 반사 후 되돌아가는 전자기파의 전달경로의 절반에 해당하는 가상면을 산정하고 이에 대해 물리광학/기하광학 혼합방법을 적용하였다 (Kim et al., 2012)
단일반사 산란 중심 위치는 첫 번째 반사면인 표적면 ⓐ에 대응하는 평면 삼각형 요소의 면적 중심(⛒)으로 산정하였다. 다중 반사 산란중심은 단일반사와 마찬가지로 가상 면에 대한 면적 중심을 산란 중심으로 산정할 수 있으나, 산란 중심이 관측 방향인 최종 표적면 ⓑ의 대응선 상에 위치하지 않고 입사 방향인 첫 번째 표적면 ⓐ 대응선 상에 위치하는 문제점이 나타난다. 이를 해결하기 위해 가상면의 등가 산란 중심(○)을 최종 표적면 ⓑ의 대응선 상의 등가 산란중심(●)으로 이동하는 수정된 산란 중심 위치 산정 방법을 적용하였다. 이는 산란중심의 위치가 표적면 ⓐ 대응선 상에 위치한 가상면 산란중심의 전달경로 길이를 유지하되, 최종 표적면 ⓑ의 면적 중심을 관통하도록 하는 방법이다.
2.4 등가 레이더 반사면적 산란 중심
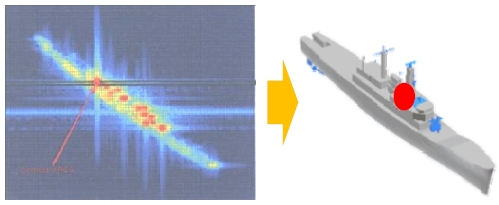
레이더 호밍 대함유도탄은 함정을 점 산란자로 인식하고 탐지추적하며, 그 RCS와 위치는 함정 상에 분포하는 산란 중심들에 대한 등가 산란 중심이 된다(Fig. 4).
본 연구에서는 대함미사일의 피격점을 산정을 위해 2.2절에서 산정한 표적의 산란 중심 분포로부터 등가 산란 중심 데이터베이스를 구축하고 이로부터 식 (3)에 의거 가중 평균(weighted-average)에 기반한 등가 산란 중심을 산정한다 (Kim et al., 2023).
| (3) |
여기서, (, , )와 (xi, yi, zi)는 대상함정의 길이, 폭, 깊이 방향 직교 좌표계에서의 등가 산란 중심 위치 좌표와 표적에 분포하는 i번째 산란 중심 위치 좌표이다. σuv,i는 i번째 산란 중심의 복소 RCS를 나타낸다.
3. SCTracer/RCS
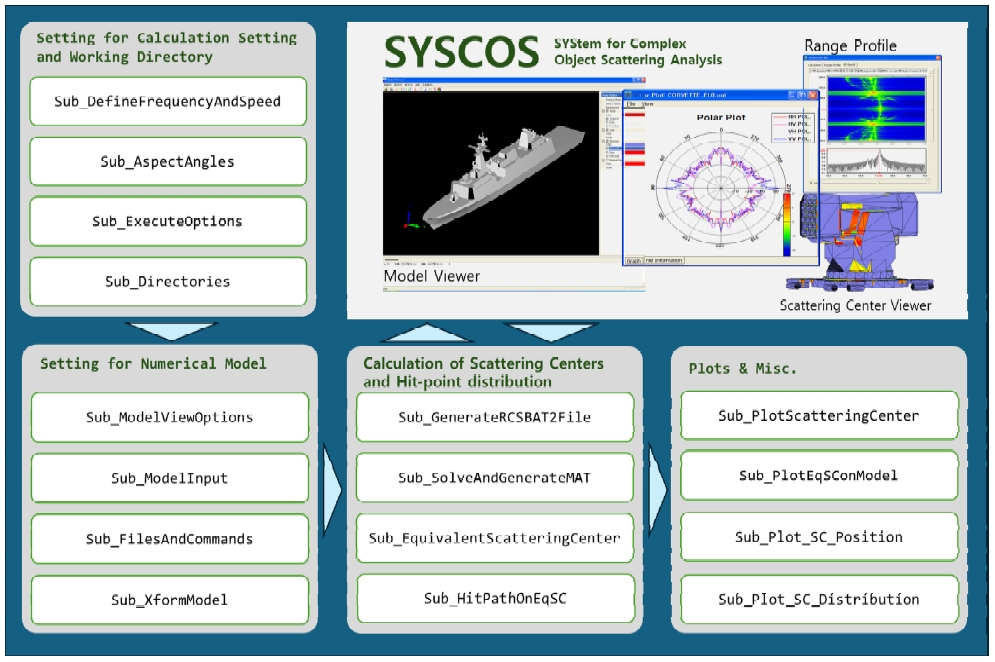
2장에서 기술된 이론을 바탕으로 수상함의 전자기파 산란자 분포 데이터베이스를 구축하고 이를 이용해 레이더 호밍 대함미사일에 의한 피격 위치 분포를 모의할 수 있는 소프트웨어 SCTrader/RCS를 개발하였다. 개발 소프트웨어는 Fig. 5에 보인 바와 같이 계산 인자 설정 모듈, 수치해석모델 입력 및 조정 모듈, 등가 산란 중심 해석 모듈, 결과 도시 모듈 등으로 구성되어 있다. 계산 인자 설정 모듈에서는 대함미사일의 레이더 운용 주파수, 운용 속도, 접근 방향 등의 피격시나리오와 계산결과 후처리를 위한 선택사항 및 작업폴더 관리 기능을 포함한다. 수치해석모델 입력 및 조정 모듈에서는 대상함정 모델의 입력과 형상확인, 출력파일 관리 기능을 포함한다. 등가산란중심 해석모듈에서는 대상함정의 산란자 분포 분석과 그에 따른 등가산란자 산정 모듈을 포함한다. 이때, 등가 산란 중심 해석 모듈은 함정 RCS 해석 전문 소프트웨어인 SYSCOS(SYStem for Complex Object Scattering analysis, Kim et al. 2012)와 연동하여 산란 중심을 산정하고 데이터베이스화하고 이로부터 등가 산란 중심과 피격점 분포를 해석한다. 결과 도시 모듈에서는 산정된 산란자 분포, 등가산란중심, 등가산란중심 분포 등을 가시화한다.
4. 레이더 반사면적 해석 및 결과
4.1 수치해석모델과 해석 조건
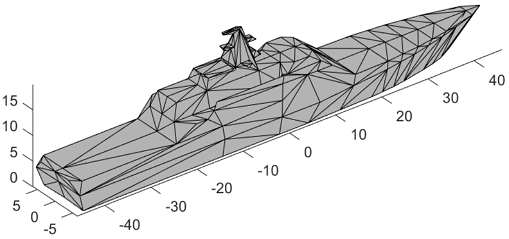
제안된 등가 산란 중심 산정기법의 타당성과 실무적용성을 검토하기 위해 90m급 가상함정에 대한 수치해석을 수행하였다. RCS 해석에서 다중 반사 현상을 많이 고려할수록 해석 시간이 많이 소요된다. 따라서, 무장 및 통신 체계와 같은 함정에 설치되는 탑재 장비는 제외하고 해석을 수행하였다. 수치해석모델은 길이, 폭, 높이가 각각 90m, 13m, 20m이며, 평면 삼각형 요소 374개로 구성하였다(Fig. 6). 선체 표면은 완전 도체라고 가정하였으며, 다중 반사는 최대 3차까지 고려하였다.
RCS 해석 주파수는 9GHz이며, 전기장 벡터 가 x-y 평면과 평행한 HH-편파를 고려하였다. 방위각은 0°에서 360°까지 0.2°간격으로, 고각은 5°로 설정하였다.
4.2 산란중심 분포와 등가 산란중심 산정
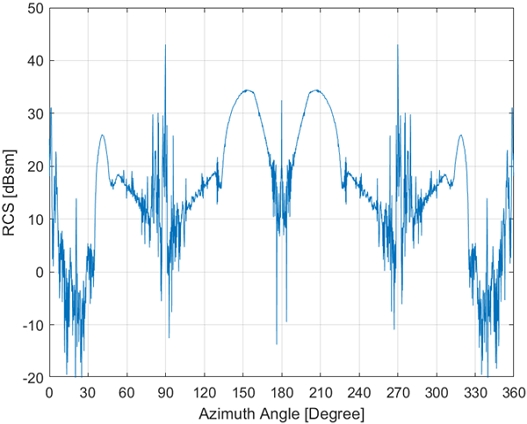
물리광학/기하광학 혼합방법을 이용해 산란중심 분포를 해석하고 그 결과를 데이터베이스에 저장하였다. 이를 이용해 식 (2)에 의거 대상모델의 전체 RCS를 복원하고 그 결과를 Fig. 7에 도시하였다. 참고로, Cardinal point에 해당하는 0°, 90°, 180°, 270°, 360°에서 빔폭이 작은 강한 피크성분이 나타나고 있으며, 대상 함정의 다중 반사에 의해 40°, 150°, 210°, 320° 부근에서 빔폭이 넓은 피크성분들이 나타남을 알 수 있다. 이는 일반적인 함정의 RCS 특성이다.
산란중심 분포 데이터를 이용한 RCS 복원결과의 신뢰성을 검토하기 위해 SYSCOS(SYStem for Complex Object Scattering analysis, Kim et al. 2012)을 이용한 RCS 해석결과와 비교하여 정확히 일치함을 확인하였다.
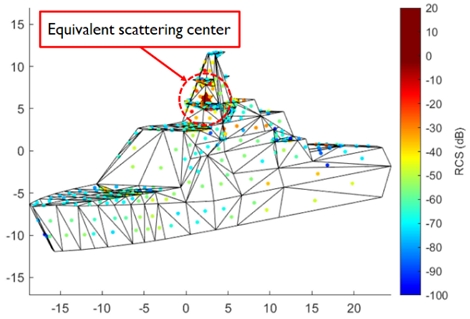
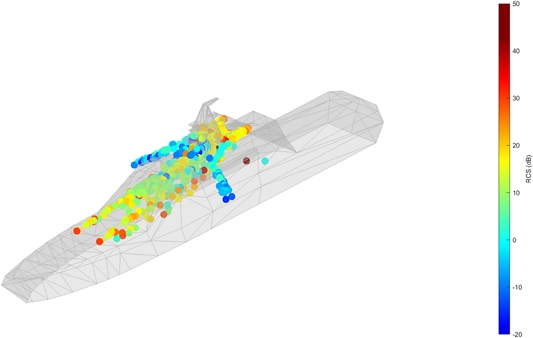
Fig. 8은 산란중심 분포 데이터베이스 중에서 방위각 24°, 고각 5°에 대한 결과를 예시한 것이다. 대상함정을 구성하는 산란자에 대응하는 산란중심들이 선루(superstructure), 선체(hull), 마스트 등 함 전체에 걸쳐 분포하고 있으나 큰 RCS를 갖는 산란중심들이 마스트 근방에 집중되어 있음을 알 수 있다. 또한, 식 (3)에 의거 등가 산란중심(★)을 산정하고 그 결과를 Fig. 7에 함께 도시하였다. 이로부터 대함미사일에 의한 피격점은 함수와 함미 보다는 중앙부임을 직관적으로 알 수 있다.
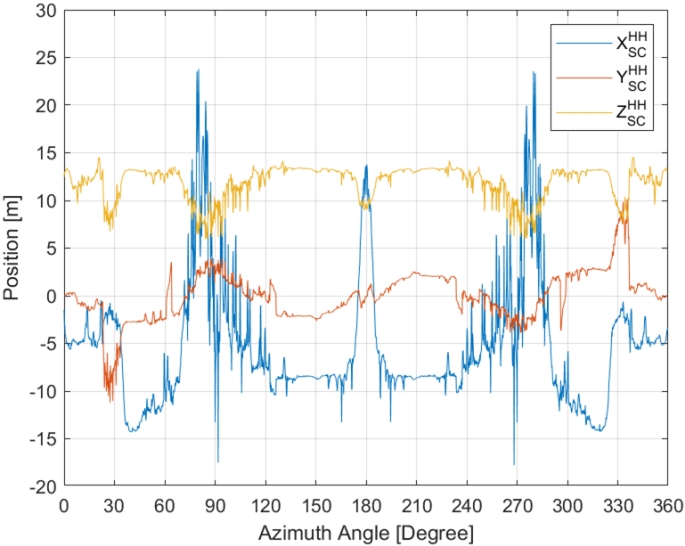
Fig. 9는 해석 방위각과 고각에 대한 산란중심 분포 데이터베이스를 활용해 식 (3)에 의거 산정한 등가 산란중심의 위치를 그래프로 나타낸 것이다. 대함미사일의 접근 방향에 따라 등가 산란중심 위치가 변화하고 있으며, 와 는 180°에 대해 축 대칭성을, 는 180°에 대해 점대칭성을 보이고 있다.
Fig. 10은 모든 대함미사일 접근방향에 대한 등가 산란중심 위치를 대상함정 수치해석모델 상에 표시한 것이다. 등가 산란중심들이 대상함정 중앙부에 집중되어 나타나고 있다.
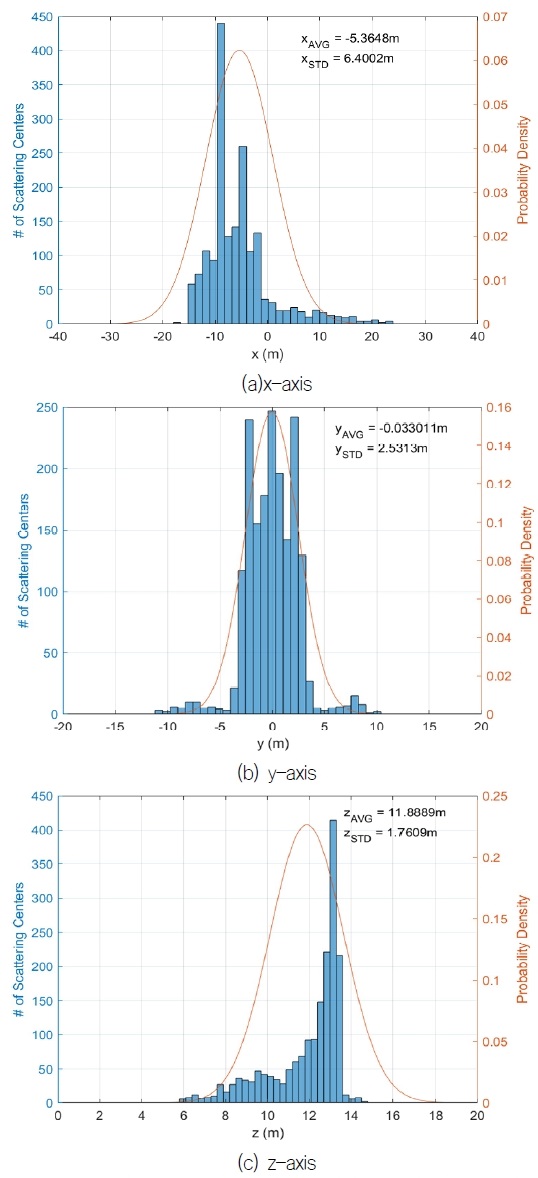
대상함정의 길이방향 분포를 살펴보기 위해 등가 산란중심의 길이방향 위치 데이터 , 폭방향 위치 데이터 및 높이방향 위치데이터 의 발생빈도와 그에 따른 확률밀도함수를 구하고 Fig. 11(a)-(c)에 함께 도시하였다. Fig. 11(a)에서 볼 수 있듯이, 대상 함 중앙부로부터 함미 방향으로 약 9m, 수선면으로부터 위로 약 13m 지점에서 등가 산란 중심의 발생 빈도가 가장 높게 나타났다. 확률 밀도 함수로는 정규분포를 적용했으며, 이때 평균값과 표준편차는 각각 함 길이 방향에 대해 –5.36m와6.40m로, 폭방향에 대해 –0.03m와 6.40m로, 깊이방향에 대해 11.89m와 1.76m로 산정되었다. 이는 확률적으로 대상 함정 중앙부로부터 함미 방향으로 5.36m와 우현 방향으로 0.03m, 수선면으로부터 위로 11.89m 지점이 대함미사일에 피격될 가능성이 가장 높은 위치임을 의미한다.
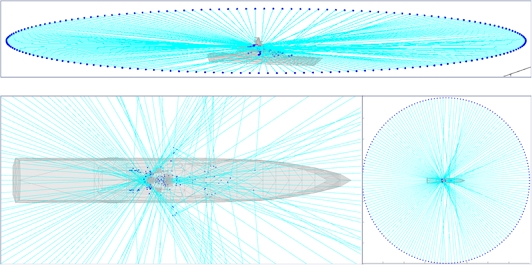
등가 RCS 산란중심 계산 결과와 대함미사일이 함정으로 접근하는 방위각을 고려하여 피격 경로를 Fig. 12에 보였다. 앞서 살펴본 바와 같이 대부분의 피격점은 마스트, 조타실 등 중앙부임을 확인할 수 있다. 이 결과는 함정의 취약성 해석, 분석 그리고 평가 과정에서 중요한 자료로 활용될 것으로 보인다.
5. 결 론
본 연구에서는 레이더 호밍 대함미사일의 함정으로의 접근방향에 따른 피격점을 추정하기 위한 등가 산란중심 산정기법을 제안하고 그 타당성과 실무적용성을 검토하였다. 이를 위해 고주파수 해석이론에 기반한 산란자의 RCS 해석방법과 이에 대응하는 산란중심 위치 추정방법을 정립하였다. 이로부터 대함미사일 접근 방향에 따른 등가 산란중심을 산정하고 피격점 분포 산정 방법을 제안하였다. 이를 바탕으로 함정 등가 산란중심 해석을 위한 소프트웨어 SCTracer/RCS를 개발하였다.
개발 소프트웨어의 타당성을 검토하기 위해 90m급 가상함정에 대한 수치해석을 수행하였다. 산란중심 분포 데이터로부터 복원한 대상함정 RCS를 기존 RCS해석결과와 비교해 그 신뢰성을 확인하였다. 또한, 대함미사일의 접근 방향에 따른 산란중심 분포 데이터로부터 산정한 등가 산란중심 위치, 즉 피격점을 발생빈도와 확률밀도함수로 분석해 실무적용성을 확인하였다.
함정의 RCS특성은 함의 외형에 매우 큰 영향을 받는 것으로 알려져 있다. 본 연구의 결과는 특정 함정에 국한 되어 있고, 탑재장비 등 복합형상들이 포함되어 있지 않다. 향후, 다양한 크기와 형상을 갖는 함정과 탑재 장비에 따른 영향성 연구가 필요하다. 또한, RCS는 대함미사일 접근 방향뿐 아니라 표적과의 거리에 따라 다르게 나타나므로 근거리장에서의 피격 위치 산정에 관한 연구가 필요하다.
Acknowledgments
It is noted that this paper is a revised edition based on the proceedings of Naval Ship Technology & Weapon Systems Seminar 2024 in Changwon.
본 과제(결과물)는 2023년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 지자체-대학 협력기반 지역혁신 사업의 결과입니다.(2023RIS-007). 본 연구는 부산광역시의 대학혁신연구단지조성사업 중 “동명대학교 대학혁신연구단지조성사업(IURP2401)” 지원으로 수행되었습니다.
References
-
Choi, W.S., Ruy, W.S., Lee, H.Y., Shin, Y.H., Chung, J.H. and Kim, E.Y., 2020. Development of a simplified formula for the damage radius of a naval ship due to an AIR EXplosion (AIREX). Journal of the Society of Naval Architects of Korea, 57(4), pp.207-212.
[https://doi.org/10.3744/SNAK.2020.57.4.207]

-
Jang, M.U., Myong, R.S., Jang, I.M. and Lee D.H. 2014. A hybrid RCS analysis code based on physical optics and geometrical optics. Journal of The Korean Society For Aeronautical and Space Sciences, 42(11), pp.958-967.
[https://doi.org/10.5139/JKSAS.2014.42.11.958]

-
Kim, K., Kim, J.H. and Cho, D.S. 2005a. RCS Analysis of complex structures using object precision method. Journal of the Society of Naval Architects of Korea, 42(2), pp.159-164.
[https://doi.org/10.3744/SNAK.2005.42.2.159]

-
Kim, K., Kim, J.H. and Cho, D.S. 2005b. A study on the effective scattering center analysis for radar cross section reduction of complex structures. Journal of the Society of Naval Architects of Korea, 42(4), pp.421-426.
[https://doi.org/10.3744/SNAK.2005.42.4.421]

-
Kim, K., Kim, J.H., Choi, T.M. and Cho, D.S. 2012. Development of radar cross section analysis system of naval ships. International Journal of Naval Architecture and Ocean Engineering, 4(1), pp.20-32.
[https://doi.org/10.2478/IJNAOE-2013-0075]

-
Kim, K.S., Hwang, S.Y. and Lee, J.H. 2014. Naval ship’s susceptibility assessment by the probabilistic density function. Journal of Computational Design and Engineering, 1(4), pp.266-271.
[https://doi.org/10.7315/JCDE.2014.026]

- Kim, K., Park, S.J. and Kim, E.Y. 2023. Estimation of anti-ship missile hit point considering the distribution of the RCS scattering center of the ship. 2023 Naval Ship Technology & Weapon System Seminar, 8-9 June 2023.
-
Knott, E.F., Shaeffer, J.F. and Tuley, M.T. 2004. Radar cross section, 2nd Edition. Artech House.
[https://doi.org/10.1049/SBRA026E]

-
Lee, G.H., Yoon, S.T. and Cho, Y.J. 2023. A feasibility study on the estimation of a ships susceptibility based on the effectiveness of its anti-air defense systems. Journal of the Society of Naval Architects of Korea, 60(1), pp.57-64.
[https://doi.org/10.3744/SNAK.2023.60.1.57]

- Yoon, S.T., Cho, Y.J. and Ko, D.E. 2017. A study on the diffuser design of exhaust pipes for the infra-red signature reduction of naval ship. Journal of the Korea Academia Industrial cooperation Society, 18(12), pp.793-798.
-
Wang, S.Y. and Jeng, S.K. 1997. A deterministic method for generating a scattering center model to reconstruct the RCS pattern of complex radar targets. IEEE Transactions on Antennas and Propagations, 39(4), pp.315-323.
[https://doi.org/10.1109/15.649821]