기계학습 모델을 활용한 선박 공칭반류장 예측
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this paper, we introduce the machine learning model to estimate the nominal wake field of a ship from the afterbody hullform using a 3 dimensional CNN (Convolutional Neural Network) model. The convolution layers extract the features of the hullform and they are connected to the nominal wake field. In this research, two different models were tested. The one learns the velocity field itself while the other learns the Fourier coefficients expressing the wake field. Both models showed about 4% volumetric mean velocity error for the test data not used in the learning process. In the case study of two sample ships included in the test data, the direct prediction model showed the better estimation results than the Fourier coefficient based model. Application cases for estimating cavitation performance using the developed model were also introduced.
Keywords:
Nominal wake field, Neural network, Propeller, Regression키워드:
공칭반류장, 신경망, 프로펠러, 회귀분석1. 서 론
프로펠러 설계 관점에서 볼 때, 선박에서 프로펠러가 작동하는 위치의 반류장(공칭반류장; nominal wake field)은 매우 중요하다. 평균 반류장(mean wake field)은 선박의 동력, 속력과 프로펠러 제원을 결정하는 데 영향을 미치며, 평균 반류에 대한 반류장의 변화는 프로펠러 날개 단면 설계와 국부 피치(local pitch) 결정에 크게 관련되어 있다 (Carlton, 2007). 또한 공칭반류장은 프로펠러의 캐비테이션 발생 가능성을 예측하는 데 필요한 입력 정보로 사용될 수 있으며, 공칭반류장의 조화해석(harmonic analysis)을 통해서 프로펠러 작동시 기진력을 예측할 수 있다. 이렇듯 공칭반류장의 분포는 선미 선형 개선 및 프로펠러 설계에 유용하게 활용될 수 있다.
현재 가장 신뢰도 높은 공칭반류장 예측은 모형시험을 이용한 방법이다. 선미 프로펠러 위치에 피토관이 부착된 반류 레이크(wake rake)를 이용해서 계측하거나 PIV(Particle Image Velocimetry), LDV(Laser Doppler Velocimetry) 등을 활용한 방법이 이용된다. 이러한 실험적 방법은 초기 선형 설계 단계 시 선형의 변화에 대한 대응이 어렵기 때문에 보통 최종 선형 결정 단계에서 사용할 수 있다. 다른 방법으로 CFD(Computational Fluid Dynamics)를 이용하는 방법으로 점성유동장 해석을 통해서 프로펠러 위치에서의 유동 분포를 얻어낼 수 있다. 하지만 CFD를 이용한 방법 역시 변화하는 선형에 따른 격자 생성 및 해석에 많은 자원과 시간을 요구한다. 최근 데이터 분석 기법의 발전으로 인하여 산업 전반에 걸쳐서 인공지능 및 기계학습 모델들이 데이터 분석을 통해 복잡한 비선형성 관계를 찾아내고 빠른 예측 결과를 줄 수 있다는 장점으로 인해 각광을 받고 있으며, 선박의 저항 추진 분야 역시 적극적인 활용을 위한 연구들이 진행되고 있다. 기존의 회귀분석에 의한 선박 성능 추정 (Holtrop, 1984; Holtrop and Mennen, 1978, 1982)에 기계학습 기법을 적용한 연구들(Bertram and Mesbahi, 2004; Cho et al., 2019; Kim et al., 2020; Kim et al., 2022; Kim et al., 2023)이 소개된 바 있으며, 정수중 성능 예측에서 나아가 파랑중 부가 저항을 예측하기 위한 기계학습 활용 연구들 (Cepowski, 2020; Martic et al., 2021, 2023)로 확장되고 있다. 또한, 유동장 예측 분야에서도 기계학습 모델의 활용이 시도되고 있으며, 활발한 연구가 진행되고 있다.
본 연구에서는 기계학습 기법을 활용하여 선형 정보로부터 공칭반류장을 예측하는 방법을 소개한다. 회귀식에 의한 평균 공칭반류계수의 추정은 Schoenherr (1939), Taylor (1933), Harvald (1977) 등에 의해서 제안된 바 있으며 반류장의 반경별 평균값의 추정은 전통적으로 Van Lammeren의 다이어그램 (Van Lammeren, 1942)이 사용되었다. 최근의 기계학습 기반 연구로는 2012년에 Kang (2012)이 선형 변수를 입력으로 구성한 인공 신경망을 활용하여 반류분포 예측을 소개한 바 있으며, Ichinose and Taniguchi (2022)는 CFD 계산 결과와 선체 표면 격자점을 이용하여 공칭반류장 예측 결과를 발표하였다. 최근에는 Lee and Lee (2023)가 유동조절핀(flow control fin)의 위치에 따른 선미 유동장 예측을 심층신경망과 전이 학습을 이용하여 시도한 바 있다. 그러나, 이 연구들은 CFD 해석 결과만을 활용한 한계가 있으며, 본 연구에서는 기존 연구와는 달리 실제 모형시험 결과와 선체 형상 정보를 합성곱 신경망을 활용하여 학습하여 공칭반류장을 예측하는 모델을 소개한다. 본 논문의 구성은 1장의 연구 배경 소개에 이어, 2장에서는 학습 모델에 대한 개요를 보이며, 3장과 4장에서는 학습에 사용된 데이터 및 학습 방법을 소개하고 학습 결과를 보인다. 마지막으로 예측 모델을 활용한 프로펠러 캐비테이션 예측 결과에 대한 case study를 소개한다.
2. 기계학습 모델 구성
2.1 공칭반류장
공칭반류장은 선박에서 프로펠러가 작동하지 않는 상태의 선미 프로펠러 위치에서의 속도분포를 의미한다. 프로펠러 평면으로 유입되는 유동이 프로펠러 단독상태와는 달리 선체의 형상에 의해 교란되고 점성 영향으로 발달하는 경계층 유동과 혼합된 복잡한 형태를 가지게 된다. 앞서 언급한 바와 같이 모형시험에서 공칭반류장을 계측하기 위해서는 보통 다수의 피토관으로 구성된 반류 레이크를 선미 프로펠러 평면에 설치하고 다수의 각도에서 속도를 계측하여 원형 평면에서의 속도분포를 얻어낸다. 선박해양플랜트연구소(KRISO)의 반류 레이크(Fig. 1)는 반경 방향으로 총 5개의 점에서 0도에서 360도까지 측정을 실시한다. 본 연구에서는 반경 방향 5개, 원주 방향 21개(0도-180도, 대칭 고려) 지점에서의 선속으로 무차원화된 축 방향 속도(Vx) 계측 결과를 이용하여 학습을 진행하였다. 반경 및 회전 방향 속도는 프로펠러의 추력에 대한 기여가 크지 않기 때문에 고려하지 않았다.
2.2 학습 모델
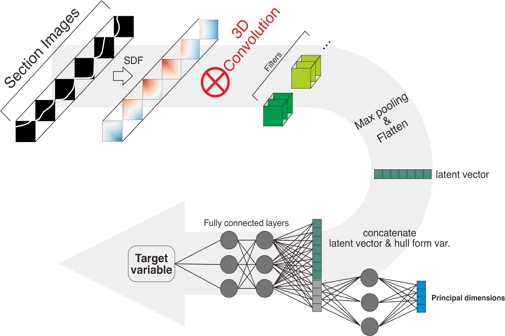
학습 모델은 총 2개로 하나는 공칭반류장의 속도분포를 그대로 학습하는 모델과 공칭반류장을 조화해석(harmonic analysis)하여 얻어진 푸리에(Fourier) 계수를 학습하는 모델이다. 입력 변수는 선미 12개 스테이션의 무차원화된 선체 형상이 사용되었으며 각 단면은 폭과 흘수로 무차원화되어 있는 정보이기 때문에 실제 선체 형상 정보를 표현하기 위하여 길이-폭비(L/B), 폭-흘수비(B/T), 방형계수(CB)가 추가로 사용되었다. 선미 선체 형상을 입력으로 고려하기 위하여 Kim et al. (2023)이 사용한 선체 형상을 이미지로 변환하여 합성곱 신경망 모델에 적용하는 방법을 사용하였다. 자세한 방법에 대한 소개는 본 논문에서는 생략한다. 본 모델에서, 96x96 픽셀 이미지 텐서 형태(96x96x12)로 입력된 선체 형상(선미 12개 스테이션)은 복수의 3차원 합성곱 층(convolution layer)을 통과한 후에 1차원 텐서 형태로 만들어 선형의 특성 정보(latent vector)를 갖게 되며, 한 개의 완전 연결층(fully connected layer)을 통과한 선형 변수(principal variables)와 결합(concatenate)된다. 이렇게 결합된 1차원 텐서는 복수의 완전연결층을 거쳐서 최종 학습 목표인 반류장 데이터에 연결되는 형태를 갖는다(Fig. 2).
반류장 데이터는 속도분포를 그대로 학습하는 모델의 경우 반경 방향 5개, 원주 방향 21로 구성된 105개의 위치에서의 속도값이 되며, 푸리에 계수를 학습하는 모델의 경우 푸리에 차수를 n이라 할 때, 반경 방향 5개, 푸리에 계수 (n+1)개가 되어 총 5x(n+1)개의 푸리에 계수가 반류장을 표현하는 데이터의 개수가 된다. 통상적인 단축 추진 상선의 경우로 고려하여 공칭반류장은 좌우 대칭을 가정하였고, 푸리에 코사인 시리즈로 표현하였다.
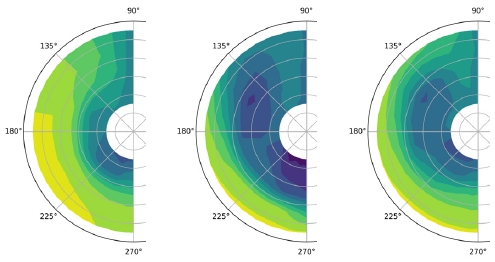
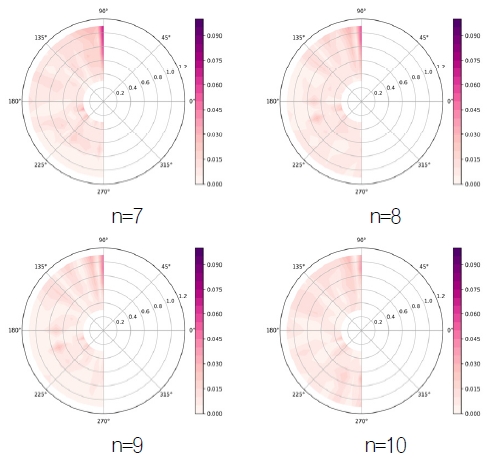
공칭반류장을 표현하기 위한 적절한 푸리에 차수를 정하기 위해서 최고 차수 7, 8, 9, 10의 푸리에 시리즈 변환에 대하여 샘플 데이터 3개를 선정하여 비교를 수행하였다. Fig. 3은 선정된 샘플의 공칭반류장을 보인다.
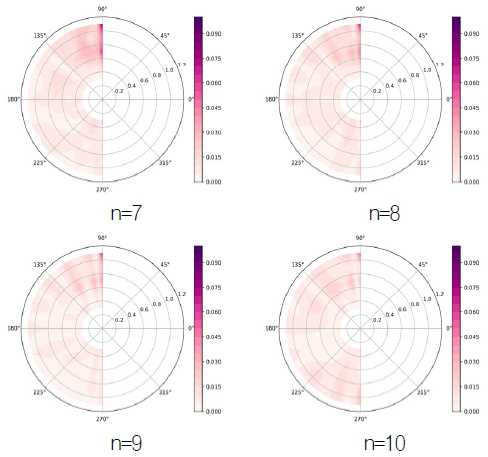
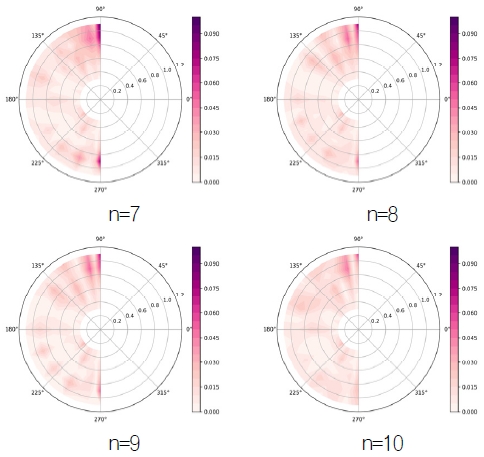
Fig. 4, 5, 6은 각각 선정된 샘플에 대한 공칭반류장을 푸리에 차수 7, 8, 9, 10으로 나타내고, 이를 재 복원하여 공칭반류장과의 절대오차를 도시한 것이다. 차수 7인 경우 12시 방향의 오차가 대체로 크게 나타났으며, 8차 이상인 경우는 유사한 결과를 보였다. 본 연구에서는 샘플 결과를 바탕으로 푸리에 차수를 9로 설정하여 학습 모델의 출력단의 개수는 50개가 된다.
3. 데이터 구성 및 학습 방법
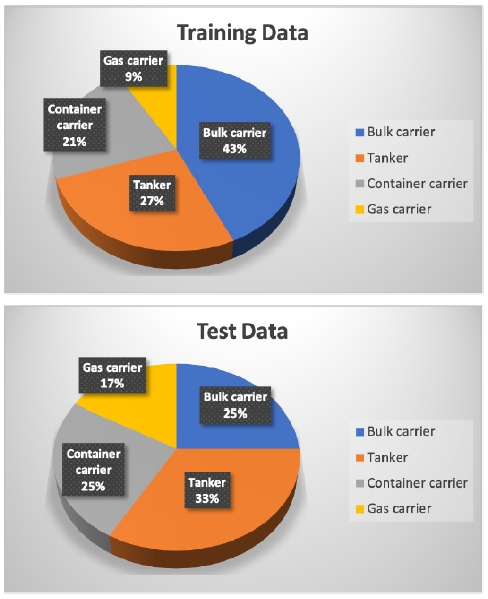
학습에 사용된 데이터는 KRISO의 반류장 시험 데이터가 존재하는 단축 선형중에 선형 정보 데이터베이스화가 완료된 선형의 설계흘수(design draft)에서의 공칭반류장이 사용되었다. 선종은 벌크선, 탱커, 컨테이너선, 가스운반선이 포함되어 있고, 모형 프로펠러의 크기가 기준 크기(0.25m)와 달라서 공칭반류장의 측정 위치가 상이한 선형들은 제외되었다. 최종적으로 사용된 데이터는 총 117개 선형의 공칭반류장으로 이 중, 93개가 훈련데이터(training data)로, 24개가 평가데이터(test data)로 사용되었다. 각 데이터에 속해있는 선종의 분포는 Fig. 7과 같다. 각 선종은 대체로 골고루 분포되어 있는 것으로 확인된다. 입력값으로 사용된 선형변수들과 출력 변수인 공칭반류장, 이를 표현하기 위한 푸리에 계수들은 학습의 효율을 높이기 위하여 정규화 과정(standard scaling)을 수행하여 평균 0, 표준편차 1을 갖도록 변형하였다.
합성곱 신경망 층, 완전연결층의 수 및 각 층의 노드 수를 결정하기 위하여 그리드 탐색(grid search) 방법을 사용하였다. 과적합을 방지하기 위해 흔히 사용되는 드롭아웃은 전체 데이터 규모가 크지 않을 경우 오히려 더 좋지 않은 학습 결과를 줄 수 있기 때문에 사용하지 않았고, 일부 완전 연결층에서 L2 규제(L2 regularization)를 적용하였다. 각 층의 활성화 함수(activation function)는 ReLU를 적용하였고, 마지막 출력층에서는 선형 함수를 적용하였다. 그리드 탐색을 수행할 때, 훈련 데이터를 3개의 폴드로 나누고, 각 폴드의 검증 결과를 평균한 값을 모델의 훈련 결과로 해서 비교하였다. 그리드 탐색시에는 총 에포크(epoch)를 200으로 설정하고 훈련 점수가 높은 6개의 모델을 선정한 후, 각각의 모델로 훈련 데이터 전체를 학습한 후, 가장 좋은 결과를 보이는 모델을 최종 모델로 선정하였다. 최종 모델 선정을 위한 학습 과정에서는 충분한 에포크를 설정하고 조기 종료(early stopping)를 적용하였다. 그리드 탐색에 사용된 신경망층은 Kim et al. (2023)이 반류계수 예측을 위해 사용했던 것과 비슷한 수준으로 정하였으며 3개의 합성곱층 [8-8-4, 16-8-4, 64-64-32], 3개의 선형변수 완전연결층 [8, 16, 32], 결합층에 사용되는 2개의 완전연결층 [64-64, 32-32]이 사용되어 총 18개의 모델을 테스트하였다. 학습률(learning rate)은 0.005가 사용되었고, 손실함수(MSE: Mean Squared Error)를 최소화 하기 위한 최적화 기법(optimizer)으로는 RMSprop (Ruder, 2016)을 사용하였다. 또한, Keras의 함수형 API를 사용하여 다중 입력(선형 단면 이미지, 선형변수)-다중 출력(공칭반류장 혹은 푸리에계수) 모델을 만들고 학습을 진행하였다.
4. 학습 결과
18개의 테스트 모델의 학습 결과 가장 좋은 성적을 보여주는 6개 모델을 선정하고, 훈련 데이터 전체에 대하여 학습을 진행하였다. 얻어진 예측 모델의 평가는 예측된 공칭반류장을 이용하여 체적 평균값(volumetric mean)을 계산하여 모형시험 결과로부터 얻어진 체적 평균값과의 오차를 기준으로 하였다. 즉, 학습에 사용되지 않은 평가데이터에 대하여 공칭반류장 예측을 수행하고 모형시험의 체적 평균속도와의 평균 절대 오차(mean absolute percentage error)를 계산하여 오차율이 작은 모델을 최종 예측 모델로 선정하였다.
4.1 반류장 직접 학습
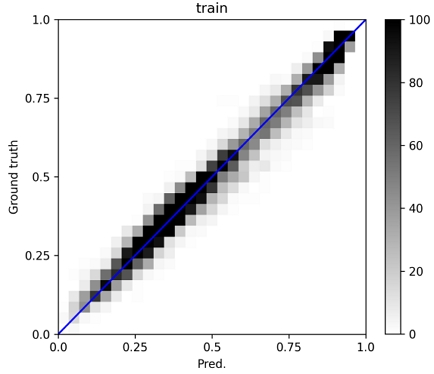
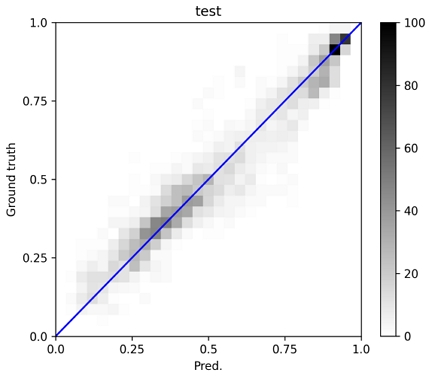
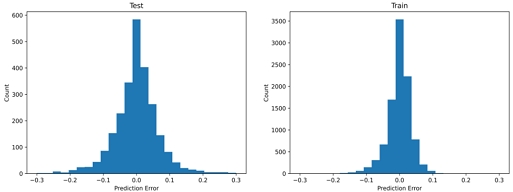
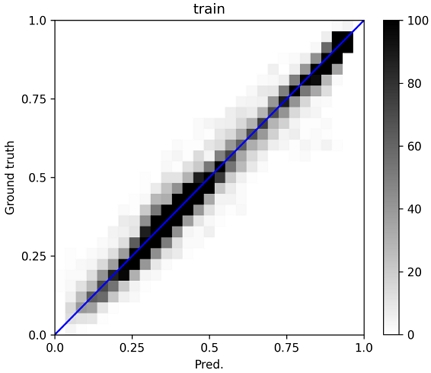
그리드 탐색으로 선정된 최종 예측 모델은 [16-8-4]의 3차원 합성곱 층과 [16]의 선형 정보 완전연결층, [64-64]의 결합층으로 구성된 모델이다. 출력층은 총 105개의 위치에서의 반류장 속도 값이 된다. Fig. 8과 9는 각각 훈련데이터와 평가데이터에 대한 예측값(x축)과 실험값(y축)을 도시한 것으로 0부터 1사이를 30등분한 셀 안에 해당하는 데이터의 수를 명암으로 표시한 것이다. 대부분의 예측 결과가 대각선상에 위치하는 것을 확인할 수 있다. 학습 결과 훈련데이터에 대한 R2는 약 0.98, 평가데이터에 대한 R2는 약 0.93이다. 체적 평균속도에 대한 평균 절대 오차율은 훈련데이터가 약 1.88%, 평가데이터가 약 3.73%로 계산되었다. Fig. 10은 평가 및 훈련데이터에 대한 예측 오차 히스토그램을 보인다.
4.2 푸리에 계수 학습
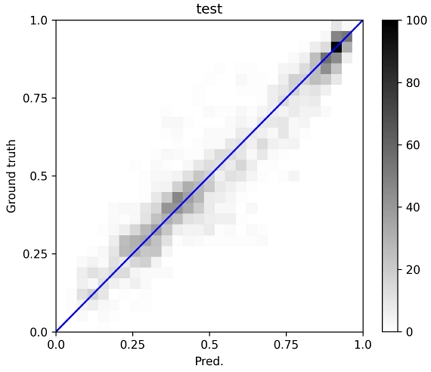
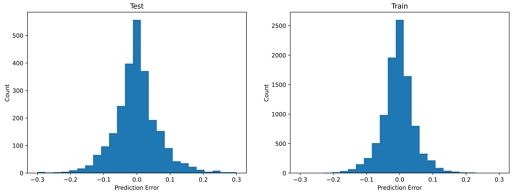
그리드 탐색으로 선정된 최종 예측 모델은 [8-8-4]의 3차원 합성곱 층과 [32]의 선형 정보 완전연결층, [32-32]의 결합층으로 구성된 모델이다. 출력층은 총 50개의 푸리에 계수가 되며, 결과에 대한 평가는 예측된 푸리에 계수를 이용하여 속도장을 재구성한 후 비교를 통해서 수행되었다. Fig. 11, 12는 각각 훈련데이터와 평가데이터에 대한 예측 결과를 보인다. 대체적으로 반류장 직접 예측 모델과 유사한 수준의 예측 결과를 보이나 훈련데이터에 대한 예측 정도는 다소 떨어지는 모습을 보인다. 학습 결과 훈련데이터에 대한 R2는 약 0.96, 평가데이터에 대한 R2는 약 0.92이다. 체적 평균속도에 대한 평균 절대 오차율은 훈련데이터가 약 4.13%, 평가데이터가 약 3.71%로 계산되었다. Fig. 13은 평가 및 훈련데이터에 대한 예측 오차 히스토그램을 보인다.
4.3 샘플 테스트 결과
평가데이터에 속한 컨테이너선과 벌크선 각 1척에 대하여 본 연구의 예측 모델을 활용하여 공칭반류장을 예측한 결과를 살펴보면, Fig. 14와 15는 공칭반류장 직접 학습 모델로 예측된 샘플 컨테이너선, 벌크선의 공칭반류장과 실험 결과 비교를 보인다. 좌측이 예측모델에 의한 결과이며 우측이 모형시험 결과이다. 컨테이너 샘플의 경우 180도 부근의 저속 영역 예측이 부족한 모습을 보이며, 벌크 샘플의 경우는 매우 좋은 예측 결과를 보인다.
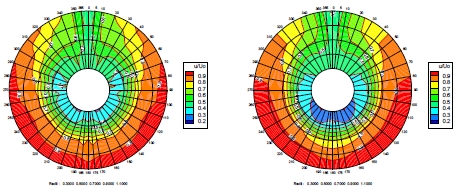
Nominal wake field comparison of the sample container carrier (direct prediction model, left: Pred., right: Exp.)
Nominal wake field comparison of the sample bulk carrier (direct prediction model, left: Pred., right: Exp.)
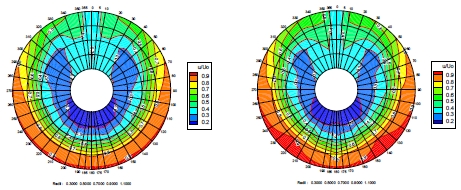
Fig. 16과 17은 각 샘플 선형의 푸리에 계수 학습 모델에 의한 공칭반류장 비교를 보인다. 푸리에 계수 학습 모델 쪽이 직접 학습 모델에 비해 조금 더 완만한 변화의 윤곽선을 보이는 경향이 있다. 고차 진동 성분의 계수 예측 정도가 다소 낮아 보이는 현상으로 생각된다. 벌크선 샘플의 경우, 반류장 분포 내에서 갈고리 모양(hook shape)의 저속 영역에 대한 과소평가가 관측되었다.
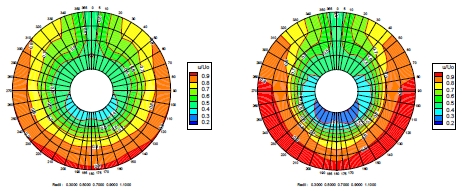
Nominal wake field comparison of the sample container carrier (Fourier coeff. prediction model, left: Pred., right: Exp.)
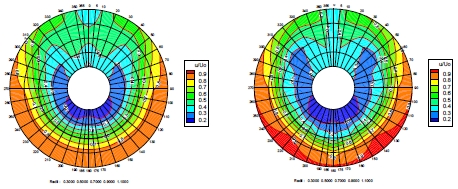
Nominal wake field comparison of the sample bulk carrier (Fourier coeff. prediction model, left: Pred., right: Exp.)
Fig. 18은 직접 학습 모델로 예측된 반경별 평균속도 분포를 비교한 그림이다. 원형 기호가 예측된 값을 나타내며, x 기호가 모형시험의 값을 표시한다. 컨테이너선의 경우 프로펠러 뿌리 근처의 속도 오차가 다소 관찰된다. 무차원 반경(r/R) 0.3에서 1.0 사이의 체적 평균 오차율은 컨테이너 샘플이 약 1.6%, 벌크선 샘플이 약 5.9%로 계산되었다. 벌크선의 경우 전체적인 속도장이 저속 영역이라서 오차율 계산의 기준이 되는 값이 작아서 오차율이 더 크게 계산된 경향이 있다.
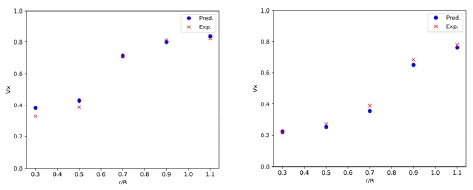
Radial mean velocity distribution from the direct prediction model (left: container carrier, right: bulk carrier)
Fig. 19는 푸리에 계수 학습 모델로 예측된 반경별 평균속도 분포를 보인다. 공칭반류장 직접 예측 모델 대비 다소 큰 오차를 보여준다. 체적 평균 오차율은 컨테이너 샘플이 약 2.4%, 벌크선 샘플이 약 8.9%로 수치에서도 확인할 수 있다.
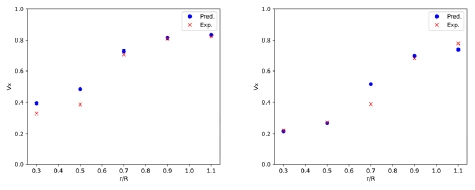
Radial mean velocity distribution from the Fourier coeff. prediction model (left: container carrier, right: bulk carrier)
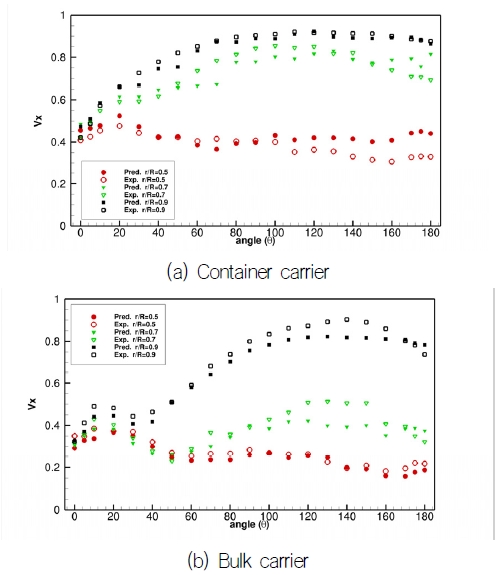
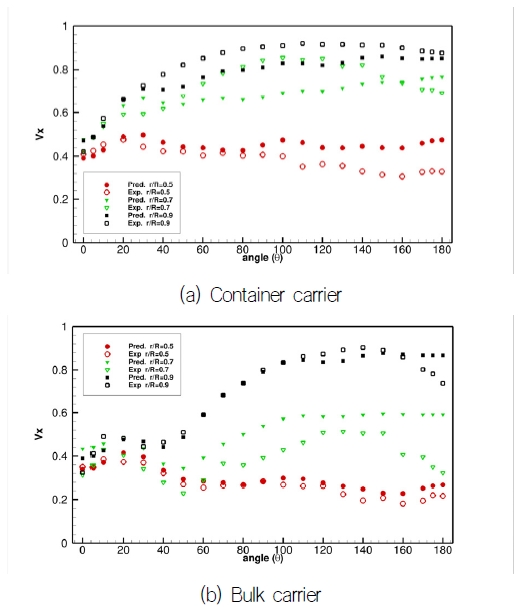
Fig. 20, 21은 각각 직접학습 모델과 푸리에 계수 학습 모델로 얻어진 샘플 선형에 대한 무차원반경 0.5, 0.7, 0.9에서의 속도 분포를 비교한 그림이다. 직접학습 모델 쪽이 반경별 속도 분포를 더 잘 예측하고 있음을 확인할 수 있다.
훈련데이터와 평가데이터에 대한 예측 결과, 샘플 선형들에 대한 개별 예측 결과를 종합해 볼 때, 본 연구에서 생성된 모델중 푸리에 계수 학습 모델보다 직접학습 모델이 더 나은 예측도를 보여줌을 확인할 수 있다.
5. 활용 예
본 연구에서 생성된 예측 모델을 활용하여 프로펠러의 캐비테이션 예측에 적용한 예를 보인다. 대상선은 앞서 선정한 샘플 컨테이너선과 벌크선을 사용하였으며, 각각의 반류 환경에서 캐비테이션 해석을 수행하였다. 수치계산에는 양력면이론(Kerwin and Lee, 1987)을 적용한 캐비테이션 성능 추정 프로그램을 이용하였다. 본 연구에서는 반류분포 변화에 따른 자항점의 변화를 수치적으로 예측하기 어려운 점이 있고, 반류분포 변화에 따른 캐비테이션 발생량의 상대적인 변화만을 조사하기 위한 제한된 목적이기 때문에 해석시 프로펠러 작동조건의 전진비(Ja)를 고정하여 수행되었다. 각 선형의 프로펠러의 주요 제원과 수치해석 조건은 Table 1과 같다. 캐비테이션 성능 추정 해석은 모형시험 반류, 직접학습 모델 예측 반류, 푸리에 계수 학습 모델 예측 반류 입력으로 수행되었다.
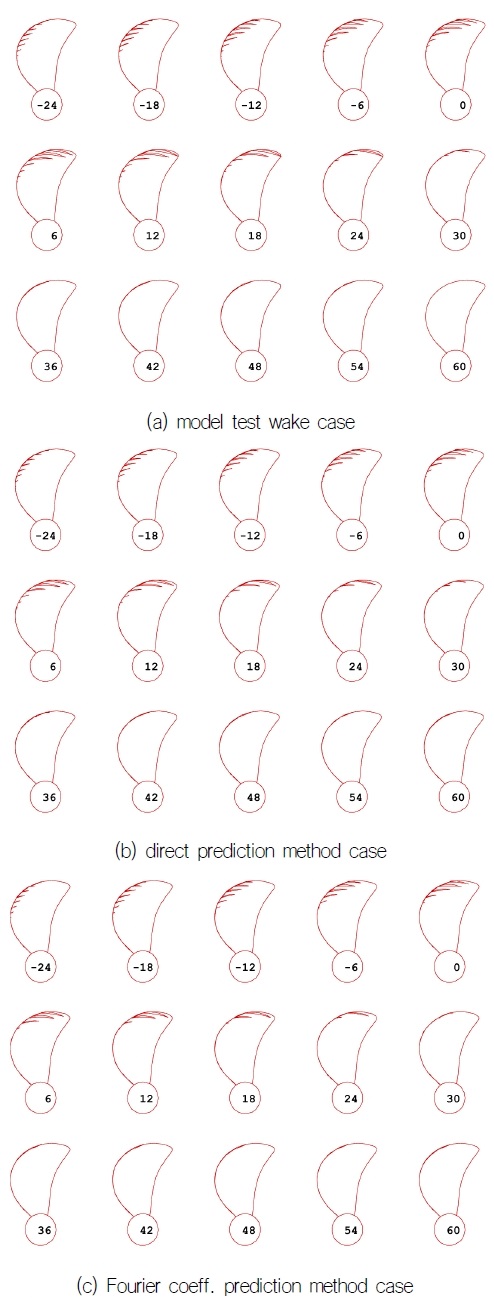
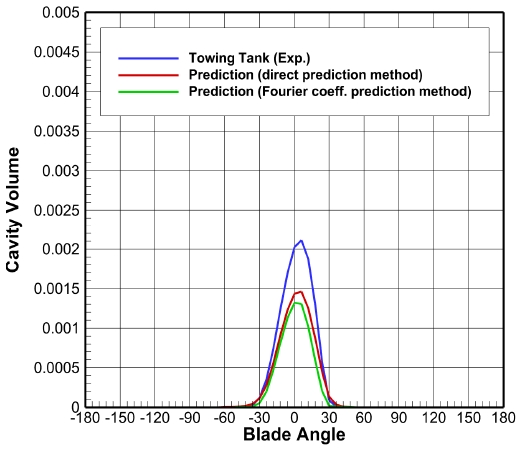
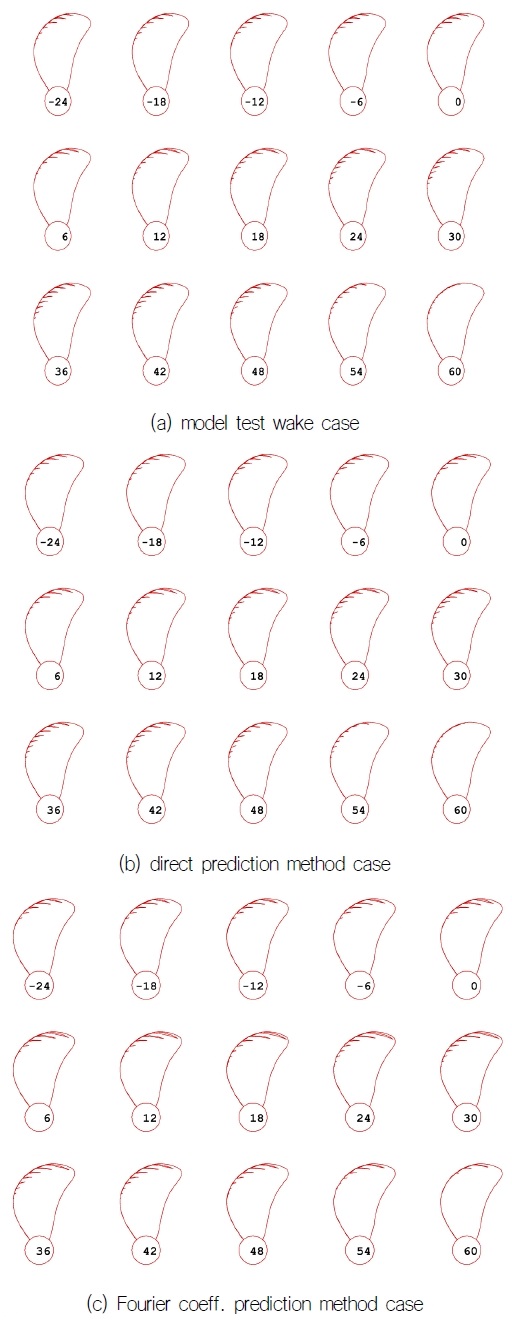
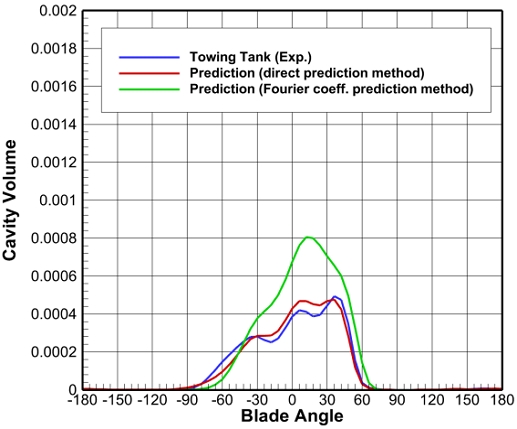
Fig. 22는 샘플 컨테이너선의 캐비테이션 해석을 통해 얻어진 –24도에서 60도 사이의 캐비테이션 패턴을 비교한 그림이다. 전반적으로 예측 모델의 반류장에서 얻어진 캐비테이션이 모형시험 결과에 비해 다소 과소평가되는 것을 확인할 수 있다(6도, 12도 등). Fig. 23의 캐비티 체적(cavity volume) 비교에서도 확인할 수 있다.
Fig. 24와 25는 샘플 벌크선의 반류장을 입력으로 얻어진 캐비테이션 패턴과 캐비티 체적을 비교한 그림이다. 푸리에 계수 학습 모델의 경우 캐비테이션을 과대평가하는 결과를 보이고 있으나, 직접 학습 모델의 경우 반류장 비교 결과(Fig. 15)에서 예상할 수 있듯이 모형시험 결과를 입력으로 예측된 결과와 상당히 유사한 결과를 보이고 있다. 푸리에 계수 학습 모델의 경우, 체적 평균 속도가 가장 큰 값을 보여주었고, 이는 Ja를 고정하였을 경우, 상대적으로 가장 작은 선체 전진비(Js) 조건이 되기 때문에 큰 공동 체적 예측 결과를 보이는 것으로 판단된다. 공동 체적의 양상도 푸리에 계수 학습 모델이 모형시험 결과와 차이를 보이는 것은 반류장 분포 예측의 차이가 큰 것에서 기인한다.
6. 결 론
본 연구에서는 기계학습 기법 중의 하나인 3차원 합성곱 신경망을 이용하여 선체의 선미 형상의 특성을 추출하고 모형시험에서 얻어진 반류장 정보를 학습하여 선체 형상이 주어질 경우 반류장을 예측하는 기계학습 모델을 소개하였다. 학습 모델은 선미 형상 정보(오프셋)로부터 특성을 얻어내는 합성곱 층과 이를 반류장에 연결하는 완전연결층의 결합으로 구성되었으며, 반류장 정보는 각 위치에서의 선속으로 무차원화 된 축 방향 속도를 그대로 학습하는 모델과 반류장을 나타내는 푸리에 계수를 학습하는 모델이 검토되었으며, 학습 결과 속도장을 직접 학습하는 모델의 예측 정도가 더 좋은 것으로 나타났다. 두 모델 모두 학습에 사용되지 않은 평가 데이터에 대하여 체적 평균속도의 오차율이 약 4%로 유사한 수준으로 나타났으나, 훈련데이터와 개별 샘플에 대한 속도장 예측 정도는 속도장 직접 학습 모델의 결과가 더 우수한 결과를 보였다. 다만 푸리에 계수 학습 모델의 경우는, 출력층의 수가 푸리에 차수에 의해 결정되기 때문에 CFD의 결과로 얻어지는 촘촘한 반류장에 적용할 경우 장점을 가질 수 있을 것으로 판단된다. 이러한 경우, 푸리에 계수 학습 모델에 더 적합한 모델 구성에 대한 연구가 필요할 것으로 판단된다. 본 연구에서 제안된 예측 모델은 선체의 형상이 주어질 경우, 공칭 반류장을 예측하고 이를 이용하여 프로펠러 캐비테이션을 예측하는 과정에도 활용될 수 있을 것으로 기대한다. 다만, 예측 모델의 정도 향상을 위해서는 더 많은 데이터의 확보가 필요하다. 모형시험 계측 결과를 활용할 때, 모형 프로펠러의 직경이 달라질 경우, 동일 위치에서의 직접적인 반류장 데이터 확보가 쉽지 않기 때문에 CFD 등을 활용한 데이터 확충이 필요할 것으로 생각된다. 향후, 선형 정보와 반류장 정보를 결합하여, 선형 생성 등에 활용할 수 있는 심층 생성 신경망(deep generative model)으로의 기계학습 기법 연구도 필요할 것으로 보인다.
Acknowledgments
본 논문은 선박해양플랜트연구소 주요사업 “극한환경상태의 선박성능 평가기술 개발(PES5090, 2520000278)” 및 “디지털 플랫폼 활용 선박 성능 추정 기술 개발(PES5220, 2520000291)”로 수행된 결과입니다.
References
- Bertram, V. and Mesbahi, E. 2004. Estimating resistance and power of fast monohulls employing artificial neural nets. Proceedings of the International Conference High Performance Marine Vehicles, Rome, Italy, 27–29 September 2004.
-
Carlton, J., 2007. Marine propellers and propulsions. Butterworth-Heinemann.
[https://doi.org/10.1016/B978-075068150-6/50012-7]

-
Cepowski, T. 2020. The prediction of ship added resistance at the preliminary design stage by the use of an artificial neural network. Ocean Engineering, 195, 106657.
[https://doi.org/10.1016/j.oceaneng.2019.106657]

-
Cho, Y.I., Oh, M.J., Seok, Y.S., Lee, S.J. and Roh, M.I., 2019. Resistance estimation of a ship in the initial hull design using deep learning. Korean Journal of Computational Design and Engineering, 24(2), pp.203-210.
[https://doi.org/10.7315/CDE.2019.203]

-
Harvald, Sv. Aa., 1977. Estimation of power of ships. ISP.
[https://doi.org/10.3233/ISP-1978-2528302]

- Holtrop, J., 1984. A statistical re-analysis of resistance and propulsion data. International Shipbuilding Progress, 31, pp.272-276.
-
Holtrop, J. and Mennen, G.G.J., 1978. A statistical power prediction method. International Shipbuilding Progress, 25, pp.253.
[https://doi.org/10.3233/ISP-1978-2529001]

-
Holtrop, J. and Mennen, G.G.J., 1982. An approximate power prediction method. International Shipbuilding Progress, 29, pp.166-170.
[https://doi.org/10.3233/ISP-1982-2933501]

- Kang, S., 2012. A study of hull form design and performance prediction using neural networks. KIIS fall conference, 22(2), pp.61-64.
- Kerwin, J.E., Lee, C.-S., 1987. Prediction of steady and unsteady marine propeller performance by numerical lifting surface theory. Trans. SNAME, 86, pp.218-258.
-
Kim, Y.C., Kim, K.S., Hwang, S.H., and Yeon, S., 2022. Prediction of residual resistance coefficient of ships using convolutional neural network. Journal of the Society of Naval Architects of Korea, 59(4), pp.243-250.
[https://doi.org/10.3744/SNAK.2022.59.4.243]

-
Kim, Y.C., Kim, K.S., Yeon, S., Lee, Y.Y., Kim, G.D. and Kim, M.S., 2023. Power prediction method for ships using data regression models. Journal of Marine Science and Engineering, 11, 1961.
[https://doi.org/10.3390/jmse11101961]

-
Kim, Y.C., Yang, K.K., Kim, M.S., Lee, Y.Y. and Kim, K.S., 2020. Prediction of residual resistance coefficient of low-speed full ships using hull form variables and machine learning approaches. Journal of the Society of Naval Architects of Korea, 57(6), pp.311-321.
[https://doi.org/10.3744/SNAK.2020.57.6.312]

- Lammeren, W.P.A. van, Troost, L. and Koning, J.G., 1942. Weerstand en voortsluwing van schepen. R-1.
-
Martić, I., Degiuli, N. and Grlj, C.G., 2023. Prediction of added resistance of container ships in regular head waves using an artificial neural network. Journal of Marine Science and Engineering, 11, 1293.
[https://doi.org/10.3390/jmse11071293]

-
Martić, I., Degiuli, N., Majetić, D. and Farkas, A., 2021. Artificial neural network model for the evaluation of added resistance of container ships in head waves. Journal of Marine Science and Engineering, 9, 826.
[https://doi.org/10.3390/jmse9080826]

- Ruder, S., 2016. An overview of gradient descent optimization algorithms. arXiv:1609.04747, .
- Schoenherr, K.E., 1939. Propulsion and propellers. principles of naval architecture, 2, The Society of Naval Archtects and Marine Engineers.
- Taylor, D.W., 1933. Speed and power of ships. John Wiley & Sons, Inc.