슬로싱이 멤브레인 타입 LNG 화물창의 수직벽면 열전달계수에 미치는 영향
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
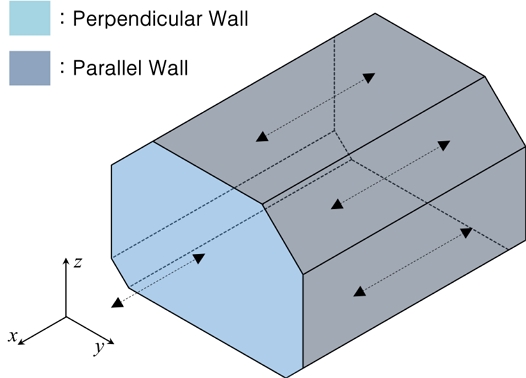
In this study, sloshing effects on the heat transfer coefficient of the vertical walls in a membrane type LNG cargo containment system (CCS) were analyzed. To develop correlations of the heat transfer coefficient incorporating sloshing effects, experiments were conducted to measure the heat transfer coefficient of an oscillating vertical plate. Based on experiments, two different correlations were developed which are each applicable to vertical and horizontal oscillations. Using the developed correlations, the heat flow rate penetrated into the vertical walls in KC-1 CCS was investigated under sloshing conditions. The results showed that the penetrated heat flow rate increases with the sloshing speed, which is defined as the product of the sloshing amplitude and the frequency. The maximum increase ratio of the heat flow rate was found to be about 7.5% at the sloshing speed of 10m/s. Also, it was found that the penetrated heat flow rate more increases when the CCS oscillates in the perpendicular direction to the vertical walls, than the parallel direction to the vertical walls. This study suggests that the increase in wall heat transfer coefficients has to be considered when evaluating the boil-off rate of CCSs that are shaking due to sloshing.
Keywords:
LNG cargo containment system, Boil-off rate, Sloshing effect, Heat penetration, Mixed convection키워드:
액화 천연가스 화물창, 자연 기화율, 슬로싱 효과, 열 침입, 혼합대류1. 서 론
Liquefied Natural Gas (LNG) 화물창의 Boil-Off Rate (BOR)은 열 침입에 의해 하루 동안 증발되어 소실되는 LNG 양의 비율로, LNG 운송사업의 경제성을 결정하는 주요한 변수이다. 따라서 운송선을 운용하는 기업들은 지금까지 누적된 운송 데이터와 이론 모델을 기반으로 운송 중 화물창의 열 침입량을 계산하고, 이에 기반하여 BOR을 예측하고 있다. 하지만 BOR 예측을 위한 이론 모델이 아직 정립되지 않은 영역이 있는데, 바로 슬로싱 환경에 노출된 화물창의 BOR을 예측하는 경우이다.
LNG선이 선적 혹은 양하를 위해 인수기지에 정박하면, 화물창은 파력에 의해 일정한 주기로 흔들리는 슬로싱 상황에 노출된다. 이러한 슬로싱이 화물창의 BOR을 증가시킨다는 사실은 널리 알려져 있지만, 어떠한 메커니즘에 의해 BOR이 증가하는지는 아직 명확히 규명된 바 없다. 따라서 연구자들은 실험과 전산 해석을 통해 슬로싱이 BOR을 증가시키는 원인에 대해 분석하였고, 다양한 메커니즘을 그 원인으로써 제시하였다. (Park and Hwang, 2023)은 슬로싱에 의해 화물창 내부에 액적 분열이 발생하고, 이러한 액적 분열이 액체연료의 기화/증발률을 증가시킨다고 주장하였고, (Lee et al., 2022)는 슬로싱이 발생하면 기체 및 액체연료 사이 계면이 깨지며 상대적으로 온도가 높은 기체연료로부터 액체연료로의 열전달이 촉진되어 BOR이 증가한다고 언급하였다. 이와는 다른 관점으로, (Lee et al., 2020)은 슬로싱이 발생하면 액체연료와 화물창 내벽 사이의 접촉 면적이 증가하게 되고, 이로 인해 화물창 열 침입량이 증가하여 BOR이 증가한다고 주장하였고, (Jung, 2023)은 액체연료의 접촉 면적 증가보다는 기체연료와 맞닿아 있던 높은 온도의 화물창 내벽에 상대적으로 온도가 낮은 액체연료가 접촉하는 것이 BOR 증가의 주요 원인이라고 주장하였다. (Jeon, 2021)은 슬로싱에 의해 화물창 내부 압력이 순간적으로 감소할 때가 있는데, 이때 액체연료의 끓는점이 낮아져서 기화/증발률이 증가하는 것이 BOR 증가의 원인이 될 수도 있다고 언급하였다.
이처럼 기존 연구자들은 화물창의 BOR 증가 원인으로 다양한 메커니즘을 제시했지만, 아직까지 슬로싱에 의한 화물창 내/외벽 열전달계수의 증가를 BOR의 증가 원인으로 지목한 연구자는 없었다. 대류열전달의 특성 상, 슬로싱에 의해 화물창이 흔들리게 되면 화물창 내/외벽에 추가적인 유동이 발생하면서 필연적으로 벽면 열전달계수가 증가하게 되는데, 이는 화물창의 열 침입량을 증가시켜 BOR 증가로 이어진다. 따라서 본 연구에서는 슬로싱이 화물창 벽면의 열전달계수에 미치는 영향에 대해 분석하고, 과연 이러한 영향이 LNG 화물창의 열 침입량을 얼마나 증가시킬 것인지 정량적으로 확인하고자 한다.
일반적으로 화물창 설계에 사용되는 모델은 자연대류 열전달 모델이며, 식 (1)과 같은 Nu 수에 대한 Gr과 Pr 수의 상관식 형태를 띠고 있다. 여기서 상수 a와 b는 중력 방향에 대한 화물창 벽면의 각도에 의해 결정되며, 그 값은 (Churchill and Chu, 1975)에서 확인할 수 있다.
| (1) |
식 (1)에서 Pr 수는 화물창 벽면 부근의 유체 물성치이며, Nuw 수는 화물창 벽면의 열전달계수 (hw)에 의해, Grw 수는 화물창 벽면과 유체 사이의 온도 차이 (Tf - Tw)에 의해 결정되는 무차원 수이다.
| (2) |
| (3) |
식 (2) ~ (3)에서 βf, νf, kf는 각각 유체의 팽창계수, 동점도, 열전도율을 의미하며, g는 중력가속도, Lc는 화물창 벽면의 특성 길이 (Characteristic Length)를 의미한다. 화물창의 벽면 온도가 주변 유체의 온도보다 높거나 낮아지게 되면 밀도 차이에 의한 유동이 발생하는데, 이 유동의 크기를 Gr 수로, 유동에 의해 발생하는 열전달의 정도를 Nu 수로 파악할 수 있다.
식 (1)의 꼴을 가진 자연대류 열전달 모델은 지금까지 다양한 실험 데이터들을 통해 보정되어 왔기 때문에 높은 정확도를 보인다. 하지만, 이는 정지된 화물창에 대해 국한되며, 파력에 의해 화물창이 전후좌우, 혹은 중심축으로 기준으로 회전하는 슬로싱이 발생하면 그 정확도가 매우 떨어지게 된다. 이는 슬로싱에 의한 유동이 기존에 존재하던 밀도 차이 유동에 더해지기 때문이다. 이 때, 밀도 차이 유동에 의한 열전달은 자연대류 열전달, 슬로싱 유동에 의한 열전달은 강제대류 열전달이라고 정의될 수 있다. 따라서, 슬로싱 환경에 놓인 화물창 벽면에서 발생하는 열전달은 이 두 가지 타입의 열전달이 복합적으로 발생하는 혼합대류 열전달로 정의할 수 있으며, 이러한 상황에서의 벽면 열전달계수를 예측하기 위해서는 기존의 자연대류 열전달 모델이 아닌 혼합대류 열전달 모델이 새롭게 필요하다.
화물창 벽면 설계에 사용 가능한 혼합대류 열전달 모델을 개발하기 위해서는 슬로싱에 의해 공급되는 유동의 크기를 나타낼 수 있는 변수가 도입되어야 한다. 이를 위해 기존 연구자들은 식 (4)와 같이 진동 Re 수를 도입하였다.
| (4) |
여기서 Vs 는 슬로싱 속도를 의미하며, 이는 식 (5)와 같이 슬로싱 진폭과 진동수의 곱으로 정의된다. 여기서 Ps는 슬로싱 진폭, fs는 슬로싱 진동수를 의미한다.
| (5) |
즉, 혼합대류 열전달 모델은 밀도 차이 유동과 슬로싱에 의한 유동을 동시에 고려하여 열전달을 예측할 수 있어야 하며, 이를 위해 식 (6)과 같이 Gr 수와 Re 수를 포함하는 상관식의 형태를 가져야 한다.
| (6) |
(Lemlich, 1955)는 식 (6)의 무차원 변수들을 포함하는 혼합대류 열전달에 대한 Nu 상관식을 제시하였다. 하지만 (Lemlich, 1955)의 모델은 평판이 아닌 수평으로 놓인 와이어에 관한 것으로, LNG 화물창 설계에 적용하기에는 대상이 되는 물체의 형태가 너무 다르다는 한계가 있었다. (Prasad and Ramanathan, 1972)는 진동하는 수직평판의 열전달계수를 측정하는 실험을 수행하였는데, 이들은 가진기를 통해 10~20Hz로 상하 진동하는 상황을 만들어 슬로싱에 의해 평판의 표면 열전달계수가 얼마나 변하는 지를 측정하였다. 이들은 이러한 실험 데이터에 기반하여 다양한 표면온도 및 슬로싱 속도에서 평판의 열전달계수를 예측할 수 있는 모델을 개발하였다. 다만 (Prasad and Ramanathan, 1972)의 연구는 진동 방향이 평판과 나란할 때로 국한되었다는 한계가 있었고, 제시한 상관식 또한 닫힌 형태가 아니기에 사용하기 어렵다는 단점이 있었다.
멤브레인 화물창은 Fig. 1과 같이 눕혀진 팔각기둥 형상을 가지는데, 슬로싱에 의해 화물창이 x, y, z 방향 중 한 방향으로 진동하게 되면 일부 벽면은 면에 나란한 방향으로, 일부 벽면은 면에 수직한 방향으로 움직이게 된다. 따라서 슬로싱에 의한 화물창 벽면의 열전달계수 변화를 온전히 예측하기 위해서는 면에 수직한 방향으로 벽면이 움직일 때 열전달계수를 예측할 수 있는 상관식이 추가적으로 개발되어야 할 것이다. 또한, 상관식의 형태는 다양한 슬로싱 조건에서 손쉽게 열전달계수를 예측할 수 있는 형태를 가져야 할 것이다.
본 연구에서는 수직 평판이 면에 수직한 방향으로 진동할 때, 열전달계수가 얼마나 증가하는 지를 관측하고, 이에 기반한 열전달계수 상관식을 개발하고자 한다. 또한, 수직 평판이 면에 나란한 방향으로 진동할 때의 열전달계수 상관식 또한, (Prasad and Ramanathan, 1972)의 실험결과에 기반하여 새롭게 개발하고자 한다. 상관식을 개발한 후에는 개발한 상관식을 토대로, 화물창이 수직 혹은 수평방향으로 진동할 때 수직벽면을 통한 열 침입량의 변화를 분석하고자 한다. 열 침입량 분석을 위한 화물창의 멤브레인 형상은 KC-1 CCS를 기준으로 하고, 열 침입량을 분석을 위한 열저항 모델은 (You et al., 2023)의 모델을 참조하고자 한다.
2. 열전달계수 측정 실험
2.1 실험장치 구성
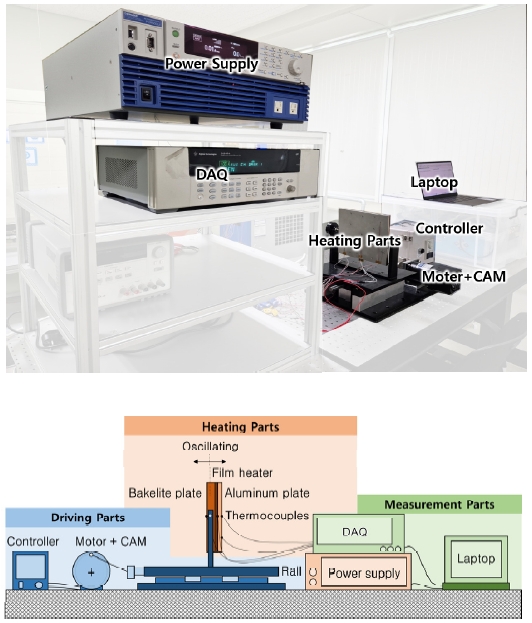
슬로싱이 벽면 열전달계수에 미치는 효과를 확인하기 위해 Fig. 2와 같이 구동부, 가열부, 그리고 온도 측정부로 구성된 실험장치를 제작하였다. 구동부는 수직 평판을 좌우로 왕복운동 시키는 역할을 수행하며, 레일을 따라 움직이는 지지대, 지지대를 왕복운동 시키는 모터 및 캠기구, 왕복운동의 주기를 조절하는 컨트롤러로 구성하였다. 다만, 모터의 스펙 상 조절 가능한 주기는 0.2~1.33초로 제한되었다 (45~300RPM). 왕복운동의 진폭은 캠 지름에 의해 고정되며, 이중 캠을 사용하여 진폭을 1cm와 2.5cm 중 하나를 선택할 수 있도록 설계되었다. 가열부는 일정한 저항을 가지는 필름히터 (Serpentine type, 60 Ω, 200×200)와 히터에 전압을 공급해주는 전원공급기 (KIKUSUI PCR500LE), 히터로부터 나오는 열량이 한쪽으로만 빠져나가도록 해주는 단열재 평판(Bakelite, 200×200×6), 그리고 표면 열전달계수를 측정할 알루미늄 평판(Al, 200×200×4)으로 구성하였다. 접촉 열저항을 최소화하기 위해 평판과 필름히터는 볼트와 너트를 통해 압착되었으며, 필름히터 열량은 전원공급기에서 계측되는 전압 및 전류값을 이용하여 계산되었다. 온도 측정부는 표면온도를 측정하기 위해 평판에 설치된 열전대와 열전대에서 나오는 신호를 계측하는 DAQ (Agilent 34980A), 그리고 계측된 값을 저장하는 노트북으로 구성되었다. 열전대는 필름히터와 단열재, 알루미늄 평판 사이에 각각 1개씩 설치되었으며, 단열재와 알루미늄 외부 표면에도 각각 3개씩의 열전대가 설치되었다. 필름히터와 평판 사이에 열전대를 설치할 때, 열전대가 압착을 방해하지 않도록 열전대가 경로를 따라 평판에 작게 홈을 내었다. 표면 열전달계수를 계산할 때는 알루미늄 평판 외부에 설치된 3개의 열전대의 측정값의 평균을 사용하였다. 알루미늄의 높은 열전도도에 의해 알루미늄 평판 표면에 설치된 3개의 열전대 측정값은 0.2℃ 내의 작은 편차를 보였다.
2.2 열전달계수 측정 방법
알루미늄 평판의 표면 열전달계수는 알루미늄 평판을 통해 전달되는 열량과 표면적, 표면온도, 그리고 외기온도로 정의된다.
| (7) |
식 (7)에서 열전달 면적(A)은 평판의 가로와 세로 길이의 곱으로 계산되었으며, 표면온도(Ts)와 외기온도(T∞)는 각각 평판 표면과 표면에서 일정 거리 떨어진 곳에 설치된 열전대를 통해 측정되었다. 식 (7)에서 열량(Q)은 필름히터에서 발생하는 열량이 아닌, 알루미늄 평판 앞면에서 대류(Convection)에 의해 빠져나가는 열량을 의미한다. 따라서 식 (7)의 열량(Q)을 계산하기 위해서는 필름히터에서 발생하는 열량(Qtotal)에서 복사 열전달로 빠져나가는 열량(Qrad)과 단열재 평판 앞면에서 대류열전달(Qconv,bak,fr)로 빠져나가는 열량을 빼줘야 한다. 평판의 두께가 평판의 너비에 비해 얇기 때문에 단열재와 알루미늄 평판 옆면으로 빠져나가는 대류열전달은 무시 가능하다고 가정하였다.
| (8) |
식 (8)에서 복사로 빠져나가는 열량(Qrad)은 단열재 평판 앞면과 옆면으로 빠져나가는 복사열전달(Qrad,bak,fr, Qrad,bak,side)과 알루미늄 평판 앞면과 옆면으로 빠져나가는 복사열전달(Qrad,Al,fr, Qrad,Al,side)로 나뉘는데, 단열재 평판 앞면으로 빠져나가는 복사열전(Qrad,bak,fr)달과 대류열전달(Qconv,bak,fr)은 합쳐서 식 (9)와 같이 전도식으로 표현된다.
| (9) |
여기서 kbak, tbak은 단열재의 열전도도와 두께이며, Tf,은 필름히터의 온도, Ts,bak은 단열재 평판의 표면온도를 의미한다.
| (10) |
복사열전달은 슈테판-볼츠만 법칙을 통해 계산되었으며, 이때 평판 옆면의 복사열전달을 계산할 때 표면온도로는 평판 앞면의 표면온도와 필름히터 온도의 평균값이 쓰였다. 단열재와 알루미늄 평판의 방사율(ϵ)은 각각 0.15와 0.9를 사용하였다. 최종적으로, 식 (7) ~ (10)을 사용하여 알루미늄 평판의 표면 열전달계수(hs,Al,fr)를 측정하였다.
2.3 불확실도 분석
| (11) |
열전달계수의 불확실도(Uh)는 식 (11)과 같이 정의된다. 열전달계수가 온도 차이와 열량에 의해 결정되는 까닭에, 열전달계수의 불확실도 또한 온도 차이의 불확실도(UΔT)와 열량의 불확실도(UQ)에 의해 결정되는 것을 알 수 있다. 식 (11)에 식 (7)을 대입하면 열전달계수의 불확실도를 식 (12)와 같이 표현할 수 있다.
| (12) |
식 (12)에서 확인할 수 있듯이 표면과 외기온도의 차이가 작아질수록 열전달계수의 불확실도가 커지는 경향이 있다. 본 실험에서 온도 차이의 불확실도(UΔT)는 최대 0.392℃, 열량의 불확실도(UQ)는 최대 0.028W로 확인되었으며, 열전달계수의 불확실도(Uh)는 최대 0.518W/m2-K로 확인되었다.
2.4 슬로싱이 열전달계수에 미치는 영향
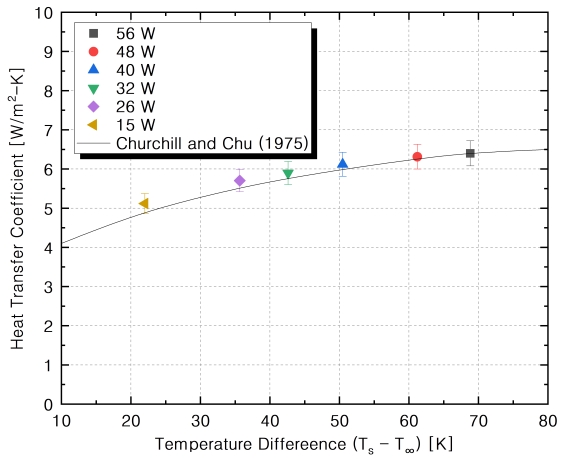
필름히터를 통해 알루미늄 평판에 일정한 열량이 가해지면 초기에는 평판 온도가 급격히 상승하다가 시간에 지남에 따라 그 증가율이 점점 줄어 평형상태에 도달하게 된다. 구동부에 의한 왕복운동이 없을 때 이러한 평형상태에 도달하기까지에는 약 3시간 정도가 소요되었으며, 시간에 따른 온도 변화가 0.4℃ 이내가 되면 완전한 평형상태라고 판단하였다. 본 실험에서는 슬로싱 효과를 확인하기에 앞서, 구성한 실험장치와 열전달계수 측정 방법을 검증하기 위해 왕복운동이 없는 상태로 필름히터 열량을 15W에서 56W로 변화시키면서 평형상태의 열전달계수를 측정하였다. Fig. 3에서 확인할 수 있듯이, 식 (13)으로 표현되는 자연대류 상관식 (Curchill and Chu, 1975)과 측정한 열전달계수가 5% 이내의 작은 오차를 보였다.
| (13) |
식 (13)에서 Ts와 T∞는 알루미늄 표면과 외기의 온도를 뜻하며, Lc은 평판의 길이(200mm)를 의미한다.
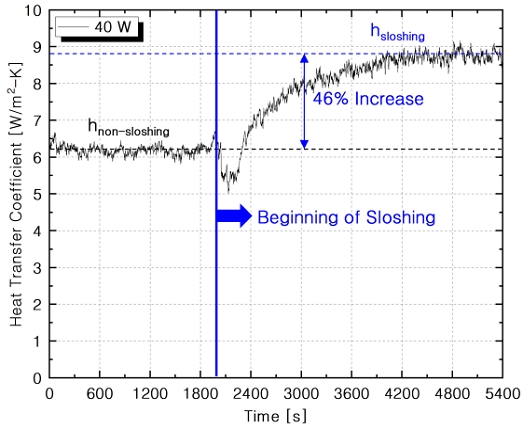
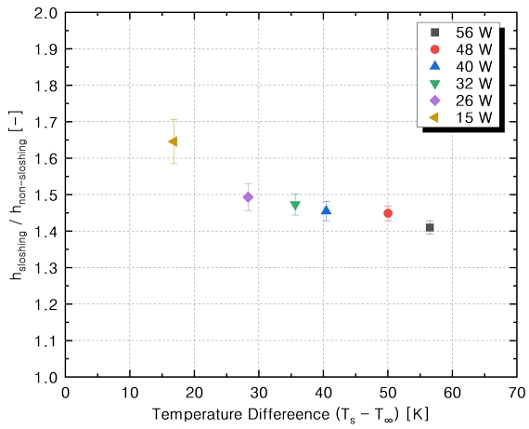
실험장치 검증 후에는 평판을 왕복운동 시키며 슬로싱이 표면 열전달계수에 미치는 효과를 확인하였다. Fig. 4는 슬로싱이 발생한 전후 시간에 따른 열전달계수의 변화를 보여주는 그래프이다. 슬로싱이 발생하면 표면 열전달계수는 즉각적으로 증가하며, 시간이 충분히 흐름에 따라 새로운 정상상태에 도달하는 것을 알 수 있다. Fig. 4는 필름히터 열량이 40W일 때의 결과로, 슬로싱이 발생할 시의 열전달계수 증가율은 46%인 것을 확인할 수 있다. 이러한 열전달계수의 증가율은 가해진 열량이나 표면과 유체 사이 온도 차이에 따라 달라지는데, Fig. 5에 볼 수 있듯이 열량이 15W에서 56W로 증가함에 따라 열전달계수 증가율은 65%에서 40% 정도로 감소하는 것을 알 수 있다. 이때, 슬로싱 진폭은 2.5cm, 슬로싱 주기는 0.5초였다.
3. 화물창 수직벽면 열전달계수 모델
3.1 수평 방향 슬로싱
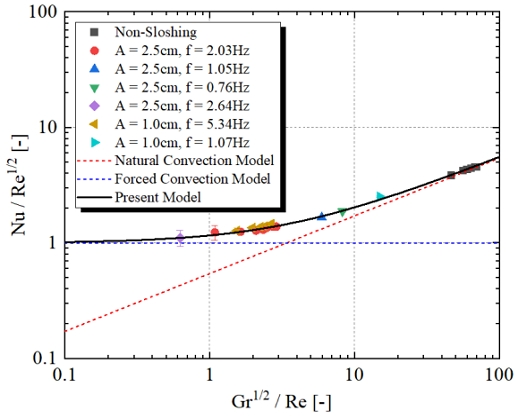
식(6)에서 설명한 것과 같이 자연대류와 강제대류가 동시에 발생하는 혼합대류의 경우, 벽면 열전달계수를 의미하는 Nu 수는 Re 수와 Gr 수에 의해 결정된다. 이처럼 두 개의 변수로 결정되는 Nu 수를 1개의 변수에 대한 함수로 표현하기 위해 본 연구에서는 Fig. 6과 같이 Nu/Re1/2과 Gr1/2/Re라는 새로운 무차원 수를 도입하였다. Fig. 6에서 Symbol은 본 연구에서 얻은 실험 데이터를 의미하며, Nu는 측정한 열전달계수를 식 (2)에 대입하여 얻었으며, Gr 수는 측정한 표면과 외기온도를 식 (3)에 대입하여 얻었다. Re 수는 왕복운동의 진폭과 진동수를 식 (4)와 (5)에 대입하여 얻었다.
Fig. 6에서 파란색 점선으로 표시된 것은 (Eckert, 1942)의 충돌제트 열전달 상관식을 나타낸 것으로, 상관식의 형태는 식 (14)와 같다.
| (14) |
| (15) |
반대로 붉은색 점선은 자연대류 상관식인 식 (13)을 나타낸 것으로 식 (16)과 같이 나타낼 수 있다.
| (16) |
혼합대류 열전달에서, 슬로싱에 의한 강제대류 효과가 벽면과 유체 사이 온도 차이에 의한 자연대류 효과보다 커지게 되면 Re 수가 Gr 수보다 상대적으로 커지게 된다. 이는 Fig. 6에서 x값 (=Gr1/2/Re)의 감소로 이어지게 되며, 또한 자연대류 효과가 무시 가능해짐에 따라 Nu 수는 오로지 식 (15)의 강제대류 상관식에 의해 결정된다. 반대로 슬로싱에 의한 화물창의 움직임이 약해지면 자연대류 효과가 강제대류 효과보다 커지게 되면서 Re 수가 Gr 수보다 상대적으로 작아지게 된다. 이는 Fig. 6에서 x값의 증가로 이어지며, Nu 수는 식 (16)의 자연대류 상관식에 의해 결정된다. 이러한 이유로 Fig. 6에서 실험값들이 x값이 작아짐에 따라 강제대류 상관식에 가까워지고, 반대로 x값이 커짐에 따라 자연대류 상관식에 가까워지는 것을 확인할 수 있다. 문제는 강제대류와 자연대류 효과의 정도가 비슷할 때인데 (x값: 0.1 ~ 10 영역), 이때 실험값은 강제대류 상관식에도, 혹은 자연대류 상관식에도 근접하지 않게 된다. 이러한 문제는 식 (17)과 같은 형태를 적용하여 해결할 수 있다.
| (17) |
식 (17)에서 강제대류 효과가 지배적일 때는 Nufc가 Nunc보다 커지게 되어 자연스럽게 Nu도 Nufc값으로 수렴하게 되고, 같은 원리로 자연대류 효과가 지배적일 때는 Nu 수가 Nunc로 수렴하게 된다. 다만 이러한 방식으로 혼합대류 열전달을 예측하기 위해서는 적절한 상수 n 값을 선정해야 하는데, 본 연구에서는 실험 데이터와 최소자승법에 의해 n = 1.85을 선정하였다. 선정한 n 값을 이용하여 좌 – 우 방향 슬로싱에 대한 화물창 수직 벽면의 열전달계수 상관식을 표현하면 식 (18)과 같다.
| (18) |
3.2 수직 방향 슬로싱
상 – 하 방향 슬로싱에 사용 가능한 열전달계수 상관식도 점근방법을 통해 구할 수 있다. 다만, 수평 방향 슬로싱과의 차이점이라면, 강제대류 상관식으로 충돌제트 상관식이 사용되는 것이 아니라 평행유동에 대한 강제대류 상관식 (Elzy and Sisson, 1967)이 사용된다는 점이다.
| (19) |
| (20) |
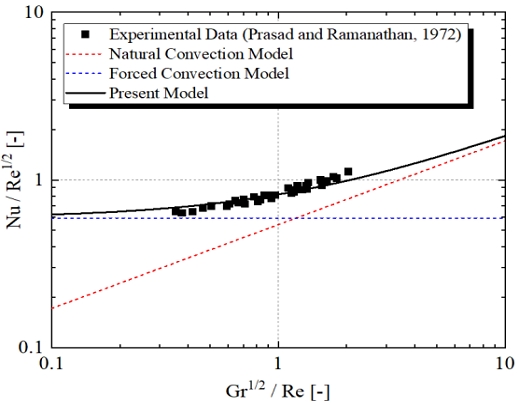
이러한 차이점은 슬로싱 방향이 벽면에 평행하게 바뀌었다는 사실에 기반하며, 최종 열전달 상관식은 동일하게 식 (17)의 형태를 가진다. 다만, 상황이 바뀌었기 때문에 상수 n 값을 새롭게 선정할 필요가 있는데, 본 연구에서는 (Prasad and Ramanathan, 1972)의 실험 데이터를 이용하여 n = 1.88을 선정하였다. 선정한 n 값을 이용하여 상 – 하 방향 슬로싱에 대한 화물창 수직 벽면의 열전달계수 상관식을 표현하면 식 (21)과 같다. Fig. 7은 식 (21)과 (Prasad and Ramanathan, 1972)의 실험 데이터를 비교한 결과이다. 그림에서 확인할 수 있듯이 개발한 상관식이 실험 값을 잘 예측하는 것을 확인할 수 있다.
| (21) |
4. 화물창 열 침입량 분석
4.1 열저항 네트워크 모델
Fig. 1의 화물창이 슬로싱에 의해 y축, 혹은 z축으로 진동하게 되면, 공기와 닿아있는 화물창 외벽과 LNG와 닿아있는 화물창 내벽에 강제대류 유동이 발생한다. 이러한 강제대류 유동은 슬로싱 방향에 따라 벽면에 충돌하는 방향으로, 혹은 벽면에 나란한 방향으로 발생할 수 있는데, 방향에 관계없이 강제대류 유동의 발생은 결과적으로 화물창 내/외벽 표면의 열전달계수 증가로 이어진다.
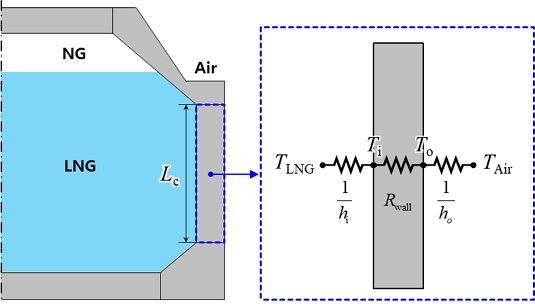
Fig. 8은 화물창 수직 벽면의 열저항 네트워크 모델을 보여주는 그림이다. (You et al., 2023)에 의하면 Fig. 8에서 화물창 수직 벽면의 단위 면적당 열 침입량은 식 (22)와 같이 나타낼 수 있다.
| (22) |
식 (22)에서 확인할 수 있듯이 화물창 벽면의 열유속 (q′′in)은 화물창 벽면의 열저항 (Rwall)과 화물창 내벽과 외벽의 열전달계수 (hi, ho)에 의해 결정된다. 따라서 슬로싱에 의한 화물창의 열 침입량 변화를 분석하기 위해서는 우선 화물창의 벽면 열저항과 내/외벽의 열전달계수 값을 얻어야 한다.
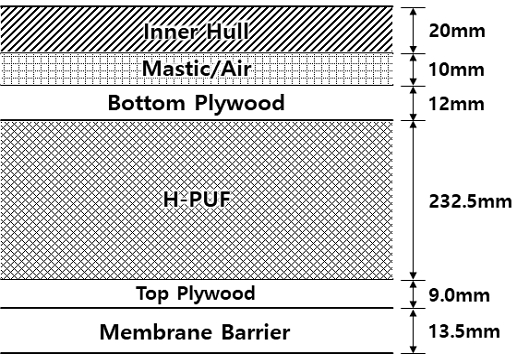
화물창 벽면의 열저항을 계산하기 위해서는 화물창 벽면 구조에 대한 정보가 필요하다. 본 연구에서는 KC-1 화물창의 벽면 구조를 참고하여 벽면 열저항을 계산하였는데, 이때 참고한 KC-1의 벽면 구조에 대한 상세정보는 Fig. 9와 같다.
| (23) |
식 (23)에서 n = 1은 벽면의 가장 안쪽에 있는 Membrane barrier 영역을 의미하고, n이 증가하는 방향에 따라 차례대로 Top plywood, H-PUF, Bottom plywood, Mastic/Air, Inner hull을 의미한다. 또한, kw,n은 n번째 층의 열전도율을 의미하며, tw,n은 두께를 의미한다. 벽면 열저항을 계산하기 위해 필요한 각 재료의 열전도율 (kw,n) 정보는 Table 1과 같다.
벽면 열저항 계산을 위해 Table 1과 곡선 접합을 통해 각 층에서의 열전도율을 온도에 대한 함수로 만들었으며, 구체적인 열전도율 함수에 관한 내용은 (You et al., 2023)에서 확인할 수 있다. 또한, LNG 온도는 –165℃, Air 온도는 5℃로 설정하였으며, 각 유체의 물성치는 REFPROP 프로그램에서 제공하는 Natural gas와 Air의 물성치를 사용하였다. 벽면 열전달계수를 결정할 때 필요한 특성 길이 (Lc)의 경우 KC-1 화물창 수직 벽면의 내벽 길이인 16.51m를 사용하였다.
4.2 슬로싱이 화물창 열 침입량에 미치는 영향
식 (22)를 통해 화물창 열 침입량을 계산하기 위해서는 벽면 열저항 (Rth,w) 값 뿐만 아니라, 내/외벽의 열전달계수 (hi, ho) 값 또한 필요하다. 슬로싱이 발생하게 되면 강제대류 유동이 추가적으로 발생하기 때문에 이를 고려할 수 있는 열전달계수 상관식을 이용해야 하는데, 본 연구에서는 식 (18)과 (21)을 사용하여 화물창의 열 침입량을 분석하였다.
Fig. 10은 식 (18)과 (21)을 이용하여 슬로싱 속도에 따라 화물창 내/외벽의 열전달계수가 어떻게 변하는지 예측한 그래프이다. Fig. 10에서 hi,v-sloshing과 hi,h-sloshing은 각각 수평방향과 수직방향 슬로싱이 발생할 때 안쪽 수직벽면의 열전달계수를 의미하며, ho,v-sloshing과 ho,h-sloshing은 각각 수평방향과 수직방향 슬로싱이 발생할 때 바깥쪽 수직벽면의 열전달계수를 의미한다. Fig. 10에서 볼 수 있듯이 내벽의 열전달계수가 외벽의 열전달계수에 비해 10~100배 높은 값을 가지는 것을 알 수 있다. 이는 화물창 내벽과 맞닿아 있는 LNG의 경우 공기에 비해 훨씬 높은 열전도율 (kf)을 가지고 있기 때문이다. Fig. 10(a)는 슬로싱 속도에 따른 화물창 내벽의 열전달계수 변화를 보여주는 그래프인데, 푸른색 선은 수직 방향 슬로싱이 발생할 때를, 붉은색 선은 수평 방향 슬로싱이 발생할 때의 결과를 의미한다. Fig. 10(a)에서 볼 수 있듯이 수평 방향 슬로싱이 수직 방향 슬로싱 보다 더 높은 열전달계수 증가를 야기하는 것을 확인할 수 있다. 이는 수평 방향 슬로싱이 발생할 때 수직 벽면에 충돌제트 유동이 발생하기 때문이다. 수평 방향 슬로싱 때, 슬로싱 속도 10m/s에서 화물창 내벽의 열전달계수가 정지했을 때와 비교하여 8배 가량 증가하는 것을 확인할 수 있다. Fig. 10(b)는 슬로싱 속도에 따른 화물창 외벽의 열전달계수 변화를 보여주는 그래프이다. 화물창 내벽의 경우와 동일하게 수평 방향 슬로싱이 수직 방향 슬로싱보다 높은 열전달계수 증가율을 보였다. 다만, 수평 방향 슬로싱 때, 슬로싱 속도 10 m/s 에서 외벽 열전달계수는 정지했을 때와 비교하여 3.5배 가량 증가하는 것을 확인할 수 있었다. 이는 내벽 열전달계수의 증가율보다 작은 수치인데, 이러한 증가율의 차이는 유체의 물성치 차이 때문으로 추측된다.
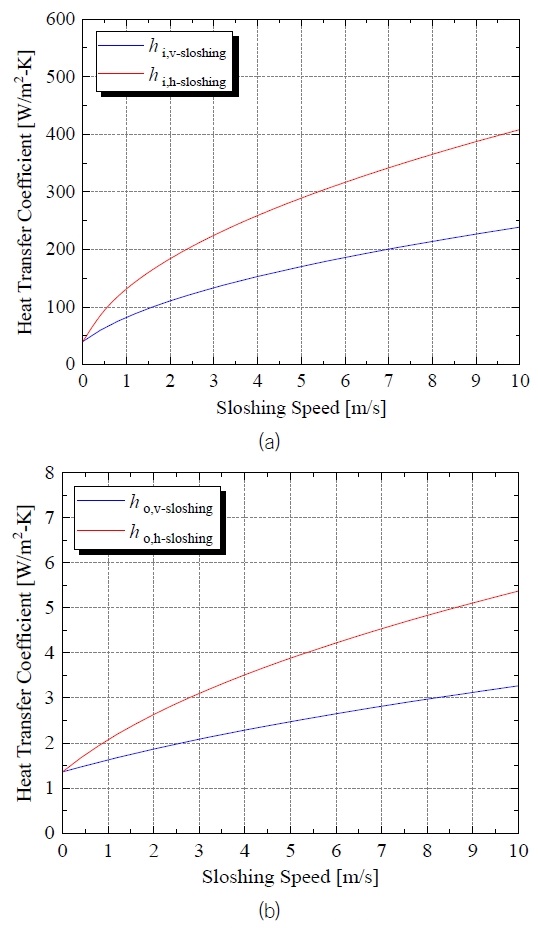
Heat transfer coefficients of (a) inner and (b) outer vertical walls in KC-1 varying with sloshing speed
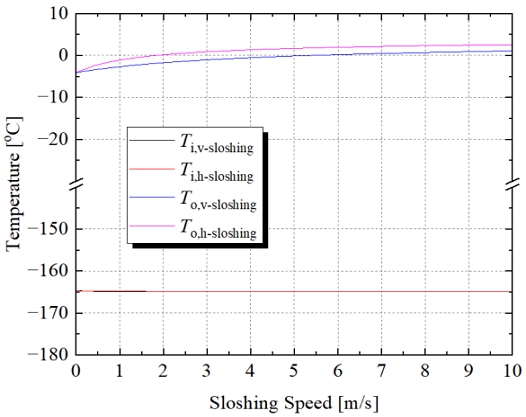
열저항 네트워크 모델을 이용하면 식 (22)를 통해 화물창 열 침입량 (q″in)을 계산할 수 있을 뿐만 아니라, 식 (24)와 (25)를 이용하여 화물창의 내/외벽의 온도 (Ti, To) 또한 알 수 있다. Fig. 11은 식 (22)와 (24), 그리고 (25)를 이용해서 예측한 슬로싱 속도에 따른 화물창 내/외벽의 온도이다. Fig. 11에서 Ti,v-sloshing과 Ti,h-sloshing은 각각 수직방향과 수평방향 슬로싱이 발생할 때 안쪽 수직벽면의 온도를 의미하며, To,v-sloshing과 To,h-sloshing은 각각 수직방향과 수평방향 슬로싱이 발생할 때 바깥쪽 수직벽면의 온도를 의미한다.
| (24) |
| (25) |
화물창 내벽의 온도는 슬로싱 방향과 슬로싱 속도에 상관없이 거의 일정한 것을 확인할 수 있으며, 화물창 외벽의 온도는 슬로싱 속도가 증가함에 따라 같이 증가하는 경향을 확인할 수 있다. 화물창 내벽의 온도가 슬로싱에 상관없이 일정한 이유는 이미 열전달계수가 충분히 높기 때문이다. 정지된 상태에서도 이미 내벽의 열전달계수가 높은 까닭에 LNG 온도와 내벽의 온도 차이가 1도 미만으로 작고, 이 때문에 슬로싱에 의해 열전달계수가 증가해도 유의미한 내벽온도 차이를 보이지 않는 것이다. 같은 논리로, 외벽의 경우에는 열전달계수가 작기 때문에 슬로싱에 유의미한 영향을 받는다. 수평 방향 슬로싱 때 외벽의 온도가 더 높게 상승하는 이유는 앞서 Fig. 10에서 설명한 것과 같이 열전달계수가 더 크게 증가하기 때문이다. 높은 열전달계수는 외기온도 (5℃)와의 작은 온도 차이를 야기한다.
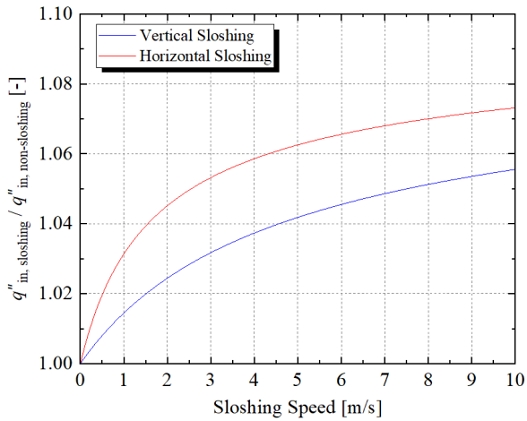
Fig. 12는 식 (22)를 통해 예측한 슬로싱 속도에 따른 화물창 열 침입량의 증가율이다. 수평 방향 슬로싱이 발생할 때 열전달계수가 더 높게 증가하므로 화물창의 열 침입량 또한 더 크게 증가하는 것을 확인할 수 있다. 슬로싱 속도 10m/s에서 화물창의 열 침입량은 정지했을 때 대비 약 7% 가량 증가하는 것을 확인할 수 있다. 다만, 슬로싱 방향에 상관없이 슬로싱 속도가 일정 값 이상으로 커지게 되면 열 침입량의 증가율 기울기가 점차 감소하는 것을 확인할 수 있는데, 이는 화물창의 벽면 열저항 때문이다. 슬로싱 속도가 계속 증가하면 화물창 내/외벽의 열전달계수 또한 같이 증가하는데, 이렇게 되면 식 (22)에서 열전달계수와 관련된 분모 항이 0으로 수렴하게 된다. 하지만 이때도 벽면 열저항 Rth,w 항은 일정 값을 유지하기 때문에 화물창 열 침입량이 무한대로 증가하는 것이 아니라 특정 값으로 수렴하는 것이다. 이는 반대로 말하면 슬로싱 속도가 아무리 빠르더라도 화물창의 열 침입량은 식 (26)의 값을 넘기 어렵다는 것을 시사한다.
| (26) |
또한, 식 (22)에서 내벽의 열전달계수(hi)는 이미 외벽의 열전달계수(ho)에 비해 매우 크기 때문에 화물창 열 침입량에 크게 영향을 끼치지 않는 것을 확인하였다. 즉, 슬로싱에 의해 내벽의 열전달계수가 8배가 증가해도 이미 1/hi이 무시 가능할 정도록 작기 때문에 열 침입량은 크게 바뀌지 않았다. 반대로 외벽의 열전달계수는 그 값이 작기 때문에 슬로싱에 의해 2배, 3배만 증가해도 화물창 열 침입량이 민감하게 바뀌는 것을 확인했다.
5. 결 론
왕복 운동하는 수직 평판의 표면 열전달계수를 측정하는 실험을 통해 슬로싱 환경에 노출된 화물창 내/외벽의 열전달계수를 예측할 수 있는 상관식을 개발하였다. 또한, 이를 KC-1 화물창에 적용하여 실제로 화물창 수직 벽면 내/외벽의 열전달계수와 온도, 그리고 열 침입량이 슬로싱에 의해 얼마나 증가하는지 정량적으로 분석하였다. 분석을 통해 알게 된 사실은 다음과 같다.
- 1. 슬로싱의 규모는 슬로싱 속도(진폭 × 진동수)로 정량화할 수 있으며, 슬로싱 속도가 증가함에 따라 화물창 내/외벽의 열전달계수도 같이 증가한다.
- 2. 화물창이 수평 방향으로 슬로싱할 때 수직 방향으로 슬로싱할 때보다 높은 열전달계수 증가율을 보이는데, 이는 수직 벽면에 충돌제트 유동이 형성되기 때문이다.
- 3. 슬로싱 발생 시 화물창 내벽의 열전달계수는 외벽의 열전달계수 보다 항상 그 값과 증가율이 높은데, 이는 LNG와 공기의 물성치 차이에 기인한다.
- 4. 화물창 내벽의 온도는 슬로싱에 상관없이 일정하며, 외벽의 온도는 슬로싱이 심하게 발생할수록 점점 외기온도에 가까워진다.
- 5. 슬로싱 발생 시 화물창의 열 침입량은 증가하며, 슬로싱 속도가 10m/s일 때 KC-1 화물창 수직벽면의 열 침입량은 최대 7.5% 정도 증가하였다.
- 6. 화물창 열 침입량의 변화는 대부분 외벽 열전달계수 증가에 의한 것이며, 내벽의 열전달계수 증가가 열 침입량 증가에 미치는 영향은 미비하다.
Acknowledgments
본 연구는 산업통상자원부 소재부품기술개발 사업의 ‘액화수소용 섭씨 영하 200 도 이하 100 MPa 급 컴팩트형 열교환기 설계(1세부)/제작(2세부) 기술개발’ 과제(1 세부:20022461, 2 세부: 20022454)와 한국기계연구원에서 수행 중인 2024년 액체수소공급시스템 핵심 기자재 개발사업(NK249B)의 연구비 지원에 의해 수행되었습니다.
References
-
Churchill, S.W. and Chu, H.H.S., 1975. Correlating equations for laminar and turbulent free convection from a vertical plate. International Journal of Heat and Mass Transfer, 18, pp.1323.
[https://doi.org/10.1016/0017-9310(75)90243-4]

- Eckert, E.R.G., 1942. Die Berechnung des Warmeuberganges in der laminaren gren-zschicht um stromter korper. VDI-Forschungsheft, 416, pp.1-24.
- Elzy, E. and Sisson, R.M., 1967. Tables of similar solutions to the equations of momentum, heat and mass transfer in laminar boundary layer flow. Bulletin no. 40, Engineering Experiment Station, Oregon State University, Corvalis, Oregon, February.
- Jeon, G.M., 2021. A numerical study on multiphase-thermal flow considering phase change and sloshing effect in cryogenic tank. Ph.D. Pusan National University.
- Jung, S.M., 2023. Multiphase-thermal analysis for efficient transportation and long-term storage of liquid hydrogen energy. Ph.D. Pusan National University.
-
Lee, J.H., Hwang, S.Y., Lee, S.J. and Lee, J.H., 2022. Numerical study of heat flux and BOG in C-type liquefied hydrogen tank under sloshing excitation at the saturated state. Journal of the Computational Structural Engineering Institute of Korea, 35(5), pp.299-308.
[https://doi.org/10.7734/COSEIK.2022.35.5.299]

- Lee, Y., Choi, S. and Son, G., 2020. Numerical study of producing BOG in a LNG-tank with sloshing effect. The Korean Society of Mechanical Engineers, Seoul, Republic of Korea, 16-24 December 2020.
-
Lemlich, R., 1955. Effect of vibration on natural convective heat transfer. Industrial & Engineering Chemistry, 47(6), pp.1175-1180.
[https://doi.org/10.1021/ie50546a024]

- Park, S. and Hwang, J., 2023. Analysis of droplet breakup and boil off rate due to sloshing phenomena inside liquid fuel tank. The Korean Society of Mechanical Engineers, Incheon, Republic of Korea, 01-04 November 2023.
-
Prasad, K.K. and Ramanathan, V., 2007. Heat transfer by free convection from a longitudinally vibrating vertical plate. International Journal of Heat and Mass Transfer, 15, pp.1213-1223.
[https://doi.org/10.1016/0017-9310(72)90186-X]

-
You, H., Kim, T., Kim, C., Kim, M., Kim, M., Han, Y.S., Nguyen, L.D., Chung, K., Choi, B. and Do, K.H., 2023. Scale effect analysis of LNG cargo containment system using a thermal resistance network model. Journal of the Society of Naval Architects of Korea, 60(4), pp.222-230.
[https://doi.org/10.3744/SNAK.2023.60.4.222]