경항모 내항성능 평가 연구
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this study, a combined seakeeping performance evaluation method has been developed for the design purpose of the light aircraft carrier CVX of Korean Navy. A frequency domain analysis method was developed for evaluation of safe operating envelope up to sea state 6, while a time domain analysis method was developed for survival condition of sea state 7 and higher. The frequency-domain solver AdFLOW-Navy was developed by adding empirical formula of roll damping and fin-stabilizer to the existing AdFLOW by KRISO, which was based on the three-dimensional higher order boundary element method (HOBEM). For the estimation of the roll damping coefficient, a two-dimensional cross-section was automatically extracted from the three-dimensional panel, and the roll damping coefficient was analyzed for the two-dimensional cross-section. As for the time domain analysis method, KIMAPS-Navy was developed by improving and expanding the KIMAPS series developed by KRISO which is based on the impulse response function by utilizing the hydrodynamic coefficients obtained from the AdFLOW-Navy. In addition, a weakly nonlinear analysis approach was applied to analyze highly nonlinear motion under heavy sea states. Finally numeraical analysis results were compared with model tests, which showed practical usefulness of the present combined seakeeping analysis approach.
Keywords:
Light aircraft carrier, Seakeeping, Roll damping, Fin stabilizer, Nonlinear motion키워드:
경항공모함, 내항성능, 횡동요 감쇠, 핀 안정기, 비선형 운동1. 서 론
제2차 세계대전을 전후하여 본격적으로 운용되어온 항공모함의 설계에 있어 내항성능은 선형 개발 시부터 중요하게 고려되었다. 따라서 다양한 환경조건에서 체계적인 내항성능 해석을 위한 노력이 전개되었으며, STANAG 4154 (NATO, 2000), Comstock and Keane Jr. (1980), Comstock (1982)에서 항공모함의 내항성능평가 기준개발, 다양한 해역에서의 불규칙 해상파의 모델링 표준화 및 내항성능평가 절차 개발, 이를 체계적으로 수행하기 위한 전산화 연구 등이 잘 정리되어 있다. Table 1은 그동안 여러 나라에서 함정 개발 시 내항성능해석을 위해 개발하여 사용되어온 프로그램을 요약한 것이다 (NATO, 2000). 대부분 설계목적의 내항성능 해석 프로그램은 선형 2차원 스트립이론에 기반하고 있음을 알 수 있는데 이는 항공모함 선형 개발이 1980년대 집중적으로 이루어진 이후 후속 연구가 미진했던 점도 있으나, 함정은 기본적으로 스트립이론을 적용하기에 충분한 세장선형인 동시에 설계목적의 내항성능평가는 다양한 해상조건, 파향, 함속의 조합에 대한 체계적 계산을 요구하는데, 스트립 방법이 이러한 목적의 주파수 영역에서의 계산 및 결과를 일목요연하게 정리해주는 편리함을 제공하기 때문이다. 일부는 비선형 스트립이론이 적용되는 경우가 있는데 이는 슬래밍, 갑판침수에 의한 스프링잉, 휘핑 등의 강한 비선형 현상 해석 목적에 국한된다. Table 1에서 확인할 수 있듯이 3차원 이론에 기반한 내항성능 해석 프로그램은 아주 제한적으로 사용된다. 미 해군에서 3차원 랜킨패널법을 적용한 시간 영역 내항성능 해석프로그램 NLOAD3D (SAIC, 2006)와 서울대학교에서 비스플라인 랜킨패널법을 적용하여 개발한 WISH (Kim and Kim, 2010a) 등이 현재 3차원 이론에 기반 한 대표적인 시간영역 해석 프로그램이다. 그러나 시간영역 해석 프로그램은 수많은 조합조건에 대한 설계목적의 선형해석결과를 얻기에는 적합하지 않다. 한편 전진속도를 고려한 3차원 그린함수를 적용한 시간영역에서의 해석이론이 있으나, 설계해석에 적용을 위해서는 충분한 신뢰성을 담보할 지속적인 연구가 요구된다 (Choi et al., 2023).
최근에 CFD를 적용하여 유체충격하중과 같이 비선형성이 강한 문제에 적용되고 있으며 최근 컴퓨터 계산용량 및 속도 발달에 따라 파랑 중 함정의 운동 해석도 시도되고 있으나 해석 시간과 자원이 많이 요구되기 때문에 현재까지 함정설계 목적의 내항성능 해석에 적용하기는 어려운 상황이다.
경항모의 가장 기본적인 임무인 이·착함 성능기준은 함의 횡동요에 가장 크게 영향을 받는 것으로 알려져 있다. 횡동요 응답 자체는 물론, 이로 인해 유기되는 이·착함 위치에서의 수직속도, 갑판에서 작업하는 승무원에게 작용하는 수직 및 수평 가속도 등에도 큰 영향을 미친다. 횡동요는 다른 운동보다 함 자체의 감쇠력이 작기 때문에 빌지킬, 핀 안정기 등과 같은 부가물의 감쇠력 고려가 중요하다. 2차원 스트립 방법에서는 전통적으로 선체단면 형상, 빌지킬, 양력효과로 인한 감쇠력을 경험식으로 고려해왔다 (Ikeda et al., 1978). 3차원 해석법의 경우 통상적으로 모형실험 및 유사선형의 감쇠계수를 임계감쇠의 퍼센티지로 고려하여 내항성능 해석을 수행하지만 경항모와 같이 특수한 선형의 경우 초기 설계단계에서 모형시험 및 유사선형의 감쇠계수의 사전 확보가 용이하지 않다. 하지만 모형시험을 수행하기 전 설계단계해서도 내항성능평가를 통한 안전임무 수행범주(SOE: Safe Operating Envelope) 식별을 위해서는 합리적이고 체계적인 횡동요 감쇠계수 추정이 요구된다. 상대적으로 중, 고속으로 운항하는 경항모의 횡동요를 줄이기 위한 장치로 핀 안정기(fin stabilizer)의 성능추정도 설계 단계에서 중요한 평가요소 중 하나이다. 핀 안정기는 알려진 바에 의하면 10~15knots 이상의 속도에서 핀을 능동적 제어를 할 경우에 횡동요 진폭을 적어도 50% 감소시키는 것으로 되어있다 (Lloyd, 1991). Cho et al. (2004)의 연구를 보면 모형시험에서 횡동요 진폭이 50% 감소하는 것을 확인할 수 있다.
본 연구에서는 개념설계 및 기본설계 단계에서 경항모의 종합적인 내항성능평가를 위해 임무 운용조건(해상상태 6이하)에서 우수한 내항성능을 갖는 함정개발 목적의 주파수영역 해석법과 해상상태 7이상의 생존조건에서 내항성능 평가를 위한 시간영역 해석법을 개발하여 경항모의 내항성능 해석에 적용하였다. 주파수 영역 해석법은 3차원 고차경계요소법(HOBEM)을 기반으로 KRISO에서 기개발한 AdFLOW를 확장, 개선하여 AdFLOW-Navy를 개발하였다. 3차원 고차경계요소법은 기본적으로 zero-speed 그린함수를 적용하므로 2차원 스트립이론과 유사한 조우주파수 개념의 전진 속도 효과를 고려하지만 2차원 방법에 비해 선수, 선미부의 함정 형상을 정교하게 반영할 수 있고, 전후동요를 정확하게 해석할 수 있는 장점을 가지고 있으며 선수부 상대파고 예측에 있어 교란파 효과를 고려할 수 있다. 선형 변화 및 부가물로 인한 횡동요 감쇠계수의 추정을 위해서 3차원 패널로부터 2차원 단면을 자동으로 추출하고 2차원 단면에 대해서 횡동요 감쇠계수를 해석하였다. 시간영역 해석법은 주파수 영역에서 얻은 유체동역학 계수 및 파랑 기진력을 활용하여 충격응답함수 기반의 시간 영역 내항성능 해석 방법 (Cummins, 1962)을 채용하여 KRISO에서 개발한 KIMAPS series를 개선, 확장하여 KIMAPS-Navy를 개발하였다. 또한 비선형 운동응답 해석을 위해서 weakly-nonlinear 해석 기법을 적용하였다.
2. 이론적 배경
본 연구에서 개발된 AdFLOW-Navy는 기존 프로그램 AdFLOW-Speed를 개선, 확장한 것이다. 따라서 기존의 프로그램에서 추가적으로 적용된 기능을 위주로 설명하였다.
2.1 전진속도 효과
유체는 비점성, 비압축성인 이상유체로 가정하고 비회전성 유동을 한다고 가정하면 유체장은 속도 포텐셜로 기술할 수 있다. 속도 포텐셜의 지배방정식은 라플라스(laplace)방정식이다. 선박이 수심 h에서 자유표면 상을 U 속도로 전진하면 방사파(radiation) 포텐셜(j = 1,...,6)과 산란파(scatter) 포텐셜(j = 7)의 선형화된 경계조건은 다음과 같다 (Newman, 1979).
| (1) |
여기서 we는 조우주파수, n은 법선벡터, g는 중력 가속도, mj는 정상상태(steday) 포텐셜과 비정상상태(unsteady) 포텐셜의 상호 작용, 는 선박의 평균위치, ϕ0는 입사파의 포텐셜을 나타낸다. 정상상태 포텐셜을 선박의 형상을 고려하지 않고 균일한 유동(uniform flow)으로 가정하고 선형화(Neumann-Kelvin linearization)를 수행하면, mj는 아래와 같이 나타낼 수 있다.
| (2) |
선박의 형상이 세장체(slender body)이고 가 we보다 작다고 가정하면, 선체주위의 자유수면 경계조건은 아래와 같다(Newman, 1979).
| (3) |
식 (2), (3)을 적용하여 식 (1)을 해석하면 방사파 포텐셜과 산란파 포텐셜을 얻을 수 있다. 이를 선체에 대해서 적분하면 부가질량(added mass) 및 감쇠(damping) 계수, 파랑기진력(wave exciting force)을 얻을 수 있다. 전진속도 효과를 고려한 부가질량 및 감쇠 계수, 파랑기진력은 STF 스트립 (Salvesen et al., 1970)과 유사한 형태로 유도된다. 이러한 방법은 전진속도 효과를 엄밀하게 반영하지는 못한다. 그러나 지금까지 운동응답에서 좋은 결과를 주는 것으로 알려져 내항성능 해석에서 많이 사용되고 있다. 4장에서 전진속도 효과를 엄밀하게 고려한 수치해석의 결과, 모형시험의 결과와 비교를 통해서 이러한 방법의 정도와 한계점을 살펴볼 것이다.
2.2 횡동요 감쇠 계수
횡동요 감쇠 계수를 추정하는 방법은 1950년대부터 많은 연구들이 수행되었으며 1970년대 후반 Ikeda et al. (1978)가 횡동요 감쇠 계수를 추정하는 방법을 정리하였다. 이후에도 많은 연구들이 수행되었으며, ITTC (2011)와 Falzarano and Somayajula (2015)에 상세하게 정리되어 있다. 본 연구에서는 위의 두 논문을 기준으로 횡동요 감쇠 계수를 프로그램에 적용하였다. 추정된 횡동요 감쇠 계수는 정확한 값을 제시하기 보다는 선형 설계 초기에 선형변화로 인한 감쇠 계수를 추정하는데 활용된다. 최종 내항성능 평가를 수행할 때는 모형시험을 통해서 횡동요 감쇠계수를 추정하고 이를 활용하여 내항성능 평가를 수행한다.
횡동요 감쇠 계수는 아래와 같이 여러 가지 구성성분으로 나눌 수 있다.
| (4) |
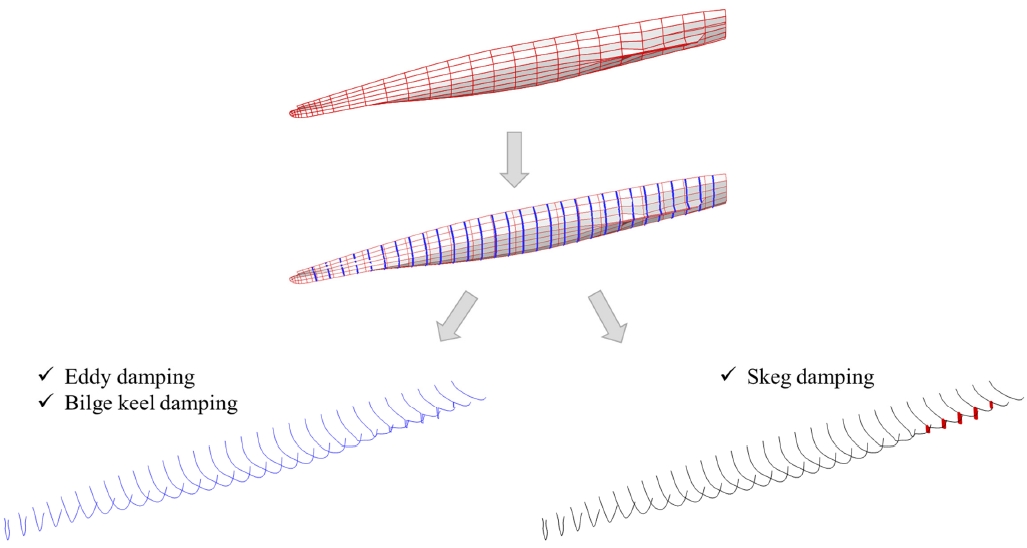
BWave, BFriction, BLift는 선박의 주요 치수로부터 얻을 수 있는 값이다. 따라서 본 연구에서 다루는 3차원 해석코드에서 바로 적용할 수 있다. 반면 BEddy, BSkeg, BBilge는 2차원 단면에 대해서 추정방법이 정의되어 있다. 따라서 2차원 기반의 스트립 해석 코드에서 많이 적용되어 있지만 3차원 해석 코드에는 바로 적용이 쉽지 않다. 본 연구에서는 Fig. 1에 나타낸 것과 같이 3차원 패널로부터 2차원 단면을 자동으로 추출하고, 2차원 단면에 대해서 횡동요 감쇠 계수를 추정하고 이를 해석 코드에 반영하였다. 2차원 단면은 주어진 단면과 3차원 패널의 교차점을 이용해서 찾았으며 단면의 개수는 수렴도 테스트를 통해서 30개로 정하였다.
파 감쇠(BWave) 계수는 식 (1)에서 제시한 경계조건문제를 해석하고 선체표면에 대해서 적분을 수행하면 얻을 수 있는 값이다.
표면 마찰 감쇠(BFriction)는 선체 표면에 작용하는 점성 표면 마찰 응력으로 인해 발생한다. 층류 운동에 대한 표면 마찰 감쇠 계수에 대한 경험식은 Kato (1958)에 의해 제시되었으며 아래 식을 사용하여 해석하였다.
| (5) |
여기서 ρ는 유체의 밀도, Sf는 접수 표면적, rf는 유효 빌지 반경, R0는 횡동요 크기, ω는 횡동요 주파수, Cf는 마찰 계수를 나타낸다. 표면 마찰 감쇠는 횡동요의 크기와 횡동요 주파수에 비례한다.
Schmitke (1978)는 전진 속도 U로 이동하는 선박의 경우에 대한 수정식을 아래와 같이 제시 하였으며 본 연구에서 아래 식을 사용하였다.
| (6) |
여기서 L은 선박의 길이를 나타낸다. 표면 마찰 감쇠는 속도가 증가하면 증가한다.
Ikeda et al. (1978)는 식 (7)과 같이 선체에 의한 양력 감쇠(BLift)를 추정하기 위한 간단한 경험식을 제시하였으며 본 연구에서 아래의 식을 사용하였다.
| (7) |
여기서 D는 선박의 흘수, OG 는 선박의 무게 중심에서 자유수면까지 거리, CM은 선박 중앙 단면 계수를 나타낸다. 위 식에서 알 수 있듯이 양력 감쇠 계수는 속도 U에 따라 선형적으로 변하며 횡동요 운동의 주기와 무관하다.
와류 감쇠(BEddy)는 유체의 분리와 선박 바닥 주변의 소용돌이의 박리로 인해 발생한다. 세장선의 경우 선미와 선미에서 떨어져 나가는 반면, 비대칭 형태를 가진 선박의 경우 선박 중앙이 와류 감쇠에 크게 기여한다. 와류 감쇠 계수를 추정하는 경험식은 항력 계수를 사용하여 실린더에 대한 항력을 추정하는 것과 유사하다. 단면에 대한 단위 길이 당 와류 감쇠는 아래의 식을 사용하였다.
| (8) |
여기서 CR는 와류 감쇠 계수이다. 와류 감쇠는 횡동요의 크기와 횡동요 주파수에 비례한다.
전진 속도가 있는 경우, 와류 감쇠 계수는 아래 경험식에 따라 급격하게 감소한다.
| (9) |
빌지킬 감쇠(BBilge)는 정상 압력 감쇠(BBKN)와 선체 감쇠(BBKH)의 두 가지 구성 요소로 분리할 수 있다.
| (10) |
단위 길이 당 빌지킬 감쇠의 수직 성분은 아래의 식을 사용하였다.
| (11) |
여기서 rcb는 횡동요 중심으로부터 빌지킬까지 거리, bBK는 빌지킬의 폭, f는 빌지에서 유속 증가 보정 계수, CBKN는 빌지킬 항력 계수이다. 빌지킬 감쇠의 수직 성분은 빌지킬의 폭, 횡동요 주파수, 횡동요 크기에 비례한다.
단위 길이 당 빌지킬 감쇠의 선체 성분은 아래의 식을 사용하였다.
| (12) |
여기서 CBKH는 빌지킬 압력 계수이다.
스케그(skeg) 감쇠(BSkeg) 성분은 스케그와 선체 표면에 걸쳐 스케그에 의해 생성된 압력을 통하여 얻을 수 있다. 본 연구에서 다루는 함정은 쌍축의 추진기를 가지고 가운데 스케그를 가지고 있다. 스케그에 의한 단위 길이당 감쇠 성분은 아래의 식을 사용하였다.
| (13) |
여기서 l 은 횡동요 중심에서 스케그까지의 거리, CSK는 스케그 압력 계수이다.
2.3 핀 안정기
핀 안정기는 핀에서 발생하는 양력을 이용하여 모멘트를 만들고 이를 이용하여 횡동요를 감소시킨다. 양력이 발생하기 위해서는 핀에 일정 크기 이상의 유속이 필요하기 때문에 비교적 높은 속도에서 그 성능이 발휘된다.
핀 안정기는 횡동요 운동에 따라서 핀의 각도가 변하는 능동 핀(active Fin)과 핀의 각도가 변하지 않는 수동 핀(passive fin)이 있다. 먼저 수동 핀에 대해서 설명하고 아울러 능동 핀에 대해서 설명하기로 한다.
한 쌍의 핀에 의해서 발생하는 횡방향 모멘트는 아래와 같다.
| (14) |
여기서 AFin은 핀의 단면적, CL은 핀의 양력계수, lfin은 횡동요 중심에서 핀의 압력 중심까지의 거리이다. 수동 핀의 경우 핀의 양력계수는 하나의 고정된 값이고 아래와 같이 나타낼 수 있다.
| (15) |
여기서 는 양력계수의 기울기를 나타내며 본 연구에서는 상수로 가정한다. β0는 횡동요 운동과 전진속도로 인한 핀의 받음각을 나타내며 다음과 같다.
| (16) |
식 (16)을 Taylor’s expansion하고 첫 번째 항만 고려하면 한쌍의 핀에 의해서 발생하는 횡방향 모멘트는 아래와 같다.
| (17) |
여기서 괄호 안의 값은 횡동요 감쇠 계수와 같은 역할을 수행한다.
능동 핀에서는 핀의 받음각이 횡동요 변위, 속도, 가속도에 따라서 제어를 한다. 핀의 받음각은 아래와 같이 나타낼 수 있다.
| (18) |
여기서 Kϕ는 횡동요 변위에 비례하는 P(Proportional) 게인, 는 횡동요 각속도에 비례하는 D(Derivative) 게인, 는 횡동요 가속도에 비례하는 A(Acceleration) 게인 이다. 본 연구에서 A게인은 1을 사용하였다. D게인은 핀 구동부 성능에 영향을 받는데 본 연구에서는 10 이하의 값을 사용하였다. P게인은 횡동요 고유 주파수의 제곱 값을 가진다.
2.4 약한 비선형(Weakly-nonlinear)
황천 시에는 파도와 운동으로 인해 접수면적이 크게 변하므로 이로 인한 선형의 비선형성을 일부 고려할 수 있는 weakly-nonlinear 기법을 도입할 수 있는 시간영역 해석을 적용하였다. 경항모는 선수 플레어로 인해 흘수에 따른 수선면 변화가 크고, 황천과 같은 거친 해상 상황에서 기동을 평가해야 하기 때문에 weakly-nonlinear 기법의 적용이 필요하다. 운동방정식은 다음과 같이 Cummins (1962) 모델로 나타낼 수 있으며, 선박의 실제 입수면적을 고려한 비선형 복원력과 Froude-Krylov 힘을 적용하였다 (Seo et al., 2013).
| (19) |
여기서, mij + aij, Rij(t - τ), cij, , FDiffi, Fexti, FN.Res.i, FN.F.K.i는 각각 질량행렬, 메모리효과 행렬, 복원행렬, 전진속도에 의한 복원력행렬, 파랑기진력, 부가물 외력, 비선형 복원력 및 비선형 Froude-Krylov 힘을 나타낸다. 비선형 복원력과 비선형 Froude-Krylov 힘은 아래와 같은 식으로부터 얻을 수 있다.
| (20) |
여기에서 SB는 입사파 및 선박 운동을 고려한 실제 접수 면적이고 는 평균 접수 면적이다.
3. 모형 시험
KRISO에서 자체 설계한 경항모 모델 KRISO-CVX1선형이 본 연구에서 대상선형이며 해석결과 비교검토를 위해 KRISO 해양공학수조에서 모형시험이 수행되었다. Fig. 2는 모형선의 사진을 나타내었으며 Table 2는 KRISO-CVX1의 주요치수를 나타내었다. 선박의 길이는 250m이고 폭은 32m이며 흘수는 9.5m이고 배수량은 약 41,500톤이다. 모형선은 1/60 스케일로 제작되었다. 모형시험에 대한 구체적인 내용은 Cho et al. (2024)에 기술되어있다.
4. 내항성능 해석 결과
4.1 운동응답
함정의 내항성능 해석에서 가장 기본이 되는 것은 운동응답 RAO이다. 운동응답 RAO와 파랑 스펙트럼으로부터 내항성능의 주요지표들이 결정되기 때문이다. 운동응답은 스트립 해석 결과, 서울대학교 WISH 프로그램 해석 결과, 그리고 본 연구에서 얻을 결과를 비교하였다. 스트립 결과는 스트립 해석 프로그램의 대표적인 프로그램인 SMP의 해석 결과를 이용하였다. WISH 프로그램에서 WISH-DB는 Double body 선형화의 결과이고 WISH-NK는 Neumann-Kelvin 선형화의 해석 결과이다. Neumann-Kelvin 선형화는 전진속도에 의한 정상유동을 균일유동으로 가정하며 Double body 선형화는 정상유동을 Double body 유동으로 가정한다. 선형화 기법에 따른 선박 내항성능 해석의 정확도 및 신뢰도에 대한 연구는 Kim and Kim (2007), Kim and Kim (2010b), Lee et al. (2017)에서 확인할 수 있다.
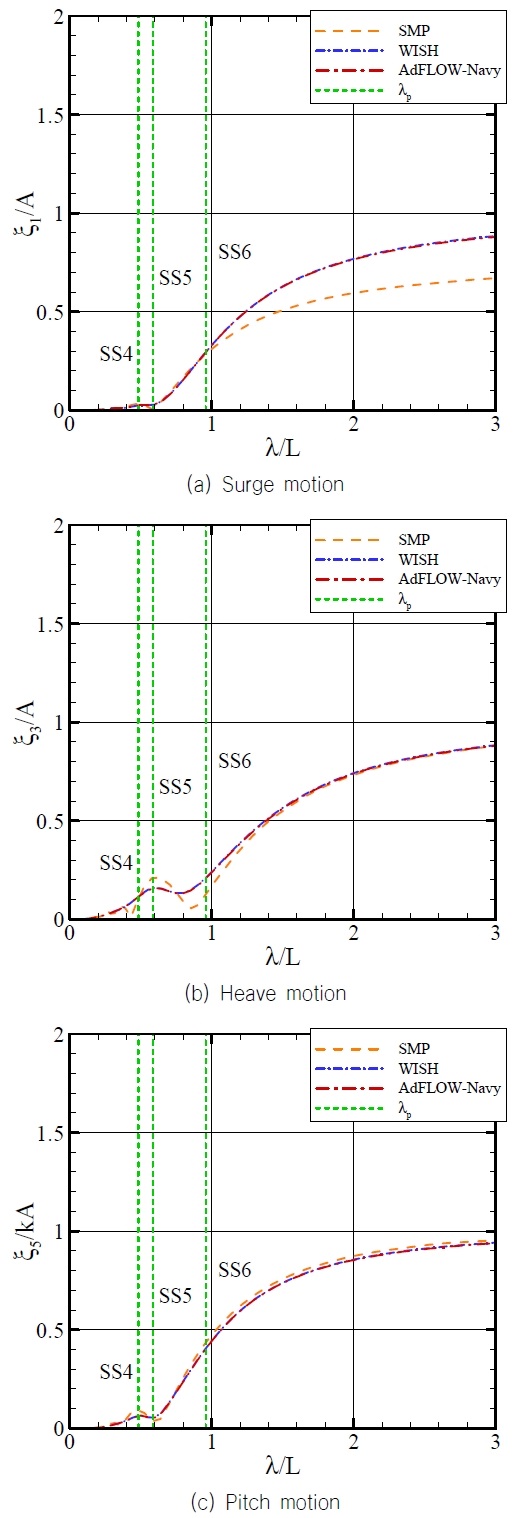
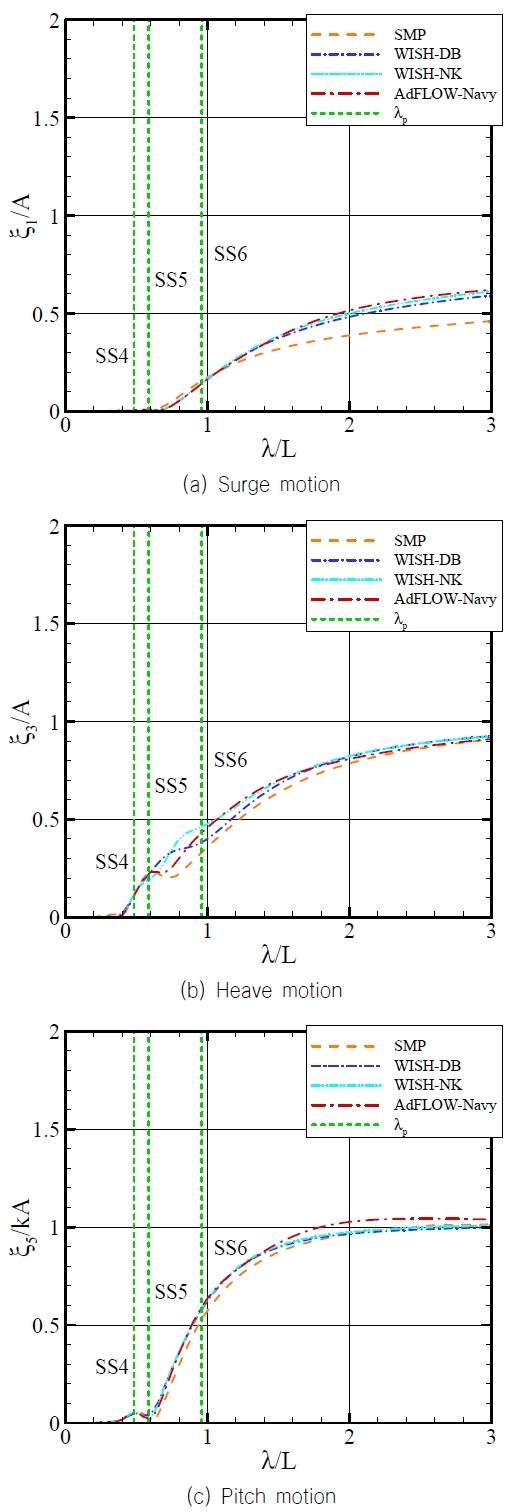
우선 스트립 프로그램과 결과 비교를 위해서 전진 속도가 없는 조건에서 전후동요(surge), 상하동요(heave), 종동요(pitch)의 결과를 Fig. 3에서 비교하였다. 전진속도가 없는 조건에서는 WISH-DB와 WISH-NK가 동일하기 때문에 WISH로 표기하였다. Fig. 3에서 수직 점선으로 표시한 것은 함정의 내항성능 해석에서 중요한 해상상태 (Hong et al., 2024)인 SS4, SS5, SS6의 모달 주기(TP)에 해당하는 파장(λP)을 표시한 것이다. 전후동요의 결과를 살펴보면 SMP 결과는 다른 프로그램의 해석 결과보다 작은 값을 보였다. 2차원 기반의 SMP는 전후동요를 엄밀하게 해석하지 못하고 선수와 선미의 형상을 정확하게 반영할 수 없기 때문에 다른 해석 프로그램의 결과와 차이를 보인다. 반면 WISH-DB, WISH-NK, AdFLOW-Navy의 해석 결과는 거의 동일하다. WISH의 해석 결과와 AdFLOW-Navy의 해석 결과가 거의 동일한 것은 전진 속도의 영향이 없기 때문이다. 상하동요 해석 결과를 보면 SMP의 결과는 다른 해석 프로그램의 해석 결과와 전반적인 경향을 비슷하지만 파장비 1.0이하에서 차이를 보이고 있다. 특히 파장비 0.5~1.0부분은 해상상태 4, 5, 6에서 파랑 에너지가 가장 큰 부분으로 내항성능 지표에도 영향을 줄 것이다. 종동요 운동응답은 상하동요 운동응답과 유사한 경향을 보여주었다. Fig. 4는 15.0knots 조건에서 운동응답을 나타낸 것이다. 전진 속도가 있는 조건에서는 3가지 해석 프로그램의 결과들이 모두 조금씩 차이를 보였다. 전후동요 응답에서 SMP 결과는 WISH, AdFLOW-Navy 보다 작은 운동응답을 보여주었다. WISH-DB, WISH-NK, AdFLOW-Navy의 결과도 장파장 영역에서 미세한 차이를 보여주었다. 상하동요는 파장비 0.5~1.0 사이에서 운동응답은 다소 차이를 보이며 SMP의 해석 결과가 가장 작았고, WISH-NK의 결과가 가장 큰 값을 보여주었다. AdFLOW-Navy 결과는 SMP와 WISH-NK의 사잇값을 보이고 있으며 WISH-DB에 근접한 결과를 나타내고 있다. 이는 AdFLOW-Navy가 스트립이론과 동일한 전진속도 효과를 고려하고 있지만 3차원 형상효과를 충실히 반영하여 나타난 결과로 생각된다.
이러한 차이는 전진 속도의 영향으로 발생하는 것으로 해상상태 SS5, SS6의 모달 주기 주변이기 때문에 내항성능 지표에도 영향을 미칠 것으로 예상된다. 종동요 응답은 단파장 영역에서 SMP의 해석 결과가 WISH의 해석 결과보다 작았고, 장파장 영역에서 AdFLOW-Navy의 해석 결과가 WISH의 해석 결과보다 큰 값을 보여주었다.
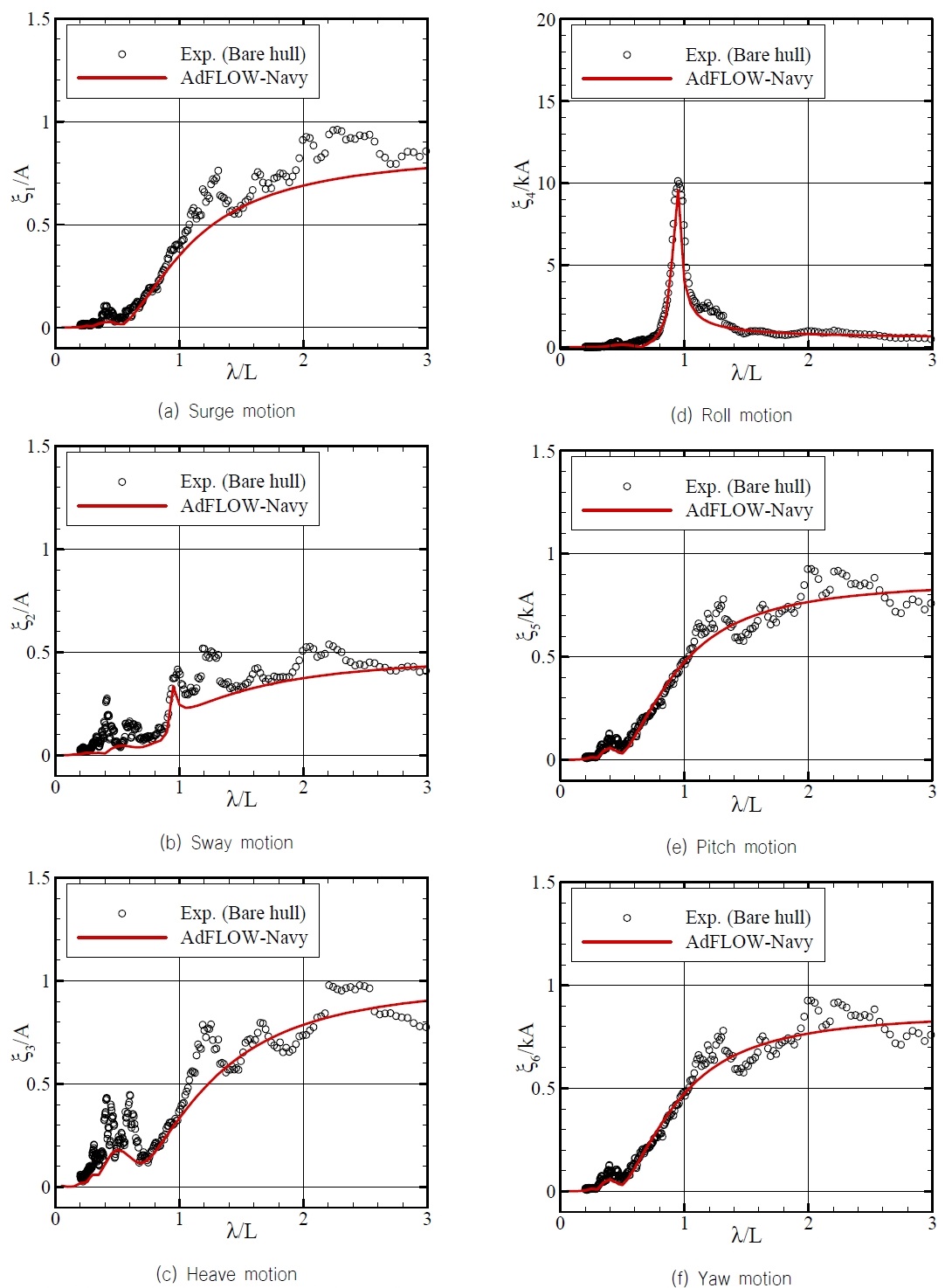
Fig. 5는 모형시험 결과와 AdFLOW-Navy 결과를 비교한 것이다. 모형시험 결과는 백색 잡음파(white noise) 조건의 해석결과를 나타낸 것이다. 모형시험에서 RAO는 운동응답 스펙트럼에서 계측된 파의 스펙트럼을 나누고 이동평균(moving average)을 통해서 얻었다. 전진 속도가 있는 조건에서 모형시험 결과와 수치해석 결과를 비교하려고 하였으나 전진 속도가 있는 조건에서는 계측 시계열의 데이터가 충분하지 않아서 운동응답의 RMS는 얻을 수 있었지만 RAO는 결과들이 분산되어 있어서 수치해석 결과와 비교하는 것이 쉽지 않았다. 모형시험의 결과는 점으로 나타내었으며 수치해석의 결과는 실선으로 나타내었다. 파장비 0.2 이하와 파장비 2.0 이상에서는 백색 잡음파의 에너지가 충분하지 않고 반사파의 영향으로 모형시험 결과들이 좀 더 분산되는 경향을 보여주었다. 그리고 이동평균을 취할 때 이동평균을 취하는 구간에 따라서 횡동요의 고유주기에서 운동응답의 크기가 변하였다. 본 연구에서는 다른 운동응답에 큰 영향을 주기 않는 범위에서 이동평균 구간을 정하였다. 모형시험 결과와 AdFLOW-Navy의 결과는 전반적으로 잘 일치하는 경향을 보였다.
4.2 횡동요 감쇠 계수
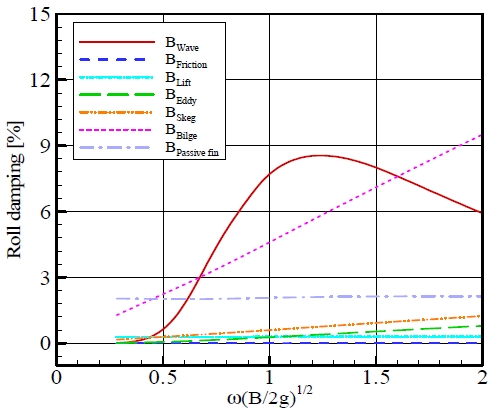
3.2절에서 설명한 추정식을 이용해서 횡동요 감쇠 계수의 영향을 살펴보고 모형시험의 결과와 비교하였다. Fig. 6은 12 knots, 횡동요 변위 10.0 도 조건에서 횡동요 감쇠 계수를 나타낸 것이다. X축은 주파수의 무차원화 값이며 Y축은 임계 감쇠 계수에 대한 비율을 나타낸 것이다. 무차원화된 값으로 KRISO-CVX1의 횡동요 고유주기는 약 0.65의 값을 가진다. 수동 핀의 경우 횡동요 감쇠 계수의 형태로 나타낼 수 있기 때문에 여기에서 같이 비교하였다.
파 감쇠(BWave) 계수는 주파수의 변화에 따라 변동이 크고 절대적인 값의 크기도 큰 것을 확인할 수 있다. 표면 마찰 감쇠(BFriction)는 다른 횡동요 감쇠 계수와 비교하면 아주 작은 값을 가진다. 양력 감쇠(BLift) 계수는 횡동요 주기와 무관하게 일정한 값을 가지며 식(7)을 보면 횡동요 변위에 무관하다. 와류 감쇠(BEddy) 계수와 스케그(skeg) 감쇠(BSkeg) 계수는 횡동요 주파수에 비례하여 증가하는 경향을 보였다. 빌지킬 감쇠(BBilge)는 주파수에 비례하여 증가하며 절대적인 값의 크기도 크다. 수동 핀(BPassive fin)은 주파수 변화에 따라서 값의 변화가 거의 없이 일정한 값을 가졌다. 횡동요 고유주기에서 파 감쇠 계수, 빌지킬 감쇠 계수, 수동 핀 감쇠 계수가 비교적 큰 값을 가졌고 나머지 감쇠 계수들은 비교적 작은 값을 가졌다.
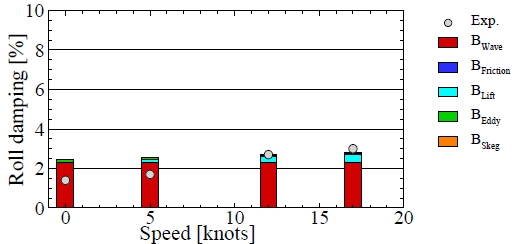
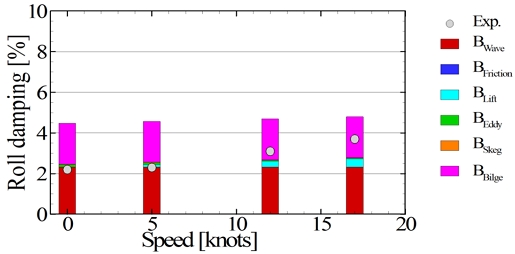
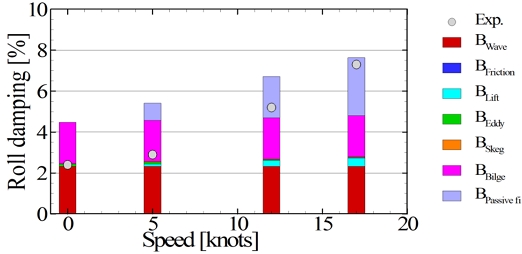
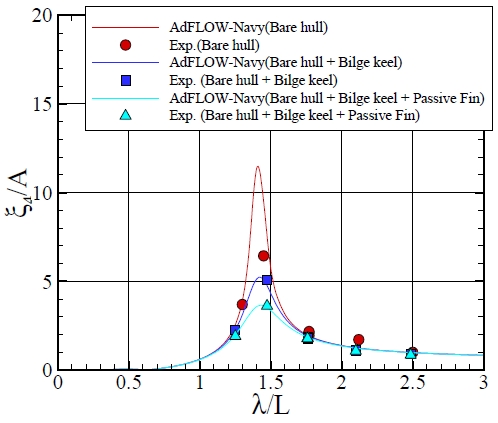
모형선의 자유 감쇠 시험을 3가지 부가물 조건(bare hull, bare hull + bilge keel, bare hull + bilge keel + passive fin)과 4가지 속도(0, 5, 12, 17knots)에서 수행하고 추정식과 비교하였다. 모형시험에서 감쇠 성분의 각각을 분리할 수 없기 때문에 각 조건에서 얻은 감쇠 계수의 값을 하나로 나타내었고 추정식에서는 각각의 성분을 합하여 나타내었다. 자유 감쇠 시험의 초기 각도는 약 5~6도이며 추정식에서 횡동요 변위 4도에 대해서 해석을 수행하였다. Fig. 7은 나선(bare hull)의 자유 감쇠 시험 결과를 나타낸 것이다. 나선에서 파 감쇠가 가장 크고 속도가 증가하면서 양력 감쇠가 증가하는 것을 확인할 수 있다. 속도가 낮은 조건에서는 모형시험 결과보다 추정한 감쇠 계수가 크고 속도가 증가하면서 모형시험과 추정한 감쇠 계수는 유사한 값을 보여주었다. Fig. 8는 나선에 빌지킬을 부착하고 자유 감쇠 시험을 수행한 결과이다. 추정식에서 파 감쇠와 빌지킬의 감쇠가 주요한 감쇠 성분이었다. 저속에서는 모형시험의 결과가 추정된 감쇠 계수보다 작았고 속도가 증가하면서 모형시험과 추정된 감쇠 계수는 유사한 값을 보여주었다. Fig. 9는 나선에 빌지킬과 수동 핀을 부착한 조건에서 결과를 정리한 것이다. Fig. 7, 8에서의 결과와 유사하게 저속에서는 추정식이 감쇠 계수를 과대 추정하고 속도가 증가하면 모형시험 결과와 유사해지는 것을 확인할 수 있다. 그리고 속도가 증가해서 17.0knots가 되면 수동 핀의 감쇠 성분이 가장 커지는 것을 확인할 수 있다. 추정식에 의한 횡동요 감쇠 계수는 정확한 값을 제시하는 것이 아니라 모형시험을 수행하기 전에 참고 값으로 활용할 수 있다는 관점에서 접근해야 한다.
Fig. 10은 3가지 부가물 조건(bare hull, bare hull + bilge keel, bare hull + bilge keel + passive fin)에서 횡동요 운동응답을 나타낸 것이다. 모형시험은 규칙파 조건에서 수행되었으며 파고는 실선 기준 2.0m이다. 나선 조건에서 조금 차이를 보였지만 전반적인 경향성은 모형시험 결과와 수치해석 결과가 잘 일치하였다.
4.3 핀 안정기
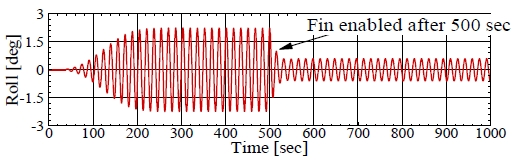
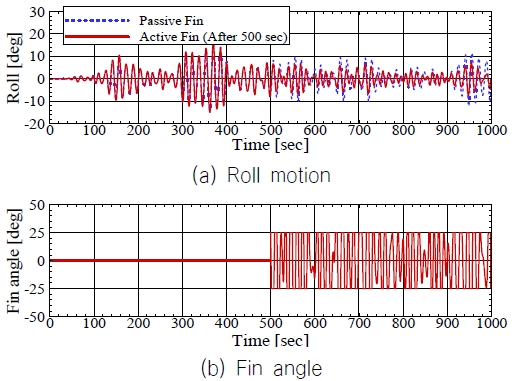
시간영역 내항성능 해석 프로그램인 KIMAPS-Navy에 능동 핀을 적용하여 횡동요 운동응답을 살펴보았다. Fig. 11은 규칙파 조건에서 능동 핀 효과를 나타낸 것이다. 처음에는 핀이 움직이지 않은 수동 핀의 결과이며 500초에서 핀이 움직이면서 횡동요 운동이 급격하게 감소하는 것을 확인할 수 있다. 핀 안정기가 작동하면서 75%의 횡동요 감소효과를 보였다. Fig. 12는 불규칙파 조건에서 핀 안정기의 영향을 나타낸 것이다. 규칙파와 동일하게 500초 이후에 핀이 작동하면서 횡동요 운동이 줄어든 것을 확인할 수 있다. 또한 핀 각도의 변화를 바로 확인할 수 있다.
4.4 교란파
경항모는 격납고(hangar)와 갑판사이에 엘리베이터가 두 개 설치되어 있으며 엘리베이터에 상대파고가 닿는지가 중요한 내항성능 지표이다. 기존의 스트립 기반의 내항성능 해석 프로그램은 교란파(disturbed wave)의 영향을 고려하지 않고 상대파고를 해석하였다. 즉 입사파(incident wave)와 함정의 운동에 의한 변위만을 고려하였다. 본 연구에서는 교란파를 고려하여 상대파고를 해석 하였다.
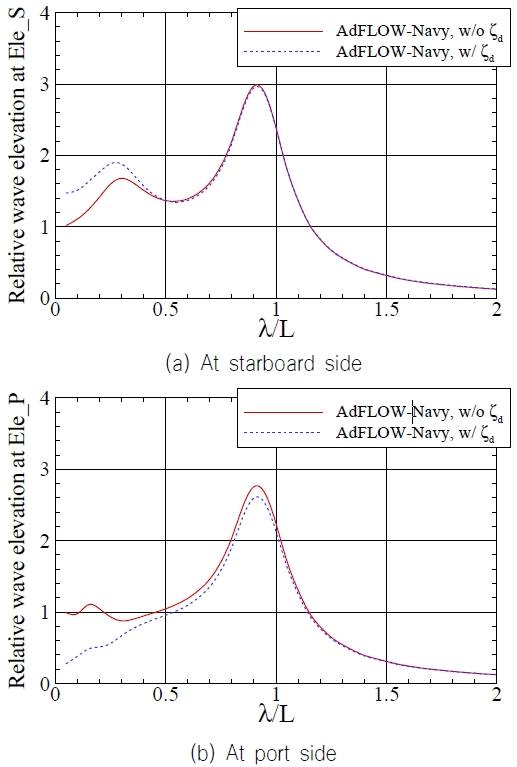
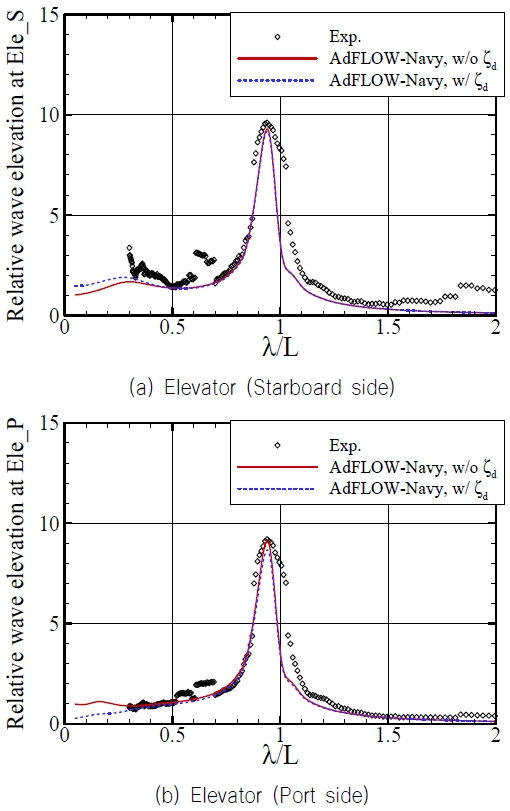
Fig. 13은 엘리베이터에서 상대파고의 응답을 나타낸 것이다. 입사파의 방향은 우현에서 오고 있으며 전진속도는 없는 조건이다. 교란파의 영향을 고려하지 않는 것을 붉은색 실선으로 나타내었고 교란파의 영향을 고려한 것을 청색 점선으로 나타내었다. 교란파의 영향은 단파장 영역에서 뚜렷하게 나타나며 선박의 길이 이상의 파장에서는 교란파의 영향이 거의 없었다. 단파장 영역에서 교란파의 영향을 고려하지 않는 상대파고는 1으로 수렴한다. 반면 교란파의 영향을 고려하면 입사파 방향(weather side)의 방향에서는 상대파고 응답이 1보다 증가하고, 입사파를 받지 않는 방향(lee side)에서는 상대파고 응답이 1보다 감소한다. Fig. 14는 함정주위 파랑장을 나타낸 것이다. 파장은 단파장에 해당하는 선박길이의 1/20 이다. 경항모의 우현에서 입사파가 반사되어 파고가 증가하는 것을 볼 수 있으며, 좌현에서 경항모의 영향으로 파가 거의 발생하지 않는 것을 확인할 수 있다.
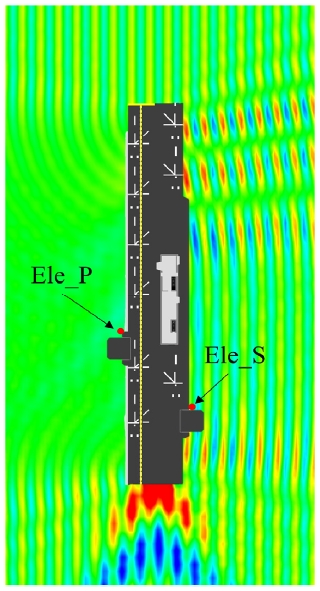
Wave contour around KRISO-CVX1 (V = 0.0knot, β = 90.0deg., λ/L = 0.05, Bare hull+Bilge keel+Passive fin)
Fig. 15는 엘리베이터에서 상대파고의 모형시험 결과와 수치해석 결과를 비교한 것이다. 모형시험 결과는 점으로 나타내었고 수치해석 결과는 실선과 점선으로 나타내었다. 모형시험이 백색 잡음파(white noise)에서 얻은 결과이기 때문에 에너지가 거의 없는 파장비 0.3이하에서는 모형시험 결과를 나타내지 않았다. 모형시험 결과와 수치해석의 결과는 전반적으로 유사하며 단파장 영역에서 교란파의 영향을 고려한 것와 모형시험의 결과가 좀 더 유사한 것으로 보인다.
4.5 불규칙파 중 운동응답
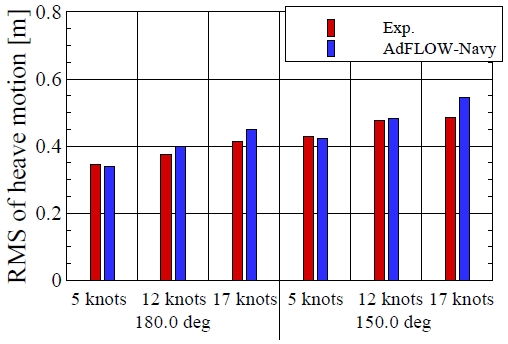
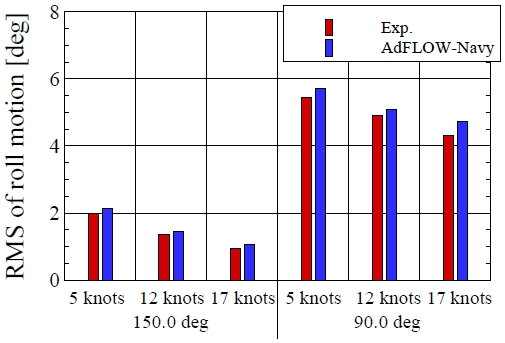
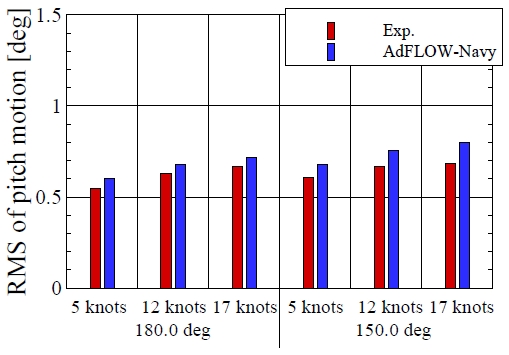
주파수영역 내항성능 해석 기법은 일반적으로 해상상태 6(Sea state 6)이하에서 사용된다. 해상상태 6에서 상하동요, 횡동요, 종동요 운동의 RMS 값을 모형시험 결과와 비교하였다. 상하동요, 종동요는 선수파(180.0deg), 선수사파(150.0deg) 조건에서 결과를 비교하였고 횡동요 운동은 선수사파(150.0deg), 횡파(90.0deg)조건에서 결과를 비교하였다. 선속은 5.0, 12.0, 17.0 knots 세 가지 조건에서 결과를 비교하였다. Fig. 16은 상하동요 결과를 나타낸 것이다. 5.0knots 조건에서 선수파 및 선수사파에서 모형시험 결과와 수치해석 결과는 잘 일치하였다. 반변 속도가 증가하면서 모형시험과 비교해서 수치해석의 결과가 조금 더 크게 해석되었다. Fig. 17은 횡동요 운동응답을 나타낸 것이다.
횡동요 운동응답은 속도가 증가할수록 줄어든 경향을 보여주었다. 모형시험과 비교해서 수치해석의 결과는 모든 조건에서 조금 큰 값을 보여주었다. Fig. 18은 종동요 운동응답의 결과를 나타낸 것이다. 앞에서 살펴보았던 상하동요, 횡동요에서 보였던 경향과 동일하게 수치해석 결과는 모형시험 결과보다 전반적으로 큰 값을 보여주었다.
4.6 비선형 운동
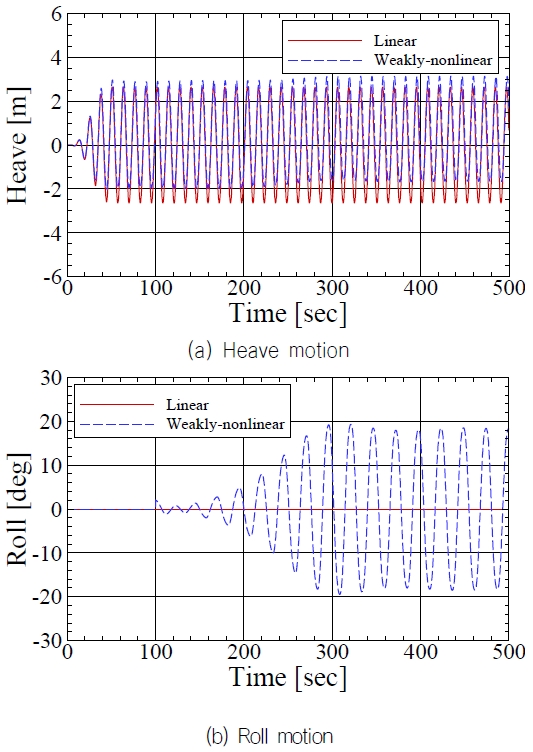
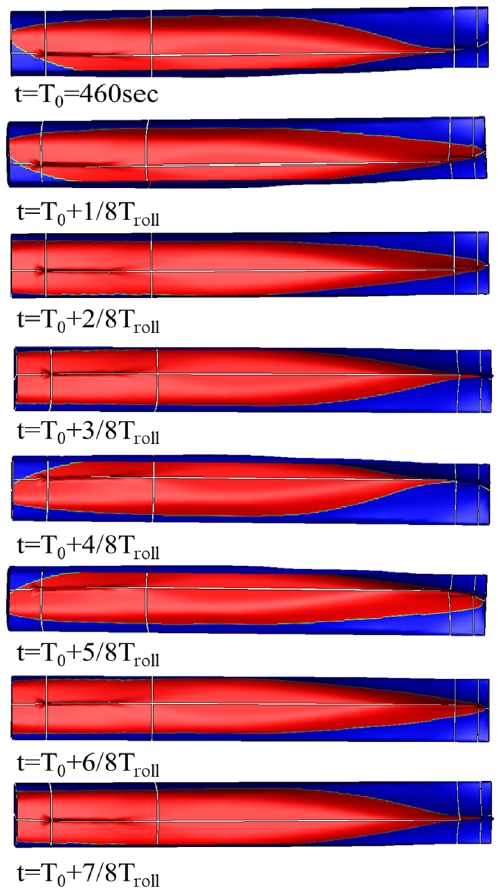
Weakly-nonlinear를 적용하면 플레어가 큰 선박의 대표적 비선형 운동인 파라메트릭 횡동요(parametric roll)를 해석할 수 있다. 파라메트릭 횡동요는 컨테이너선과 같이 플레어가 큰 선형에서 수선면적의 변화가 주기적인 복원력의 변화를 발생시켜 나타나는 대표적인 비선형 운동응답으로 횡동요의 고유 주파수(ωn)의 2배에 해당하는 입사파 조우주파수(ωe) 근처에서 발생한다. Fig. 19는 파장비 λ/L = 1.4, 파고 5미터, 입사파 주기 15초인 경우 파라메트릭 횡동요의 발생의 예를 보여주고 있다. 파라메트릭 횡동요의 발생이 가능한 조건 설정을 위해 초기 설계 무게중심을 3.9 미터 증가시켜 횡동요 고유주기를 12.4초에서 25.5초로 변화시킨 조건에서 해석을 수행하였다. Fig. 19(b)를 보면 선수파 조건에서 100초에서 2deg의 교란을 주었을 때 횡동요 운동응답이 20도까지 증가하는 것을 볼 수 있다. 또한 횡동요는 입사파의 2배 주기인 횡동요 고유주기로 진동하는 전형적인 파라메트릭 횡동요 현상을 나타내고 있다. 횡동요 운동이 커지면서 상하동요 운동응답은 줄어드는 에너지 변환현상도 관찰된다. Fig. 20은 급격한 입수면적 변화가 파라메트릭 횡동요를 발생시킴을 보여주고 있다. 본 계산을 통해 경항모 설계 시 무게중심 변화로 인한 파라메트릭 횡동요 발생가능성에 대한 검토가 필요함을 알 수 있다.
경항모 설계 시에는 전통적인 주파수영역에서의 내항성능평가와 아울러 시간영역에서 weakly-nonlinear 해석 기법을 적용하면 선형해석에서는 나타나지 않는 비선형 현상 예측이 가능하다. 모든 설계조건에서 비선형 해석을 수행할 필요는 없지만 임무가 예상되는 특정한 조건에서 경항모의 내항성능을 파악할 때 비선형 효과를 고려하는 것이 필요할 것으로 사료된다.
5. 결 론
본 연구에서는 경항모의 내항성능 평가를 위해, 선형 내항성능 해석을 위한 주파수영역 해석 프로그램 AdFLOW-Navy와 비선형 내항성능 해석을 위한 시간영역 해석 프로그램 KIMAPS-Navy를 개발하였다. 이로부터 다음과 같은 결론을 얻었다.
- - 스트립 기반의 해석 프로그램과 비교해서 본 연구에서 개발한 AdFLOW-Navy는 전후동요를 엄밀하게 반영할 수 있으며 선수 및 선미의 형상을 정밀하게 반영할 수 있음을 확인하였다. 또한 전진속도가 있는 조건에서 운동응답은 조금 차이가 있지만 전진 속도를 엄밀하게 고려한 해석 결과와 전반적인 경향성은 잘 일치하는 것을 확인하였다.
- - 3차원 패널로부터 2차원 단면을 자동으로 추출하고 2차원 단면에 대해서 횡동요 감쇠계수를 추정하고 모형시험 결과와 비교하였다. 추정된 횡동요 감쇠계수는 저속구간에서는 모형시험과 다소 차이를 보였지만 설계 초기에 모형시험을 수행하기 전에 활용 가능함을 확인하였다.
- - 상대파고를 해석할 때 교란파의 영향을 고려하였으며 단파장 영역에서 교란파의 영향이 크게 나타나는 것을 확인하였다. 해상상태 6에서 주파수 영역 내항성능 해석 프로그램의 결과는 모형시험의 결과와 유사한 값을 주는 것을 확인하였다.
- - 시간영역에서 weakly-nonlinear 해석 기법을 적용하여 특정 조건에서 비선형 운동응답인 파라메트릭 횡동요의 발생을 확인하였다. 경항모는 수선면 위 형상의 변화가 심하고 좌우가 비대칭인 경우도 있기 때문에 비선형 효과가 고려된 시간영역 해석이 필요함을 확인하였다.
Acknowledgments
It is noted that this paper is a revised edition based on the proceedings of SNAK 2024 in Jeju.
본 논문은 국방신속획득기술연구원으로부터 연구비를 지원(계약번호:UC200006D)받아 선박해양플랜트연구소에서 “함재기 이·착함 시뮬레이션 기술”(PGS4280)로 수행된 연구결과입니다. SMP 해석 결과는 Gibbs & Cox에서 제공하였으며 WISH는 서울대학교 김용환 교수님 연구실에서 제공받았습니다.
References
-
Cho, S.K., Hong, S.Y. and Jang, T.S., 2004. Experiment and simulation study on performance evaluation and design of fin-stabilizer. Journal of the Society of Naval Architects of Korea, 41(6), pp.1-7.
[https://doi.org/10.3744/SNAK.2004.41.6.001]

- Cho, S.K., Hong, S.Y., Song, H.D., Yon, Y.W., Oh, Y.J., Park, D.M. and Oh, S.H., 2024. Seakeeping performance model test technology of an aircraft carrier, The Korean Association of Ocean Science and Technology Societies, Session I, Jeju, Korea, 23-24 May, 2024.
-
Choi, Y.M., Bouscasse, B., Clement, A.H., Gentaz, L., Ferrant, P., Kim, Y.J. and Malenica, S., 2023. An alternative expression of the time domain free surface green function for deep water. Ocean Engineering, 267, 113267.
[https://doi.org/10.1016/j.oceaneng.2022.113267]

-
Comstock, E.N. and Keane Jr. R.G., 1980. Seakeeping by design, Naval Engineers Journal, 92(2), pp.157-178.
[https://doi.org/10.1111/j.1559-3584.1980.tb05267.x]

-
Comstock, E.N., 1982. Seakeeping performance comparison of air capable ships, Naval Engineers Journal, 94(2), pp.101-117.
[https://doi.org/10.1111/j.1559-3584.1982.tb02432.x]

- Cummins, W.E., 1962. The Impulse response function and ship motion. Report 1661, Department of the Navy, David W. Taylor Model Basin, Hydromechanics Laboratory, Research and Development Report, October 1962.
-
Falzarano, J. and Somayajula, A., 2015. An overview of the prediction methods for roll damping of ships. Ocean Systems Engineering, 5(2), pp.55-76.
[https://doi.org/10.12989/ose.2015.5.2.055]

-
Hong, S.Y. Park, D.M., Jung, J.H., Seo, M.G. and Cho, S.K., 2024, A study on Short-Take and Vertical Landing(STOVL) performance evaluation of a light aircraft carrier and a consistent analysis of Safe Operating Envelope (SOE), Journal of the Society of Naval Architects of Korea, 61(2), pp.126-135.
[https://doi.org/10.3744/SNAK.2024.61.2.125]

-
Ikeda, Y., Himeno, Y. and Tanaka, N., 1978. Components of roll damping of ship at forward speed. Journal of the society of Naval Architects of Japan, 143, pp.113-125.
[https://doi.org/10.2534/jjasnaoe1968.1978.113]

- International Towing Tank Conference (ITTC), 2011, Recommended Procedures ans Guidelines – Numerical Estimation of Roll Damping (7.5-02-07-04.5), pp.1-32.
-
Kato, H., 1958. On the frictional resistance to the rolling of ships. Journal of Zosen Kiokai, 102, pp.115-122.
[https://doi.org/10.2534/jjasnaoe1952.1957.102_115]

-
Kim, B. and Shin, Y.S., 2007, Steady flow approximations in three-dimensional ship motion calculation, Journal of Ship Research, 51(3), pp.229-249.
[https://doi.org/10.5957/jsr.2007.51.3.229]

-
Kim, K.H. and Kim, Y., 2010a. Numerical analysis of added resistance on ships by a time-domain rankine panel method, Journal of the Society of Naval Architects of Korea, 47(3), pp.398-409.
[https://doi.org/10.3744/SNAK.2010.47.3.398]

- Kim, K.H. and Kim, Y., 2010b. Comparative study on ship hydrodynamics based on Neumann-Kelvin and double-body linearizations in time-domain analysis. International Journal of Offshore and Polar Engineering, 20(04), pp.265-274.
- Lee, J.H., Kim, B.S. and Kim, Y., 2017. Study on steady flow effects in numerical computation of added resistance of ship in waves. Journal of Advanced Research in Ocean Engineering, 3(4), pp.193-203.
-
Lloyd, A.R.J.M., 1991. Seakeeping. philosophical transactions of the royal society of London. Series A: Physical and Engineering Sciences, 334(1634).
[https://doi.org/10.1098/rsta.1991.0012]

-
Newman, J.N. (1979). The theory of ship motions. Advances in applied mechanics, 18, pp.221-283.
[https://doi.org/10.1016/S0065-2156(08)70268-0]

- North Atlantic Treaty Organization(NATO), 2000. Common procedures for seakeeping in the ship design process, standardization agreement, STANAG 4154 NAV(Edition 3).
- Salvensen, E.O. Tuck, O. and Faltinsen, O., 1970. Ship motions and sea loads. Transactions of the Society of Naval Architects and Marine Engineers, 78, pp.250-287.
- Science Applications International Corporation(SAIC), 2006. Nonlinear 3D Seakeeping and Load Prediction Program, Annapolis, Maryland, USA.
- Schmitke, R.T., 1978. Ship sway, roll, and yaw motions in oblique seas. SNAME Transactions. 86, pp.26-46.
-
Seo, M.G., Kim, K.H., Park, D.M. and Kim, Y., 2013. Comparative study on added resistance for different hull forms by using weakly-nonlinear seakeeping formulations. Journal of the Society of Naval Architects of Korea, 50(1), 49-58.
[https://doi.org/10.3744/SNAK.2013.50.1.49]