전산유체역학 해석을 통한 프로펠러의 상하동요 운동 중 유체력 특성 연구

1. 서 론

오랫동안 선박의 유체역학적 성능은 정속 직진 중의 저항/추진, 긴 주기의 수평면 상 운동에 대한 조종, 짧은 주기의 파랑으로 인한 운동을 다루는 내항의 분야로 나누어 해석되었다. 하지만 최근 들어 선박의 유체역학적 성능을 실제 운항 조건을 기준으로 평가하게 되면서 앞서의 구분이 적용되지 않는 통합적인 유체역학적 성능의 해석이 요구되고 있다. 실해역 조건은 일반적으로 불규칙파 중 운항을 의미하므로, 결국 선박의 유체역학적 성능 해석은 앞으로는 불규칙파 중 저항, 추진, 조종이 통합된 문제로 귀결될 것이다.

전통적인 선박의 내항 문제는 추진 성능과의 연계는 고려하지 않고 파랑으로 인한 선체의 운동만을 다뤘다. 파랑 중 저항 문제인 부가저항 관련 연구에서는 초기에는 전후동요 없이 일정한 속도로 직진하는 선체의 파랑 중 종동요와 상하동요 운동에 집중하였고 (Simonsen et al., 2013; Yang et al., 2013; Yang et al., 2015; Ozdemir and Barlas, 2017; Seo and Park, 2017; Kim et al., 2018; Lee et al., 2022a), 스프링 계류를 이용해 파랑 중 전후동요를 약하게 제한하는 운동을 추가로 다루게 되었다 (Sadat-Hosseini et al., 2013; Seo et al., 2014; Park et al., 2015; Yu et al., 2017; Sigmund and el Moctar, 2018).

최근에는 부가저항의 상위개념으로 부가동력에 대한 연구가 수행되고 있다 (Lee et al., 2019; Seo et al., 2020; Kim et al., 2021a; Lee et al., 2022b; Sanada et al., 2022). 부가동력에서는 파랑 중 선체 운동과 이로 인한 유동 안에서 추진기의 성능과 선체-추진기 상호작용의 변화를 부가저항 문제에 더하여 고려해야 한다 (Sigmund and el Moctar, 2017; Eom et al., 2021a). 수치해석 분야에서는 계산 자원의 절약을 위해 실제 회전하는 추진기 대신 추진기로 인한 추력만을 반영하는 방식의 해석이 부가동력 연구에 적용되기도 하였다 (Lee et al., 2021; Zhang et al., 2021; Lee et al., 2022b). 이런 접근에서는 추진기의 축방향 추력만을 반영하기 때문에 다른 유체력 요소의 영향은 무시된다. 하지만 Seo et al. (2023)의 연구에서는 추진기의 영향으로 선수파 중 선체운동과 이로 인한 부가저항이 달라지는 것을 실험을 통해 확인하였으므로, 실제 추진기 대신 추력항만을 적용하는 접근에는 물리적 현상의 정확성에 한계가 있을 것으로 보인다.

파랑 중 운동하는 선박의 추진기에는 규칙적으로 유입류의 방향이 변하면서 축방향의 추력 외에도 다른 방향의 유체력이 발생할 수 있다. 이에 대한 연구로, 추진기의 단독 조건에서 수면의 영향에 대한 연구 (Eom et al., 2021b)와 사항 중 유체력의 해석 사례가 있다 (Dubbioso et al., 2013; Dubbioso et al., 2014; Yao, 2015; Hou and Hu, 2019). 사항 조건에 놓인 추진기에서는 추진기 날개 각각의 하중 변화와, 사항 유동의 속력에 비례하여 유체력과 모멘트가 발생하는 경향이 보고되었다. 그리고 추진기의 축방향 외의 유체력과 모멘트 성분은 조종 운동 중의 베어링 하중의 관점에서 연구된 바가 있다 (Dubbioso et al., 2017; Muscari et al., 2017).

이들 추진기 단독 성능에 대한 연구 결과를 선체 운동과 연계하여 추진기가 장착된 선체의 내항과 조종 문제를 더욱 잘 설명할 수 있다. 선체 중앙에서 멀리 떨어져 있는 추진기는 사항 조건에서 축방향 외의 유체력을 발생하여 선체의 종동요, 선수동요 방향의 회전 운동에 대한 모멘트를 발생시킨다. 조종 운동 모델에 추진기의 단독 사항 상태의 횡방향 유체력 모델을 적용한 선박 조종 연구에서는 이러한 유체력이 조종 성능에 큰 영향을 미치지 못함을 보인 바 있다 (Kinaci and Ozturk, 2023). 하지만 전산유체역학(computational fluid dynamics, CFD)을 통한 Zhang et al. (2020)의 연구에서 선체 반류 안에서는 축방향 외의 유체력이 단독 조건보다 더욱 커짐을 보였으므로, 선체 상호작용을 고려하면 조종 성능에 추진기의 축방향 외의 유체력이 영향을 줄 것으로 생각된다.

이외에도 추진기가 운동 중인 선체에 미치는 영향으로 가속 운동 중 발생하는 부가질량을 생각할 수 있다. Park et al. (2020)는 수중무인운동체의 조종 성능 해석을 위한 구속모형시험에서 추진기로 인한 유체력의 차이가 가속도에 비례하는 것을 보여 부가질량의 측면에서 실험 결과를 설명한 바 있다.

본 연구에서는 추진기의 상하동요 운동 중 사항 유입류와 가속도로 인해 발생하는 유체력의 특성을 파악하기 위해 CFD를 이용하였다. 축 방향 유속으로 정의된 전진비 조건에 더하여 사항 유속 조건을 적용하여 수치해석을 하였고, 추가로 가속도 유무에 따른 6분력의 변화로부터 가속 운동 중 유체력 성분을 얻어내었다. 이 유체력 성분이 가속도에 비례하는지를 확인하여 부가질량의 관점에서 이해할 수 있는지를 확인하고, 운동 중인 추진기의 유체력에서 어떤 비중을 차지하는지 확인하였다.

논문은 다음과 같이 구성되었다. 2장에서는 해석 대상 프로펠러와 해석 조건을 다뤘다. 3장에 전산 해석에 사용한 프로그램의 주요한 내용을 소개하였다. 4장에는 사항, 가속도로 인한 6분력의 비교 결과를 설명하였다. 5장에 논문의 결론을 정리하였다.

2. 해석 대상과 조건

2.1 대상 모형

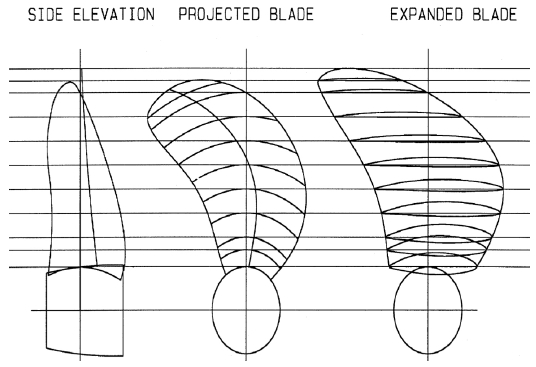
연구에 사용된 추진기 모형은 KP505이다. 이는 선박해양플랜트연구소(Korea Research Institute of Ships and Ocean Engineering, KRISO)에서 연구목적으로 선형과 실험 결과가 공개된 3,600TEU급 컨테이너선 KRISO Container Ship(KCS)를 위해 설계되었다 (Kim et al., 2001). 추진기의 지름(D)은 대상선형을 활용한 연구를 참고하여 선정하였다 (Kim et al., 2021a; Kim et al., 2021b). 연구에 사용한 KP505의 형상과 주요 제원은 Fig. 1과 Table 1에 나타내었다.

Fig. 1

Design of KP505 propeller blade

Table 1

Principal particulars of KP505

2.2 좌표계

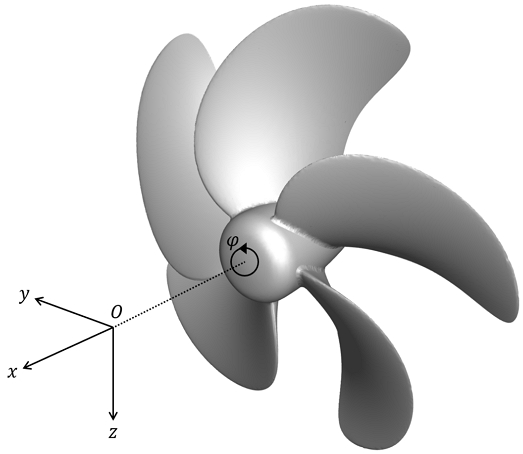
본 연구의 CFD 해석에 선체를 포함하지는 않았지만, 선박의 운동 해석과의 연계를 고려하여 좌표계는 가상의 선체에 고정된 것으로 정하였다. 따라서 추진기의 회전을 따라 좌표계가 회전하지 않는다. Fig. 2는 좌표계의 구성이다. 운동 해석의 좌표계는 원점(O)이 선체의 길이방향 중심을 지나는 수직선과 추진기 축의 연장선의 교점에 위치한 오른손 직교 좌표계(O - xyz)이다.

Fig. 2

Ship-fixed coordinate system

x, y, z축의 양의 방향은 각각 추진기의 축을 따라 상류 방향, 축에 수직인 우현 방향, 아래 방향으로 정의하였다. 추진기는 x축을 중심으로 회전하며 x와 z방향으로 전진하도록 하였다. 추진기 날개의 위상(ϕ)은 날개의 기준선과 z축이 이루는 각도로, x축을 중심으로 하는 회전 방향 상에서 정의된다. 선수파 중 선박 운동을 고려한다면 z축은 선체의 파랑 중 종동요, 상하동요의 영향을 직접 받는 방향, y축은 운동이 없는 방향으로 볼 수 있다. 따라서 본 논문에서는 z방향 운동을 주된 시험 조건으로 정의하였다.

2.3 해석 조건

실제 선박의 선수파 중 운동은 x - z평면 상에서 전후동요, 상하동요, 종동요로 이뤄진다. 추진기의 운동 또한 이 세 운동이 복합적으로 나타날 것으로 기대된다. 하지만 추진기 성능에 대해 세 가지 운동의 속도와 가속도의 복합적 영향을 전체적으로 이해하기는 어려운 일이므로, 해석에 적용할 운동 성분을 줄여 문제를 단순화할 필요가 있다.

가속도를 포함한 해석 조건을 정하는데 있어 Park et al. (2020)의 연구를 참고하여 부가질량의 개념으로 추진기의 영향을 가정하였다. 전체 모형선의 원점 기준 부가질량(m_z)과 부가관성모멘트(J_yy)는 각각 식 (1)과 (2)와 같이 나타낼 수 있다. 여기서 x_P는 선체 길이 방향 중심에서 본 추진기의 x방향 위치이다.

$\[ m_z=m_{zH}+m_{zP} \]$

(1)

$\[ J_{yy}=J_{yyH}+J_{yyP}+x_P^2{m}_{zP} \]$

(2)

만약 선체가 상하동요와 종동요 운동을 한다면 선체의 상하동요 운동에 대한 부가질량(m_zH)과 부가관성모멘트(J_yyH)에 더하여 추진기의 상하동요의 부가질량(m_zP)과 종동요의 부가관성모멘트(J_yyP)가 발생할 것이다. 식 (1)의 우변의 두 성분에 대해서, 선체의 상하동요 중 투영되는 면적이 추진기보다 월등히 크기 때문에 추진기의 부가질량은 무시할만한 수준으로 생각된다. 같은 이유로 식 (2)의 J_yyP 또한 J_yyH에 비할 수준은 아닌 것으로 판단하였다.

반면 식 (2)에서는 추진기가 무게중심에서 가장 먼 위치인 선체의 후방에 위치하면서 $$ x_P^2{m}_{zP}$$항이 전체 J_yy에 영향을 줄 수 있을 것으로 보았다. 따라서 추진기의 상하동요 병진 운동으로 인한 가속도 관련 항이 선체의 종동요 운동에 미치는 영향을 식별하는 방향으로 해석 조건을 한정하였다.

추진기의 작동 조건은 전진 속도(U_A), 회전수(n), 추진기의 축에 수직인 종방향의 운동 속도(W), 같은 방향의 가속도($$ \dot{W}$$)의 네 가지로 구성된다. 앞의 두 가지는 추진기 성능과 관련하여 필수적으로 사용되는 전진비(advance ratio, J_A)로 무차원화하여 식 (3)과 같이 나타내었다.

$\[ J_A=\frac{U_A}{nD} \]$

(3)

W는 사항각과의 연계를 고려하여 식 (4)와 같이 U_A로 무차원화하여 W'로 나타내었다. 본 연구에서 다룰 시험 조건에서는 W'가 크지 않기 때문에 W'는 추진기 사항각과 거의 비례한다고 볼 수 있다.

$\[ W^{\mathrm{\text{'}}}=\frac{W}{U_A} \]$

(4)

$$ \dot{W}$$의 무차원화를 위해 $$ \dot{W}$$로 인한 추진기의 유체력이 어떤 양상을 보일지를 먼저 고려해야 한다. 추진기는 양력이 지배적이므로 유체력에 대해 점성의 영향이 작은 편이기 때문에, 해석 조건의 선정에서는 비점성 유동을 가정할 수 있다. 따라서 부가질량의 관점에서 가속도 영향을 받는 성분의 크기는 U_A, W에는 무관하고 $$ \dot{W}$$에 비례할 것으로 예상하여, 실험 조건 전체에서 고정된 값인 n, D를 이용해 식 (5)와 같이 $$ {\dot{W}}^{\mathrm{\text{'}}}$$으로 무차원화하였다.

$\[ {\dot{W}}^{\mathrm{\text{'}}}=\frac{\dot{W}}{n^{2}D} \]$

(5)

Table 2에 전체 해석 조건을 정리하여 나타내었다. 시험은 정속 직진(straightforward), 정속 사항(steady drift), 수직 가속(vertical acceleration)의 세 가지로 구성된다. 정속 직진 조건은 같은 조건의 모형시험과 비교검증을 위해 다양한 J_A 조건에서 해석을 수행하였다. 사항 조건의 J_A 는 본 연구가 참고한 자항시험(Kim et al., 2021b)의 조건에서 사용한 모형선 자항 상태에서 추진기의 작동 조건을 바탕으로 구하였다. 모형선의 전진속도(V_S), 반류비(w_P0), n가 주어진다면 식 (6)을 통해 J_A 를 구할 수 있다.

$\[ J_A=\frac{\left(1-w_{P0}\right)V_S}{nD} \]$

(6)

Table 2

Test conditions

KP505의 상하 운동과 가속도는 추진기의 장착 선형인 KCS의 선수파 중 부가동력에 대한 CFD 해석 결과를 이용해 그 범위를 구하였다 (Kim et al., 2021a). 파장 별로 얻어진 선체의 운동과 추진기의 수직방향 변위로부터 W와 $$ \dot{W}$$의 최대값을 구했고, 이를 포함하도록 CFD 해석 조건의 범위를 정하였다.

정속 사항 조건의 해석이 수행된 W'의 최대값은 0.38로, 이를 입사각으로 환산하면 20.8°이다. 정속 사항 조건의 해석은 최대 W'에 대해 25, 50, 75, 100% 조건에서 수행하였다.

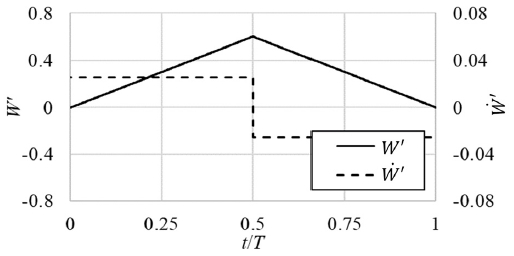
Fig. 3은 제안된 수직 방향 가속 운동을 적용한 시계열 속도, 가속도의 예시이다. 가속도 조건의 해석은 다음의 순서로 수행되었다. 우선 J_A = 0.535 조건에서 추진기를 직진한다. 그리고 시험 조건으로 정해진 0.026, 0.052의 $$ {\dot{W}}^{\mathrm{\text{'}}}$$를 적용하여 W'이 0.6이 될 때까지 수직 방향 속도를 증가시킨다. 이후 $$ -{\dot{W}}^{\mathrm{\text{'}}}$$를 적용해 W'이 0까지 감소하도록 한다. 운동 주기 (T)동안 하나의 W' 조건에 대해 $$ +{\dot{W}}^{\mathrm{\text{'}}}$$, $$ -{\dot{W}}^{\mathrm{\text{'}}}$$의 두 가지 가속도 조건의 유체력 변화를 확인할 수 있다.

Fig. 3

Time history of W˙ and W˙' in periodic vertical motion (W˙'=±0.026)

3. 전산 해석 기법

3.2 해석 영역 구성 및 격자계

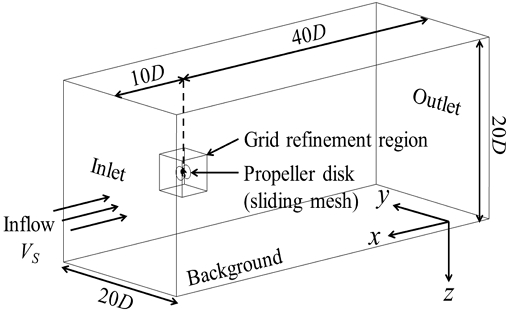
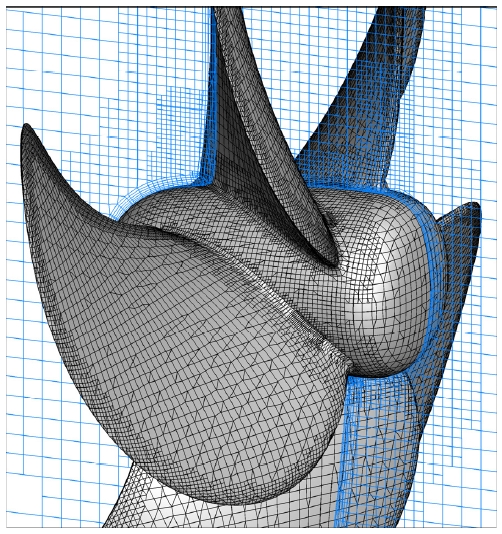
본 연구에서는 추진기의 회전, 축방향의 직진운동에 더하여 축에 수직인 방향의 가속 운동을 구현해야 한다. 해석 영역은 크게 배경 유체 영역과 회전운동을 하는 추진기 영역으로 구성된다. Fig. 4는 계산 영역의 구성이다.

Fig. 4

Computational domain and grid regions

격자계는 영역별로 배경(Background), 격자 재분할 구역(Grid refinement region), 추진기 원반(Propeller disk)으로 나뉘며 각각 구성된 격자수는 Table 3에서 보인 바와 같다. 추진기 원반 영역은 슬라이딩 메쉬(sliding-mesh)로 회전을 구현하였다.

Table 3

Cell counts of grid regions

경계 조건은 Table 2에서 보인 직진과 정속 사항/수직 가속 조건에 대해 각각 적용되었다. 직진 조건에서는 Fig. 4의 유입면(Inlet)에 속도 및 압력 경계조건은 각각 Dirichlet과 Neumann 경계조건을 적용하였고, 유출면(Outlet)에는 속도에 대해 Neumann, 압력에 대해 Dirichlet 경계조건을 적용하였다. 배경 영역의 나머지 경계면으로의 유동 유입이나 유출은 고려하지 않았다. 추진기 표면의 속도 경계조건은 속도값은 0으로 고정된 Dirichlet 경계조건, 압력은 Neumann 경계조건을 적용하였다. 정속 사항과 수직 가속 조건에서는 배경 격자를 포함한 전 계산 영역이 주어진 속도나 가속도로 수직운동을 하도록 하여, 유입면과 유출면을 상하부에도 정의하였다.

Fig. 5는 해석을 위한 프로펠러의 표면과 x - z평면 상의 격자 구성이다. 벽면에서의 전단력(τ_w) 보정을 위한 벽함수(Wall function)를 사용하기 위해 추진기 날개면과 허브에는 9개 층의 프리즘 격자를 배치하였다. 벽으로부터 법선 방향의 첫 번째 격자 높이(Δs)는 식 (13)을 통해 y⁺가 30보다 작은 값을 가지도록 설정하였다.(Versteeg and Malalasekera, 2007)

$\[ y^{+}=\frac{\mathrm{\Delta }s{U}^{\mathrm{*}}}{\nu },{ U}^{\mathrm{*}}=\sqrt{\frac{{\tau }_w}{\rho }} \]$

(13)

Fig. 5

Grid distribution on the model surface and x - z plane

여기서 ρ와 ν는 각각 유체의 밀도와 동점성 계수이다.

4. 해석 결과와 고찰

4.1 정속 사항 조건

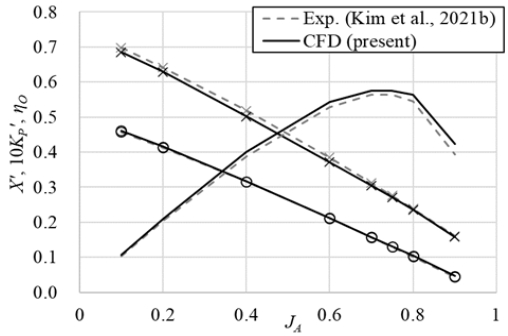
CFD를 이용한 정속 직진 중의 추진기 성능 해석 결과를 실험과 비교하여 검증하였다. Fig. 6은 같은 조건의 실험을 통해 얻은 추진기 단독 성능 곡선과의 비교이다. 추진기 효율(η_O)은 식 (14)를 통해 정의하였다. 토크에서 약간의 차이는 있으나, 본 연구에서 주요하게 다룰 추력에서는 실험 결과와 잘 일치하는 것을 확인할 수 있다.

$\[ {\eta }_O=\frac{J_A{X}^{\mathrm{\text{'}}}}{2\pi K_P{}^{\mathrm{\text{'}}}} \]$

(14)

Fig. 6

Comparison of propeller performance for straight forward test

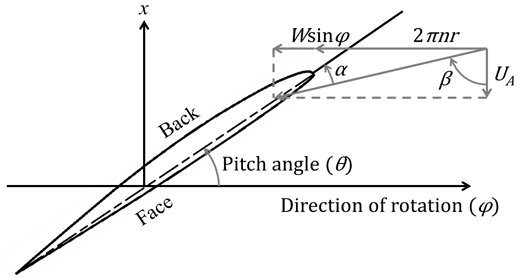
수직 방향 운동에 따른 유체력과 모멘트의 변화를 살펴보기에 앞서 Dubbioso et al. (2013, 2014)를 참고하여 Fig. 7과 같이 KP505 프로펠러의 2차원 날개 단면에서 사항각 중 받음각 변화를 분석하였다.

Fig. 7

Schematic of the angle of attack of the propeller blade in oblique flow

추진기 날개의 받음각(α)은 식 (15)를 통해 구할 수 있다.

$\[ \alpha =\beta +\theta -{90}^{\circ } \]$

(15)

여기서 β, θ는 각각 날개 단면을 포함한 평면에서 추진기 유입류가 이루는 각도와 추진기 날개의 피치각으로, 식 (16), (17)을 통해 반지름 위치(r), 추진기 피치(P)로부터 계산할 수 있다.

$\[ \beta ={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\frac{2\pi nr+W\mathrm{s}\mathrm{i}\mathrm{n}\varphi }{U_A}\right) \]$

(16)

$\[ \theta ={\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\frac{P}{\pi D}\right) \]$

(17)

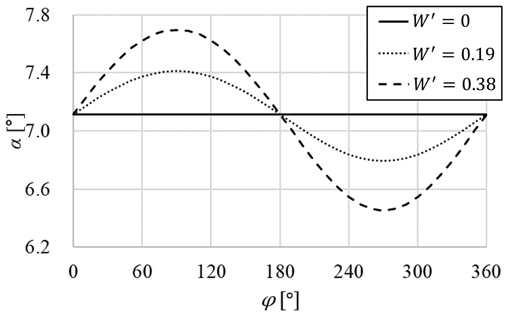
Fig. 8은 본 연구의 정속 사항 시험 조건에서 구한 ϕ에 따른 α의 추세로, r = 0.35D 위치에서 구한 값이다. 프로펠러 날개의 중앙선이 +z축에 놓였을 때를 ϕ = 0˚로 정의하여 나타냈다.

Fig. 8

Angle of attack of the propeller blade with respect to the phase angle

사항 유입류의 영향으로 α는 90˚, 270˚ 위상에서 서로 반대로 나타났다. W' = 0.38에서 그 진폭은 1.3˚로, 이는 W' = 0조건에서 J_A가 0.48에서 0.59까지 ±10% 정도 변화하는 수준의 α 변화에 대응한다. 이런 추진기 날개의 위상에 따른 하중 변화는 유체력의 불균형을 유발하여 진동의 원인이 될 수 있다. 하지만 평균 α는 W에 무관하게 일정하므로 각 날개의 유체력의 총합인 추진기의 추력, 토크는 W 조건에 대해서 큰 변화가 없을 것으로 생각된다.

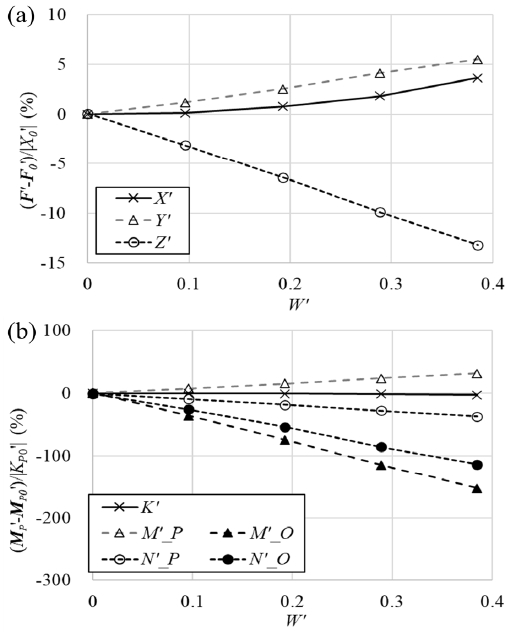
모형선 자항 조건인 J_A = 0.535에서 W' 의 변화에 따른 6방향 유체력과 모멘트의 변화를 조사하였다. x축 방향 외의 유체력 성분 중에는 수직 방향 유입류의 방향인 z방향의 유체력(Z)과 x - z평면 상의 모멘트인 y방향 모멘트(M)가 주로 발생할 것으로 예상하였다. 본 연구의 해석 범위와 유사한 30° 이내의 입사각에서의 선형적인 유체력과 모멘트의 증가 양상을 보인 Dubbioso et al. (2013)의 연구 결과에서는 사항 유입류 방향의 유체력 성분이 그렇지 않은 방향 성분에 비해 약 5배 더 큰 것으로 확인되었고, 모멘트는 두 방향이 서로 비슷한 크기를 보였다.

Fig. 9는 정속 사항 조건의 유체력, 모멘트 결과이다. 모든 유체력과 모멘트는 J_A = 0.535, W' = 0 조건의 X₀', K_P0'로써 무차원화하여 나타내었다. Dubbioso et al. (2013)의 연구에서 보인 바와 같이 W'에 따른 Z'의 변화는 운동 방향과 반대로 나타났다. 그리고 그 크기는 운동이 없는 방향인 Y'보다 크게 나타났지만, 그 비율은 2.5배 정도로 Dubbioso et al. (2013)의 연구보다는 두 방향 성분 간의 차이가 작게 얻어졌다. 이는 본 연구에서 사용된 추진기의 형상이 스큐(skew)를 가져 더 복잡한 3차원 형상을 가지기 때문에 z방향 유입류도 날개 표면을 따라 y방향으로 흘러나가는 비율이 증가함에 따른 반작용으로 생각된다.

Fig. 9

Hydrodynamic force and moment of the propeller with the vertical inflow speed variation

유체 모멘트 성분인 M_P'와 N_P'의 크기가 비슷한 것은 Dubbioso et al. (2013)의 연구에서도 지적되었던 내용으로, 유체력 결과와는 다르게 본 연구에서도 이와 같은 경향을 보였다. 좌표계 원점인 선체의 길이방향 중심에 작용하는 모멘트인 M_O'와 N_O'에 대해서는 추진기 자체에서 발생하는 모멘트인 M_P'와 N_P'보다 추진기의 유체력과 추진기 선미 배치로 인한 모멘트 성분(x_P × F)이 더 지배적인 것으로 확인되었다. 그리고 M_O'이 추진기의 수직방향 속도와 반대로 발생하기 때문에 선미 위치에서 작동하는 추진기는 종동요에 대한 일종의 감쇠 작용(Damping)을 수행하는 것으로 볼 수 있다.

Fig. 8에서 설명한대로 W'의 변화에 따른 X', K_P'의 변화는 그렇게 두드러지지 않았다. 이는 선체의 상하동요, 종동요 운동이 발생하더라도 추진기의 추력, 토크는 전진 속도만을 기준으로 산정해도 큰 문제가 없음을 의미한다. 따라서 이전 연구에서 사용해 온 전진비에만 의존한 추진기 모델이 사항각을 포함한 유동 조건에 놓이더라도 x방향 유체력의 해석에 한해서는 타당한 결과를 낸다고 볼 수 있다.

Fig. 9에서 보인 결과를 이용해 J_A = 0.535 조건에서 W'에 따른 F', M_P'을 식 (18)과 같이 근사하여 나타낼 수 있었다. X_P', K_P'은 추세의 개형을 감안하여 W'의 2차 함수로, 나머지 유체력과 모멘트 성분은 W'의 1차 함수로 근사하였다.

$\[ \begin{array}{c}{X}^{\mathrm{\text{'}}}=0.0586W^{\mathrm{\text{'}}2}+X_0{}^{\mathrm{\text{'}}}\hfill \\ Y^{\mathrm{\text{'}}}=0.0331W^{\mathrm{\text{'}}}\hfill \\ Z^{\mathrm{\text{'}}}=-0.0803W^{\mathrm{\text{'}}}\hfill \\ K_P{}^{\mathrm{\text{'}}}=-0.0076W^{\mathrm{\text{'}}2}+K_{P0}{}^{\mathrm{\text{'}}}\hfill \\ M_P{}^{\mathrm{\text{'}}}=0.0331W^{\mathrm{\text{'}}}\hfill \\ N_P{}^{\mathrm{\text{'}}}=-0.0385W^{\mathrm{\text{'}}}\hfill \end{array} \]$

(18)

4.2 가속도 조건

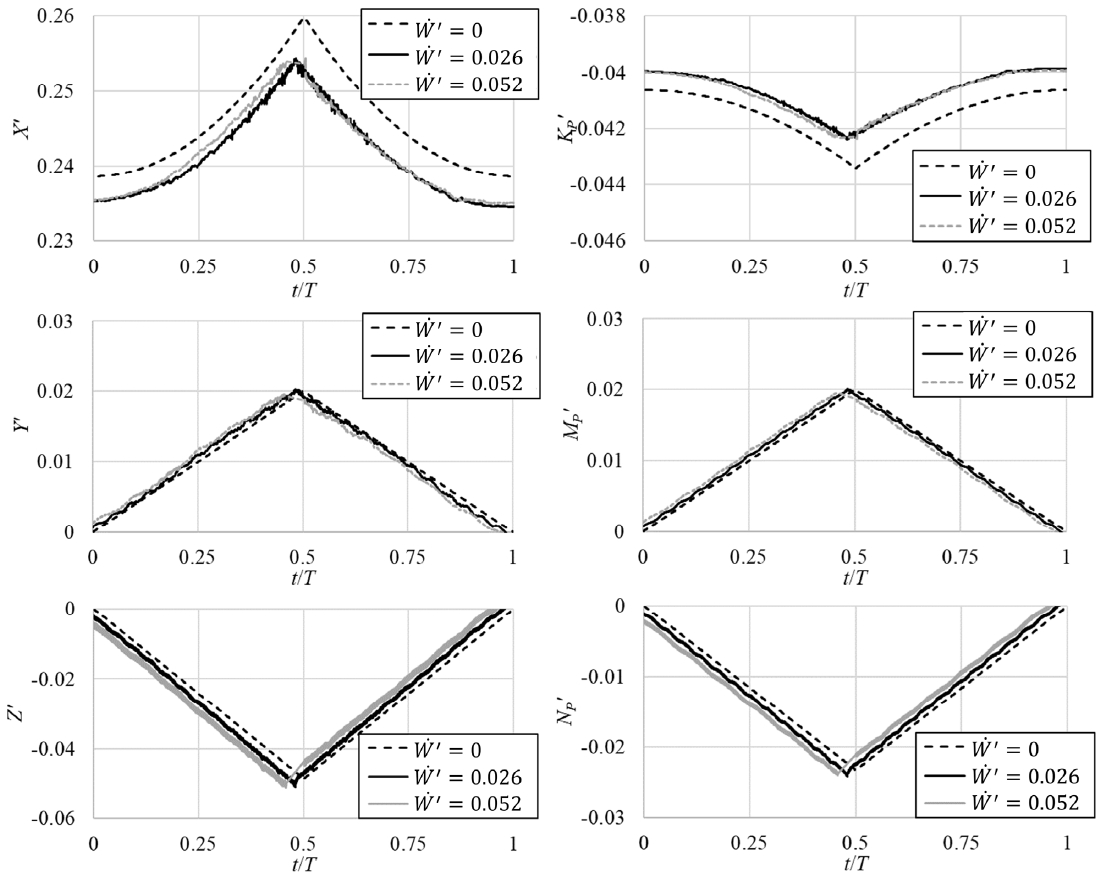
Fig. 10은 $$ {\dot{W}}^{\mathrm{\text{'}}}=0.026$$, $$ 0.052$$ 조건의 수직 가속도 운동 중 얻은 W'와 F', M_P'의 시계열로, 식 (18)을 이용해 추정한 $$ {\dot{W}}^{\mathrm{\text{'}}}=0$$ 조건의 W' 에 따른 유체력과 모멘트도 함께 나타내었다. 시계열 자료에서는 추진기 날개의 위상 변화로 인한 짧은 주기의 유체력과 모멘트의 요동이 나타났으나, 이는 크기가 작아 가속도 조건의 영향 분석에서 무시하였다. 전체적으로 유체력의 변화는 W'의 변화를 따르는 경향을 보였는데, X'와 K'는 4.1장에서 다룬 대로 W'에 대해 선형적인 반응을 보이지는 않았다.

Fig. 10

Time series of hydrodynamic force and moment of vertical acceleration test

Fig. 10에서 실제 결과와 식 (18)을 이용해 추정한 결과의 차이가 식 (11), (12)의 $$ \Delta {\mathit{F}}^{\mathrm{\text{'}}}\left({\dot{W}}^{\mathrm{\text{'}}}\right)$$, $$ \Delta {\mathit{M}}_P{}^{\mathrm{\text{'}}}\left({\dot{W}}^{\mathrm{\text{'}}}\right)$$이다. Fig. 11에 이를 추세선과 함께 나타내었다. 앞에서 언급한 유체력과 모멘트의 위상에 따른 요동으로 인해 데이터가 산포되었으나, 전체적인 경향의 확인에는 문제가 없었다.

Fig. 11

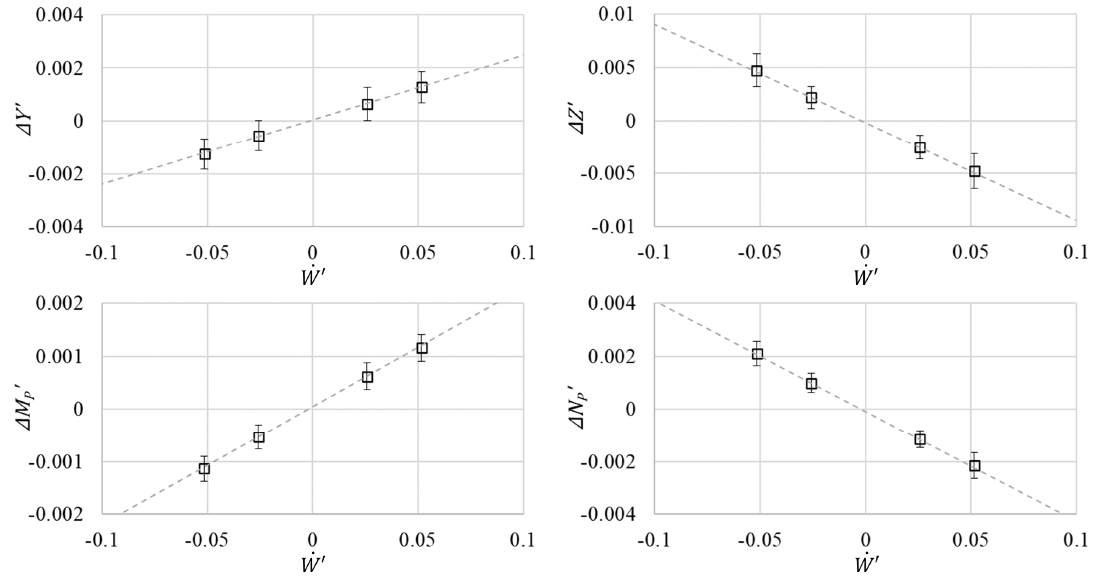
Off-axial components of ΔF' and ΔM' with variation of acceleration (symbol: mean, error bar: 95% confidence interval)

$$ {\dot{W}}^{\mathrm{\text{'}}}$$에 비례하여 나타나는 유체력 성분을 Y', Z', M', N'에 대해서 잘 확인할 수 있었으므로, 부가질량의 개념으로 이를 설명하고자 하는 접근이 타당함을 확인할 수 있었다. Y', Z', M', N'의 네 가지 운동 성분에 대해 가속도의 영향을 받는 성분과 $$ {\dot{W}}^{\mathrm{\text{'}}}$$와의 비례상수를 Table 4에 나타내었다. Y', Z'간의 크기 차이는 약 4배로 얻어져 정속 사항 중 유체력의 추세와 마찬가지로 z방향 유체력의 변화가 지배적임을 알 수 있다.

Table 4

Proportionality of acceleration-induced term of off-axial hydrodynamic force and moment

그 중 수직 방향 운동에 대해 직접적인 영향을 받는 Z'에 대한 부가질량을 해석하였다. 식 (19)와 같이 Table 4의 비례상수에 차원을 적용하면 종동요 가속에 대한 부가질량 m_z를 구할 수 있다.

$\[ m_z=-\frac{\Delta Z^{\text{'}}}{{\dot{W}}^{\text{'}}}\times \rho D^3=0.074\left(kg\right) \]$

(19)

이를 식 (2)에 대입하면 선체의 가속 운동에서 추진기가 미치는 영향을 구할 수 있다. 식 (2)의 $$ x_P^2{m}_{zP}$$ 항은 0.126 kgm²로 계산되었다. 이는 본 연구의 대상 선형인 KCS의 종동요 방향 관성 모멘트(I_yy) (Kim et al., 2021b)인 38.58 kgm²의 0.3% 정도로, 운동에 영향을 줄 만한 크기는 아닌 것으로 판단된다.

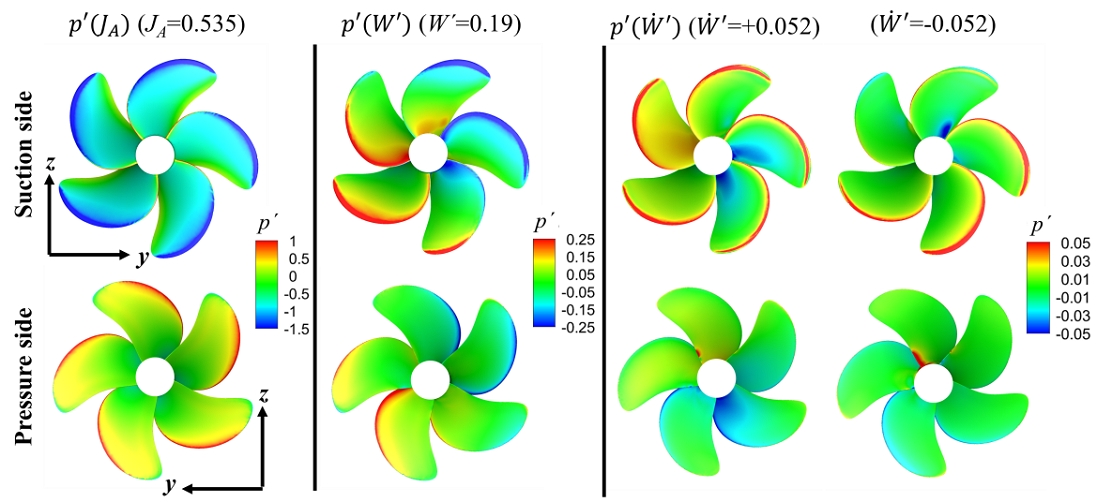
가속도로 인한 유체력 변화를 확인하기 위해 Fig. 12에 추진기의 표면 압력 분포를 정리하여 나타내었다. 표면 압력은 식 (20)에서 보인 바와 같이 nD를 이용해 무차원화되었으며, 식 (21)과 같이 직진 상태를 기준으로 사항각의 영향 성분, 가속도 성분을 분리하여 나타냈다.

$\[ p^{\text{'}}=p/\left(\frac{1}{2}\rho n^2{D}^2\right) \]$

(20)

$\[ p^{\text{'}}\left(J_A,W^{\text{'}},{\dot{W}}^{\text{'}}\right)=p^{\text{'}}\left(J_A\right)+p^{\text{'}}\left(W^{\text{'}}\right)+p^{\text{'}}\left({\dot{W}}^{\text{'}}\right) \]$

(21)

Fig. 12

Composition of pressure coefficient (p') on the propeller surface in heave motion

압력 성분 중 사항각에 대한 p'(W')은 위상에 따른 변화가 앞날에서 명확히 드러났으며, 이는 Fig. 8에서 추진기 날개의 사항 중 받음각 변화에 대해 설명한 내용을 뒷받침한다. 위상이 0° - 180°일 때에서는 추진기 날개의 받음각 증가로 인해 압력면의 압력이 더 높아지고 흡입면의 압력은 낮아지는 양상이 발생했다.

$$ p^{\mathrm{\text{'}}}\left({\dot{W}}^{\mathrm{\text{'}}}\right)$$은 $$ +{\dot{W}}^{\mathrm{\text{'}}}$$, $$ -{\dot{W}}^{\mathrm{\text{'}}}$$에 대해 각각 나타내었다. 가속도 영향에 대해, 앞서 전체 유체력과 모멘트에서는 가속도에 비례한 유체력 변화가 얻어졌으므로 가속도의 방향에 따라 $$ p^{\mathrm{\text{'}}}\left({\dot{W}}^{\mathrm{\text{'}}}\right)$$이 반대 부호로 얻어질 것으로 기대하였다. 하지만 국부 압력 분포에서는 이러한 경향이 나타나지 않았으며, 가속도로 인한 압력의 변화는 주로 90° 내외의 위상에서 허브 근처 압력의 감소로 얻어졌다. 이는 Fig. 7과 식 (15)에서 알 수 있듯, 허브 근처는 r이 작아지면서 추진기 날개의 받음각에 W'가 미치는 영향이 증가하기 때문에 가속 운동에서 유선의 급격한 변화는 허브 근처에서 발생하는 것을 의미한다. 추가로, 유동의 받음각이 바뀌면서 정체점의 위치가 변하게 되는 앞날에서도 압력의 국부적인 변화가 나타났다.

5. 결 론

본 연구에서는 상하동요 운동 시 추진기에 작용하는 유체력의 특성을 파악하기 위해 CFD 해석을 수행하였다. 사항 조건은 동일 추진기가 적용된 선형의 선수파 중 운동의 크기를 바탕으로 선정하였고, 해석을 통해 정속 사항, 수직 가속 운동 중의 6분력을 얻었다. 사항 중의 추진기 유체력 특성을 우선 설명하고, 가속 중의 유체력이 부가질량의 측면에서 설명될 수 있는지를 파악하였다.

사항 상태에서는 축 방향 유체력과 모멘트를 제외하면 사항각에 따라 선형적인 유체력과 모멘트의 증가 양상이 나타났다. 선체 운동에 대한 추진기의 영향은 추진기 자체의 유체모멘트보다는 선미 배치로 인한 성분이 지배적임을 확인하였다.

가속도로 인한 유체력과 모멘트의 변화는 추진기 축 방향 성분을 제외하면 모두 가속도에 비례하는 것으로 나타났다. 따라서 가속도 영향 성분은 비점성 유동의 부가질량의 관점에서 해석될 수 있음을 확인하였지만, 그 크기는 전체 유체력에 비하면 작은 수준으로 나타났다.

본 연구에서는 사항과 수직 가속도 조건의 추진기 성능을 추진기 자체의 유체력과 모멘트에 집중하여 해석하여 사항 유입류 속도가 전체 유체력의 변화에 지배적인 영향을 미침을 확인하였다. 본 연구에서 확인한 사항 중 유체력 발생을 선체의 조종이나 파랑 중 운동 모델에 결합하여 선체 운동 모델을 개선할 수 있을 것으로 생각되며, 이러한 기법을 일반화하여 적용하기 위해 설계 요목의 변화에 따른 6방향 유체력과 모멘트의 추정 모델을 구하는 후속 연구가 요구된다.

Acknowledgments

2024년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임(P0023684, 2024년 산업혁신인재성장지원사업).

References

• Dubbioso, G., Muscari, R. and Di Mascio, A., 2013. Analysis of the performances of a marine propeller operating in oblique flow. Computers & Fluids, 75, pp.86-102. [https://doi.org/10.1016/j.compfluid.2013.01.017]
• Dubbioso, G., Muscari, R. and Di Mascio, A., 2014. Analysis of a marine propeller operating in oblique flow. part 2: very high incidence angles. Computers & Fluids, 92, pp.56-81. [https://doi.org/10.1016/j.compfluid.2013.11.032]
• Dubbioso, G., Muscari, R., Ortolani, F. and Di Mascio, A., 2017. Analysis of propeller bearing loads by CFD. part Ⅰ: straight ahead and steady turning maneuvers. Ocean Engineering, 130, pp.241-259. [https://doi.org/10.1016/j.oceaneng.2016.12.004]
• Eom, M.-J., Paik, K.-J., Jang, Y.-H., Ha, J.-Y. and Park, D.-W., 2021a. A method for predicting propeller performance considering ship motion in regular waves. Ocean Engineering, 232, Article No. 109135. [https://doi.org/10.1016/j.oceaneng.2021.109135]
• Eom, M.-J., Jang, Y.-H. and Paik, K.-J., 2021b. A study on the propeller open water performance due to immersion depth and regular wave. Ocean Engineering, 219, Article No. 108265. [https://doi.org/10.1016/j.oceaneng.2020.108265]
• Hou, L. and Hu, A., 2019. Theoretical investigation about the hydrodynamic performance of propeller in oblique flow. International Journal of Naval Architecture and Ocean Engineering, 11(1), pp. 119-130. [https://doi.org/10.1016/j.ijnaoe.2018.02.013]
• Kim, W.J., Van, S.H. and Kim, D.H., 2001. Measurement of flows around modern commercial ship models. Experiments in Fluids, 31, pp.567-578. [https://doi.org/10.1007/s003480100332]
• Kim, Y.-C., Kim, Y., Kim, J. and Kim, K.-S., 2018. Added resistance and 2DOF motion analysis of KVLCC2 in regular head waves using dynamic overset scheme. Journal of the Society of Naval Architects of Korea, 55(5), pp.385-393. [https://doi.org/10.3744/SNAK.2018.55.5.385]
• Kim, D.-H., Sanada, Y., Sadat-Hosseini, H. and Stern, F., 2021a. URANS simulations for a free-running container ship: part 2. added power. Journal of hydrodynamics, 33(3), pp.448-467. [https://doi.org/10.1007/s42241-021-0053-5]
• Kim, D.-H., Sanada, Y., Park, s., Sadat-Hosseini, H. and Stern, F., 2021b. URANS simulations for a free-running container ship: part 1. turning-circle. Journal of hydrodynamics, 33(3), pp.421-447. [https://doi.org/10.1007/s42241-021-0052-6]
• Kinaci, O.K. and Ozturk, D., 2023. Turning circle tests with system-based simulations in irregular waves including wave drift and propeller side forces. Ocean Engineering, 274, Article No. 114082. [https://doi.org/10.1016/j.oceaneng.2023.114082]
• Lee, C.-M., Seo, J.-H., Yu, J.-W., Choi, J.-E. and Lee, I., 2019. Comparative study of prediction methods of power increase and propulsive performances in regular head short waves of KVLCC2 using CFD. International Journal of Naval Architecture and Ocean Engineering, 11, pp.883-898. [https://doi.org/10.1016/j.ijnaoe.2019.02.001]
• Lee, S.-H., Paik, K.-J., Hwang, H.-S., Eom, M.-J. and Kim, S.-H., 2021. A study on ship performance in waves using a RANS solver, part 1: comparison of power prediction methods in regular waves. Ocean Engineering, 227, Article No. 108900. [https://doi.org/10.1016/j.oceaneng.2021.108900]
• Lee, S.-H., Paik, K.-J. and Lee, J.-H., 2022a. A study on ship performance in waves using a RANS solver, part 2: comparison of added resistance performance in various regular and irregular waves. Ocean Engineering, 263, Article No. 112174. [https://doi.org/10.1016/j.oceaneng.2022.112174]
• Lee, S.-H., Paik, K,-J., Cho, J.-H., Kim, G.-H., Kim, H.-S. and Kim, S.-H., 2022b. A numerical study on self-propulsion performance in regular waves and power prediction in irregular waves. International Journal of Naval Architecture and Ocean Engineering, 14, Article No. 100454. [https://doi.org/10.1016/j.ijnaoe.2022.100454]
• Muscari, R., Dubbioso, G., Ortolani, F. and Di Mascio, A., 2017. Analysis of propeller bearing loads by CFD. Part Ⅱ: transient maneuvers. Ocean Engineering, 146, pp.217-233. [https://doi.org/10.1016/j.oceaneng.2017.09.050]
• Ozdemir, Y.H. and Barlas, B., 2017. Numerical study of ship motions and added resistance in regular incident waves of KVLCC2 model. International Journal of Naval Architecture and Ocean Engineering, 9, pp.149-159. [https://doi.org/10.1016/j.ijnaoe.2016.09.001]
• Park, D.-M., Lee, J. and Kim, Y., 2015. Uncertainty analysis for added resistance experiment of KVLCC2 ship. Ocean Engineering, 95, pp.14-156. [https://doi.org/10.1016/j.oceaneng.2014.12.007]
• Park, J., Rhee, S.H., Yoon, H.K., Lee, S. and Seo, J., 2020. Effects of a propulsor on the maneuverability of an autonomous underwater vehicle in vertical planar motion mechanism tests. Applied Ocean Research, 103, Article No. 102340. [https://doi.org/10.1016/j.apor.2020.102340]
• Sadat-Hosseini, H., Wu, P.-C., Carrica, P.M., Kim, H., Toda, Y. and Stern, F., 2013. CFD verification and validation of added resistance and motions of KVLCC2 with fixed and free surge in short and long head waves. Ocean Engineering, 59, pp.240-273. [https://doi.org/10.1016/j.oceaneng.2012.12.016]
• Sanada, Y., Kim, D.-H., Sadat-Hosseini, H., Stern, F., Hossain, M.A., Wu, P.-C., Toda, Y., Otzen, J., Simonsen, C., Abdel-Maksoud, M., Scharf, M. and Grigoropoulos, G., 2022. Assessment of EFD and CFD capability for KRISO Container Ship added power in head and oblique waves. Ocean Engineering, 243, Article No. 110224. [https://doi.org/10.1016/j.oceaneng.2021.110224]
• Seo, M.-G., Yang, K.-K., Park, D.-M. and Kim, Y., 2014. Numerical analysis of added resistance on ships in short waves, Ocean Engineering, 87, pp.97-110. [https://doi.org/10.1016/j.oceaneng.2014.05.011]
• Seo, S. and Park, S., 2017. Numerical simulations of added resistance and motions of KCS in regular head waves. Journal of the Society of Naval Architects of Korea, 54(2), pp.132-142. [https://doi.org/10.3744/SNAK.2017.54.2.132]
• Seo, J.-H., Lee, C.-M., Yu, J.-W., Choi, J.-E. and Lee, I., 2020. Power increase and propulsive characteristics in regular head waves of KVLCC2 using model tests. Ocean Engineering, 216, Article no. 108058. [https://doi.org/10.1016/j.oceaneng.2020.108058]
• Seo, M.-G., Park, I.-B., Park, D.-M. and Hwang, S., 2023. A study on soft-mooring model test techniques for the evaluation of added resistance on ships. Journal of the Society of Naval Architects of Korea, 60(5), pp.320-331. [https://doi.org/10.3744/SNAK.2023.60.5.320]
• Sigmund, S. and el Moctar, O., 2017. Numerical and experimental investigation of propulsion in waves. Ocean Engineering, 144, pp.35-49. [https://doi.org/10.1016/j.oceaneng.2017.08.016]
• Sigmund, S. and el Moctar, O., 2018. Numerical and experimental investigation of added resistance of different ship types in short and long waves. Ocean Engineering, 147, pp.51-67. [https://doi.org/10.1016/j.oceaneng.2017.10.010]
• Simonsen, C. D., Otzen, J. F., Joncquez, S. and Stern, F., 2013. EFD and CFD for KCS heaving and pitching in regular head waves, Journal of Marine Science and Technology, 18, pp.435-459. [https://doi.org/10.1007/s00773-013-0219-0]
• Versteeg, H.K. and Malalasekera, W., 2007. An Introduction to Computational Fluid Dynamics: The Finite Volume Method (2nd edition), Pearson Education.
• Yang, K.-K., Lee, J.-H., Nam, B.-W. and Kim, Y., 2013. Analysis of added resistance using a Cartesian-grid-based computational method. Journal of the Society of Naval Architects of Korea, 50(2), pp.79-87. [https://doi.org/10.3744/SNAK.2013.50.2.79]
• Yang, K.-K., Seo, M.-G. and Kim, Y., 2015. Analysis of added resistance in short waves. Journal of the Society of Naval Architecture of Korea, 52(4), pp.338-348. [https://doi.org/10.3744/SNAK.2015.52.4.338]
• Yao, J., 2015. Investigation on hydrodynamic performance of a marine propeller in oblique flow by RANS computations. International Journal of Naval Architecture and Ocean Engineering, 7(1), pp.56-69. [https://doi.org/10.1515/ijnaoe-2015-0005]
• Yu, J.-W., Lee, C.-M., Choi, J.-E. and Lee, I., 2017. Effect of ship motions on added resistance in regular head waves of KVLCC2. Ocean Engineering, 146, pp.375-387. [https://doi.org/10.1016/j.oceaneng.2017.09.019]
• Zhang, Y.-X., Chen, K. and Jiang, D.-P., 2020. CFD analysis of the lateral loads of a propeller in oblique flow. Ocean Engineering, 202, Article No. 107153. [https://doi.org/10.1016/j.oceaneng.2020.107153]
• Zhang, L., Zhang, J. and Shang, Y., 2021. A practical direct URANS CFD approach for the speed loss and propulsion performance evaluation in short-crested irregular head waves. Ocean Engineering, 219, Article No. 108287. [https://doi.org/10.1016/j.oceaneng.2020.108287]