열 네트워크와 열역학적 평형 기반 방법을 활용한 극저온 탱크의 장기 증발가스 예측
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This study proposes an analytic model to predict boil-off gas (BOG) generation in cryogenic liquid storage tanks. The model simulates evaporation under isobaric conditions, where the liquid phase remains saturated, and the vapor phase is superheated. The simulation is divided into two stages: heat transfer analysis and thermodynamic response. In the first stage, a steady-state thermal network is developed to quantify heat ingress into the tank. This includes external heat convection, insulation conduction, and natural convection within the liquid and vapor phases. Additionally, heat transfer at the liquid-vapor interface is incorporated, calculating heat inputs to both phases. In the second stage, the liquid and vapor are modeled as lumped masses with uniform temperature in each phase. Their temperature variations and evaporation rates are analyzed based on heat inputs from the thermal network. The integration of steady-state heat transfer and dynamic thermodynamic responses allows for time-dependent predictions of evaporation behavior over extended periods. The model was validated using a 1.0 m³ liquid nitrogen storage tank, demonstrating close agreement with the BoilFAST model in predicting BOG generation, heat inputs, and vapor temperatures. This study provides a computationally efficient and reliable method for predicting long-term evaporation in cryogenic systems.
Keywords:
Cryogenic Liquid Tank, Boil-off Gas(BOG), Steady-State Thermal Network, Lumped Mass, Thermodynamic Model(TDM), Convective Heat Transfer키워드:
극저온 액체 탱크, 증발가스, 정상 상태 열 네트워크, 집중 질량, 열역학 모델, 대류 열전달1. 서 론
1.1 연구 배경과 목적
친환경 에너지 운송 및 활용 선박의 필요성이 증가하면서, 액화천연가스뿐만 아니라 액체수소(LH2)를 저장하고 활용하는 선박의 중요성이 부각되고 있다. 특히, 액체수소는 낮은 열용량과 증발 잠열로 인해 상대적으로 높은 증발률(Boil-Off Rate, BOR)을 보이며, 증발을 방지하기 위해 높은 단열 성능을 갖춘 극저온 탱크에 저장된다. 대형 액체수소 탱크에는 주로 파우더 단열 재료를 충진하고 고진공 상태를 유지하는 방식이 사용된다 (Ratnakar, 2023). 극저온 단열 탱크 설계에서 가장 중요한 과제는 BOG를 최소화할 수 있는 적절한 단열층을 선택하고, 장기적인 BOG 발생량을 예측하는 것이다. BOG 발생의 주요 원인은 외부로부터 유입되는 대류 열 유속이며, 이는 단열 재료의 열전도 및 탱크 내외부의 대류 열전달 특성에 따라 결정된다. BOG를 예측하기 위해서는 탱크 내부와 외부의 대류 열전달, 액상-기상 계면에서의 열전달, 그리고 상변화를 포함한 현상을 종합적으로 고려해야 한다. 전산유체역학해석(CFD)은 액상과 기상의 다상 대류 흐름과 열확산, 그리고 상변화를 모사할 수 있는 장점이 있으므로 BOG 현상을 세밀하게 분석하는 용도로 사용된다. 그러나 CFD는 수분 이내의 단시간 동안의 BOG 현상을 시뮬레이션에 수십 시간 이상의 전산 자원이 요구되므로, 수 시간 이상의 장기적인 BOG 현상의 모사에 비효율적 한계를 가진다 (Sakowski et al., 2019). 이에 본 연구는 수 시간 이상의 장시간 BOG 발생량을 효율적으로 예측하는 방안을 제시하고자 한다.
1.2 관련 연구 동향
BOG 발생에 영향을 미치는 주요 요인으로는 극저온 탱크의 단열 성능, 적재율(Filling Ratio, FR), Sloshing 유동, 탱크 내부 액상 및 기상의 상태, 외부 열 유입, 그리고 혼합물의 조성 변화 등이 있다 (Lin et al., 2018; Khan et al., 2020; Migliore, 2015). 극저온 탱크 내 액체의 기화량을 예측하기 위해서 다양한 방법이 시도되었다. CFD 기반의 다상 열 유동 해석과 열평형 방정식 기반의 열역학 모델(Thermodynamic Model, TDM)이 주로 활용되었다. TDM 또는 Thermal Homogeneous Model(THM)은 액체에 유입되는 열 유속과 온도를 열전도 해석을 수행한 후에 기상과 액상의 온도와 압력을 예측하는 효율적인 방법으로 알려져 있다 (Nam et al., 2024). Lin et al. (2018)은 유한요소해석을 사용하여 Type C LNG 탱크의 열 유입을 자연대류 효과를 보정한 열전도 방정식으로 계산하고, 적재율에 따른 BOR(Boil-Off Rate)을 예측하였다. Hwang et al. (2016)은 NO96-GW와 NO96-L03 단열 시스템의 열저항 값을 계산하여, 준정적 열평형 상태에서의 열 유속을 바탕으로 BOG 및 BOR 값을 도출하였다. 이러한 방법은 외부 입열량에만 관심을 갖는 방법이다. 한편, BOG 예측에서 열전달뿐만 아니라 대류 열전달, 상변화, 난류 모델링까지 포함하는 CFD 기반의 해석 사례도 많은 연구자에 의하여 시도되었다 (Yu et al., 2016; Huerta & Vesovic, 2021). Ferrin et al. (2020)은 0.5m3 용량의 LNG 저장 탱크를 대상으로, 복합 열전달을 통해 단열재의 두께와 재료에 따른 열 유입을 분석하였다. 이 연구는 CFD를 적용하여 자연대류 유동 및 액상-기상 계면에서의 증발과 응축을 모두 포함하여 BOG 예측 사례를 제시하였다. 그러나 CFD 기반의 해석은 높은 계산 자원과 시간이 요구되며, 모델의 초기 조건 및 매개변수 선택에 따라 결과의 민감도가 크게 달라지는 한계를 가진다. 이와 달리 TDM 또는 THM은 액상과 기상을 집중 질량으로 단순화하고, 열 유입량을 바탕으로 액상과 기상의 온도, 압력, 그리고 BOG 발생량을 예측한다. 극저온 탱크 해석 특화된 소프트웨어 BoilFAST (Ghafri et al., 2022) 및 SINDA/FLUINT (Agrawal et al., 2015)도 TDM 기반의 해석 방법을 구현하였다. Perez et al. (2021)과 Ghafri et al. (2022)는 Cylinder 형상의 극저온 탱크에서 BOG 계측 실험을 수행하였고, BoilFAST를 이용한 BOG 예측 결과와 비교하였다. 이들의 예측 결과는 실험 데이터와 일관성을 보여주었으나, 기상과 액상 계면에서의 열전달 계수를 이론적으로 산정하지 못하고, 시행착오를 통해 그 값을 역산하는 한계를 지니고 있다. Agrawal et al. (2015)은 직경 0.5m, 높이 1.0m의 Cylinder 형상 극저온 추진제 탱크를 대상으로, SINDA/FLUINT를 활용하여 장기적인 열 유속, BOG, 압력 및 온도 변화를 예측하였다. 이 연구는 액상과 기상을 집중 질량 모델로 가정하여 두 상 간의 상변화를 계산하는 Two-Phase Thermodynamic Lumped Model을 제안하고, LH2 탱크 실험 데이터를 통해 모델의 정확성을 검증하였다. 그러나 벽면의 대류 열전달 경험 식을 고정값으로 설정하여 실제 물리적 조건의 복잡성을 충분히 반영하지 못한 한계를 가지고 있다.
1.3 연구 목적 및 주요 내용
본 연구의 목적은 극저온 저장 탱크의 외부 열 환경에 따른 수 시간 이상 BOG 발생량과 온도 변화를 예측하는 해석 모델을 구현하는 것이다. 앞 절에서 언급한 바와 같이 CFD를 이용한 다상 열 유동 해석은 저장 탱크 내부 유체의 열 유동과 상변화 과정을 반영하여 정밀한 해석이 가능한 장점이 있지만, 높은 연산 자원과 시간의 제약이 따른다. 반면, 열평형 방정식 기반의 열역학 방법은 액상과 기상의 평균 온도만을 반영하는 단점이 있으나, 상변화와 대류 열전달을 동시에 고려하여 장기간의 BOG 예측을 단시간 내 해석할 수 있게 한다. 이에 본 연구는 열역학 모델을 기반으로 극저온 탱크의 입열 환경 단순화 과정, 열저항을 이용한 대류 열전달 및 열확산 정식화 과정, 그리고 상변화 및 BOG 발생 과정을 집중 질량 법을 통해 모사하는 과정을 제시하고자 한다.
2. BOG 발생 과정의 모델링
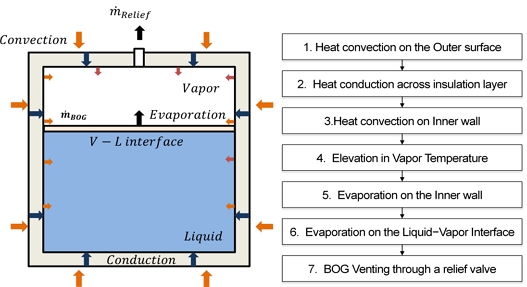
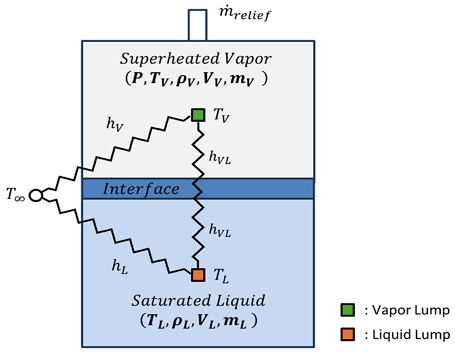
극저온 탱크에서 발생하는 Boil-Off는 외부로부터의 열 유입, 탱크 내 기상의 온도 변화, 그리고 액상의 기화가 밀접하게 관련되어 있다. 본 장에서는 BOG 발생 과정을 단순화하고 이를 모델링하기 위한 해석적 접근법을 제안한다. 먼저, 문제의 단순화를 위하여 액상은 포화 상태로, 기상은 과열 상태로 가정하였다. 증발 가스는 밸브로 배출된다고 가정하여 탱크 내부 압력은 정압 상태로 가정하였다. 외부 공기로부터의 대류 열전달, 단열재 층을 통한 열전도, 그리고 액상과 기상의 경계면에서 전달되는 대류 열전달이 기상의 온도 상승 및 액상의 기화를 발생시킨다고 가정할 수 있다. 이러한 과정을 Fig. 1에 간략하게 표현하였다.
2.1 탱크의 열전달률(Heat flow rate) 성분
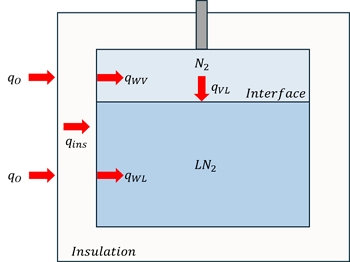
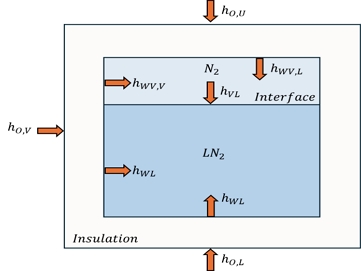
대류 열전달에 의한 열 유입은 외부 공기로부터 탱크 외벽에 가해지는 열전달률(qo), 단열재를 통해 탱크 내벽까지 전도에 의한 열전달률(qins), 탱크 내부의 액상 접촉면의 대류 열전달률(qWZ), 그리고 기상 접촉면의 열전달률(qWV)로 구분할 수 있다. 또한, 기상과 액상의 온도 차에 의한 열전달률(qVL)이 액상에 전달된다. 열전달률과 대류 계수를 각각 Fig. 2와 Fig. 3에 제시하였다. 그림에서 hO,U, hO,V 와 hO,L는 각각 탱크 외벽의 상단, 수직, 그리고 하부 표면에서 대류 열전달 계수를 의미하며, hWV,L과 hWV,V는 각각 내벽 기상의 수직 및 수평 면에서 대류 열전달 계수를 의미한다. hWZ은 액상이 탱크와 접하는 면에서 대류 열전달 계수를 의미한다. hVL은 액상-기상 계면에서 대류 열전달 계수를 의미한다. 따라서 액상으로 전달되는 열전달률(qL)과 기상에 전달되는 열전달률(qV)은 각각 qL=qWL+qVL과 qV=qWV-qVL로 가정할 수 있다. 그리고 액상과 기상으로 유입되는 열에너지 QV와 QL은 각각 qL과 qV을 시간으로 적분하여 계산할 수 있다.
탱크 외벽의 대류 열전달은 공기의 밀도 변화에 따른 자연대류 현상으로 가정하였다. 수직 및 수평 여부, 그리고 밀도에 따른 유동의 방향을 고려하여 대류 계수를 가정하였다. 탱크 외벽의 상단에서 대류 열전달 계수(hO,U)는 식 (1)을 적용하였다. 이는 전도체 상면에 온도가 높은 유체가 존재하는 자연대류 열전달로 가정할 수 있기 때문이다(McAdams, 1954; Guyer et al.,1989). 탱크 외벽의 하단에서 일어나는 대류 열전달 계수(hO,L)는 식 (2)를 적용하였다. 탱크 수직 표면의 대류 열전달 계수(hO,V)는 수직 평판에서의 자연대류 열전달로 가정하여 식 (3)을 적용하였다(Churchill and Chu, 1975).
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
여기서, Raair와 kair는 각각 공기의 Rayleigh 수와 열전도율을 의미하며, Lc는 대류 면적의 특성 길이로 대류 면적의 주변 길이를 의미한다. Prair과 Grair는 각각 공기의 Prandtl 수와 Grashof 수이며, g는 중력 가속도, βair는 공기의 체적 열팽창 계수, Ts는 대류 표면의 온도, T∞는 외부 공기의 온도, νair는 공기의 동점성 계수, μair는 공기의 점도, Cp,air는 공기의 정압 비열을 의미한다.
탱크 내벽에서 기상 및 액상 면으로의 열전달은 자연대류에 의해 발생한다. 탱크 내벽 상부에서 기상으로의 대류 계수(hWV,L)와 탱크 수직 벽면에서 기상으로의 자연대류 계수(hWV,V)는 각각 식 (7) 및 식 (8)과 같다. kV, RaV와 PrV는 각각 기상의 열전도율, Rayleigh 수, 그리고 Prandtl 수를 의미한다.
| (7) |
| (8) |
탱크 내벽에서 액상 면으로의 대류 열전달 계수(hWL)는 식 (9)와 같이 Rohsenow (1952)의 Pool boiling 대류식을 사용하였다. 식 (9)에서 μL는 액상의 점도, ΔT는 액상의 온도(TL)와 탱크 내벽 온도(TW) 차이, ρL과 ρV는 각각 액상과 기상의 밀도, Cp,L는 액상의 비열, ReL는 액상의 Reynolds 수, PrL는 액상의 Prandtl 수, s는 Prandtl 수의 지수로서 Rohsenow et al.(1998)이 제시한 1.7을 사용하였다. 식 (10)과 식 (11)과 같이 액상 Rayleigh 수(RaL)는 Grashof 수(GrL)와 Prandtl 수(PrL)로 계산된다. βL, νL과 kL은 각각 액상의 체적 열팽창 계수, 동점성 계수, 그리고 열전도율을 의미하며, TV는 기상의 온도를 의미한다.
| (9) |
| (10) |
| (11) |
액상-기상 계면은 얇은 평면이므로, 평판의 대류 열전달로 가정할 수 있다 (Joseph et al., 2016). 즉, 액상과 기상을 각각 전도영역과 대류 조건으로 가정할 수 있다. 따라서 계면의 대류 열전달 계수(hVL)는 식 (12)과 식 (13)을 이용하여 계산하였다.
| (12) |
| (13) |
여기서, CVL은 계면에서 열전달 상수이며, 기상-계면에서는 0.27, 계면-액상에서는 0.54를 사용하였다(Joseph et al, 2016). RaVL는 계면에서 Rayleigh 수를 의미한다. Lc,VL는 액상-기상 계면의 특성 길이 βV, νV, μV와 Cp,V는 각각 기상의 체적 열팽창 계수, 동점성 계수, 점도, 그리고 정압 비열을 의미한다.
2.2 열저항 네트워크 모델을 이용한 입열 계산
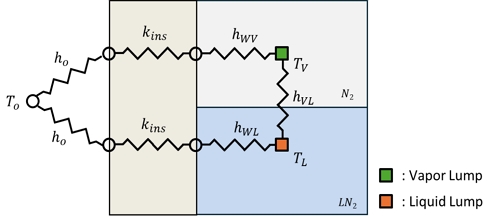
액상 및 기상으로 전달되는 입열은 대류 열전달 계수 및 단열재의 열전도율, 그리고 외기 온도와 액상 및 기상 온도에 의하여 결정된다. 증발되는 순간을 준정적 상태로 가정하면 Fig. 4와 같이 열저항 모델로써 단순화하여 열유입을 계산할 수 있다. 즉, 단열재의 열전도와 대류 열전달 계수를 포함한 열저항 네트워크를 이용하면 액상과 기상으로 전달되는 입열을 계산할 수 있다. 액상의 열저항(RL) 및 기상에서 열저항(RV)은 각각 식 (14)와 식 (15)로 표현할 수 있다. 따라서, 외기로부터 액상으로 전달되는 입열(QOL)과 기상으로 전달되는 입열(QOV)는 각각 식 (16)과 식 (17)로 표현할 수 있다. 또한, 계면으로부터 액상에 전달되는 입열(QVL)은 식 (18)과 같이 계산할 수 있다.
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
여기서, hO는 외부 공기의 평균 대류 열전달 계수, AO는 단열재 외부 표면의 접촉 면적, kins는 단열재 열전도율, tins는 단열재 두께, Ains는 단열재 두께의 평균 면적이다. hWL과 hWV는 각각 내벽 액상과 기상의 대류 열전달 계수를 의미한다. AWL과 AWV는 탱크 내벽에서 액상과 기상의 대류 면적이며, 증발이 진행되면서 변하는 값이다. 그리고 Δt는 대류 열전달이 가해진 시간을 의미한다. 액상은 포화 상태이므로 온도(TL)는 일정하며, 기상의 온도 변화(ΔTV)는 QOV/mVCp,V로 계산하였다. 여기서 mV와 Cp,V는 각각 기상의 질량과 정압 비열을 의미한다.
2.3 집중 질량을 이용한 BOG 예측
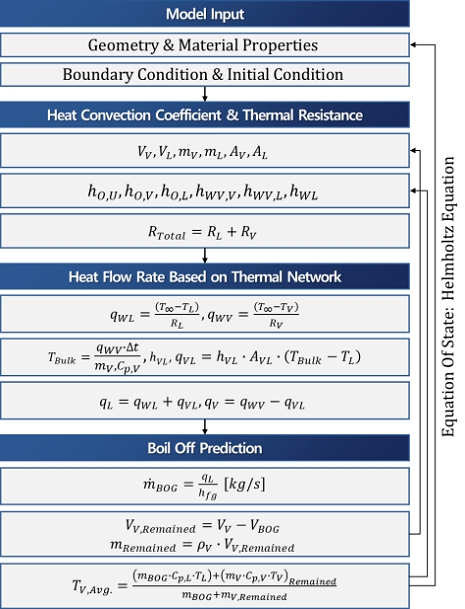
탱크 내부 액상과 기상은 모두 집중 질량으로 가정하고, 증발하는 순간에 열역학적 평형 상태라고 가정하였다. 앞 절에서 설명한 열저항 네트워크를 이용하면 입열을 계산할 수 있다. 따라서, 시간에 따른 액상과 기상별로 집중 질량의 상태 변화를 갱신하고, 이를 시간 증분하여 반복 계산함으로써 BOG의 시계열을 예측하였다. 이 과정에서 외부로부터 액상과 기상의 열전달률 qOL과 qOV는 에너지 보존 법칙에 의해 탱크 내벽에서 각 상으로의 열전달률 qWL과 qWV과 같다고 가정하여 식 (16)과 식 (17)로 계산하였다. 외부에서 기상으로 열 유입에 의하여 변화하는 기상 온도(TBulk)는 식 (19)와 같이 계산할 수 있다. TBulk의 증가는 기상에서 액상으로 전달되는 열전달률(qVL)을 증가시키며, hVLAVL(TBulk-Tl)으로 계산된다. TBulk와 TL은 각각 기상과 액상 온도를 의미한다. 따라서 액상으로 전달되는 모든 열전달률(qL)은 식 (20)과 같이 qWL과 qVL의 합으로 가정하였다. 식 (21)은 qL에 의한 액상의 증발량이며, hfg는 기화열을 의미한다. 증발된 기체는 기존의 기상과 혼합됨과 동시에 밸브로 기체가 배출되므로, 잔여 기상 부피(VV,Remained)와 질량(mV,Remained)은 기상 부피(VV)와 증발한 기상 부피(VBOG), 기상의 밀도(ρV) 관계를 이용하여 식 (22)와 식 (23)과 같이 계산하였다. 식 (24)는 기존 기체, 배출된 기체, 그리고 증발 기체의 혼합을 고려한 온도(TV,Avg)를 의미한다. 즉, TV,Avg는 증발 질량(mBOG)와 잔여 기체 질량(mV,Remained)의 비율을 고려한 평균 온도이며, 이 과정에서 Helmholtz 상태 방정식을 이용하여 상태 변화를 반영하였다. 모든 액체가 증발할 때까지 식 (19) ~ 식 (24)를 반복 수행하면, BOG 발생 및 기체의 온도 이력을 계산할 수 있다. 이 과정을 Fig. 5에 정리하였다. Fig. 5에서 mL과 mV는 각각 액상과 기상 질량을 뜻하며, VL는 액상의 부피를 의미한다.
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
2.4 BoilFAST의 BOG 예측 모델
본 연구에서 제안한 BOG 예측 절차를 BoilFAST의 해석 절차 와 비교하였다. BoilFAST는 과열 증기의 집중 질량과 과냉각 액체의 집중 질량을 기반으로 BOG를 예측하는 모델이다 (University of Western Australia, 2001). 이는 액체가 포화 상태에 도달한 이후에 증발이 발생하며, 기체는 비평형 열역학 상태에서 온도와 압력이 증가하는 과열 상태로 존재한다는 것을 의미한다. 이 과정에서 액상-기상 간 경계면에서 열전달을 통해 열역학적 평형이 유지된다. BoilFAST의 주요 열전달 및 상태 변수를 Fig. 6에 요약하였으며, 과열 증기와 포화 액체 사이의 상태 변수와 계면에서의 열전달 과정을 나타낸다. BoilFAST와 본 연구의 모델은 동일한 상태 변수를 사용한다. 그림과 같이 기상의 상태 변수는 압력 PV, 온도 TV, 밀도 ρV, 기체 부피 VV, 기체 질량 mV로 나타냈다. 액상은 포화 상태를 유지하며, 상태 변수로는 온도 TL, 밀도 ρL, 부피 VL, 질량 mL을 포함한다. 액상-기상 경계면에서 증발이 발생하는 것으로 가정하였으며, mBOG와 qVL는 각각 증발량과 계면에서 열전달률을 의미한다. 그러나 BoilFAST는 극저온 탱크의 크기와 형상별로 BOG 계측 실험을 수행하여 액상-기상 계면의 열전달 계수(hVZ)를 경험적으로 결정하며 상수 값으로 가정하는 한계를 가지고 있다 (Ghafri et al., 2022). 이에 반해, 본 연구는 식 (12)에 보인 바와 같이 기상의 온도 변화에 따라 결정되는 변수로 가정하였다.
먼저 BoilFAST는 식 (14) ~ 식 (18)을 이용하여 외부로부터 열 유입은 먼저 계산하여 입력해야 한다. 액상의 열전달률(qL), 기상의 열전달률(qV), 그리고 계면에서 액체로 열전달률(qVL)로부터 액상의 엔탈피(HL) 변화는 식 (25)와 같으며, 기상의 엔탈피(HV) 변화는 식 (26)과 같이 표현할 수 있다.
| (25) |
| (26) |
위 식에서, 와 은 각각 증발 기체와 방출된 기체의 단위 시간당 질량의 변화율이다. h는 가스의 비엔탈피을 의미한다. 연성된 식 (25)와 식 (26)으로부터 와 기상의 온도를 계산한다. 액상과 기상의 열역학적 특성은 Helmholtz 표준 상태 방정식을 사용하고 있다(Span et al., 2000).
3. 장기 BOG 예측 결과
3.1 저장 탱크의 개요
본 절에서는 액체 질소를 저장한 가상의 사각 탱크를 선정하여 BOG 발생량을 예측한 결과를 제시하였다. 액체 질소는 BOG 실험 또는 극저온 관련 실험에 주로 사용하는 매체이므로, 본 연구에서 개발한 모델의 실험적 검증 가능성을 염두에 두고 대상 액체로 선정하였다. 탱크 외벽에 단열재 EPS(Expanded Polystyrene)를 가진 1.0 m3 체적의 Rectangular cuboid 형상을 가정하여, 액상의 부피 분율, 입열량 및 액상-기상 간 면적 변화 계산, 시간별 기상의 온도 및 증발량을 계산하였다. 기상과 액상의 상태 방정식 및 물성은 미국 국립표준기술연구소(NIST)의 REFPROP(Lemmon et al., 2018)를 적용하였다. 단열재의 열전도율은 계산의 편의를 위하여 0.02W/mK로 가정하였다.
3.2 탱크의 열적 환경
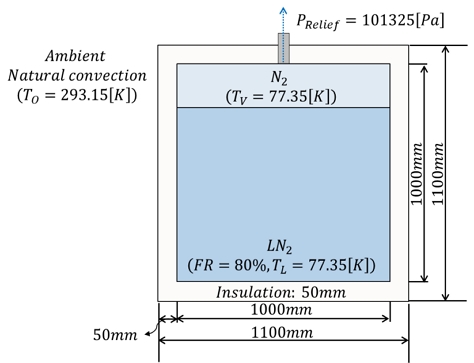
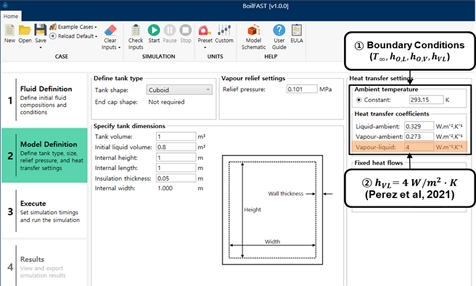
초기의 탱크는 정압 상태에서 액상과 기상이 약 77K의 포화 온도 상태에 있다고 가정하였다. 초기 액체의 적재율은 80%로 설정하였으며, 외부 온도 T∞는 293.15 K로 가정하였다. Fig. 7은 해석에 반영된 외부 열환경 및 초기 조건을 간략하게 보여주고 있다. Prelief를 1기압으로 가정하여, 정압조건을 부여하였다.
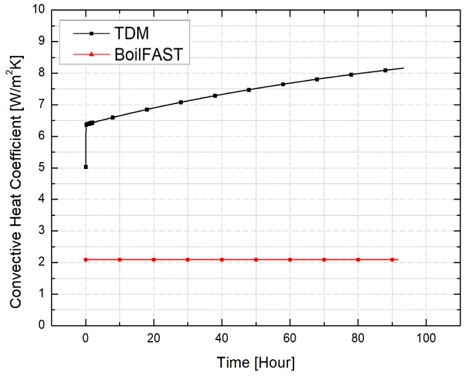
Fig. 8은 본 연구(TDM)와 BoilFAST의 대류 열전달 계수를 비교하였으며, 앞 장에서 제시한 식 (1)~식 (13)을 적용하여 각각의 대류 열전달 계수를 계산하였다. TDM은 시간이 지남에 따라 기상 온도가 상승하므로 탱크 내벽의 대류 열전달 계수와 액상-기상 계면에서 대류 열전달 계수 값이 달라지는 점을 반영하였다. 앞 절에서 언급한 바와 같이 Δt는 5초 간격으로 기상의 온도 변화 및 BOG를 계산하여, 총 8시간까지 반복하여 계산하였다. 각 시간 간격 별로 변화된 대류 열전달 계수는 열저항 네트워크에 반영하여, 적재율 별로 액상 및 기상으로 입열량이 변하는 과정을 모사하였다.
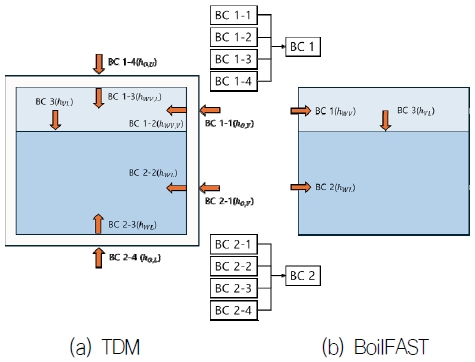
외부-탱크 표면의 대류 열전달 계수(hO,U, hO,L, hO,V)는 각각 3.63 W/m2K, 7.14 W/m2K 그리고 10.79 W/m2K이며, 식 (1)~(3)을 기반으로 계산하였다. 내벽-액상의 대류 열전달 계수(hWL)는 식 (6)을 통해 1924.0 W/m2K로 계산되었다. 탱크 기상의 수평 및 수직면, 그리고 액상-기상 경계면에서 대류 열전달 계수(hWV,L, hWV,V, hVL)는 각각 식(4), 식(5), 그리고 식 (7)을 사용하여 계산하였다. 즉, 본 연구에서 제시한 모델(TDM)과 비교하기 위해 동일한 대류 경계조건을 BoilFAST에 적용하여 BOG의 시간 변화를 계산하였다. 2.4절에서 언급한 바와 같이 BoilFAST는 열 유입량과 등가 열전달 계수를 상수로 가정하여 적재율 변화를 반영하지 못하는 특징을 가지고 있으며, 이는 본 연구에서 제안한 적재율 변화를 반영한 대류 열전달 계수 계산과정과 중요한 차이점 중 하나이다. 즉, 본 연구의 해석적 모델에서는 경계조건을 외부-탱크 표면, 내벽-유체(액상 및 기상), 그리고 액상-기상 경계면으로 세분화하여 정의하였지만, BoilFAST는 외부-유체(액상 또는 기상) 및 액상-기상 경계면으로 단순화하여 정의하고, 대류 열전달 값을 상수로 적용하는 특징이 있다. 따라서 식 (14)~식 (18)을 이용하여 등가 열전달 계수로 변환한 후에 그 값들을 BoilFAST 모델에 반영하였다. BoilFAST의 해석 조건을 Fig. 9에 제시하였다. 그림의 우측 상단에서 ① Boundary conditions 외부 온도(T∞), 외벽-액상 대류 열전달 계수(hO,L)과 외벽-기상의 대류 열전달 계수(hO,V), 그리고 액상-기상 계면에서 대류 열전달 계수(hVL)이 상수 값으로 적용됨을 확인할 수 있다. hO,L과 hO,V는 각각 0.366 W/m2K, 0.299 W/m2K로 적용하였다. ② hVL는 Perez et al. (2021)가 실험 데이터를 기반으로 보정하여 제시한 4.0 W/m2K를 적용하였다. BoilFAST는 기상의 온도 변화를 반영하지 않고 대류 열전달 계수를 상수로 사용하고 있는 것과 달리, 본 연구의 TDM은 기상의 온도 변화, 대류 면적 변화를 반영하여 대류 열전달 계수를 시간 별로 다시 계산하였다.
3.3 장기 BOG 예측 및 분석
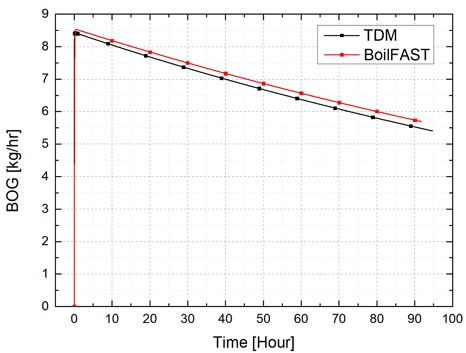
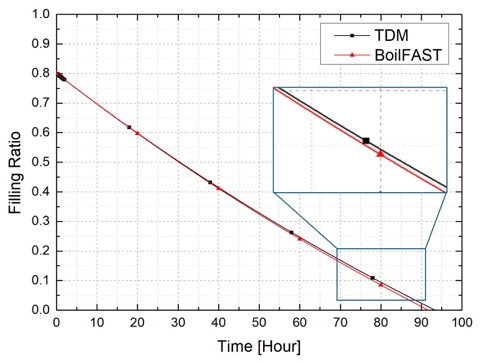
본 절에서는 TDM 기반의 해석 모델로부터 예측된 시간에 따른 BOG 이력, Filling Ratio 및 열전달률을 BoilFAST의 결과와 비교하였다. 인텔 i7 CPU 전산 환경에서 해석 시간은 약 1분 이내에 모두 종료되었다. Fig. 10과 Fig. 11은 BOG 발생량과 Filling Ratio 변화를 비교한 결과이며, 초기 단계에서 급격한 상승을 보인 후 특정 시점부터 완만하게 감소하는 양상을 보였으며, 탱크 내부 Filling Ratio 변화 역시 유사한 감소 경향을 나타내었다. 초기 BOG의 급격한 증가는 평형 상태의 액상에 열 침입으로 인한 증발량 증가로 설명되며, 시간이 지남에 따라 점차 안정화되는 현상을 확인할 수 있었다. 탱크 내부의 액화 질소는 약 92시간 이내에 완전히 증발하고, BoilFAST의 결과가 TDM 결과보다 약 16% 더 많은 BOG 발생량을 예측하였다. Filling Ratio의 경우, 두 모델 모두 유사한 경향을 보였으나, 약 45시간 이후부터 BoilFAST 결과가 더 낮은 값을 나타냈다.
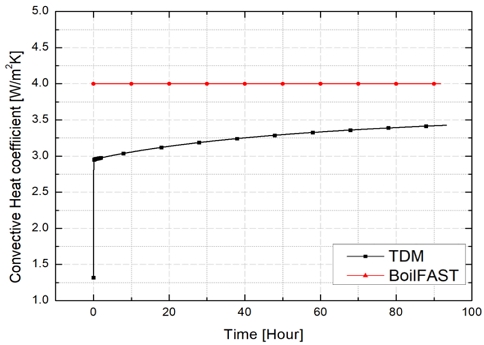
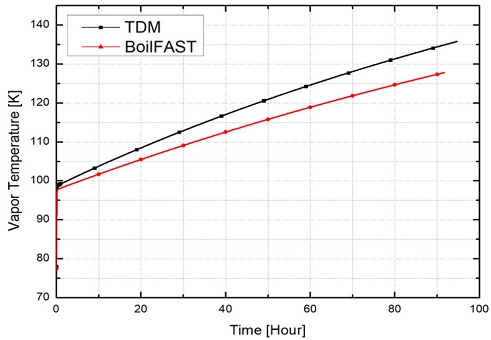
BOG 예측 모델 결과의 차이는 입열 조건에서 적용된 대류 열전달 계수와 열전달률의 차이로부터 기인하는 것으로 판단된다. 이러한 차이는 상대적으로 증발량이 높은 BoilFAST 모델에서 시간이 지남에 따라 누적되며, 두 모델 간의 차이가 점차 확대된 결과로 판단된다. 이에 따라 각 모델의 입열 조건에 따른 열전달률과 대류 열전달 계수를 비교하여 BOG 발생에 미치는 영향을 파악하였다. Fig. 12와 Fig. 13은 BOG 발생 구간 동안 탱크 액상-기상 계면의 대류 열전달 계수 (hVL) 및 내벽-기상의 대류 열전달 계수(hWV,V)를 보여준다. BoilFAST 모델은 고정된 대류 열전달 계수를 적용했지만, TDM 모델은 온도 의존적인 값을 적용하였다. 먼저, Fig. 12에 보인 바와 같이 TDM의 hVL보다 BoilFAST의 값이 큼을 알 수 있다. hVL의 차이는 증발량에 영향을 끼친 것으로 판단된다. Fig. 13의 hWV,V은 TDM의 대류 계수가 큰 값이지만, 열저항에서의 영향은 단열재보다 매우 작으므로 BOG에 영향을 거의 미치지 않은 것으로 판단된다. 기상 온도는 Fig. 14와 같은 경향을 보였다. 대류 열전달 계수 및 기상 온도는 복합적으로 작용하여 Fig. 15와 같이 액상, 기상, 그리고 액상-기상 계면에서 열전달률로 나타났다.
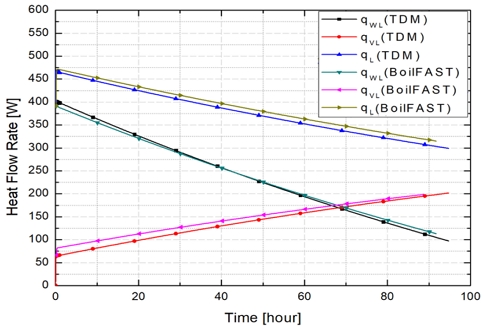
Fig. 15와 같이 BoilFAST 모델이 TDM 기반 예측 모델과 비교하여 더 높은 열전달률을 보이는 것으로 나타났다. 그림에서 qWL은 탱크 내벽으로부터 액상에 직접 전달되는 열전달률을 의미한다. qVL은 액상-기상 경계면에서의 열전달률을 의미한다. 따라서 액상으로 전달되는 모든 열전달률(qL)은 qWL과 qVL의 합이며, 이 값은 BOG의 발생 열원을 의미한다. 초기에는 적재율이 높으므로 액상의 대류 면적이 넓으며 당연히 qWL의 값이 큰 비율을 차지하였다. 그러나, 증발이 진행되면서 적재율이 낮아지면서 qWL의 값이 감소함을 알 수 있다. 또한, 누적되는 입열에 의하여 기상 온도가 상승하고, 기상에서 액상으로 전달되는 열전달률(qVL)이 상승하는 것을 알 수 있다. 이때, qVL의 최대 비율은 TDM에서 67%, BoilFAST에서 64%까지 증가하였다. 위 결과는 BOG 발생 초기에는 액상으로 유입되는 대류 열전달이 주요한 BOG의 원인임을 보여주며, 시간이 지남에 따라 기상의 열유입 및 온도가 증가하면서 경계면에서 액상으로 유입되는 열의 비중이 증가함을 나타낸다. 이러한 결과는 적재율의 변화, 그에 따른 대류 접촉 면적의 변화, 그리고 기상의 온도 변화에 BOG 발생 민감하게 반응한다는 사실을 확인시켜 주었다.
4. 결 론
본 연구에서는 액체수소 및 LNG와 같은 극저온 액체 저장 탱크에서 장기간 발생하는 증발 가스를 신속하게 예측할 수 있는 해석적 모델을 제시하였다. 제안된 모델은 정적 열전도 네트워크를 활용하여 열전달률과 열적 환경을 경계조건으로 반영하였으며, 액상과 기상을 각각 Lumped Mass로 치환하여 열역학 평형 모델(TDM)을 통해 탱크 내 상변화를 반영하였다. 해석 모델의 타당성을 검증하기 위해 가상의 극저온 저장 탱크를 대상으로 BoilFAST의 예측 결과와 비교하였다. 약 92시간에 걸친 장기간 BOG 발생 경향을 예측한 결과, 두 모델 간에 약 10% 내외의 차이가 발생하였다. 특히, BoilFAST가 대류 열전달 계수를 상수로 설정하고 기상의 온도 및 대류 면적의 변화와 같은 열적 환경의 동적 변화를 반영하지 못한 점은 본 연구의 예측값과 차이를 가져온 원인으로 판단된다. 본 연구의 TDM 모델은 기상의 온도 변화 및 액상과 기상의 적재율 변화에 따른 대류 열전달 계수의 변화를 반영하여 BOG 변화를 예측하였다. 이를 통해 극저온 탱크 외부 및 내부의 열적 환경을 세밀하게 반영함으로써, 장기 BOG 예측의 타당성을 향상하고자 하였다. 예측된 결과로부터, 대류 열전달 조건이 극저온 탱크의 BOG 발생에 미치는 원인에 대해 분석하였으며, 적재율이 높은 BOG 발생 초기에는 액상으로 유입되는 열이 BOG 발생의 주요한 요인임을 확인하였다. 시간의 경과에 따른 적재율의 감소는 기상 온도가 증가함에 따라 기상-액상 경계면에서의 열전달이 BOG에 큰 영향을 미침을 확인하였다. 이는 장기 BOG 발생에서 적재율 변화 및 그에 따른 대류 면적의 변화, 기상의 온도 변화, 그리고 액상-기상 계면에서 열전달 계수가 중요한 요인임을 확인하게 하였다. 다만, 본 연구는 열저항 모델에서 단열재의 열전도의 온도 의존성을 제외하였으며, 이를 개선할 필요가 있다. 또한, 열전도 유한요소해석 또는 CFD 기반의 다상 열유동 해석을 수행하여 각 탱크 내벽의 위치별로 대류 열전달 계수의 적절성을 검토할 필요가 있다. 마지막으로, BOG 계측 실험 데이터를 이용하여 TDM 모델의 BOG 발생 경향을 평가하여 제시된 모델의 정확성을 확인할 필요가 있다.
Acknowledgments
이 논문은 2024년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임 (P0023684, 2024년 산업혁신인재성장지원사업)
References
- Agrawal, G., Joseph, J., Agarwal, D.K. and Kumar, S.S., 2015. Effect of insulation thickness on evolution of pressure and temperature in a cryogenic tank. Proceedings of the 23rd National Heat and Mass Transfer Conference and 1st International ISHMT-ASTFE Heat and Mass Transfer Conference. Thiruvananthapuram, 17-20 December 2015.
-
Al Ghafri, S.Z., Swanger, A., Park, K.H., Jusko, V., Ryu, Y., Kim, S. and May, E.F., 2022. Advanced boil-off gas studies of liquefied natural gas used for the space and energy industries. Acta Astronautica, 190, pp.444-454.
[https://doi.org/10.1016/j.actaastro.2021.10.028]

-
Cullimore, B.A., 1998. Optimization, data correlation, and parametric analysis features in SINDA/FLUINT version 4.0. 28th International Conference On Environmental Systems. Danvers 13-16 July 1998.
[https://doi.org/10.4271/981574]

- Guyer, E.C., 1999. Handbook of Applied Thermal Design. CRC Press: Boca Raton.
- Hasan, M.M., Lin, C.S. and Vandresar, N.T., 1991. Self-pressurization of a flightweight liquid hydrogen storage tank subjected to low heat flux. Proceedings of the 1991 ASME/AIChE National Heat Transfer Conference. Minneapolis, 28-31 July 1991.
-
Heestand, J., Shipman, C.W. and Meader, J.W., 1983. A predictive model for rollover in stratified LNG tanks. AIChE Journal, 29(2), pp.199-207.
[https://doi.org/10.1002/aic.690290205]

-
Huerta, F. and Vesovic, V., 2019. A realistic vapour phase heat transfer model for the weathering of LNG stored in large tanks. Energy, 174, pp.280-291.
[https://doi.org/10.1016/j.energy.2019.02.174]

-
Joseph, J., Agrawal, G., Agarwal, D.K., Pisharady, J.C. and Kumar, S.S., 2017. Effect of insulation thickness on pressure evolution and thermal stratification in a cryogenic tank. Applied Thermal Engineering, 111, pp.1629-1639.
[https://doi.org/10.1016/j.applthermaleng.2016.07.015]

-
Kashani, A., Ponizhovskaya, E., Luchinsky, D., Smelyanskiy, V., Sass, J., Brown, B. and Patterson-Hine, A., 2014. Physics based model for online fault detection in autonomous cryogenic loading system. AIP Conference Proceedings, 1573(1), pp.1305-1310.
[https://doi.org/10.1063/1.4860857]

-
Kumar, L. and Sleiti, A.K., 2024. Modeling and analysis of effect of various tank geometries and relief pressure on liquid hydrogen (LH2) Boil-Off Losses. Energy Proceedings, 44, pp.11076
[https://doi.org/10.46855/energy-proceedings-11076]

-
Lemmon, E.W., Bell, I.H., Huber, M.L. and McLinden, M.O., 2018. NIST standard reference database 23: Reference fluid thermodynamic and transport properties - REFPROP, Version 10.0 [Software]. National Institute of Standards and Technology. Available at: [Accessed 23 December 2024].
[https://doi.org/10.18434/T4/1502528]

-
Lin, Y., Ye, C., Yu, Y.Y. and Bi, S.W., 2018. An approach to estimating the boil-off Rate of LNG in type C independent tank for floating storage and regasification unit under different filling ratio. Applied Thermal Engineering, 135, pp.463-471.
[https://doi.org/10.1016/j.applthermaleng.2018.02.066]

-
Ma, L., Yin, X., Shang, L. and Ji, Z., 2018. Modelling of two-phase closed thermosyphon based on SINDA/FLUINT. Applied Thermal Engineering, 130, pp.375-383.
[https://doi.org/10.1016/j.applthermaleng.2017.10.156]

-
Migliore, C., Tubilleja, C. and Vesovic, V., 2015. Weathering prediction model for stored Liquefied Natural Gas (LNG). Journal of Natural Gas Science and Engineering, 26, pp.570-580.
[https://doi.org/10.1016/j.jngse.2015.06.056]

-
Perez, F., Al Ghafri, S.Z., Gallagher, L., Siahvashi, A., Ryu, Y., Kim, S. and May, E.F., 2021. Measurements of boil-off gas and stratification in cryogenic liquid nitrogen with implications for the storage and transport of liquefied natural gas. Energy, 222, pp.119853.
[https://doi.org/10.1016/j.energy.2021.119853]

-
Ratnakar, R.R., Sun, Z. and Balakotaiah, V., 2023. Effective thermal conductivity of insulation materials for cryogenic LH2 storage tanks: A Review. International Journal of Hydrogen Energy, 48(21), pp.7770-7793.
[https://doi.org/10.1016/j.ijhydene.2022.11.130]

-
Rohsenow, W.M., 1952. A method of correlating heat-transfer data for surface boiling of liquids. Transactions of the American Society of Mechanical Engineers, 74(6), pp.969-975.
[https://doi.org/10.1115/1.4015984]

-
Sakowski, B. A., Hauser, D. M., and Kassemi, M., 2019. SINDA/FLUINT and thermal desktop multi-node settled and unsettled propellant tank modeling of zero boil off test. In AIAA Propulsion and Energy 2019 Forum, pp. 4281.
[https://doi.org/10.2514/6.2019-4281]

-
Shu, Q.S., Fast, R.W. and Hart, H.L., 1986. An experimental study of heat transfer in multilayer insulation systems from room temperature to 77K. Advances in Cryogenic Engineering, 31, pp.455-463.
[https://doi.org/10.1007/978-1-4613-2213-9_52]

-
Wang, Z., Sharafian, A. and Mérida, W., 2020. Non-equilibrium thermodynamic model for liquefied natural gas storage tanks. Energy, 190, pp.116412.
[https://doi.org/10.1016/j.energy.2019.116412]

-
Wei, W., Li, X., Wang, R. and Li, Y., 2009. Effects of structure and shape on thermal performance of perforated multi-layer insulation blankets. Applied Thermal Engineering, 29(5-6), pp.1264-1266.
[https://doi.org/10.1016/j.applthermaleng.2008.06.024]

-
Woodfield, P.L., Monde, M. and Mitsutake, Y., 2007. Measurement of averaged heat transfer coefficients in high-pressure vessel during charging with hydrogen, nitrogen or argon gas. Journal of Thermal Science and Technology, 2(2), pp.180-191.
[https://doi.org/10.1299/jtst.2.180]

-
Yu, K., Ge, Z. and Korpus, R., 2016. CFD predictions of FLNG BOG including the influence of filling, offloading, and vessel motion. Offshore Technology Conference 2016. Houston, 2-5 May Curran Associates: New York.
[https://doi.org/10.4043/27228-MS]