실시간 응력 평가를 위한 향상된 축소 모델 기반 동적 해석 기술

1. 서 론

선박 및 해양구조물은 엔진의 진동, 해류, 파랑과 같은 다양한 동적 하중을 지속해서 받으며, 이러한 하중은 고유 진동수와 외부 진동 간의 공진을 통해 큰 변형을 초래할 수 있다. 반복적이고 지속적인 하중은 구조물의 피로 파괴를 유발할 가능성이 있어 이를 정확히 평가하고 관리하는 기술이 필수적이다.

특히, 최근 디지털 트윈(digital twin) 기술의 발전으로 물리적 구조물의 상태를 실시간으로 모니터링하고, 동적 하중 및 응력 변화를 평가하는 기술이 중요한 연구 분야로 주목받고 있다 (Byun et al., 2024). 디지털 트윈은 물리적 시스템의 동적 응답을 디지털 환경에서 모사하여 구조물의 건전성을 예측하고 유지보수 전략을 최적화하는 데 활용된다. 그러나 복잡한 구조 시스템에서 실시간 해석을 구현하기 위해서는 유한요소(Finite Element, FE) 해석의 높은 계산 비용을 줄이는 것이 반드시 요구된다 (Ko and Boo, 2022; Jeong et al., 2023).

이 문제를 해결하기 위해 차원 축소 모델(Reduced-Order Model, ROM) 기법이 다시금 주목받고 있다. ROM은 구조 시스템의 해석 효율성을 획기적으로 향상하는 방법으로, 정적 해석에서 사용되는 정적 응축 기법 (Guyan, 1965; Boo and Oh, 2017)과 동적 해석에서 활용되는 IRS 방법 (O'Callanhan, 1989), 부분 구조 합성(Component Mode Synthesis, CMS) 방법 (Craig and Bampton, 1968), 자동화된 다단계 하위 구조화(Automated Multi-Level Sub-Structuring, AMLS) 방법 (Bennighof and Lehoucq, 2004) 등이 대표적이다. 하지만 복잡한 구조물의 국부 영역에서 발생하는 세부적인 동적 응답을 분석하는 데 기존의 저차 모드 기반 방법은 정확도의 한계를 드러낸다.

이를 해결하기 위해 개발된 향상된 ROM 기법 중 대수적 동적 응축(Algebraic Dynamic Condensation, ADC) 방법(Boo and Lee, 2017)은 전체 질량 및 강성 행렬을 대수적 하위 구조와 인터페이스 경계 영역으로 분리하고, 관성 효과를 포함해 구조 시스템을 축소하는 기법이다. ADC 기법은 기존의 모드 기반 축소 기법보다 높은 정확도와 효율성을 제공하며, 동적 해석 및 응력 평가를 실시간으로 수행하는 데 적합하다.

본 연구의 목적은 향상된 ROM 기법을 기반으로 효율적이고 정확한 동적 해석 기술을 개발하고, 이를 통해 실시간 응력 이력을 평가하는 것이다. 이를 위해 ADC 기법을 사용하여 축소된 동적 운동 방정식을 구성하고, 이를 활용해 시간-변위 응답을 계산한다. 이후 계산된 변위를 바탕으로 구조 시스템 각 요소의 응력 이력을 효율적으로 평가한다. 제안된 방법의 정확성과 효율성을 검증하기 위해, 상용 유한요소 소프트웨어와의 결과를 비교 분석하였다.

본 논문의 구성은 다음과 같다. 2장에서는 동적 해석을 위한 향상된 ROM 기법 기반의 축소 질량 및 강성 행렬 도출 과정을 설명한다. 3장에서는 제안된 방법을 활용하여 과도 응답 및 응력 이력 해석 절차를 기술한다. 마지막으로 4장에서는 다양한 수치 예제를 통해 제안된 방법의 정확성과 효율성을 검증하고 결론을 제시한다.

2. Improved Reduced-Order Model

구조물의 동적 해석을 위한 지배방정식 (Bathe, 1996)은 다음과 같은 행렬 및 벡터 미분 방정식 형태로 표현된다.

여기서 M_g, C_g, K_g는 각각 구조물의 질량, 감쇠 그리고 강성 행렬을 나타내며, $$ {\ddot{\mathit{u}}}_g$$, $$ {\dot{\mathit{u}}}_g$$, u_g는 각각 구조물의 가속도, 속도, 변위 벡터를 의미한다. F_g는 하중 벡터를 나타낸다. 각 행렬은 특정 요소 m에 대하여 표현할 수 있으며, ρ는 밀도이고, κ는 감쇠 특성 매개변수이다.

감쇠 행렬 C_g는 Rayleigh 감쇠 원리에 따라 질량 및 강성 행렬의 선형 조합으로 표현되며, 다음과 같이 나타낼 수 있다.

이때, α와 β는 특정 주파수 대역에 대해 원하는 감쇠 특성을 조정할 수 있는 계수이다.

그러나 식 (1)의 동적 지배방정식을 직접 해석하려면 높은 전산 비용과 자원이 요구되며, 실시간 응력 평가를 수행하기에는 추가적인 어려움이 따른다. 이를 해결하기 위해 본 연구에서는 계산 효율성과 정확도를 극대화할 수 있는 축소모델 구성 과정을 제안한다. 대수적 동적 응축 방법을 적용하여 축소된 동적 방정식을 구성하였으며, 이를 위한 ADC 기법의 네 가지 주요 절차를 정리하였다.

2.1 대수적 하위 구조화

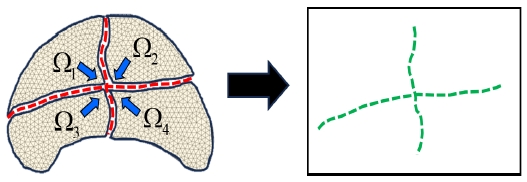
복잡한 유한요소 모델은 주로 크고 희소한 질량 및 강성 행렬을 다루므로, 전체 행렬을 행과 열 기준으로 재배열하고 여러 개의 하위 행렬로 구분할 수 있다. 여기서 행렬의 재배열 방법은 실제 구조물의 물리적인 특성을 변화시키지 않고 유한요소 모델의 절점 번호를 다시 부여하는(node renumbering) 방법을 사용하여 수행된다. Fig. 1은 하위 구조(sub-structures) 및 인터페이스 경계 영역(interface boundary)을 정의하는 과정과 물리적 관점에서 대수적 하위 구조화(algebraic sub-structuring) 방법을 보여준다.

Fig. 1

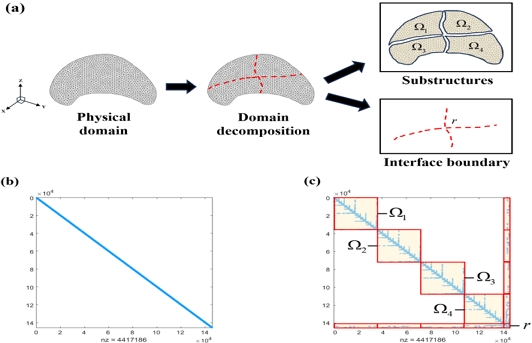
Algebraic sub-structuring procedure : (a) Decomposition of FE model into substructures and interface boundary, (b) Nonzero pattern of a FE matrix, (c) Matrix sub-structuring.

대수적 하위 구조화 후 전체 질량 및 강성 행렬은 하위 구조와 인터페이스 경계 영역으로 다음과 같이 나타낼 수 있다.

$\[ {\mathit{M}}_g=\left[\begin{array}{cc}{\mathit{M}}_n& {\mathit{M}}_n^c\\ {\left({\mathit{M}}_n^c\right)}^T& {\mathit{M}}_r\end{array}\right],{\mathit{ }\mathit{K}}_g=\left[\begin{array}{cc}{\mathit{K}}_n& {\mathit{K}}_n^c\\ {\left({\mathit{K}}_n^c\right)}^T& {\mathit{K}}_r\end{array}\right] \]$

(3)

여기서 M_g와 K_g는 각각 대각 성분을 기준으로 대칭인 전체 질량 및 강성 행렬을 의미한다. 대각 성분(diagonal term)의 아래 첨자 n은 하위 구조, r은 인터페이스 경계 영역을 의미한다. 비대각 성분(off-diagonal term)의 위 첨자 c는 하위 구조와 인터페이스 경계 영역의 연관성(coupled)을 의미한다.

2.3 인터페이스 경계 축소

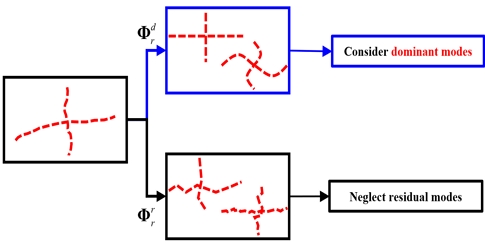
시스템의 자유도 수가 증가함에 따라 하위 구조뿐만 아니라 인터페이스 경계 영역의 자유도 수도 급격히 증가한다. 이에 따라 증가하는 계산 비용을 줄이기 위해 인터페이스 경계 영역의 크기를 줄이는 절차가 필요하다. Fig. 2와 같이 전체 인터페이스 고유벡터 행렬 Φ_r는 주요 인터페이스 모드 행렬(Dominant interface mode matrix) $$ {\mathit{\Phi }}_r^d$$과 잔여 인터페이스 모드 행렬(Residual interface mode matrix) $$ {\mathit{\Phi }}_r^r$$로 구분할 수 있다.

Fig. 2

Interface boundary reduction

구분된 인터페이스 모드 행렬을 기반으로 인터페이스 변위 벡터 u_r는 다음과 같이 정리할 수 있다.

$\[ {\mathit{u}}_r={\mathit{\Phi }}_r{\mathit{q}}_r=\left[{\mathit{\Phi }}_r^d {\mathit{\Phi }}_r^r\right]\left[\begin{array}{c}{\mathit{q}}_r^d\hfill \\ {\mathit{q}}_r^r\hfill \end{array}\right] \]$

(9)

여기서 $$ {\mathit{q}}_r^d$$와 $$ {\mathit{q}}_r^r$$는 각각 $$ {\mathit{\Phi }}_r^d$$와 $$ {\mathit{\Phi }}_r^r$$에 대응하는 일반화된 좌표 벡터이다. 시스템의 주된 거동을 결정하는 주요 인터페이스 모드 행렬​만을 고려하여, 인터페이스 변위 벡터를 표현하면 다음과 같이 근사화된 형태로 나타낼 수 있다.

$\[ {\mathit{u}}_r\approx {\overline{\mathit{u}}}_r={\mathit{\Phi }}_r^d{\mathit{q}}_r^d \]$

(10)

여기서 $$ {\overline{\mathit{u}}}_r$$은 축소된 인터페이스 변위 벡터이다.

식 (10)를 식 (8)에 적용하면, 축소된 인터페이스 경계 영역의 고유값 문제를 다음과 정식화할 수 있다.

$\[ \begin{array}{c}{\stackrel{\mathit{―}}{\mathit{K}}}_r{\mathit{q}}_r^d=\overline{\lambda }{{\stackrel{\mathit{―}}{\mathit{M}}}_r\mathit{q}}_r^d\hfill \\ with {\stackrel{\mathit{―}}{\mathit{M}}}_r={\left({\mathit{\Phi }}_r^d\right)}^T{\hat{\mathit{M}}}_r{\mathit{\Phi }}_r^d,{\stackrel{\mathit{―}}{\mathit{K}}}_r={\left({\mathit{\Phi }}_r^d\right)}^T{\hat{\mathit{K}}}_r{\mathit{\Phi }}_r^d\hfill \end{array} \]$

(11)

여기서 $$ {\stackrel{\mathit{―}}{\mathit{M}}}_r$$와 $$ {\stackrel{\mathit{―}}{\mathit{K}}}_r$$는 각각 축소된 인터페이스 경계 영역의 질량 및 강성 행렬을 의미하며, $$ \overline{\lambda }$$는 근사화된 고유값으로 주요 인터페이스 모드 행렬의 열 개수와 같은 개수의 크기를 가진다.

2.4 관성 효과를 고려한 하위 구조 응축

근사화된 시스템에서 해의 정확도를 향상시키기 위해 하위 구조의 관성 효과를 추가적으로 고려해야 한다. Fig. 3은 관성 효과가 배제된 빨간 점선에 각 하위 구조의 관성 효과 항을 포함하여 초록 점선과 같이 응축한 결과를 도식적으로 나타낸 것이다.

Fig. 3

Sub-structural inertial effect condensation

식 (5)에서 제외했던 미지의 고유값 λ에 대한 1차 관성 항을 고려하여 축소된 하위 구조 변위 벡터 $$ {\stackrel{\mathit{―}}{\mathit{u}}}_s$$​는 다음과 같이 재정의할 수 있다.

$\[ {\overline{\mathit{u}}}_s=\left({\mathit{\Psi }}_c+\lambda {\mathit{K}}_s^{-1}{\hat{\mathit{M}}}_c\right){\mathit{u}}_r \]$

(12)

식 (10)과 식 (12)을 결합하면, 식 (7)에서 축소된 전체 변위 벡터 u_g는 다음과 같이 표현할 수 있다.

$\[ \begin{array}{c}{\overline{\mathit{u}}}_g=\left[\begin{array}{c}{\overline{\mathit{u}}}_s\\ {\overline{\mathit{u}}}_r\end{array}\right]={\mathit{\Psi }}_1{\mathit{q}}_r^d with\hfill \\ {\mathit{\Psi }}_1=\stackrel{\mathit{―}}{\mathit{\Psi }}+\lambda {\mathit{\Psi }}_a,\stackrel{\mathit{―}}{\mathit{ }\mathit{\Psi }}=\left[\begin{array}{c}{\mathit{\Psi }}_c\\ I\end{array}\right]{\mathit{\Phi }}_r^d, {\stackrel{\mathit{―}}{\mathit{\Psi }}}_a=\left[\begin{array}{c}{\mathit{K}}_s^{-1}{\hat{\mathit{M}}}_c{\mathit{\Phi }}_r^d\\ 0\end{array}\right]\hfill \end{array} \]$

(13)

여기서 Ψ₁은 λΨ_a에 의해 하위 구조의 관성 효과를 고려하여 새롭게 정의된 인터페이스 제약 모드 행렬이며, $$ \overline{\mathit{\Psi }}$$는 축소된 인터페이스 제약 모드 행렬이다.

따라서 강성과 관성 효과가 모두 반영된 축소모델은 다음과 같이 정의할 수 있다.

$\[ {\tilde{\mathit{M}}}_r={\mathit{\Psi }}_1^T{\mathit{M}}_g{\mathit{\Psi }}_1, {\tilde{\mathit{K}}}_r={\mathit{\Psi }}_1^T{\mathit{K}}_g{\mathit{\Psi }}_1 \]$

(14)

축소된 감쇠 행렬 $$ {\tilde{\mathit{C}}}_r$$는 식 (2)와 같이 Rayleigh 감쇠 원리를 적용하여 축소된 질량 및 강성 행렬의 선형 조합으로 다음과 같이 나타낼 수 있다.

$\[ {\tilde{\mathit{C}}}_r=\alpha {\tilde{\mathit{M}}}_r+\beta {\tilde{\mathit{K}}}_r \]$

(15)

최종적으로 식 (14)와 식 (15)를 기반으로 축소된 동적 운동 방정식은 다음과 같이 정의할 수 있다.

$\[ {\tilde{\mathit{M}}}_r{\ddot{\mathit{u}}}_r+{\tilde{\mathit{C}}}_r{\dot{\mathit{u}}}_r+{\tilde{\mathit{K}}}_r{\mathit{u}}_r={\tilde{\mathit{F}}}_r with{ \tilde{\mathit{F}}}_r={\mathit{\Psi }}_1^T{\mathit{F}}_g \]$

(16)

여기서 $$ {\tilde{\mathit{F}}}_r$$는 전체 힘 벡터와 변환 행렬의 곱으로 얻어진 축소된 힘 벡터이다. 제안된 방법에서는 새롭게 정의된 인터페이스 제약 모드 행렬 Ψ₁을 대수적 동적 응축을 위한 핵심 변환 행렬로 정의한다.

3. Improved ROM 기반 동적 해석

본 장에서는 축소된 운동 방정식을 기반으로 과도 응답 및 응력 이력 해석에 대한 수식을 정의한다. 대표적인 유한요소 해석 프로그램인 Abaqus에서 채택하는 과도 응답 해석 방법인 Hilber-Hughes-Taylor(HHT) method를 사용하여 시간에 따라 변화하는 변위 응답을 계산하고 얻은 변위 결과를 응용하여 응력 이력을 계산한다.

식 (16)을 기반으로 시간에 따라 변화하는 미지수 u_r, $$ {\dot{\mathit{u}}}_r$$, $$ {\ddot{\mathit{u}}}_r$$에 대한 동적 운동 방정식을 다음과 같이 정의할 수 있다.

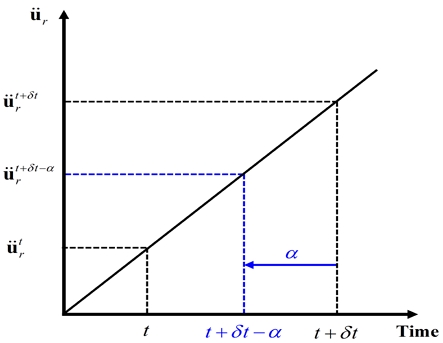
여기서 t와 δt는 각각 시간과 시간 증분을 나타낸다. Fig. 4와 같이 HHT 방법은 시간에 따른 선형 가속도 근사를 사용하여 다음과 같이 표현할 수 있다.

Fig. 4

Linear acceleration approximation

여기서 α는 중간점 근사 매개변수로 해의 수렴성을 개선하는 역할을 한다.

Newmark time integration의 상수 평균 가속도 가정을 이용하여, 가속도와 속도에 대한 방정식은 다음과 같이 가정할 수 있다.

여기서 β와 γ는 해의 안정성과 정확도를 높이기 위해 결정하는 매개변수로써 다음과 같이 정의할 수 있다.

따라서 식 (22)와 식 (23)을 식 (18)에 대입하여 정리하면 과도 응답 해석의 최종 식을 다음과 같이 나타낼 수 있다.

따라서 시간에 대한 축소 변위 $$ {\mathit{u}}_r^{t+\delta t}$$는 축소된 강성 행렬의 역행렬과 힘 벡터의 행렬 곱을 통해 다음과 같이 계산된다.

최종적으로 시간에 대한 전체 변위 $$ {\mathit{u}}_g^{t+\delta t}$$는 식 (13)에서 계산된 변환 행렬 Ψ₁과 시간에 대한 축소 변위의 곱으로 다음과 같이 표현할 수 있다.

앞서 정의한 식들과 FEM 이론을 기반으로 쉘 요소에서의 국부 변형률 보간 행렬 $$ {\stackrel{\mathit{―}}{\mathit{B}}}_{ij}$$는 다음과 같이 계산할 수 있다.

여기서 아래 첨자 i와 j는 쉘 요소 각 절점에서의 좌표 번호를 의미하며, g_i는 공변 벡터로 국부 좌표계(Local coordinate)에서 정의된 벡터를 전체 좌표계(Global coordinate)로 변환하기 위한 매핑(Mapping) 기준 벡터를 의미한다. 따라서 국부 변형률 보간 행렬과 매핑 기준 벡터를 결합하여 쉘 요소의 전체 변형률 보간 행렬 B_ij는 다음과 같이 정의할 수 있다.

여기서 $$ {\overline{e}}_i$$는 전체 좌표계에서의 방향벡터를 의미한다. 응력-변형률 관계 행렬 C_g는 재료 법칙(Material law)에 따라 쉘 요소의 탄성계수 E와 포아송 비 ν의 단순 곱을 통해 정의할 수 있다. 최종적으로 시간에 따른 응력 이력은 변형률-응력 관계 행렬, 전체 변형률 보간 행렬 및 식 (29)에서 도출된 시간에 따라 변화하는 전체 변위 행렬의 곱으로 다음과 같이 표현할 수 있다.

본 연구의 핵심 과제는 실시간 응력 해석이 가능한 성능을 확보하는 것이다. 이를 위해 기존의 단순 수식 기반 접근법을 넘어, 수식 계산 과정을 세분화하고 부분 행렬 기반의 계산 전략을 구현하는 것이 필수적이다(Boo and Lee, 2017). 그러나 이러한 성능을 달성하려면 ROM 구성을 포함한 전체 프로세스의 최적화가 필요하며, 이를 뒷받침하기 위한 계산 전략의 정교화와 코드의 고도화가 요구된다. 특히, 디지털 트윈 및 실시간 응력 해석과 같은 다양한 실시간 해석 기능을 실현하기 위해서는 상용 소프트웨어 수준의 높은 코딩 성능이 필수적이다.

4. 해석 수치 예제

본 연구에서는 제안한 응력 이력 해석의 성능을 검증하기 위해 조선소 내업 공정에서 일반적으로 직면하는 Rectangular plate, Stiffened plate model 그리고 Semi-submersible rig 구조물을 평가하였다. 유한요소모델링 및 시스템 행렬 추출은 상용 유한요소 프로그램인 Abaqus를 이용하였으며, 동일한 변위 및 응력 이력을 계산하기 위해 HHT 매개변수 α값을 –0.05로 설정하였다. 계산 과정은 자체 개발한 코드(In-house code)를 기반으로 수행되었다. 먼저, 상용 FE 프로그램에서 전체 시스템 행렬 M_g와 K_g 행렬 데이터를 추출하여 앞서 정의한 식 (3)부터 식 (16)까지 자체 개발한 코드를 기반으로 축소모델을 구성한다. 구축된 축소모델을 기반으로 식 (17)부터 식 (29)까지 과도 응답 해석 모듈을 통해 시간에 따라 변화하는 변위를 계산한다. 마지막으로 축소모델을 구축하기 위해 사용된 변환 행렬 Ψ₁과 계산된 변위 결과 $$ {\mathit{u}}_g^{t+\delta t}$$ 그리고 FEM을 기반으로 구축된 전체 변형률 보간 행렬 B_ij를 활용하여 응력 이력을 계산하는 코드가 수행된다.

축소모델이 적절하게 구축되었는지 확인하기 위해 전체 모델과 축소모델의 고유값을 비교하고, 다음과 같이 오차율 ξ_k을 계산하였다.

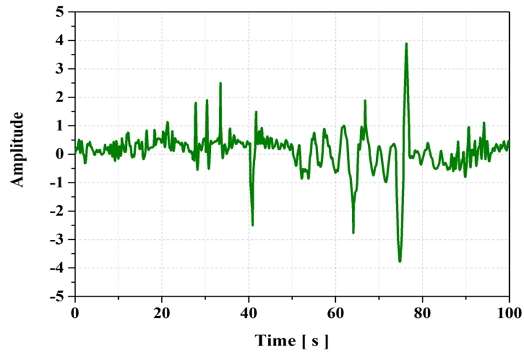
모든 수치 예제에 대하여 FE 모델 구성 시 S4 shell element를 사용하였으며 재료의 물성은 탄성계수 E = 206,000MPa, 포아송 비율 ν= 0.3인 연철(Mild steel)을 적용하였다. 그리고 복잡하고 현실적인 하중을 수치 예제에 반영하기 위해 아래 Fig. 5와 같이 하중 프로파일(Force profile)을 만들었으며, 100초 동안 0.1초의 시간 간격을 설정하여 해석을 수행하였다.

Fig. 5

Force profile for numerical examples

4.1 Rectangular plate problem

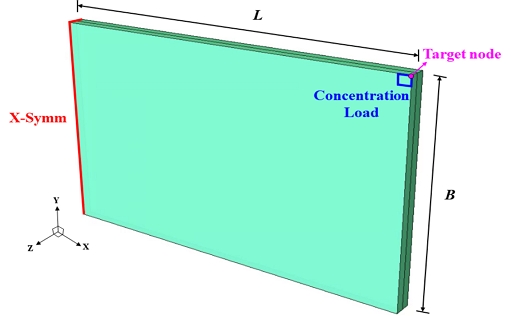
본 예제에서는 Fig. 6과 같이 B = 20m, H = 12m, 두께 t = 0.01m의 제원을 가지는 자유도 145,926개의 Rectangular plate model을 사용하였다. 축소모델은 전체 모델의 자유도 개수 대비 약 0.2% 수준으로 축소하였다. 하중 및 경계 조건은 실제 구조를 고려하여 한쪽 끝단에 X축 대칭 조건을, 반대쪽 끝단 상단 요소에 Z축 방향 100N 집중 하중 조건으로 동적 해석을 수행하였다. Fig. 5의 각 진폭(Amplitude) 값에 100배를 곱한 이력을 해석에 적용하였으며, Target 노드에서 도출된 결과를 시각화하였다.

Fig. 6

Rectangular plate problem

여기서 $$ {\omega }_k^2$$와 $$ {\overline{\omega }}_k^2$$은 각각 전체 시스템과 축소 시스템에 대한 고유값을 의미한다. 아래 첨자 k는 오차율을 계산하기 위해 사용된 정규모드의 개수를 나타낸다. 각 수치 예제의 자유도 개수 및 축소비율은 아래 Table. 1에 명시하였다.

Table 1

Number of DOFs in numerical examples

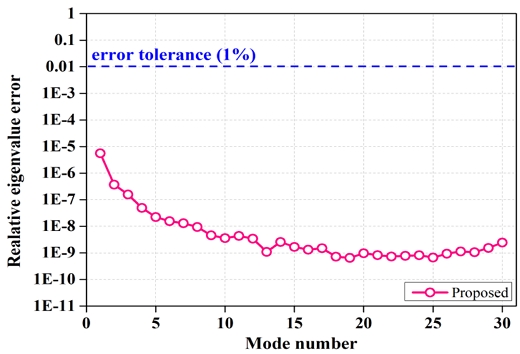
Fig. 7은 모드 번호(mode number)에 따른 상대 고유값 오차(relative eigenvalue error)를 로그 스케일로 나타낸 것이다. 그래프에서 확인할 수 있듯이, 제안된 방법의 상대 고유값 오차는 대부분 10^-6 이하로 매우 낮은 수준을 유지하고 있으며, 특히 일부 모드에서는 10^-9 수준에 도달하여 높은 정확도를 보인다.

Fig. 7

Relative eigenvalue error of rectangular plate

이는 제안된 방법이 고유값 계산에서 매우 정밀한 결과를 제공함을 의미하고, 적절한 축소모델이 구성되었음을 의미한다. 또한, 파란색 점선은 1%의 오차 허용 한계(error tolerance)를 나타내며, 제안된 방법의 결과는 모든 모드 번호에서 허용치를 훨씬 밑돌고 있다. 이를 통해 제안된 방법이 안정적이고 신뢰할 수 있는 성능을 발휘함을 확인할 수 있다.

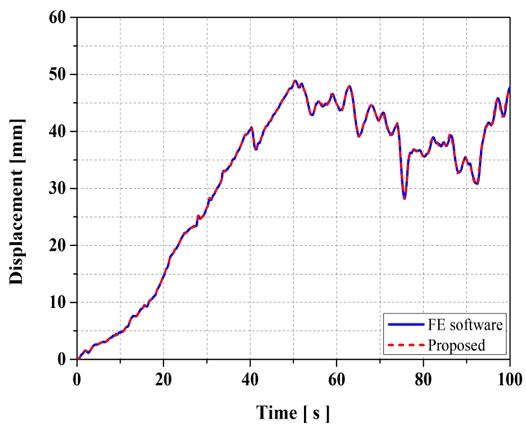
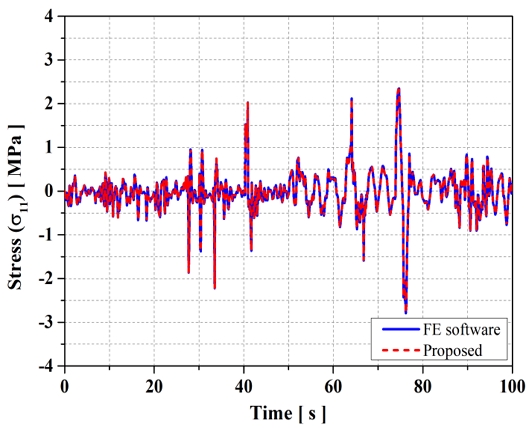
제안한 해석 기법의 변위 및 응력 이력의 정확도를 확인하기 위해서 유한요소 프로그램의 해석 결과와 비교하여 Fig. 8, 9와 같이 제시하였다. Fig. 8은 하중이 작용한 Z축 방향의 변위 결과이고, Fig. 9는 굽힘 효과가 크게 작용하는 X축 방향의 응력 결과를 도식화하였다. 또한, 전산 효율을 검증하기 위해 단계별 해석

Fig. 8

Displacement result of rectangular plate

Fig. 9

Stress history of rectangular plate

4.2 Stiffened plate problem

시간을 비교하여 Table. 2에 정리하였다. 축소모델을 활용하여 동적 해석을 수행한 결과, 100초 동안의 응력 이력을 도출하는 데 약 1.5초가 소요되며 정확도 또한 동일 수준으로 실시간 해석에 가까운 효율성을 보임을 확인할 수 있다.

Table 2

Computational cost for rectangular plate

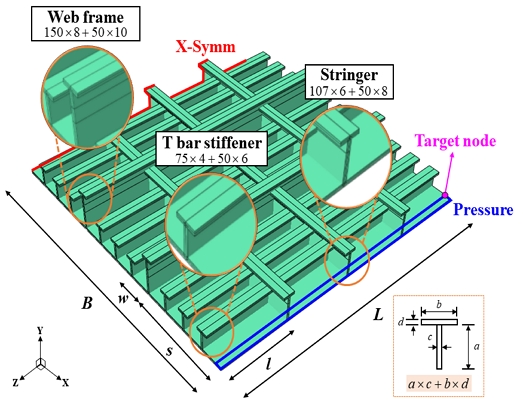
본 예제에서는 Fig. 10과 같이 B = L = 1.2m, 두께 t = 0.01m의 제원을 가지는 자유도 36,606개의 Stiffened plate model을 사용하였다. 축소모델은 전체 모델의 자유도 개수 대비 약 0.3% 수준으로 축소하였다. 하중 및 경계 조건은 Longitudinal 방향을 기준으로 한쪽 끝단에 X축 대칭 조건을, 반대쪽 Free edge에는 Y축 방향으로 0.1MPa 압력을 가하여 동적 해석을 수행하였다. Fig. 5의 하중 프로파일에서 각 진폭 크기에 0.1배 곱한 값을 최종 하중으로 사용하였으며, Target 노드에서의 변위 및 응력 이력을 계산하였다.

Fig. 10

Stiffened plate problem

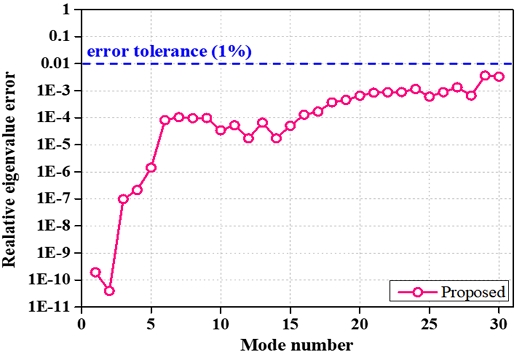
축소모델과 전체 모델의 고유값 간 오차율을 분석한 결과, Fig. 11에서 저차 모드에서는 오차가 거의 없음을 확인할 수 있다. 특히, 상대 오차가 매우 낮은 수준을 유지하며, 제안된 방법이 고유값 계산에서 높은 정확도를 제공함을 보여준다.

Fig. 11

Relative eigenvalue error of stiffened plate

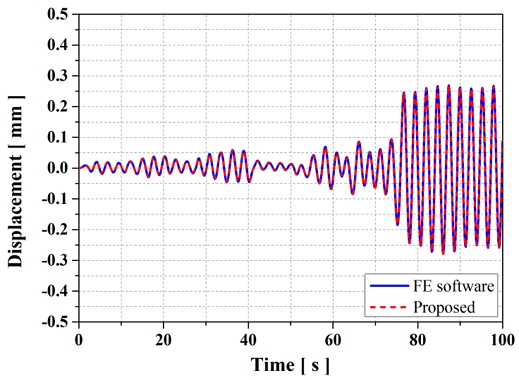
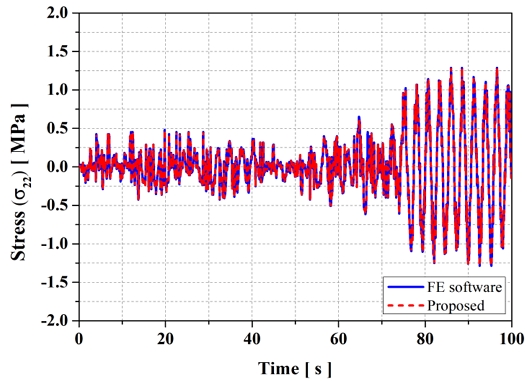
Fig. 12, 13은 보강판 문제에 가해진 Y축 방향 하중과 동일한 방향의 변위 및 응력 해석 결과를 시간에 따라 나타낸 것으로, 이는 구조적 강성과 설계 기준을 평가하는 주요 요소이다. 파란색 선은 유한요소 소프트웨어를 사용한 해석 결과를, 빨간색 점선은 제안된 방법의 결과를 나타낸다. 두 결과는 전체 시간 영역에서 매우 유사하게 나타나며, 특히 고주파 진동 영역에서도 큰 차이가 없음을 확인할 수 있다. 이는 제안된 방법이 유한요소 해석과 일치하는 높은 정확도를 가지며, 시간 이력 해석에서도 신뢰할 수 있는 결과를 제공함을 입증한다.

Fig. 12

Displacement result of stiffened plate

Fig. 13

Stress history of stiffened plate

또한, 전산 효율성을 검증하기 위해 단계별 해석 시간을 비교하여 Table. 3에 정리하였다. 본 예제에서는 100초 동안의 응력 이력을 도출하는 데 약 0.1초가 소요되며, 실시간에 준하는 높은 해석 효율성을 보였다. 이는 제안된 방법이 디지털 트윈 기반 실시간 구조해석에 매우 적합함을 보여주는 중요한 결과이다.

Table 3

Computational cost for stiffened plate

4.3 Semi-submersible rig problem

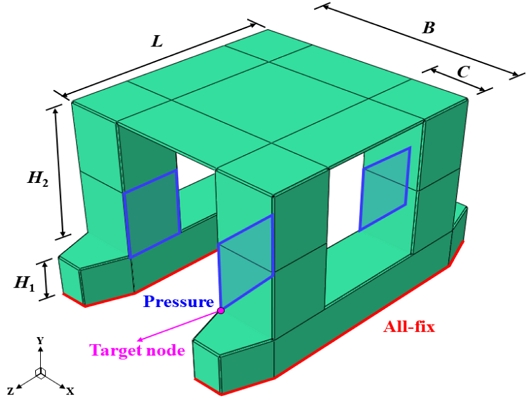
Fig. 14는 B = 80m, L = 110m, C = 20m, H1 그리고 H2는 각각 15m, 50m이며 두께 t = 0.015m의 제원을 가지는 자유도 58,278개의 Semi-submersible rig model을 보여준다.

Fig. 14

Semi-submersible rig problem

본 예제에서는 전체 모델의 자유도 개수 대비 약 0.3%에 해당하는 축소모델을 구축하였다. 하중 및 경계 조건은 폰툰(Pontoon) 바닥에 전단 고정(All-fix) 조건을, 칼럼(Column) 외벽에는 10MPa 압력을 가하여 동적 해석을 수행하였다. 앞선 예제들과 마찬가지로, Fig. 5의 하중 프로파일 진폭에 10배 확장한 값을 최종 하중으로 적용하여 해석을 수행하였으며, Target 노드에서의 동적 해석 결과를 도출하였다.

Fig. 15

Relative eigenvalue error of semi-submersible rig

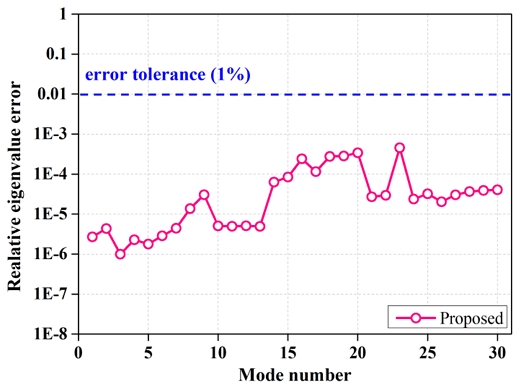
Fig. 15에서 확인할 수 있듯이, 제안된 방법의 상대 고유값 오차는 10^-3 에서 10^-6 사이에 분포하며, 모든 모드에서 안정적인 성능을 유지한다. 특정 모드에서 상대적으로 오차가 증가하는 경향이 관찰되기도 하지만, 전체적으로 오차 수준은 매우 낮다. 또한 1%의 오차 허용 한계(error tolerance)와 비교했을 때, 제안된 방법은 모든 모드에서 허용치를 충분히 만족하며, 이는 제안된 방법의 계산 결과가 신뢰할 수 있는 수준임을 보여준다.

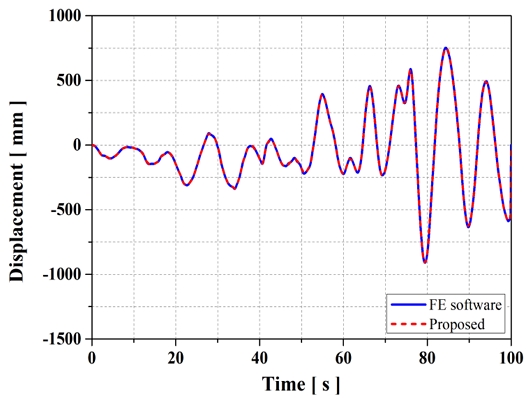
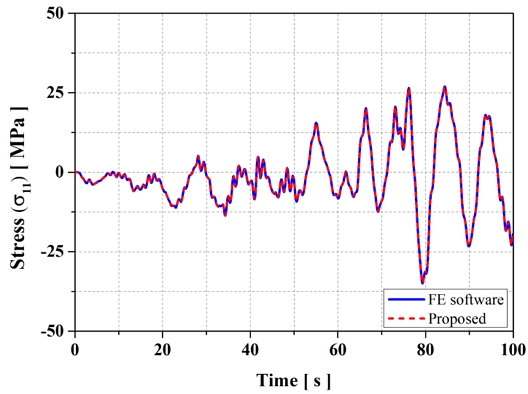
Fig. 16, 17은 동적 안정성, 하중 저항 능력 등 구조적 강성을 평가하기 위해 각각 총 100초 동안 0.1초 간격으로 하중이 가해진 X축 방향의 변위 및 응력 해석 결과를 나타낸 것이다. 제안된 기법의 결과는 상용 프로그램의 결과와 전체 시간 영역에서 매우 잘 일치하며, 특히 변위와 응력의 고주파 진동 구간에서도 높은 정확도를 유지하는 것을 확인할 수 있다.

Fig. 16

Displacement result of semi-submersible rig

Fig. 17

Stress history of semi-submersible rig

Table. 4는 계산 시간 비교 결과를 보여준다. 기존의 Abaqus 기반 해석에서는 Transient analysis에 1353.3초가 소요된 반면, 본 연구에서 제안한 방법을 적용한 경우, 단 0.4초만 소요되었다. 특히, 제안된 방법은 기존 방법 대비 계산 비용을 약 2.8% 수준으로 절감하며, 뛰어난 계산 효율성을 입증하였다.

Table 4

Computational cost for semi-submersible rig

이 결과는 본 연구에서 제안된 계산 전략이 실시간 응력 평가 및 구조물 해석에서 매우 높은 효율성을 제공함을 보여준다. 계산 시간의 획기적인 단축은 실시간 데이터를 기반으로 구조물의 상태를 평가하고 예측하는 디지털 트윈 기술 구현에 필수적인 요소이다. 따라서, 본 연구의 제안 방법은 디지털 트윈 기반 실시간 구조해석 기술의 실현 가능성을 크게 향상시키며, 다양한 실시간 응용 분야에 중요한 기여를 할 수 있다.

5. 결 론

본 연구에서는 향상된 차원 축소 모델(Reduced-Order Model, ROM) 기법을 활용하여 구조물의 변위 및 응력 이력을 효율적으로 계산하는 방법을 제안하였다. 대수적 동적 응축(Algebraic Dynamic Condensation, ADC) 기법을 사용하여 동적 해석을 위한 축소모델을 구축하고, 이를 통해 시간-변위 응답을 계산한 후 구조물의 실시간 응력 이력을 평가하였다. 제안된 방법의 효율성과 정확성을 검증하기 위해 Rectangular plate, Stiffened plate, 그리고 Semi-submersible rig와 같은 다양한 구조물을 대상으로 축소모델을 구축하고, 상용 유한요소(Finite Element, FE) 해석 결과와 비교 분석을 수행하였다.

해석 결과, 제안된 방법은 기존 유한요소 해석보다 수십 배 이상의 빠른 계산 속도를 달성하였으며, 해석 정확도에서도 상용 해석 프로그램과 동등한 수준을 유지하였다. 이러한 결과는 대규모 구조 시스템에서 실시간 구조해석 및 응력 평가를 가능하게 하는 제안 기법의 유용성과 잠재력을 명확히 입증한다.

또한, 본 연구는 디지털 트윈(Digital Twin) 기술과 결합하여 구조물의 상태를 실시간으로 모니터링하고, 잠재적 손상이나 피로 상태를 조기에 감지하여 효율적인 유지보수를 지원할 가능성을 보여준다. 제안된 ROM 기반 해석 기술은 구조해석의 효율성을 극대화하고, 전산 비용과 설계 공수를 줄이는 데 기여할 수 있을 것으로 기대된다. 궁극적으로 본 연구는 실시간 응력 평가 및 구조해석 분야에서의 응용 가능성을 확장하며, 엔지니어링 실무에서 실용적인 해석 도구로 활용될 수 있음을 제시한다.

Acknowledgments

이 연구는 2022년도 한국해양대학교 연구년 전임교원 교내연구비 지원을 받아 수행되었음. 또한, 본 연구는 산업통상자원부 조선해양산업기술개발사업 (RS-2024-00460088)의 연구비 지원으로 수행되었음.

References

• Bathe, K.J., 1996. Finite Element Procedures. Prentice Hall: Englewood Cliffs.
• Bennighof, J.K. and Lehoucq, R.B., 2004, An automated multi-level substructuring method for eigenspace computation in linear elastodynamics. SIAM Journal on Scientific Computing, 25(6), pp.2084–2106 [https://doi.org/10.1137/S1064827502400650]
• Boo, S.H. and Lee, P.S., 2017a, A dynamic condensation method using algebraic substructuring. International Journal for Numerical Methods in Engineering, 109(12), pp.1701–1720. [https://doi.org/10.1002/nme.5349]
• Boo, S.H. and Lee, P.S., 2017b, An iterative algebraic dynamic condensation method and its performance. Computers and Structures, 182, pp.419-429. [https://doi.org/10.1016/j.compstruc.2016.12.011]
• Boo, S.H. and Oh, M.H., 2017c, Automated static condensation method for local analysis of large finite element models. Structural Engineering and Mechanics, 61(6), pp.807-816. [https://doi.org/10.12989/sem.2017.61.6.807]
• Byun, S.J., Lee, S.J. and Boo, S.H., 2024, Load recovery using d-optimal sensor placement and full-field expansion method. Journal of the Society of Naval Architects of Korea, 61(2), pp.115-124. [https://doi.org/10.3744/SNAK.2024.61.2.115]
• Guyan, R.J., 1965, Reduction of stiffness and mass matrices. AIAA Journal, 3(2), pp.380. [https://doi.org/10.2514/3.2874]
• Jeong, Y.H., Boo, S.H. and Yim S.C., 2023, Block-partitioned Rayleigh–Ritz method for efficient eigenpair reanalysis of large-scale finite element models. Journal of Computational Design and Engineering, 10(3), pp. 959-978. [https://doi.org/10.1093/jcde/qwad030]
• Ko, D.H. and Boo, S.H., 2022, Efficient structural dynamic analysis using condensed finite element matrices and its application to a stiffened plate. Journal of Marine Science & Engineering, 10(12), pp.1958. [https://doi.org/10.3390/jmse10121958]
• O'Callanhan, J., 1989, A procedure for an improved reduced system (IRS) model. Proceedings of the 7th International Modal Analysis Conference, pp.17-21.
• Craig, R.R. and Bampton, M.C.C., 1968, Coupling of substructures for dynamic analysis. AIAA Journal, 6(7), pp. 1313–1319. [https://doi.org/10.2514/3.4741]