NARX 모델을 이용한 비선형 선박 구조 응답 시계열의 선형화
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this paper, a method to linearize the nonlinear response of Ultra Large Container Ship(ULCS) with a bow flare is studied by using the Nonlinear Auto-Regressive with External inputs(NARX) model. Response linearization is closely related with the development of digital twin model of a ship, where ocean wave spectrum around sea-going vessel is trageted based upon linear theory between wave and ship response. Linearization scheme is based on the system identification approach using NARX(Nonlinear Autoregressive with External Input) method, which is popularly used for nonlinear dynamic system identification. For the acquisition of data, the nonlinear time domain analysis was performed, where the nonlinear Froude-Krylov force and restoring force and restoring force of the external forces acting on the vessel were considered. Obtained structural response, such as vertical bending moment at the midship section of the ship, was analyzed using NARX, and linear transfer function was extracted using harmonic probing method. To validate the accuracy of the proposed methodology, a structural response in irregular waves was computed in time domain and compared with the linearized responses obtained from transfer function and probability of peak sagging moment exceedance. In terms of the probability exceedance peak responses, the linearized responses turned out to be in good accordance with direct linear analysis results.
Keywords:
Volterra series, NARX, Nonlinear transfer function, Linear transfer function키워드:
볼테라 급수, 비선형 자기 회귀법, 비선형 전달함수, 선형 전달함수1. 서 론
불규칙한 파랑 중 항해하는 선박은 비선형 구조 응답을 가진다 (Jensen and Pedersen 1981). 이는 피로 손상을 유발하고 선박의 수명에 영향을 미친다. 따라서 항해하는 선박의 구조 응답을 정확히 예측하는 것은 기초 설계의 효율성과 안정성을 높이는 데 필수적이다. 이를 추정하기 위한 다양한 연구들이 이어져 왔지만, 최근에는 센서를 통해 얻은 데이터를 활용할 수 있는 디지털 트윈 개념이 주목받고 있다 (Finotti et al. 2019; Khazaee et al. 2022). 디지털 트윈은 계측 데이터를 바탕으로 미계측 위치의 실시간 구조 응답을 추정하여 유지보수 계획 및 전략 수립에 활용될 수 있다.
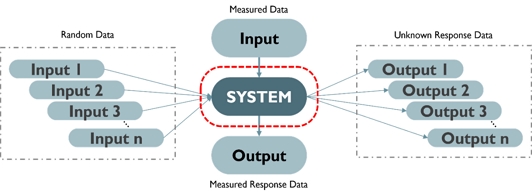
미계측 위치의 구조 응답을 정확히 추정하기 위해서 선체 주변의 방향파 스펙트럼을 추정하는 것이 가장 중요하다. Nielsen (2006)은 선박의 운동 응답 데이터를 기반으로 방향파 스펙트럼을 추정하는 방법을 제시하고 수조 실험으로 얻은 데이터로 검증하였다. 또한 Chen et al. (2020)은 14,000TEU 대형 컨테이너선의 선체 응력 데이터를 이용하여 방향파 스펙트럼을 추정하는 방법을 제안하였다. 이때 기존의 방향파 스펙트럼 추정법은 파랑과 응답의 관계를 선형 시스템으로 가정한다. 그러나 실제 해상에서는 선박이 불규칙한 파랑으로 인해 비선형 구조 응답을 가지기 때문에, 이러한 선형 가정은 실제 응답과의 오차가 발생한다. 따라서 계측 데이터에서 비선형 효과를 포함한 선형 성분을 정확히 추출하는 것이 중요하다. 본 연구에서는 인공 신경망을 사용해 계측 데이터에서 선형 성분을 식별하고자 하였으며, 이를 통해 파랑 하중이 아닌 다른 출력 데이터를 입력으로 사용하여 시스템을 효과적으로 식별할 수 있음을 제안하였다. Fig. 1은 연구의 개념도를 나타내며, 계측된 데이터를 활용해 시스템을 식별하고 이를 기반으로 원하는 응답을 추정하는 방법을 도식화한 것이다.
따라서 본 연구에서는 인공 신경망을 이용하여 비선형 구조 응답에서 선형화 응답을 추출하였다. 방법을 검증하기 위해, 13,000TEU 대형 컨테이너 선박의 비선형 해석을 통해 시계열 데이터를 얻고 외부 입력이 있는 비선형 자기 회귀 방법인 NARX (Nonlinear autoregressive with external input) 모델을 사용하여 신경망을 식별하였다. 이러한 신경망의 특성을 harmonic probing을 적용하여 비선형 효과가 고려된 선형 전달함수로 추정하였다. 또한 볼테라 급수를 이용하여 파랑 하중 데이터와 선형 전달함수를 곱해 응답을 구하고 선형 해석결과와 비교하였다. 특히 서로 다른 출력 데이터를 이용하여 비선형 구조 응답에서 선형 성분을 추출하는 방법을 검증하기 위해, 상하 운동 응답과 종동요 응답을 사용하여 선형 전달함수와 응답을 추정하였다. 세 개의 추정된 응답을 비교하여 본 연구에서 제안하는 방법의 유효성을 검증하였다.
2. 이론적 배경
2.1 NARX Model
인공 신경망은 인간의 뇌 구조를 모방한 컴퓨팅 모델로, 입력된 데이터를 바탕으로 규칙을 학습하여 새로운 데이터에 대해 예측하거나 분류할 수 있다. 연구에서는 시계열 데이터를 이용하여 비선형 동적 시스템을 분석하는데 특화된 NARX(Nonlinear autoregressive with external input) 모델을 사용하였다. 이는 TDNN(Time Delay Neural Network)와 달리 과거 출력값을 입력으로 반환하며, RNN(Recurrent Neural Network)보다 긴 시간 의존성을 효과적으로 처리하는 특징이 있다.
NARX 모델은 입력 X과 출력 Y의 과거 데이터를 비선형 시스템 함수 f로 계산하여 현재의 출력을 예측하는 식 (1a)와 같이 표현할 수 있다.
| (1a) |
여기서, 는 현재 시간에서의 시스템의 출력값을, 은 과거 N 시간 간격(NΔt)까지 시스템의 출력값을 의미하며 은 과거 N 시간 간격까지의 시스템의 외란을 의미한다.
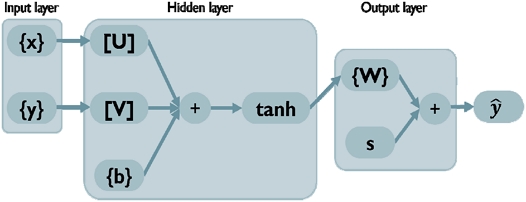
NARX 모델은 Fig. 2와 같이 입력층(input layer), 은닉층(hidden layer), 출력층(output layer)의 3층 구조로 구성된다. 입력층은 외부 데이터를 신경망에 전달하는 역할을 하며, 은닉층은 입력 데이터의 비선형적 특성을 학습하는 중간층으로, 뉴런 수에 따라 여러 개의 층으로 구성될 수 있다. 뉴런의 수가 많을수록 더 복잡한 패턴을 학습할 수 있어 딥러닝 구조에서 고차원적인 문제 해결에 효과적이다. NARX 신경망에서 예측된 출력값은 식 (1b)와 같이 수식으로 나타낼 수 있다.
| (1b) |
여기서, 시스템의 b는 은닉층에서의 편향값이고 tanh는 비선형 활성화 함수이며, s는 출력층의 편향값을 의미한다. [U]와 [V]는 각각 은닉층과 출력층에서의 시스템 파라미터 행렬이다.
이러한 신경망은 예측값과 목표값의 오차를 계산하고 이를 기반으로 가중치와 바이어스를 조정하는 역전파 과정을 거친다. 오차는 식 (2a)와 같이 예측값과 목표값의 평균 제곱 오차로 계산되며, 과적합을 방지하기 위해 가중치 크기를 조절하는 정규화 항이 추가된다. 신경망은 기울기 하강법을 통해 식 (2b)와 같이 가중치를 업데이트하고, 최적의 가중치를 학습하여 오차를 최소화한다.
| (2a) |
| (2b) |
여기서, 는 네트워크 모델의 추정값을, yi는 계측 데이터를 의미하고, wi는 네트워크 모델에 포함된 파라미터를 의미한다.
2.2 Volterra Series
볼테라 급수 출력이 과거의 입력값으로 표현 가능한 비선형 동적 시스템의 수학적 모델이다. 이는 식 (3a)처럼 출력 y(t)는 볼테라 커널과 입력의 과거를 합성 곱하여 적분한 형태로 정의된다.
| (3a) |
여기서, hn(τ1,⋯,τn) 볼테라 커널을, x(t-τj)는 과거 특정 시점 τj에서의 시스템에 작용하는 외란을 의미한다.
일반적으로 비선형성이 약한 동적 시스템 문제에 자주 사용되며, 연구에서 비선형 시스템을 선형화하기 때문에 1차 볼테라 커널까지 전개하여 식 (3b)로 나타냈다.
| (3b) |
이때 1차 볼테라 커널은 충격 응답 함수(Impulse Response Function, IRF)로 정의될 수 있다. 충격 응답 함수를 푸리에 변환하여 식 (4)과 같이 나타내면 1차 전달함수인 LTF(Linear Transfer Function)이다.
| (4) |
이 전달함수와 파랑 하중을 곱하면 응답을 계산할 수 있다. 불규칙파는 n개의 정현파 합인 식 (5a)와 같이 나타내며, 1차 응답은 파랑 하중을 곱하여 식 (5b)로 표현할 수 있다.
| (5a) |
| (5b) |
여기서 Am은 해당 정현파의 진폭을, ωm과 ϕm은 해당 정현파의 각주파수와 위상 각을 나타내며 Re는 복소수의 실수부를 의미한다.
한편 1.1절에서 설명한 NARX 모델은 외부 입력을 사용하는 구조로 선박 비선형 시스템에 적용할 때, 다른 출력 데이터를 입력으로 사용하여 신경망을 식별할 수 있으며 이 관계를 나타내기 위해 볼테라 모델 식 (3b)를 이용하여 다음과 같이 표현하였다. 식 (6a)에서 는 외부 입력으로 사용하는 출력 데이터이고, g1(τ1)을 푸리에 변환하면 식 (6b)와 같이 출력 간의 선형 전달함수로 정의할 수 있다.
| (6a) |
| (6b) |
또한 입력으로 사용한 출력을 파랑 하중과 같은 형태의 식 (5a)처럼 가정하면 식 (7a)로 나타낼 수 있으며, 입력과 전달함수를 곱하여 1차 응답을 식 (7b)로 계산할 수 있다.
| (7a) |
| (7b) |
2.3 Harmonic Probing
조화 탐색(harmonic probing) 방법은 Bedrosian and Rice (1971)이 처음으로 제안한 연속 시간에서 시스템의 주파수 응답을 분석하는 것이다. 이후 Billings and Tsang (1989)는 이산 시계열로 확장하면서 디지털 시스템이나 이산 신호의 처리에서도 사용할 수 있게 되었다. 이 방법은 특정 주파수 신호를 입력으로 제공하고 그에 따른 시스템의 출력을 분석하여 주파수 응답을 계산한다. 또한 2.1절 NARX 모델을 이용하여 식별된 신경망의 특성으로 비선형 시스템을 분석할 수 있다.
이를 적용하여 크기가 1이고 하나의 주파수를 가지는 외력을 가정하면, 입력과 출력을 다음과 같이 표현할 수 있다.
| (8a) |
| (8b) |
이 입력과 출력을 신경망의 방정식 식 (1b)에 대입하고, 이때 하이퍼볼릭 탄젠트는 테일러 급수를 이용해 전개하면 다음 식 (9a)와 같이 선형 전달함수를 계산할 수 있다. 또한 2.2절에서 정의한 출력 간의 전달함수도 동일하게 식 (9b)로 계산될 수 있다.
| (9a) |
| (9b) |
여기서 ⊙는 행렬의 요소별 곱을 의미하고 과거의 입력과 출력을 이용하여 시스템을 식별하기 때문에, 지연 연산자 벡터 ∆ω를 정의하였다.
3. 수치 해석
3.1 Cummins Equation
연구에서 제안하는 방법을 검증하기 위해 Cummins 방정식을 따르는 프로그램을 이용하여 수치해석을 진행하였다(Cummins, 1965). 또한, 이 방정식은 주파수 영역에서 운동 방정식을 시간 영역 운동 방정식으로 변환하는 다음의 과정을 정의한다.
주파수 영역의 운동 방정식을 식 (10)과 같이 나타낸다.
| (10) |
여기서 [m]은 질량 행렬을, [A]는 부가질량 행렬, [B]는 감쇠 행렬, [C]는 복원렬 행렬을 나타낸다. 외력 항에는 유체 동역학적 힘이 고려된다. 이 방정식을 역푸리에 변환하면, 시간 영역의 운동 방정식은 식 (11)과 같다.
| (11) |
식(11)에는 무한 주파수에서의 부가량 항과 충격 응답 함수 K(t)항이 포함되는데, 충격 응답 함수 K(t)는 주파수 영역에서 감쇠 행렬 [B]로부터 식 (12a)와 같이 유도된다. 이때 외력 F(t)는 주파수 성분으로 표현하여 식 (12b)와 같이 주어진다.
| (12a) |
| (12b) |
또한 본 연구에서는 비선형 외력 Q(t)를 추가로 고려하였으며, 비선형 Froude-Krylov와 복원력을 반영하였다. 다만 플레어 선수가 있는 선박의 경우 비선형 효과를 충분히 고려했다는 가정하에, 회절과 방사에 의한 비선형 효과는 별도로 고려하지 않았다.
3.2 해석 모델
Fig. 3은 해석을 위해 대상 선박으로 13,000TEU급 대형 컨테이너선 마젤란이다. 수치해석 시, 응답에서 비선형성이 두드러지게 나타나도록 플레어 선수를 가지는 선박으로 선정하였다. 해석 모델의 주요 재원은 Table 1에 정리하였다. 선박의 중앙 단면에서의 수직 굽힘모멘트의 시계열을 얻어 계산에 적용하였다. 중앙 단면의 굽힘모멘트는 해석에 적용된 프로그램에서 자동으로 계산되는 방식으로, 선체 표면에 작용하는 유체 정/동역학적 힘과 선박 운동에 의한 관성력의 평형을 통해 계산할 수 있다.
3.3 해석 조건
비선형 응답 계산은 주파수 영역에서 수치해석을 먼저 진행 후, 시간 영역 해석을 차례로 진행하였으며 다음 Table 2와 같이 조건을 설정하였다. BV Hydrostar를 이용하여 계산하는 주파수 영역의 응답은 0.1rad/s 간격으로 해석하였으며, BV Homer를 이용하여 시간 영역은 3시간 동안 0.02s 간격으로 해석을 수행하였다. 또한 선박의 속도는 15knots로 고정하였고, 3.1절 식 (12a)에서 충격 응답 함수가 충분히 0으로 감소하는 작동 시간이 요구되기에 100s로 설정하였다. Table 2에 정리된 해석 조건은 주파수 영역에서 얻어진 유체동역학적 계수들에 대한 계산이 시간 영역으로 변환됨에 있어 시간 영역 해석의 정확도를 해치지 않는 적절한 조건으로 결정되었다. 특히 시간 영역해석의 시간 간격은 시간 적분의 정확도에 크게 영향을 미치는 값이므로 충분히 작은 값을 적용하였다.
불규칙 해상 조건은 JONSWAP 스펙트럼과 Pierson- Moskowitz (PM) 스펙트럼을 절대 주파수 영역에서 식 (13a)와 (13b)를 이용하여 계산하였다. 이때 스펙트럼의 유의 파고 Hs는 13.5m이며 피크 파 주기 Tp는 15.5s로 선정하였다. 이때 파 스펙트럼은 정면파 방향(head sea)으로 입사하고 매개변수를 높게 설정하여 극한 조건에서 시간 영역 해석을 진행하였다.
| (13a) |
| (13b) |
시간 영역 해석 후 얻어진 시계열 데이터는 선박이 항해할 때 고정된 지점에서 측정되는 절대 주파수로 분석하면 움직임을 고려하지 않기 때문에 실제 선박 응답을 제대로 예측할 수 없다. 이에 따라 조우 주파수 영역의 시계열 데이터를 이용하였고, 식 (14)에서 g는 중력 가속도이며 V는 선박의 속도, β는 입사파의 각도이다.
| (14) |
4. 수치 데이터 적용
4.1 수치 해석 결과
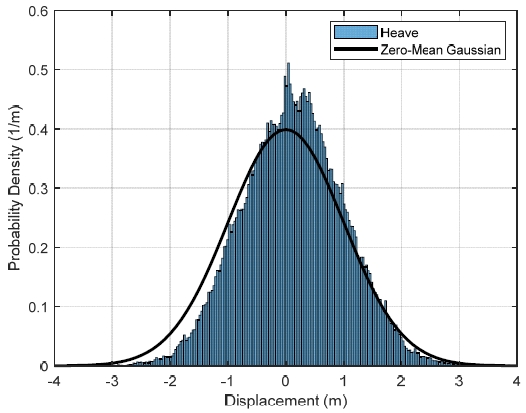
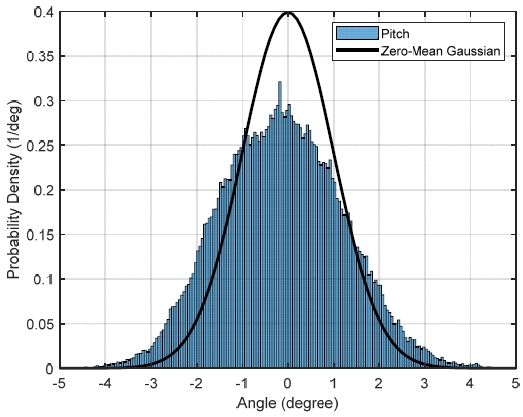
서로 다른 출력 데이터를 이용하여 시스템을 식별하기 위해, 운동 해석결과 중 상하 운동과 종동요를 시스템의 입력 데이터로 선정하였다. 이 두 개의 운동 응답은 비선형 해석결과지만, 파랑 하중과 유사하게 평균이 0인 가우시안 분포를 띄며 비선형성이 두드러지지 않아 입력 데이터로 사용하였다. 두 응답 시계열에서 확률 밀도 함수의 왜도를 계산해 비교한 결과, 상하 운동 응답의 왜도는 0.0341, 종동요 응답의 왜도는 0.1012로 나타났다. 상하 운동 응답의 경우 선형성이 뚜렷하게 나타남을 알 수 있으나, 종동요의 경우 약간의 비선형성이 포함된 것으로 판단할 수 있다. 또한 Fig. 4와 Fig. 5에서 JONSWAP 스펙트럼의 결과인 상하 운동과 종동요 운동 시계열의 분포를 평균이 0이고 분산이 1인 가우시안 분포와 비교하였다. 이를 통해 상하 운동과 종동요가 입력 데이터로 적합하다는 점을 확인하였다.
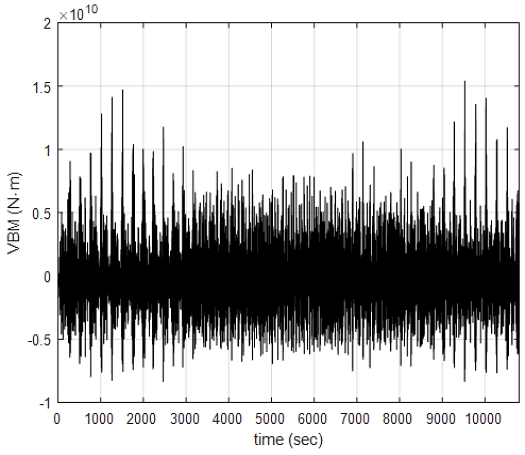
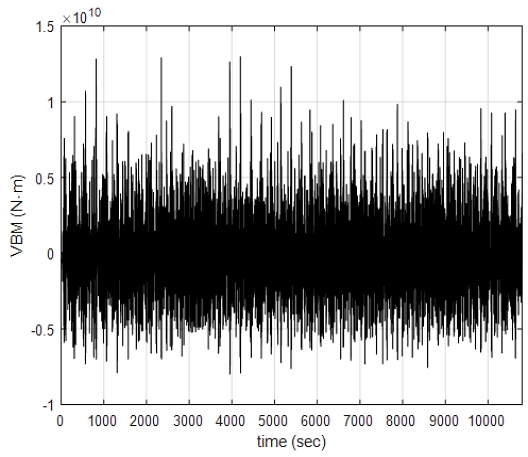
선박의 구조 응답으로 가장 비선형성이 두드러지게 나타나는 중앙 단면에서 수직 굽힘 모멘트 시계열을 출력 데이터로 선택하였다. 이 비선형 응답은 응답의 범위와 피크가 얼마나 정확하게 추정되는지 가장 중요하기 때문에, 비선형 구조 응답의 평균을 제거하고 사용하였다. Fig. 6과 Fig. 7에서 응답 그래프에서 양수인 sagging moment가 음수인 hogging moment보다 더 크게 나타남을 확인하였다. 또한 선형 구조 응답의 왜도는 –0.0079이고, 비선형 구조 응답의 왜도는 0.3468로, 굽힘 모멘트의 경우 비선형 효과가 두드러짐을 확인하였다.
시스템을 식별하여 응답을 추정하기 위해 파랑 하중과 상하 운동, 종동요를 입력 데이터로 사용하고, 수직 굽힘 모멘트를 출력 데이터로 사용하여 Table 3과 같이 6개의 case로 나누어 간략히 명명하였다. 또한 6개의 case가 NARX 모델을 적용하고 시스템 식별하는 과정을 여러 번에 거쳐, 인공 신경망의 매개변수를 최적화하였고 사용된 매개변수를 Table 4에 정리 하였다. Table 4에 정리된 매개변수를 다양한 매개변수 조건에 대한 결과를 분석하여 최적의 값이라 판단되는 값을 경험적으로 선정하였다.
4.2 유효성 검증
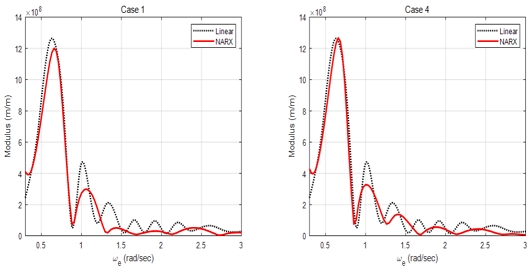
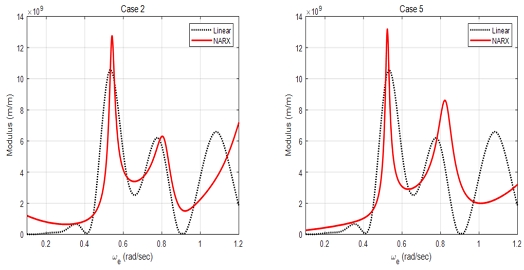
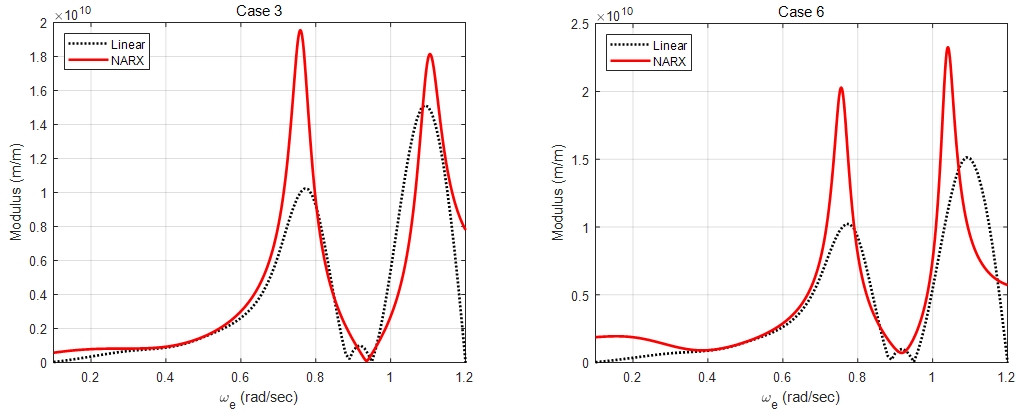
최적의 매개변수를 이용하여 식별한 시스템의 특성으로 2.3절을 통해 선형 전달함수를 추정하였으며, 주파수 영역 해석으로 얻어진 선형 전달함수의 크기와 다음과 같이 비교하였다. Fig 8에서 입력 데이터가 파랑 하중인 case 1와 case 4가 약 0.6rad/s에서 최댓값을 가지는 것을 통해 해석결과와 유사하게 나타남을 확인하였다. 또한 고 주파수로 갈수록 여러 봉우리가 생긴 것은 컨테이너선의 전형적인 전달함수 패턴으로 관찰될 수 있다. Fig 9에서 상하 운동 응답으로부터 얻어진 전달함수이며, 선형 해석결과는 약 0.5rad/s, 0.8rad/s, 1.1rad/s에서 세 개의 피크가 나타났다. 또한 case 2와 case 5의 추정된 전달함수에서는 약 0.5rad/s, 0.8rad/s에서 피크가 나타나고 1.0rad/s 이후로 발산되었다. Fig 10에서 case 3과 case 6은 종동요 응답으로부터 얻어진 전달함수이며, 약 0.9rad/s와 1.1rad/s에서 피크가 동일하게 나타났지만, 선형 해석결과 전달함수의 크기보다 더 크게 추정되었다.
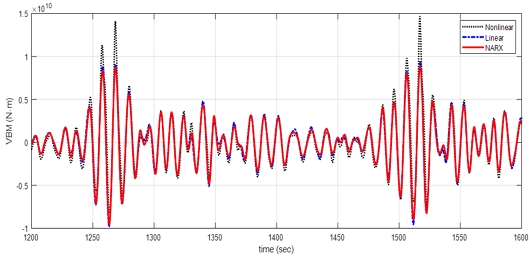
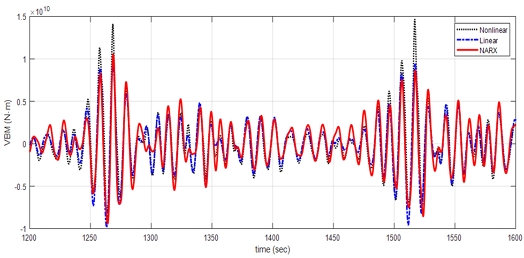
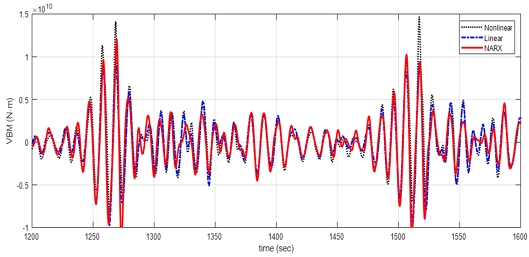
추정된 선형 전달함수로 선형 응답을 식 (5b)와 (7b)를 통해 구하였고, 비선형 해석결과 Target과 선형 해석결과 Linear, NARX와 선형 전달함수로부터 추정한 응답 세 가지를 비교하여 case 1, case 2, case 3은 1200s부터 1600s까지 결과를 나타냈다.
Fig. 11과 Fig. 13에서 case 1과 case 3은 선형 해석결과와 추정된 응답이 매우 일치함을 볼 수 있었으며, Fig. 12에서 case 2의 경우 위상 각은 거의 유사하나 1280s에서 1370s 구간에서 보수적으로 예측되었다. 이러한 경향성에 대한 정확한 원인 분석은 어려우나 NARX가 데이터를 활용한 최적화 문제임을 고려한다면 시계열의 오차는 어느 정도 발생할 수 있을 것으로 판단된다.
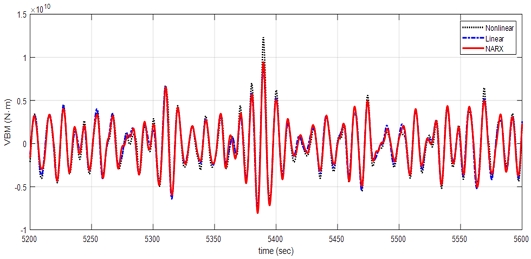
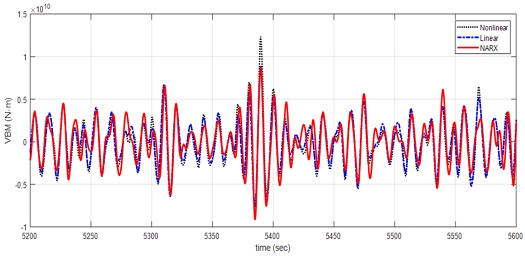
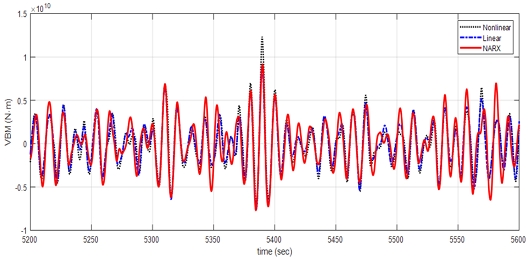
동일하게 case 4, case 5, case 6의 추정된 응답을 비선형 해석결과 Nonlinear과 선형 해석결과 Linear와 비교하여 5,200s부터 5600s까지 결과를 나타냈다. Fig. 14에서 case 4는 선형 해석결과와 추정된 응답이 매우 일치함을 볼 수 있었으며, Fig. 15와 Fig. 16에서 case 5와 case 6은 경향이 유사하나, 응답의 크기가 상대적으로 작은 구간에서 응답이 과하게 예측되어 비선형 해석결과보다 크게 나타났다.
비선형 구조 응답에 있어서 응답의 피크 추정이 중요하기 때문에, 비선형 해석결과와 선형 해석결과, 추정한 응답 세 가지 경우의 peak sagging moment를 계산하고, 피크의 초과 확률 분포도(Probability of exceedance)를 Fig. 17, Fig. 18에 나타냈다. 이 그래프는 선박 설계 시 안전성을 평가하는 데 활용되며, sagging moment의 피크 값이 발생할 확률을 보여준다. Fig. 17에서 선형 해석결과는 case 2의 확률 분포와 거의 일치하였으며, 파랑 하중으로 예측한 case 1은 뉴런의 개수를 10으로 설정한 결과, 과적합이 발생했다. 또한 case 3은 선형 해석결과보다 확률 분포가 오른쪽으로 치우친 것으로 나타났다. Fig 17에서 초과 확률이 10-2와 10-3인 경우에 대해 peak sagging moment를 비교하고 선형 해석과 각 case 간의 오차를 계산하여 Table 5와 같이 나타내었다. 두 가지 확률의 레벨에서 선형 해석결과와 case 1, case 2는 매우 유사했으며 case 3은 상대적으로 더 크 값을 보였다. 특히 종동요 응답을 입력으로 사용한 case 3의 경우 추정된 값이 선형해석의 결과와의 오차가 상대적으로 크게 나타남을 확인할 수 있는데, 이는 종동요 응답이 파랑 및 상하 운동 응답 과 비교하여 비선형 효과가 어느 정도 포함되어 있기 때문인 것으로 판단된다.
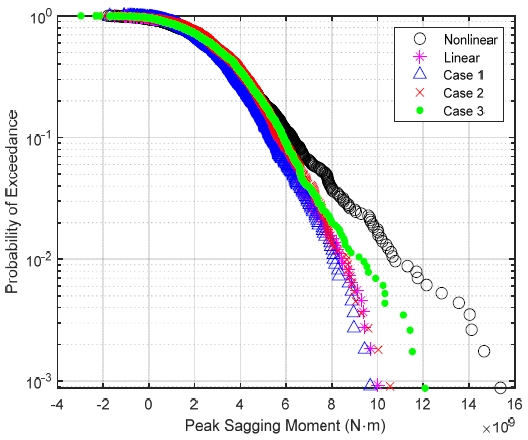
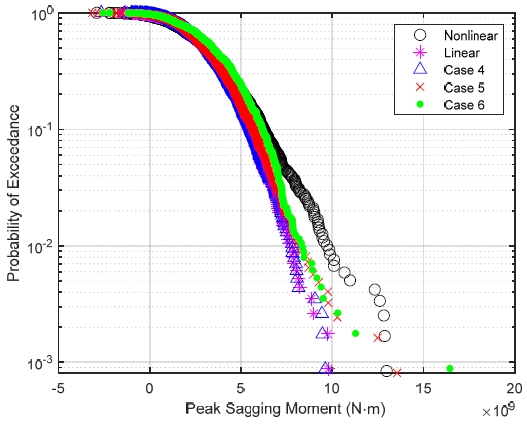
Fig. 18에서 선형 해석결과는 case 4의 확률 분포와 매우 일치하였고, case 5와 case 6은 모멘트의 피크가 커질수록 선형 해석결과보다 비선형 해석결과에 가까워지는 경향을 보여, 추정된 응답의 비선형성이 두드러졌음을 확인할 수 있었다. 또한 동일한 초과 확률 조건에서 peak sagging moment와 오차를 계산하여 Table 6과 같이 정리하였다. 초과 확률이 10-2인 경우, 선형 해석결과와 case 4는 매우 유사하게 나타났으며, case 5와 case 6은 선형 해석결과보다 더 큰 값을 보여 비선형성이 case 4보다 두드러짐을 확인하였다. 또 확률이 10-3인 경우, case 4와 선형 해석결과는 매우 유사했으나, case 5와 case 6은 비선형 해석결과보다도 더 큰 값을 보였다. 앞선 경우와 마찬가지로 종동요 응답을 입력으로 사용한 경우 여전히 오차는 크게 나타났음을 확인할 수 있고, case 5의 경우 발생한 오차는 신경망 훈련에 사용하는 매개변수를 더욱 세밀하게 조정할 필요가 있음을 시사한다.
5. 결 론
본 연구에서는 NARX 모델을 이용하여 선박의 비선형 구조 응답의 선형화하는 방법을 제안하였다. 비선형 효과를 고려하는 프로그램을 사용하여 수치 해석하고 얻어진 데이터로 방법의 유효성을 검증하였다. 비선형 응답을 선형화하는 데 효과적인 방법임을 확인하였고, 검증 결과를 바탕으로 다음과 같은 결론을 도출하였다.
- • NARX 모델은 과거의 입력과 출력 데이터를 활용하여 비선형 동적 시스템 식별에 사용하였다. 이 신경망의 입력 데이터를 파랑 하중으로 훈련하여 전달함수를 추정하고, 계측이 가능한 상하 운동 응답과 종동요를 입력 데이터로 사용하여 비선형 동적 시스템을 성공적으로 식별하였다.
- • 방법을 검증하기 위해, Homer를 사용하여 시간 영역에서 해석을 수행했으며, 이때 외력에는 비선형 Froude-Krylov와 복원력을 고려하였다. 또한 비선형 효과가 두드러지게 나타내기 위해, 대상 선박을 플레어 선수가 있는 13,000TEU급 대형 컨테이너선으로 선정하였다. 중앙 단면의 수직 굽힘 모멘트 시계열에서 양의 sagging moment가 음의 hogging moment보다 크게 나타나 비선형 효과가 두드러짐을 보여주었다.
- • 입력과 파랑 스펙트럼에 따라 6개의 케이스에 대해 신경망을 식별하고 추정된 전달함수를 주파수 영역 해석과 비교한 결과, 모든 case에 대해 선형 전달함수를 합리적으로 추정함을 확인하였다. 추정된 전달함수는 케이스 별로 약간 상이하게 도출되었으나 이는 신경망 학습 과정에서 발생한 오차로 추정된다.
- • 볼테라 급수를 이용하여 6개의 case의 추정된 전달함수로 선형 응답을 계산했다. 추정된 응답과 선형 해석결과를 비교한 결과, 두 응답이 비교적 잘 일치함을 확인할 수 있었으며, 수직 굽힘 모멘트 피크의 초과 확률 분포에서도 신뢰성 있게 예측됨을 확인할 수 있었다.
- • 종동요를 입력으로 사용한 경우 추정치의 정확도는 상대적으로 떨어짐을 확인할 수 있었다. 이는 입력으로 사용된 종동요게 미약하게나마 포함된 비선형성으로 인한 결과로 추정되므로 계측 데이터의 선형화를 위해 상하 동요를 적용하는 것이 보다 합리적임을 뒷 받침하는 결과이다.
- • 본 연구에서는 NARX에 적용되는 매개변수를 경험적으로 선정하고 이를 활용하여 시스템의 전달함수를 식별하였으나 최적의 매개변수를 선정함에 있어 보다 체계적인 접근법이 확립되어야 할 것으로 판단되며, 이는 향후 연구에 있어 중요하게 다루어져야 할 내용으로 여겨진다.
Acknowledgments
이 논문은 2024년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임. (P0023684, 2024년 산업혁신인재성장지원산업)
References
-
Bedrosian, E. and Rice, S.O., 1971. The output properties of volterra system (nonlinear systems with memory) driven by harmonic and Gaussian inputs. Proceedings of the IEEE, 59(12), pp.1688-1707.
[https://doi.org/10.1109/PROC.1971.8525]

-
Billings, S.A. and Tsang, K.M., 1989. Spectral analysis for non-linear systems, Part 1: Parametric non-linear spectral analysis. Mechanical Systems and Signal Processing, 3(4), pp.319-339.
[https://doi.org/10.1016/0888-3270(89)90041-1]

-
Chen, X., Okada, T., Kawamura, Y. and Mitsuyuki, T. 2020. Estimation of on-site directional wave spectra using measured hull stresses on 14,000 TEU large container ships. Journal of Marine Science and Technology, 25, pp.690-706.
[https://doi.org/10.1007/s00773-019-00673-w]

- Cummins, W.E., 1962. The impulse response function and ship motion. Report 1661, Department of the Navy, David W. Taylor Model Basin, Hydromechanics Laboratory, Research and Development Report, October 1962.
-
Finotti, R.P., Cury, A.A. and Barbosa, F.D.S. 2019. An SHM approach using machine learning and statistical indicators extracted from raw dynamic measurements. Latin American Journal of Solids and Structures, 16(02), e165.
[https://doi.org/10.1590/1679-78254942]

-
Jensen, J.J. and Pedersen, P.T., 1981. Bending moments and shear forces in ships sailing in irregular waves. Journal of Ship Research, 25(04), pp.243-251.
[https://doi.org/10.5957/jsr.1981.25.4.243]

-
Khazaee, M., Derian, P. and Mouraud, A. 2022. A comprehensive study on Structural Health Monitoring (SHM) of wind turbine blades by instrumenting tower using machine learning methods. Renewable Energy, 199, pp.1568-1579.
[https://doi.org/10.1016/j.renene.2022.09.032]

-
Nielsen, U.D. 2006. Estimations of on-site directional wave spectra from measured ship responses. Marine Structures, 19(1), pp.33-69.
[https://doi.org/10.1016/j.marstruc.2006.06.001]