분력계의 설치 위치가 조종성능 추정 구속모형시험 결과에 미치는 영향 연구
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The present study aims to investigate the effect of the installation location of two three-component load cells on the results of the captive model tests. The captive model tests consisted of the static drift, pure sway, and pure yaw tests. The test results were analyzed when the load cells were located at 5%, 10%, and 15% of the ship's length from its center. When two load cells were used in the captive model tests, the direction of the sway force of the two load cells was opposite. As the load cells were installed farther from the center, the magnitude and standard deviation of each load cell’s sway force decreased. However, the standard deviation of the yaw moment increased as the yaw moment was calculated by multiplying the sway force and distance. The yaw moment is the sum of the yaw moment value measured from the load cell and the value calculated by the sway force and distance. The yaw moment calculated by the sway force was more than 70% of the total yaw moment acting on the hull. As the load cell got closer to the center of pressure, the ratio of yaw moment calculated by sway force increased.
Keywords:
Arrangement of the load cell, Captive model test, Horizontal planar motion mechanism test, Maneuverability키워드:
분력계 배치, 구속모형시험, 수평면운동장치 시험, 조종성능1. 서 론
선박의 조종성능 연구는 운항 중인 선박의 이동 궤적과 자세를 정확하게 추정하기 위해 수행되고 있으며, 연구 결과들은 해상 사고 및 오염을 예방하기 위한 기초 자료로 활용되고 있다. 선박들의 충돌이나 좌초로 인한 원유 유출과 해양 오염을 방지하려면 설계 단계에서 조종성능을 정확하게 분석하여야 하고, 국제해사기구(International Maritime Organization, IMO)가 제정한 조종성능 기준 (IMO, 2002)을 만족하는지 검증하여야 한다. 최근에는 4차 산업혁명의 발전으로 스마트 선박과 친환경 기술의 중요성이 대두되고 있는데, 선박의 조종성능은 디지털 트윈과 경제 운항 기술 개발에도 필수적인 요소이다.
조종성능 추정 방법론들은 관점에 따라 다양하게 분류될 수 있다. 조종성능 분석을 위해 필요한 계수 혹은 지표들을 어떻게 얻느냐의 관점으로 바라보면, 경험식을 활용한 방법론, 실험을 이용한 방법론, 전산유체역학(Computational Fluid Dynamics, CFD) 해석을 이용한 방법론으로 분류할 수 있다. 실험을 이용한 방법론은 구속모형시험과 자유항주모형시험으로 나뉘게 된다. 구속모형시험은 수조에서 모형선을 예인전차에 구속하고 예인하며 모형선에 작용하는 외력을 측정하고, 측정된 외력 결과에 최소자승법이나 푸리에 해석법 등을 적용하여 유체력미계수를 도출하게 된다. 도출된 유체력미계수를 이용하여 외력을 모델링하고 운동방정식에 기반한 조종운동 시뮬레이션을 수행하여 조종성능 관련 지표들을 얻게 된다 (Kim et al., 2011; Kwon et al., 2022; Shin and Choi, 2011; Yoon, 2009). 자유항주모형시험은 모형선에 모터, 제어기, 컴퓨터, 계측장비, 통신장비들을 탑재하여 제어 입력에 따라 모형선이 운항할 수 있도록 설계하며, 모형선이 운항하는 동안 궤적과 자세를 계측하여 조종성능을 분석하게 된다 (Park et al., 2020; Yun and Yeo, 2019; Yun et al., 2021; Yun et al., 2022).
본 연구에서는 조종성능 분석을 위해 전통적으로 수행되고 있는 구속모형시험의 신뢰성 향상을 목표로 하였다. 두 개의 분력계가 설치되는 경우에 분력계의 설치 위치에 따른 실험 조건을 설정하고 그에 따른 실험 결과를 분석하였다. 모형선의 자세가 구속되어 움직이지 않는 경우에는 힘 평형에 따라 모형선에 작용하는 외력은 모두 분력계에 전달되게 된다. 모형선의 크기가 작은 경우에는 모형선 중앙에 분력계를 설치하여 1점 지지 방식으로 모형선을 예인하게 되지만, 모형선의 크기가 커지게 되면 프루드 상사에 의해 예인속도도 증가하게 되고 외력의 크기가 증가함에 따라 결합부에 과도한 하중이 가해지게 된다. 이를 해결하고자 두 개의 분력계를 선수부와 선미부에 각각 설치하는 2점 지지 방식이 적용되고 있으며, 분력계들에 작용하는 외력을 더하여 모형선이 받는 전체 외력을 계산할 수 있다. 각각의 분력계들의 선수동요 방향 회전을 구속하면, 모형선이 받는 선수동요 모멘트는 모두 분력계로 전달되게 된다. 선수동요 운동이 구속된 2점 지지 방식에서 선수동요 모멘트는 분력계에서 계측되는 선수동요 모멘트와 좌우동요 힘에 분력계가 설치된 위치를 고려하여 계산해주어야 한다.
분력계는 기계적인 미세한 변화를 전기 신호로 검출해주는 스트레인 게이지를 적절한 위치에 설치하는 방식으로 제작된다 (Kim et al., 1997; Kim et al., 2024). 분력계의 전기 신호는 증폭기와 데이터 수집(data acquisition, DAQ) 장비를 거쳐 디지털 신호로 변환되며, 분력계의 신호들은 잡음을 포함하게 된다. 구속모형시험을 2점 지지 방식으로 설계한다면, 선수동요 모멘트 계산 시에는 좌우동요 힘과 모형선의 중앙으로부터 분력계까지의 거리를 곱한 값도 고려하여야 하는데, 이때 분력계 신호의 잡음도 거리와 함께 곱해지게 되어 실험 결과의 신뢰성에 영향을 줄 수도 있다. 본 연구에서는 두 개의 분력계가 설치되는 위치에 따라 발생하는 실험 결과의 차이점을 분석하고자 사항시험과 수평면운동장치(Horizontal Planar Motion Mechanism, HPMM) 시험을 수행하였다.
본 논문은 다음과 같은 순서로 구성된다. 2장에서는 실험의 구성을 실험 환경, 모형선, 시험 조건 및 계측장비 순으로 설명하였다. 3장에서는 실험 결과의 분석에 필요한 좌표계, 조종운동방정식, 유체력미계수를 도출하는 과정에 대해 설명한다. 4장에서는 분력계의 배치에 따른 사항시험과 HPMM 시험 결과를 나타내었다. 5장은 연구 내용의 요약과 결론이다.
2. 실험 구성
2.1 실험시설
구속모형시험은 국립창원대학교 해양공학수조동에 있는 3차원 조파수조에서 수행되었으며, 3차원 조파수조의 전경은 Fig. 1에 나타내었다. 3차원 조파수조의 길이는 20m, 폭은 14m, 깊이는 1.8m이다. 조파수조에는 3자유도 수평면 운동을 모사할 수 있도록 길이 방향과 폭 방향으로의 병진 운동과 선수동요 회전 운동이 가능한 예인전차가 설치되어 있으며, 예인전차의 길이 방향과 폭 방향 병진 운동의 최대 속력은 1.0m/s이다. 모형선이 벽 근처에서 운동할 경우에는 측벽 효과로 인하여 실험 결과의 신뢰성이 저하될 수 있다. 3차원 조파수조의 길이 방향 끝단에는 조파기와 소파기가 각각 설치되어 있어, 측벽 효과를 피하고자 수조의 중앙을 기준으로 길이 방향 12m, 폭 방향 1m 이내의 구역에서 모형선이 예인되도록 설정하였다.
2.2 대상 선형
본 연구에서는 선박해양플랜트연구소(Korea Research Institute of Ships & Ocean Engineering, KRISO)에서 연구 목적으로 공개한 KCS (KRISO container ship) 선형의 축소 모형을 사용하였다. KCS 선형은 구속모형시험과 자유항주모형시험을 연구하는 연구자들에게 대상 선형으로 자주 활용되었으며 (Kim et al., 2011; Shin and Choi, 2011; Yun et al., 2021; Yun et al., 2022), 국내뿐만 아니라 국제학술회의들(CFD Workshop Tokyo 2005, SIMMAN 2008 등)에서도 많은 연구 결과들이 발표되었다. KCS 선형에 대한 모형시험 결과는 선행연구들에서 정리되었기에 실험 결과의 유효성과 타당성을 검증하기에 적합하다고 판단되어 대상 선형으로 선정하였다.
모형선의 축척비는 수조 크기와 예인전차의 최대 속력을 고려하여 수선간 길이가 1m가 되도록 선정하였으며, 모형선의 주요제원은 Table 1에 나타내었다.
실험에 사용된 모형선이 2점 지지 방식으로 예인전차에 구속된 모습을 Fig. 2에 나타내었으며, 구속모형시험을 진행하기에 앞서 밸러스팅시험과 관성시험을 통해 모형선의 흘수와 선수동요 회전 방향 질량관성모멘트를 상사시켰다. 분력계의 설치 위치가 실험 결과에 미치는 영향을 분석하는 데 초점을 맞추었기 때문에, 타와 프로펠러는 부착하지 않고 선체에 작용하는 외력만을 계측하였다.
2.3 시험 조건
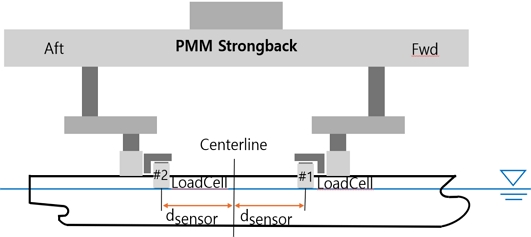
분력계의 설치 위치에 따른 실험 결과를 분석하고자 모형선의 중앙으로부터 분력계가 설치된 위치(dsensor)를 변수로 설정하였으며, 선수 방향과 선미 방향의 dsensor는 동일하도록 설계하였다. 예인전차에 두 개의 분력계를 이용하여 모형선을 설치한 개략도를 Fig. 3에 나타내었으며, 상하동요, 종동요, 횡동요 운동이 발생하지 않도록 모형선을 구속하였다.
두 개의 분력계를 설치할 경우에는 분력계에 작용하는 힘과 모멘트를 최대한 분산시키고자 모형선의 중앙에서 먼 거리에 설치하는 것이 일반적이다. 자항 상태에서 실험을 수행하게 된다면 선미 근처에는 프로펠러를 회전시키기 위한 모터와 추력 및 토크를 계측하기 위한 동력계가 설치되어 분력계 설치 시에 간섭이 발생할 수 있다. 따라서 모형선의 형상과 실험에 사용되는 장비들과의 간섭을 고려하여 중앙에서 최대한 먼 거리에 분력계를 설치한다. 본 연구에서는 선체 길이의 5%, 10%, 15% 만큼 떨어진 위치에 분력계가 설치될 수 있도록 분력계 부착판을 제작하여 실험을 수행하였다.
조종성능을 분석하기 위한 구속모형시험들 중 사항시험과 순수좌우동요(pure sway) 및 순수선수동요(pure yaw) 시험을 수행하였으며, 자세한 시험 조건은 Table 2에 나타내었다. 모형선의 예인 속도는 실선 기준 24knots에 대해 프루드 상사를 통해 계산되었다. 순수좌우동요시험은 무차원화한 좌우동요 가속도의 범위를 0.2-0.35로 설정하였다. 순수선수동요시험은 예인전차의 성능을 고려하여 무차원화한 선수동요 각속도 범위를 0.2-0.35로 설정하였다. 좌우동요 운동의 진폭은 0.15m로 설정하였다.
2.4 분력계 교정시험
실험에 사용된 분력계는 전후동요 힘, 좌우동요 힘, 선수동요 모멘트를 계측하는 3분력계로 원방포스택에서 제작되었다. 3분력계의 용량은 전후동요 힘 5N, 좌우동요 힘 10N, 선수동요 모멘트 1Nm이다. 두 개의 3분력계에 대해 교정시험을 수행하였을 때, 직진성오차, 이력오차, 반복성오차 결과를 Table 3에 나타내었다. 백분율은 각 방향의 최대 용량이 가해질 때 계측된 값을 기준으로 계산되었다. Sensor #1과 Sensor #2는 원방포스택에서 제작된 동일한 3분력계 모델(MCL-3A01)이며, 선수 방향과 선미 방향에 각각 부착되었다.
3. 조종 수학 모델
3.1 좌표계
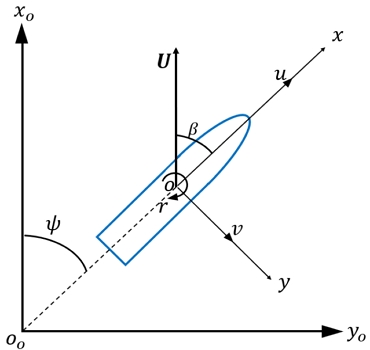
선박의 조종운동방정식은 횡동요를 고려하여 4자유도 운동방정식으로 자주 기술되지만, 본 연구의 구속모형시험에서는 횡동요 운동을 구속하였기 때문에 전후동요, 좌우동요, 선수동요에 대한 3자유도 수평면 운동에 대해 좌표계를 정의하였다. Fig. 4에 지구고정좌표계(Oo-xoyo)와 물체고정좌표계(O-xy)를 도시하였다. 물체고정좌표계의 원점(O)은 선박의 중앙에 위치하고, x축과 y축의 양의 방향은 선수방향, 우현방향이다. 좌표계들은 우수좌표계로 정의하였으며, 선수동요의 양의 방향은 선수가 우현 방향으로 회전할 때로 정의된다.
3.2 조종운동방정식
3자유도 수평면 운동에 대한 전후동요, 좌우동요, 선수동요 운동방정식은 식 (1)-(3)과 같이 나타낼 수 있다. 이 때, m은 모형선의 질량, Izz는 모형선의 z축 방향 질량관성모멘트, xG는 원점으로부터 무게중심까지 x축 방향의 거리이다. 선박은 좌우대칭 형상이기 때문에 yG는 0이며, 상하동요, 횡동요, 종동요 운동을 고려하지 않았기 때문에 zG 에 의한 영향은 고려하지 않아도 된다. u, v, r은 각각 전후동요 속도, 좌우동요 속도, 선수동요 각속도이다. 모형선에는 프로펠러와 타가 부착되지 않았으며, 선체에 의한 외력만 작용하게 된다.
| (1) |
| (2) |
| (3) |
실험 결과들은 축척비에 따라 값이 달라지지 않도록 무차원화한 결과들을 주로 비교한다. 힘과 모멘트는 식 (4)와 같이 선박의 길이를 이용하여 무차원화하였으며, 속도와 각속도는 식 (5)와 같이 무차원화되었다. 무차원화된 값임을 표현하기 위하여 프라임 기호를 사용하였다.
| (4) |
| (5) |
선박에 작용하는 외력은 속도와 각속도에 대해 테일러 급수 전개를 하고, 선박의 형상 및 외력의 특성을 고려하여 기함수 혹은 우함수 형태의 다항식으로 표현하게 된다. 외력을 표현한 다항식에서 속도와 각속도의 거듭제곱들에 곱해지는 계수들은 유체력미계수로 정의된다. 전후동요 힘, 좌우동요 힘, 선수동요 모멘트에 대한 유체력미계수들 중 사항시험, 순수좌우동요, 순수선수동요 시험을 통해 얻을 수 있는 유체력미계수들로 외력을 구성하면 식 (6)-(8)과 같다.
| (6) |
| (7) |
| (8) |
4. 시험결과
두 개의 3분력계에서 계측된 결과로 전후동요 힘, 좌우동요 힘, 선수동요 모멘트를 표현하면 식 (9)-(11)과 같이 나타낼 수 있다. 하첨자 1과 2는 선수 방향과 선미 방향에 부착된 3분력계 결과를 나타내며, 하첨자 n은 신호의 잡음을 나타낸다.
| (9) |
| (10) |
| (11) |
신호 잡음은 뚜렷한 주기, 위상, 진폭을 가지지 않아 정속 구간 계측 결과의 신뢰성을 저하시킬 수 있다. 두 개의 3분력계를 사용함에 따라 신호 잡음이 중첩되게 되며, 신호 잡음 영향은 하나의 분력계를 단독으로 사용하는 경우보다 X와 Y 결과에 대해서는 2배까지 증가할 수 있고, N 결과에 대해서는 식 (11)과 같이 Y와 N의 신호 잡음과 dsensor가 모두 고려되기 때문에 더 증폭될 수 있다.
4.1 사항시험 결과
사항시험에서는 모형선의 사항각도를 고정하고 일정한 속도로 모형선을 예인하며 선체에 작용하는 힘과 모멘트를 계측하였다. 정속 구간에서 계측된 값의 평균을 구하고 식 (4)-(5)를 이용하여 계측값과 속도를 무차원화하였다. 식 (6)-(8)의 항들 중 v와 관련된 유체력미계수를 도출할 수 있으며, 최소자승법을 이용하여 Xuu, Xvv, Yv, Yvvv, Nv, Nvvv 값을 얻을 수 있다.
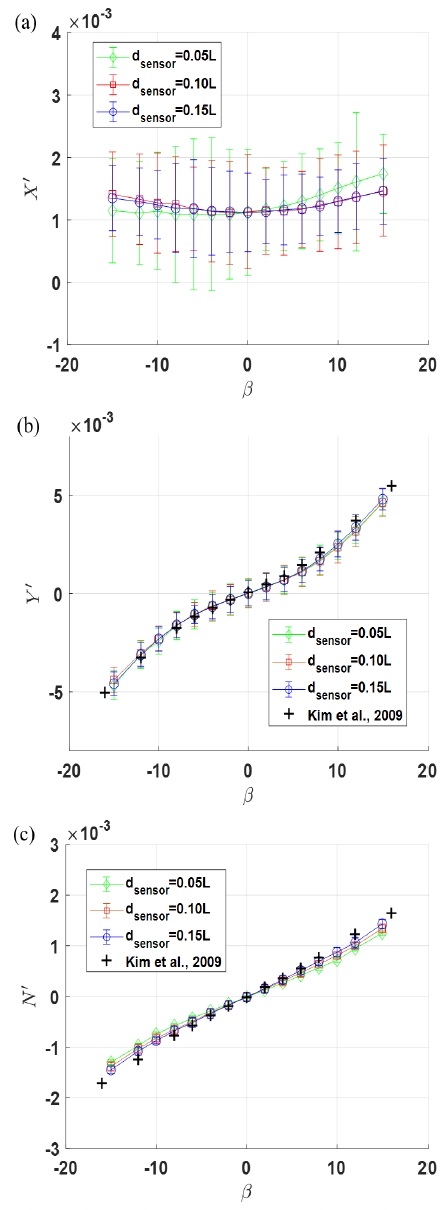
Fig. 5에는 사항시험을 통해 얻어진 전후동요, 좌우동요 힘과 선수동요 모멘트 결과를 나타내었다. 정속 구간에서의 평균값과 표준편차를 이용하여 오차막대(error bar) 형태로 실험 결과를 나타내었다. 평균값은 선체에 작용하는 외력으로 볼 수 있고, 표준편차에는 분력계의 신호 잡음과 모형선의 자세와 속도에 영향을 줄 수 있는 예인전차의 진동, 속도 정밀도 등이 포함되게 된다. 표준편차가 작을수록 실험 결과의 균일성이 보장되고 신뢰성 높은 실험 수행이 가능한 것으로 볼 수 있다. 본 연구의 실험 구성의 신뢰성을 확인하고자 사항시험에 대해 Kim et al. (2009)의 실험 결과를 Figs. 5 (b), (c)에 함께 나타내었다. 해당 선행연구 결과는 KCS 선형에 대해 자항 조건에서 수행한 실험 결과이므로, 프로펠러가 부착되지 않은 본 연구의 결과와는 약간의 차이가 발생하였다.
전후동요 힘, 좌우동요 힘, 선수동요 모멘트의 평균값 결과는 분력계의 설치 위치에 따라 거의 유사한 결과가 나타났다. 선체에 작용하는 외력은 분력계의 설치 위치와 관련 없이 동일하기 때문에, 식 (9)-(11)을 이용하여 외력을 계산하면 평균값 결과는 동일해지게 된다. 하지만, 실험의 신뢰성과 관련이 있는 표준편차의 값은 분력계의 설치 위치에 따라 다름을 확인할 수 있다.
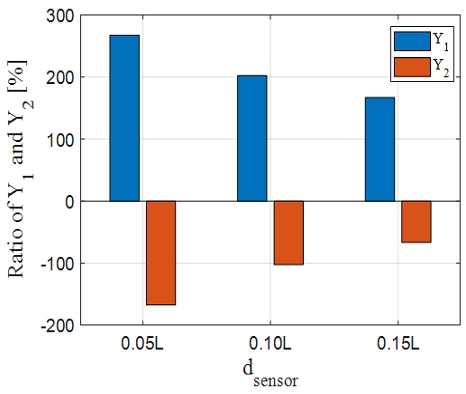
전후동요와 좌우동요 힘 결과에서는 dsensor가 0.05L일 때 다른 두 조건에 비해 표준편차가 크게 계산되었다. 분력계의 설치 위치에 따른 두 개의 분력계에서 계측되는 좌우동요 힘의 비율을 Fig. 6에 나타내었다. 선수 방향과 선미 방향에 설치된 분력계에서 계측된 좌우동요 힘의 비율을 모든 사항각도 조건에 대해 평균한 결과이다. 선수 방향과 선미 방향에 설치된 분력계에는 반대 방향의 힘이 작용하며, 그 힘의 크기는 분력계가 중앙에서 멀리 설치될수록 작아지고 그에 따라 표준편차도 Fig. 5에 나타난 것처럼 감소하였다.
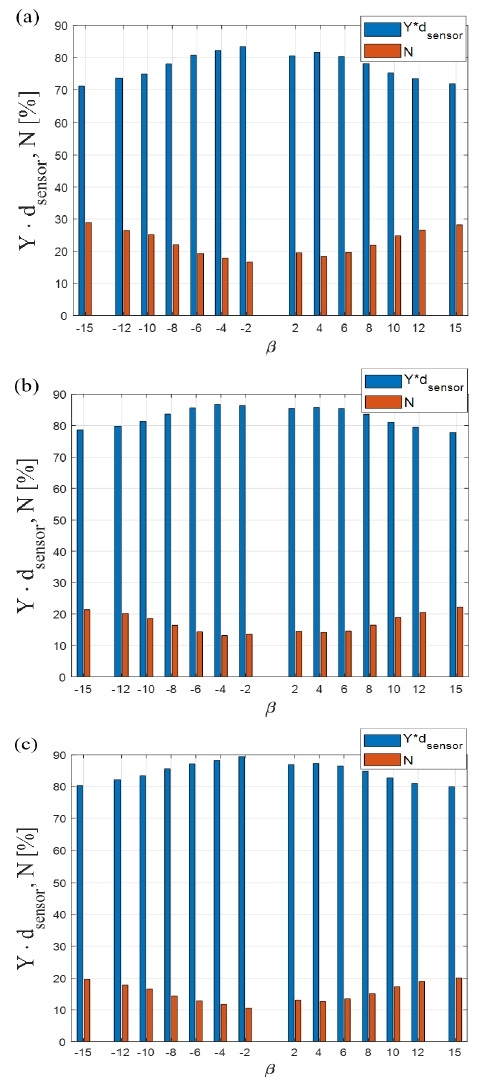
선수동요 모멘트 결과에서는 표준편차가 매우 작아 Fig. 5(c)의 오차막대 그래프에서 표준편차의 값이 잘 보이지 않았다. 선수동요 모멘트 계산 시에 Y*dsensor에 의해 계산되는 N 값과 분력계에서 계측된 N 값의 비율을 Fig. 7에 나타내었다. Y*dsensor에 의해 계산되는 값이 전체 선수동요 모멘트의 70% 이상임을 알 수 있고, N 계측값보다 Y 계측값의 영향이 더 지배적인 것을 확인할 수 있다. N’ 계산 시에 dsensor의 값은 선박의 길이로 나누어져 무차원화되고 Y 신호의 잡음에 0.05, 0.10, 0.15의 값이 곱해져 좌우동요 힘 결과에 비해 선수동요 모멘트의 표준편차는 작아지게 된다. 분력계가 중앙에서 멀리 설치될수록 Y 신호 잡음에 더 큰 dsensor 값이 곱해짐에 따라 선수동요 모멘트의 표준편차는 증가하였으며, 분력계가 중앙에서 멀리 설치될수록 표준편차가 감소하는 전후동요 및 좌우동요 힘과 반대의 경향성이 확인되었다.
사항각도가 커지면 선박에 작용하는 선수동요 모멘트가 증가함에 따라 분력계에서 계측되는 N의 비율이 증가하였으며, 분력계의 설치 위치가 중앙에서 멀어지며 압력중심에 가까워짐에 따라 N 계측값이 감소하고 Y*dsensor의 비율이 증가하였다.
4.2 순수좌우동요시험 결과
순수좌우동요시험은 선수동요 운동이 발생하지 않도록 모형선을 y축 방향으로만 강제운동시키며 x축 방향으로 일정한 속도로 직진하게 된다. 물체고정좌표계를 기준으로 본다면 모형선의 전진속도는 일정하고, 선수동요 각속도와 각가속도는 0이고, 좌우동요 속도와 가속도만 변화하게 된다. 좌우동요 속도와 가속도와 관련된 유체력미계수를 모두 추정할 수 있으나, 좌우방향 속도 변화 폭이 사항시험보다 작기 때문에 가속도 관련 변수만 구하는 것이 일반적이다 (Sung and Park, 2015).
좌우동요 변위를 사인 함수의 형태로 표현하면 속도와 가속도는 각각 코사인과 사인 함수의 형태로 표현된다. 삼각함수 꼴로 정의된 좌우동요 속도와 가속도를 식 (7)-(8)에 대입하고 삼각함수의 배각 공식을 통해 정리하면, y축 방향 변위 및 가속도와 위상이 동일한 in-phase 성분과 y축 방향 속도와 위상이 동일한 out-phase 성분으로 분리할 수 있다. 좌우동요 속도와 관련된 유체력미계수들은 out-phase 성분으로 구할 수 있으나, 사항시험을 통해 관련 유체력미계수들을 확보하였기 때문에 in-phase 성분만 분석하였다. 좌우동요 운동의 주파수에 따라 네 조건의 실험을 수행하였으며, 모든 주파수 조건의 결과를 고려한 유체력미계수를 도출하기 위해 Yoon (2009)의 연구에서 제시된 ‘Multiple-Run’ 방식을 이용하였다. 각 주파수 별 실험 결과에 대해 최소자승법을 적용하여 in-phase 성분의 최댓값을 각각 얻은 후, 모든 주파수 조건에 대한 결과를 종합하여 Fig. 8에 나타내었다.
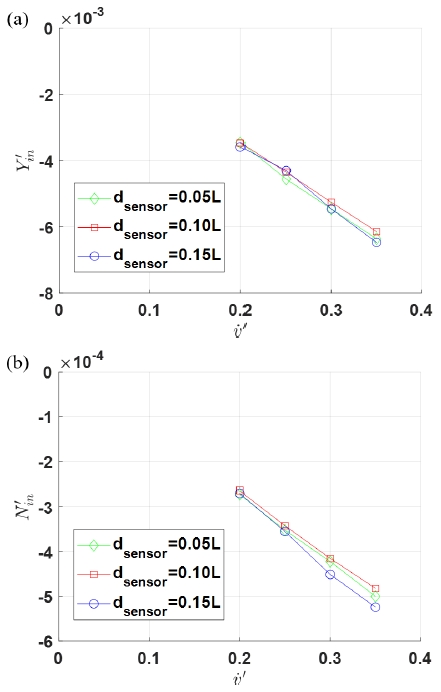
순수좌우동요시험에서 최소자승법을 통해 얻은 in-phase 성분의 결과들은 분력계의 설치 위치에 따라 큰 차이가 없음을 확인할 수 있다. 실험 결과의 신뢰성을 분석하기 위해 raw data와 곡선 적합(curve fitting)의 차이를 분석하였다. 곡선 적합은 각 주파수 조건별 시험에서 최소자승법을 통해 도출된 결과이다. raw data와 곡선 적합의 차이의 평균값은 유체력미계수 추정 정확도와 관련된 것으로 볼 수 있고, 차이의 표준편차는 신호 잡음의 영향으로 볼 수 있다. raw data와 곡선 적합 차이의 평균값은 10-19의 차수로 매우 작은 값이 계산되어 유체력미계수 추정 정확도는 보장된 것으로 볼 수 있다.
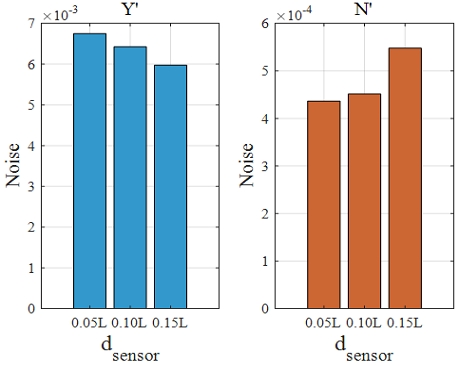
raw data와 곡선 적합 차이의 표준편차 결과를 Fig. 9에 나타내었다. 분력계의 설치 위치에 의한 영향을 분석하기 위해 모든 주파수 조건 결과의 평균값을 나타내었다. 순수좌우동요시험에서도 사항시험과 유사하게 분력계의 설치 위치가 중앙에서 멀어질수록 좌우동요 힘의 표준편차는 감소하고, 선수동요 모멘트의 표준편차는 증가하였다.
4.3 순수선수동요시험 결과
순수선수동요시험은 좌우동요와 선수동요의 위상차가 90°가 되는 선수동요 운동을 추가로 발생시켜, 모형선의 선수방향이 모형선의 운동궤적에 항상 접하도록 한 뒤 선체에 작용하는 힘과 모멘트를 계측하는 시험이다. 이 때, 좌우동요 속도와 가속도가 발생하지 않도록 선수동요 각도의 진폭을 설정하게 되며, 순수선수동요시험 설계와 관련된 내용은 Yoon (2009)의 연구에 잘 정리되어 있다.
순수좌우동요시험과 유사하게 ‘Multiple-Run’ 방식을 적용하여 모든 주파수 조건에 대한 실험 결과를 Fig. 10에 나타내었다. 선수동요 각도 및 각가속도와 위상이 동일한 in-phase 성분에 대해 좌우동요 힘과 선수동요 모멘트 결과는 Figs. 10(a), (b)에 나타내었으며, 선수동요 각속도와 위상이 동일한 out-phase 성분에 대해서는 Figs. 10(c), (d)에 나타내었다.
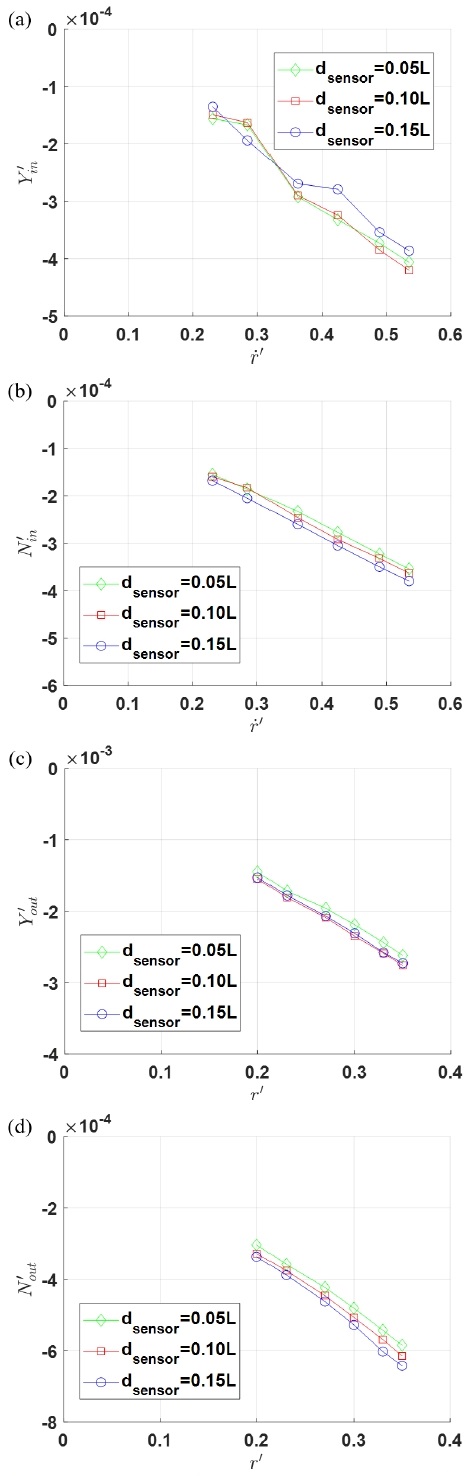
Pure yaw test results – (a): Y force (in-phase), (b): N moment (in-phase), (c): Y force (out-phase), (d): N moment (out-phase)
순수선수동요시험에서 최소자승법을 통해 얻은 in-phase 성분과 out-phase 성분 결과들은 분력계의 설치 위치에 따라 기울기의 큰 차이는 없는 것을 확인할 수 있다.
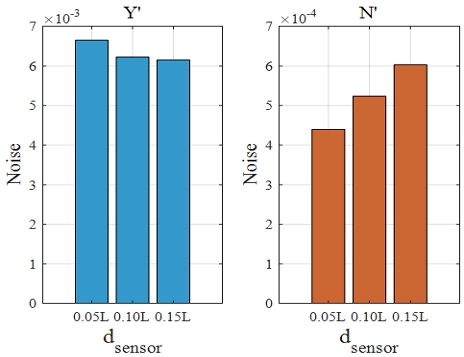
순수선수동요시험 결과의 신뢰성을 분석하기 위해 raw data와 곡선 적합의 차이를 분석하였다. raw data와 곡선 적합의 차이의 평균값은 10-19 차수로 유체력미계수 추정의 정확도는 확보된 것으로 볼 수 있다. 순수좌우동요시험과 동일한 방법으로 raw data와 곡선 적합의 차이의 표준편차 결과를 Fig. 11에 나타내었다. 분력계의 설치 위치에 의한 영향을 분석하기 위해 모든 주파수 조건 결과의 평균값을 나타내었다. 순수선수동요시험에서도 이전의 시험들과 유사하게 분력계의 설치 위치가 중앙에서 멀어질수록 좌우동요 힘의 표준편차는 감소하고, 선수동요 모멘트의 표준편차는 증가하였다.
5. 결 론
본 연구에서는 2점 지지 구속모형시험에서 분력계의 설치 위치가 실험 결과에 미치는 영향을 분석하였다. 이를 위해 KCS 선형의 축소 모형을 사용하여 3차원 조파수조에서 사항시험, 순수좌우동요시험, 순수선수동요시험을 수행하였다. 분력계의 설치 위치를 모형선 중앙으로부터 선체 길이의 5%, 10%, 15%만큼 떨어진 거리로 설정하고, 구속모형시험에서 계측되는 전후동요 힘, 좌우동요 힘, 선수동요 모멘트를 분석하였다.
2점 지지 구속모형시험에서 선수 방향과 선미 방향에 부착된 분력계에 작용하는 좌우동요 힘의 부호는 반대였으며, 모형선에 작용하는 힘보다 더 큰 힘이 선수 방향의 분력계에 작용하였다. 실험 설계 시에 분력계의 용량은 모형선에 가해질 힘을 추정하여 선정하는데, 선수 방향 분력계에는 이보다 더 큰 힘이 가해질 수 있기 때문에 실험 설계 시에 유의하여야 한다.
좌우동요 힘에 의해 계산되는 선수동요 모멘트는 선체에 작용하는 전체 선수동요 모멘트의 70% 이상이었으며, 분력계가 압력중심에 가깝게 설치될수록 선수동요 모멘트의 계측값은 감소하고 좌우동요 힘에 의해 계산되는 선수동요 모멘트의 비율은 증가하였다.
Acknowledgments
이 논문은 2023~2024년도 창원대학교 자율연구과제 연구비 지원으로 수행된 연구결과 중 일부임을 밝히며, 연구비 지원에 감사드립니다.
References
- International Maritime Organization (IMO), 2002. Standards for ship manoeuvrability. IMO Resolution MSC.137(76) (adopted on 4 December 2002).
- Kim, H., Kim, J.S., Song, M. and Rhyu, S., 1997. A design and manufacture of 6-component load cell. Journal of the Society of Naval Architects of Korea, 34(2), pp.20-26.
-
Kim, H., Shin, C., Rhyu, S. and Ham, Y., 2024. Development of a multi-component waterproof type force sensor devised with column elements under eccentric load. Journal of the Society of Naval Architects of Korea, 61(3), pp.200-207.
[https://doi.org/10.3744/SNAK.2024.61.3.200]

-
Kim, Y.G., Kim, S.Y., Yoon, K.H., Oh, B.I. and Yeo, D.J., 2009. Estimation of maneuvering performance of KCS hull form using CPMC captive model test. Journal of the Society of Naval Architects of Korea, 46(6), 553-561.
[https://doi.org/10.3744/SNAK.2009.46.6.553]

-
Kim, Y.G., Yeo, D.J., Son, N.S., Kim, S.Y., Yun, K.H. and Oh, B.I., 2011. Prediction of maneuverability of KCS with 4 degrees of freedom. Journal of the Society of Naval Architects of Korea, 48(3), pp.267-274.
[https://doi.org/10.3744/SNAK.2011.48.3.267]

-
Kwon, C.S., Kim, D.J., Lee, Y.Y., Kim, Y.G., Yun, K.H. and Cho, S., 2022. Prediction of maneuverability of a submarine at surface condition by captive model test. Journal of the Society of Naval Architects of Korea, 59(6), pp.423-431.
[https://doi.org/10.3744/SNAK.2022.59.6.423]

-
Park, J., Seo, J., Lee, T., Lee, D., Park, G., Yoon, H.K. and Rhee, S.H., 2020. Uncertainty assessment of outdoor free-running model tests for evaluating ship maneuverability. Journal of the Society of Naval Architects of Korea, 57(5), pp.262-270.
[https://doi.org/10.3744/SNAK.2020.57.5.262]

-
Shin, H.K. and Choi, S.H., 2011. Prediction of maneuverability of KCS using captive model test. Journal of the Society of Naval Architects of Korea, 48(5), pp.465-472.
[https://doi.org/10.3744/SNAK.2011.48.5.465]

-
Sung, Y.J. and Park S.H., 2015. Prediction of ship manoeuvring performance based on virtual captive model tests. Journal of the Society of Naval Architects of Korea, 52(5), 407-417.
[https://doi.org/10.3744/SNAK.2015.52.5.407]

- Yoon, H., 2009. Phase-averaged stereo-PIV flow field and force/moment/motion measurements for surface combatant in PMM maneuvers. Ph.D Thesis. University of Iowa.
-
Yun, K.H. and Yeo, D.J., 2019. An experimental study on manoeuvrability of a ship in heeled condition. Journal of the Society of Naval Architects of Korea, 56(3), pp.273-280.
[https://doi.org/10.3744/SNAK.2019.56.3.273]

-
Yun, K.H., Choi, H. and Kim, D.J., 2021. An experimental study on the manoeuvrability of KCS with different scale ratios by free running model test. Journal of the Society of Naval Architects of Korea, 58(6), pp.415-423.
[https://doi.org/10.3744/SNAK.2021.58.6.415]

-
Yun, K.H., Kim, D.J., Yeon, S., Kim, Y.C., Kim, Y.G. and Yang, K.K., 2022. A study on the manoeuvrability of 1/42.0 scaled KCS. Journal of the Society of Naval Architects of Korea, 59(5), pp.262-270.
[https://doi.org/10.3744/SNAK.2022.59.5.262]