다수 무인선의 대형 유지와 충돌 회피를 위한 군집제어 알고리즘에 관한 연구

2.1 대형 제어 시스템의 개요

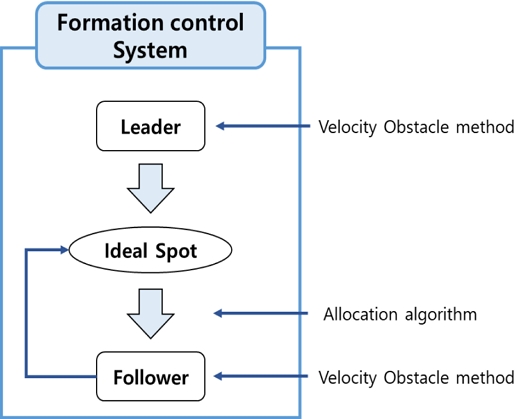
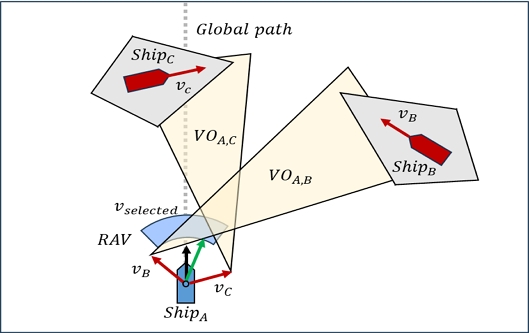
본 논문의 군집 대형 제어 시스템은 리더(leader)와 팔로워(follower), 이상 지점(Ideal spot)으로 구성되어 있다. 가변적으로 선택되는 리더를 기준으로 대형이 결정되며, 결정된 대형에 팔로워가 할당되는 방식으로 군집을 유지한다. Fig. 1은 군집 제어 시스템의 간단한 개념도이다. 팔로워의 위치 할당은 할당 알고리즘(allocation algorithm)에 의해 결정된다. 팔로워는 이상 지점을 추종함과 동시에 군집 내의 다른 선박과 장애물을 고려하여 충돌 회피를 수행한다.

Fig. 1

System of formation control

2.2 대형 행렬 정의

대형 행렬(Formation matrix)이란 이루고자 하는 대형에 대한 정보를 행렬로 표현한 것이다. 본 논문의 대형 행렬은 식 (1)과 같이 표현한다.

식 (1)에서 첫 번째 행은 리더를 기준으로 경유점까지의 거리와 각도를 나타낸다. 첫 번째 행을 제외한 나머지 행은 각 운항체가 선택할 수 있는 이상 지점 (Ideal point)에 대한 거리와 각도를 의미한다. 여기서 m은 군집에 포함된 운항체의 개수이다. 대형의 리더는 반드시 첫 번째 행을 선택하며, 나머지 행은 2.3의 할당 알고리즘에 의해 리더를 제외한 나머지 운항체가 선택하게 된다.

2.3 할당 알고리즘

2.3.2 운항체의 대형 할당

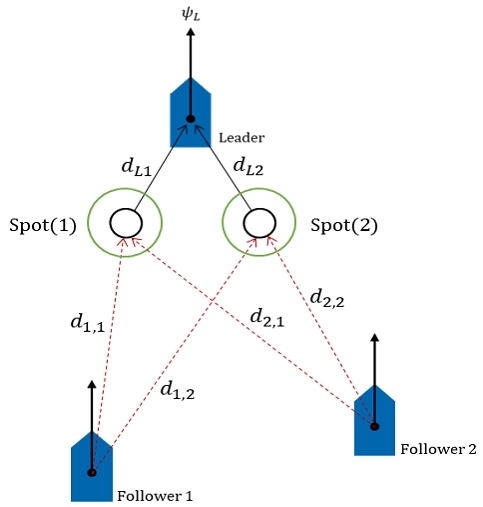
리더를 제외한 n개의 운항체는 거리 비용 행렬에 의해 이상 지점을 선택한다. 거리 비용 행렬은 n×n 크기의 행렬로 운항체로부터 각 이상 지점까지의 거리로 구성되어 있다. Fig 2는 3척의 운항체로 구성된 군집의 거리 비용 행렬 계산의 예시이다.

Fig. 2

Calculation of distance cost table

팔로워 1과 2는 리더의 위치를 기준으로 정의된 이상 지점까지의 거리를 계산한다. 각 이상 지점으로부터 가까운 거리에 위치한 팔로워부터 지점을 선택하게 되며, Fig. 2에서는 d_1.1이 d_2.1 보다 짧으므로 팔로워 1은 이상 지점 1을 선택 한다. 각 이상 지점은 1대의 팔로워만 선택할 수 있으며, 팔로워에 의해 선택된 이상 지점은 다음 팔로워가 이상 지점을 선택할 때 후보에서 제외된다. n대의 팔로워가 존재할 때, 거리 비용 행렬은 식 (4)와 같다.

$\[ D=\left[\begin{array}{ccccc}{d}_{\mathrm{1,1}}& d_{\mathrm{1,2}}& \cdots & d_{1,n-1}& d_{1,n}\\ d_{\mathrm{2,1}}& d_{\mathrm{2,2}}& \cdots & d_{2,n-1}& d_{n,n}\\ ⋮& ⋮& ⋮& ⋮& ⋮\\ d_{n-\mathrm{1,1}}& d_{n-\mathrm{1,2}}& \cdots & d_{n-1,n-1}& d_{n-1,n}\\ d_{n,1}& d_{n,2}& \cdots & d_{n,n-1}& d_{n,n}\end{array}\right] \]$

(4)

2.4 대형 유지와 경로 추종

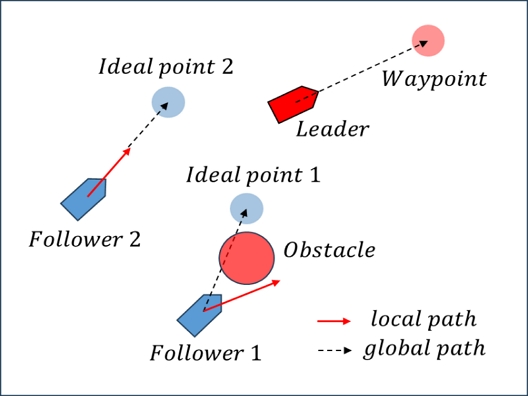
선도-추종 기법을 이용하는 군집은 대형을 유지하며 목적지로 향하기 때문에 리더와 팔로워가 추종하는 경유점이 달라진다. 리더로 선정된 선박은 군집 전체가 이동해야 하는 경유점을 향해 전역 경로를 계획한다. 반면 팔로워는 대형 행렬과 할당 알고리즘에 의해 선정된 이상 지점을 향하는 전역 경로를 계획한다. 이와 동시에 리더와 팔로워는 충돌 방지를 위한 지역 경로도 함께 계획한다. Fig. 3의 예시를 통해 리더와 팔로워가 각각 다른 전역 경로를 따르는 것을 확인할 수 있다. 리더와 팔로워 2는 충돌 위험이 없으므로 원래의 전역 경로와 동일한 방향의 지역 경로를 생성하며, 팔로워 1과 같이 충돌 위험이 있을 경우 충돌을 회피할 수 있는 지역 경로를 생성한다. 충돌 회피와 관련된 내용은 3장에서 자세히 서술한다.

Fig. 3

Global and local path planning process of leader and follower

3.1 속도 장애물 기법

운항 중 조우하는 장애물을 회피하기 위해 속도 장애물 기법을 이용한다. 대형 내에 존재하는 다른 선박은 동적 장애물로 간주하여 대형 형성 및 변경 중 발생할 수 있는 충돌을 회피하며 고정 장애물은 속도가 “0”인 동적 장애물과 같이 취급한다. 속도 장애물 기법은 이동하는 다수 장애물에 대한 회피를 위하여 제안된 알고리즘이다. (Fiorini and Shiller, 1998) 현재까지도 다양한 분야에서 사용되고 있으며, 회피 대상의 속도 벡터와 피항중인 이동체의 속도 벡터를 이용하여 충돌을 회피한다. 3.2장부터 3.4장까지 속도 장애물 기법의 수학적 표현을 기술한다.

3.2 자선과 타선의 수학적 표현

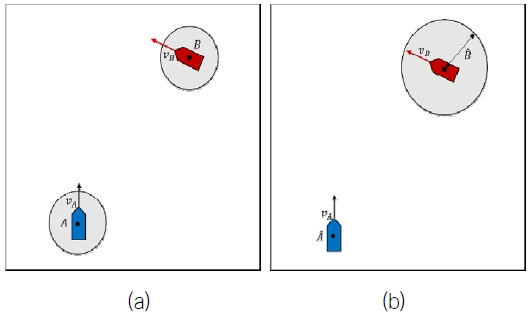
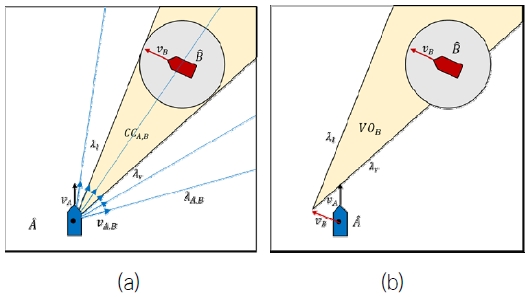
2차원 평면에 존재하는 다각형의 장애물은 다수의 원으로 표현 가능하다. (Featherstone, 1990) 속도 장애물을 도식화하기 위해 자선과 타선은 각각을 대표하는 원으로 표현한다. Fig. 4(a)에서 A는 자선을, B는 타선을 의미한다.

Fig. 4

Mathmatic Expression of Own ship and Target ship

또한 Fig. 4(b)에서 $$ \hat{A}$$은 자선을 대표하는 원의 반경을 0으로 줄여 점으로 표현한 것이고, $$ \hat{B}$$은 타선을 대표하는 원의 반경에 자선을 대표하는 원의 반경을 더한 큰 원으로 표현한 것이다. 생성된 $$ \hat{A},\hat{B}$$는 3.3절에서 충돌 원뿔을 정의하기 위해 이용된다.

3.3 충돌 원뿔과 속도 장애물 정의

충돌 원뿔은 자선과 타선이 충돌할 가능성이 있는 영역을 의미하며 Fig. 5(a)와 같이 $$ \hat{A}$$으로부터 $$ \hat{B}$$으로의 접선을 각각 λ_r,λ_f라 할 때, λ_r,λ_f 사이의 공간을 충돌 원뿔로 정의하고 CC_A,B로 표시한다. 타선에 대한 자선의 상대 속도가 충돌 원뿔 안에 존재할 경우 충돌이 발생한다고 판단한다. 또한 v_A,B는 자선이 선택 가능한 타선에 대한 자선의 상대속도 후보군이고, λ_A,B는 v_A,B 방향으로 그은 직선이라 하면, 충돌 원뿔 CC_A,B는 식 (5)와 같이 λ_A,B와 $$ \hat{B}$$의 교집합이 존재하는 영역이라고도 정의할 수 있다.

Fig. 5

Definition of Collision Cone and Velocity Obstacle

단일 선박과 조우하는 경우 상대 속도를 이용해 회피 할 수 있으나, 다수의 선박을 회피하는 경우에는 자선의 절대 속도를 이용하여 일반화된 상황에 대한 고려가 필요하다. 이를 위해 정의하는 것이 Fig. 5(b)와 같이 나타낸 속도 장애물 VO이며, VO는 식 (6)과 같이 충돌 원뿔을 타선의 속도 v_B만큼 이동시킨 것이다. 따라서 식 (7)과 같이 자선의 절대 속도 v_A가 VO에 포함되지 않으면 자선과 타선의 충돌이 발생하지 않는 것으로 정의할 수 있다.

식 (6)에서 ⊕는 Minkowski의 벡터합 연산자이다. 속도 장애물은 수학적 연산에서 상대 속도를 계산하기 위한 v_B를 이항한 것과 같으므로 충돌 원뿔을 이용하였을 때와 속도 장애물을 이용하였을 때의 물리적 의미는 같다. 다수의 속도 장애물에 대한 회피는 식 (8)과 같이 속도 장애물을 모두 합친 것과 같으며 m은 장애물의 수이다. VO_Bi는 i번째 장애물에 의해 생성된 속도 장애물을 의미한다.

3.4 가용 속도 벡터

속도 장애물 기법을 사용하기 위해 선박이 미소 시간 간격 Δt 후에 도달 가능한 속도 벡터를 계산하며 이를 가용 속도 벡터로 정의한다. 속도 장애물 기법은 속도 장애물 내에 위치한 가용 속도 벡터를 목표 속도 선택지에서 제외함으로써 이동체와의 충돌을 방지한다. 본 논문에서 가용 속도 벡터는 최대, 최소 선수각과 최대, 최소 속도를 이용하여 생성된다. 식 (9), (10)은 가용 속도 벡터를 정의하기 위한 수식이다.

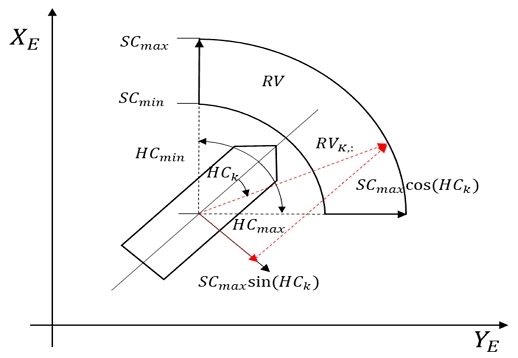
식 (9)의 SC와 HC는 속도 후보군(Speed Candidate, SC)과 선수각 후보군(Heading Candidate, HC)를 의미하며, RS와 RH는 가용 속도(Reachable Speed, RS), 가용 선수각(Reachable Heading, RH)이다. n_speed와 n_heading은 각각 SC와 HC의 길이이다. 가용 속도 벡터(Reachable Velocity, RV)는 식 (10)의 행렬과 같이 나타낼 수 있으며 첫 번째 열은 선박 고정 좌표계에서 x 방향 속도 성분을, 두 번째 열은 y 방향 속도 성분을 나타낸다. Fig. 6은 생성된 RV 를 나타내며, RV_K,:는 RV의 행 중 하나이다.

Fig. 6

Example of Reachable Velocities

RV_K,:의 길이는 SC_max이고 HC_k만큼 기울어져 있다.

3.5 COLREGs를 반영한 속도 벡터 선택 전략

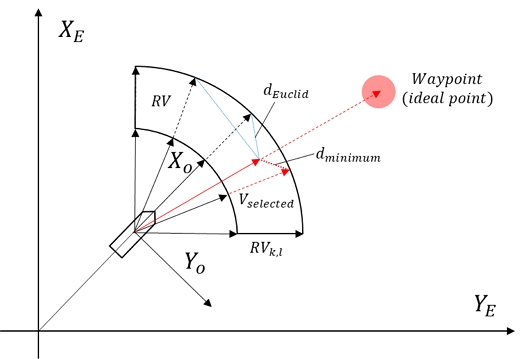
가용 속도 벡터 중 최종적으로 추종할 목표 속도는 기준 벡터로부터 RV의 각 요소까지 유클리드 거리를 계산하여 벡터의 유사도 비교를 통해 결정한다. 이는 식 (11)과 Fig. 7에서 확인 할 수 있다. Fig. 7의 V_target은 기준 벡터이며, 경유점 혹은 이상 지점을 향하는 방향을 가지고 그 크기가 목표 선속과 같은 벡터이다. d_Euclid는 기준 벡터로부터 RV까지의 유클리드 거리를 요소로 하는 행렬이며 V_selected는 최종적으로 선박의 제어를 위해 사용되는 목표 속도 벡터이다. I는 d_Euclid 중 최솟값을 가지는 요소의 인덱스이다. 유클리드 거리가 작을수록 두 벡터는 유사도는 증가하므로, 속도 장애물 영역 내에 존재하는 벡터를 제외한 나머지 벡터 중 유클리드 거리가 가장 짧은 대상을 선택하여 충돌을 방지함과 동시에 목표 속도 벡터와 가장 유사한 벡터를 선정한다.

Fig. 7

Vector selection strategy based on the Euclidean distance

선박은 국제해상충돌예방협약(CORLEGs)을 준수하여 회피하여야 한다. COLREGs에서 Starboard-Crossing 상황에서는 자선이 피항 의무선, 타선이 침로 유지선이 되며, Port-Crossing 상황에서는 자선이 침로 유지선이 되고, 타선이 피항 의무선이 된다. 또한 Port-Crossing 상황에서 타선이 충돌 회피 의사를 보이지 않을 경우 충돌 방지를 위해 방향에 상관 없이 최대한 피항하는 것을 목표로 한다. 이를 반영하기 위해 속도 벡터를 선정 할 때, 자선 기준 우현부터 가용 속도 벡터를 탐색함으로써, 우현으로 회피가 가능할 경우 우현의 속도벡터를, 우현의 회피 경로가 없을 경우 좌현으로 회피를 수행하도록 하였다.

3.6 선박안전영역을 반영한 충돌 회피

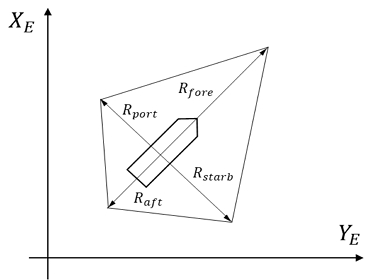
선박안전영역은 안전한 항해를 위해 정의된 타선 및 장애물이 진입할 수 없는 선박 주변의 2차원 영역을 말한다(Fujii & Tanaka,1971). 이는 Zhao et al.(1993), Wang et al.(2010) 등에 의해서 발전되었으며, 다양한 형태의 선박 안전 영역이 제시되었다. 본 논문에서 선박안전영역은 속도 장애물에서 선박을 2차원에 표현하는 과정에서 이용된다. 일반적인 속도 장애물 기법은 회피 대상과 피항체를 일정한 반경의 원으로 표현하지만, 이는 사용자에 의해 장애물의 크기가 정의된다는 단점이 존재하며, 선박의 방향에 따른 위험 영역이 반영되지 않는다. 이를 해결하기 위하여 원을 대신한 Quadrangle Ship Domain (QSD)을 적용 한다. 이는 선박 중심으로 선수, 선미, 좌현, 우현 방향의 각기 다른 길이를 가지는 사각형의 영역으로 정의되며 각 방향의 길이는 식 (12)와 같이 계산한다. Fig. 8은 QSD의 예시이다.

Fig. 8

Quadrangle Ship Domain

식 (12)의 L은 선박의 길이이며, k_AD는 선박의 전진거리와 관련된 계수, k_DT는 선박의 전술 직경과 관련된 계수이다. 이는 선박에 따라 달라지므로 식 (13)과 같이 경험식에 의해 결정한다. V_own은 knot로 표현된 선박의 속도이다.

Fig. 9은 선박 안전 영역을 포함한 다수 선박 회피 상황의 예시이다. 위험도가 높은 타선의 선수 방향으로는 안전 영역이 넓게 생성되므로 속도 장애물도 크게 생성된다. 비교적 위험도가 적은 타선의 선미 방향으로는 안전 영역이 좁으며, 속도 장애물도 작게 생성되는 것을 확인할 수 있다. 검정색 화살표는 전역 경로를 추종하기 위한 벡터이며, 초록색 화살표는 장애물을 회피하기 위한 속도 벡터이다. 초록색 화살표는 속도 장애물에 포함되지 않으며, 3.5의 속도 벡터 전략에 의해 선택된다.

Fig. 9

Collision avoidance and selection of optimum vector

4.1 대상선

선박의 동역학적 특성을 반영하여 대형제어, 충돌회피 시뮬레이션을 수행하기 위해 자율운항선박(Korea Autonomous Surface Ship, KASS) 1차 설계 선형을 대상선으로 선정하여 활용하였다. 대상선은 2축 2타선으로, Table 1은 선박의 주요 제원이며, Fig. 10는 KASS 모형선이다.

Table 1

Principal particulars of the subject ship

Fig. 10

KASS model ship (3.8 scale)

4.2 조종운동 수학모델

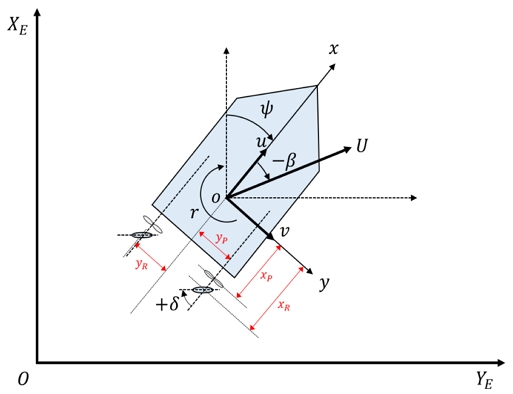
시뮬레이션 환경 구성을 위해 사용된 대상선의 조종운동 수학모델은 3자유도 운동모델이다. 지배방정식은 식 (14)와 같이 나타내며, 선체력, 추력, 타력을 수식화 한 것은 각각 식 (15), (16), (17)과 같다. 추력과 타력 표현에서 윗첨자 P는 2축 2타의 좌현(Port)을 의미한다. Fig. 11은 선박 운동 모델의 좌표계이다.

Fig. 11

Coordinate systems

식 (16)의 프로펠러 전진비 J_P는 식 (18)과 같이 나타낼 수 있다. 또한 식 (17)의 타 직압력 F_N은 식 (19)와 같이 나타낼 수 있으며 본 논문에서는 좌현의 타 직압력만을 나타내었으며 우현의 타 직압력은 생략하였다.

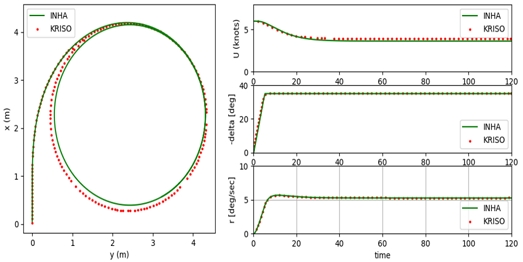
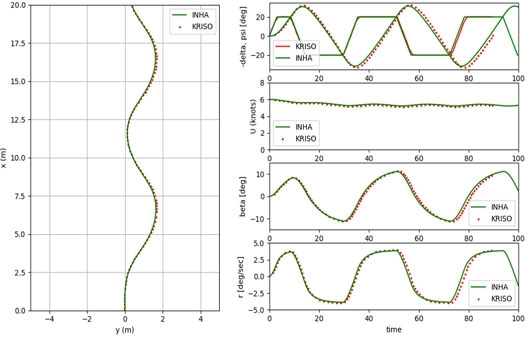
대상선의 조종운동 수학모델을 반영한 시뮬레이션 환경을 검증하기 위하여 Kim et al. (2021)에 의해 수행된 대상선의 선회 시뮬레이션과 지그재그 시뮬레이션 결과와 비교하였으며, Fig. 12, Fig. 13을 통해 시뮬레이션 환경에서 대상선의 동특성이 유효하게 반영되고 있음을 확인하였다.

Fig. 12

Validation of turning test (35°, Startboard)

Fig. 13

Validation of Zig-Zag test (20°/20°, Starboard)

4.3 속도, 선수각 제어기

리더와 팔로워가 군집을 이루어 운항하기 위해서는 속도와 선수각 제어기를 필요로 한다. 군집 내의 선박들은 속도 벡터 선택 전략에 의해 선정된 속도 벡터와 각 선박의 속도, 선수각을 이용하여 제어된다. 리더와 팔로워는 동일한 제어기를 이용하지만 목표 선수각과 목표 선속에 차이가 있다. 팔로워의 경우는 이상 지점과 자선과의 거리 오차를 이용하여 목표 선수각과 목표 선속을 결정하고 있으며, 리더의 경우는 이상 지점과 자선과의 거리 오차를 “0”으로 설정하여 목표 선수각과 목표 선속을 결정하고 있다. 목표 선수각 및 목표 선속에 도달하기 위하여 속도와 선수각 모두 P 제어기를 이용하여 제어하였으며, 각 제어기는 식 (20)과 같이 나타낼 수 있다.

식 (20)의 ψ_target은 대상선의 목표 선수각을 의미하며 ψ는 선수각을 의미한다. δ는 대상선의 타각이며, 속도는 각각의 RPS를 제어함으로써 목표에 도달한다.

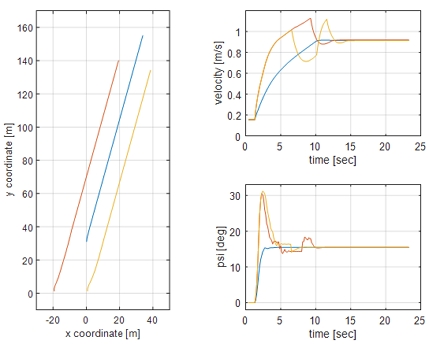
Fig 14은 대형 내의 선박의 대형 형성 및 위치 제어를 시뮬레이션 한 결과이다. 최초 시작점으로부터 대형이 형성되기 위해 팔로워의 속도가 증가하였다가 특정 지점이 지난 후 일정한 속도에 수렴하는 것을 확인할 수 있으며, 형성된 대형 또한 유지됨을 볼 수 있다. 선수각 제어기의 성능 검증은 4.4절의 대형 제어 시뮬레이션과 함께 서술한다.

Fig. 14

Formation control simulation to validate the speed controller

4.4 대형 제어 시뮬레이션

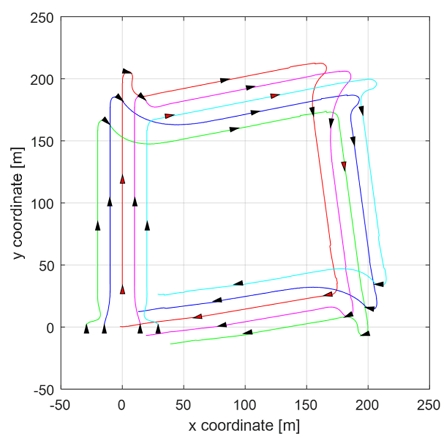
구현한 대형 제어 알고리즘과 선수각 제어 알고리즘을 검증하기 위해 5대의 선박을 이용한 대형 제어 시뮬레이션을 수행하였다. 시뮬레이션은 사각형 경유점을 설정하고, 선박이 Wedge 형태의 대형을 유지하며 운항하는 시나리오로 진행되었다. 경유점은 (0, 200), (200, 200), (200, 0), (0, 0) 순으로 시계 방향으로 이동하며, 총 3번의 경유점 변경이 이루어진다. Fig 14에서 그 결과를 확인할 수 있다. Fig 15에서 붉은색 선박은 현재 설정된 리더를 나타낸다. 첫 번째 경유점을 지난 후, 두 번째 경유점으로 향하는 과정에서 거리 비용이 가장 작은 선박이 새롭게 리더로 선정되었다. 세 번째와 네 번째 경유점을 지날 때에도 동일한 방식으로 적합한 리더가 선정되었다. 또한, 정해진 경유점을 추종하는 과정에서 선수각 제어기를 통해 타를 제어하여 원하는 방향으로 이동하는 것을 확인할 수 있다.

Fig. 15

Formation control simulation with 5 ships result

4.5 정적 장애물 회피 시뮬레이션

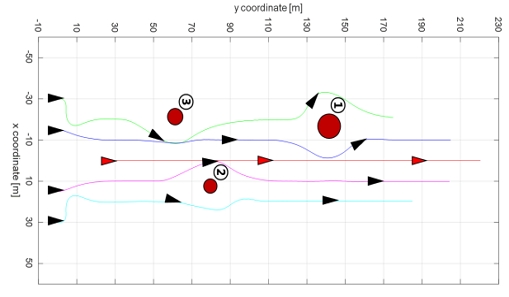
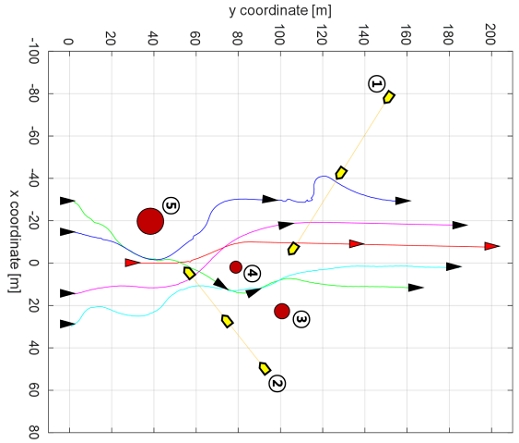
정적 장애물에 대한 회피 및 대형 유지를 검증하기 위해 Fig, 16와 같이 시나리오를 구성하였다. 장애물은 반지름 7m의 장애물 1개, 반지름 4m의 장애물 2개로 구성되며 군집이 이동하는 방향에 이동을 방해하도록 위치를 선정하였다. 장애물의 제원은 Table 2와 같다.

Fig. 16

Static obstacle avoidance simulation result

Table 2

Information of Static obstacle

시작 지점에서 y축을 기준으로 가장 위에 위치한 선박을 ship1, 가장 왼쪽에 위치한 선박을 ship2, 그 오른쪽에 위치한 선박을 ship3, 가장 오른쪽에 위치한 선박을 ship5, 마지막 선박을 ship 4라고 정의하였을 때, 3번 장애물을 회피하기 위해 ship 2가 우현으로 회피한다. 2번 장애물을 조우한 ship 4와 ship 5가 각각 좌현과 우현으로 회피하는 것을 확인 할 수 있고, 1번 장애물을 회피하기 위해 ship 2와 ship 3가 각각 좌현 우현으로 회피하는 것을 볼 수 있다. 모든 장애물을 회피 한 후 다시 대형을 유지하기 위한 경로를 추종하는 것을 확인할 수 있다.

4.6 동적 장애물 회피 시뮬레이션

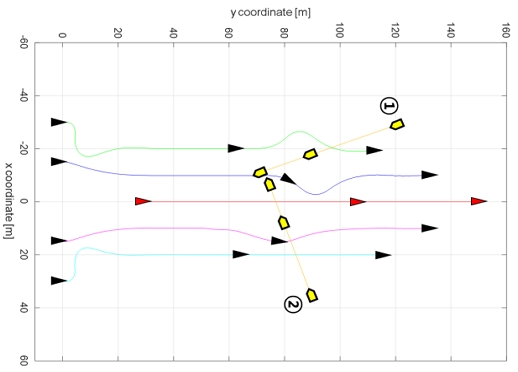
동적 장애물 회피 및 대형 유지를 검증하기 위해 Fig. 17와 같이 동적 장애물 1과 2가 대형을 가로지르며 직선 이동하는 시나리오를 구성하였다. 장애물의 제원은 Table 3과 같다.

Fig. 17

Dynamic obstacle avoidance simulation scenario

Table 3

Information of Dynamic obstacle

4.7 복합 장애물 회피 시뮬레이션

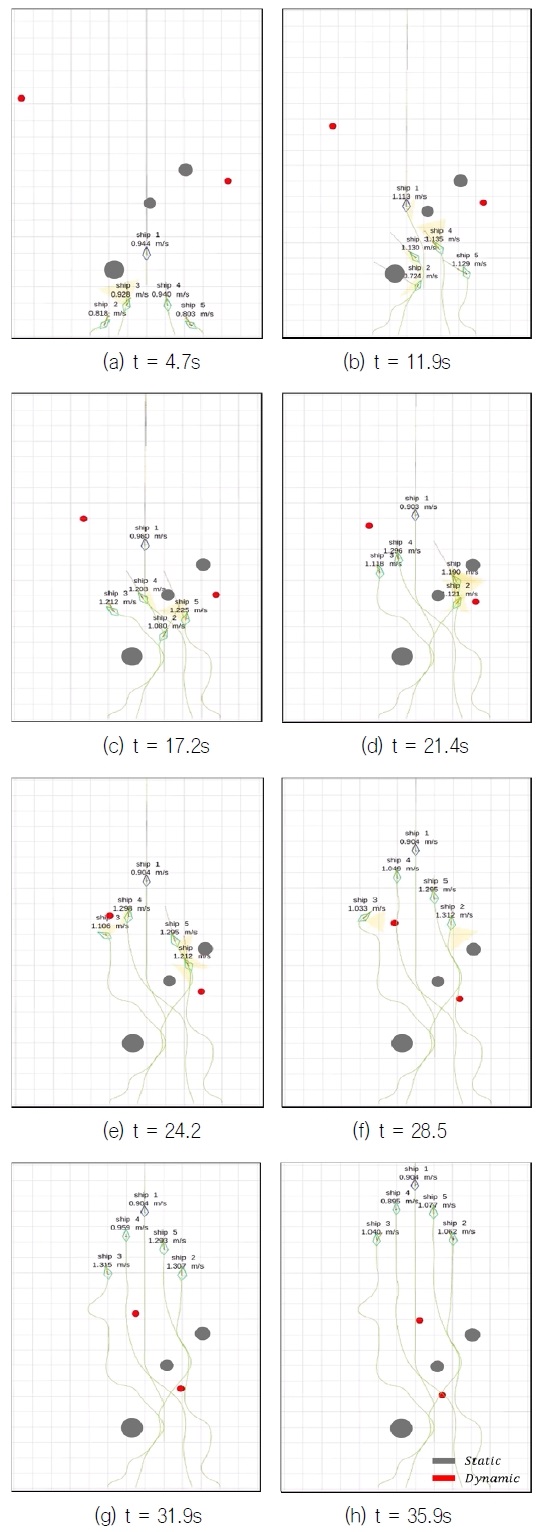
동적 장애물과 정적 장애물이 모두 존재하는 상황에서 Fig. 18와 같은 시뮬레이션을 진행하였다. (시나리오에 대한 설명 추가) 2개의 동적 운항체가 직진 운항하며 대형의 경로를 상에 3개의 정적 장애물이 존재한다. 장애물의 제원은 Table 4와 같다.

Fig. 18

Complex obstacle avoidance simulation scenario

Table 4

Information of Dynamic and static obstacle

Fig. 19는 Fig. 18 시뮬레이션의 시간에 따른 군집의 이동 경로를 나타낸다. Fig. 19(b) t = 11.9s에서 리더가 회피를 수행함에 따라 대형 내 다른 선박도 대형 유지를 위해 이동함을 확인할 수 있다. Fig. 18의 ship 2, ship 5와 같이 일반적인 상황에서는 우현으로 회피를 수행한다. Fig. 19(e)는 1번 동적 장애물을 ship3가 Port-Crossing으로 조우한 상황으로 COLREGs를 고려하면 자선은 침로 유지선이지만, 본 시뮬레이션의 동적 장애물은 회피 행동을 하지 않으므로, 침로를 유지할 경우 충돌이 발생한다. 따라서 Fig. 19(f)와 같이 1번 장애물의 선미부로 회피하여 충돌을 방지하는 것을 확인할 수 있다. 본 시나리오를 통해 정적 장애물과 동적 장애물을 동시에 회피하며 대형을 유지함을 확인할 수 있다. 또한, Fig. 18에 나타난 군집의 경로를 확인하면, 최초 군집 내의 각 운항체가 목표로 하던 이상 지점과 최종 각 운항체의 이상 지점이 달라진 것을 확인할 수 있으며, 충돌 회피와 대형 유지를 동시에 수행하면서 할당 알고리즘에 의해 새로운 대형을 형성한다는 것을 확인 할 수 있다.

Fig. 19

Complex obstacle avoidance simulation result