유체-구조 연성 해석을 통한 유연 날개 주변의 공동 유동 특성 예측

1. 서 론

최근 복합소재를 이용한 제품 개발이 급증하면서, 조선 산업에서는 선박용 복합소재 프로펠러 개발에 관심이 증가하고 있다. 기존 금속 프로펠러와 비교해 복합소재 프로펠러는 부식에 대한 저항성이 크고, 무게가 가벼워 연료 효율성 측면에도 이점이 있는 것으로 알려져 있다 (ITTC, 2005; Mouritz et al., 2001). 특히 복합소재 유연 프로펠러는 캐비테이션 성능 및 유기 소음 저감에 효과가 있어, 최근 잠수함 프로펠러에서 발생하는 캐비테이션 및 유기 소음을 해결하는 방안으로 주목받고 있다.

복합소재 프로펠러의 성능 실험 결과는 Ashkenazi et al. (1974)에 의해 최초로 발표되었다. 이 연구에서는 복합소재 프로펠러가 진동 및 소음 측면에서 기존 금속 프로펠러보다 좋은 성능을 보인다는 것을 확인하였다. 이후 Gowing et al. (1998)은 유연 수중익을 대상으로 한 실험 연구를 통해 날개 끝에서 발생하는 변형이 캐비테이션 발생을 지연시켰음을 입증한 바 있다. 또한 복합소재 프로펠러에 대한 수치해석 연구는 Lin et al. (1991)에 의해 처음 제시되었으며, 유체력 및 응력 해석을 위해 FEM과 VLM(Vortex Lattice Method)을 적용하여 유체-구조 연성 해석을 수행하였다. Ducoin et al. (2010)은 유연 수중익을 대상으로 비공동 및 공동 조건에서 유체-구조 상호작용을 수치해석 및 실험적으로 분석하였으며, 유체력에 의한 변형 및 이에 기인한 진동 특성을 면밀하게 확인하였다 (Ducoin et al., 2012).

국내에서도 복합소재 프로펠러에 대한 연구가 활발히 진행되고 있다. Jang et al. (2012)은 변형량을 고려한 유연 프로펠러의 설계 기법을 제시하였고, Lee et al. (2012)은 적층형 복합소재 유연 프로펠러를 제작하고 여러 시험을 통해 변형에 기인한 프로펠러의 성능을 검토하였다. Kim et al. (2020)은 복합소재 유연 프로펠러의 설계 알고리즘을 정립하였으며, 이어서 CFD-FEM에 대한 양방향 연성 해석을 통해 공동 조건에서 적층형 복합소재 프로펠러의 성능을 검토하였으며, 구조적 변형이 프로펠러의 주요 매개변수 및 캐비테이션 발생량에 영향을 미칠 수 있음을 확인하였다 (Kim et al., 2022).

본 연구는 복합소재 유연 프로펠러의 기본 형태인 3차원 유연 날개를 대상으로 수치해석을 수행하였다. 캐비테이션 터널 내에 날개 형상을 배치하였으며, 재료 물성치를 다르게 부여하여 강성 및 유연 재질의 날개를 모사하였다. 수치해석은 비공동 조건에 대해 먼저 수행하였으며, 비정상 유동에서 구조적 변형에 따라 나타나는 유동 특성을 파악하였다. 또한, 공동 유동 조건에서도 수치해석을 수행하여 변형량에 기인한 캐비테이션 발생 특성을 확인하였다. 강성 날개는 Leroux et al. (2004)의 실험 연구와 비교하여 결과를 검증하였으며, 유연 날개는 Ducoin et al. (2012)의 실험 연구를 통해 수치해석 결과를 검증하였다. 유동해석을 위해 상용 전산유동해석 프로그램인 STAR-CCM+를 사용되었으며, 구조해석 또한 상용 구조해석 프로그램인 Abaqus를 사용하여 유체-구조 연성해석을 수행하였다.

2. 수치해석 방법

비정상 공동 유동 해석의 엄밀한 해석을 위해 선행 연구 (Heo and Kim, 2024)를 통해 격자 및 물리 모델의 적정성을 확인한 바 있다. 본 연구에서는 해당 선행 연구를 기반으로 하여 유동해석 수치 기법을 설정하였다. 유동해석은 상용 전산유동해석 프로그램인 STAR-CCM+(ver 19.02)을 사용하였다. 비정상 난류 유동을 해석하기 위해 RANS 기법이 적용되었으며, 주요 연속 방정식 및 지배방정식은 다음과 같다.

여기서, ρ는 밀도, $$ \overline{u}$$는 시간에 대한 평균유속, p는 압력, μ는 점성계수, $$ -\rho \overline{u_i^{\prime }{u}_j^{\prime }}$$는 레이놀즈 응력 항을 나타낸다. 난류 모델은 SST K-Omega 모델을 적용하며, 지배방정식의 시간 차분, 대류항, 확산항은 2차 정확도의 암시적 방법(implicit method)으로 계산하였다. 속도와 압력의 연성은 SIMPLEC 알고리즘을 통해 수행하였으며, 면밀한 캐비테이션의 거동은 Schnerr-Sauer (2001) 모델을 통해 모사하였다.

여기서, α는 체적분율(Volume fraction)을 의미하고, l과 v는 각각 물과 증기를 나타낸다. 또한 R_B는 기포의 반경, R_e과R_c은 각각 기포의 기화와 응축을 의미한다. 유체 하중에 따른 구조적 변형을 예측하기 위해 상용 구조해석 프로그램인 ABAQUS (2021)를 사용하며, 구조체의 응력 및 변형을 해석하기 위한 지배방정식은 다음과 같이 정의된다.

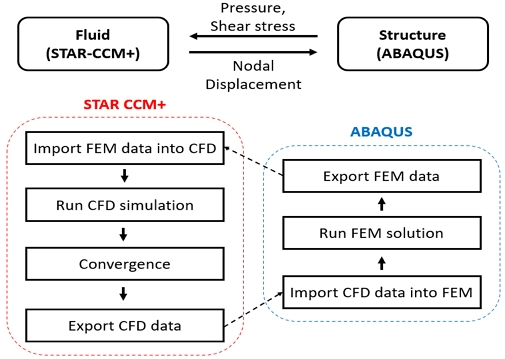
여기서 행렬 형태로 나타나는 M,C,K,F는 각각 질량, 감쇠, 강성, 외력 항을 의미하며, d와 ϵ는 변위와 변형률을 나타낸다. Fig. 1은 유체-구조 연성해석의 절차를 자세히 나타내었다. 유동해석과 구조해석의 연성해석은 양방향 결합을 적용하여 서로 상호작용이 가능하도록 설정하였다. 이는 유체와 구조가 강하게 결합된 형태로, 매시간 간격마다 압력 및 전단 응력과 변위를 교환한다. 그 과정에서 내부 반복을 통해 매개변수 교환이 진행되며 수렴 값을 찾아간다.

Fig. 1

Fluid-Structure Interaction scheme

3. 계산 영역 및 경계 조건

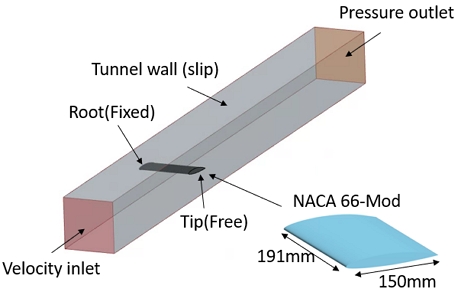
본 연구에서는 강성 날개의 경우 Leroux et al. (2004)의 실험 연구를, 유연 날개의 경우 Ducoin et al. (2012)의 실험 연구를 참고하여 해석 영역 및 조건을 구성하였다. 해석 대상인 수중익의 날개 단면은 NACA66의 수정된 형상이며, 코드 길이와 스팬 길이는 각각 150mm, 191mm에 해당한다.

강성 날개의 재료는 스테인리스 강(Stainless steel)으로 설정되었으며, 유연 날개는 폴리옥시메틸렌 수지(POM polyacetate)의 재질을 가진다. 세부적인 재료 물성치 및 수치해석에 적용된 유체 물성치는 Table 1과 Table 2에 정리하였다.

Table 1

Material properties of hydrofoils

Table 2

Material properties of fluid

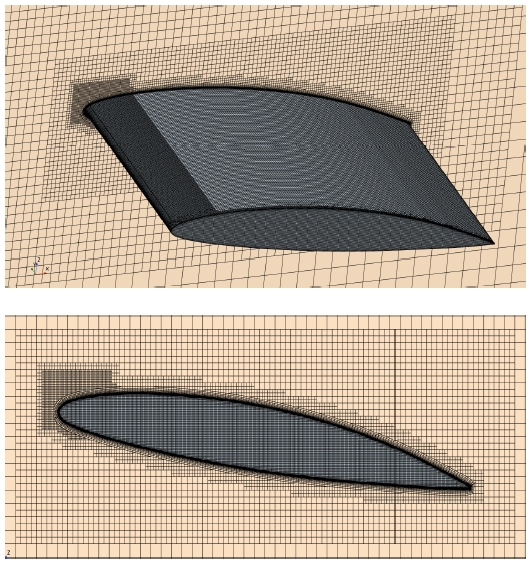
수치해석 도메인은 Fig. 2와 같이 캐비테이션 터널 제원으로 구성하였다. 캐비테이션 터널의 제원은 실험 연구 (Ducoin et al., 2012)와 동일한 폭(0.192m)과 높이(0.192m)를 가지며, 실제 시험 부(test section)의 길이는 1m이지만 해석의 안정성을 위해 길이 방향으로 더 늘려 구성하였다. 터널의 벽면은 미끄럼 벽 조건(slip-wall condition)이 적용되며, 터널의 앞쪽과 뒤쪽 면은 속도 유입 면(velocity inlet)과 압력 유출 면(pressure outlet)으로 각각 구성된다. 터널 내부에는 날개 형상이 존재하고 있으며, 날개의 뿌리부(root)는 터널과 완전히 맞닿아 고정되어 있으며, 반대쪽 끝단 부(tip)는 자유로운 변형을 위해 터널의 벽면과 간극이 존재한다. 여기서, 터널 벽면과 날개 사이의 간극은 1mm이다.

Fig. 2

Fluid domain and boundary conditions

수치해석 결과를 실험 결과와 비교 및 검증하기 위해서 공동 수와 레이놀즈수를 일치시켜 시험 조건을 선정하였다. 이때, 공동수와 레이놀즈수는 각각 아래의 식과 같이 정의된다.

여기서, V_∞와 p_∞는 유동의 속도, 압력을 의미하며, ν는 동점성 계수, p_v는 증기압이다. 또한, 수치해석은 강성 날개와 유연 날개를 대상으로 비공동 및 공동 유동에서 수행되었다. 모든 조건에서 레이놀즈수와 날개의 받음각은 고정된다. 3개의 공동수 조건에 대해 해석을 수행하였으며, 세부 계산조건은 Table 3에 나타내었다.

Table 3

Test conditions

4. 수치해석 결과

본 수치해석에 앞서 해석 격자의 타당성을 검토하기 위해 격자 수렴도 테스트를 수행하였다. 격자는 비정렬 격자인 Trimmer로 구성되며, 수중익 주변의 경계층 유동 및 캐비테이션을 잘 모사하기 위해 프리즘 층을 별도로 설정하였다. 이때, 무차원화 된 벽면 거리는 1 이하의 수준으로 적용하였다. 격자 수렴도 테스트는 강성 날개를 대상으로 수행하였으며, 이를 실험 연구인 Leroux et al. (2004)와 비교하여 검증하였다. 수렴 기준은 수중익에 발생하는 양력 계수를 중점으로 비교하였으며, 시간 간격은 1.0×10^-3초로 진행하였다. 격자 수준은 조밀도에 따라 3가지로 분류하여 수렴 수준을 확인하였다.

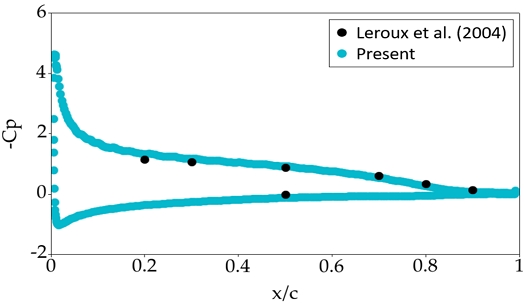
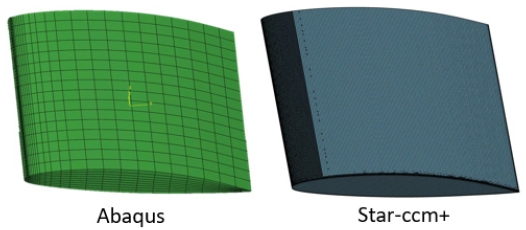
Table 4는 격자 수렴도 테스트 결과이며, 격자가 조밀해질수록 양력 계수가 수렴하는 것을 알 수 있다. 하지만, 전반적으로 실험과 비교하였을 때 오차가 존재하는데 이를 면밀히 확인하기 위해 별도로 Fig. 3에서 나타낸 바와 같이 실험과 수치해석의 압력계수 분포를 비교하였다. 결과적으로 수치해석의 결과가 실험과 잘 일치하고 있으며, 양력 계수의 오차 또한 크지 않기 때문에 합리적인 수준이라고 판단하여 본 해석에서는 중간 수준의 격자를 채택하였다. 또한, 구조 격자의 경우 ABAQUS 내에서 설정하였으며, 하중에 따른 변형 방향을 고려하여 8개의 절점을 브릭 요소인 C3D8으로 구성하였다. 유체 및 구조 격자 수준은 Fig. 4와 5에서 나타내었다.

Table 4

Grid convergence test

Fig. 3

Comparisons of pressure coefficient between the experimental and numerical results

Fig. 4

Fluid and structure meshes on the hydrofoil

Fig. 5

Representation of mesh resolution

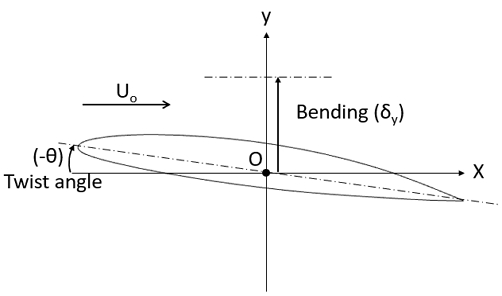
추가적으로, 시간 간격에 대한 수렴도 테스트를 수행하였으며, 시간 간격 또한 3개로 분류하여 수렴도를 판단하였다(Table 5).Table 5를 통해 시간 간격에 따라 양력 계수가 거의 일치하는 것을 확인할 수 있다. 궁극적으로 본 해석에서는 유체-구조의 연동과 캐비테이션 해석을 고려하여 1.0×10^-4초로 진행하였다. 수치해석은 먼저 비공동 조건에서 강성 및 유연 날개를 대상으로 해석을 수행하였다. 이때, 유연 날개의 경우 구조적 변형으로 인한 굽힘과 뒤틀림이 발생하게 되는데, 본 연구에서는 Fig. 6과 같이 수중익의 끝단부의 2차원 형태를 기준으로 굽힘량(δ_y)과 뒤틀림 각(θ)을 정의하였다. 여기서, 굽힘은 수중익의 중심코드를 기준으로 하여 z방향 변위를 의미하며, 뒤틀림은 수중익의 전연과 후연의 각도를 기준으로 계산된다.

Table 5

Time step convergence test

Fig. 6

Schematic view of the hydrofoil with bending and twist angle

또한, 유체-구조 연성의 경우 유연 날개의 변형에 따라 격자의 원활한 수정이 필요하다. 이를 위해 일반적으로는 Morphing 기법을 사용하여 변형량에 기반한 격자를 수정하지만, 본 연구의 경우에는 터널과 날개 사이에 1mm의 작은 간극이 존재하여 해당 부분에서 유체 격자의 수정이 원활하게 이루어지지 않았다.

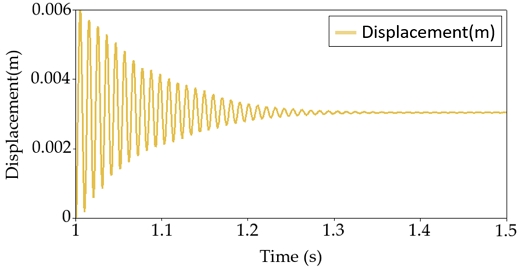
따라서, 수중익의 변형이 Fig. 7과 같이 수렴하는 과정에서 일반적인 morping 기법 이외에 remeshing solver를 적용하여 일정 시점마다 강제적으로 격자의 수정을 부여하였다. Remeshing solver는 기존 격자를 삭제하고 새로 생성하여 격자를 전체적으로 재구성하는데 중점을 두기 때문에, 빠르게 회전하는 프로펠러나 터빈 블레이드에 대한 유체-구조 연성해석 시 구조 변형으로 인해 격자가 왜곡될 때 유용하게 사용할 수 있다 (Siemens. 2019). 변형이 크게 발생하는 해석의 초반부에서는 비교적 잦은 remeshing 주기를 적용하여 해석의 안정성을 높였으며, 이후 변형량의 진폭이 안정됨에 따라 해석 시간의 절감을 위해 점진적으로 remeshing 주기를 키워나가면서 해석을 수행하였다. 다음 Table 6는 강성 및 유연 날개에 대해 비공동 조건(σ=7.0)에서 수치해석을 수행한 결과를 정리하여 나타내었다.

Fig. 7

Time series data of displacement of the flexible hydrofoil (σ=7.0)

Table 6

Lift coefficient and displacement comparison: rigid vs. flexible hydrofoil in non-cavitating condition

먼저 유연 날개에 발생하는 양력 계수가 강성 날개에 비해 증가하는 것을 확인할 수 있는데 이는 유연 날개에 유체 하중이 작용하여 날개의 받음각이 증가하는 방향으로 변형이 발생하였기 때문으로 판단된다. 이러한 굽힘 및 뒤틀림의 경향은 Ducoin et al. (2012)의 실험 결과와도 일치하는 것을 확인할 수 있으며, 받음각 변화인 뒤틀림 각의 경우 굽힘에 비해 실험 결과와 차이를 보이는데 이는 절대적인 비교 값이 작을 뿐만 아니라 실험과 계산조건을 정확하게 맞추기 어려운 점에 기인한 것으로 판단된다.

Fig. 8은 날개의 끝단 위치(y/c≈0)에서의 변형 전과 후 형상을 비교하여 나타내었다. 앞선 Table 6에서 알 수 있듯이 유연 날개가 강성 날개에 비해 연직 상방으로 상승하는 방향으로 변형이 발생한 것을 확인할 수 있다. 또한, 변형된 유연 날개의 형상이 Ducoin et al. (2012)의 실험 연구와 비교하였을 때 잘 일치하는 것을 확인하였다.

Fig. 8

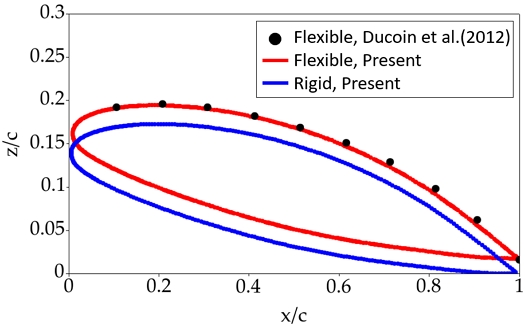
Comparison of the deformed shape between experimental and numerical results in non-cavitating condition

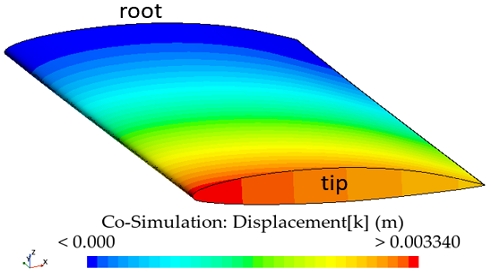
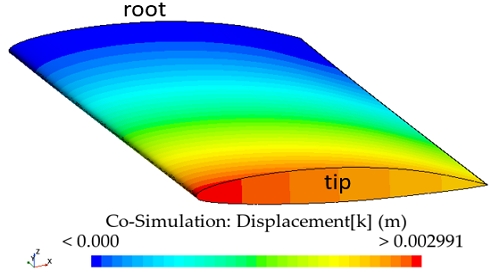
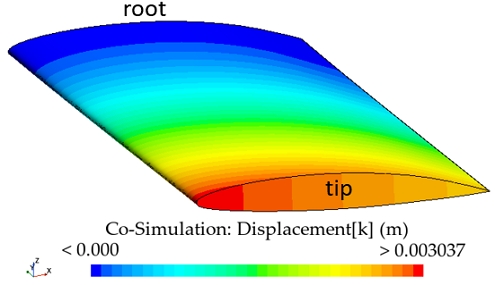
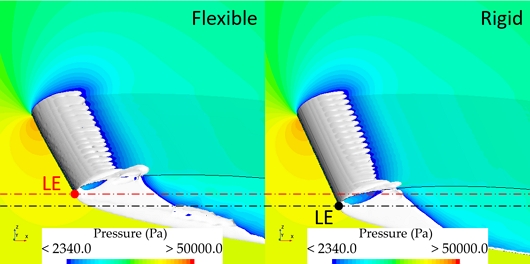
Fig. 9~11은 비공동 및 공동 조건을 포함하여 각 공동수 조건에서 유연 날개의 변형량을 보여준다. 날개의 뿌리부는 고정되어 있으므로 모든 조건에서 동일하게 변형량이 존재하지 않으며, 스팬 방향으로 변형량이 점차 증가하여 고정되어 있지 않은 날개 끝단 부에서 최대 변형량을 갖는 것을 알 수 있다. 또한, 코드 방향으로는 날개의 앞날에서 변형이 가장 크게 발생하며, 뒷날로 갈수록 변형량이 작아짐을 알 수 있다. 이러한 경향을 통해 날개의 받음각이 증가하는 방향으로 변형이 발생하였음을 알 수 있다.공동 조건에서의 기준 압력은 수중익의 중심으로부터 –x 방향으로 코드 길이의 2배 위치를 기준으로 하였다. Fig. 12는 공동수 2.6 조건에서 강성 날개 및 유연 날개 표면과 주변의 압력 분포와 캐비테이션 발생 정도를 보여준다. 이때, 캐비테이션은 수증기의 체적분율(volume fraction of vapor)이 0.1 이상인 영역을 나타내었다. 본 연구에서 사용한 RANS 기법의 한계로 비정상 유동에 따른 캐비테이션의 주기적인 거동 특성이 관측되지 않았으며, Fig. 9의 그림과 같이 캐비테이션 발생 길이가 특정 형태로 수렴하였다. 해당 결과는 기존 실험 연구 (Ducoin et al., 2010)에서 관측된 결과와 같으며, 해석 영역 및 날개 형상에 따라 달라질 수 있다.

Fig. 9

Displacement along the spanwise direction for the flexible hydrofoil(σ = 7.0)

Fig. 10

Displacement along the spanwise direction for the flexible hydrofoil(σ = 2.6)

Fig. 11

Displacement along the spanwise direction for the flexible hydrofoil(σ = 2.4)

Fig. 12

Comparison of the rigid and flexible wings in cavitating flow(σ = 2.6)

추가로, 해당 공동 조건에서 강성 날개와 유연 날개 모두 얇은 층 캐비테이션만 관측되었다. 유연 날개의 형상은 비공동 조건에서와 같이 굽힘 및 뒤틀림 변형이 발생하며, 유연 날개의 앞날이 강성날개에 비교해 상승한 것을 확인할 수 있다. 고정되지 않은 날개 끝으로 갈수록 변형량의 크기가 증가하므로, 날개 끝단 부(gap 이 존재하는 위치)에서 생성되는 캐비테이션의 규모가 강성 날개와 비교하여 더욱 커진 것을 확인할 수 있다.

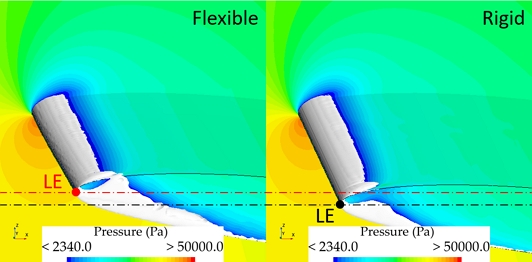
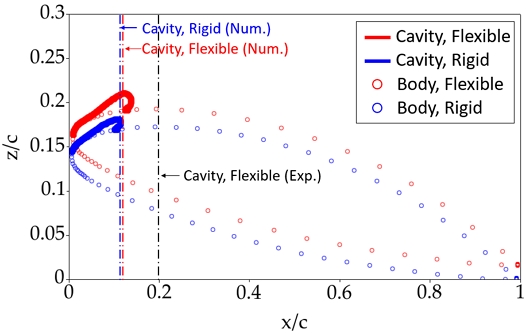
Fig. 13은 공동수 2.6 조건에서 강성 유연 날개 끝단 부에서 발생하는 캐비테이션 형상을 기존 수치해석 (Ducoin et al., 2010) 및 실험 연구 (Ducoin et al., 2012)와 비교하여 나타내었다. 동일한 유체 하중 조건에서 유연 날개에서 발생하는 얇은 층 캐비테이션의 길이가 강성 날개에 비해 길게 나타나고 있으며, 이는 뒤틀림 변형으로 인한 받음각의 상승이 원인으로 보인다. 이러한 경향은 기존 수치해석 및 실험 연구에서도 동일하게 나타나고 있으며, 유연 날개에 발생하는 캐비테이션 길이의 경우 Ducoin et al. (2012)의 실험 결과와도 잘 일치함을 확인할 수 있다.

Fig. 13

Comparison of the experimental and numerical displaced tip section in cavitating flow(σ = 2.6)

Fig. 14는 공동수 2.4 조건에서 강성 날개 및 유연 날개 표면과 주변의 압력 분포와 캐비테이션 발생 정도를 보여준다. Fig. 12와 마찬가지로 날개의 앞날에 얇은 층 캐비테이션이 발생하였으며, 공동 수가 낮아짐에 따라 전반적인 캐비테이션 발생 길이가 공동수 2.6의 결과와 비교해 강성 및 유연 날개 모두 커진 것이 확인된다. 또한, 가장 변형이 크게 발생하는 날개 끝단 부에서 캐비테이션의 규모가 두드러지게 커지는 것을 알 수 있다.

Fig. 14

Comparison of the rigid and flexible wings in cavitating flow(σ = 2.4)

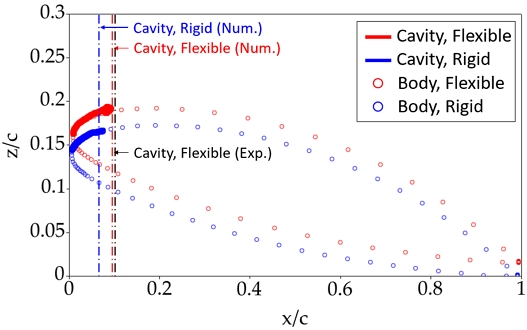
Fig. 15는 공동수 2.4조건에서 강성및 유연 날개 끝단 부에서 발생하는 캐비테이션 형상을 기존 수치해석 및 실험 연구와 비교하여 나타내었다. 마찬가지로 날개의 앞날부터 얇은 층 캐비테이션이 발생하였으며, 공동수가 낮아짐에 따라 캐비테이션 발생 길이가 강성 및 유연 날개 모두 커진 것을 알 수 있다.

Fig. 15

Comparison of the experimental and numerical displaced tip section in cavitating flow(σ = 2.4)

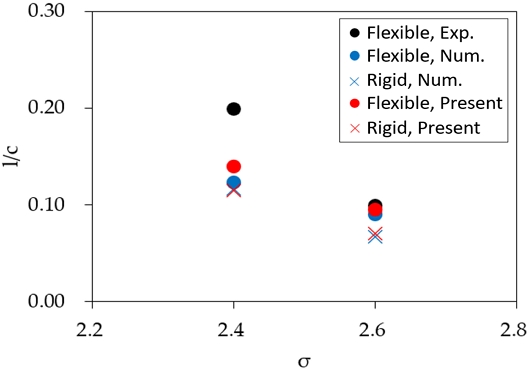
강성 날개에서 발생한 캐비테이션의 규모는 이전 수치해석 연구 결과와 유사하나, 유연 날개의 경우 기존 실험 연구와 본 수치해석 결과가 크게 차이를 보이고 있다. 다만 공동 수 2.4 조건에서 유연 날개의 경우 실험 결과와 비교해 공동 길이가 짧게 예측되는데, 이는 수치해석에서 사용한 캐비테이션 모델 내부의 물의 상태(water quality)나 기포 생성 입자(seed)에 대한 초기 조건을 실험과 온전히 맞추지 못한 점에서 기인한 것으로 판단된다. Fig. 16은 앞선 두 공동수 조건에서의 캐비테이션 발생 길이를 코드 길이로 무차원하여 기존 연구 결과와 비교한 결과이다. 마찬가지로 공동수가 낮은 조건에서 유연 날개가 변형 후 발생하는 캐비테이션 규모를 잘 예측하지 못하고 있음을 확인할 수 있으며, 이를 확인하기 위해서는 추후 정도 높은 실험 연구를 병행함으로써 수치해석 결과를 검증할 필요가 있다.

Fig. 16

Comparison of the non-dimensional cavity length between experimental and numerical results

Table 7은 강성 및 유연 날개에 대해 각 공동수 조건에서의 굽힘량과 뒤틀림 각을 정리하여 나타내었다. 기존 실험 및 수치해석 연구 (Ducoin et al., 2010) 결과와 비교하였을 때 굽힘 및 뒤틀림 각이 유사한 수준으로 예측됨을 확인할 수 있다.

Table 7

Lift coefficient and displacement comparison: rigid vs. flexible hydrofoil in cavitating condition

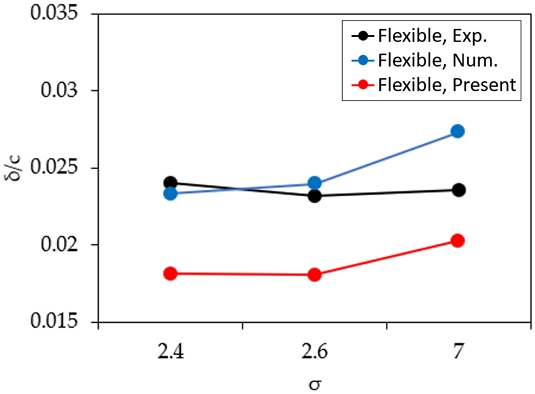
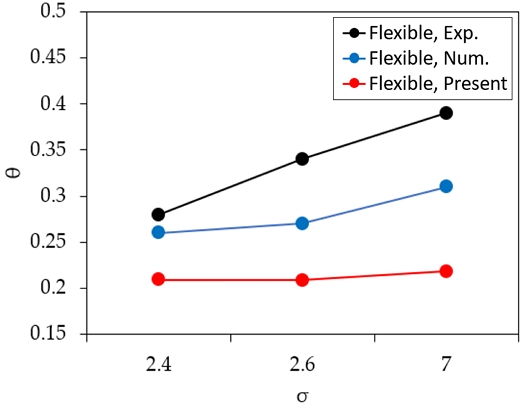
Fig. 17은 유연 날개의 굽힘량을 기존 연구 결과와 비교하여 나타내었으며, 굽힘량은 코드 길이로 무차원하였다. 실험의 경우, 공동 길이가 코드 길이의 10%가 되는 공동수 2.6 조건까지는 공동 발생량이 굽힘량에 영향을 미치지 않다가, 공동 길이가 코드 길이의 20%가 되는 공동수 2.4 조건에서는 굽힘량이 증가함을 확인할 수 있다. 이에 대해 공동의 발생이 날개 주변 밀도를 감소시켜 부가 질량이 감소하고 이에 기인하여 굽힘량이 증가하였다고 설명하고 있다 (Ducoin et al., 2012). 본 수치해석 및 기존 수치해석 결과는 이러한 실험의 경향을 따라가지 못하고 있는데, 이는 앞서 설명한 바와 마찬가지로 두 수치해석에서 사용된 난류 모사 기법은 RANS 기법이 구조물의 진동 및 유체-구조 상호작용을 충분히 고려하지 못함에 기인한 문제로 판단된다.

Fig. 17

Comparison of the non-dimensional displacement between experimental and numerical results

단순히 발생한 공동의 길이만큼 양력이 감소함에 따라 굽힘량이 작아지거나 유지하고 있는 형태로 예측된 것으로 보이며, 이에 관해 추가적인 연구가 필요할 것으로 보인다. Fig. 18은 유연 날개의 날개 끝단에서의 뒤틀림 각을 Ducoin et al. (2010)의 실험 및 수치해석 연구 결과와 비교하였다. 실험은 공동수가 낮아짐에 따라 비틀림각이 감소하는 경향이 두드러지게 나타나지만, 본 수치해석의 결과는 뚜렷한 경향을 찾아보기 어렵다. 발생한 캐비테이션의 규모 또한 이와 직결되었을 거라 예상할 수 있으며, 난류 모사 기법의 개선뿐만 아니라 날개의 진동 및 동적 거동 관점에서도 변형량 및 유동 특성을 함께 살펴볼 필요가 있음을 확인하였다.

Fig. 18

Comparison of the non-dimensional Twist angle between numerical results

5. 결 론

본 연구는 복합소재 유연 프로펠러의 공동 유동 특성을 파악하기 위한 기초 연구로, 유체-구조 연성해석을 통해 프로펠러보다 단순한 형상의 3차원 유연 날개의 변형량 및 이에 기인한 공동 유동 특성을 확인하였다. 구조적 변형에 따른 차이를 확인하기 위해 강성 및 유연 날개에 대해 각각 수치해석 기법을 정립하고 해석을 수행하였다.

비공동 조건의 경우 유체 하중이 작용함에 따라 유연 날개는 구조적 변형인 굽힘과 뒤틀림이 발생하여 받음각이 증가하면서, 동일한 압력 조건 하에서 유연 날개의 양력 계수가 강성 날개에 비해 증가하는 것을 확인하였다. 또한, 고정되지 않은 날개의 끝단 부로 갈수록 변형량이 증가하며, 날개 끝단부 앞날에서 가장 큰 변형량이 발생함을 확인하였다.

공동 조건에서는 두 개의 공동수 조건으로 수치해석을 수행하였다. 앞서 비공동 조건에서의 특성과 유사하게 유연 날개의 변형량(굽힘과 뒤틀림)은 양력 계수에 영향을 주며, 이는 캐비테이션의 발생에도 영향을 미치는 것을 확인하였다. 동일한 공동수 조건에서 날개 단면의 앞날에서 발생하는 얇은 층 캐비테이션의 규모가 강성 날개와 비교해 유연 날개 주변에서 커지는 것을 확인하였으며, 이는 받음각 증가에 기인한 것으로 판단할 수 있다.

또한, 이러한 경향은 기존 수치해석 및 실험 연구와의 비교를 통해 검증하였다. 다만 공동 수가 낮아짐에 따라 발생한 캐비테이션의 규모가 커질수록 실험 결과와 차이가 발생하였으며, 이러한 특성을 확인하기 위해서는 유체역학적인 접근뿐만 아니라 유체-구조 상호작용의 복잡성, 캐비테이션 안정성 및 비정상 거동 특성, 고유 진동수와의 상호작용 및 재료의 비선형 거동 등 각 요인을 면밀히 분석하고 이해할 필요가 있음을 확인하였다.

추후 지속적인 연구를 통해 LES 등의 고차원 난류 모사 기법 적용 및 진동 관점에서의 동적 거동 특성을 면밀하게 검토하고, 소음해석까지 연구 내용을 확장하고자 한다.

Acknowledgments

본 연구는 과학기술정보통신부 기초연구사업(NRF-2022R1G1A1011337)의 지원으로 수행되었습니다.

References

• Ashkenazi, Y., Gol’fman, I., Rezhkov, L. and Sidorov, N., 1974. Glass-fiber-reinforced plastic parts in ship machinery. Leningard: Sudostroyenniye Publishing House.
• Ducoin, A., Young, Y.L. and Sigrist, J.o., 2010. Hydroelastic responses of a flexible hydrofoil in turbulent, cavitating flow. Fluids Engineering Division Summer Meeting. [https://doi.org/10.1115/FEDSM-ICNMM2010-30310]
• Ducoin, A., Astolfi, J.A. and Sigrist, J., 2012. An experimental analysis of fluid structure interaction on a flexible hydrofoil in various flow regimes including cavitating flow. European Journal of Mechanics-B/Fluids, 36, pp.63-74. [https://doi.org/10.1016/j.euromechflu.2012.03.009]
• Gowing, S., Coffin, P. and Dai, C., 1998. Hydrofoil cavitation improvements with elastically coupled composite materials. SNAME American Towing Tank Conference. [https://doi.org/10.5957/ATTC-1998-019]
• Heo, N. and Kim, J.H., 2024. Periodic behavior and noise characteristics of cavitating flow around two-dimensional hydrofoils. Journal of Marine Engineering, 12, 1681. [https://doi.org/10.3390/jmse12091681]
• Jang, H.G., Nho, I.S., Hong, C.H. and Lee, C.S., 2012. Design algorithm of flexible propeller by fluid-structure interactive analysis. Journal of the Society of Naval Architects of Korea, 49(6), pp.528-533. [https://doi.org/10.3744/SNAK.2012.49.6.528]
• Kim, J.H., Ahn, B.K. and Kim, G.D., 2020. Design of flexible composite propellers considering fluid-structure interaction. Journal of the Society of Naval Architects of Korea, 57(2), pp.61-69. [https://doi.org/10.3744/SNAK.2020.57.2.061]
• Kim, J.H., Lee, H.S., Kim, S.H., Choi, H.Y., Hah, Z.H. and Seol, H.S., 2022. Performance prediction of composite marine propeller in non-cavitating and cavitating flow. Applied Sciences, 12(10), pp.5170. [https://doi.org/10.3390/app12105170]
• Lee, S.G., Nam, J.H., Hyun, B.S., Paik, B.G., Lee, C.S., Jang, H.G. and Nho, I.S., 2012. Enhanced manufacturing and performance analysis of flexible composite propeller. Journal of the Society of Naval Architects of Korea, 49(6), pp.521-527. [https://doi.org/10.3744/SNAK.2012.49.6.521]
• Leroux, J., Astolfi, J.A. and Billard, J.Y., 2004. An experimental study of unsteady partial cavitation. Journal of Fluids Engineering, 126(1), pp.94-101. [https://doi.org/10.1115/1.1627835]
• Lin, G., 1991. Comparative stress/deflection analyses of a thick-shell composite propeller blade.
• Mouritz, A.P., Gellert, E., Burchill, P. and Challis, K., 2001. Review of advanced composite structures for naval ships and submarines. Composite structures, 53(1), pp.21-42. [https://doi.org/10.1016/S0263-8223(00)00175-6]
• Siemens. 2019. STAR-CCM+ User Guide: Tutorial Examples. Siemens Digital Industries Software.