잠수함 모사 플랫폼의 유체력 특성 연구
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Recent advancements in unmanned submersibles, such as ROV and UUV, have revolutionized traditional submarine design by strategically relocating the sail to a forward position, optimizing spatial utilization. This significant alteration directly impacts submarine hydrodynamics, prompting extensive research through model experiments and computational analysis to comprehensively understand the resulting changes. Moreover, the development of docking systems for unmanned submersibles has stimulated further investigations into submarine attitude control and stability, particularly during docking procedures. Maintaining a stable attitude is paramount for ensuring precise docking maneuvers, necessitating careful considerations of sail configuration, control surface layout, and overall submarine geometry. In this study, CWC model tests were conducted to understand the hydrodynamic characteristics of a submarine model platform used for evaluating the UUV launch and recovery system. The tests focused on various combinations of appendages. The results, particularly in terms of the sail position and rudder configuration, show that positioning the sail forward and using the X-rudder configuration is most advantageous for the resistance reduction and position control.
Keywords:
Submarine, Resistance test, Total drag Coefficient(CT), Strouhal number(St)키워드:
잠수함, 저항시험, 전 저항계수, 스트로홀 수1. 서 론
최근 무인수상정(Unmaned Surface Vehicle, USV), 무인잠수정(Unmaned Underwater Vehicle, UUV)과 같은 여러 형태의 무인체계 관련 기술들이 발전하면서 방위산업에 큰 영향을 끼치고 있다. 특히 기존의 유인체계와 결합한 유·무인 복합체계로 운용함으로써 전략, 전술을 강화하여 결과적으로 전투력을 증대시킬 수 있어 다각적인 운용 방식에 대한 새로운 아이디어와 실행 방안에 관한 연구가 활발히 진행되고 있다. 특히 유인 수상 및 수중체계로부터 무인체계를 안전하고 신속하게 진수 및 회수하는 시스템(Launch and Recovery Rystem, LARS)의 기술개발에 대한 요구가 높아지고 있다. 수상함의 경우 크레인(crane), 대빗(davit), 선미 램프(stern ramp) 방식의 진수 시스템이 가장 일반적이다. 그러나 안전하고 신속한 회수를 위해서는 별도의 보조 장치가 필요하며 레일(rail), 슬레드(sled), 케이지(cage), 코쿤(cocoon) 및 그물(net)과 같이 다양한 방식이 제안되고 있다 (Lee, 2016). 잠수함의 LARS는 내부 탑재형과 외부 탑재형으로 구분할 수 있다. 내부 탑재형은 기존 어뢰 또는 미사일 발사관을 이용하는 방식으로 진수 시 기존의 발사 시스템을 이용하거나 UUV의 자체 추력으로 이동할 수 있다. 그러나 잠수함이 정지 또는 저속으로 이동하는 상황에서 UUV와의 상대운동을 최소화하여 안전하게 회수하기 위해서는 별도의 보조 장치가 필요하다. 외부 탑재형의 경우 상하 또는 좌우 갑판에 부착할 수 있는 고정식 혹은 착탈식 LARS가 제안되고 있다. 외부 탑재형의 경우 기존 유인 잠수함의 구조적 변경 없이 운용 가능한 시스템을 구성할 수 있다는 장점이 있어 다양한 방식이 개발되고 있다.
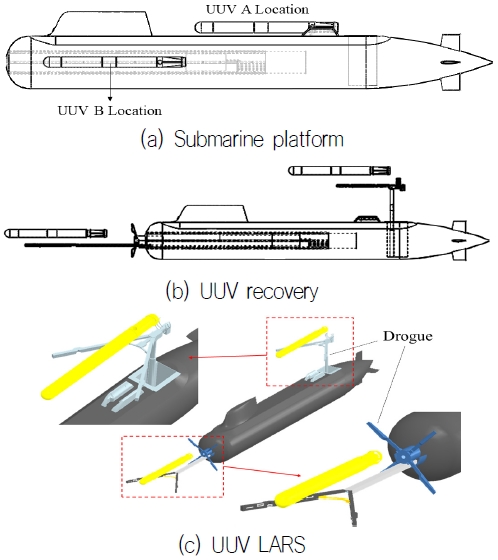
본 연구는 잠수함용 UUV 개발과 함께 외부 및 내부 탑재형 LARS 개발을 목표로 수행 중인 미래도전국방기술 과제의 하나로 개발될 LARS의 성능평가를 위해 필요한 잠수한 모사 플랫폼을 설계하고, 작용하는 유체력 특성을 계측할 목적으로 수행되었다. 개발목표인 UUV는 사전 전개가 필요한 음파 기반 측위 장치의 사용 없이 UUV의 항법 정밀도를 확보하기 위해 수중지형, 자기장 및 중력장 분포와 같은 지구 물리적 특성을 이용한 위치정보에 기반한 항법 기술을 적용하고 있고, 잠수함과 UUV의 심도를 분리하여 이동 중 도킹이 가능한 방식의 LARS 기술개발을 목표로 하고 있다. LARS는 상부 갑판 격납 방식과 내부 탑재형인 함수 발사관에 동시에 적용 가능한 방식으로, 자체 동력으로 진수하며 드로그(drogue)를 이용한 회수방식으로 구성되어 있다(Fig. 1 참조). 개발목표인 LARS의 성능을 검증하기 위해서는 잠수함의 운용 환경과 최대한 가까운 시험평가 환경이 구현되어야 한다. 이를 위해 기존 잠수함의 함형을 모사한 플랫폼을 설계, 제작하고 유체력 특성을 평가하였다. 잠수함의 유체력 특성은 크게 함수의 형상, 세일의 형상 및 위치, 함미 타의 조합에 따라 특성이 달라지며, 조합별 특성 파악을 위해 두 종의 함형을 고려하였다.
LARS and submarine platform
함형이 공개된 BB2 (Kim et al., 2012; Kwon et al., 2022)나 DARPA SUBOFF (Park et al., 2019; Seo and Park, 2021) 모델을 대상으로 수행한 모형실험 및 CFD 해석이 수행되고 있으며 다양한 방식의 LARS가 발전함에 따라 잠수함의 자세 변화와 자세 유지성에 대해서도 연구가 이루어지고 있다. Kim et al. (2012)은 BB2 잠수함 선형에 대하여 대형 제어형 예인 전차(Computerized Planar Motion Carriage, CPMC)를 이용하여 구속모형시험(captive model test)을 수행해 저항계수와 조종 유체력 계수를 구했고 본 선형이 수직면과 수평면에 대한 직진 안정성을 가진다는 것을 확인하였다. Kwon et al. (2022)은 평면운동 장치(Planer Motion Mechanism, PMM)시험을 수행해 유체력 계수와 X형 함미타의 중립타각 분석을 수행하였으며 해당 선형이 수상 조건에서도 충분한 직진 안정성과 제어 유효성을 가지고 있음을 확인하였고 상부타에서만 선체 정류효과가 나타나 선체를 안정적으로 유지시켜준다는 결과를 도출하였다. 잠수함의 함미타는 보통 X형 타와 십자형 타(P타, perpendicular rudder)를 주로 사용하며 Han et al. (2017)은 잠수함의 세일 위치와 함미타형을 변화시켜 회전 팔 시험(Rotating Arm test, RA)를 수행해 동적 안정성 분석을 하였다. 동일한 크기의 P타 또는 세일이 후방에 위치할 때가 안정적이며 세일의 위치는 수평면 운동에 대한 동적 안정성의 영향이 적지만 함미타의 크기와 형상은 동적 안정성에 큰 영향을 끼친다는 결과를 도출하였다.
2. 실험 장치 및 모형
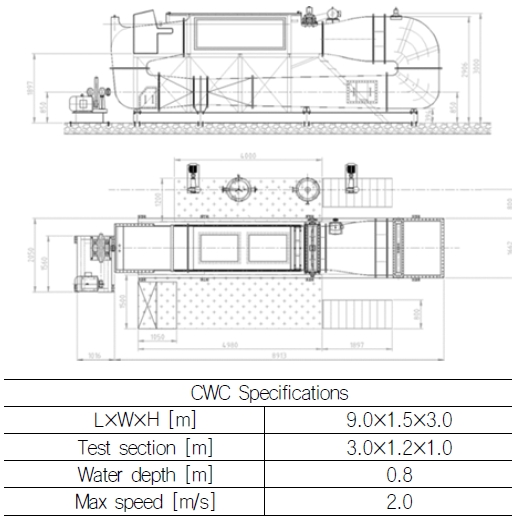
실험은 충남대학교의 회류수조(Fig. ２)에서 수행되었다. 시험부 단면은 1.2m × 1.0m(H × B), 길이는 3.0m이며 최대 유속은 2.0m/s이다.
CNU Circulating Water Channel (CWC)
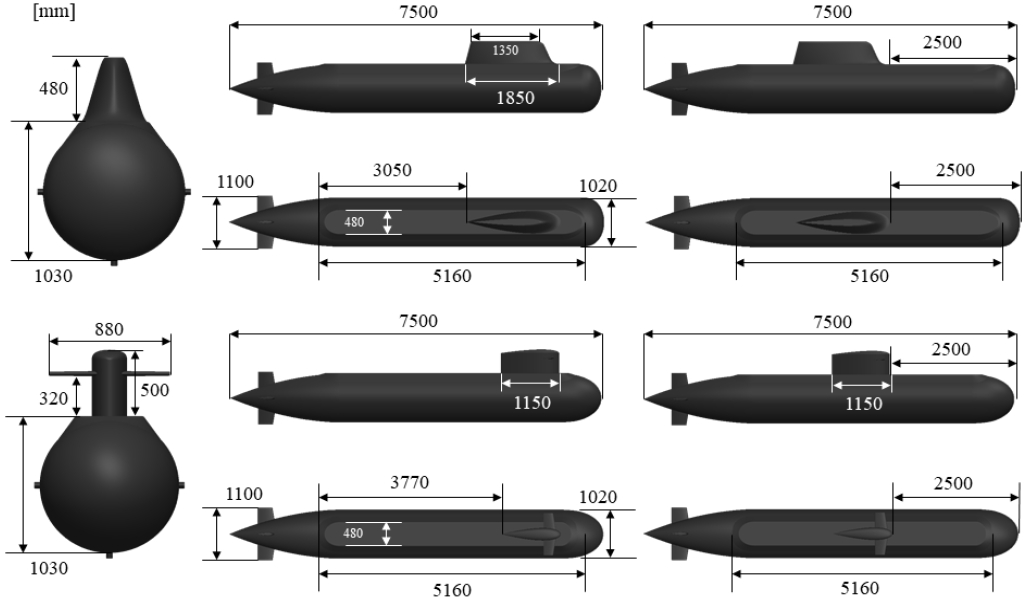
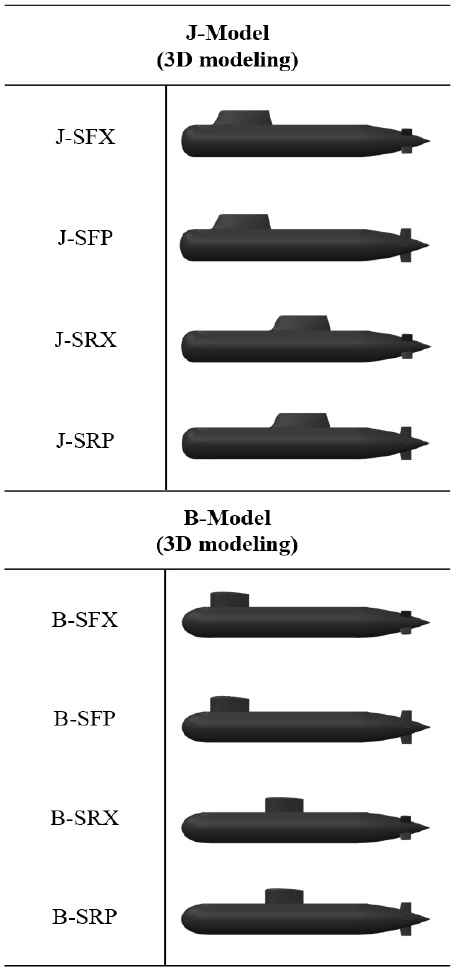
본 연구는 무인 잠수정의 LARS 성능평가를 위한 잠수함 모사 플랫폼의 성능평가를 목적으로 잠수함의 기본 형상과 세일 형상 및 위치, 함미타의 조합별 유체력 특성을 평가할 목적으로 수행되었다. Fig. 1의 (a)는 UUV가 회수된 상태로 잠수함이 항해 중인 그림이며 (b)는 각 탑재방식에 따른 UUV 회수 장면이다. 개발목표 UUV는 길이 2,500mm, 직경 200mm이며 함수 발사관은 길이 5,200mm, 직경 460mm이다. 상부 갑판의 폭은 480mm, 길이는 5,160mm로 제작하였다. 모형은 두 가지 종류(BB2, KSS)에 대해 세일이 전방(Front) 또는 후방(Rear)에 위치할 때, 함미타의 형태가 X타 또는 P타 상태로 구분하였다. BB2에 대한 모형은 ‘B’로 표기하였으며 장보고급 즉, KSS모형은 ‘J’로 표기하였다. 모형은 실제 크기의 1/10로 제작하였으며 LOA는 0.75m이며 지름은 1.02m이며, 모형에 대한 자세한 정보는 Fig. 3에 나타내었다.
Test Models (Full-scale)
본 실험에서는 유속을 0.4 ~ 1.0m/s까지 증가시켰으며 레이놀즈수의 범위는 2.89 × 105 ~ 7.23 × 105이다(Table 1 참고). 잠수함 모형에 작용하는 전저항 계수는 표면적으로 무차원화하여 평가하였으며, 여기서 물의 밀도(ρ)는 999.1kg/m3, 점성계수(μ)는 1.144 × 10-6kg/m·s, 표면적(S)은 0.247m2이다. 추가로 잠수함의 자세 유지성에 대해 평가하기 위해 Y 방향으로 작용하는 힘을 무차원화하였고 이를 드리프트 계수(CY)로 정의하였다.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Test conditions
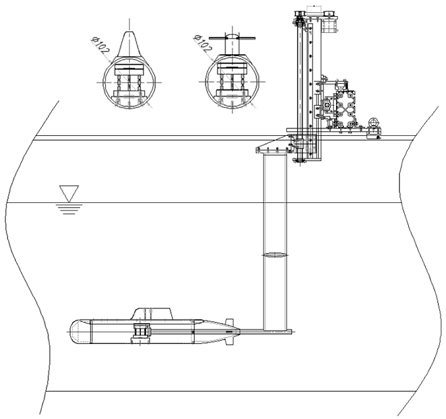
잠수함 모형의 유체력 특성을 평가하기 위해 3축 분력계를 사용하였으며 함수부로부터 300mm 떨어진 위치에서 모형과 결합하였다. 실험은 수심 0.8m에서 진행하였고 폭 방향 위치와 수심을 조절할 수 있는 트래버스(traverse)를 사용하여 모형을 수면으로부터 0.5m에 위치시켰다(Fig. 4). 모형은 조합별로 총 8종이고 모형의 종류(J, B), 세일의 위치(F, R), 함미타의 형상(X, P)로 명명하였으며 Fig. 5에 나타내었다.
Schematic view of the test-setup
Test models and classification names
3. 결과 분석
모형의 전 저항계수(CT)는 식 (6)과 같이 마찰저항계수(CF)와 잉여저항계수(CR)의 합이며, 마찰저항 계수는 ITTC 1957 식을 사용하였다(식 7).
| (6) |
| (7) |
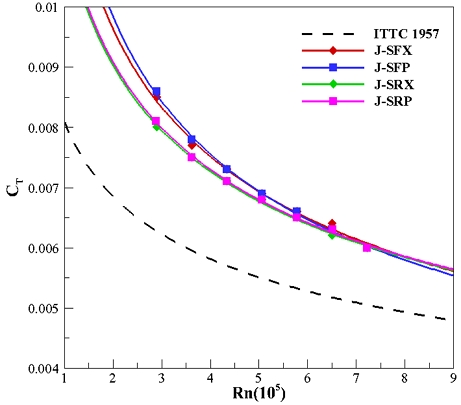
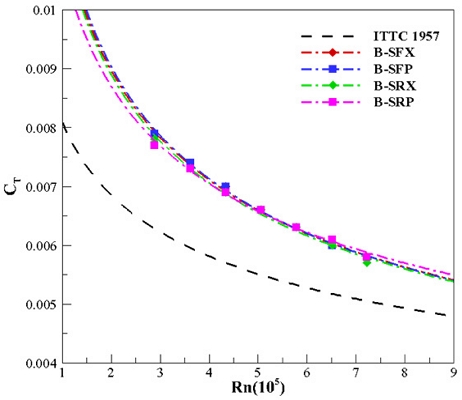
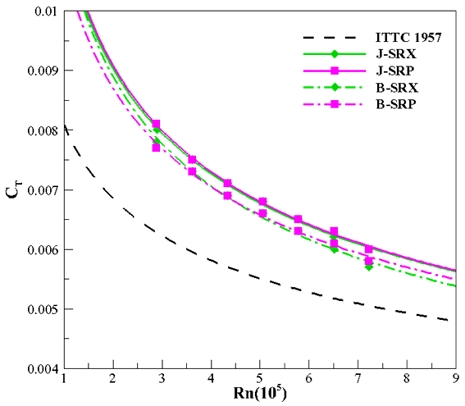
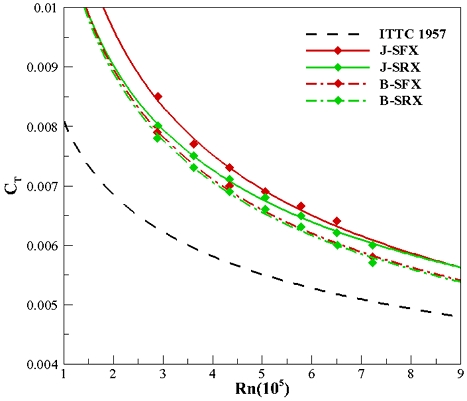
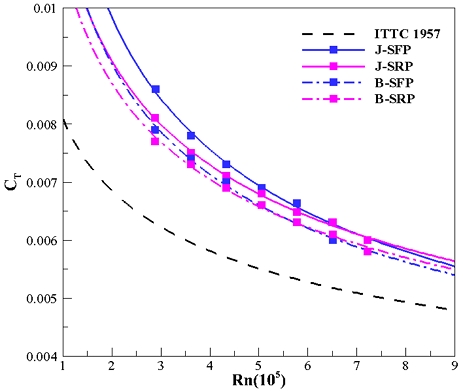
Fig. 6, 7은 J모형과 B모형에 대한 전 저항계수를 ITTC 1957 모형선-실선 상관곡선과 함께 레이놀즈수에 따라 나타낸 것이며 각각 4종(SFX, SFP, SRX, SRP)에 대해 비교하였다. 먼저, 모든 모델이 마찰 저항계수를 의미하는 ITTC 1957 상관곡선보다 전 저항계수가 높게 계측되었으며 이 둘의 차이는 잉여 저항계수 즉, 형상 및 압력저항이라고 분석하였다. Fig. 6에서 J모형은 세일이 후방에 위치하는 타입(J-SRX, SRP)이 전방에 위치하는 타입(J-SFX, SFP)보다 전 저항계수가 낮게 계측되었으며, 특히 점성에 대한 영향이 상대적으로 크게 작용하는 저유속일 때는 더 고려해야 할 필요가 있다. 함수부에서 세일까지의 거리가 길수록 잠수함 상부를 타고 흐르는 유동은 점성에 영향을 받아 유속이 느려지며 세일이 받는 압력저항이 줄어든다. 하지만 유속이 고속으로 갈수록 두 개의 모델이 수렴하게 되는 것을 보아 이에 대한 효과가 줄어드는 것으로 분석하였다. 반대로 Fig. 7의 B모형은 세일의 위치에 따른 전 저항계수 차이가 J모형만큼 확연한 차이가 나지 않았다. B모형의 함수부는 J모형보다 상대적으로 유선형에 가까운 점을 고려할 때 함수부의 선형이 세일의 위치보다 유동 및 저항에 더 영향을 준다는 것으로 분석하였다.
Comparison of total drag coefficient (J-model)
Comparison of total drag coefficient (B-mo)
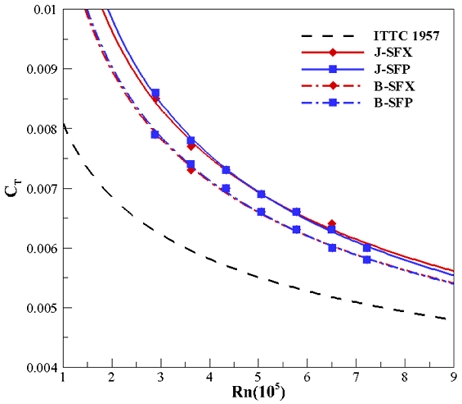
Fig. 8, 9는 세일을 전방 또는 후방에 위치시키고 J모형과 B모형, 함미타에 의한 차이를 확인하기 위해 전 저항계수를 비교한 그래프이다. B모형에 대한 전 저항계수가 J모형보다 낮게 나왔으며, 전 레이놀즈수 영역에 걸쳐 세일이 전방에 위치할 때는 약 0.0004만큼, 후방에 위치할 때는 0.0002만큼 정량적으로 차이가 났다. J모형과 B모형 전부 저항 측면에서 함미타에 의한 차이는 거의 없었으며 세일의 위치에 따른 후류 변화가 함미타에 미치는 영향은 비슷하다고 판단하였다.
Comparison of total drag coefficient (Front sail)
Comparison of total drag coefficient (Rear sail)
Fig. 10, 11는 함미타를 X타와 P타로 고정한 뒤 세일의 위치에 대한 차이를 확인하기 위한 것이다. 세일이 후방에 위치한 J모형(J-SRX, SRP)만 기울기가 다른 것을 확인할 수 있으며 낮은 유속조건에서 B모형의 모델들과 저항값이 비슷하게 측정된 것으로 보아 함수부의 형상이 변화함에 따라 세일에 미치는 영향은 유속이 낮고 세일이 전방에 있을 때만 적용된다고 해석할 수 있다. B모형의 함수부는 유선형에 가까워 세일의 위치에 따른 유동 변화가 거의 없고 상대적으로 뭉툭한 함수부를 가진 J모형은 세일이 전방에 있을 때 다른 모델들과 차이를 보인다. 따라서 함수부의 선형이 저항 측면에서 가장 큰 영향을 끼치나 유선형에 가깝지 않을수록, 또 낮은 유속일수록 세일의 위치에 대한 고려가 필요하다고 판단된다.
Comparison of total drag coefficient (X rudder)
Comparison of total drag coefficient (P rudder)
결과적으로, B모형이 J모형보다 모든 경우의 저항 측면에서 약 3% 우수했으며 J모형에서는 세일이 후방에 있는 모델이 전방에 있는 모델보다 낮은 유속조건에서만 최대 5% 우수했다. 하지만 B모형은 연구목적으로 개발된 모형이며 실험의 결과값인 3%의 저항 증가는 기능적 측면에서 충분히 절충이 가능할 것으로 보이기에 Y방향 드리프트 힘에 관해 고려해야 할 필요가 있다.
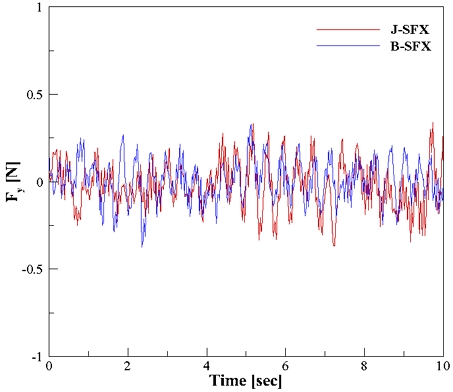
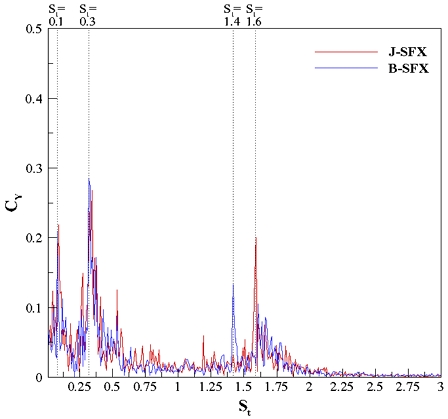
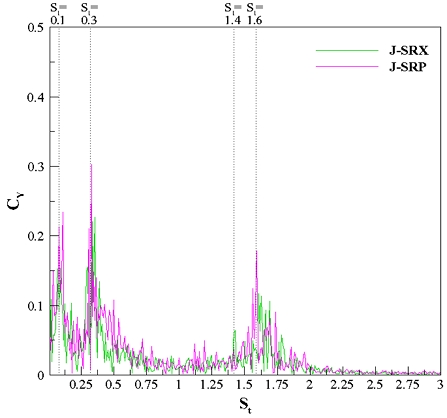
Fig. 12~19는 잠수함 모델의 자세 유지성을 확인하기 위해 수평방향의 힘을 분석한 것이다. 각 모델에 대해서 3분력계를 통해 수평방향 힘인 Fy를 얻었으며 낮은 유속조건에서는 계측량이 낮아 분석의 어려움이 있어 최고 유속인 0.8m/s 조건에서만 분석을 진행하였다. 유동은 잠수함 모델의 길이 방향으로 수평하게 흘러가지만 유동이 흘러가며 세일 및 함미부의 후류나 함수부로부터 나오는 보오텍스 등 폭방향으로 힘이 작용하기 때문에 Fig. 12과 같이 0을 중심으로 폭방향 힘이 진동하는 것을 확인할 수 있다. 이를 모델별로 비교 및 분석을 하기 위해 고속푸리에변환(Fast Fourier Fransform, FFT)을 수행하여 힘의 주파수 특성을 파악하고 이를 무차원화한 스트로홀 수(St)에 따라 드리프트 계수를 표시하였다. Fig. 13과 같이 J모형과 B모형이 폭방향으로 드리프트를 일으키는 스트로홀 수가 상이했으며 스트로홀 수 0.1, 0.3, 1.4, 1.6으로 J모형은 세 개, B모형은 네 개의 특정 스트로홀 수가 존재했다.
Measurement of Fy (SFX)
Comparison of Y drift force coefficient (SFX)
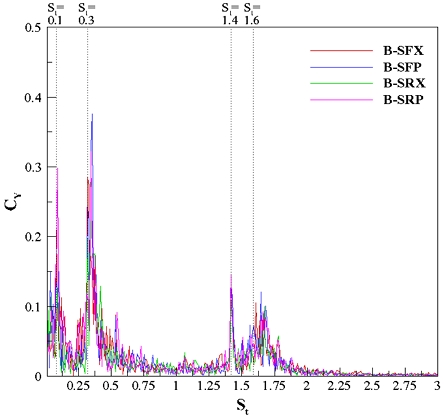
Fig. 14, 15는 전체 J모형, B모형에 대해 드리프트 계수를 비교한 그래프로 상대적으로 낮은 스트로홀 수 1 이하의 범위에서는 B모형의 드리프트 계수가 같거나 높고 1 이상의 범위에서는 B모형이 확연히 낮은 것을 확인할 수 있다. J모형은 스트로홀 수 1.6에 하나의 특정 스트로홀 수를 가지며, B모형은 1.4, 1.6으로 두 개의 특정 스트로홀 수를 가진다. 이는 모형이 각각 갖는 특성으로 판단하였으며 정량적으로는 두 모형이 가지는 드리프트 계수는 차이가 없었지만, 진동을 일으키는 스트로홀 수가 다르며 J모형이 상대적으로 크고 긴 주기성의 진동이 일어나는 것으로 분석할 수 있다. 따라서 높은 스트로홀 수 범위에서만 봤을 때 B모형이 상대적으로 안정적이었으며 이는 함수부의 선형이 유선형인 것이 저항뿐만 아니라 자세 유지 측면에서도 우수한 것으로 판단된다. 하지만 폭방향 힘에 대한 제어는 특정 스트로홀 수가 적을수록 제어 로직이 간결해지기 쉬울 것으로 예상할 수 있기에 J모형이 실제 운용에는 효과적이라고 판단할 수 있다.
Comparison of Y drift force coefficient (J-model)
Comparison of Y drift force coefficient (B-model)
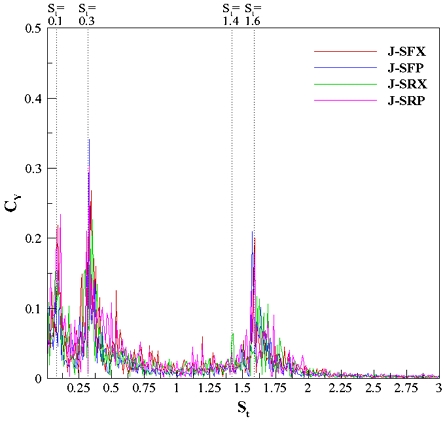
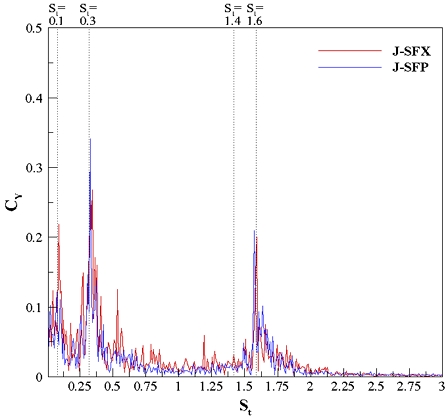
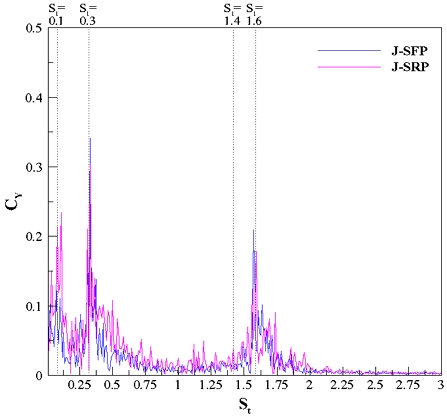
Fig. 16, 17은 J모형에서 세일이 전방 또는 후방에 위치할 때 함미타의 형태에 대해 비교한 그래프이다. 우선 세일이 전방에 위치할 때는 스트로홀 수 0.3에서 P타가 X타보다 드리프트 계수가 20% 높게 계측되었으며 스트로홀 수 1.6에서는 거의 같게 계측되었다. P타가 특정 스트로홀 수를 제외하고는 값이 0.2~0.3정도 낮게 계측되었지만, 드리프트 계수에 있어서는 특정 스트로홀 수의 영향이 지배적이라고 판단된다. 세일이 후방에 위치하는 경우, 직진 주행시 P타의 드리프트 계수가 전체 스트로홀 수 범위에서 크게 계측되었다. 잠수함의 폭방향 힘은 함수부나 세일의 후류영역에서 떨어져 나가는 보오텍스가 지배적이라고 판단되며 P타의 경우 상부 함미타의 양측면에 직접적으로 보오텍스가 작용하게 된다. 이에 따라 드리프트 계수가 높게 계측되었으며 직진 안정성에 있어서는 X타가 유리하다고 판단된다.
Comparison of Y drift force coefficient (Front sail)
Comparison of Y drift force coefficient (Rear sail)
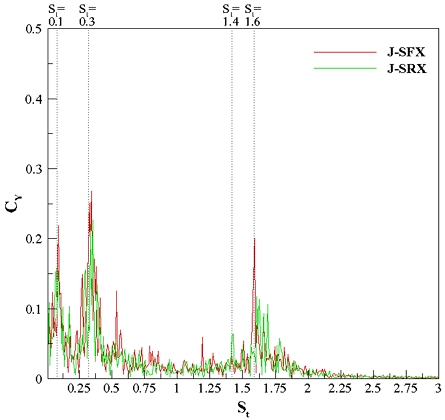
Fig. 18~19는 함미타가 X타 또는 P타일 때 세일의 위치에 대해 비교한 그래프이다. X타의 경우 세 개의 특정 스트로홀 수에서 세일이 전방에 위치할 때(J-SFX, SFP) 약 35%만큼 높게 계측되었으며 전체적으로 후방에 세일이 위치한 것(J-SRX, SRP)이 더 안정적이였다. 이는 세일이 함미타와 멀어질수록 후류영역 안에서 보오텍스가 상대적으로 크게 작용한다는 것으로 판단하였으며 수치해석이나 PIV, LDV등을 이용한 유동가시화를 통해 유동장에 대한 해석이 요구된다.
Comparison of Y drift force coefficient (X rudder)
Comparison of Y drift force coefficient (P rudder)
전체적으로 모든 모델을 비교하자면, 세일이 후방에 위치하며 함미타의 형상이 X타인 ‘J-SRX’모형이 가장 효율적인 것으로 결과가 도출하였으며, 실제 설계에서는 본 연구에서 수행한 유체력 특성과 UUV의 운용을 복합적으로 고려하여 설계를 진행해야 할 것이다.
4. 결 론
본 연구는 UUV 탑재를 위한 잠수함 모형을 여러 조합에 따라 저항시험을 수행하였으며 세일이 전방에 있고 함미타의 형태가 X타일 때 저항 및 자세 유지 측면에서 가장 효율적이라는 것을 실증하였다. 실제 잠수함에서 운용되는 선속 범위를 고려하여 프루드 상사를 통해 실험하였으며 작용하는 항력과 폭방향 힘을 계측하여 전 저항계수와 드리프트 계수를 평가하였다. 본 연구를 통해 도출된 결론은 다음과 같다.
- • 잠수함 모형에서 세일의 위치와 함미타의 형태, 함수부의 선형을 달리하며 저항을 계측하였으며 함수부의 선형이 전 저항계수에 가장 많은 영향을 끼친다. 함미타의 형태는 저항 측면에서 큰 차이는 없었으며 세일의 위치는 전방에 있을 때만 함수부의 선형과 큰 상관관계를 보인다. 전반적으로 함수부의 선형이 유선형에 가까울수록, 또 세일의 위치가 후방에 있을수록 전 저항계수는 낮게 계측되었으며 상대적으로 뭉툭한 함수부를 가지는 J모형이 B모형보다 대략 3% 높게 계측되었다.
- • 잠수함의 자세 유지성을 검토하기 위해 드리프트 계수를 평가하였으며 전 저항계수와는 달리 드리프트 계수는 세일, 함미타, 함수부, 총 세가지 요인들이 유기적으로 영향을 끼치고 특히 특정 스트로홀 수에서 극명한 차이를 보였다. J모형과는 달리 B모형에서는 스트로홀 수 1.4에서 폭방향 힘을 일으키는 성분이 계측되었으며 이는 함수부의 선형이 특정 스트로홀 수에 직결된다고 분석하였다. 세일의 위치와 함미타의 형태는 각 특정 스트로홀 수에서 드리프트 계수가 차이가 났다. P타는 X타보다 스트로홀 수 0.3에서 약 20%, 세일이 전방에 위치할 때는 35% 높게 계측되었다.
Acknowledgments
이 연구는 2024년 정부(방위사업청)의 재원으로 국방과학연구소의 지원을 받아 수행된 미래도전국방기술 연구개발사업임(No. 915071101).
References
- Han, J.H., Jeong, J.H., Lee, S.B., Jang, K.Y. and Lee, S.K., 2017. Dynamic stability analysis of a submarine by changing conning tower position and control planes. Journal of Navigation and Port Research, 41(6), pp.389-394.
-
Kim, Y.G., Yun, K.H., Kim, S.Y. and Kim, D.J., 2012. Captive model test of submerged body using CPMC. Journal of the Society of Naval Architects of Korea, 49(4), pp.296-303.
[https://doi.org/10.3744/SNAK.2012.49.4.296]
-
Kwon, C.S., Kim, D.J., Lee, Y.Y., Kim, Y.G., Yun, K.K. and Cho, S.R., 2022. Prediction of maneuverability of a submarine at surface condition by captive model test. Journal of the Society of Naval Architects of Korea, 59(6), pp.423-431.
[https://doi.org/10.3744/SNAK.2022.59.6.423]
-
Park, I.R., Kim, J.I., Suh, S.B., Seol, H.S., 2019. Numerical study on the resistance and self-propulsion of the SUBOFF submarine model in the cavitation tunnel. Journal of computational fluids engineering, 24(3), pp.50-58.
[https://doi.org/10.6112/kscfe.2019.24.3.050]
-
Suh, S.B. and Park, I. R., 2021. Numerical simulation of the flow around the SUBOFF submarine model using a DES method. Journal of the Society of Naval Architects of Korea, 58(2), pp.73-83.
[https://doi.org/10.3744/SNAK.2021.58.2.073]
