일반화된 확장 상태 관측기 기반 과작동 특성을 가진 자율무인잠수정 비선형 제어 알고리즘 개발

1. 서 론

무인 잠수정은 해양탐사, 수중 구조물, 해양 데이터 수집 등 다양한 분야에서 활용할 수 있다. 또한 무인화 작업을 중점으로 두고 있어 인명 손실을 줄일 수 있고, 장시간 운용이 가능해 국방 분야에서도 활용되고 있으며, 그 역할이 점차 중요해지고 있다 (Sahoo et al., 2019). 정해진 임무를 수행하기 위해 무인 잠수정은 고도의 제어 기술과 성능이 요구된다. 그러나 무인 잠수정의 동역학적 모델은 측정 오차, 유체 계수들의 부정확성, 조류와 같은 외부 요인으로 인한 문제로 인해 정확한 수학적 모델링이 어려우며, 이러한 문제점으로 인해 정밀하게 제어하기가 쉽지 않다 (Roy et al., 2013).

이를 극복하기 위해 슬라이딩 모드 제어기(Sliding Mode Controller; SMC)와 같은 모델 불확실성과 외란에 강인한 특성을 가진 비선형제어 알고리즘이 연구되고 있다 (Utkin and Vadim, 1977). SMC는 견고성과 설계 단순화 장점이 있지만, 선형 스위칭 매니폴드로 인해 유한 시간 내 수렴을 보장하지 못한다. 이를 극복하기 위해 터미널 슬라이딩 모드 제어기(Terminal SMC; TSMC)가 개발되었으나, 시스템 상태가 평형에서 멀리 떨어지면 성능이 저하되며 특이점 문제를 가지고 있다 (Yu and Man, 1996). 본 논문에서는 특이점을 제거하고 빠른 수렴성을 보장하는 비특이성 고속 터미널 슬라이딩 모드 제어기(Non-singular fast terminal SMC; NFTSMC)를 무인 잠수정 제어에 적용하였다(Patre et al., 2018).

NFTSMC는 빠른 수렴 능력을 가지며 모델 불활실성과 외란에 견고하지만 예상치 못하거나 큰 외란에 대하여 제어 성능이 저하될 수 있다. 따라서 외란과 시스템 상태변수를 빠르고 정확하게 추정하여 보상해주는 제어 전략이 필요하다.

확장 상태 관측기(Extended state observer; ESO)는 시스템 상태와 외란을 추정 및 보상하여 제어 시스템의 견고성과 효율성을 높인다 (Han, 2009). 전통적인 ESO는 주로 저주파 외란에 중점을 두어 고주파 외란을 효과적으로 처리하지 못하고, 추정 지연이 발생할 수 있으므로 향상된 ESO가 필요하다 (Madoński and Herman, 2015). 그중 일반화된 확장 상태 관측기(Generalized extended state observer; GESO)는 고주파 외란 처리 능력과 빠른 추정 속도로 다양한 주파수 대역의 외란을 빠르게 보상하여, 시스템의 비선형성과 불확실성에도 견고성을 제공한다 (Shi et al., 2018).

본 연구의 주요 내용은 다음과 같이 요약할 수 있다.

• 1. 6 자유도를 가진 무인 잠수정의 비선형 모델을 모델 불확실성, 외란에 강인한 NFTSMC 제어기를 이용하여 목표 궤적을 빠르게 추적하도록 설계하였다.
• 2. 3^rd GESO를 이용하여 기존의 NFTSMC의 한계를 극복하고 고주파 외부 외란을 빠르고 정확하게 보상한다.
• 3. 제어력 분배를 적용하여 추진기에 할당되는 힘을 최적화하여 전체 시스템의 에너지 효율을 높여 정밀한 운동 제어를 유도하였다.
• 4. 전체 폐루프 안정성과 유한 시간 수렴 특성을 Lyapunov stability 함수를 이용하여 입증하였다.

이에 본문 2장에서 무인 잠수정 모델에 관한 내용을 다루고 3장에서 일반화된 확장 상태 관측기, 4장에서 비특이성 고속 터미널 슬라이딩 모드 제어기, 5장에서 제어력 분배, 6장에서 시뮬레이션 결과를 정리하고 7장에서 본 연구에서 얻은 결론을 정리한다.

2. 무인 잠수정 모델

본 논문에서는 사우스 햄튼 대학에서 개발한 Delphin2 잠수정 모델을 사용하였다. Delphin2 모델의 재원은 Table 1에 나온 정보를 이용하였고, 크게 운동방정식과 추진기 모델로 나누어서 설명하고자 한다(Tanakikorn, 2017).

Table 1

Delphin2 particulars and key performances (Tanakikorn, 2017)

2.1 운동방정식

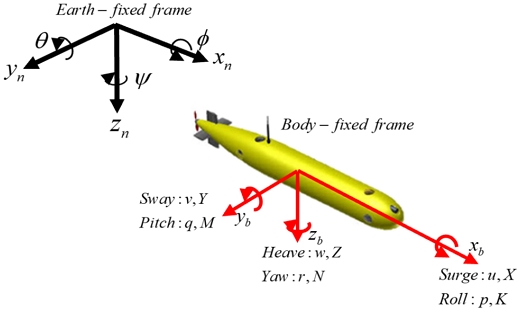
Delphin2 모델은 지구 고정 좌표계(earth-fixed frame)과 선체 고정 좌표계(body-fixed frame)으로 Fig. 1과 같이 나타내었다. 식 (1)을 통해 지구 고정 좌표계에서의 잠수정의 위치, 오일러 각도는 η로 나타내었고, 선체 고정 좌표계에서 잠수정의 선속도와 각속도는 ν로 나타내었다. 두 좌표계 사이의 변환 행렬은 식 (2)과 같으며 R₁(η), R₂(η)은 식 (3)과 식 (4)로 표현한다. 여기서 s(ㆍ), c(ㆍ)와 t(ㆍ)는 sin(ㆍ), cos(ㆍ), tan(ㆍ)을 의미한다.

$\[ \begin{array}{c}\eta ={\left[{\eta }_1 {\eta }_2\right]}^T,{\eta }_1={\left[x y z\right]}^T,{\eta }_2={\left[\varphi \theta \psi \right]}^T\hfill \\ v={\left[v_1 v_2\right]}^T,v_1={\left[u v w\right]}^T,v_2={\left[p q r\right]}^T\hfill \end{array} \]$

(1)

$\[ \begin{array}{c}\dot{\eta }=R\left(\eta \right)v\hfill \\ \left[\begin{array}{c}\dot{{\eta }_1}\\ {\dot{\eta }}_2\end{array}\right]=\left[\begin{array}{cc}{R}_1\left({\eta }_2\right)& 0_{3\times 3}\\ 0_{3\times 3}& R_2\left({\eta }_2\right)\end{array}\right]\left[\begin{array}{c}{v}_1\\ v_2\end{array}\right]\hfill \end{array} \]$

(2)

$\[ R_1\left(\eta \right)=\left[\begin{array}{ccc}c\theta s\psi & -c\theta s\psi +s\varphi s\theta c\psi & s\varphi s\psi +c\varphi s\theta c\psi \\ s\psi c\theta & c\psi c\varphi +s\varphi s\theta s\psi & -c\psi s\varphi +s\theta s\psi c\varphi \\ -s\theta & s\varphi c\theta & c\varphi c\theta \end{array}\right] \]$

(3)

$\[ R_2\left(\eta \right)=\left[\begin{array}{ccc}1& s\varphi t\theta & c\varphi t\theta \\ 0& c\varphi & -s\varphi \\ 0& s\varphi /c\theta & c\varphi /c\theta \end{array}\right] \]$

(4)

Fig. 1

Body-fixed and Earth-fixed Coordinate systems

Delphin2 비선형 동역학 운동방정식은 Fossen (2011)의 운동방정식을 기반으로 나타내었으며, 이는 식 (5)와 같다. 여기서 사용한 동역학 계수는 Table 3을 통하여 확인할 수 있다. 여기서 M∈R^6×6은 총질량 행렬, C(v)∈R^6×6은 코리올리스와 구심성 행렬, D(v)∈R^6×6은 유체 감쇠 계수 행렬, G(η)∈R^6×6은 중력과 부력에 대한 행렬, τ는 식 (6)과 같이 힘과 모멘트로 이루어진 행렬이다 (Fossen, 2011).

$\[ Mv+C\left(v\right)v+D\left(v\right)v+G\left(\eta \right)=\tau +{\tau }_d \]$

(5)

$\[ \tau =\left[X Y Z K M N\right] \]$

(6)

τ_d는 선체에 가해지는 외부 외란이다. 식 (2)의 좌표계 변환을 식 (5)에 적용하여 지구 고정 좌표계에 대한 행렬로 식 (7)과 같이 나타낼 수 있다. M_η, C_η, D_η, G_η와 τ_η, d은 식 (8)으로 나타내었다 (Fossen, 1994).

$\[ M_{\eta }\ddot{\eta }+C_{\eta }\dot{\eta }+D_{\eta }\dot{\eta }+G_{\eta }\left(\eta \right)={\tau }_{\eta }+d \]$

(7)

$\[ \begin{array}{c}{M}_{\eta }=J^{-T}\left(\eta \right)M{J}^{-1}\left(\eta \right)\hfill \\ C_{\eta }=J^{-T}\left(\eta \right)\left[C-M{J}^{-1}\left(\eta \right)\dot{J}\left(\eta \right)\right]J^{-1}\left(\eta \right)\hfill \\ D_{\eta }=J^{-T}\left(\eta \right)D{J}^{-1}\left(\eta \right)\hfill \\ G_{\eta }\left(\eta \right)=J^{-T}\left(\eta \right)G\left(\eta \right)\hfill \\ {\tau }_{\eta }=J^{-T}\left(\eta \right)\tau \hfill \\ d=J^{-T}{\tau }_d\hfill \end{array} \]$

(8)

2.2 추진기 모델

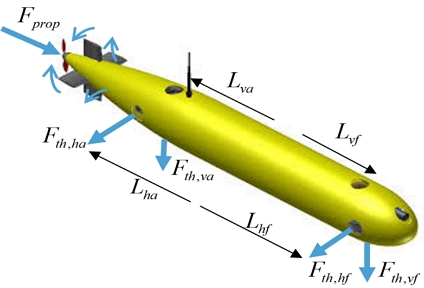
추진기는 주 프로펠러 추진기, 4개의 제어 평면(러더, 스턴)과 중앙에 2개의 전·후방 수평 터널 추진기, 2개의 전·후방 수직 터널 추진기로 구성되어 있다. 각 추진기의 (+) 기호는 Fig. 2와 같으며 힘과 모멘트의 러더, 스턴 기호 규칙은 Table 2로, 4개의 터널 추진기에 대한 기호 규칙은 Table 3으로 나타내었다(Tanakikorn, 2017).

Fig. 2

Regarding the positive actuator demands and distance between central axis and thrusters

Table 2

Forces and moments regarding positive control surface deflections

Table 3

Forces and moments regarding positive thrusters and propeller set-points

각 추진기의 힘과 추진기를 통해 발생한 힘 벡터(τ)는 m개의 자유도와 n개 성분의 추진기로 구해진 힘과 모멘트이며, 이를 식(9)으로 나타낼 수 있다. f = [f₁, ⋯, f_n]^T∈Rⁿ는 각 추진기에서 발생한 힘과 모멘트의 합을 벡터 성분으로 나타냈으며,T = [t₁, t₂, ⋯, t_m]∈R^m×n는 선체 고정 좌표계의 원점에 작용하는 등가 힘과 모멘트로 변환하는 힘 구성 행렬이다(Fossen, 1994).

$\[ \tau =Tf \]$

(9)

주 프로펠러 모델은 기준 프로펠러 이론 (Molland et al., 2011)을 따라 전진 비(J)와 추력계수(K_T,prop)로 특성화하였다. 여기서 w_t는 반류비, D_prop는 프로펠러 지름, n_prop는 실험으로 구한 프로펠러 요구값(u_prop)으로 계산된 프로펠러 속도이다. 여기서 u_prop는 [10,22]의 범위에서 구동한다. u_prop가 10 미만이 되면, Deadband 구간에 들어서므로 동작하지 않는다. 여기서 u_prop은 모터에 인가되는 무차원의 프로펠러 요구값이다.

$\[ J=\frac{u}{n_{prop }{D}_{prop }}\left(1-w_t\right) \]$

(10)

$\[ K_{T,prop}=K_{T_0, prop }\left(1-{\left[\frac{J}{c_{prop,1}}\right]}^{c_{prop,2}}\right) \]$

(11)

$\[ n_{prop }=-0.0055u_{prop }^2+0.4136u_{prop }-1.7895 \]$

(12)

위의 식을 이용하여 주 프로펠러 힘(F_prop)을 식 (13)으로 나타낼 수 있다. t는 추력 감소 계수이다.

$\[ F_{prop }=\rho n_{prop }^2{D}_{prop }^4{K}_{T, prop }\left(1-t\right) \]$

(13)

주 프로펠러 모델의 힘 구성 행렬과 주 프로펠러의 힘 벡터는 식 (14)와 같이 표현한다.

$\[ t_1={\left[\begin{array}{c}1 0 0 0 0 0 0\hfill \end{array}\right]}^T,f_1=F_{prop} \]$

(14)

터널 추진기는 Quasi-steady 모델을 사용하였으며, 추력 힘은 식 (15)로 나타낼 수 있다. 여기서 n_th는 추진기 속도, D_th는 추진기 지름, K_T,th는 추력계수를 의미한다. 추진기의 회전속도(u_th)는 [-2500,-150] ∪ [150,2500]rpm(=rev/m)의 범위에서만 동작하며, [-150,150]rpm의 범위는 Deadband 구간으로 동작하지 않는다.

$\[ F_{th}=\rho \left|n_{th}\right|n_{th}{D}_{th}^4{K}_{T,th}\cdot e^{\left(-c_{th,l}{\left(u\right)}^2\right)}\cdot \left[1-c_{th,2}\left(\frac{v}{n_{th}{D}_{th}}\right)\right] \]$

(15)

추진기의 요구값(u_th)에 대하여 추진기 속도(n_th)의 값은 다음 식과 같이 과도 응답(transient response)를 가지며 1차 저주파 통과 필터(low-pass fileter) 형태로 모델링된다 (Fossen, 1999).

$\[ {\dot{n}}_{th}=K_{th,u}{u}_{th}-K_{th,n}{n}_{th} \]$

(16)

러더와 스턴 요구값에 대하여 출력값은 과도 응답을 가지며 1차 저주파 통과 필터 형태로 다음과 같은 전달함수로 모델링된다. 여기서 τ는 시정수로 값이 작을수록 반응속도가 빨라진다(Fig. 3 참조).

$\[ G_T=\frac{Y\left(s\right)}{R\left(s\right)}=\frac{G\left(s\right)D\left(s\right)}{1+G\left(s\right)D\left(s\right)H\left(s\right)}=\frac{1}{\tau s+1} \]$

(17)

$\[ H\left(s\right)=1,D\left(s\right)=\frac{1}{\tau },G\left(s\right)=\frac{1}{s} \]$

(18)

Fig. 3

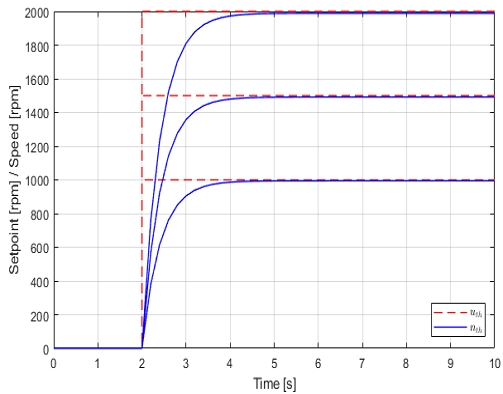
Transient thruster model regarding three different setpoints; Kth,u=2.3992, Kth,n=2.4124 (Tanakikorn, 2017)

터널 추력기의 힘 구성 행렬과 터널 추력기의 힘 벡터는 식 (19)로 표현한다. l은 회전 중심으로부터 추력기까지의 거리를 의미하며 hf와 ha는 수평면의 전방 터널 추력기, 수평면의 후방 터널 추력기를 의미한다.

$\[ t_2=\left[\begin{array}{cccc}0& 0& 0& 0\\ -1& -1& 0& 0\\ 0& 0& -1& -1\\ 0& 0& 0& 0\\ 0& 0& L_{vf}& -L_{va}\\ L_{hf}& -L_{ha}& 0& 0\end{array}\right], f_2=\left[\begin{array}{c}{F}_{th,hf}\\ F_{th,ha}\\ F_{th,vf}\\ F_{th,va}\end{array}\right] \]$

(19)

러더와 스턴으로 인한 힘과 모멘트는 식 (20), (21)로 주어진다. 러더 각도(δ_R)와 스턴 각도(δ_S)는 [-30°, 30°]의 범위를 가지며, 러더와 스턴의 힘 구성 행렬과 러더와 스턴의 힘 벡터는 식 (23)로 표현한다. X_|u|uδRδR와 X_|u|uδSδS는 러더와 스턴으로 인한 전후 동요 감쇠 계수이고, Y_|u|uδR은 러더로 인한 좌우 동요 감쇠 계수, Z_|u|uδS와 M_|u|uδS은 스턴의 깊이, 종 동요 힘과 모멘트의 감쇠 계수, N_|u|uδR은 선수동요 모멘트의 감쇠 계수이다.

$\[ \begin{array}{c}{X}_R=X_{\left|u\right|u{\delta }_R{\delta }_R}\left|u\right|u{\delta }_R^2,\hfill \\ Y_R=Y_{\left|u\right|u{\delta }_R}\left|u\right|u{\delta }_R,\hfill \\ N_R=N_{\left|u\right|u{\delta }_R}\left|u\right|u{\delta }_R\hfill \end{array} \]$

(20)

$\[ \begin{array}{c}{X}_S=X_{\left|u\right|u{\delta }_S{\delta }_S}\left|u\right|u{\delta }_S^2,\hfill \\ Z_S=Z_{\left|u\right|u{\delta }_S},\left|u\right|u{\delta }_S,\hfill \\ M_S=M_{\left|u\right|u{\delta }_S}\left|u\right|u{\delta }_S\hfill \end{array} \]$

(21)

$\[ t_3=\left[\begin{array}{cccccc}-1& 0& 0& -1& 0& 0\\ 0& -1& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 1& 0& 0& 0\end{array}\right], f_3=\left[\begin{array}{c}{X}_R\\ Y_R\\ N_R\\ X_S\\ Z_S\\ M_S\end{array}\right] \]$

(22)

3. 일반화된 확장 상태 관측기

외란을 정확하게 추정하고 보상하여 제어기의 견고성과 효용성을 높이기 위하여 본 연구에서는 제어기에 GESO를 적용하였다. GESO는 향상된 확장 상태 관측기로 빠른 외란에 대하여 높은 추정 정확도를 보이며 고차의 일반화된 확장 상태 관측기일수록 더 정확한 추정 성능을 가진다(Shi et al., 2018).

N차의 GESO를 설계하기 위하여 Delphin2 잠수정의 운동방정식 제어입력 항을 식 (23)으로 정의하여 식 (24)와 같이 선형화하였다.

외란을 식 (25)와 같이 새롭게 정의하여 x_η를 다음과 같이 정의한다.

추정 변수 벡터는 $$ {\dot{\widehat{x}}}_{\eta }$$는 다음과 같이 정의하며 여기서 L은 추정 이득 값이다.

시스템 변수와 추정 변수의 차이를 $$ {\dot{e}}_{\eta }={\dot{x}}_{\eta }-{\dot{\widehat{x}}}_{\eta }$$로 정의하여 다음과 같이 식을 정리한다.

외란에 대한 외란의 추정 오차를 전달함수로 정리하면 다음과 같으며 GESO의 추정 이득 값은 전달함수 계산 결과와 대역폭(bandwidth) w_b의 관계를 통하여 결정된다.

GESO의 차수와 대역폭이 추정 성능에 미치는 영향을 보기 위해서 1, 2, 3차의 GESO 전달함수에 대하여 대역폭이 일정할 때 차수에 따른 보드 선도와 차수가 일정할 때 대역폭에 따른 보드 선도를 비교하였다. 그 결과 Fig. 4와 같이 저주파에서 차수와 대역폭이 커질수록 전달함수의 크기가 작아지므로 외란 추정 정확도가 높아지는 것을 확인하였다. 하지만 너무 높은 차수는 계산의 부담을 줄 수 있고 너무 큰 대역폭은 노이즈를 증폭시키므로 적절한 차수와 대역폭을 선택하는 것이 중요하다.

Fig. 4

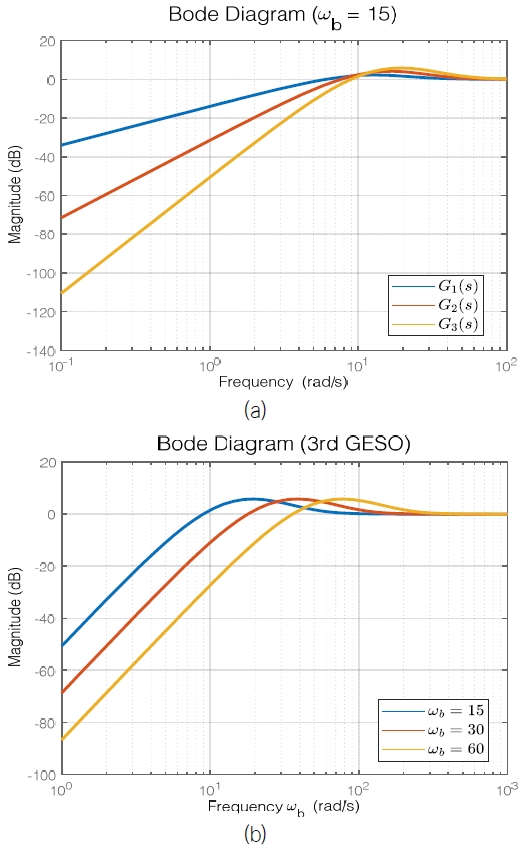
Bode plots for Gn(s): (a) Different order with fixed bandwidth ωb=15 rad/s; (b) Different bandwidth width fixed order n=3

본 논문에서는 실험 과정을 거쳐 외란 추정 정확도가 높고 계산의 부담이 적은 n = 3와 w_b = 60rad/s를 선택하여 제어기에 외란을 추정하고 보상해주었다.

GESO의 안정도를 분석하기 위하여 에너지 관점에서 안정도를 분석하는 방법인 Lyapunov stability 분석을 하였으며 Positive definite한 Lyapunov candidate function (LCF) V₁을 다음과 같이 정의하였다.

V₁의 시간에 대한 미분값은 식 (34)과 같은 LCF와 $$ ‖P{B}_d‖={\lambda }_1‖d_M^{\left(n\right)}‖=\gamma $$으로 최댓값이 제한되어 있다고 가정하면 negative definite 값을 가져 다음과 같이 안정도를 만족한다.

4. 비특이성 고속 터미널 슬라이딩 모드 제어기

기존 슬라이딩 모드 제어기에서 발생하는 유한 시간 내 수렴하지 않는 문제점과 터미널 슬라이딩 모드 제어기에서 발생하는 평형점에서 멀리 떨어져 있을 때의 수렴 속도 문제점, 그리고 특이점으로 인해 수렴하지 않는 문제점을 보완하기 위하여 Delphin2 잠수정에 비특이성 고속 터미널 슬라이딩 모드 제어기를 적용하였다. 무인 잠수정에 적용한 NFTSMC를 설계하고 Lyapunov stability 분석을 통해 안정성을 검증한다.

5. 제어력 분배

Delphin2 잠수정은 Overactuated 시스템이다 (Tanakikorn, 2017). Overactuated 시스템이란 잠수정의 자유도보다 구동 장치의 개수가 더 많은 시스템을 말하며, Overactuated 시스템의 사용으로 다양한 방향으로 자유롭게 움직일 수 있으며, 정밀 제어가 가능하다. Delphin2 잠수정의 구동 장치는 후방의 주 프로펠러 추진기, 러더, 스턴, 중앙에 전·후방 수평 터널 추진기, 전·후방 수직 터널 추진기로 구성되어 있다. Delphin2와 같은 과잉 구동 시스템은 여러 추진기를 통해 힘과 모멘트를 생성한다. 이를 제어력 분배를 통해 각 추진기에 할당되는 힘을 최적화하여 전체 시스템의 에너지 효율을 높이고, 정밀한 운동 제어를 할 수 있다.

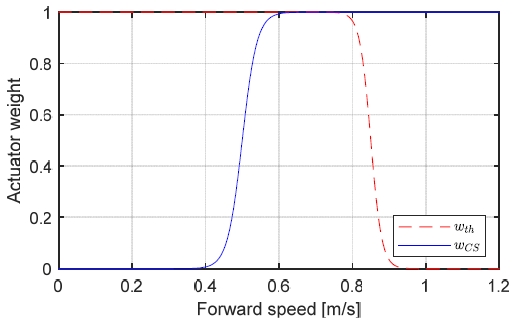
Delphin2 잠수정은 저속에서 러더나 스턴과 같은 조종 면을 사용해도 힘을 내지 못한다. 이를 해결하기 위해 천이 과정을 사용하는 추진기 가중치 함수를 적용하여 제어력을 분배한다. 이는 Fig. 5로 도식화하였으며, 전진 속도가 작을 때 추진기의 사용 비율이 높아지고, 전진 속도가 일정 값보다 커지게 되면 조종 면의 사용 비율이 높아진다. 가중치 함수는 식 (45), (46)과 같으며 식에 사용되는 가중치 변수는 $$ u_{th}^{\mathrm{*}}=0.85,{\sigma }_{th}^{\mathrm{*}}=0.03,u_{cs}^{\mathrm{*}}=0.5,{\sigma }_{cs}^{\mathrm{*}}=0.04$$으로 설정한다 (Tanakikorn, 2017).

Fig. 5

Actuator weighting function

5.1 수평면 제어

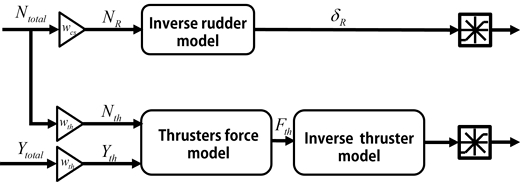
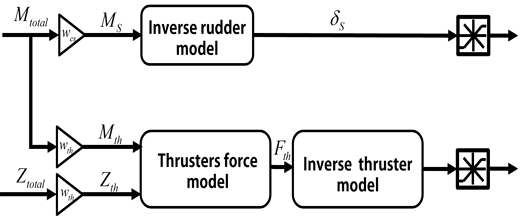
제어기를 통해 계산된 선수동요 모멘트와 좌우 동요 모멘트는 다음 식과 같이 가중치 함수가 곱해져 러더 선수동요 모멘트(N_R)와 추진기 선수동요 모멘트(N_th), 추진기 좌우 동요 힘(Y_th)으로 변환된다. 이후 추진기 모델에 대한 역 모델을 적용하여 러더 각도(δ_R)와 수평 터널 추진기 RPM(u_th)을 구하여 추진기 요구값을 결정한다(Fig. 6 참조).

$\[ N_R=w_{cs}{N}_{total } \]$

(47)

$\[ N_{th}=w_{th}{N}_{total } \]$

(48)

$\[ Y_{th}=w_{th}{Y}_{total } \]$

(49)

Fig. 6

Regarding the positive actuator demands for yawing moment

요구되는 러더 각도는 식 (50)와 같이 역 러더 모델을 이용하여 구한다. 전방 수평 터널 추진기 힘(F_th,hf)과 후방 수평 터널 추진기 힘(F_th,ha)은 식 (51)와 같이 추진기 힘 모델을 이용하여 구할 수 있다. 그 후 각 수평 터널 추진기의 요구 RPM은 식 (52)의 역 추진기 모델을 이용하여 구한다.

$\[ {\delta }_R=\frac{N_R}{N_{\left|u\right|u{\delta }_R}\left|u\right|u} \]$

(50)

$\[ \left[\begin{array}{c}{F}_{th,hf}\\ F_{th,ha}\end{array}\right]={\left[\begin{array}{cc}{L}_{hf}& L_{ha}\\ 1& 1\end{array}\right]}^{-1}\left[\begin{array}{c}{N}_{th}\\ Y_{th}\end{array}\right] \]$

(51)

$\[ u_{th}=\mathrm{s}\mathrm{i}\mathrm{g}\mathrm{n}\left(F_{th}\right)\sqrt{\frac{\left|F_{th}\right|}{L_h\rho D_{th}^4{K}_{T,th}}} \]$

(52)

5.2 심도 제어

깊이 제어도 수평면 제어와 동일한 방식으로 가중치 함수가 곱해져 스턴 종 동요 모멘트(M_S), 추진기 종 동요 모멘트(M_th), 추진기 상하동요 힘(Z_th)으로 변환된다. 이후 추진기 모델에 대한 역 모델을 적용하여 스턴 각도(δ_S)와 수직 터널 추진기 RPM(u_th)을 구하여 추진기 요구값을 결정한다(Fig. 7 참조).

$\[ M_S=w_{cs}{M}_{total} \]$

(53)

$\[ M_{th}=w_{th}{M}_{total} \]$

(54)

$\[ Z_{th}=w_{th}{Z}_{total} \]$

(55)

$\[ {\delta }_S=\frac{M_S}{M_{\left|u\right|u{\delta }_S}\left|u\right|u} \]$

(56)

$\[ \left[\begin{array}{c}{F}_{th,vf}\\ F_{th,va}\end{array}\right]={\left[\begin{array}{cc}{L}_{vf}& L_{vf}\\ 1& 1\end{array}\right]}^{-1}\left[\begin{array}{c}{M}_{th}\\ Z_{th}\end{array}\right] \]$

(57)

Fig. 7

Regarding the positive actuator demands for pitching moment

요구되는 스턴 각도는 식 (56)와 같이 역 스턴 모델을 이용하여 구한다. 전방 수평 터널 추진기 힘(F_th,vf)과 후방 수평 터널 추진기 힘(F_th,va)은 식 (57)와 같이 추진기 힘 모델을 이용하여 구할 수 있다. 구한 터널 추진기의 힘은 역 추진기 모델을 이용하여 각 수직 터널 추진기의 요구 RPM을 구한다.

6. 시뮬레이션 결과

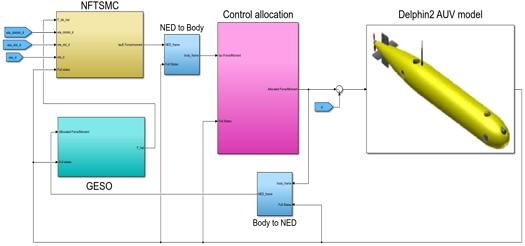
본 논문에서 제안된 제어기의 성능을 입증하기 위해 Delphin2 잠수정에 Table 4의 시뮬레이션 변수를 이용하여 MATLAB/Simulink 시뮬레이션을 수행하였다. 시뮬레이션의 MATLAB Simulink 블록 다이어그램 프로그램은 Fig. 8과 같다.

Table 4

Parameters of the simulation

Fig. 8

Simulation program using MATLAB-Simulink

선체 고정 좌표계에서 Delphin2 AUV MATLAB-Simulink model을 구성하였고, 지구 고정 좌표계에서 NFTSMC 제어기와 GESO를 이용한 외란 관측기를 개발하였다. 제어 목표값과 외란 관측기로 추정된 외란을 입력받아 제어기를 통해 계산된 힘과 모멘트는 식 (2)을 통한 좌표계 변환 과정을 거쳐 선체 고정 좌표계 형태로 입력되어 제어력 분배 과정을 거쳐 Delphin2 잠수정에 제어입력을 주게 된다.

제어기의 강인성을 검증하기 위해 강체의 질량과 관성, 유체력과 같은 계수 값들은 ±30%의 오차 범위로 설정하였으며 100s까지 η_d = [x_d, y_d, z_d, ϕ_d, θ_d, ψ_d]를 추종하도록 시뮬레이션을 진행하였다.

외란은 다양한 대역 대의 외란이 합쳐진 형태로 다음과 같은 값의 외란을 가해주었으며 시뮬레이션 중에는 외란이 지속적으로 가해진다고 가정하였다.

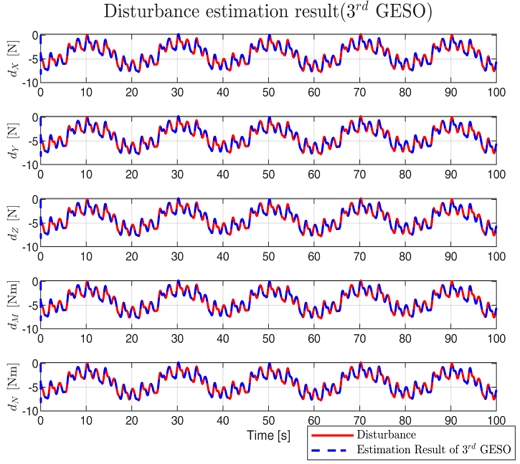
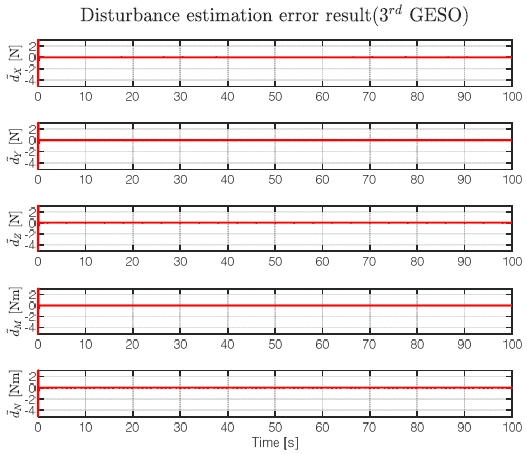
Fig. 9는 3^rd GESO를 통하여 외란을 추정한 결과 그래프이다. 빨간색 그래프가 가해지는 외란이며, 파란색 그래프가 3^rd GESO를 통해 추정한 외란이다. 다양한 대역 대의 외란을 Fig. 10과 같이 빠르게 추정하여 추정 오차는 0으로 수렴함을 나타내었다.

Fig. 9

True disturbance(red line) and estimated of 3rd GESO(blue line)

Fig. 10

Result of disturbance estimation error(3rd GESO)

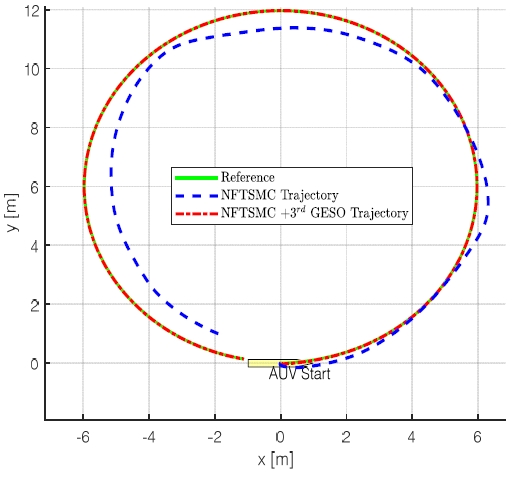
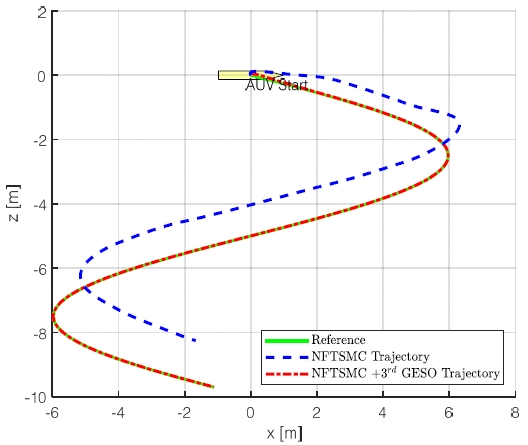
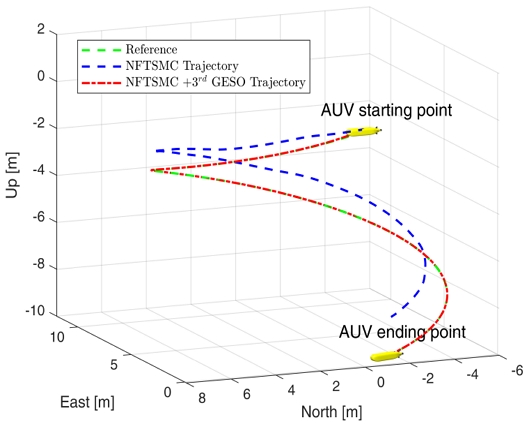
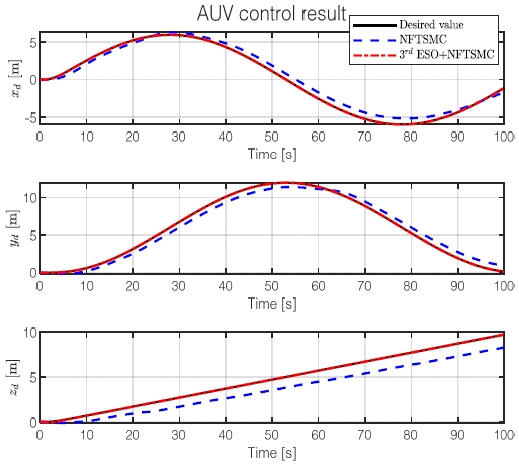
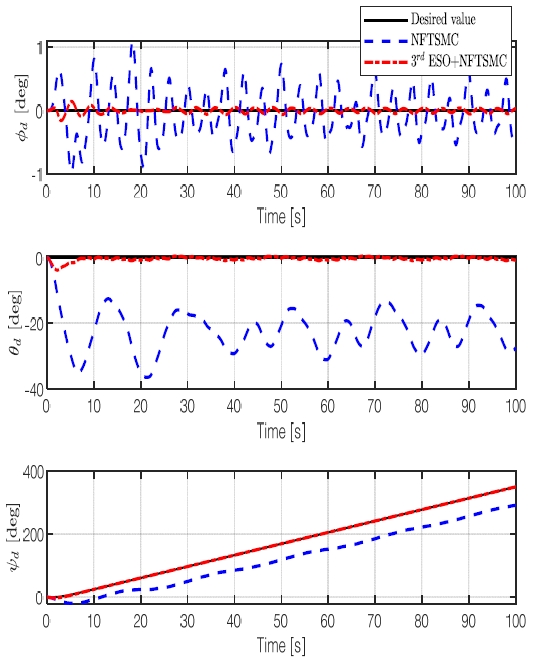
제안된 제어기의 성능을 검증하기 위하여 NFTSMC만 사용한 모델과 3^rd GESO를 적용한 NFTSMC의 위치와 자세의 제어 결과를 비교하였다. Fig. 11에서는 x, y 평면, Fig. 12에서는 x, z 평면, Fig. 13에서는 3차원 공간에서의 Delphin2 잠수정 모델의 궤적과 도착점의 방위각을 표현하였다. 또한 Fig. 14을 통해 시간에 따른 x, y, z, θ, ψ의 제어 결괏값을 비교하였다.

Fig. 11

Trajectory tracking curves in x-y plane by NFTSMC vs NFTSMC+3rd GESO

Fig. 12

Trajectory tracking curves in x-z plane by NFTSMC vs NFTSMC+3rd GESO

Fig. 13

Trajectory tracking curves in 3D space by NFTSMC vs NFTSMC+3rd GESO

Fig. 14

Comparison plot of x, y, z control by NFTSMC vs NFTSMC+3rd GESO

Fig. 15

Comparison plot of θ, ψ control by NFTSMC vs NFTSMC+3rd GESO

그 결과 NFTSMC만을 사용하였을 경우 제어 목표값을 추종하지 못하고 오차가 크게 발생하지만 3차 GESO를 적용한 NFTSMC는 제어 목표값을 잘 추종하는 것을 확인하였다. 이를 제어 오차값의 제곱 평균 제곱근(root mean square error, RMSE)을 구하여 오차값의 차이를 비교하였다. 그 결과 Table 5와 같이 NFTSMC와 3차 GESO를 사용한 제어기가 NFTSMC만을 사용한 제어기보다 오차가 최대 약 163배 이상 감소한 것을 확인하였다.

Table 5

Performance measures using RMSE for NFTSMC and NFTSMC+3rd GESO

7. 결 론

무인 잠수정이 수중에서 목표 작업을 성공적으로 수행하려면 모델의 불확실성이나 강한 조류와 같은 외란을 극복하고 목표 위치와 자세를 유지할 수 있는 견고한 제어 성능을 갖춘 제어기가 필수적이다. 본 연구에서는 외란에 강인한 성능을 가진 NFTSMC와 NFTSMC의 한계를 보완 해줄 3^rd GESO를 설계하여 무인 잠수정이 외란을 보상하여 제어를 수행하도록 하였다. 이를 시뮬레이션을 통하여 알고리즘의 유효성을 검증하였다. 향후 무인 잠수정 제어를 Hardware In the Loop Simulation (HILS)로 검증하기 위해 임베디드 보드로 제어기를 구성하고 동역학 모델을 리얼 타임 하드웨어인 Speedgoat에 빌드하여 제어기의 성능을 실증할 것이다.

Table 6

6-DOF AUV parameter

Acknowledgments

이 연구는 2024년 정부(방위사업청)의 재원으로 국방과학 연구소의 지원을 받아 수행된 미래 도전 국방 기술 연구 개발 사업임(No. 915071101).

References

• Fossen, T.I., 1994. Guidance and Control of Ocean Vehicles. A John Wiley & Sons Ltd: USA.
• Fossen, T.I., 2011. Handbook of marine craft hydrodynamics and motion control. A John Wiley & Sons Ltd: USA. [https://doi.org/10.1002/9781119994138]
• Han, J., 2009. From PID to active disturbance rejection control. IEEE transactions on Industrial Electronics, 56(3), 900-906. [https://doi.org/10.1109/TIE.2008.2011621]
• Ji, S.B., Yoo S.J., and Youn W.K., 2024. Autonomous underwater vehicle control using a nonlinear disturbance observer based sliding mode controller. Journal of the Society of Naval Architects of Korea, 61(4), pp.216-225. [https://doi.org/10.3744/SNAK.2024.61.4.216]
• Kim, J., Joe, H., Yu, S.C., Lee, J.S. and Kim, M., 2015. Time-delay controller design for position control of autonomous underwater vehicle under disturbances. IEEE Transactions on Industrial Electronics, 63(2), pp.1052-1061. [https://doi.org/10.1109/TIE.2015.2477270]
• Madoński, R., and Herman, P., 2015. Survey on methods of increasing the efficiency of extended state disturbance observers. ISA transactions, 56, pp.18-27. [https://doi.org/10.1016/j.isatra.2014.11.008]
• Patre, B.M., Londhe, P.S., Waghmare, L.M. and Mohan, S., 2018. Disturbance estimator based non-singular fast fuzzy terminal sliding mode control of an autonomous underwater vehicle. Ocean Engineering, 159, pp.372-387. [https://doi.org/10.1016/j.oceaneng.2018.03.082]
• Roy, S., Nandy, S., Shome, S.N. and Ray, R., 2013. Robust position control of an autonomous underwater vehicle: a comparative study. IEEE International Conference on Automation Science and Engineering, pp.1002-1007. [https://doi.org/10.1109/CoASE.2013.6653951]
• Sahoo, A., Dwivedy, S.K. and Robi, P.S., 2019 Advancements in the field of autonomous underwater vehicle. Ocean Engineering, 181, pp.145-160. [https://doi.org/10.1016/j.oceaneng.2019.04.011]
• Tanakitkorn, K., 2017. Guidance, control and path planning for autonomous underwater vehicles. Ph.D. Southampton.
• Tanakitkorn, K., Wilson, P.A., Turnock, S.R. and Phillips, A.B., 2017. Sliding mode heading control of an overactuated, hover-capable autonomous underwater vehicle with experimental verification. Journal of Field Robotics, 35(3), pp.395-415. [https://doi.org/10.1002/rob.21766]
• Utkin, V., 1977. Variable structure systems with sliding modes. IEEE Transactions on Automatic control, 22(2), pp.212-222. [https://doi.org/10.1109/TAC.1977.1101446]
• Shi, D., Wu, Z. and Chou, W., 2018. Generalized extended state observer based high precision attitude control of quadrotor vehicles subject to wind disturbance. IEEE Access, 6, 32349-32359. [https://doi.org/10.1109/ACCESS.2018.2842198]
• Yu, X., and Man, Z., 1996. Model reference adaptive control systems with terminal sliding modes. International Journal of Control, 64(6), pp.1165-1176. [https://doi.org/10.1080/00207179608921680]