Unet 기반 인공지능 모델을 활용한 잠수함의 표면 압력 분포 예측

1. 서 론

잠수함의 선형은 함수 부와 함미 부의 형상뿐만 아니라 상부 케이싱과 세일, 그리고 제어판의 형상 등 다양한 구성요소를 가지고 있어 최적화의 대상이 되는 파라메터의 수가 많다. 한편, 잠수함은 저항 추진 성능과 운동 조종 성능 등 기동 성능뿐만 아니라 표적강도와 유동소음 등으로 대표되는 피탐 성능 또한 그 최적화의 대상이 된다. 따라서 잠수함의 선형 설계는 고도화된 유동 해석을 포함한 다목적 최적화의 대표적인 예시라고 할 수 있다.

잠수함 주변의 유동을 실험적으로 관측하고 해석하는 연구는 여러 가지 선형에 대하여 수행되어 왔다. 잠수함의 수식 선형으로 공개된 DARPA SUBOFF (Groves et al., 1989)는 대상 선형으로서 가장 활발하게 활용되어 왔다. Crook et al. (1990)은 DARPA SUBOFF에 대하여 함교, 선미 부가물, 그리고 Ring wing의 설치 여부에 따른 저항 실험을 수행하고 그 결과를 비교하였다. Liu and Huang (1998)은 풍동 실험을 수행하여 반류 분포와 경계층내의 속도 분포 등을 계측하고 부가물의 부착 여부에 따른 표면 압력과 저항을 계측하였다. SUBOFF의 자항 성능에 대한 연구는 대부분 INSEAN에서 개발한 E1619 프로펠러를 사용하여 수행되어 왔으며 실험적 연구는 Özden et al. (2019)에 의하여 최초로 수행되었다. Roddy (1990)는 SUBOFF 함형에 대한 PMM(Planar motion mechanism) 실험을 수행하여 부가물이 모두 설치된 SUBOFF 잠수함이 수평면과 수직면 운동 중 불안정성을 가지고 있음을 확인하였다. Park et al. (2017)은 큰 입사각을 가지는 경우에 대한 운동 조종 모델을 개발하기 위하여 예인 수조 및 풍동 실험을 수행하였다. 한편 Park and Seok (2023)은 PPM 실험에서 필수적으로 설치되는 스트럿이 사항 조건에서 잠수함에 주는 영향을 면밀히 관찰하기 위하여 CFD(Computational Fluid Dynamics)를 활용한 연구를 수행하였다.

CFD를 활용하여 잠수함의 저항 추진 및 운동 조종 성능을 예측하는 연구 또한 오랜 기간 수행되어 왔다. Yang and Lohner (2003)은 선미 부가물이 없는 SUBOFF 주변의 유동을 비 정렬 격자에 대한 RANS(Reynolds averaged Navier Stokes)방정식으로 해석하여 실험과 높은 일치를 보임을 확인하였으며, 받음각 조건에 따라 해석을 수행하고 가시화된 유동장을 분석하였다. Chase (2012)는 RANS, DES(Detached eddy simulation), 그리고 DDES(Delayed detached eddy simulation) 기법을 사용하여 부가물이 설치된 SUBOFF에 대한 저항 해석을 수행하였으며 E1619를 대상 프로펠러로 하여 POW 해석 및 자항 해석을 수행하였다. 그 결과 저항의 경우 대체로 실험 결과와 높은 일치성을 보임을 확인하였으나 부가물에 의해 생성된 난류 유동을 다소 크게 예측하는 경향이 있음을 확인하였다. 한편, Cho et al. (2020)은 X 타를 가지는 BB2에 대하여 CFD 기반 구속 모형 실험을 수행하고 MMG(Mathematical modeling group) 모델을 구성하였다. 이후 동일한 조건에서 시뮬레이션된 잠수체의 궤적과 자유 항주 실험 결과를 비교하여 높은 일치를 보임을 확인하였다.

잠수함과 수상함의 함형을 최적화 하기위한 SBD(Simulation based design)는 일반적으로 함형의 자동 변형 기법, 유동 해석 기법, 그리고 최적화 알고리즘을 포함하고 있다. 한편, 설계 파라메터와 CFD 연산량의 증가는 SBD를 어렵게 하는 가장 큰 원인이 되며 함형 최적화에 관한 최신의 연구에서는 차원 축소(dimensionality reduction) 기법이나 예측 모델(surrogate model), 그리고 실험계획법(Design of experiments)을 활용하여 이 문제를 해결하고 있다.

차원 축소 기법의 경우 설계 공간에 대한 차원 축소를 수행하여 효율을 높이거나 CFD 해석 속도를 가속화하는 방식으로 다양한 연구가 진행되어 왔다. Diez et al. (2015)은 KLE(Karhunen–Loeve Expansion)를 이용하여 설계 변수를 95%가량 줄임으로서 더 효율적인 SBD가 가능함을 보여주었다. Demo et al. (2018) 은 고차원 시계열 데이터의 차원 축소에 적합한 DMD(Dynamic Mode Decomposition)을 활용하여 유동 해석의 초기 단계에서 얻은 유동장 데이터만을 이용하여 충분히 수렴된 상태의 유동장을 높은 정확도로 예측할 수 있음을 보였으며, AS(Active Subspace)를 활용하여 매개 변수 공간의 크기를 획기적으로 줄일 수 있음을 보여주었다.

한편, 예측 모델의 경우 최적화 알고리즘에서 시뮬레이션 직접 수행하는 경우 소요되는 시간이 비현실적으로 커지는 문제를 해결하기 위하여 많은 연구에서 사용해 왔다. Chen et al. (2022) 은 잠수함의 저항 및 조종 성능의 최적화를 MOCPSO(Multi-Objective Constrained PSO) 알고리즘을 기반으로 수행하였으며 CFD 해석 결과를 근사하여 대체하기 위하여 Kriging model을 활용하였다. Luo et al. (2021) 은 SA(Simulated Annealing)를 기반으로 SUBOFF 함형을 최적화 하였으며 RBF(Radial Basis Function)를 기반으로 한 동적 예측 모델을 활용하여 CFD 해석을 대체하였다. 한편, Mai et al. (2023)은 CFD를 활용하여 BB2 잠수함의 설계 변수(세장비, 세일의 길이 방향 위치, 세일 높이)의 변화에 따른 유체력 미계수를 계산하고 이를 기반으로 한 실험식을 제안하였다.

실험계획법을 활용한 잠수함의 최적 설계는 더 적은 개수의 함형을 생성하여 SBD의 효율을 높일 수 있어 잠수함 설계에서도 활용되고 있다. Wu et al. (2020)은 다구치 실험계획법을 활용하여 세일과 조종면의 형태를 최적화하는 연구를 수행하였다.

오늘날 인공지능을 활용한 연구는 분야를 가리지 않고 점점 더 늘어나고 있으며 Wang and Wang (2021)은 그 주요 원인으로서 (1) 하드웨어의 발전, (2) 방대한 데이터 생성, (3) 특정 분야에서 AI 알고리즘의 높은 정확도, 그리고 (4) AI의 일반화 능력을 제시하였다. 인공지능을 활용한 선박의 성능 예측이나 최적화에 대한 몇몇 연구가 수행되어 왔으며 특히 대부분의 연구는 저항 계수와 같은 적분 변수형 유동 성능 지표를 예측하는 모델로서 인공지능을 활용하였다. Ai-gui and Jia-wei (2009)는 선형 매개변수를 입력받아 저항 계수를 예측하는 인공 신경망 모델을 제시하였으며, Zhang et al. (2021)은 인공 신경망을 기반으로 한 네 가지 예측 모델을 비교하고 DBN(Deep Belief Network)을 사용하여 Wigley 선형의 조파 저항을 최적화하였다.

한편, 배열 형태 데이터 학습에 적합한 CNN(Convolution Neural Network)을 활용하여 성능 변수가 아닌 유동장의 모습을 직접 예측하기 위한 다양한 연구가 수행되어 왔다. 특히 Unet (Ronneberger et al., 2015)은 합성곱 신경망과 역 합성곱 신경망을 순차적이고 대칭적으로 배열한 인공신경망으로 정렬 격자형 데이터의 입출력에 적합하여 유동 해석 결과를 예측하는 연구에 활용되어 왔다. Thuerey et al. (2020) 은 2차원 날개 주변에 대한 유동장을 예측에 Unet을 활용하였으며 유속과 압력분포에 대하여 높은 예측 정확도를 보여주었다. Zhu et al. (2024)는 어텐션 구조를 추가한 Unet을 도입 함으로써 유동장 예측에 중요한 날개의 형상적 특성에 더욱 민감하게 반응하도록 하여 날개 주변 유동장에 대한 예측정확도를 높였다. 또한 Zuo et al. (2024)은 익형 주변 유동에 대한 학습 정확도 향상을 위하여 CBAM (Convolutional Block Attention Module)을 추가한 Unet을 활용하여 익형 주변 유동을 학습하였다. Hou et al. (2022)은 시계열 데이터 해석에 적합한 LSTM(Long Short-Term Memory) 과 Unet을 결합하여 직진 가속 운동하는 SUBOFF 주변 유동장에 대한 스냅샷 데이터를 예측하였다.

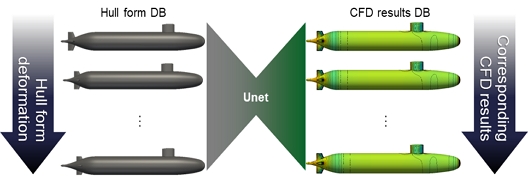
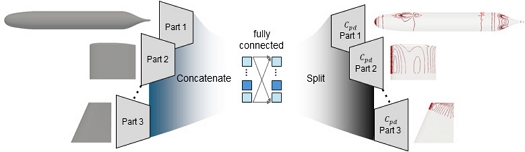
잠수함 주변의 유동장을 직접 예측하는 인공지능 연구는 함형의 변화가 주변 유동장에 미치는 영향을 높은 정확도로 예측하여 잠수함의 표면 압력의 변화나 부가물에 의해 생성된 와류 구조를 분석하는 방식으로 활용할 수 있을 것으로 기대되나, 전술한 연구의 경우 대부분 익형 주변의 유동장 학습에 국한되어 있거나 학습 데이터가 스냅샷에 국한되어 있기 때문에 공학적인 목적의 응용이 어려울 것으로 판단된다. 본 연구에서는 이러한 어려움을 극복하기 위하여 SUBOFF의 3차원 격자 데이터와 유동장 데이터의 3차원 구조를 그대로 유지하며 학습에 적합하도록 전처리 하는 기법을 제시하였다. 이후 행렬형 데이터의 입출력에 적합한 Unet을 활용하여 함형의 변화에 따른 표면 압력 변화를 학습하고 그 결과를 분석하였다(Fig. 1).

Fig. 1

The schematic image of overall structure of Unet based pressure distribution prediction system

2. 본 론

2.1 함형 변형 기법을 활용한 함형 데이터 구축

학습에 사용할 함형 데이터 세트는 DARPA SUBOFF 함형을 변형하여 생성하였다. 먼저 기본 함형이 되는 SUBOFF는 Groves et al. (1989)에서 공개한 수식을 만족하는 STL(stereolithrography) 형식의 정렬 격자로 출력하도록 하였다(Fig. 2). 이때 SUBOFF 함형은 축대칭형 선형, 세일, 그리고 선미 부가물의 크게 세 개의 파트로 구성되며 각 곡면을 표현하는 매개변수 방향별 노드의 숫자는 형상의 표현에 충분한 개수가 되도록 지정하였다(Table 1). 이는 행렬형 데이터로 정리하였다. 예를 들어 하나의 축 대칭 선체는 (128×128×3)의 크기를 가지는 행렬로 표현하였으며, 행렬의 첫 번째 열과 마지막 열은 Fig. 2a의 붉은색 곡선으로 표시한 잠수함 상부 12시 방향의 곡선 위의 점이 되도록 전처리하였다. 이때 CNN에 삽입되는 데이터의 차원 표현은 일반적으로 폭(width), 높이(height), 그리고 채널(channel)로 표현하며 본 논문에서 마지막 차원은 각 노드의 3-D 공간에서의 좌표를 표현하기 위해 필요한 숫자의 개수로서 세 가지 채널(channel) 데이터로 준비하였다.

Fig. 2

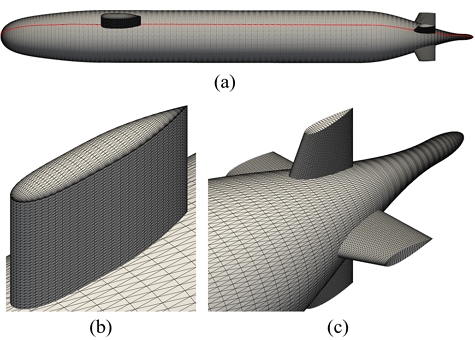
Structured grid for DARPA SUBOFF 5475 model(a: overall view; b: sail; c: afterbody and stern appendages)

Table 1

Size of grid for each part

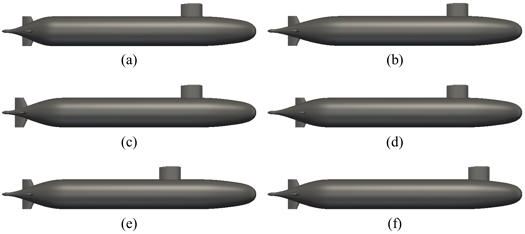
선형을 변형하기 위하여 총 세 가지 선형 변환 기법을 적용하였으며 순서대로 선미부의 배수량 분포, 세일의 길이 방향 위치 변화, 그리고 선미 부가물의 길이 방향 위치 변화를 수행하였다. 먼저 선미부의 배수량 분포는 선미 수선(X_AP)과 중앙 평행 부의 시작 지점(X_PP) 사이에서 단면의 길이 방향 이동량(ΔX)을 길이 방향 위치에 대한 4차 다항식으로 정의하여 변형을 수행하였다(Eq 1). 이때 Eq 1은 X_AP와 X_PP에서 변형량과 기울기가 0이 되고 그 중심에서 ΔX_max가 되도록 다항식의 계수를 결정하였으며, 이때 변형의 매개변수가 되는 ΔX_max는 단면의 길이 방향 이동량의 최댓값을 의미한다. 한편, 세일의 길이 방향 위치나 선미 부가물의 길이 방향 위치는 모두 기존의 격자를 길이 방향으로 평행 이동하여 변형을 수행하였으며 세 가지 변형에 대한 변형량의 범위는 Table 2에 기술하였다. 이때 세일의 길이 방향 최대 변형량(ΔX_S)은 세일의 길이(L_sail)와 동일하며 선미 부가물의 길이 방향 변형량(ΔX_A)은 Groves et al. (1989)에 주어진 선미 부가물의 세 가지 부착 위치를 참조하여 그 최대값을 결정하였다. 각 변형에 대해 가장 극단적인 변형 예시는 Fig. 3에 도시하였으며 각 변형은 변형 범위 내에서 일정한 간격으로 네 번씩 중복을 허용하여 변형함으로써 총 64개의 함형 데이터를 제작하였다.

$\[ \Delta X=\frac{16\Delta X_{\text{max}}}{{\left(X_{AP}-X_{PP}\right)}^4}{\left(X-X_{AP}\right)}^2{\left(X-X_{PP}\right)}^2 \]$

(1)

Table 2

Deformation range for each variation method

Fig. 3

Hull form variation examples for each deformation (the largest deformed cases for a, b: afterbody slenderness; c, d: stern appendages longitudinal position; e, f: sail longitudinal position)

2.2 전산 유체 해석을 통한 유동장 데이터 구축

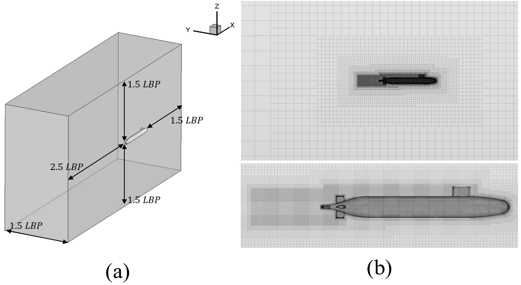
2.1절에서 제작된 함형들에 대하여 학습 데이터로 사용될 점성 유동에 의한 표면 압력 분포를 확보하기 위하여 Starccm+(Siemens dgital industries software, 2020)를 활용하여 CFD 해석을 수행하였다. 대상 잠수함의 형태가 온전히 좌우 대칭이기 때문에 해석에 소요되는 시간을 줄이기 위하여 대칭 경계 조건을 포함한 좌현 영역을 계산 영역으로 구성하였으며 해석 격자 모습은 Fig. 4와 같다. 난류 모델은 RSM(Reynolds Stress Model)로 선정하여 RANS 방정식을 풀었으며, 잠수함 벽면 경계층 해석의 정도를 높이기 위해 prism layer 격자를 사용하고 그 첫 번째 격자의 무차원 거리 y+는 60수준을 가지도록 하였다. 이때 Crook (1990)의 저항 실험 결과와 CFD 해석 결과를 비교하여 검증을 수행하였으며 12knots의 선속에서 총저항 기준 0.7% 수준의 차이를 보임을 확인하였다.

Fig. 4

Size of CFD domain and mesh distribution around submarine model

해석을 완료된 표면 압력 데이터는 이후 인공 신경망의 입력 데이터가 되는 선체 표면 격자의 노드에서 다시 내삽하여 구한 후 행렬의 형태로 정리하였다. 이때 내삽 기법으로 가우시안 커널 보간법을 활용하였으며 함체를 이루는 각 부분에 대하여 Table 1과 동일한 가로 세로 크기를 가지는 채널 1의 행렬로 표면 압력 데이터를 전처리 하였다.

2.3 Unet기반 압력 분포 예측 모델 구축 및 학습

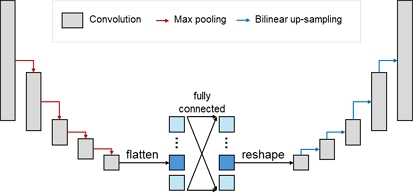
Unet은 고차원의 행렬 데이터의 입출력에 우수한 성능을 보여준다. 특히 배열 데이터가 가지고 있는 공간적 특성을 합성곱 신경망을 바탕으로 추출하고 비선형성이 큰 데이터 패턴을 분석한 후 그에 알맞은 정답 데이터를 다시 생성하기 위하여 Fig. 5의 기본 구조를 가진다. 데이터 흐름의 순서대로 구조와 목적을 상술하면 다음과 같다. 1) 합성곱(convolution) 및 풀링(max pooling) 층에서는 데이터의 공간적 특성을 추출하고 해상도를 낮춤으로써 데이터에 내제된 특성을 낮은 차원의 배열 데이터, 즉 특성맵으로 변환한다. 2) 완전 연결 신경망에서는 특성맵을 1차원 배열로 변형(flatten)하여 모든 노드가 연결된 완전 연결 인공 신경망(fully connected)으로 전달하며 특성치에 내재된 정보를 바탕으로 더욱 복잡한 패턴을 찾을 수 있도록 한다. 3) 역 합성곱 및 업샘플링 층에서는 축소된 차원을 본래의 차원으로 회복시킴과 동시에 합성곱 연산을 수행하여 고차원 데이터의 변화를 예측할 수 있도록 한다. 이때 기존의 특성맵의 차원으로 재배열(reshape)한 데이터의 해상도를 복원하기 위하여 이중 선형 업샘플링(bilinear up-sampling)을 사용하였다.

Fig. 5

Overall structure of Unet

한편, 본 연구에서는 함체의 형상 데이터가 여러 파트로 구성되어 있음을 고려하여 파트별로 전술한 과정을 수행하되 그 사이에서 발생하는 상호 작용을 예측할 수 있도록 하기 위하여 Fig. 6과 같이 병렬적 구조의 특성 추출 이후 각 특성맵을 연쇄적으로 연결한 구조의 Unet을 적용하였다. 각 파트는 총 5번의 합성곱 연산을 거치며 특성이 추출되며 각 합성곱 연산이 끝난 후 인코더의 경우 풀링을 디코더의 경우에는 업샘플링을 수행하도록 하였다. 이때 인코더 필터의 크기와 개수는 모든 파트에 대하여 (3×3) 크기를 가지는 필터 16개를 적용하였으며 디코더의 경우 인코더와 대칭적인 구조를 가지되 가장 마지막 층에서는 각 노드 별로 동압에 대한 압력계수(C_pd) 값이 하나씩 할당됨으로 하나의 필터를 가지는 합성곱 연산을 추가하였다.

Fig. 6

Overall structure of Unet based pressure distribution prediction network extracting features from multi-part data

2.4 표면 압력 및 저항 계수 예측 결과

학습이 완료된 신경망을 활용한 압력분포의 예측 정확도 평가는 정성적인 방법과 정량적인 방법으로 수행하였다. 우선 예측된 압력 분포의 형태적 유사성을 정성적으로 평가하기 위하여 학습데이터에 대하여 각 파트에 따라 재건된 압력 분포와 정답 데이터로 사용된 압력분포의 컨투어를 비교하였다. 한편, 64개의 데이터 중 5개의 데이터는 테스트 데이터로 구별하여 사용하였다.

학습에 사용된 데이터에 대한 축 대칭 몸체에 대한 표면 압력 분포의 비교는 Fig. 7과 같았으며, 전반적으로 압력의 분포가 높은 수준으로 일치하는 것을 확인할 수 있었다. 특히 세일과 선미 부가물의 부착 위치가 변화함에 따른 국소적인 변화를 높은 수준으로 재건할 수 있었다. 또한 선미부의 비대도 증감에 따라 발생하는 선미부 전반에 걸친 압력 변화 또한 잘 예측할 수 있음을 확인하였다. 그러나 재건된 압력분포의 경우 전반적으로 노이즈가 발생함을 확인할 수 있었으며 특히 몸체의 상부 12시 방향에서 그 노이즈가 더 심하게 발생하는 경향이 있었다. 한편, 세일과 부가물에 대한 표면 압력 분포는 Fig. 8과 같았으며 몸체에 비하여 예측 정확도가 높고 노이즈는 작음을 확인할 수 있었다. 이는 몸체에 비하여 상대적으로 형태적 변화에 따른 압력 분포의 변화가 적기 때문으로 사료된다.

Fig. 7

Comparison of pressure distribution of ground truth and prediction for axisymmetric body (black: CFD; red: AI; a: overall view; b: enlarged)

Fig. 8

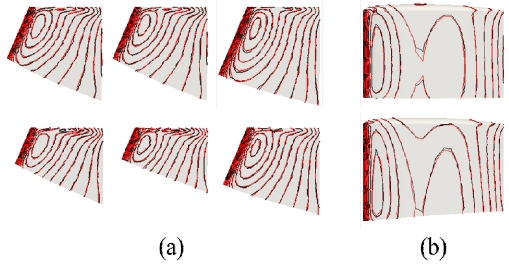
Comparison of pressure distribution of ground truth and prediction for sail and stern appendages (black: CFD; red: AI

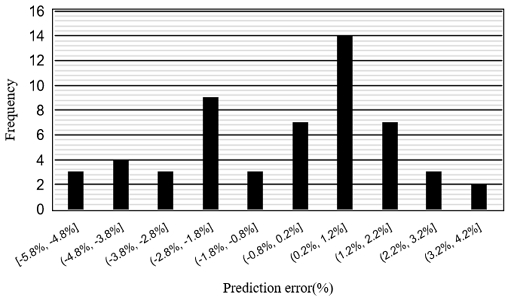
정량적인 재건 성능의 비교를 위하여 예측된 압력분포를 적분하여 총저항 계수를 비교하였으며 Fig. 7에 도시된 함형에 대한 총 저항 계수는 Table 3에 표기하였다. 이때 예측된 압력 분포만으로는 총저항을 예측할 수 없으므로 마찰저항의 경우 Schoenherr 곡선으로부터 그 값을 추정하여 계산하였다. 이후 학습 데이터에 전체에 대한 전 저항 오차를 분석하기 위하여 오차 범위에 따른 빈도수를 히스토그램으로 표현하였다(Fig. 9). 그 결과 학습 데이터에 대한 예측 오차는 [+3%,-3%] 수준에서 대부분 분포함을 확인하였으며, 절대 오차에 대한 평균치는 2.0%임을 확인하였다. 한편, 함형 변화에 따른 예측 오차 경향을 분석하기 위하여 변형의 종류별로 변형량에 따른 평균 예측 오차를 비교하였다(Table 4). 그 결과 다른 변형에 비하여 선미 부가물의 길이 방향 변화에 따른 예측 오차가 큰 것을 확인하였으며 선미 부가물과 선미 선형의 상호 작용에 따른 압력 분포 비선형적 변화는 상대적으로 예측하기 어려움을 확인할 수 있었다.

Table 3

Resistance coefficient prediction results for example hull forms in training data

Fig. 9

Histogram of reconstruction error for total resistance coefficient of training data set

Table 4

Comparison of mean prediction errors at different deformation stages

Table 5

Prediction results of total resistance for test data

추가로, 5개의 테스트 데이터에 대한 압력 분포 예측을 수행하여 총저항을 확인한 결과 평균적으로 –8.51% 수준의 예측정확도를 보여주었다. 또한 전 케이스에 대한 오차가 음의 값으로 편향되어 있음을 확인하였다. 이는 학습에 사용한 데이터의 숫자가 충분하지 않아 테스트 오차가 학습 오차보다 비교적 크게 산정되는 것으로 사료된다.

3. 결 론

본 연구는 잠수함의 형태 변화에 따른 표면 압력 변화를 예측하기 위하여 Unet의 구조를 기반으로 한 인공 신경망 모델을 제안하였다. 학습 데이터는 행렬의 형태로 전처리한 잠수함의 정렬 격자 데이터와 각 노드 지점에서 압력계수를 사용하였으며, 축 대칭형 몸체와 기타 부가물들의 형상을 병렬적으로 특성추출 할 수 있도록 구역별 특성맵을 연쇄적으로 이어 붙여 사용하는 Unet 구조를 사용하였다.

그 결과 예측된 압력분포는 CFD 해석 결과와 높은 수준으로 일치함을 확인할 수 있었으며, 적분한 압력분포와 경험식으로부터 구한 마찰저항 계수를 합하여 구한 총저항계수를 비교한 결과에서도 평균 2.0% 수준의 오차를 보임을 확인할 수 있었다. 그러나, 인공 신경망에 의하여 예측된 압력분포의 경우 다소 큰 노이즈를 가지고 있음을 확인하였으며, 3차원 형상을 2차원 행렬의 형태로 전처리하는 과정에서 발생한 불연속 지점, 즉 잠수함의 상부 12시 방향에서 그 노이즈가 심화됨을 확인할 수 있었다. 이는 학습 데이터의 크기를 키우고 합성곱 연산의 패딩을 전처리 과정 및 원본 데이터에 어울리도록 수정함으로써 개선할 수 있을 것으로 사료된다.

한편, 변형의 종류에 따라 평균 예측 오차를 비교한 결과 선미 부가물의 위치에 따른 예측 오차가 상대적으로 큰 것을 확인할 수 있었다. 이는 선미 형태와 부가물 위치의 복합적인 변화에 따른 압력의 비선형적 거동을 정밀하게 예측하지 못하여 발생한 것으로 사료되며, 구역별 특성 정보가 교환되는 연쇄적 연결 구조가 가진 한계와 학습 데이터의 부족이 주요 원인으로 사료된다.

Acknowledgments

이 과제는 부산대학교 기본연구지원사업(2년)과 2023년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 지자체-대학 협력기반 지역혁신 사업 (2023RIS-007) 의 결과입니다.

References

• Ai-guo, C. and Jia-wei, Y. 2009. Research on the genetic neural network for the computation of ship resistance. In 2009 International Conference on Computational Intelligence and Natural Computing, IEEE, Vol. 1, pp.366-369. [https://doi.org/10.1109/CINC.2009.34]
• Chase, N., 2012. Simulations of the DARPA Suboff submarine including self-propulsion with the E 1619 propeller. M.S. thesis. Iowa: The University of Iowa.
• Chen, G., Wu, J. and Wan, D. 2022. Optimization of submarine resistance and manoeuvrability based on SBD technique. In ISOPE International Ocean and Polar Engineering Conference, pp.ISOPE-I
• Cho, Y.J., Seok, W., Cheon, K.H. and Rhee, S.H. 2020. Maneuvering simulation of an X-plane submarine using computational fluid dynamics. International Journal of Naval Architecture and Ocean Engineering, 12, pp.843-855. [https://doi.org/10.1016/j.ijnaoe.2020.10.001]
• Crook, B. 1990. Resistance for DARPA SUBOFF as represented by model 5470. David Taylor Research Center, Bethesda, Md.
• Demo, N., Tezzele, M., Mola, A. and Rozza, G. 2018. An efficient shape parametrisation by free-form deformation enhanced by active subspace for hull hydrodynamic ship design problems in open source environment. In ISOPE International Ocean and Polar Engineering Conference, pp. ISOPE-I.
• Diez, M., Campana, E. F. and Stern, F. 2015. Design- space dimensionality reduction in shape optimization by Karhunen–Loève expansion. Computer Methods in Applied Mechanics and Engineering, 283, 1525-1544. [https://doi.org/10.1016/j.cma.2014.10.042]
• Groves, N.C., Huang, T.T. and Chang, M.S. 1989. Geometric characteristics of DARPA SUBOFF models (DTRC Model Nos. 5470 and 5471). David Taylor Research Center.
• Hou, Y., Li, H., Chen, H., Wei, W., Wang, J. and Huang, Y. 2022. A novel deep U-Net-LSTM framework for time-s equenced hydrodynamics prediction of the SUBOFF AFF-8. Engineering Applications of Computational Fluid Mechanics, 16(1), pp.630-645. [https://doi.org/10.1080/19942060.2022.2030802]
• Liu, H.L. and Huang, T.T. 1998. Summary of DARPA SUBOFF experimental program data. [https://doi.org/10.21236/ADA359226]
• Luo, W., Guo, X., Dai, J. and Rao, T. 2021. Hull optimization of an underwater vehicle based on dynamic surrogate model. Ocean Engineering, 230, 109050. [https://doi.org/10.1016/j.oceaneng.2021.109050]
• Mai, T. L., Jeon, M., Vo, A. K., Yoon, H. K., Kim, S. and Lee, J. 2023. Establishment of empirical formulae for hydrodynamic derivatives of submarine considering design parameters. International Journal of Naval Architecture and Ocean Engineering, 15, 100537. [https://doi.org/10.1016/j.ijnaoe.2023.100537]
• Özden, Y. A., Özden, M. C., Demir, E. and Kurdoglu, S. 2019. Experimental and numerical investigation of DARPA Suboff submarine propelled with INSEAN E1619 propeller for self-propulsion. Journal of ship research, 63(04), 235-250. [https://doi.org/10.5957/JOSR.09180084]
• Park, J.Y., Kim, N. and Shin, Y.K. 2017. Experimental study on hydrodynamic coefficients for high-incidence-angle maneuver of a submarine. International Journal of Naval Architecture and Ocean Engineering, 9(1), pp.100-113. [https://doi.org/10.1016/j.ijnaoe.2016.08.003]
• Park, J. and Seok, W. 2023. Computational analysis of strut effects on a BB2 submarine at drift angle 0, 6, and 12°. International Journal of Naval Architecture and Ocean Engineering, 15, 100555. [https://doi.org/10.1016/j.ijnaoe.2023.100555]
• Roddy, R.F. 1990. Investigation of the stability and control characteristics of several configurations of the DARPA SUBOFF model (DTRC Model 5470) from captive-model experiments. David Taylor Research Center, Ship Hydromechanics Department, DTRC/SHD-1298-08.
• Ronneberger, O., Fischer, P. and Brox, T. 2015. U-net: Convolutional networks for biomedical image segmentation. In Medical image computing and computer-assisted intervention–MICCAI 2015: 18th international conference, Munich, Germany, October 5-9, 2015, proceedings, part III 18 (pp. 234-241). Springer International Publishing. [https://doi.org/10.1007/978-3-319-24574-4_28]
• Siemens Digital Industries Software. Simcenter STAR-CCM+, version 2020.3.1. Siemens 2020.
• Thuerey, N., Weißenow, K., Prantl, L. and Hu, X. 2020. Deep learning methods for Reynolds-averaged Navier–Stokes simulations of airfoil flows. AIAA Journal, 58(1), 25-36. [https://doi.org/10.2514/1.J058291]
• Wang, B. and Wang, J. 2021. Application of artificial intelligence in computational fluid dynamics. Industrial & Engineering Chemistry Research, 60(7), 2772-2790. [https://doi.org/10.1021/acs.iecr.0c05045]
• Wu, S. J., Lin, C. C., Liu, T. L. and Su, I. H. 2020. Robust design on the arrangement of a sail and control planes for improvement of underwater Vehicle’s maneuverability. International Journal of Naval Architecture and Ocean Engineering, 12, pp.617-635. [https://doi.org/10.1016/j.ijnaoe.2020.06.002]
• Yang, C. and Lohner, R. 2003, September. Prediction of flows over an axisymmetric body with appendages. In The 8th International Conference on Numerical Ship Hydrodynamics, Busan, Korea.
• Zhang, S., Tezdogan, T., Zhang, B. and Lin, L. 2021. Research on the hull form optimization using the surrogate models. Engineering Applications of Computational Fluid Mechanics, 15(1), pp.747-761. [https://doi.org/10.1080/19942060.2021.1915875]
• Zhu, Z., Zhao, G. and Zhao, Q. 2024. Fast and high-precision compressible flowfield inference method of transonic airfoils based on attention UNet. Physics of Fluids, 36(3). 036111. [https://doi.org/10.1063/5.0188550]
• Zuo, K., Ye, Z., Bu, S., Yuan, X. and Zhang, W. 2024. Fast simulation of airfoil flow field via deep neural network. Aerospace Science and Technology, 150, 109207. [https://doi.org/10.1016/j.ast.2024.109207]