주성분 분석을 통한 선박 조종 중 4자유도 동역학 특성 연구
1충남대학교 첨단수송체연구소2충남대학교 자율운항시스템공학과
3충남대학교 선박해양공학과
2Department of Autonomous Vehicle System Engineering, Chungnam National University
3Department of Naval Architecture and Ocean Engineering, Chungnam National University
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The present study concerns a feasibility study for applying principal component analysis to ship dynamics in maneuver. Using the four degrees of freedom standard modular model for ship dynamics maneuver simulations of large angle zigzag tests with rudder deflection angle variations are conducted. The datasets of ship motion, hydrodynamic force, and moment during the maneuver are acquired to identify the principal modes. The covariance matrix of obtained ship dynamics variables shows a strong linear correlation between the motion, hydrodynamic force, and moment, except the surge force. Four eigenvectors of the covariance matrix are selected as the principal modes of ship dynamics. Using the principal modes, ship motion in turning circle and zigzag tests is reconstructed, showing good agreement with the original data.
Keywords:
Ship maneuverability, Dynamics model, Principal component analysis키워드:
선박 조종성능, 동역학 모델, 주성분 분석1. 서 론
선박의 조종은 선박의 동역학적 특성을 이해하여 목표한 운동이나 항로를 달성하기 위해 추진기와 방향타에 대한 적절한 제어 명령을 내리는 과정으로 볼 수 있다. 여기서 선박의 동역학적 특성은 실제 유체역학적 해석을 하여 알기보다는 현재의 운동에 대응하는 유체역학적 외력이나 모멘트의 관계식으로 구성된 운동 모델을 시스템 식별(system identification)을 통해 얻는다 (Lee and Shin, 1998; Sung and Park, 2015).
일반적으로 조종 운동 모델은 모든 선체를 하나의 운동체로 보아 조종 운동과 조종 입력을 테일러급수로 전개하는 전선 모델 (Shin et al., 2009)이나 선체, 추진기, 방향타의 유체력을 각각 계산하여 이를 합하는 모듈형/컴포넌트 모델(modular/component model)에 기반한다. 이 중 모듈형 모델은 이를 정식화한 Mathematical Modeling Group의 이름을 따서 MMG 모델이라고 부르기도 한다. 이 모델에서 선체의 유체력은 통상적으로 운동 변수에 대한 테일러 급수를 이용해 근사하여 표현되나, 추진기와 방향타의 유체력, 모멘트는 추진기 단독시험 결과와 방향타의 직압력에 근거한 유체역학적 이론을 통해 추정한다.
전통적으로 조종 운동은 수평면에서만 이뤄지는 것으로 보아 조종을 위한 운동 모델은 전후동요(surge), 좌우동요(sway), 선수동요(yaw)의 3가지만을 다루는 3자유도 운동으로 구성한다. 이러한 접근방법은 다양한 사례에 대해 그 신뢰성을 인정받았다. 이후 3자유도 조종 운동에 더하여 선박의 조종운동에서 횡동요(roll)의 영향을 고려한 4자유도 운동을 해석하려는 연구가 수행되었다. 이는 횡경사각에 따라 선체의 수면 아래 형상이 비대칭으로 나타나면서 선체의 횡동요 유체력이나 선수동요 모멘트가 발생한다는 점에 착안한 것이다 (Sohn and Kim, 2003; Yun and Yeo, 2019). 이러한 횡경사를 포함한 조종 운동 모델을 개발하기 위해서 전통적인 구속모형시험 기반의 접근에서는 실험 분량이 늘어나고, 횡동요와 다른 운동을 결합한 새로운 실험의 설계가 요구된다 (Kim et al., 2011).
4자유도 운동 모델의 개발을 위한 구속모형시험의 설계와 수행의 어려움을 극복하기 위해 자유항주 모형시험이나 시운전으로부터 바로 운동 모델을 구하려는 시도가 이뤄져왔다. 초기에는 일반적인 운동 모델의 구성을 그대로 적용해 선체의 유체력 항에 대한 유체력 미계수를 칼만 필터(Kalman filter)를 통해 찾아내려는 연구가 주로 수행되었다 (Lee and Shin, 1999; Yoon et al., 2007; Perera et al., 2015). 칼만필터 외에도 최적화 알고리즘을 이용한 조종계수의 식별이 이뤄지기도 하였다 (Sutulo and Soares, 2014; Xu et al., 2016; Xu et al., 2018; Kim and Kim, 2020; Wang et al., 2020a; Wang et al., 2020b; Kim et al., 2022).
앞에서 논한 테일러 급수 기반의 선체 유체력 모델을 대체하기 위해서는 테일러 급수 외의 다른 방식으로 운동과 유체력의 관계를 규정해야 한다. 이를 위해 자주 제안된 방식은 인공신경망이다 (Moreira and Soares, 2003; Wakita et al., 2022). 다만 인공신경망 기반의 조종 모델 개발은 운동과 유체력간의 관계가 수식으로 명확히 나타나는 전통적인 운동 모델에 비해 그 속을 알기 어렵기 때문에 사용자가 모델을 완전히 이해하기가 어렵다는 한계가 있다.
조종 계수 추정에 대한 Kim and Kim (2020)의 연구에서는 작은 타각의 조종 시험 결과로부터 선형 조종계수를 결정한 후 큰 타각의 조종 시험 결과를 이용해 비선형 조종 계수를 얻는 방안을 제안하고 검증하였다. 이로부터 선박의 조종 운동은 선형적 특성을 기반으로 하여 비선형적 특성의 반영이 가능함을 알 수 있다. 따라서 이러한 문제에는 완전 비선형적 문제에 대한 접근법인 인공신경망보다는 더 직관적이고 이해하기 쉬운 선형적 이론에 기반한 해석법이 더 유용할 것으로 생각된다.
어느 정도의 선형성을 갖는 문제를 몇 가지의 유효한 선형 문제의 결합으로 나타내는 기법 중 대표적인 것으로 주성분 분석(Principal Component Analysis, PCA)이 있다. PCA는 분야에 따라 적합직교분해(Proper Orthogonal Decomposition, POD), 특이값분해(Singular Value Decomposition, SVD)라고도 부른다(Lee, 2017). 이는 데이터의 주요 패턴을 구성하는 한정된 수의 정규고유벡터의 선형결합으로 데이터를 나타내는 기법이다. PCA를 통해 구한 정규고유벡터 기저에서 주요한 몇 가지만을 활용해서도 대부분의 데이터를 재구성해낼 수 있으므로 데이터의 저차원화가 가능해진다. 그리고 기저 벡터의 구성을 해석하여 대상 데이터의 특성을 설명할수도 있다는 장점이 있기 때문에, 난류 구조, 진동 특성과 같이 비선형적인 물리 현상의 해석에 사용되고 있다 (Hong and Lee, 2010; Shin et al., 2017). 이외에도 빅데이터에서 의미있는 데이터 패턴을 추출하거나 잡음을 제거하는 등의 데이터 처리 분야에서도 활용되고 있다 (Yoo, 2020; Jung and Yoon, 2021).
위에서 살펴본 바와 같이 선박의 조종 운동 문제에 PCA를 적용한다면 선박의 주요한 선형적 동역학 요소들을 조합해 약한 비선형성을 갖는 선박 조종 운동 모델의 개발이 가능할 것으로 판단된다. 상세하게 설명하자면, Kim et al.(2022)에서 제안한대로 구속모형시험이 아닌 자유항주모형시험의 결과로부터 선체 운동과 유체력의 데이터를 구하고, 이 데이터 세트에 PCA를 통한 시스템 식별을 적용해 주요한 운동-유체력 관계를 찾아 이를 바탕으로 다른 선체 운동을 설명할 수 있는 선체 유체력의 모델을 개발하는 방안을 제안할 수 있을 것으로 전망된다. 이를 위해서는 다음의 사항에 대한 검토가 선행되어야 한다.
- - 선박의 조종 시 운동을 PCA를 통해 저차원화해 나타낼 수 있는가?
- - PCA의 주요 모드를 이용해 주어진 운동에 대응하는 유체력을 추정할 수 있는가?
- - 조종 운동 모델을 개발하기 위한 자유항주 모형시험은 어떻게 구성되어야 하는가?
본 연구에서는 첫 번째 문제에 집중하여 전통적인 선박의 조종 운동을 MMG 모델을 통한 조종 시뮬레이션으로 구현하고, 그 결과를 PCA를 통해 분석하여 운동의 저차원화가 가능함을 보였다. 논문은 다음과 같이 구성된다. 2장에서는 조종 해석을 위한 4자유도 운동 모델의 구성을 다뤘다. 3장에서는 PCA의 수학적 원리와 이를 선박 유체력 모델링에 적용하기 위한 방안을 설명하였다. 4장은 MMG 모델을 이용한 조종 시뮬레이션 결과와 PCA를 이용한 재구성 결과를 보였다. 5장에 조종 운동의 PCA 결과를 보였다. 6장은 본 연구의 결론이다.
2. 조종 운동 모델
2.1 대상 선형
연구에 사용된 선형은 선박해양플랜트연구소(Korea Research Institute of Ships and Ocean Engineering, KRISO)에서 개발한 3,600TEU급 컨테이너선 KCS이다. 해당 선형은 다양한 스케일에 대해 조종 성능의 평가를 위한 모형시험과 전산유체역학(Computational Fluid Dynamics, CFD)해석이 수행된 바 있다 (Kim et al., 2011; Yasukawa et al., 2018; Yun et al., 2021; Sanada et al., 2021; Kim et al., 2021; Yang et al., 2022; Yun et al., 2022; Okuda et al., 2023).
Fig. 1과 Table 1에 각각 대상 선형의 형상과 주요 요목을 보였다. 본 연구에서는 자유항주 모형시험과의 비교를 통해 검증된 Okuda et al. (2023)의 조종 모델을 그대로 사용하기 위해 축척비는 해당 연구와 동일하게 1:65.83으로 하였다. 해당 연구의 데이터에서 유의할 점으로, 추진기를 KCS 선형을 위해 설계된 KP505 대신 지름과 날개 수가 같은 다른 프로펠러를 사용했음을 일러둔다. 다만 본 연구는 선체의 유체력을 주로 다루고 있고, 추진기의 추력에 대한 주요 수치가 해당 논문에서 함께 제공되고 있는 점을 감안해 조종 모델에 KP505 프로펠러를 위한 추력 모델로 교체해 적용하지는 않았다.
2.2 좌표계
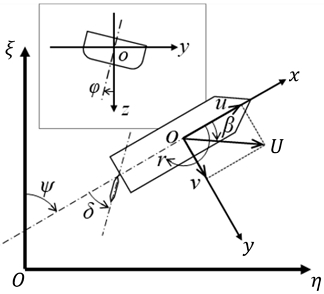
4자유도 조종 운동을 위한 좌표계는 지구고정좌표계와 운동좌표계가 사용되었다. Fig. 2에 좌표계를 표시하였다. 지구고정좌표계의 ξ, η, ζ축은 각각 조종 시작 시 선체의 직진 방향, 같은 시점의 우현 방향, 중력 방향으로 정의하였다.
Okuda et al. (2023)의 연구에서 사용된 수평면선체고정좌표계는 원점을 선체의 길이 방향 중앙(midship)에 놓는다. 수평면선체고정좌표계에 대한 상세한 설명은 본 논문의 부록에서 따로 다뤘다. 이 좌표계에서 유체력과 모멘트는 무게중심에서 얻어지나 이를 원점에서 해석하므로, 이동 좌표계에서 무게중심 위치의 좌표(xG, 0, zG)를 고려해야 한다. 여기서 zG는 수평면에서 무게중심까지의 거리이다.
원점의 x방향 운동 속도(u)는 무게중심과 좌표계 원점에 대해 동일하나, y방향 운동 속도(vm)는 무게중심의 y방향 속도(v)에 선체의 선수동요 각속도(r)와 횡경사의 시간변화율()로 인한 회전을 고려해 식 (1)과 같이 계산한다.
| (1) |
본 연구에서 사용된 4자유도 운동방정식은 식 (2)와 같다.
| (2) |
여기서 X, Y는 각각 x, y방향 힘의 합력, K와 N은 각각 x, z방향 모멘트의 합력이다. m, Ixx, Izz는 각각 모형선의 질량과 x, z 축 방향의 관성모멘트이다. 관성모멘트는 무게중심이 아니라 좌표계 원점 기준으로 계산되므로 평행축정리(parallel-axis theorem)가 적용되었다.
mx, my, Jxx, Jzz는 각 방향의 부가질량과 부가관성모멘트로, Okuda et al. (2023)의 연구를 따라 같은 값을 적용하였다. 그 중 Jxx에 대해서 따로 설명하자면 KCS 선형에 대해 제안된 Ixx값의 10%를 부가관성모멘트로 가정하였다. kxx값은 Ixx와 Jxx의 합에 대한 관성반경 값으로, 일반적으로 KCS 선형에 적용되던 값인 0.4b (Yun et al., 2021)가 아니라 0.44b임을 일러둔다. αz는 my가 작용하는 지점의 z방향 위치로, Yasukawa et al. (2019)에서 제안된 값을 사용하였다. 조종 시뮬레이션에서는 식 (2)의 병진, 회전 방향 가속도를 순차적 반복계산법을 통해 0.02초 간격으로 계산하였다. 반복계산에서 설정된 임계값은 10-10이다.
2.3 조종 모델의 구성
본 연구에서는 대표적인 모듈러 모델인 MMG 모델을 이용하였다. 이전에도 모듈러 모델은 각 기관마다 적절한 변형을 거쳐 이용되었으나, Yasukawa and Yoshimura (2015)의 연구를 통해 MMG 모델의 표준안이 MMG standard method라는 이름으로 제안되었고, Yasukawa et al. (2019)의 연구에서는 여기에 횡동요의 영향을 추가하여 4자유도 운동으로 확장하였다.
본 연구에서 참고한 Okuda et al. (2023)의 연구에서는 축척비 1:65.8의 KCS 선형에 Yasukawa et al. (2019)의 조종 운동 모델을 적용하여 유체력 미계수와 그 외의 조종계수들을 구하였다. 본 연구에서도 동일한 모형선을 가정하여 같은 조종모델과 조종 계수를 사용하였는데, 그 구성과 값은 부록에 상세히 나타내었다.
MMG 모델은 식 (3)과 같이 선체, 추진기, 방향타의 유체력을 나누어 구하여 식 (2)의 운동방정식의 좌변인 X, Y, K, N을 구성한다. 식 (3)의 우변에서 아래첨자의 H, P, R은 각각 힘과 모멘트에서 선체, 추진기, 방향타 성분을 의미한다.
| (3) |
2.4 선체 유체력 모델
Okuda et al. (2023)의 조종 모델에서 선체 유체력 모델은 식 (4)와 같이 구성된다. 차원을 갖는 선체 유체력과 모멘트 XH, YH, NH는 무차원화된 좌우동요 속도(v'm = vm/U)와 선수동요 각속도(r' = rL/U), ϕ에 대한 함수로 얻어지는 X'H, Y'H, N'H를 이용해 구한다. 여기서 U는 순간 속도의 벡터합의 크기이다.
| (4) |
전통적인 조종 운동 모델은 X'H, Y'H, N'H를 v'm, r', ϕ에 대한 테일러 급수 전개를 통한 다항식으로 표현한다. Okuda et al. (2023)의 연구에서 사용된 수식은 부록의 식 (11)과 같고, 여기에 사용된 조종계수의 값을 부록의 Table 3에 나타내었다.
3. 주성분 분석
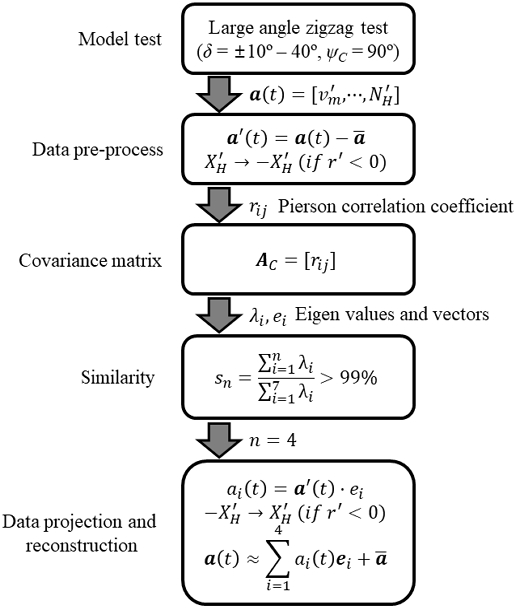
본 연구의 PCA 과정을 Fig. 3에 정리하여 나타내었다. 선박 조종 운동에 PCA를 적용하면 조종 운동 중 자주 발생하는 동역학적 변수, 즉 운동과 유체력 및 모멘트에 대한 패턴인 주요 모드를 얻을 수 있다. 이 주요 모드의 선형 결합으로 다른 조종 운동을 표현할 수 있는지를 확인하는 것이 본 연구의 목표이다.
3.1 기본 개념
선박의 조종 운동은 4자유도 운동을 다루나 제어 입력은 프로펠러 회전수(nP)와 δ 두 가지뿐이므로 선박의 4자유도 운동을 모두 제어하지는 못한다. nP는 전후동요와 추진기 후류의 유속 변화를 통해 조종에 영향을 줄 수 있지만, 본 연구에서는 nP가 고정값이므로 운동 성분은 δ의 제어에만 영향을 받는 것으로 가정하였다.
Kim et al. (2022)에서 다룬 바와 같이 δ의 변화로 인한 선회에서 v'm, r', ϕ 운동은 강한 상관관계를 보인다. 따라서 식 (4)에서 좌변의 X'H, Y'H, N'H도 v'm, r', ϕ을 따라 일관된 경향을 보일 것으로 생각할 수 있다. 식 (3)의 KH는 YH와 연관된 함수이므로, K'H를 식 (5)와 같이 정의하면 식 (6)과 같이 무차원화된 선체 유체력과 모멘트 전부를 운동 변수에 대한 함수로 정리할 수 있다. 이 함수를 테일러 급수 전개로 나타낸 것이 부록의 식 (11)의 선체 동역학 모델이다.
| (5) |
| (6) |
PCA는 식 (6)의 변수의 입출력 관계가 아니라 입출력 변수 전체를 하나의 데이터로 보아 이들의 패턴을 구성하는 주요 기저(basis)를 구한다. 따라서 이를 입력-출력 관계로 재구성하는 것은 후속 연구에서 PCA 기반의 조종 모델을 개발할 때 고려할 점으로 보았다.
조종 운동 시 특정 순간의 운동과 유체력, 모멘트를 식 (6)처럼 구분하는 대신 1×7 행벡터 a(t) = [v'm, r', ϕ, X'H, Y'H, K'H, N'H도 v'm]로 나타내었다. a(t)는 식 (7)과 같이 시간에 무관한 7개의 정규 직교 기저(orthonormal basis) ei의 선형결합으로 나타낼 수 있다.
| (7) |
여기서 a는 시계열 데이터의 평균이며, 직교 기저를 이용한 표현은 요동성분에 국한됨을 알 수 있다. ai(t)는 ei가 직교 기저임을 이용해 a'(t)와 ei의 내적을 통해 구할 수 있다. 이는 ai(t)가 aˊ(t)를 해당 기저로 사영한 크기와 같기 때문이다.
이 때, a'(t)를 유효하게 나타낼 수 있는 7보다 작은 개수의 ei가 있다면, 식 (8)과 같이 n개의 ei들과 a로 a(t)를 근사할 수 있을 것이다. 이를 통해 조종 모델을 표현하는 변수의 수를 원래의 운동 변수 7개에서 식 (8)을 구성하는 ai(t)의 개수인 n으로 저차원화가 가능하다.
| (8) |
PCA에서 ei는 a'(t) 데이터의 공분산행렬(AC)의 고유벡터를 이용해 얻는다. 우선 자유항주 조종 시험에서 a'(t)의 시계열을 얻는다. 시계열 a'(t)를 구성하는 변수(vi, vj)에 대해 식 (9)의 피어슨상관계수(Pierson correlation coefficient) (rij)를 원소로 갖는 행렬 AC를 만든다.
| (9) |
식 (9)로부터 AC는 대칭행렬임을 알 수 있으므로, AC의 고유벡터들은 서로 직교함을 알 수 있다. 고유벡터들을 정규화하여 식 (7)과 (8)을 위한 기저로 사용할 수 있다. AC의 고유벡터는 데이터의 상호상관도를 반영한 전반적인 데이터의 변화 경향을 나타낸다. 그리고 고유벡터에 대응되는 고유값(λi)이 크면 고유벡터 방향으로 데이터의 변화 폭이 크다는 의미로, a'(t)의 지배적인 변화를 잘 설명한다고 볼 수 있다. 따라서 고유값의 크기 순으로 고유벡터를 나열한 뒤 유의미한 수의 고유벡터만을 취해 동역학적 변수를 표현하게 된다.
3.2 데이터 전처리
PCA는 선형 변환에 기반하므로 해석을 위한 데이터도 최대한 선형성을 확보할 필요가 있다. 이는 주어진 데이터를 그대로 해석하기보다는 데이터의 평균이 0에 위치해야 하고, 데이터는 원점 대칭의 기함수(odd function) 형태를 갖춰야 한다는 의미이다.
부록의 식 (11)에서 X'H를 제외한 모든 변수는 함수의 개형이 기함수에 가까워 좌선회와 우선회 시 서로 반대되는 부호를 갖는 것을 가정했음을 알 수 있다. 따라서 PCA 해석을 위한 데이터를 자유항주 조종 시험을 통해 얻을 때, 조종 시험을 좌우현에 대해 수행한 데이터를 함께 모아서 해석하는 것으로 선형성을 강조한 데이터 세트를 만들 수 있다. 물론 이렇게 구한 평균값이 완전히 0은 아닐 것이므로, 식 (7)에서 시계열 데이터의 평균 a를 빼준 a'(t)에 대한 PCA를 수행해 주요 모드를 구해야 한다.
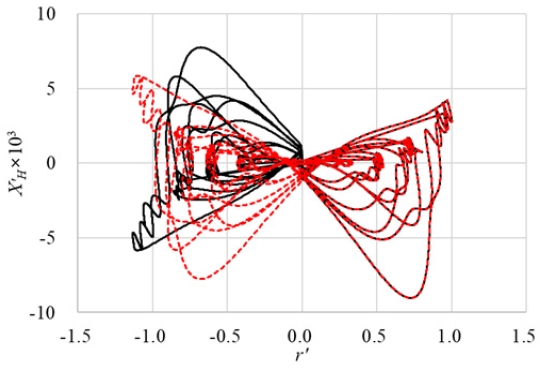
조종 운동 모델에서 X'H는 우함수(even function)이므로 선체의 선회 방향에 무관하게 음수 방향으로 증가하는 선형성이 없는 특성을 보인다. 이에 대응하기 위해 X'H를 기함수 형태로 변환하여 PCA를 적용하는 방안을 제안하였다. Fig. 4에서 보인대로 r'의 부호에 따라 X'H의 부호가 함께 바뀌도록 전처리를 하여 r'과 X'H에 대해 기함수의 관계를 구성하였다.
4. 조종 시뮬레이션
4.1 시뮬레이션 조건
3장의 조종 모델을 이용하여 대각도 지그재그 조종 시험의 시뮬레이션을 수행하고 PCA를 통해 주요 모드를 추출하였다. 모든 조종 시험은 3.2장에서 제안한 대로 좌선회, 우선회를 모두 수행한 결과를 합하여 PCA 해석을 위한 데이터 세트로 사용하였다. 시뮬레이션이 수행된 직진 중 선속(U0) 조건은 Fr = 0.26으로, 설계속도인 24kts에 대응한다. 방향타의 회전 속도는 Okuda et al. (2023)에서 사용된 값을 그대로 적용하였다. 이는 모형선 기준으로 19.0˚/s인데, 실선 기준으로 SOLAS 조약에서 제안하는 최소값인 2.32˚/s에 대응한다.
조종 시나리오로 사용된 대각도 지그재그(large angle zigzag) 조종 시험은 Araki et al. (2012)에서 제안되었다. 이는 지그재그 시험에서 타각의 변화를 주는 선수각(ψC) 조건을 전통적인 지그재그 시험의 방향타각(δ = ψC)보다 크게 주는 시험이다. 통상적인 지그재그 시험이 정속 선회에 접어들기 전에 반대방향으로 타각을 주어 조종 운동이 천이영역의 초입에서만 일어나는데 반해, 대각도 지그재그 시험은 정속 선회 중의 타각 변화에 따른 조종 운동을 파악할 수 있다. Araki et al. (2012)의 연구에서는 대각도 지그재그 조종 시험의 결과를 이용하여 조종모델의 계수를 유효하게 추정할 수 있음을 보였다. 따라서 PCA의 주요 모드에 대응하는 운동 조건을 식별하는데 적절한 것으로 판단하였다.
Araki et al. (2012)의 연구에서는 ψC를 ±90˚로 하였는데, 본 연구에서도 이 값을 따라 조종 시뮬레이션을 수행하였다. 조종 시험을 위한 δ는 10˚, 20˚, 30˚, 40˚를 적용하였다. 일반적인 선박의 최대 δ는 35˚이나 더 큰 δ까지 조종 시뮬레이션을 수행해야 δ = 35˚ 정속 선회 조종의 운동 범위를 포함한 운동-유체력 데이터가 확보될 것으로 판단하였다. 이후에 MMG 모델을 이용한 시뮬레이션 이외에도 자유항주 모형시험이나 CFD 해석에서 PCA를 수행하는 과정을 위해서도 이러한 δ = 40˚ 조건의 구현은 충분히 가능할 것으로 보인다.
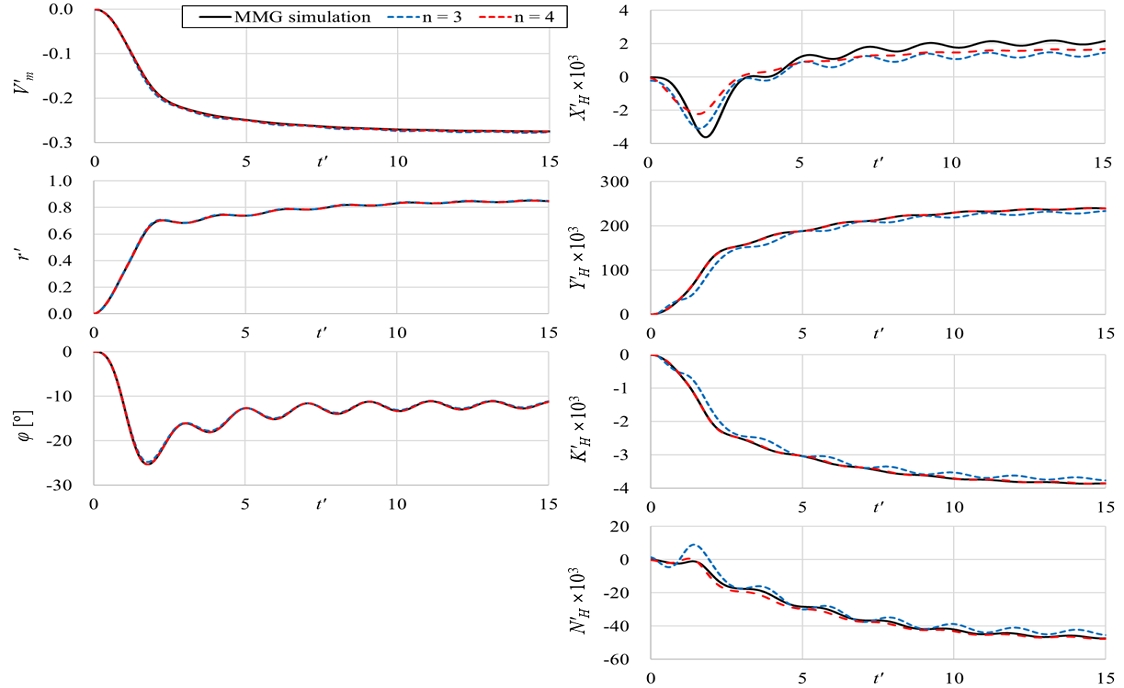
마지막으로 대각도 지그재그 조종시험을 통해 얻은 주요 모드들이 다른 조종 운동의 동역학적 특성을 잘 반영하는지 확인하기 위해 통상적인 35˚ 선회, 10˚/10˚, 20˚/20˚ 지그재그 조종 시험의 시뮬레이션을 수행하였다. 이 조종 시험의 동역학적 변수들은 대각도 지그재그 조종 시험의 주요 모드들을 통해 재구성하여 비교하였다. 본 연구에서 사용된 조종 시뮬레이션 자체의 신뢰도는 Okuda et al. (2023)의 연구에서 자유항주 모형시험과의 비교를 통해 수행된 바 있으므로, 본 연구에서 직접 다루지는 않았다.
4.2 대각도 지그재그 조종 시험
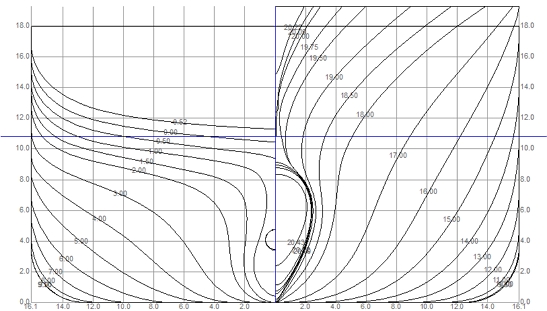
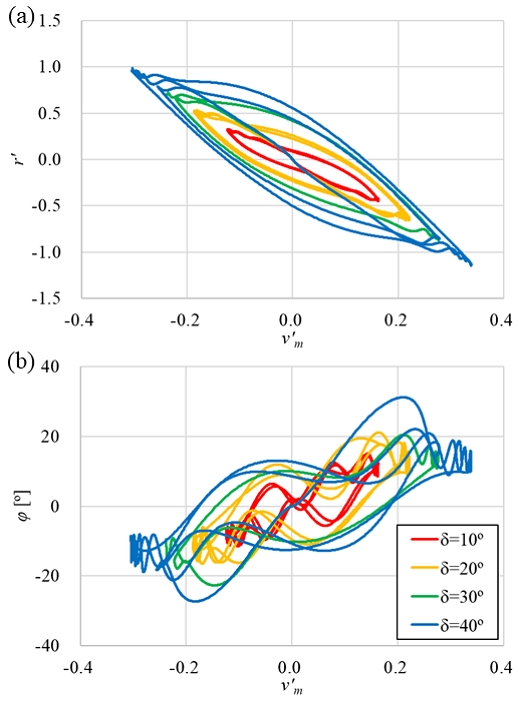
Fig. 5에 대각도 지그재그 조종 시험의 시뮬레이션 결과를 보이고 조종 운동의 과정을 세 영역으로 분류하였다. A 영역에서는 직진 중에 방향타를 트는 조종의 초기 천이단계로, 선체가 선회하면서 선속이 크게 줄어들게 된다. B 영역은 안정된 선회로, 선체의 운동에 변화가 없이 일정한 각속도로 선회를 한다. C 영역은 선회 중 반대로 방향타를 트는 경우로, A 영역과는 다르게 낮은 전진비에서 추진기의 추력이 크게 발생하고 있는 상태이므로 선속의 급격한 감소 없이 선회를 한다. 일반 지그재그 조종 시험에서는 A, C 영역이, 정속 선회 시험에서는 A, B 영역이 나타나는데 반해 대각도 지그재그 조종 시험에서는 A, B, C 모든 영역의 조종 운동 경향을 얻을 수 있었다.
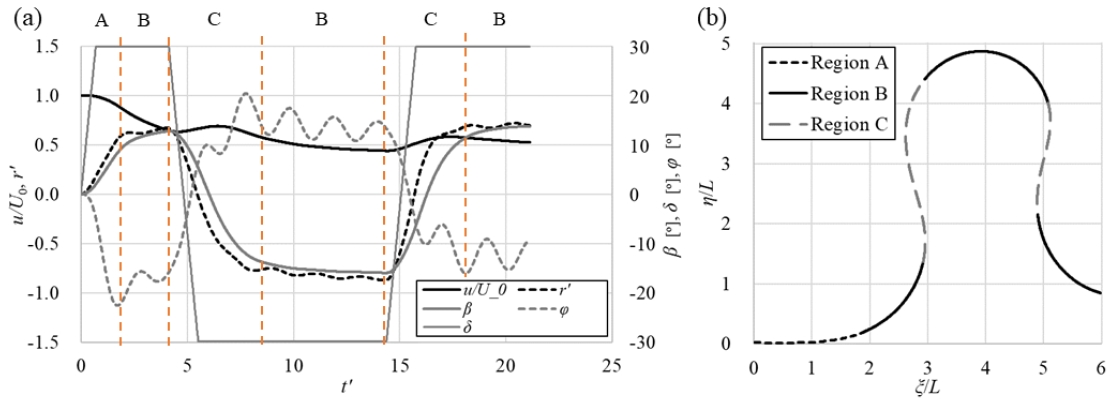
30˚/90˚ large angle zigzag test results and identification of dynamics regions: (a) time history of u/U0, rˊ, β, δ, φ and (b) trajectory
30˚/90˚ 대각도 지그재그 조종 시뮬레이션 결과에서 얻어진 주요 운동 변수인 v'm, r', ϕ을 Fig. 6에 나타내었다. Fig. 5에서 보인 운동의 세 영역도 구분하여 함께 나타내었다. A 영역은 직진 상태인 원점에서 시작하여 운동 영역의 끝단까지 발달하는 천이구간이다. B 영역은 운동 분포의 양 끝단으로, 선체 횡동요 운동의 고유 주기로 인해 국소적으로 요동하는 경향이 나타났다. C 영역은 운동 분포의 양 끝단을 연결하나, 원점을 거치지 않고 1, 3사분면을 거쳐가며 운동이 발생하는 특성을 보인다.
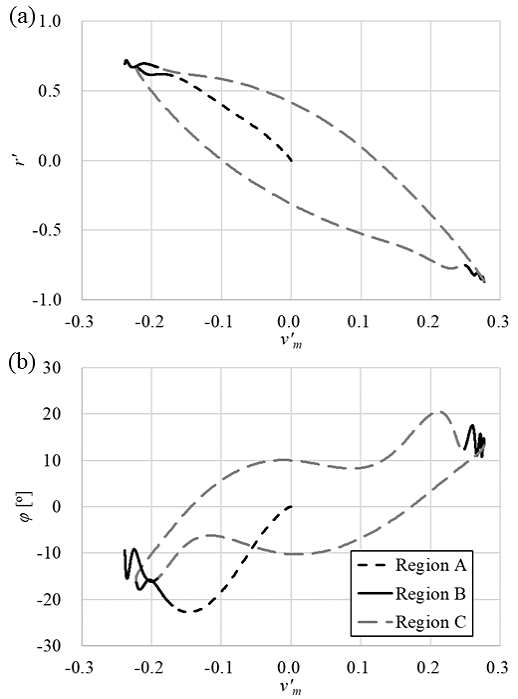
Results of 30˚/90˚ large angle zigzag test and identification of dynamics regions: (a) vˊm vs rˊ and (b) vˊm vs φ
Fig. 6(b)의 v'm, ϕ의 관계에서 ϕ의 요동으로 인한 운동 변수간의 상호상관도의 감소가 더욱 뚜렷하게 확인되었다. 빌지 킬(bilge keel)이 달린 텀블홈(tumblehome) 함형의 조종 운동 모델 개발을 다룬 Kim et al. (2022)의 결과에서는 v'm, ϕ의 관계가 잘 식별된 점과 다른 결과이다. 이는 본 연구의 대상선형인 KCS가조종 운동 중 횡동요가 더 크게 발생하는 탓으로 생각된다.
Fig. 7은 모든 δ에 대한 대각도 지그재그 조종 시험의 결과를 합쳐 나타낸 결과이다. 조종 시험에서 적용한 δ가 커질수록 전체 운동의 범위가 넓어지는 것을 알 수 있다. 그리고 v'm, r'의 관계는 아주 뚜렷하게 나타난데 반해 ϕ는 고유 횡동요 운동의 영향을 추가로 받아 다른 변수와의 연관성이 다소 약하게 나타났지만, 전체적으로 v'm과 양의 상관관계를 보였다.
자유항주 조종 운동의 결과로부터 PCA를 통해 조종 운동 모델을 개발한다면 v'm, r', ϕ이 최대한 다양하게 얻어져 PCA의 주요 모드가 다양한 조종 운동을 포함하도록 조종 시나리오를 구성해야 한다. Fig. 7을 바탕으로 생각하자면 v'm, r', ϕ 각각의 범위는 최대한으로 얻어지면서 각 운동 성분 간의 상호상관도는 낮은 조종 시나리오가 필요할 것으로 보인다. 후속 연구에서 최적의 조종 시나리오를 개발하려 한다면 운동의 다양성을 정량화할 수 있는 기준의 수립이 필요할 것으로 생각된다.
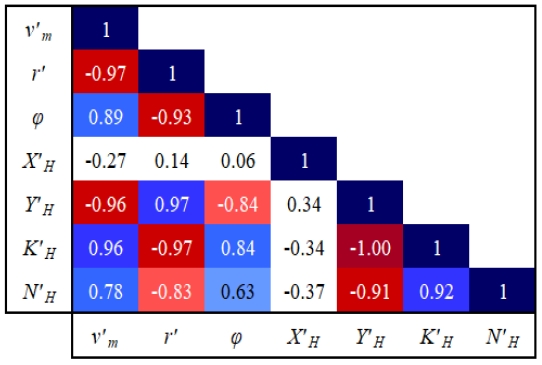
Fig. 8은 대각도 지그재그 시험의 조종 시뮬레이션에서 얻어진 동역학적 변수(v'm, r', ϕ, X'H, Y'H, K'H, N'H)를 이용해 구한 AC이다. 선체의 운동 변수인 v'm, r', ϕ에서는 0.9 내외의 높은 상호상관도가 나타났으므로 운동의 연성이 강하게 발생한 것을 알 수 있다. 그리고 유체력 및 모멘트 항인 X'H, Y'H, K'H, N'H에 대해서는 X'H를 제외하면 서로 간의 강한 상관관계를 확인할 수 있다.
이는 자유항주 모형시험 결과에 대해 최적화를 통한 조종 운동 모델의 개발을 다룬 연구인 Kim et al. (2022)에서 지적된 사항과 동일한다. 운동 변수와 유체력 및 모멘트간의 관계는 Y'H, K'H에 대해서는 비슷한 수준으로 강하게 나타났는데, 이는 식 (3)에서 보인 대로 K'H는 Y'H로부터 바로 계산되기 때문이다. N'H는 운동 변수와의 상호상관도가 Y'H보다 작게 나타났다.
5. 조종 시험 결과의 주성분 분석
5.1 주요 모드의 분석
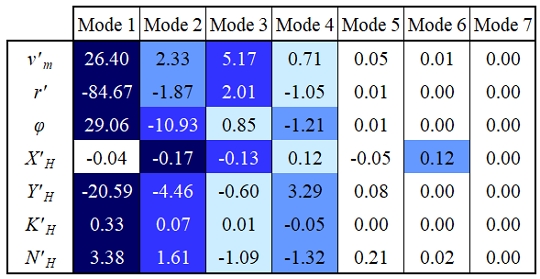
4.2장에서 구한 공분산 행렬에 대한 고유벡터와 고유값을 구해 KCS 모형선 운동의 주요 모드로 이용하였다. Table 2에 각 고유 벡터에 대응하는 고유값과 식 (10)으로 정의된 유사도(similarity) sk를 나타냈다. 이는 원래 데이터와 제한된 수의 고유벡터를 이용해 재구성한 데이터가 얼마나 유사한지를 보인다.
| (10) |

Eigen values of the covariance matrix and similarity with respect to the number of principal modes of the large angle zigzag test results
유사도의 해석을 통해 4개의 고유벡터를 이용할 경우 대각도 지그재그 조종 시험 중 운동의 99%를 재구성할 수 있음을 확인하였다. 이렇게 구한 4개의 주요 모드로 다른 조종 운동을 효과적으로 재구성할 수 있는지를 5.2장에서 다뤘다.
Fig. 9는 7개 모드에 대한 λiei의 분포이다. Table 2에서 분석한대로 상위 4개 모드에서 대부분의 운동의 지배적인 성분이 나타났다. 첫 번째 주요 모드에 대해, Fig. 8의 공분산 행렬에서 확인한대로 v'm, r', ϕ의 상관관계가 잘 나타났다. 이로 인한 유체력에 대해서는 Y'H, K'H의 관계가 두드러졌다. X'H는 본 연구에서는 배제한 6차 모드에서 세 번째로 강한 영향이 나타난 만큼 다른 운동 변수나 유체력, 모멘트 항과 명확한 선형적 관계를 기대하기는 어려운 것으로 보인다. 따라서 이후 PCA 기반의 조종 모델을 개발할 때 X'H항의 신뢰성 검토를 중요하게 봐야 할 것으로 생각된다.
5.2 주요 모드를 이용한 조종 운동의 재구성
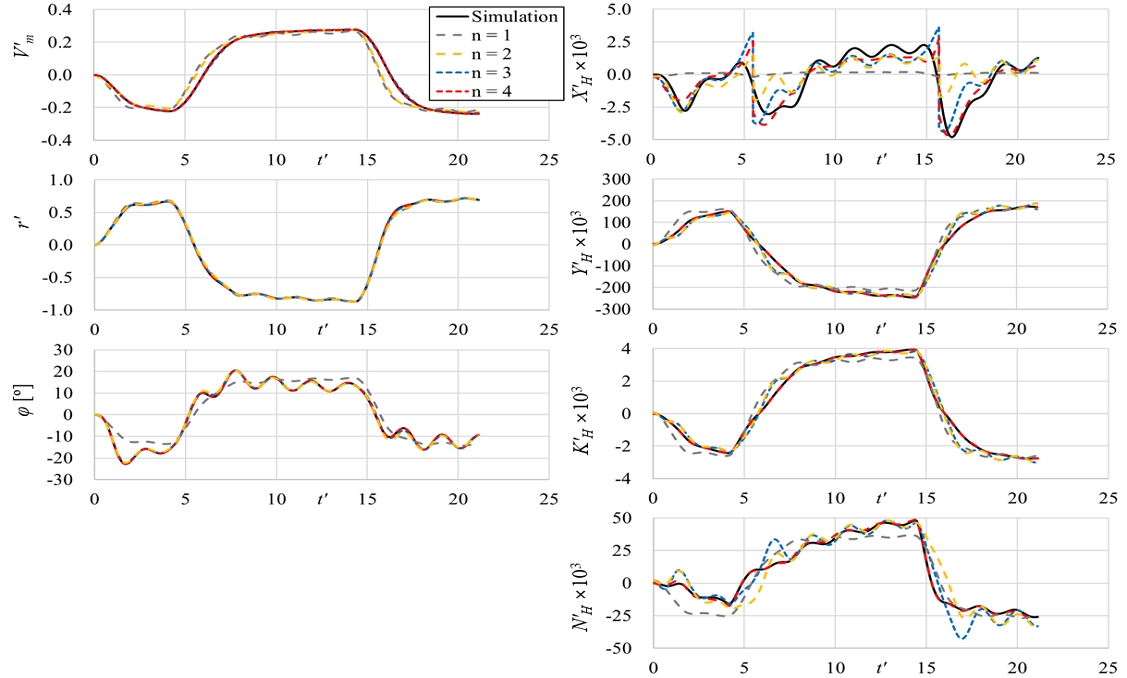
5.1장의 대각도 지그재그 조종 시험 결과에서 얻은 주요 모드(ei)와 Fig. 5의 시계열 데이터를 전처리한 결과(a'(t))를 식 (8)에 대입해 30˚/90˚ 대각도 지그재그 조종 운동을 저차원화해 재구성하는 과정을 보였다. Fig. 9와 함께 논한 바와 같이 본 연구에서는 4개의 주요 모드를 이용해 조종 운동을 재구성한 결과를 원래의 운동 데이터와 비교했다. 그리고 주요 모드 수에 따른 재구성 정확도의 변화를 확인하기 위해 그보다 낮은 n에 대한 재구성 결과도 함께 보였다.
Fig. 10은 30˚/90˚ 대각도 지그재그 조종 시험에 대한 재구성 결과의 비교이다. 5.1장에서 다른 변수와의 연관성이 낮은 것으로 확인된 X'H를 제외하면 첫 번째 주요 모드만 이용해도 전체적인 동역학적 변수의 경향을 잘 구현할 수 있었다. 운동 변수에 대해서는 r', ϕ는 2개의 주요 모드로도 운동을 잘 구현하였지만 v'm은 3개의 주요 모드가 필요했다. 이는 Fig. 9를 통해 주요 모드 별 요소의 크기 비교를 통해 예상할 수 있는 내용이다.
유체력 및 모멘트의 재구성에서는 더 많은 주요 모드가 필요한 것으로 판별되었다. Fig. 9에서 다룬대로 PCA를 통한 데이터 저차원화에서 X'H는 n = 6 이하의 조건에서는 정확도가 떨어질 것으로 예상하였다. 하지만 전체적인 결과는 원래의 데이터를 잘 추종하는 것으로 확인되었다. 다만 X'H의 급격한 변화가 발생하는 영역의 재구성에서 불연속적인 경향이 나타났다. 이는 Fig. 9와 함께 논한 대로 원래는 여섯 번째 주요 모드를 통해 설명되어야 하나, 저차원화 과정에서 이를 배제한 영향으로 보인다. 그리고 이 영역은 Fig. 5에서 방향타가 최대로 꺾이는 시점과 일치하는데, 이러한 방향타 운동과 X'H의 연관성에 대해서는 추가적인 연구가 필요한 것으로 보인다.
네 번째 주요 모드로 인한 재구성 결과의 차이는 Y'H, K'H이 급격한 변화를 겪는 영역에서 나타났다. 그리고 N'H에서의 차이가 유의미하게 나타났다. 3개의 주요 모드를 이용한 재구성 결과에서는 N'H가 횡동요 운동의 주기를 따라 요동하는 경향이 나타났는데, ϕ와 N'H의 관계가 강조되는 네 번째 주요 모드가 빠지면서 횡동요와 다른 운동의 분리가 제대로 이루어지지 않은 탓으로 보인다.
식 (8)을 통해 운동을 재구성하는 과정에서 얻은 ai(t)의 시계열과 Fig. 5의 조종 운동 영역 구분을 비교하여 A – C 영역에서 어떤 모드가 지배적으로 작용하는지를 알 수 있다. Fig. 11에 30˚/90˚ 대각도 지그재그 조종 시험의 재구성 과정에서 얻어진 a1(t)부터 a4(t)의 변화를 나타냈다. a1(t)는 A, B, C 영역 모두에서 전체적인 v'm, r', ϕ의 경향을 잘 따라갔으므로, 선체 동역학의 주된 경향을 의미한다. ϕ는 고유 주기로 계속해서 요동하는 운동이 추가로 발생했는데, 이는 두 번째 주요 모드에서 해석될 수 있었다. 이는 두 번째 주요 모드에서 ϕ 관련 값이 크게 나타났던 Fig. 10의 내용과 부합한다. 세 번째와 네 번째 주요 모드는 선회 중 반대 방향으로 방향타를 꺾는 과정인 C 영역의 운동에 주로 관여하는 것을 알 수 있다.
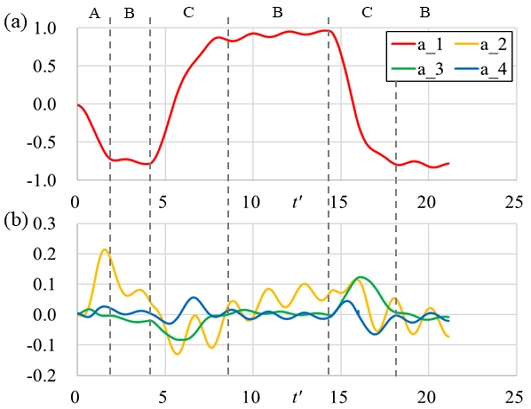
Time history of ai(t) for reconstruction of 30˚/90˚ large angle zigzag test results: (a) a1 and (b) a2, a3, and a4
대각도 지그재그 조종 시험을 통해 얻은 주요 모드로 다른 조종 운동을 재구성할 수 있다면 대각도 지그재그 조종 시험이 선박의 동역학적 특성을 충분히 잘 반영하는 시나리오라고 할 수 있다. MMG 조종 모델을 이용해 35˚ 선회 시험, 10˚/10˚, 20˚/20˚ 지그재그 조종 시험 시뮬레이션을 수행하고, 그 결과에 대해 식 (8)을 이용해 조종 운동을 재구성하였다.
우선 각 조종 운동에 대한 a(t)를 MMG 모델을 이용해 구하였다. 그리고 식 (8)을 이용해 a'(t)를 구하였다. 여기서 a는 각 조종 운동의 평균이 아니라 5.1장에서 구한 대각도 지그재그 조종 시험의 평균값임에 유의한다. a'(t)와 ei의 내적으로 ai(t)를 구하고 a(t)를 재구성하는 과정은 식 (10)과 같다.
Fig. 12는 35˚ 선회 시험의 재구성 결과에서 각각 운동 변수와 유체력 및 모멘트 변수의 비교이다. A 영역에서 B 영역으로의 천이 과정 전반에 대해 3개의 주요 모드보다 4개의 모드를 이용한 재구성 결과가 좋은 일치 정도를 보이는 점은 대각도 지그재그 시험의 재구성 결과와 같았다.
Fig. 13은 35˚ 선회 시험의 재구성 과정에서 얻어진 a1(t)부터 a4(t)의 변화이다. a1(t)의 변화는 전체적인 운동을 따라가는 가운데 a2(t)로 횡동요가 모사되는 것은 앞서의 대각도 지그재그 시험과 같다. 그리고 Fig. 12에서 설명한대로 세 번째, 네 번째 주요 모드는 C 영역의 운동에 관계하므로, A, B 영역의 운동으로만 구성된 선회 시험에서는 거의 나타나지 않음을 알 수 있다.
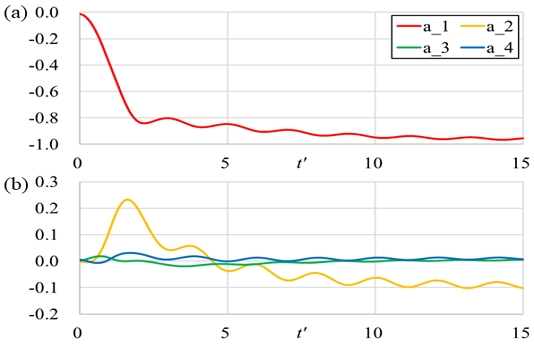
Time history of ai(t) for reconstruction of 35˚ turning circle test results: (a) a1 and (b) a2, a3, and a4
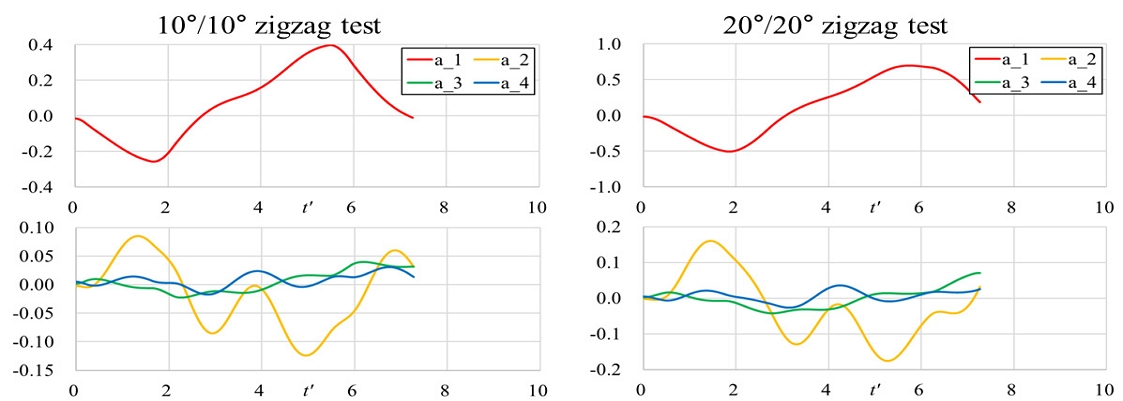
Fig. 14와 Fig. 15는 10˚/10˚과 20˚/20˚ 지그재그 조종 시험에 서 운동 변수와 유체력 및 모멘트 변수에 대한 원 데이터와 재구성 결과의 비교이다. 재구성에 사용한 주요 모드의 개수가 3개에서 4개로 늘어남에 따라 N'H 재구성의 수준이 개선되었으나, 앞의 두 조종 조건과 달리 네 번째 주요 모드까지 사용하더라도 N'H에서 차이가 확인되었다. 이는 지그재그 조종 시험은 조종 운동이 A 영역에서 B 영역으로 진입하기 전에 바로 C 영역으로 넘어가는 천이 운동으로 구성되기 때문에, 완전히 발달된 B 영역과 C영역이 구분되는 대각도 지그재그 조종 시험에서 이러한 천이 운동 영역을 설명할 데이터가 얻어지지 않은 탓으로 보인다. 만약 일반적인 지그재그 시험과 같이 A 영역에서 C 영역으로 바로 천이되는 조종 시나리오의 운동 변수들을 PCA 해석을 위한 데이터에 포함시킨다면 이러한 운동도 잘 재구성할 수 있을 것으로 생각된다.
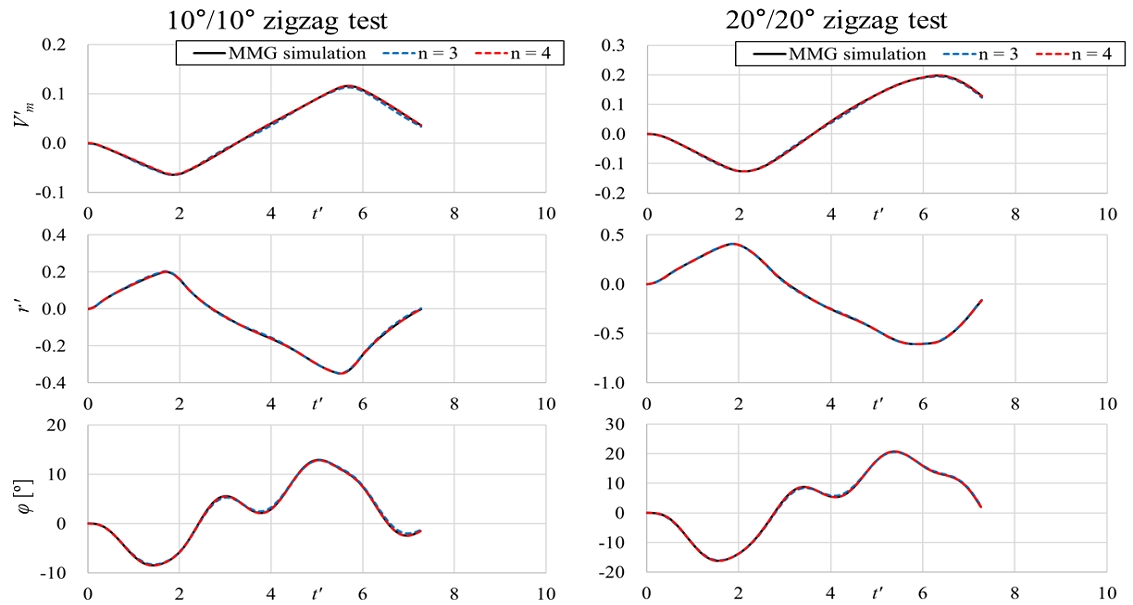
Reconstruction of motion variables of 10˚/10˚ and 20˚/20˚ zigzag test results by principal modes of large angle zigzag tests

Reconstruction of hydrodynamic forces and moments of motion variables of 10˚/10˚ and 20˚/20˚ zigzag test results by principal modes of large angle zigzag tests
X'H에 대해서 재구성에 오차가 있는 점은 다른 운동과 동일하였다. 이를 통해 재구성에 사용하지 않은 여섯 번째 모드가 X'H의 추정에 큰 영향을 주는 것을 다시 확인할 수 있다. 하지만 이 모드는 다른 변수의 영향이 없이 X'H만을 주로 보이기 때문에 다른 변수와의 상관관계로부터 전체적인 경향을 추출해내는 PCA의 목적에는 부합하지 않는다는 문제가 있다. 따라서 PCA를 이용한 조종 운동 모델의 개발에서 고려할 수는 없는 것으로 판단된다.
Fig. 16은 지그재그 조종 시험 결과의 재구성 과정에서 얻은 a1(t)부터 a4(t)의 변화이다. 지그재그 조종 시험은 A, C 영역으로 구성되므로 대각도 지그재그 시험과 같이 천이 운동 영역에서 세 번째와 네 번째 주요 모드가 조종 운동에 영향을 줄 것으로 기대하였으나, a3(t)와 a4(t) 모두 Fig. 11에서와 같은 두드러진 변화는 나타나지 않았다. 따라서 세 번째와 네 번째 주요 모드를 이용한 N'H 추정의 정확도가 앞서 대각도 지그재그 조종 시험의 결과와는 다르게 얻어졌다.
6. 결 론
본 연구에서는 선박의 조종 운동의 저차원화를 위한 PCA의 적용 가능성을 검토하였다. 검증된 MMG 조종 모델을 이용한 대각도 지그재그 조종 운동 시뮬레이션을 수행하고, 여기서 얻은 선체 유체력 데이터와 운동 변수의 상호상관도를 해석하였다. 이를 통해 조종 운동에서 각 변수들간의 선형적 관계의 수준을 확인하였다. 대각도 지그재그 조종 시험은 선박의 조종 과정에서 발생할 수 있는 다양한 운동 양상을 잘 포함하였으며, 이 조종 시나리오를 기반으로 조종 운동 모델 개발을 위한 자유항주 조종 시험을 기획할 수 있을 것으로 보인다.
상호상관도 해석 결과를 이용해 선체 운동과 유체력에 대한 PCA 해석을 수행하였다. 주요 모드에 대응하는 고유값의 분석을 통해 전체 7개의 모드 중 4개로 운동의 99%를 재구성할 수 있었다. 이를 통해 구한 선체의 운동-유체력 관계는 X'H를 제외하고는 원래의 운동을 잘 복원하는 것을 확인하였다.
조종 운동에 대응되는 주요 모드를 식별하였고, 첫 번째 모드는 전반적인 선박의 거동을, 두 번째는 고유 횡동요 운동에 관련한 동적 특성을, 세 번째와 네 번째는 선회 중 반대 방향의 방향타 조종에 대한 운동을 설명할 수 있었다. PCA 해석을 통해 얻은 대각도 지그재그 조종 시험의 주요 운동 모드를 다른 조종 시나리오에 적용하여 한정된 수의 운동 모드로도 다른 조종 운동을 효과적으로 재구성할 수 있음을 확인하였다.
위의 사항을 고려하여, 후속 연구에서는 대각도 지그재그 시험이나 다른 조종 시나리오의 수행을 통해 얻은 운동-유체력 데이터의 주요 모드들을 가지고 운동 입력에 대한 유체력의 출력이 가능한 조종 모델을 개발할 수 있을 것으로 보인다. 그리고 본 연구에서는 조종 시나리오의 수행을 MMG 모델을 이용한 조종 시뮬레이션으로 대체했으나, CFD나 모형시험을 통한 자유항주 시험의 수행 결과로 PCA 해석을 구현하여 본 연구에서 제안된 개념의 실제 적용 사례를 보일 수 있을 것으로 생각된다.
Acknowledgments
이 논문은 2023년도 해양수산부 재원으로 해양수산과학기술진흥원의 지원을 받아 수행된 연구임(RS-2023-00256122, 해양 무인시스템 통합실증 시험·평가기술 개발).
References
-
Araki, M., Sadat-Hosseini, H., Sanada, Y., Tanimoto, K., Umeda, N. and Stern, F., 2012. Estimating maneuvering coefficients using system identification methods with experimental, system-based, and CFD free-running trial data. Ocean Engineering, 51, pp.63-84.
[https://doi.org/10.1016/j.oceaneng.2012.05.001]

-
Hamamoto, M. and Kim, Y.-S., 1993. A new coordinate system and the equations describing manoeuvring motion of a ship in waves. Journal of the Society of Naval Architects of Japan, 173, pp.209-220.
[https://doi.org/10.2534/jjasnaoe1968.1993.209]

-
Hong, S. H. and Lee, S. I., 2010. Vibration analysis of the tapping AFM microcantilevers using proper orthogonal decomposition. Transactions of the Korean Society for Noise and Vibration Engineering, 20(4), pp.414-421.
[https://doi.org/10.5050/KSNVE.2010.20.4.414]

-
Jung, Y. and Yoon, D., 2021. Analysis of null steering anti-jamming performance based on SVD in tactical communication network for small military unit. Journal of Korean Institute of Information Technology, 19(6), pp.65-72.
[https://doi.org/10.14801/jkiit.2021.19.6.65]

-
Kim, Y.-G., Yeo, D.-J., Son, N.-S., Kim, S.-Y., Yun, K.-H. and Oh, B.-I., 2011. Prediction of maneuverability of KCS with 4 degrees of freedom. Journal of the Society of Naval Architects of Korea, 48(3), pp.267-274.
[https://doi.org/10.3744/SNAK.2011.48.3.267]

-
Kim, D.J. and Kim, Y.-G., 2020. Tune of hydrodynamic coefficients based on empirical formula by using menoeuvring performance indices of a ship. Journal of the Society of Naval Architects of Korea, 57(6), pp.331-344.
[https://doi.org/10.3744/SNAK.2020.57.6.331]

-
Kim, D.-H., Sanada, Y., Park, S., Sadat-Hosseini, H. and Stern, F., 2021. URANS simulations for a free-running container ship: Part 1. turning circle. Journal of Hydrodynamics, 33(3), pp.421-447.
[https://doi.org/10.1007/s42241-021-0052-6]

-
Kim, K., Kim, H., Choi, S., Na, K.-I., Lee, H. and Seo, J., 2022. Development of ship dynamics model by free-running model tests and regression. Journal of the Society of Naval Architects of Korea, 59(3), pp.173-182.
[https://doi.org/10.3744/SNAK.2022.59.3.173]

- Lee, H.-Y. and Shin, S.-S., 1998. Approximate technique for ship’s manoeuvrability prediction. Journal of the Society of Naval Architects of Korea, 35(4), pp.19-26.
- Lee, H.-Y. and Shin, H.-K., 1999. Estimation of maneuvering mathematical model by system identification techniques. Journal of Ocean Engineering and Technology, 13(4), pp.118-123.
- Lee, J.H., 2017. Proper orthogonal decomposition and its application: parametric reduced order models. Computational Structural Engineering, 30(1), pp.29-35.
-
Moreira, L. and Soares, C.G., 2003. Dynamic model of manoeuvrability using recursive neural networks. Ocean Engineering, 30(11), pp.1669-1697.
[https://doi.org/10.1016/S0029-8018(02)00147-6]

-
Okuda, R., Yasukawa, H. and Matsuda, A., 2023. Validation of maneuvering simulations for a KCS at different forward speeds using the 4-DOF MMG method. Ocean Engineering, 284, 115174.
[https://doi.org/10.1016/j.oceaneng.2023.115174]

-
Perera, L.P., Oliveira, P. and Soares, C.G., 2015. System identification of nonlinear vessel steering. Journal of Offshore Mechanics and Arctic Engineering, 137(3), 031302.
[https://doi.org/10.1115/1.4029826]

-
Sanada, Y., Park, S., Kim, D.-H., Wang, Z., Stern, F. and Yasukawa, H., 2021. Experimental and computational study of hull-propeller-rudder interaction for steady turning circles. Physics of Fluids, 33, 127117.
[https://doi.org/10.1063/5.0073098]

-
Shin, H., Jung, J.-H. Lee, H.-Y., 2009. Prediction of ship maneuverability by circular motion test. Journal of the Society of Naval Architects of Korea, 46(3), pp.259-267.
[https://doi.org/10.3744/SNAK.2009.46.3.259]

-
Shin, S.-Y., Jung, K.-H., Kang, Y.-D., Suh, S.-B, Kim, J. and An, N.-H., 2017. A study on the effect of large coherent structures to the skin friction by POD analysis. Journal of the Society of Naval Architects of Korea, 54(5), pp.406-414.
[https://doi.org/10.3744/SNAK.2017.54.5.406]

-
Sohn, K.-H. and Kim, Y.-M., 2003. A study on new mathematical model of ship manoeuvring motion taking coupling effect of roll into consideration. Journal of Korean Navigation and Port Research, 27(5), pp.451-458.
[https://doi.org/10.5394/KINPR.2003.27.5.451]

-
Sung, Y.J. and Park, S.-H., 2015. Prediction of ship manoeuvring performance based on virtual captive model tests. Journal of the Society of Naval Architects of Korea, 52(5), pp.407-417.
[https://doi.org/10.3744/SNAK.2015.52.5.407]

-
Sutulo, S. and Soares, C.G., 2014. An algorithm for offline identification of ship manoeuvring mathematical models from free-running tests. Ocean Engineering, 79, pp.10-25.
[https://doi.org/10.1016/j.oceaneng.2014.01.007]

-
Wakita, K., Maki, A., Umeda, N., Miyauchi, Y., Shimoji, T., Rachman, D. and Akimoto, Y., 2022. On neural network identification for low-speed ship maneuvering model. Journal of Marine Science and Technology, 27, pp.772-785.
[https://doi.org/10.1007/s00773-021-00867-1]

-
Wang, Z., Soares, C.G. and Zou, Z., 2020a. Optimal design of excitation signal for identification of nonlinear ship manoeuvring model. Ocean Engineering, 196, 106778.
[https://doi.org/10.1016/j.oceaneng.2019.106778]

-
Wang, Z., Xu, H., Xia, L., Zou, Z. and Soares, C.G., 2020b. Kernel-based support vector regression for nonparametric modeling of ship maneuvering motion. Ocean Engineering, 216, 107994.
[https://doi.org/10.1016/j.oceaneng.2020.107994]

-
Xu, H. and Soares, C.G., 2016. Vector field path following for surface marine vessel and parameter identification based on LS-SVM. Ocean Engineering, 113, pp.151-161.
[https://doi.org/10.1016/j.oceaneng.2015.12.037]

-
Xu, H., Hinostroza, M.A. and Soares, C.G., 2018. Estimation of hydrodynamic coefficients of a nonlinear manoeuvring mathematical model with free-running ship model tests. International Journal of Maritime Engineering, 160(3), pp.213-225.
[https://doi.org/10.3940/rina.ijme.a3.2018.448]

-
Yang, K.-K., Kim, Y.-C., Kim, K.-S. and Yeon, S.M., 2022. Numerical analysis on turning and yaw checking abilities of KCS in calm water a based on free-running simulations. Journal of the Society of Naval Architects of Korea, 59(1), pp.1-8.
[https://doi.org/10.3744/SNAK.2022.59.1.1]

-
Yasukawa, H. and Yoshimura, Y., 2015. Introduction of MMG standard method for ship maneuvering predictions. Journal of Marine Science and Technology, 20, pp.37-52.
[https://doi.org/10.1007/s00773-014-0293-y]

-
Yasukawa, H., Hirata, N. and Yamazaki, Y., 2018. Effect of bilge keels on maneuverability of a fine ship. Journal of marine Science and Technology, 23, pp.302-318.
[https://doi.org/10.1007/s00773-017-0474-6]

-
Yasukawa, H., Sakuno, R. and Yoshimura, Y., 2019. Practical maneuvering simulation method of ships considering the roll-coupling effect. Journal of Marine Science and Technology, 24, pp.1280-1296.
[https://doi.org/10.1007/s00773-019-00625-4]

-
Yoo, C., 2020. Estimation of cosine similarity change in singular value decomposition. Journal of Korean Institute of Information Technology, 18(3), pp.31-37.
[https://doi.org/10.14801/jkiit.2020.18.3.31]

-
Yoon, H.K., Son, N.S. and Lee, G.J., 2007. Estimation of the roll hydrodynamic moment model of a ship by using the system identification method and the free running model test. IEEE Journal of Oceanic Engineering, 32(4), pp.798-806.
[https://doi.org/10.1109/JOE.2007.909840]

-
Yun, H.K. and Son, N.S., 2004. Estimation of roll related coefficitnes of a ship by using the system identification method. Journal of the Society of Naval Architects of Korea, 41(4), pp.53-58.
[https://doi.org/10.3744/SNAK.2004.41.4.053]

-
Yun, K. and Yeo, D.J., 2019. An experimental study on the manoeuvrabiilty of a ship in heeled condition. Journal of the Society of Naval Architects of Korea, 56(3), pp.273-280.
[https://doi.org/10.3744/SNAK.2019.56.3.273]

-
Yun, K., Choi, H. and Kim, D.J., 2021. An experimental study on the manoeuvrability of KCS with different scale ratios by free running model test. Journal of the Society of Naval Architects of Korea, 58(6), pp.415-423.
[https://doi.org/10.3744/SNAK.2021.58.6.415]

-
Yun, K., Kim, D.J., Yeon, S.M., Kim, Y.-C., Kim, Y.G. and Yang, K.-K., 2022. A study on the manoeuvrability of 1/42.0 scaled KCS. Journal of the Society of Naval Architects of Korea, 59(5), pp.262-270.
[https://doi.org/10.3744/SNAK.2022.59.5.262]

Appendix
부록: 4DOF MMG Standard 기법
부록에서는 Yasukawa and Yoshimura (2015)에서 제안한 선박 조종 운동 모델인 MMG Standard 기법에 대한 상세한 내용을 다룬다. Okuda et al. (2023)의 연구에서는 이 조종 운동 모델에 횡동요 운동을 추가해 4자유도 운동 모델을 개발해 이용하였다.
수평면선체고정좌표계
3자유도 조종 모델에서는 운동좌표계의 원점은 선체의 길이방향 중심이나 무게중심이 수면에 투영된 점에 놓이고 운동 방향은 선수, 우현, 아래를 향하는 선체고정좌표계가 이용된다. 이 좌표계에서는 횡동요가 없기 때문에 x, y축은 항상 수평면에 놓인다.
횡동요를 더한 4자유도 조종모델에서 선체고정좌표계를 이용하면 선체의 횡경사각(ϕ)으로 인해 좌우동요 운동이 수평면에 대해 기울어져 해석되어야 한다. 하지만 조종 시 운동은 수평면상에서 이뤄지므로 운동의 주된 방향이 선체고정좌표계에서 정의되는 좌우동요와 불일치하는 문제가 있어, 횡동요 운동 시 추가적인 좌표계 변환이 요구된다.
Hamamoto and Kim (1993)은 선체 운동의 해석을 위한 운동좌표계는 수평면에 고정하고 ϕ은 선체의 상태변수로만 사용하는 수평면선체고정좌표계(horizontal ship-fixed coordinate system)를 제안했다. 이는 지구고정좌표계에서 물체고정좌표계로의 오일러 각(Euler angle) 변화에서 선수동요 방향의 좌표계 회전만을 운동좌표계에 반영한다는 의미이다. 이러한 좌표계는 4자유도 선박 운동의 해석에서 자주 사용되었다 (Sohn and Kim, 2003; Kim et al., 2011; Araki et al., 2012; Yasukawa et al., 2018).
선체 유체력 모델
선체 유체력 모델은 식 (11)과 같은 다항식으로 나타낼 수 있으며, 여기에 사용된 조종계수는 Table 3과 같다.
| (11) |
횡동요 운동 모델
횡동요 운동에 대한 모델은 식 (3)에서 보인 바와 같이 좌우동요운동의 유체력, 복원모멘트, 감쇠항으로 구성되며, 별도의 조종계수로 표현하지 않았다. 이렇게 좌우동요 힘으로부터 횡동요 모멘트를 설명하는 모델이 Sohn and Kim (2003)과 Araki et al.(2012)에서도 사용된 바 있다. 방향타 성분도 마찬가지로 좌우동요 유체력에 대한 모멘트 암 길이(zR)만을 고려한다. 만약 조종 계수가 직접 반영된 횡동요 운동 모델을 다루려 한다면 Yasukawa et al. (2018)의 연구를 참고할 수 있다.
본문의 식 (3)에서 횡동요 운동은 선체와 방향타 성분으로 구성되는데, 선체 성분은 좌우동요 유체력과 모멘트 암 길이(zH), 복원력, 횡동요에 대한 선형 및 비선형 감쇠항으로 계산한다. Okuda et al. (2023)은 횡동요에 대한 선형, 비선형 감쇠항을 식 (12)와 (13)을 통해 계산하였다.
| (12) |
| (13) |
aϕ, bϕ는 횡동요 감쇠시험(roll decay test)를 통해 구할 수 있으며, Okuda et al. (2023)의 연구에서 제안된 값은 설계속도에서 각각 0.031, 0.002으로, 이 값을 본 연구에서도 적용하였다.
추진기 유체력 모델
추진기는 단독 성능 곡선을 이용하되, 직진과 조종 운동 중의 반류비를 고려해 유입류의 속도를 정한다. 추력(T)에 대한 추력감소비(tP)를 고려하여 선체에 실질적으로 가해지는 XP는 식 (14)와 같이 나타낸다.
| (14) |
여기서 T는 식 (15)와 같이 추진기의 전진비(JP)의 함수로 나타나는 추력계수(KT)를 추진기 회전수(nP), 추진기 지름(DP), 물의 밀도(ρ)를 이용해 차원화한 값이다. KT는 JP에 대한 이차함수로 근사한다.
| (15) |
JP는 모형선의 전진속도(u)와 반류비(wp)를 고려하여 식 (16)을 이용해 계산한다.
| (16) |
wP는 자항 해석에서 다루는 직진상태의 반류비(wP0)와 추진기 유입류가 갖는 사항각(βP)을 이용해 식 (17)로 계산된다.
| (17) |
여기서 x'P 와 z'P 은 각각 xP와 zP를 L로 나눠 무차원화한 값이다.
추진기의 조종 계수를 Table 4에 정리하였다. 앞서 설명하였듯 본 연구에 사용된 추진기는 KCS를 위해 개발된 프로펠러인 KP505가 아니므로, nP는 KP505 프로펠러를 이용한 KCS 모형선의 자유항주 시험 결과와 다소 다를 수 있다.
방향타 유체력 모델
방향타의 유체력과 모멘트는 방향타의 유입류 속력(UR)과 받음각(αR)에 따른 양력으로부터 구한다. 방향타의 코드(chord)방향에 대해 수직인 방향의 힘(FN)은 식 (18)과 같이 계산한다.
| (18) |
여기서 fα는 방향타 단면 형상의 받음각에 따른 양력 크기의 변화율로, 받음각-양력계수 그래프의 기울기로 볼 수 있다 (Yasukawa et al., 2018). 원래 양력은 유동 방향에 수직인 성분으로 정의되지만 여기서는 방향타에 수직인 방향 성분만을 취하게 된다.
방향타의 x방향, y방향 유입류 속도를 각각 UR, vR이라 하면 Ur과 αR은 각각 식 (19), (20)과 같이 나타낼 수 있다.
| (19) |
| (20) |
여기서 uR은 추진기의 추력으로 인해 가속되는 유속으로 보아 식 (21)을 이용해 구한다. 그리고 ϵ은 추진기와 방향타의 유입류 속도의 비율, κ는 보정을 위한 상수인데, Okuda et al. (2023)의 연구에서는 둘 모두 모형시험을 통해 구하였다.
| (21) |
vR은 추진기와 마찬가지로 선체 전체의 좌우동요와 선체의 선수동요로 인한 횡방향 속도 성분의 합으로 구한다.
| (22) |
여기서 γR은 정류계수(flow straightening coefficient), l'R은 방향타의 길이방향 유효 위치를 L에 대한 비율로 나타낸 값이다. 방향타가 좌우 비대칭의 유입류에 놓이기 때문에 좌우현에 대해 γR은 다른 값을 갖는다. l'R은 실제 방향타의 위치가 아니라 U라는 균일한 유속에 놓인 방향타에서 발생하는 선수동요의 모멘트에 대응되는 모멘트 암 길이로 이해할 수 있다.
이제 FN으로부터 XR, YR, KR, NR을 구할 수 있다. 그 결과는 식 (23)과 같다. 수평면선체고정좌표계의 특성 상 y방향 힘 성분은 cosϕ를 고려해줘야 한다.
| (23) |
여기서 tR은 선체-방향타 상호작용 계수로 방향타 유체력 중 x방향 성분의 증가율을 의미한다. aR는 방향타 유체력 중 y방향 성분의 증가계수, xH는 y방향 유체력의 작용점의 x방향 위치이다. 앞에서 열거한 방향타의 조종 계수를 Table 5에 정리하였다.