수압시험 시 관 단면적 비 및 충수 속도별 탱크 내부 과압 발생에 관한 해석
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This study was conducted based on the case of an accident (excessive deformation) that occurred during the hydraulic test of a shipboard tank manufactured in accordance with the design regulations. Over-pressure phenomenon was noted as the main cause of accidents in the process of testing tanks without physical damage, which can be found in external factors such as cross-sectional difference between inlet pipe and air pipe and higher water filling rate than the recommended one. The main goal of this paper is to establish a safe water filling rate according to the range of sectional area ratio(SAR) reduced below the regulations for each test situation. The simulation was conducted in accordance with the hydraulic test procedure specified in the Ship Safety Act, and the main situation was divided into two types: filling the tank with water and increasing the water head to the test pressure. The structural safety evaluation of the pressure generated inside the tank and the effect on the structure during the test was reviewed according to the SAR range. Based on the results, guidelines for the optimal filling rate applicable according to SAR during the hydraulic test were presented for the shipboard tanks used in this study.
Keywords:
Shipboard tank, Hydraulic test, Sectional Area Ratio(SAR), Water filling rate키워드:
선상 탱크, 수압 시험, 단면적 비, 충수 속도1. 서 론
산적화물선 및 유조선 공통구조규칙에 따르면 유체 저장을 목적으로 하는 탱크의 경우, 준공 이후 수압시험을 통해 탱크와 수밀경계의 수밀성 및 탱크의 구조적 안전성을 확인하도록 명시하고 있다. 하지만 규정에 따라 설계되어 물리적인 결함이 없는 선상 탱크의 수압시험 과정에서 과도한 변형이 발생한 사례가 있다. 과도 변형의 경우 수압 해제 후에도 탱크 외판에 영구 변형이 발생하며, 영구 변형이 발생한 경우 외부 도장을 제거한 후 곡직 작업(fairing)을 수행하여 변형된 판을 복원시키고 보강 후 재시험을 실시한다. 추가 작업으로 인해 발생한 예상치 못한 작업 기한의 연기는 조선소 내 한정된 도크의 전체 작업 공정에 부정적인 영향을 미친다.
선상 탱크의 수압시험 사고 예방을 위해 원인을 파악하고 분석하기 위한 사고 사례 및 선행 연구를 찾고자 하였으나, 조선소 내부 문제와 연계되어 한계가 있었다. 이러한 이유로 수압시험 사고의 원인을 파악하기 위해 다른 산업군에서 발생한 수압시험 사고 사례를 조사하였다. 2013년 볼트 접합 방식의 육상용 저장 탱크에 대한 수압시험 도중, 부품의 결함으로 인해 누수가 발생하였음에도 시험을 지속하다 하중을 견디지 못하고 물탱크가 붕괴하는 사고가 발생하였다 (Lee, 2013). 이 사고는 탱크의 제조 관점에서 재료의 결함 혹은 용접부 불량 등의 문제가 발생하지 않도록 주의해야 함을 시사한다.
또 다른 사고 사례로, 저온의 청수를 이용하여 수직형 압력용기의 수압시험 중 용기 상단 취성 파단사고가 발생하였다 (Parthiban, 2012). 또 다른 수직형 압력용기 폭발 사고의 발생 원인은 과압(over-presuure)이다. 용기 내 주수되는 유량에 비해 빠져나가는 공기의 양이 적어 내부에 과압이 발생하였으며, 이는 상단부 환기용 파이프가 비닐 등의 물체에 의해 막혔던 것으로 밝혀졌다 (Dey, 2017). 수압시험의 절차와 진행에 관련된 규정이 존재하여도 시험 과정에서 사고가 발생하였으며, 그 결과 구조물의 심각한 손상과 심한 경우 인명피해까지 발생하였다.
본 연구에서는 물리적 결함이 없는 탱크의 수압시험 과정에서 과도한 변형이 발생한 사고의 원인을 탱크 내부 공기에 의한 과도 압력으로 가정하였다. 물리적 결함 없이 제작된 탱크의 경우 시험 압력에 대해서도 내하력을 가져야 하므로 이론적으로는 과도 변형이 발생하지 않아야 하기 때문이다. 하지만 시험 과정에서 탱크 내부의 공기가 압축될 경우, 기존 수두 압력에 추가적인 하중이 가해져 탱크 구조에 변형을 야기할 수 있다. 본 연구에서는 위 가정을 해석적으로 증명하고자 한다.
우선 과압을 유발할 수 있는 상황을 확인하고자 운용적 측면에서의 외적 요인을 검토하였다. 조선소 작업 현장에서 탱크 수압시험 시 과압을 유발할 수 있는 상황으로는 탱크 내부의 부유성 이물질에 의한 관막힘(Fig. 1(a)), 부적절한 크기의 수두 측정용 호스 체결(Fig. 1(b)), 복잡한 작업 환경에서의 호스 접힘(Fig. 1(c)) 등이 있다. 이러한 시험 환경은 공기관의 단면적을 감소시키는 예이다.
그리고 예정된 작업 일정을 준수하기 위해 적정 충수 속도 이상으로 작업을 진행할 경우 탱크 내부에 과압을 유발할 수 있다. 이를 근거로 주요 해석 변수를 주수관(water inlet pipe)과 공기관의 단면적 비(Sectional Area Ratio, SAR)와 충수 속도 두 가지를 설정하여 사례 연구(case study)를 수행하였다.
본 연구에서는 물리적 결함이 없는 선상 탱크의 수압시험 과정에서 과도 변형 발생 사고에 대한 주요 원인으로 공기 압축에 의한 과압 현상에 주목하였다. 과압을 유발할 수 있는 상황을 수압시험 현장 실태를 바탕으로 파악하고, 발생 가능한 상황을 조합한 해석 시나리오를 시뮬레이션하였다. 분석 결과를 바탕으로 탱크 내부에 발생한 압력이 구조물에 과도 변형을 유발하지 않도록 하는 상황별 충수 속도에 대한 가이드라인을 제시하였다.
2. 수압시험 변형 원인 분석 및 해석 시나리오 수립
2.1 수압시험 정의 및 과압 선정 기준
수압시험이란 규정된 높이만큼 물을 탱크에 채운 뒤 수두압력을 바탕으로 구조적 안전성을 만족하는지 테스트하고, 충수 과정에서 구조물의 균열과 같은 결함에 의한 누수 여부를 확인하는 시험이다. 시험은 공기관과 수두 측정용 호스를 연결하여 규정의 시험 수두까지 호스를 올리고 물 넘침(overflow) 여부를 통해 적정 시험 압력(testing pressure)이 가해졌는지 확인한다. 수압시험의 절차는 선박 검사관이 입회하여 탱크 내 · 외부의 배수설비의 개방을 확인하고, 탱크 내부의 부유성 이물질이 없도록 관리하며, 규정 충수 높이별로 충수를 진행한 뒤 변형의 정도와 누수 여부 등을 체크리스트에 작성하는 것이다 (MOF, 2020). 시험 압력까지 올린 호스에서 물 넘침이 발생하게 되면 주수를 중단하고 시험 압력 하에서 24시간 유지한 채 변형과 누수 여부를 확인한다. 실무에서는 탱크 이면에서 불빛을 이용하여 변형 여부를 검사하고(Fig. 2(a)), 균열 또는 체결 불량 등 결함부에서 발생하는 누수를 육안으로 확인하거나 미세균열 등의 경우 비눗물 테스트를 이용하여 결함 여부를 확인하게 된다(Fig. 2(b)).
탱크의 수압시험에 관련된 규정으로 미국석유협회(API)의 기술기준 코드 650에서는 수압시험 중 수위가 올라가는 속도인 충수 속도를 탱크의 높이에 따라 Table 1과 같이 구분하여 제시하고 있다 (API, 2020). 그리고 본 연구에서는 과압의 기준을 선정하기 위해 국제선급연합회(IACS)의 산적화물선 및 유조선 공통구조규칙(CSR-H)과 노르웨이 선급 협회(DNV-GL)의 설계 규정을 참조하였다. CSR-H에서는 공기관 또는 넘침관에서의 설계압력은 25kPa 이상일 것을 요구하고 있으며 (IACS, 2021), DNV-GL piping system 규정에 따르면 펌프의 용량이 공기관의 단면적에 비해 클 경우 공기관의 물 넘침 발생 시 동적 압력 증가가 25kPa을 초과하지 않을 것을 명시하고 있다 (DNV, 2021). 이를 바탕으로 본 연구에서는 최소 설계압력이자 최대 동적압력 기준인 25kPa을 과압에 대한 기준으로 평가하고자 하였다. 하지만 설계하는 탱크의 강성에 따라 구조물 변형에 영향을 주는 압력이 과압에 대한 기준치와 상이할 수 있으므로 유의할 필요가 있다.
2.2 공기관 단면적 감소에 의한 과압 현상
수압시험 과정에서는 공기관의 단면적 감소를 유발할 수 있는 다양한 상황이 발생할 수 있다. 시험 과정에서 과압을 유발할 수 있는 첫 번째 상황은 공기관의 단면적 감소이다. 탱크의 준공 이후 수압시험을 실시하기 전 부유성 이물질을 미처 파악하지 못하고 진행하였을 경우 이러한 이물질들이 시험 과정에서 공기관을 막게 되어 탱크 내부에 과압을 유발할 수 있다. 수압시험이 원활하게 진행된다 하더라도 수두 높이를 측정하기 위해 실제 공기관의 직경보다 작은 크기의 수두 측정용 호스를 체결할 경우에도 유사한 문제가 발생할 수 있다. 또는, 작업 환경에 따라 호스의 접힘 등의 이유로 과압이 발생할 수 있다. 예를 들어, 공기관의 단면적 감소로 인해 발생하는 주수관과 공기관의 단면적의 차이가 2.5배로 가정하여 연속방정식을 적용한 관의 유속 관계는 v2 = 6.25 v1이다. 관의 유속 관계를 베르누이 방정식에 적용하여 식 (1)와 같이 단면적 차에서 기인한 주수관과 공기관의 압력차 (P1-P2)를 도출할 수 있다. 여기서, 우변의 첫 번째 항은 동압력(dynamic pressure) 성분이며, 우변의 두 번째 항은 정수압(hydraulic pressure) 성분이다.
| (1) |
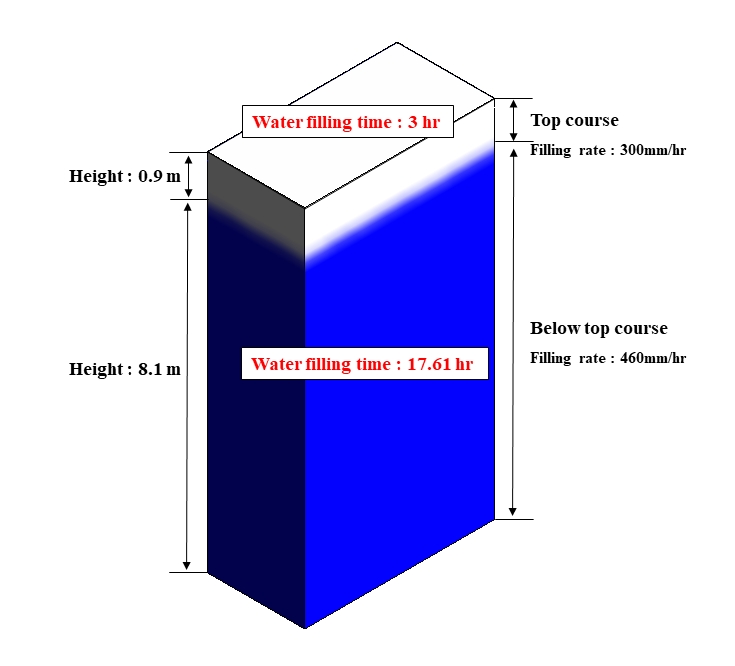
계산을 위한 기본 조건으로 주수관의 직경 100mm (단면적 7,854mm2), 공기관의 직경 40mm ~ 100mm (단면적 1,257mm2 ~ 7,854mm2)를 가지는 높이 9m의 탱크에 2시간 동안 총 유량 101.1m3을 채웠다고 가정할 때, 위의 과정을 통해 소요 시간에 따른 두 관의 압력 차이를 계산할 수 있으며 그 결과는 Table 2와 같다. 계산에 사용된 밀도는 청수의 충수를 고려하여 ρ = 999 kg/m3 을 사용하였으며, 주수관의 위치는 탱크 최하단으로 가정하였다. 주수관과 공기관의 단면적 차이를 위의 예와 같이 0.16~1.00배로 하여 수압시험을 진행하게 되면 관의 단면적 차에서 기인하는 압력 차이로 인해 구조 변형 가능성이 상존함을 알 수 있으며, 단면적 비를 변수로 하여 과압의 발생 여부를 추가적으로 검토할 필요가 있다.
2.3 적정 속도 이상의 충수에 의한 과압 현상
유량의 경우 주수관의 단면적과 관을 통해 들어오는 유체의 속도에 의해 결정된다. 이와 관련된 규정인 API 650에서는 수압시험 시 물이 차오르는 속도인 충수 속도를 규정하고 있으며 그 값은 앞서 설명한 Table 1과 같다. 규정 충수 속도를 바탕으로 본 연구의 해석 대상인 요소수 저장탱크(urea water storage tank)의 수압시험에 소요되는 시간을 계산하면 만수까지 약 20시간 이상이 걸리는 것을 확인할 수 있다(Fig. 3).
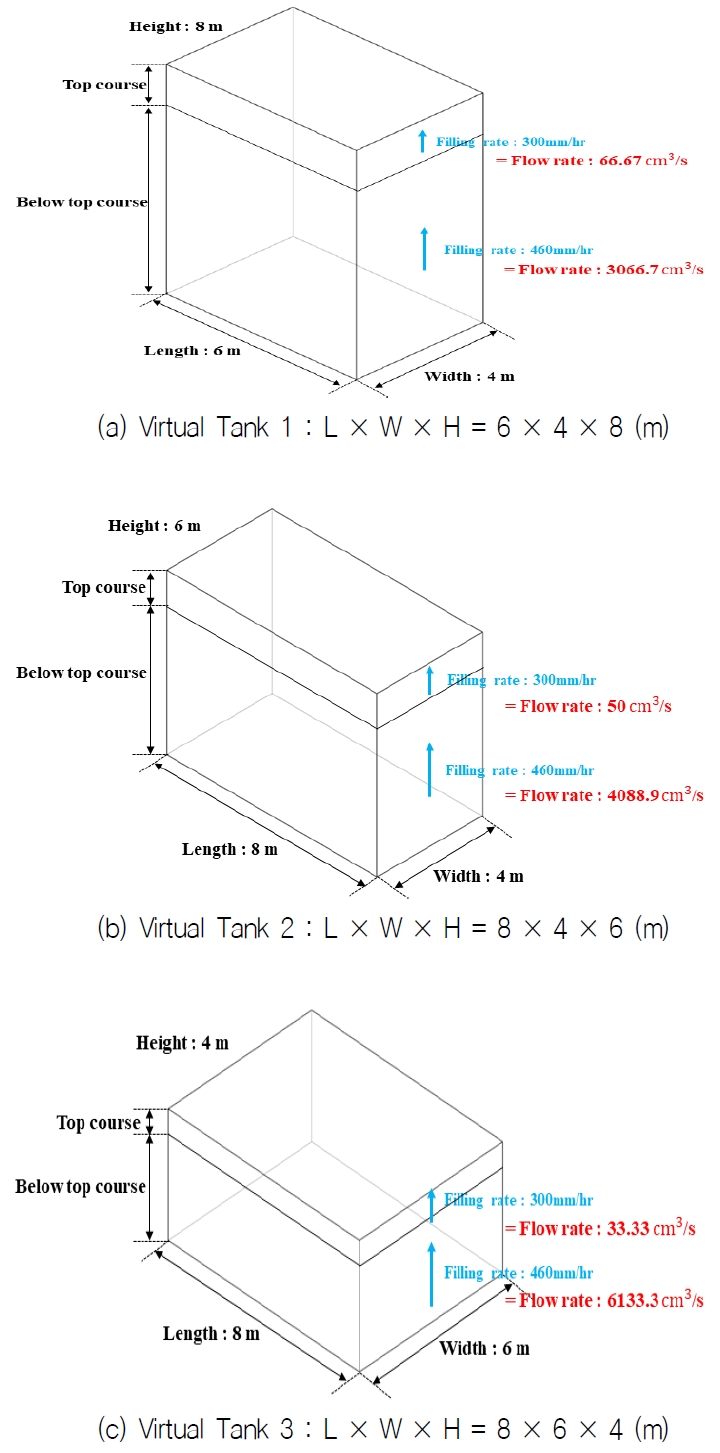
API 규정 내 권장 충수 속도는 탱크 구획에 따라 제안된다. 하지만 탱크의 용적에 따른 구분이 없기 때문에, 동일한 용적을 가지는 높이가 다른 탱크의 경우 규정 충수 속도라 할지라도 주수되는 실제 유량에 차이가 발생한다. 이를 설명하고자 동일 용적의 높이가 다른 가상의 탱크를 대상으로 주수되는 유량의 차이와 소요시간을 Fig. 4에 나타내었다. 결과적으로 규정에서 제안하는 충수 속도는 동일 용적의 탱크 내에서 단면적 대비 높이가 높은 탱크일수록 보수적인 제안이 되는 것을 의미한다.
이 절에서는 API에서 제안하는 충수 속도를 기준으로 시험을 진행할 경우 특정 탱크에서는 상당한 소요 시간이 발생할 수 있음을 확인하였다. 또한, 탱크의 제원에 따라서 보수적인 접근이 될 수 있음을 확인하였다. 그러므로 실제 수압시험 환경에서 사용가능한 속도를 변수로 하여 탱크 내부의 발생 압력에 대해 추가적으로 검토할 필요가 있다.
2.4 해석 시나리오 선정
해석 시나리오를 선정하기 위해 본 연구에서 채택한 첫 번째 주요 변수는 관의 직경 차이에 따른 단면적 감소이다. 관련 설계 기준인 노르웨이 선급 협회(DNV-GL)의 규정에 따르면, 탱크가 가장 큰 펌프로 과도 주수되는 경우에도 탱크 구조가 압력을 견딜 수 있도록 공기관의 치수가 지정되어야 함을 명시하고 있다. 또한, 펌프의 용량이 공기관의 단면적에 비해 클 경우 물 넘침 시 공기관의 압력 강하를 계산한 문서를 요구하고 있다. 물 넘침이 발생할 경우 동적 압력 증가가 25kN/m2을 초과하지 않는지 계산으로 확인하여야 하며, 공기관의 내부 지름은 50mm 이상일 것과 공기관 단면적은 주수관 단면적의 125% 이상일 것을 요구하고 있다.
설계 관점에서 규정 요구치를 만족하는 선상 탱크라 할지라도, 2.2절에서 고려한 수압시험 과정에서 공기관의 단면적 감소를 유발할 수 있는 다양한 상황을 반영하여 이를 설계 변수로 지정하였다. 실제 설비되는 요소수 저장탱크의 주수관과 공기관의 단면적 비(2.56)를 바탕으로 DNV 규정에서 요구하는 단면적 제한 범위를 고려하였다. 추가적으로 시험 과정에서 발생할 수 있는 단면적이 감소된 상황을 고려하여, 실제 현장에서 사용하는 수두 측정 호스 제원을 바탕으로 계산한 주수관과 공기관의 면적 비(0.16)까지 일정 간격으로 분할하여 해석 시나리오를 설정하였다. 다음으로 유속 선정 기준으로서 옥내 · 외 소화전설비 안전기준에 명시된 설비 가압송수장치의 성능 기준인 정격토출압력 1.7 ~ 7bar 내외의 방수 압력을 일정 간격으로 분할하여 유속에 대한 변수를 설정하였다. 방수 압력으로부터 방수량(liter/min)을 계산하는 식은 아래 식 (2)~(4)을 적용할 수 있다(NFA, 2013).
| (2) |
| (3) |
| (4) |
여기서, P1과 P2는 방수압력을 나타내며(각각 kg/cm2,MPa), D1과 D2는 주수관 직경을 나타낸다(각각 mm, m).
본 연구에 사용된 요소수 저장탱크의 경우 관의 단면적 비가 DNV-GL 규정 공기관 설계 요구치를 만족하는 사례(Case A~C) 및 단면적 비가 감소한 사례(Case D~G)로 구분하여 시나리오를 설정하였다. 그리고 소방 설비 안전기준을 만족하는 가압송수장치의 방수량(liter/min)을 유량(m3/s)으로 환산하여 위 사례들과 조합한 결과 Table 3과 같은 해석 시나리오를 선정할 수 있었다.
3. 유동해석을 통한 수압시험 시뮬레이션
2.2절에서 베르누이 방정식을 이용하여 관의 단면적 차에 기인한 압력 차 계산식을 정리하였다. 하지만 이는 물을 비압축성, 비점성 상태로 가정하여 계산되었다. 실제 탱크의 수압시험 과정에서는 충수에 따른 물과 탱크 벽면의 마찰이 고려되어야 하며, 수위의 상승에 따라 공기관을 통해 빠져나가지 못한 내부 공기의 압축이 반영된 탱크 내 압력을 확인할 필요가 있다. 이와 같은 상황을 반영하여 유동해석을 수행함으로써 탱크 내부의 과압 현상을 시뮬레이션하였고, 해석 시나리오별 탱크 내부에 발생한 압력 결과를 구조 해석의 작용 하중으로 사용하였다.
3.1 모델링 및 해석 조건
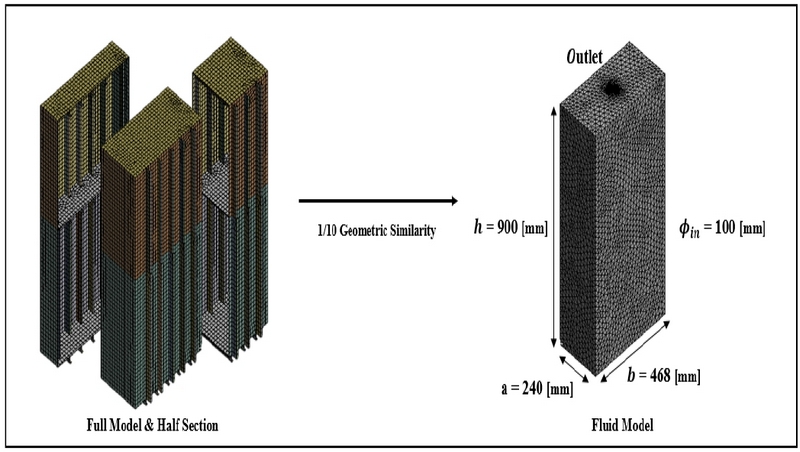
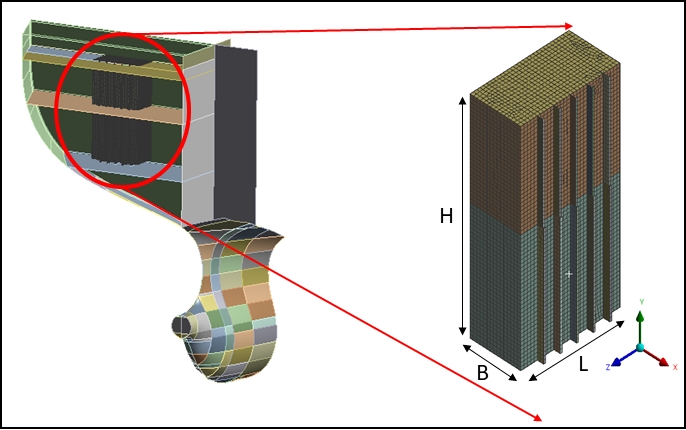
유동 해석을 수행하기 위해 ANSYS 2022 R1 상용 해석 프로그램 내 모델링 프로그램인 SpaceClaim을 이용하여 모델링을 수행하였다. 체적 추출(volume extract) 기능을 통해 구조 해석용 모델의 내부 체적을 추출하여 유동 영역으로 설정하였으며, 추출한 유동 영역은 1/10 축척비로 상사하였다(Fig. 5).
본 유동해석에서는 경계조건인 입구영역 및 출구영역 지정에 있어 주수관과 공기관의 모델링이 불가피하다. 그러나 해석 대상의 특성상 전체 탱크의 사이즈에 비해 상대적으로 매우 작은 크기인 관을 모델링하는 것은 상당한 문제를 유발할 수 있다. 즉, 전체 모델 영역 대비 미소한 길이를 가지는 영역에 대해 모델링을 진행하고 요소망을 생성할 경우 요소 크기의 급격한 변화로 인해 해석의 수렴성이 저해된다. 또한 유체의 점성을 반영할 경계층(boundary layer)을 구현하기 위해서 더 작은 크기의 요소로 요소망을 생성해야 하며, 이는 해석을 위한 전체 요소 수 증가의 요인이 된다. 이러한 경우, 해석 목적을 명확하게 함으로서 해석 과정에서 불필요한 계산을 줄일 수도 있다.
본 연구에서 유동해석을 수행하는 주요 목적은 앞서 가정한 시나리오별 충수 과정에 따라 발생하는 탱크 내부의 압력을 확인하는 것이다. 주수관으로부터 물이 뿜어져 나오는 유동 현상이나 구조물과 유체의 충격에 의해 발생하는 수격현상(water hammer)은 고려 대상이 아니게 된다 (Heo et al., 2001). 그러므로 시나리오별 주수관을 통해 유입되는 유량을 바탕으로, 식 (5)과 (6)을 이용하여 충수 속도를 계산한 뒤 이를 해석에 반영하여 수압시험 과정을 비 원형 관의 유동으로 해석하였다. 비 원형 관내 유동해석 수행 절차에 대한 도움은 Chung et al. (2021)의 튜브 내 다상 열유동해석을 위한 조건 셋업 절차를 참고하였다. 결과적으로 주수관을 모델링할 필요 없이 충수 과정과 그 과정에서 발생하는 탱크 내부의 압축현상을 잘 모사할 수 있도록 하였다.
| (5) |
| (6) |
여기서, Qinlet과 vinlet및 vfill은 각각 주수관을 통한 유량(m3/s)과 유속(m/s) 그리고 탱크 내부의 충수 속도(m/s)를 나타내며, Ainlet과 At는 각각 주수관 단면적(m2)과 탱크의 단면적(m2)을 나타낸다.
본 연구에서의 유동해석은 여러 해석 시나리오를 효과적으로 수행하기 위해 실물 크기의 원형(prototype)이 아닌 1/10 스케일 축소를 한 유동영역 모형(model)에 대해서 진행하였다. 수압시험 현상 시뮬레이션을 통해 구하고자 하는 목적을 바탕으로 시험 과정을 비원형 관내 유동으로서 단순화하였으며, 관내 유동은 점성력과 관성력이 지배적인 유동으로 잘 알려져 있으므로 원형과 모형 간의 레이놀즈 수(Reynolds number, Re)를 일치시켰다.
| (7) |
| (8) |
여기서, ρ는 유체의 밀도(kg/m3), v는 유속(m/s), μ는 유체의 점성계수(m2/s), Dh는 수력 직경(m)을 의미한다.
원형과 모형에서 동일한 유체에 대해 고려하므로 식 (7)에서 밀도와 점성계수는 같은 값을 사용하며, 비원형 관에 대한 해석이므로 관의 길이 대신 수력직경을 사용하여 레이놀즈 수를 계산하였다. 수압시험 과정을 역학적으로 상사한 모형을 통해 유동 해석을 수행하였으며 대응하는 원형 점에서의 압력 값으로의 변환은 식 (9)에서 나타낸 압력에 관한 무차원 수인 오일러 수(Euler number, Eu)를 이용하여 변환하였다 (Nam, 2014).
| (9) |
본 연구에서 유동해석을 수행하는 주요 목적은 앞서 가정한 시나리오별 충수 과정에서 탱크 내부에 발생하는 압력을 확인하는 것이다. 충수 과정별 해석 결과로부터 내부 과압이 발생하는 시점과 그 정도를 파악하기 위해서는 시간에 따라 내부 유동이 달라지는 비정상 유동(unsteady flow)을 수행하여야 한다. 또한, 탱크 내부에 존재하는 공기는 환기가 제대로 이루어지지 않을 경우 충수가 진행됨에 따라 압축되므로 압축 여부에 따라 밀도가 변화하는 이상기체(ideal gas)로 물성을 부여하였다.
수압시험에서 고려하는 유체는 공기와 물이므로 서로 다른 상(phase)을 가진 유체에 대한 해석인 다상유동(multiphase flow) 해석을 수행하였다. 서로 다른 섞이지 않는 두 유체에 대한 유동해석을 수행하기 위해서 VOF 모델(Volume of Fluid)을 적용하였다. VOF 모델이란 섞이지 않는 두 유체의 유동에 대해 하나의 운동량방정식으로 해석영역의 각 유체의 체적율(volume fraction)을 계산하는 방법이다 (KAERI, 2007). 충수가 진행됨에 따라 상간의 경계면을 추적하기 위한 임의의 q번째 상에 대한 체적 분율 연속방정식은 식 (10)과 같다 (Ansys Inc., 2012).
| (10) |
여기서, α는 셀에서의 부피 분율, Sα는 각 상에 대한 사용자 정의 추가 질량 상수, 는 p상에서 q상으로의 물질 전달을 의미한다.
| (11) |
모든 셀은 식 (11)과 같이 각 상의 체적율 합이 항상 1을 만족하여야 한다. 예를 들어, α1 = 1은 첫 번째 상에 해당하는 유체로 가득 채워진 상태를 의미하고, 0 < α1 < 1 은 셀 내 첫 번째 유체와 다른 유체 사이의 인터페이스를 포함하는 것을 의미한다.
다상유동 모델의 계산은 각 상에 대해 질량, 에너지 및 운동량 방정식을 독립적으로 수행한다. 이후 서로 다른 상끼리 질량, 에너지 및 운동량 교환을 수행하기 위해 수송방정식을 통해 계산에 필요한 물성치를 체적율 평균(volume fraction averaged)으로 변환하여 계산에 반영한다. 2상 시스템에서 두 번째 상의 체적 분율을 계산하고자 할 경우, 예를 들어 밀도 ρ = α2ρ2+ (1 - α2)ρ1 과 같이 계산되며, 밀도의 체적율 평균을 계산하는 일반식은 (12)와 같이 표현한다(Cho et al., 2008).
| (12) |
| (13) |
| (14) |
여기서, keff는 유효 열 전도도(effective thermal conductivity), Sh는 방사(radiation) 및 기타 열원을 고려한 상수이다.
식 (13), (14)는 프로그램을 통해 계산되는 유동영역 내 운동량 방정식과 에너지 방정식을 나타낸다. 각 상은 보존법칙을 만족하며 유체의 거동은 서로 비슷한 유형의 보존방정식으로 표현된다. 서로 다른 상에 대한 각 방정식들의 연계는 물리적 상관관계를 규정하는 상호 구성방정식을 통해 궁극적으로 결과 해를 도출하게 된다.
3.2 시나리오별 유동해석 결과 분석
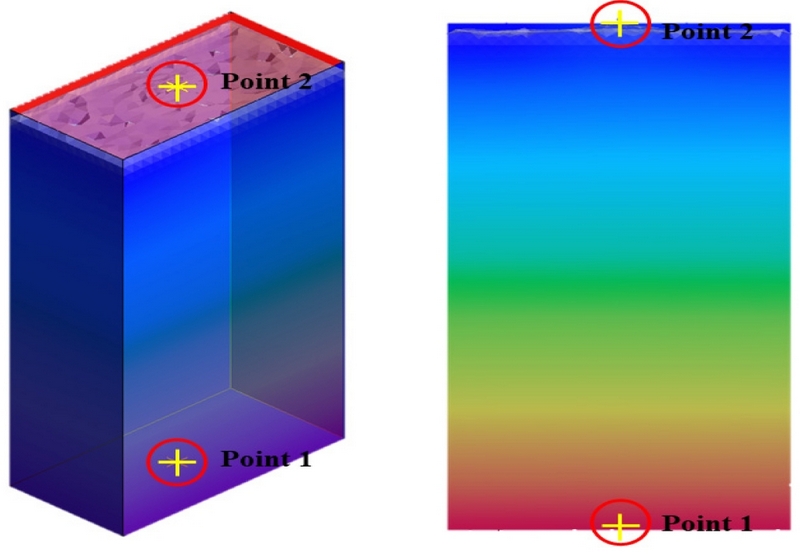
해석 결과를 데이터로 추출하기 위한 데이터 계측 지점은 Fig. 6과 같다. 충수가 진행됨에 따라 탱크의 무게중심(0.12, 0.45, 0.234 [m])이 지나는 중심축을 기준으로 y좌표(탱크 높이방향)에 차이를 두어 계측 지점을 선정하였다. 지점 1(point 1 : 0.12, 0, 0.234 [m])의 경우 탱크 내부가 충수되고 차오른 물에 의한 정수압과 내부 유체의 유동에 의한 동압이 함께 계측된다. 지점 2(point 2 : 0.12, 0.9, 0.234 [m])의 경우 충수 시나리오에 따라 공기의 압축으로 인한 밀도 변화가 나타나며, 이러한 압축된 공기의 영향으로 탱크 구조에 가해지는 내부 하중을 계측할 수 있다. 지점 2를 통해 확인 가능한 공기의 압축 현상을 통해, 해석 변수인 SAR에 따른 탱크 내부 압축 공기에 의한 동적 압력 발생 여부를 확인 가능하다.
1/10 상사 모형에 대한 유동해석 결과는 식 (9)를 이용하여 모형의 계측 지점에서의 결과를 원형의 대응점에서의 결과로 변환하였다. 레이놀즈 상사를 만족하는 모형과 원형 사이에서, 원형의 대응점에서의 압력은 아래 식 (15), (16)의 과정으로부터 무차원 수인 레이놀즈 수 및 오일러 수의 비교를 통해 계산이 가능하다.
| (15) |
| (16) |
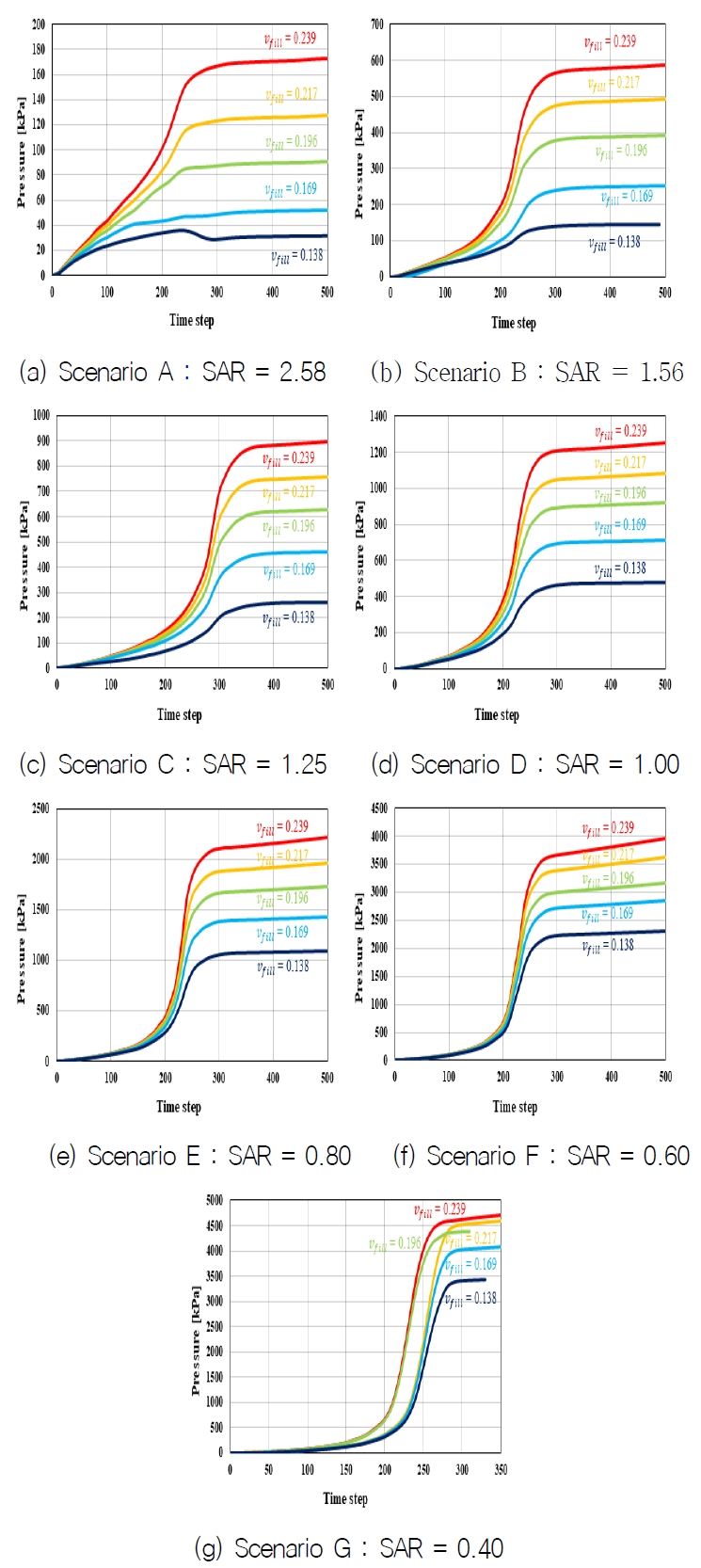
수압시험 내 충수 과정을 모사한 시뮬레이션 결과를 검토하였다. A1 시나리오(SAR=2.56)와 G1 시나리오(SAR=0.16)의 경우 동일한 충수 속도 (vfill = 0.239 [m/s])에서 수행된 사례로 시간에 따른 시뮬레이션의 두드러진 시각적 차이는 확인할 수 없다. 하지만 해당 시뮬레이션 결과에서 SAR의 차이로 인해 시간에 따라 발생하는 탱크 내부 압력에 주목할 필요가 있다.
충수가 탱크의 25%만큼 진행된 t = 10.67s의 경우, 시나리오 A에서 발생한 최대 압력은 26.7kPa, 시나리오 G에서 발생한 최대 압력은 36.2kPa이 탱크 최하단에서 발생하였으며, 충수 초기 서로 다른 시나리오 사이에서 발생 압력 값의 차이는 상대적으로 크지 않다. 하지만, 수위가 탱크의 50%를 넘어서는 순간부터 SAR에 따른 탱크 내부 발생 압력은 빠르게 증가하는 경향을 보인다. 탱크 수위의 50%를 나타내는 t = 21.32s와 75% 수위를 나타내는 t = 31.98s에서의 SAR에 따른 압력 증가량은 시나리오 A의 경우 1.6배 증가하였으며, 시나리오 G의 경우 3배 증가하였다. 90% 충수 된 t = 38.38s의 경우 t = 31.98s 대비 시나리오 A의 경우 약 1.5배, 시나리오 G의 경우 약 5배 증가하는 것을 확인하였다.
충수 과정 시뮬레이션을 통해 DNV-GL 설계 규정의 공기관 단면적 요구치를 만족하는 시나리오 A와 단면적 요구치를 만족하지 못하는 시나리오 G의 비교를 통해 충수 과정에 따른 탱크 내부의 압력 증가량에 대한 경향을 파악할 수 있었다. 또한, 시나리오 A1의 경우 만수 시 탱크 내에 발생한 최대 압력이 약 180kPa 임을 확인할 수 있다. 하지만 식 (16)을 적용하면 동일한 환경의 원형에 대응하는 지점에서의 최대 발생 압력은 1.8kPa로 추정할 수 있다. 이는 원형 탱크의 만수 시 작용하는 정수압이 88.3kPa임을 감안하면 2% 내외의 압력이 동압으로 작용하는 것이므로, DNV-GL 설계 규정을 만족하는 탱크에서는 고속의 주수 환경일지라도 탱크 내부에 발생한 압력이 과압으로 작용하지 않는다고 정리할 수 있다.
하지만 본 연구에서는 물리적 결함이 없는 탱크의 수압시험 시 과도 변형의 문제를 다루고 있으므로, 시험 과정 중 단면적이 감소된 상황에서 탱크 내부에 발생한 최대 압력에 주목하여야 한다. 공기관의 단면적 감소를 고려한 시나리오 중 가장 위험한 환경인 시나리오 G1의 경우, 유동 해석을 통해 탱크 모형의 내부 발생 최대 압력이 4,706kPa 임을 확인할 수 있다. 마찬가지로 식 (16)을 적용하여 원형의 대응점에서의 최대 발생 압력은 47kPa로 추정되며, 이는 시험 수두인 만수 + 2.4m에서 발생하는 시험 압력 111kPa의 42%인 압력 값에 해당하며 시험 압력과 조합하여 구조물에 작용할 경우 탱크에 과도한 변형을 유발시킬 수 있다고 판단된다.
모든 충수 과정에 대해 시뮬레이션을 수행하고 모니터링한 결과, 탱크 내부의 압력 증가 추세는 충수 초기에는 점진적이지만 일정 시점에서 급격히 상승한 이후 수렴하는 경향을 확인할 수 있다. 즉, 충수 초기에는 수위에 따른 정수압에 의해 압력 곡선이 서서히 상승한다. 이후 탱크 높이 50% 이상의 수위부터 SAR에 따른 탱크 내부 공기 압축이 반영되어 체적의 변화가 발생한 기상(gas phase)에서의 동압에 의해 압력 곡선의 급격한 상승을 나타내는 것으로 정리할 수 있다.
시험 진행에 따른 탱크 내부 압력 경향에 대한 그래프는 해석 시나리오에서 구분한 단면적 비에 따라 Fig. 7에 정리하였다. DNV 규정을 만족하는 시나리오 A, B, C의 압력 곡선은 모든 과정의 일반적인 유형과 같이 점진적인 상승을 보이다 급격한 상승 후 수렴하였다. 하지만, SAR ≧ 1.25를 만족하는 세 시나리오 모두 시간에 따라 발생한 압력 상승 폭이 2.1절에서 정의한 과압 기준에 미치지 못하는 것을 알 수 있다. 이는 단면적 규정을 만족하는 경우 공기관을 통해 내부 공기가 배출되어, 충수 시 공기 압축에 의한 동압의 증가량이 구조물에 유의미한 영향을 미치지 않기 때문으로 보인다.
반면에 시험 환경에 의해 DNV 규정 단면 요구치보다 감소한 시나리오인 D, E, F, G의 압력 곡선의 경우 일반적인 경향을 따르지만, 그 상승 폭에 큰 차이를 나타낸다. 2.1절에서 설정한 과압 판정 기준인 25kPa에 약간 못 미치는 E1(21.1[kPa]) 사례와 F5(23.04[kPa]) 사례부터 기준치를 초과하는 F, G 시나리오 모두 탱크의 50% 수위 이전까지 점진적 상승을 보이다 급격한 압력 상승이 발생한다. 이는 규정 요구치 이하로 감소한 공기관을 통해 충수 과정 중 공기 압축이 발생하며, 높은 동압에 의한 가파른 압력 상승 곡선을 나타내는 것으로 판단된다.
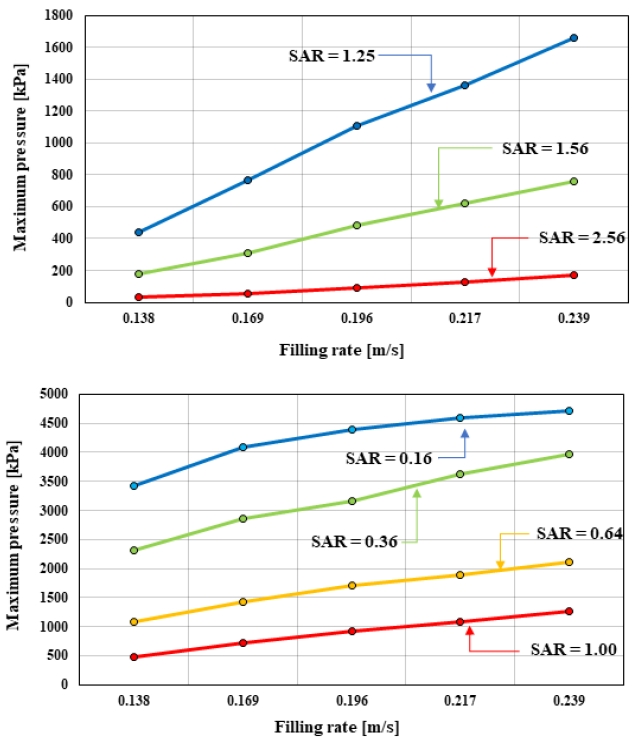
Fig. 8은 가압송수장치를 이용한 수압시험 시 탱크의 충수 속도에 따른 시나리오별 최대 발생 압력을 그래프로 정리하였다. 유동 해석 결과 데이터는 선정 시나리오별, 충수 속도별, 그리고 모형 시험의 최대 발생 압력과 원형의 대응점에서의 값으로 구분하여 Table 4에 정리하였다. SAR과 충수 속도를 변수로 한 시나리오 별 원형에서의 발생한 최대 압력은, 수압시험 절차를 고려하였을 때 만수 상황에서 정수압과의 상호작용, 시험 수두까지 상승시킨 상황에서 시험 압력과의 상호작용을 고려할 필요가 있다. 본 연구에서 선정한 과압 기준을 초과하지 못하는 사례라도 구조물의 강성을 고려하여 변형에 유의미한 값으로 작용하는지 구조해석을 통한 발생 압력에 대한 분석이 필요하다.
4. 과압에 의한 탱크 외벽의 변형해석
4.1 모델링 및 해석조건
본 연구에서는 요소수 저장탱크를 해석 대상으로 선정하여 연구를 수행하였다. 모델링 및 정적 구조해석은 ANSYS 2022 R1 상용 해석 프로그램을 이용하였으며, 탱크의 주요 구성요소인 판 및 보강재의 경우 쉘 요소를 이용하여 제작하였다. Fig. 9는 이 탱크의 구조를 보여주고 있으며, 주요 제원은 Table 5와 같다. 해석 모델의 요소 크기는 KR선급 강선규칙 제 3편 선체구조의 부록 3-2 직접강도평가에 관한 지침을 참고하였으며, 사용한 허용 응력 산정 기준을 만족하기 위해 150 × 150mm로 요소 크기를 선정하였다 (KR, 2021).
이 탱크는 직육면체의 한 면이 횡격벽에 용접되어 있고 수직 보강재들에 의해 외부가 보강되어 있으며, 나머지 탱크를 둘러싼 판의 경우 내부 보강의 구조를 가진다. 탱크의 바닥판으로부터 5m 높이에 중간 갑판(platform deck)이 존재하고, 탱크의 최상단부와 최하단부는 각각 계류갑판(mooring deck)과 하부갑판 사이에 I형 보를 통해 용접 지지되고 있는 구조이다.
선박의 제작에 사용되는 구조용 강(structural steel) 재료의 물성을 해석 모델에 반영하였으며, 탱크 내부 과압에 의해 발생할 수 있는 재료의 항복 이후 소성 거동은 소성 영역 재료 모델링에 사용되는 이중 선형 변형률 경화(bilinear strain hardening) 모델을 사용하였다. 이중 선형 변형률 경화 재료 모델은 변형률 경화가 발생하는 지점부터 재료의 극한 강도까지의 거동을 직선 형태로 가정하는 모델이다 (Vince and Abraham, 2009). 적용한 구조용 강에 대한 재료 물성치는 Table 6에 정리하였다.
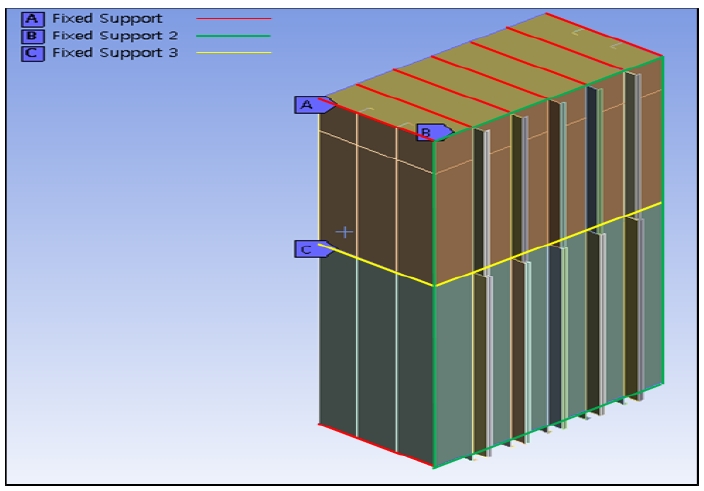
탱크의 구조해석을 수행함에 있어 지지점에 대한 경계조건 부여가 필요하다. 경계조건은 구조물의 실제 거동을 잘 반영할 수 있도록 지정해야 한다. 해석 대상인 요소수 저장탱크의 실제 거동을 고려하였을 때, 해석 대상은 탱크 상 · 하부 I형 빔과의 용접부(A), 횡격벽의 일부로서 용접 부착되는 지점(B) 및 중간갑판과의 용접부(C)의 자유도 구속을 반영하여야 한다. 즉, Fig. 10에서 나타낸 각 지지부의 모든 병진(Tx, Ty, Tz) 및 회전(Rx, Ry, Rz) 방향 자유도를 구속하는 것이 실제 거동을 묘사할 수 있다고 판단하였다.
구조해석 수행을 위한 하중조건으로는 수압시험 시 탱크 구조물 내 작용할 수 있는 하중들에 대해 고려하여 조합하였으며 Table 7에 정리하였다. 구조용 강을 재료로 제작된 해당 탱크의 자중은 20.6톤이며, 자중의 경우 구조물에 중력가속도를 인가해 줌으로서 해석에 반영할 수 있다. 또한, 수압시험 과정을 통해 충수된 물에 의한 정수압을 고려하였으며, 정수압 계산을 위한 청수의 밀도는 999.9kg/m3, 자유 수면 높이는 탱크 높이 9,000mm를 적용하여 구조물에 높이 별로 하중을 인가하였다. 마지막으로 유동해석 결과로서 Table 4에 정리한 탱크 내부 공기 압축에 의한 과압을 시나리오별로 탱크 벽면에 부여하는 것으로 수압시험 과정에서 발생할 수 있는 하중 조합을 재현하였다.
4.2 변형해석의 결과 분석
4.1.3절 하중조합을 고려한 시나리오별 구조해석 결과를 고찰하기 전에, 강으로 제작되는 일반적인 구조물의 변형에 대한 허용기준을 조사하였다. 한국강구조학회의 ‘강 구조 설계기준’ (KSSC, 2019)과 대한건축학회의 ‘강 구조 계산 규준 및 해설’ (AIK, 2005)에서는 동일하게 단순지지의 강제 보는 전체 하중에 대한 변형이 스팬 길이(span length, L)의 1/300 이하, 캔틸레버 보에서는 L/250 이하가 되어야 함을 명시하고 있다. 또한, 노르웨이 선급의 해양구조물 강 구조 설계 지침에서는 갑판 보의 경우 시간에 따라 변하는 하중과 영구 하중에 의해 발생한 최대 처짐이 L/300 이하로 제시하고 있다 (DNV, 2018).
실무에서는 조선소마다 각기 다른 설계 규정이 적용되고 있으며, 관련 부서에 변형 기준에 대해 문의한 결과, 변형 허용 기준을 L/1000 ~ 3L/1000 범위 사이의 값으로 구역마다 구분하여 설정하고 있었다. 횡격벽과 같은 큰 강성을 가진 주요 부재 일부에 용접되어 구성되는 구조의 경우 변형 허용치를 경감하여 적용하여 판단하기 때문이다. 위의 규정과 함께 검토하였을 때 본 연구의 부재 처짐에 대한 허용 기준을 식 (17)과 같이 설정하였다. 이 값을 초과하는 변형이 발생한 시나리오의 경우 시험 과정에서 Table 7의 조합하중이 과압으로 작용하여 탱크 내 과도 변형을 발생시킬 수 있는 것으로 판단할 수 있다.
| (17) |
여기서, δallow는 허용 최대 처짐량을 의미한다.
주요 해석 시나리오별 구조해석은 Ansys Structural Analysis에서 제공하는 파라미터 해석(parameter analysis)기법을 이용하여 수행하였다 (DNDE, 2021). 유동해석 결과인 구조물 내부에 작용하는 과압을 구조해석에서의 주요 입력 파라미터로, 출력 파라미터는 그에 해당하는 변형 및 응력으로 설정하였다. 식 (17)에서 계산된 허용 최대 처짐을 임계점(critical point)으로 설정하여, 이를 초과하는 변형이 발생한 경우를 찾아냄으로써 여러 해석 시나리오에 대해서 문제 발생 소지가 있는 시나리오를 확인할 수 있었다.
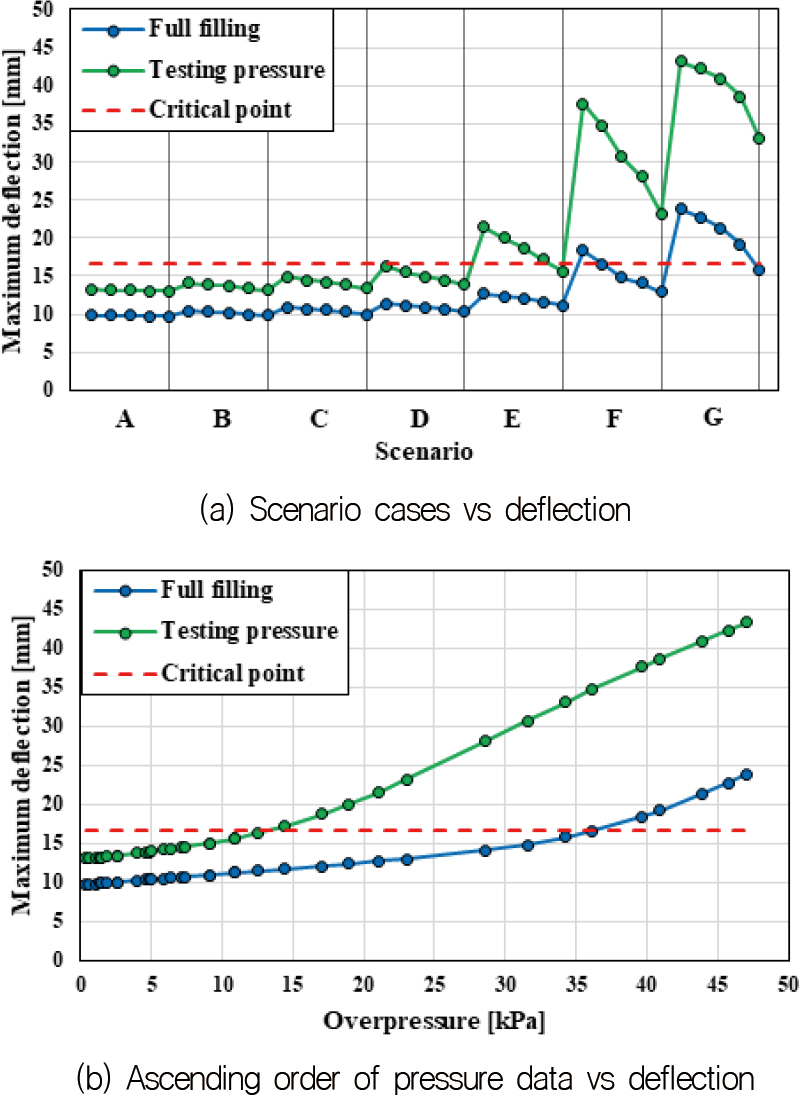
Fig. 11에서 청색 선은 만수 기준 정수압과 내부 동압의 조합 하중(이를 full filling condition으로 표시)으로 인한 탱크의 변형 결과이며, 녹색 선은 수압시험 과정에서 만수 후 2.4m 수두높이를 증가시킨 시험 압력과 탱크 내부 동압의 조합 하중(이를 testing pressure condition으로 표시)에 의한 탱크 변형 결과를 나타낸다. 또한 A~G의 각 시나리오 내 5개의 점들은 Table 4에 정리된 유량으로부터 계산된 충수 속도에서의 탱크 내부 압력 결과를 나타낸다. Fig. 11(a)의 해석 결과에서 full filling condition 시험 상황에서는 F1 사례와 G 시나리오에 해당하는 동압이 탱크에 가해졌을 경우, 충수 과정에서 최대 허용 처짐 이상의 변형이 발생하는 것을 확인할 수 있다. 이는 SAR이 0.36 이하로 감소한 상황에서 연구에서 사용한 충수 속도 범위 내에서 시험을 진행할 경우 탱크에 과도 변형이 발생하는 것을 의미한다.
다음으로, 허용 범위 이내의 탄성 변형을 유지하며 만수까지 충수를 진행하였더라도 시험 압력을 맞추기 위해 수두 높이를 증가시킬 경우, D1, E1~E4 및 F, G 시나리오에서 발생한 내부압이 탱크 내부에 과도 변형을 발생시키는 것으로 나타난다. D1 사례는 동일한 단면적의 관을 가지더라도 빠른 충수 속도로 탱크 내부를 시험 압력까지 증가시킬 경우 최대 허용 처짐량에 가까운 위험 수준의 변형이 발생하는 것을 확인할 수 있다.
마지막으로, 주수관과 공기관의 단면적 비(SAR)가 DNV 규정에서 제안하는 값인 125% 이상임을 만족하는 시나리오 C라 할지라도, 시험 압력 하에서 압력을 유지하는 시간 동안 추가 처짐이 발생하여 최대 허용 처짐을 초과할 수 있으므로 유의할 필요가 있다.
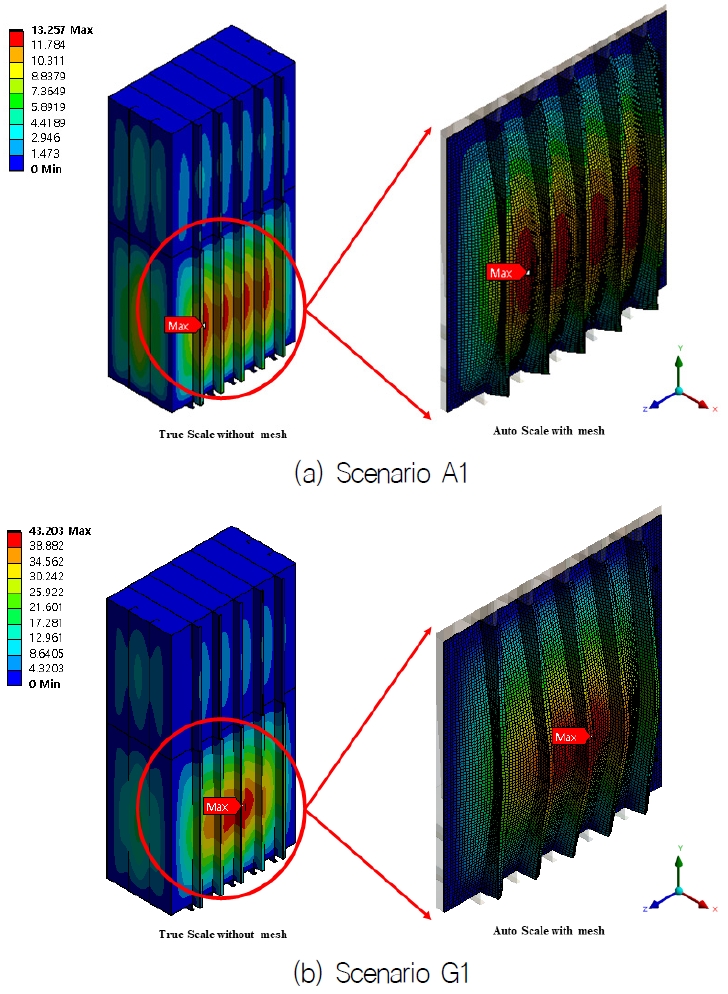
4.1절의 해석모델에 대해 경계 및 하중조건을 적용한 유한요소모델 주요 변형 결과는 Fig. 12에 도시하였다. 도시한 변형 결과는 유동 시뮬레이션과 마찬가지로 A1와 G1의 사례를 통해 나타내었다. 변형해석 시나리오 모두 탱크 하부 횡격벽에 용접되는 판에서 최대 변형이 발생한 것을 확인할 수 있다. 이는 작용하중에서 자유수면 높이에 따른 정수압이 가장 지배적인 하중으로 탱크의 하부일수록 높은 압력을 받기 때문이다. 또한, 판을 보강하는 보강재의 시공 위치가 기하학적 강성에 반영되었으며, 횡격벽에 해당하는 판을 제외한 탱크를 구성하는 나머지 판 부재는 고장력강 재료로 구성되어 있으므로 동일한 하중 대비 변형의 정도가 낮기 때문이라 판단한다.
해석 시나리오별 작용 하중에 대한 최대 변형 결과와 최대 허용 처짐에 따른 구조안전성 평가를 Table 8에 정리하였다. 시나리오 A, B, C에서는 해당하는 SAR 기준 충수 속도에 의한 동압의 영향이 구조물에 유의미한 영향을 미치지 않았으며, 만수 시 정수압과 시험 압력이 각 상황의 지배적인 하중으로 구조물에 작용한 변형 결과이기에 배수를 통한 수두 제거 이후 탄성 복원이 예상된다. 하지만 SAR이 규정 요구치 미만으로 줄어든 상황에서는 각 상황별 동압과의 조합하중을 고려할 필요가 있다.
따라서 본 연구의 해석 모델인 요소수 저장 탱크와 같이 탱크의 단면적 대비 높이가 높은 선상 탱크의 경우, 수압시험을 두 가지 상황(full filling 및 testing pressure condition)으로 구분하여 다음과 같이 상황에 따른 최적의 충수 속도를 제안한다.
- 1.0 ≦ SAR : 탱크의 충수 과정에서는 가압송수장치의 기준에 따라 어떠한 충수 속도를 사용하여도 무방하나, 만수 후 시험 수두를 높이는 과정에서는 0.0196m/s 이내일 것 (4bar에 해당하는 충수 속도).
- 0.64 ≦ SAR ≦ 1.00 : 탱크의 충수 과정에서는 가압송수장치의 기준에 따라 어떠한 충수 속도를 사용하여도 무방하나, 만수 후 시험 수두를 높이는 과정에서는 0.0137m/s 이내일 것 (2bar에 해당하는 충수 속도).
- 0.36 ≦ SAR ≦ 0.64 : 빠른 속도(5bar 이상의 빠른 충수 속도)로 시험을 진행할 경우 충수 과정에서 문제가 발생하므로, 만수까지 물을 채우는 과정에서는 0.0196m/s 이내의 충수 속도로 진행하되, 만수 후 시험 수두를 높이는 과정에서는 0.0097m/s 이내일 것 (2bar의 방출압력 하에서 밸브 조절을 통해 유량을 3/4 이하로 낮출 것).
- 0.16 ≦ SAR ≦ 0.36 : 만수까지 물을 채우는 과정에서는 0.0137m/s 이내의 충수 속도로 진행하되, 만수 후 시험 수두를 높이는 과정에서는 0.00685m/s 이내일 것 (2bar의 방출압력 하에서 밸브 조절을 통해 유량을 절반 이하로 낮출 것).
5. 결 론
본 논문은 설계 규정을 만족하여 제작된 선상 탱크의 수압시험 시 발생한 실제 사고 사례(과도 변형)를 바탕으로 진행되었다. 물리적인 결함이 없는 선상 탱크 준공 후 조선소 내 수압시험 환경에서 과도 변형 사고를 유발할 외부 요인으로 과압 현상에 주목하여 분석을 수행하였다.
시험 과정에서 탱크 내 과압 발생 상황을 두 가지 주요 변수(공기관의 단면적 감소 및 빠른 충수 속도)로 가정하였다. 조선소 내 수압시험에 사용 가능한 충수 속도 범위를 산정하고 실제 사용되는 수두 측정용 호스의 제원을 바탕으로, 충수 속도와 관의 단면적 비를 조합하여 35가지의 해석 시나리오를 선정하였다.
탱크 내부 공기의 압축에 의한 동압을 확인하고자 유동해석 시뮬레이션을 수행하였다. 해석 시나리오에 따른 유동 해석 결과 탱크 내부에 최소 0.35kPa ~ 최대 47.06kPa의 동압이 추가로 발생하는 것을 확인할 수 있었으며, 최대값인 47.06kPa은 시험 압력 111kPa의 42%에 해당하는 수치이다. 시험 압력만을 요소수 저장 탱크에 내부 하중으로 가하였을 경우 13mm의 변형이 발생하는 것을 확인할 수 있으며, 기존 하중 대비 최대 42% 내의 추가적인 하중은 탱크 내 과도 변형을 유발하기에 충분한 수치로 판단하였다.
수압시험 중 탱크 내부에 발생한 압력이 과도한 변형을 유발하는지 확인하고자 구조해석을 실시하였다. 그 결과, 설계 규정을 만족하는 경우 만수 시 탱크에 발생한 최대 변형은 최대 허용 처짐량 대비 65.5%, 시험 압력하에서 탱크에 발생한 최대 변형은 최대 허용 처짐량 대비 89%에 해당하는 변형을 확인하였다. 이는 수두 제거 시 발생한 변형이 탄성 복원되지만, 시험 압력 상태를 유지하는 동안에는 주변 작업 환경에서 발생할 수 있는 추가적인 하중을 주의할 필요가 있음을 시사한다.
반면에 설계 규정을 만족하지 못하는 SAR〈 1.25인 상황에서, 본 연구의 과압 판정 기준 25kPa의 근처(사례 E1) 또는 초과(시나리오 F, G)하는 사례를 확인하였다. 이는 선상 탱크의 수압시험 환경에서 불가피하게 발생할 수 있는 상황이기 때문에, SAR의 범위와 시험 상황(filling condition 및 testing pressure condition) 별로 구분하여 구조 안전성을 만족하는 충수 속도에 대한 가이드라인을 제안하였다.
불가피하게 SAR이 감소한 상황에서 수압시험을 진행하여도 단면적에 따라 제안하는 충수 속도를 초과하지 않는 범위 내에서 시험을 진행한다면 최대 허용 처짐 이하의 변형이 발생할 것이고, 수압시험의 목적을 달성함과 동시에 기존 권장 속도 대비 시험에 소요되는 시간을 단축시킬 수 있을 것이다. 하지만 제안한 충수 속도는 요소수 저장 탱크와 같이 탱크의 단면적 대비 높이가 높은 탱크에 한정한 연구 결과이므로, 향후 탱크 단면적과 높이에 따라 선상 탱크의 적용 범위를 구분하고 권장 충수 속도에 대한 가이드라인을 추가 정의할 필요가 있다.
References
- Architecturlal Institute of Korea (AIK), 2005. Architectural structural design standards. [Online] Available at: https://www.codil.or.kr, [Accessed 19 August 2023].
- Ansys Inc., 2012. ANSYS FLUENT 12.0/12.1 Documentation. [Online] Available at: https://www.afs.enea.it/project/neptunius/docs/fluent/, [Accessed 07 August 2023].
- American Petroleum Institute (API), 2020. Welded tanks for oil storage. [Online] Available at: https://www.yumpu.com/en/document/view/64162102/api-650-2020, [Accessed 16 July 2023].
- Cho, H.K., Park, I.K., Yoon, H.Y., Kim, J.T. and Jeong, J.J., 2008. The semi-implicit numerical scheme for transient two-phase flows on unstructured grids. Journal of Energy Engineering, 17(4), pp.218–226.
-
Chung, S.M., Seo, Y.S., Jeon, G.M., Kim, J.W. and Park, J.C., 2021. Parameter study of boiling model for CFD simulation of multiphase-thermal flow in a pipe. Journal of Ocean Engineering and Technology, 35(1), 50-58.
[https://doi.org/10.26748/KSOE.2020.071]

- Det Norske Veritas (DNV), 2018. Design of offshore steel structures (DNVGL-OS-C101).
- Det Norske Veritas (DNV), 2021. Rules for classfication : Ships (RU-SHIP).
- Dey, A.K., 2017. 5 Examples of hazards of pressure testing. [Online] Available at: https://whatispiping.com/hazards-of-pressure-testing/, [Accessed 15 August 2023].
- DNDE, 2021. Ansys mechanical basic. pp.221–266.
- Heo, J., Kim, T.H., Moon, B.H., Choi, H.Y., Lee, K.W. and Ro, T.S., 2001. Effects of valve characteristics and pipe diameter on water hammer phenomena. Proceedings of the Korean Nuclear Society Autumn Meeting, Seoul, Korea.
- International Association of Classification Societies (IACS), 2021. Common structural rules for bulk carriers and oil tankers.
- Korea Atomic Energy Research Institute (KAERI), 2007. Two-phase flow models and numerical methods of the commercial CFD codes.
- Korean Register (KR), 2021. Rules for the classification of steel ships(Part 3-Hull Structures).
- Korean Society of Steel Construction (KSSC), 2019. Steel structural member design criteria. [Online] Available at: https://www.kcsc.re.kr/Search/List, [Accessed 19 August 2023].
- Lee, S,H., 2013. Three months before the Samsung’s Water Tank Disaster, There was a ‘Preview’. [Online] Available at: http://www.yna.co.kr/view/AKR20130806141500057, [Accessed 09 November 2023].
- Ministry of Oceans and Fisheries (MOF), 2020. Ship safety act. Additional shipbuilding inspection, Article 11, Clause 2.
- National Fire Agency (NFA), 2013. National fire safety code 109.
- Nam, J.K., 2014. Engineering fluid mechanics. [Online] Available at: http://www.kocw.net/home/index.do, [Accessed 19 August 2023].
- Parthiban, K.K., 2012. An accident with brittle fracture during hydrotest. [Online] Available at: http://www.venus-boiler.com/technical_papers.php, [Accessed 15 August 2023].
- Vince, A. and Abraham, A. 2009. Building better products with finite element analysis. 3rd Ed. Paju, Korea: Sci-Tech Media Publisher.