동역학 시뮬레이션을 이용한 함재기 견인차량의 주행특성 분석 기법에 관한 연구
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper deals with the dynamic simulation method for analysis of driving characteristics of aircraft and towing vehicles (TUG) on carrier vessel in wave motions. For prompt deployment in a short period of time, optimization of the movement of carrier aircraft becomes a major issue. In this regards, strategy studies using real-time simulation technology and optimal decision-making technologies are being conducted. In the present work, the dynamic characteristics of carrier aircraft and TUG connected by towbar or towbarless mechanism were investigated by means of multi-body dynamics model. Meanwhile, for real-time simulation, Dugoff’s model of tire loads calculation was adopted. Through comparative analysis it was confirmed that the similarity of results between the multi-body contact model and the tire load calculation model can be achieved by coefficients tuning.
Keywords:
Naval Aircraft, Tow Tractor, Driving Characteristics, Dynamic simulation, Tire Contact Simulation Model키워드:
함재기, 견인 트랙터, 주행특성, 동역학 시뮬레이션, 타이어 접촉 시뮬레이션 모델1. 서 론
항공모함은 바다의 영토 방어와 국민의 안전 수호를 위해 사용되는 군사작전 함정으로 최근 한반도 인근 해역 및 해상교통로의 보호를 목적으로 대한민국 해군의 항공모함 확보 필요성이 논의되고 있다 (Shim et al., 2022). 이러한 항공모함에는 전투기와 헬리콥터, 수상기 등과 같은 함재기를 탑재하여 작전에 운용 및 활용하고 있다.
항공모함 내의 정해진 구역 내에서는 함재기의 자체 동력으로 이동하는 것이 안전상 위험 요인이 됨에 따라, TUG라 불리는 항공기 견인차량을 이용하여 격납고 및 활주로 등의 구역 이동과 함재기 이착함을 위한 활주로 정위치 이동을 하게 된다.
TUG는 고출력의 디젤 및 전기모터 엔진을 이용한 함재기 견인이 주요 역할임에 따라, 견인 방식에 의해 그림 1과 같이 towbar TUG와 towbarless TUG로 구분할 수 있다. Towbar TUG는 견인바인 towbar를 사용하여 견인하는 차량으로 항공기 기종별로 길이와 직경 등의 종류가 달라 다양한 종류의 towbar를 구비해야 하는 어려움이 있다. 또한, 긴급 상황 시에도 운용 절차에 따라 작업해야 하므로 towbar 설치 및 해체의 어려움이 존재하고, 전진 및 후진 시 towbar의 위치를 변경해야 하는 단점이 존재하지만, 고하중을 단순한 구조를 통해 쉽게 이송할 수 있다는 장점이 있다. Towbarless TUG는 towbar 사용 시 발생하는 문제점을 해소하기 위해 개발된 TUG 차량 일체형 견인차량으로 항공기 바퀴를 차량에 직접 체결하도록 되어 있다. 이에 따라, 연결 및 분리 시간이 적게 소요되고, 기종에 따라 다양하게 구비하지 않고 견인에 사용할 수 있기 때문에 유지보수 비용이 현저히 적게 발생하게 된다. 또한, 차량이 직접 연결되기 때문에, 항공기 제어 및 운용이 단순하며 정밀하다. 하지만, 차량이 수십에서 수백 톤의 고하중을 직접 견뎌야 하기 때문에 구조적 안전성 및 운전자의 안전에 대한 문제점이 존재한다.
이와 같은 이유로, 항공모함에서도 다양한 종류의 함재기를 운용하기 위해 towbar TUG 및 towbarless TUG를 복합적으로 활용하고 있다.
항공기와 TUG의 견인 시스템은 여러 환경 변수 및 운동제약을 고려하여 궤적 계획 및 스케쥴링을 최적의 제어 문제로 변환하고 효율이 높은 최적 운용 제어 관점의 기술이 요구되고 있다(Liu et al., 2019). 기존에 개발된 최적 제어 알고리즘들은 기구학 기반으로 연구가 진행되어 추진력, 마찰력, 관성력 등을 고려하지 않았기 때문에, 함정의 거동 등에 의한 가속도 영향에 대한 현실적인 문제를 반영하는데 한계가 있다. 이와 같은 이유로, 함재기-TUG 견인 시스템의 경우 궤적 계획 최적화를 위해서는 가속도를 고려할 수 있는 동역학 기반의 물리모델 도입과 이를 이용한 최적화 연구가 진행되어야 한다.
본 연구에서는 항공모함 내 함재기 전술 효율화를 위해 시뮬레이션 기반의 전략 도출 연구를 진행 중에 있으며, 특히, 거동을 갖는 항공모함 내에서의 함재기와 TUG의 운용 최적 계획 및 skidding, jackknifing 현상 (Etienne, 2011)과 같은 고중량의 항공기 견인 시 발생 가능한 상황을 분석하기 위해 동역학 시뮬레이션 기반의 해석 기법을 적용하고자 한다.
따라서, 본 논문에서는 함재기와 TUG의 견인 시스템 동역학 모델을 위한 해석 기법 고찰과 항공모함 내 견인 시스템 해석을 위한 방법을 소개하고자 한다.
2. 견인차량 시뮬레이션 기술
견인 시스템은 견인체와 피견인체로 구분할 수 있으며, 모두 차량 모델로 구현할 수 있다. 이러한, 차량 시뮬레이션 모델은 기구학 모델과 동역학 모델로 구분하여 개발될 수 있다.
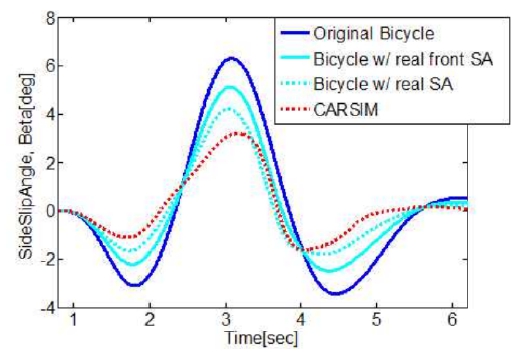
기구학 모델은 차량의 종방향과 횡방향으로 2 자유도로 표현되는 자전거 모델(bicycle model) (Choi and Park, 2017)과 4개의 바퀴로 구현하는 4 타이어 모델 (Paszkowiak et al., 2021)이 존재한다. 자전거 모델은 차량의 좌우 타이어 조향각이 동일하고 현가장치 및 수직방향에 대한 움직임으로부터 기인한 효과는 무시, 회전관성 영향을 배제하기 위해 5 m/s (18 KPH) 이하의 저속 주행 조건, 지면의 변화가 없는 평탄 노면 등의 가정이 가능할 경우 사용이 가능하다. 4 타이어 모델은 좌우 타이어의 서로 다른 조향각을 입력할 수 있지만, 자전거 모델과 유사한 조건일 경우에만 사용이 가능하다.
동역학 모델은 차량에 가해지는 모든 기본적인 제어력과 외력은 타이어와 지면의 접촉에 의해 발생하며 이에 따라, 차량의 운동 특성이 결과로 도출된다는 정의에 의해 개발이 진행되었다. 이에 따라, 차량 차체는 강체동역학 기반으로 구현이 되고, 타이어의 특성들을 다양한 연구 수식들이 적용된 외력으로 활용되고 있다. 타이어 동역학 모델은 견인력(longitudinal force), 횡력(lateral force), 수직력(normal force)의 3방향에 대한 병진하중과 전복 모멘트(overturning), 구름저항 모멘트(rolling resistance), 정렬 모멘트(aligning)의 3방향에 대한 회전하중, 타이어의 주행 중 자세 표현을 위한 slip angle과 inclination angle, 회전각속도로 표현된다 (Virtual Motion, 2020).
타이어의 6방향 하중 중 회전하중은 병진하중으로 변형하여 총 3방향의 수평하중, 측면하중, 수직하중인 병진하중으로 표현할 수 있다. 여기서, 수평하중은 가속과 감속, 저항력 등 주행을 모사하는 진행방향 힘을, 측면하중은 미끌림, 코너링 등을 모사하는 측면방향 힘을, 수직하중은 지면과의 지지 및 충격, 저항력 등을 모사하는 수직방향 힘을 의미한다.
타이어 하중을 산출하기 위해서 많은 연구가 진행되었으며, 대표적으로 Fiala Tire (Fiala, 1954), MF Tire (Pacejka, 2006), Brush Tire (Kim et al., 2017), Dugoff`s Tire (Dugoff et al., 1969) 등의 타이어 하중 산출 모델과 접촉 질점을 세분화하여 각질점의 위치, 속도로 하중을 산출하는 contact 모델 (Virtual Motion, 2021)이 존재한다.
타이어 하중 산출 모델의 기본 수식은 아래와 같이 타이어 마찰력과 주행력에 의한 진행방향 힘(식 (1))과 타이어 조향에 따른 슬립과 선회력에 의한 측면방향 힘(식 (2)), 타이어의 변형에 의한 수직방향 힘(식 (3))으로 나타낼 수 있다.
| (1) |
| (2) |
| (3) |
여기서, μ는 지면과 타이어 사이의 마찰계수, Ttire와 Rtire는 타이어 구동 토크 및 반경, η는 구동 효율, cα는 코너링 강성계수, α는 조향 시 발생하는 타이어 슬립각, kver와 cver는 지면과 타이어 사이의 수직 강성계수 및 감쇠계수를 의미한다.
위와 같은 x-y-z 방향의 타이어 하중 산출을 위한 기본 수식을 바탕으로 슬립각을 산출하는 방법, 선회력을 계산하는 방법, 마찰력과 저항력을 계산하는 방법 들을 경험식 또는 실험 기반 도출된 수식들을 추가적으로 사용하여 식 (4)와 (7)의 Fiala Tire 모델(중력 방향 힘(Fz)은 식 (3)과 동일)과 같은 다양한 형태의 모델이 도출되었다 (Michael, 2015).
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
여기서, ksx와 ksy는 x-y 방향의 타이어 슬립 강성계수, σs는 슬립율, σc는 임계 슬립율, α*는 임계 슬립각을 의미한다.
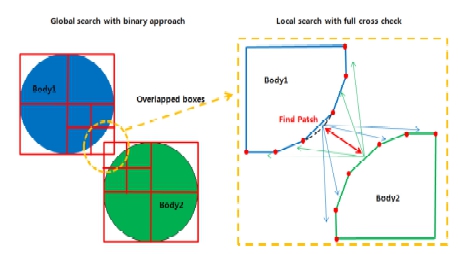
접촉 모델을 이용한 타이어 모델은 아래 수식과 같이 각각의 접촉 질점의 침하량(p)과 침하속도를 이용하여 지면과 타이어 사이의 접촉 강성계수와 감쇠계수, 마찰계수를 통한 모든 접촉 질점의 수직방향 힘과 수평방향 힘을 합력하여 진행방향, 측면방향, 수직방향의 힘으로 환산하여 도출된다.
| (9) |
| (10) |
여기서, k*와 c*, μ*는 지면과 타이어 사이의 접촉 강성계수와 감쇠계수, 마찰계수를 의미한다.
접촉 모델을 이용한 타이어 모델은 타이어 면의 모든 질점의 정보를 계산하여 하중을 산출하기 때문에 높은 정확도를 갖지만, 그림 3과 같이 모든 질점의 접촉 여부를 판단하고 접촉 시 접촉질점의 침투된 양과 이에 따른 접지력을 계산하기 때문에 해석시간이 오래 걸린다. 이와 같은 이유로 빠른 주행성능 분석을 위해서 강체 동역학 기반의 타이어 하중 산출 모델이 도출되었다. 하지만, 타이어 하중 산출 모델의 경우, 결정된 계수에 의해 주행성능이 도출됨에 따라서 계수 값에 의해 정확도의 차이가 크게 변화하게 된다. 이에 따라, 기존에 타이어 하중 산출 모델의 정확도를 높이기 위해 여러 파라미터의 값을 경험과 실험을 바탕으로 추정하는 연구가 진행되고 있다.
본 연구에서는 항공모함에서 운용될 TUG에 대한 주행 특성 고찰을 위해 접촉 모델을 이용하여 연구에 활용하였고, 타이어 하중 산출 모델의 활용 가능성을 판단하기 위해 실제 차량의 평지 주행 시 제어 알고리즘 및 해석 기술에 다수 활용되고 있는 Dugoff`s Tire 모델을 이용하여 비교하였다.
3. TUG 동역학 시뮬레이션
3.1 접촉 메커니즘 기반 동역학 시뮬레이션
TUG 주행 차량의 접촉 모델 기반 동역학 시뮬레이션 모델은 상용 소프트웨어인 ANSYS/Motion(구 DAFUL) (Virtual Motion, 2021)을 이용하여 단일 주행 차량 모델을 구축하였다. 단일 주행차량의 제원은 항공기-트랙터(TUG) 시뮬레이션 모델 구축에 사용되었던 Liu et al. (2018)의 모델을 참고하였으며, 제원은 표 1과 같다.
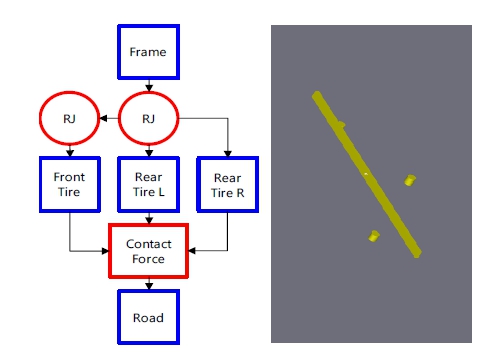
구축된 TUG 모델은 그림 4와 같이 강체 모델로 차체, 타이어로만 구성되었으며, 타이어는 전륜 타이어는 조향과 구동의 두 방향 회전을 위해 pitch와 yaw 방향의 revolute joint (Virtual Motion, 2020) 2기를 후륜 타이어는 구동을 위해 pitch 방향 revolute joint를 이용하여 모델링하였다. 타이어와 지면은 접지 및 주행을 위해 접촉 메커니즘을 적용하였고, 주행력을 인가하기 위해 각각의 revolute joint에 요구되는 주행 속도가 도출되도록 회전속도의 환산을 통해 인가하였다.
3.2 환경 변수 변화에 따른 주행 특성 분석
TUG 동역학 모델의 주행 특성 분석을 위해 적용된 환경 변수는 지면과 타이어 사이의 마찰계수, 항공모함 거동으로 정의하였다.
마찰계수는 주행 특성에 가장 큰 영향을 주는 인자로서 항공모함 활주로 재질인 고장력 특수강(HY-100)과 TUG 타이어 재질인 고무 사이의 마찰계수를 의미한다. 하지만, 고장력 특수강과 고무 타이어 사이의 정확한 마찰계수의 확보가 어렵기 때문에, 표 2와 같이 공항당국이 제공하는 제동기능 분류(Noh, 2016)에 의거 하여, 최소마찰계수를 추정하여 활용하였다. 자료 분석 결과, 최소 0.30 이상의 마찰계수를 갖는 환경에서 항공기의 정상운항이 가능하였다. 이에 따라, 활주로에서 운용 가능한 최소마찰계수는 0.3 임을 알 수 있으며, 마찰계수의 범위를 0.3 ∼ 0.9까지로 분석 영역을 정의하였다.
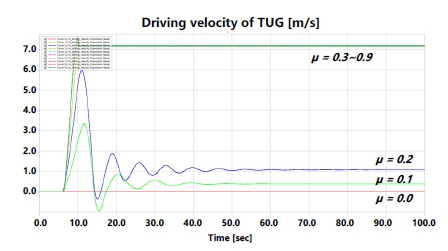
마찰계수에 따른 주행 특성 분석 결과, 마찰계수 0.3 이하의 영역에서는 무게 대비 주행에 필요한 마찰력이 부족하여 정상적인 주행이 불가능하였다. 특히, 마찰계수가 0.0인 경우에는 마찰력이 발생하지 않아, 주행이 되지 않음을 확인할 수 있었다. 0.3이상의 마찰계수인 경우 그림 5와 같이 목표하는 주행 속도 7.5m/s를 만족하였으며, 각각의 마찰계수에 따른 선회 반경은 표 3과 같이 정상 주행이 가능한 0.3 이상 영역에서 큰 차이가 없음을 알 수 있다. 따라서, 공항당국의 제동기능 분류 기준에 따라, TUG 차량모델에 요구되는 마찰계수는 추정 제동기능 medium이상인 0.3이며, 안정적인 시뮬레이션을 위해서는 추정 제동기능 good 영역인 0.4 이상을 사용하는 것이 적절하다.
함재기 TUG는 항공모함 내에서 운용되는 장비임에 따라, 해양파에 의한 항공모함 거동에 따른 특성 변화의 검토가 필요하다. 항공모함의 경우 거동 결과의 부재로 Oh et al. (2021)의 선박 탑재 장비 해석 기술 연구 결과에 의해 선박의 heave와 roll, pitch 거동을 반영하였다. 선박의 거동은 타이어가 접지되는 지면에 heave 거동을 위한 translational joint 1기와 roll과 pitch 거동을 위한 revolute joint 2기를 인가하여 모사하였다. Heave와 roll, pitch의 최댓값은 영향도 검토를 위해 극한값을 적용하여, 각각 6초 주기의 0.5 m, 5.0 deg로 정의하였으며, Oh et al. (2021)의 연구 결과에 따르면, 6,000톤급 선박이 pitch 최댓값 1.5 deg를 갖는 것으로 보아, 수만 톤급의 항공모함은 더 낮은 pitch 각으로 운동할 것으로 추정할 수 있어, 본 연구에서 적용한 값들이 충분히 극한값이라고 할 수 있다.
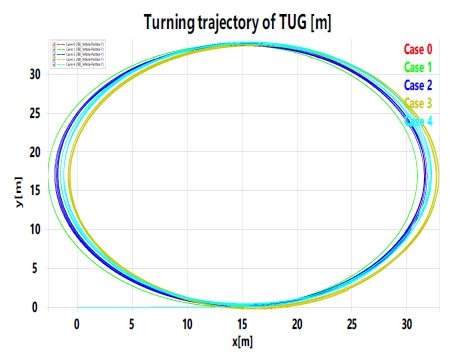
선박 거동에 따른 주행 특성 분석 결과는 표 4와 같이 각각의 조건에 따른 선회직경으로 나타내었으며, 선박 거동이 존재하더라도 TUG 주행 특성에 크게 영향을 주지 않음을 확인할 수 있다. 하지만, 선회직경의 변화가 없더라도 선회 궤적의 차이가 발생함을 그림 6을 통해 확인할 수 있었다.
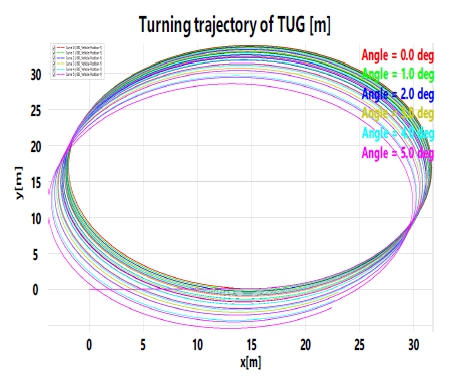
이에 따라, 상세 분석을 위해 선박 거동 중 영향도가 높은 roll과 pitch 각도를 정적인 상태의 경사도로 모사하여 분석을 수행하였다. 정의한 경사각도는 선박 거동의 극한값 이내의 경사인 0.0, 1.0, 2.0, 3.0, 4.0, 5.0 deg로 roll 방향에 대해 정의하였다. 경사도에 따른 주행 특성 분석 결과, 그림 7과 같이 roll 방향의 경사면을 따라 경사각이 클수록 유사한 선회직경을 그리면서 점점 더 미끄러지는 주행 특성을 보였다.
4. 함재기 TUG의 실시간 동역학 해석을 위한 타이어 하중 산출 모델 활용 기법
4.1 타이어 모델에 따른 주행 특성 비교
TUG 동역학 시뮬레이션 모델 구축 시 환경 변수 이외에 중요한 요소는 타이어 모델이다. 본 연구에서 사용된 접촉 메커니즘 기반 타이어 모델은 실시간성 효율이 낮기 때문에, 분석에 많은 시간이 소요된다. 이에 따라, Dugoff`s Tire 모델(식 (11),(12))을 이용하여 실시간 모델을 구성하였고, 접촉 메커니즘 모델과 비교 분석을 수행하였다.
| (11) |
| (12) |
| (13) |
| (14) |
여기서, μ는 지면과 타이어 사이의 마찰계수, cσ는 진행방향 강성계수, cα는 코너링 강성계수, σ는 슬립율, α는 슬립각을 의미한다.
타이어 모델에 따른 주행 특성 분석에 사용된 모델은 Baarath et al. (2018)이 검증한 단일 차량 모델을 이용하여 그림 8과 같이 동역학 모델을 구현하였으며, 제원은 표 5와 같다.
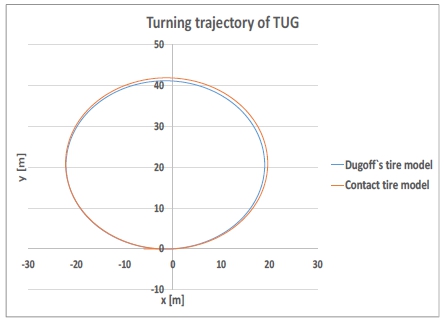
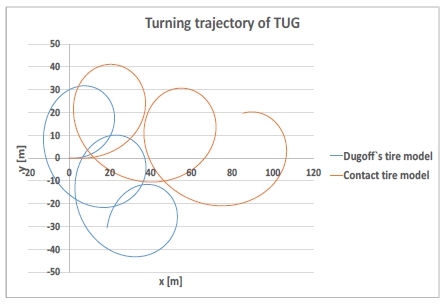
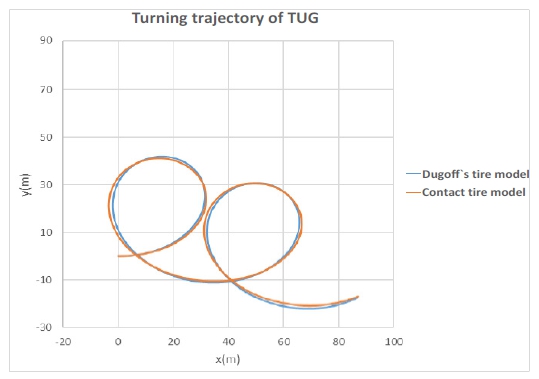
평지 선회 결과, 그림 9와 같이 선회 직경은 Dugoff`s Tire 모델이 41.14 m로 접촉 메커니즘은 41.86 m로 1.7 %의 오차를 보였으며, 유사한 평지 주행 성능 결과를 도출함을 확인하였다. 하지만 경사도가 있는 경우, 그림 10과 같이 경사각이 주어진 pitch 방향의 경사면으로 미끄러지는 현상은 유사하게 나타나지만, 선회 궤적의 차이가 발생함을 확인할 수 있다.
경사도가 있는 경우, 타이어 모델링 방법에 따라서 다음과 같은 차이가 발생한 이유는 타이어 하중 산출 모델은 다수의 가정 및 단순화로 인해 그림 11과 같이 많은 오차 유발 요인을 갖게됨에 따라 경사면 주행 결과의 오차 특성이 더 극대화되기 때문에 차이가 발생하게 된다. 특히, Dugoff`s Tire 모델의 경우 횡력에 대한 입력인자를 최소화한 모델로 더 큰 차이가 발생하게 된다.
또한, 경사각이 커지게 되면 차체의 무게로 인하여 구심력이 감소함에 따라, 선회운동의 곡률반경이 커지게 되고, 이로 인해 전후륜의 미끄럼각 차이가 증가하여 전륜이 미끄러지는 부족조향이 발생함을 Bang and Lee (2014)의 연구를 통해 고찰된 바있다. 이에 따라, 실시간성을 갖는 선형 타이어 모델을 적용하기 위해서 현재 튜닝 파라미터를 이용하여 오차를 최소화하는 계수를 추정하여 활용하는 연구들이 (Bang and Lee, 2014; Cho et al., 2022; Han and Ko, 2015) 진행되고 있다.
4.2 실시간 선형 타이어 모델의 활용 방법
실시간성을 갖는 Dugoff`s Tire 모델을 Contact Tire 모델을 대체하여 효율적으로 활용하기 위해서는 Dugoff`s Tire 모델의 종방향과 횡방향의 강성계수를 경사각에 따라 최적화하여 활용해야 함을 타이어 모델 분석을 통해 도출할 수 있었다.
이에 따라, 본 연구에는 TUG의 Contact Tire 모델과 Dugoff`s Tire 모델의 경사도에 따른 선회 주행 궤적 결과를 비교하여 최적의 종/횡방향 강성계수를 도출하기 위해 파라미터 수정을 통한 주행 궤적의 변화를 고찰 및 파라미터 수정의 반복과정을 이용한 파라미터 업데이트 방법을 사용하였고, 이를 Baarath 차량 모델에 적용하였다. 그 결과 그림 10과 같이 발생하던 궤적의 오차를 그림 12와 같이 최소화가 가능함을 확인하였고, 추정된 종/횡방향 강성계수의 결과는 표 6과 같다.
연구 결과를 통해, 종/횡방향 계수 업데이트 기법을 이용하여 타이어 하중 산출 모델의 실시간성 확보 및 정확도 증가 효과를 확인할 수 있었다.
5. 결 론
항공모함 내에서는 여러 함재기들을 짧은 시간 동안 작전에 투입해야 함에 따라, 함재기의 이동에 대한 최적화가 주요 이슈가 된다. 이러한 이유로, 실시간 시뮬레이션 기술과 최적 의사결정 기술들을 활용한 전략 연구들이 수행되고 있다. 본 연구에는 여러 요소 기술 중에서 함재기의 이착함 및 항공모함 내 이동 작전에 투입되는 견인차량(TUG)에 대한 동역학 시뮬레이션 모델의 분석 및 실시간 시뮬레이션을 적용하기 위한 타이어 하중 산출 모델의 활용 방법에 대해 고찰을 수행하였다.
함재기 견인차량의 주행 성능에 영향을 미치는 인자는 지면과 타이어 사이의 마찰계수, 해양파에 의한 선박의 거동이다. 이러한 특성을 반영하여 주행 성능을 평가하기 위해서는 동역학 기반의 시뮬레이션 기술을 적용해야 한다.
동역학 시뮬레이션 모델의 구축에 있어, 다양한 주행 메커니즘 표현 방법들이 존재하는데 여기서는 주행 메커니즘을 대표하는 접촉 모델과 실시간 주행 성능 평가를 위한 타이어 하중 산출 모델 중 Dugoff`s Tire 모델을 적용하여 비교 분석을 수행하였다. 접촉 모델은 주행 시 타이어 표면의 모든 질점의 비선형 특성을 고려할 수 있어 비교적 정밀한 결과를 도출할 수 있으나, 해석 시간이 오래 걸려 실 작전에 활용되기 어렵다. 타이어 하중 산출모델은 타이어 중심에서의 하중만 계산하기 때문에 실시간 해석이 가능하여 실제 작전에 활용이 가능하나, 타이어 모델링 방법에 따라서 적용이 필요한 입력 인자의 종류가 다르며, 적합한 수치를 인가하지 않으면 큰 오차를 갖는 결과가 도출될 수 있다. 이러한 오차는 사용하고자 하는 타이어 모델 기법을 선정한 후 계수 파라미터 튜닝 기법으로 보완이 가능함을 연구를 통해 확인하였으며, 검증 결과 접촉모델과 타이어 하중 산출 모델의 결과 유사성을 계수 파라미터 튜닝 기법을 통해 가능함을 고찰하였다.
향후 연구에서는 함재기에서 사용되는 다양한 견인차량 각각에 대한 주행속도와 선박 거동 조건에 따른 계수 보간 모델을 개발하여 실시간으로 정밀한 결과를 도출하는 함재기 견인차량 주행 성능 예측 시뮬레이션 모델 개발 및 실제 TUG 차량의 주행 특성 계측값을 이용하여 Contact Tire 모델 vs Dugoff`s Tire 모델 결과와 Real Data vs Dugoff`s Tire 모델의 결과를 비교하여 상호보완적으로 활용할 수 있는 방법론을 도출할 예정이다.
Acknowledgments
본 논문은 방위산업기술지원센터로부터 연구비를 지원(계약번호:UC200006D)받아 선박해양플랜트연구소에서 “함재기 이·착함 시뮬레이션 기술”(PGS4280)로 수행된 연구결과입니다.
References
-
Baarath, K., Zakaria, M.A. and Zainal, N.A., 2018. An investigation on the effect of lateral motion on normal forces acting on each tires for nonholonomic vehicle. Intelligent Manufacturing & Mechatronics, pp.611-621.
[https://doi.org/10.1007/978-981-10-8788-2_55]

-
Bang, J. and Lee, B., 2014. A roll-behavior analysis of SUV in turning motion on a slope. Transaction of Korean Society of Automotive Engineers, 22(4), pp.131-137.
[https://doi.org/10.7467/KSAE.2014.22.4.131]

-
Cho, K., Kim, J., Lee, H., You, S. and Cho, W., 2022. Data-driven based accuracy improvement for vehicle lateral model. Transaction of Korean Society of Automotive Engineers, 30(2), pp.133-142.
[https://doi.org/10.7467/KSAE.2022.30.2.133]

-
Choi, C. and Park, J., 2017. Game-based lateral longitudinal coupling control for autonomous vehicle trajectory tracking. IEEE Access, 4, pp.1-10.
[https://doi.org/10.1109/ACCESS.2021.3135489]

- Dugoff, H., Fancher, P. and Segel, L., 1969. Tire performance characteristics affecting vehicle response to steering and braking control inputs. University of Michigan.
- Etienne, C., 2011. Modelling and nonlinear analysis of aircraft ground manoeuvres. University of Bristol.
- Fiala, E., 1954. Lateral forces on rolling pneumatic tires. Zeitschrift V.D.I.
- Han, S. and Ko, K., 2015. Forklift truck vehicle dynamics modeling and stability analysis. KSAE 2015 Annual Conference and Exhibition, Gyeongju, Republic of Korea, 18-21 November 2015.
- Kim, J., Jung, S. and Yoo, W., 2017. Analysis of limitation and improvement of degree of freedom for brush tire model. Transactions of Korean Society of Mechanical Engineers, 41(7), pp.585-590.
-
Liu, H., Yang, X., Li, Y. and Guo, H., 2018. Adaptive backstepping controller to improve handling stability of tracctor-aircraft system on deck. 15th International Conference on Ubiquitous Robots, Hawaii, USA, 27-30 June 2018.
[https://doi.org/10.1109/URAI.2018.8441769]

-
Liu, J., Han, W. and Wang, X., 2019. Trajectory planning and tracking control for towed carrier aircraft system. Aerospace Science and Technology, 84, pp.830-838.
[https://doi.org/10.1016/j.ast.2018.11.027]

- Michael, T., 2015. Implementation and validation of the fiala tire model in chrono. Technical Report TR-2015-13, MSC Software.
-
Noh, K., 2016. A study on the application of runway friction measurements. Journal of the Korean Society for Aviation and Aeronautics, 24(3), pp.62-68.
[https://doi.org/10.12985/ksaa.2016.24.3.062]

- Oh, J., Kim, H. and Kwon, O., 2021. A study on the development of safety operation guideline for onboard a-frame system using dynamic simulation. Journal of the Korea Society of Industry Convergence, 24(5), pp.625-633.
- Pacejka, H.B., 2006. Tyre and Vehicle Dynamics. Butterworth Heinemann.
-
Paszkowiak, W., Bartkowiak, T. and Pelic, M., 2021. Kinematic model of a logistic train with a double ackermann steering system. International Journal of Simulation Modelling, 20(2), pp.243-254.
[https://doi.org/10.2507/IJSIMM20-2-550]

-
Shim, H., Chung, J., Cho, T., Lee, S. and Song, G., 2022. A research of the flow-field measurement above the flight deck on LHP by PIV system. Journal of Society of Naval Architects of Korea, 59(4), pp.225-234.
[https://doi.org/10.3744/SNAK.2022.59.4.225]

- Virtual Motion, 2020. DAFUL 2020 R1 Verification Manual. Virtual Motion, Inc.
- Virtual Motion, 2021. DAFUL 2021 R1 User`s Manual. Virtual Motion, Inc.
- You S.H., 2017. The accuracy improvement of vehicle lateral single track model. Korea University of Technology and Education.