다방향 불규칙파에 대한 조파 기법 및 방향 스펙트럼 추정 연구

1. 서 론

해양구조물은 항시 파랑에 노출되기 때문에 실해역의 파랑을 잘 모사하여 구조물의 응답을 평가해야 한다. 실해역은 여러 방향에서 진행되는 파의 중첩으로 생성된 다방향 불규칙파(multi-directional irregular waves)이지만 장파정 불규칙파(long crested irregular waves)와 비교하여 상대적으로 복잡하기 때문에 모형수조에서는 주로 장파정 불규칙파 시험을 한다. 그러므로 보다 현실적인 해상상태를 반영하기 위해서는 다방향 불규칙파가 고려되어야 하며 다방향 불규칙파의 생성과 해석기법에 대한 연구가 요구된다. 하지만 다방향 불규칙파의 조파는 조파기의 총길이와 수조제원에 제한되기 때문에 경사파 조파 범위가 한정됨에 따라 목표로 하는 다방향 불규칙파가 존재하는 영역이 한정된다(Takayam, 1982). 이와 같은 이유로 다방향파에 대한 많은 연구자료가 공개되어 있지 않은 실정이다.

최근 해양과학기술원 부설 선박해양플랜트연구소(Korea Research Institute of Ships and Ocean Engineering, KRISO)에서는 심해공학수조(Deep Ocean Engineering Basin, DOEB)가 건설되어 다양한 해양구조물의 파랑 중 성능을 평가하고 있다. 따라서 효율적이고 정밀한 모형시험을 위해 심해공학수조의 조파성능에 대한 연구가 지속적으로 진행되고 있다 (Oh et al, 2022). 심해공학수조는 사각수조로 L type의 스네이크 조파기를 보유하고 있다. 해당 조파기와 스네이크 원리를 이용하여 경사 규칙파, 장파정 불규칙파 그리고 다방향 불규칙파를 생성할 수 있다. 목표하는 파랑을 생성하기 위해서는 적절한 조파판(wave paddle)들의 운동이 구현되어야 하며 해당 조파판의 변위들은 조파 프로그램인 AwaSys (Andersen and Figaard, 2014)를 통해 구현된다. 따라서 AwaSys가 제공하는 심해공학수조의 조파판 변위의 생성기법을 확보함은 물론 다방향파의 특성 파악이 요구된다.

다방향파의 특성은 파성분의 방향분포를 통해 파악되며 이를 추정하기 위한 다양한 방법이 제안되었다. MLM(Maximum Likelihood Method)은 대표적인 상호스펙트럼을 이용한 추정법이며 정확성을 위해 파고계 배치의 각별한 주의가 요구된다(Goda, 1985). 파고계 배치 및 상호스펙트럼의 오차를 극복하기 위하여 MEM(Maximum Entropy Principle Method)이 제안되었다. van den Berg (2011)에 의해 두 방법에 대한 비교연구가 수행되었으며 MEM이 더 정확한 방향분포를 추정하지만 때때로 잘못된 결과를 제공하는 것으로 확인하였다. 이와 달리 MLM의 경우, MEM과 비교하여 상대적으로 부정확하지만 빠르고 강건한 결과를 제공하는 것으로 보고하였다.

다방향파 재현과 정량적인 검증을 위한 모형시험은 고려할 변수가 다양하기 때문에 수치수조를 통한 파랑 생성 특성 파악은 수조시험의 시간과 비용을 절약할 수 있다. CFD와 같은 점성수치수조 (Jia et al., 2020)와 비교하여 효율적인 측면에서 비점성, 비압축성을 가정한 스펙트랄 방법 (Lee et al., 2005; Oh et al., 2020)과 경계요소법이 주로 사용된다 (Sung et al., 1997; Oh et al., 2018). 특히 경계요소법이 수조의 기하학적 특성을 반영하는데 더 유리하다.

본 연구에서는 심해공학수조와 같이 스네이크 조파기의 조파판 변위 시계열을 생성하고 검증하기 위하여 경계요소법 기반 3차원 선형 수치수조를 개발하였다. 규칙 경사파, 장파정 불규칙 경사파 그리고 다방향 불규칙파 생성을 위한 조파판 변위 시계열 생성기법을 구현하였다. 불규칙파의 경우, 속도면에서 우수한 FFT(Fast Fourier Transform) 및 IFFT(Inverse Fast Fourier Transform) 알고리즘을 활용하였다. 생성된 조파판의 변위 시계열을 이용하여 수치수조에서 조파 시뮬레이션을 수행하였고 시뮬레이션 결과의 스펙트럼을 이용하여 생성된 조파판 변위 시계열의 적정성을 검증하였다. 다방향 불규칙파 생성의 적정성을 검증하기 위하여 방향파 추정이 필수적이다. 따라서 다방향파의 특성을 파악하기 위하여 MLM을 이용한 방향파 추정 코드를 작성하여 검증하였다. 검증된 방향파 추정코드를 이용하여 수조모형시험의 방향분포 특성은 물론 조파 시뮬레이션의 방향분포 특성을 파악하였다. 다방향 불규칙파의 방향분포 교정 절차를 수립하였고 수치수조를 이용하여 방향분포함수의 교정 가능성을 확인하다.

2. 3차원 경계요소법을 이용한 수치수조

2.1 경계치 문제

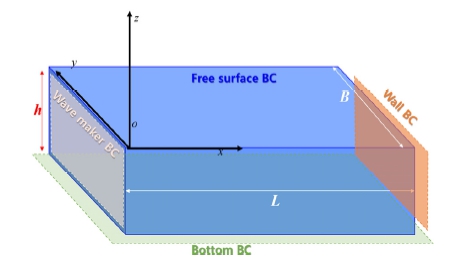
본 연구에서는 Fig. 1과 같이 3차원 직교좌표계(x, y, z)를 사용하였고 z는 평균수면을 기준으로 상방으로 정의하였다. 자유수면경계, 조파경계, 바닥경계 및 벽 경계조건으로 구성된 수치수조의 경계치 문제를 구성하였다. 유체의 비압축과 비점성 그리고 유동의 비회전을 가정하면 유체속도는 속도 포텐셜 Φ의 구배로 표현될 수 있고 지배방정식인 연속 방정식은 식 (1)과 같이 라플라스방정식으로 치환된다.

Fig. 1

Coordinate system for 3D wave maker problem

$\[ {\nabla }^2\Phi =0\mathrm{ }\mathrm{i}\mathrm{n}\mathrm{ }\mathrm{f}\mathrm{l}\mathrm{u}\mathrm{i}\mathrm{d}\mathrm{ }\mathrm{r}\mathrm{e}\mathrm{g}\mathrm{i}\mathrm{o}\mathrm{n} \]$

(1)

자유수면 경계면의 압력은 대기압과 동일해야하며 경계면의 속도는 유체입자의 속도와 동일하다. 이러한 물리적 특성을 동역학적 경계조건과 운동학적 경계조건이라 하며 선형화된 경계 조건은 식 (2)와 (3)과 같다.

$\[ \frac{\partial \Phi }{\partial t}=-g\eta \mathrm{ }\mathrm{o}\mathrm{n}\mathrm{ }\mathrm{f}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{ }\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{ }\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y} \]$

(2)

$\[ \frac{\partial \eta }{\partial t}=\frac{\partial \Phi }{\partial z} \mathrm{o}\mathrm{n}\mathrm{ }\mathrm{f}\mathrm{r}\mathrm{e}\mathrm{e}\mathrm{ }\mathrm{s}\mathrm{u}\mathrm{r}\mathrm{f}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{ }\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y} \]$

(3)

여기서 g는 중력가속도 그리고 η는 자유표면의 변위를 나타낸다.

깊이 h에 위치한 수저면과 벽면은 불투과 경계조건으로 식 (4)로 표현된다.

(4)

조파기 경계면은 식 (5)와 같이 조파면 속도 U_n으로 정의된다. 피스톤(piston) 방식또는 플랩(flap) 방식과 같은 조파기의 형태에 따라 U_n을 정의할 수 있다.

$\[ \frac{\partial \Phi }{\partial n} = U_n\left(t\right) \mathrm{o}\mathrm{n}\mathrm{ }\mathrm{w}\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{ }\mathrm{m}\mathrm{a}\mathrm{k}\mathrm{e}\mathrm{r}\mathrm{ }\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y} \]$

(5)

2.3 심해공학수조 모델

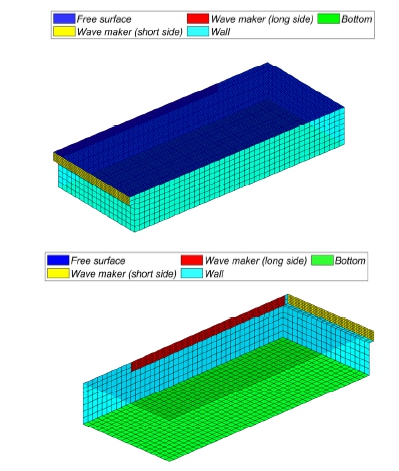
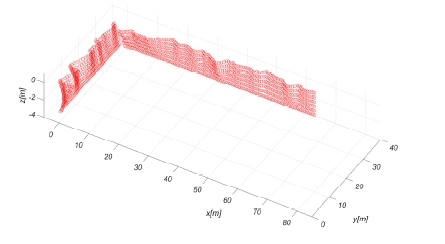
본 연구는 심해공학수조의 다방향 조파기 신호생성을 목표로 하기 때문에 심해공학수조의 기하학적 형상을 반영하는 것이 중요하다. 심해공학수는 100 m x 50 m x 15 m의 규모이며 L type의 스네이크 조파기가 설치되어 있다. 조파기는 단변(short side)으로 35 m 그리고 장변(long side)으로 65 m의 길이에 대하여 0.5 m 조파판이 동일한 간격으로 배치된다. 각각의 조파기의 조파판은 수면으로부터 3 m 아래 힌지를 기준으로 회전하는 플랩 플랩(flap) 방식이다 (Oh et al., 2022). 심해공학수조의 형상을 반영하여 Fig. 2와 같이 경계요소법에 활용할 격자를 생성하였다. 8,520개의 자유수면 panel을 포함하여 총 11,256개의 panel로 구성되어 있다. 조파기의 panel은 조파판 간격을 고려하여 0.5 m 간격으로 격자를 구성하였다.

Fig. 2

Panel model for Deep Ocean Engineering Basin

3. 다방향 불규칙파 생성을 위한 조파기 신호 생성

3.1 규칙 경사파 생성

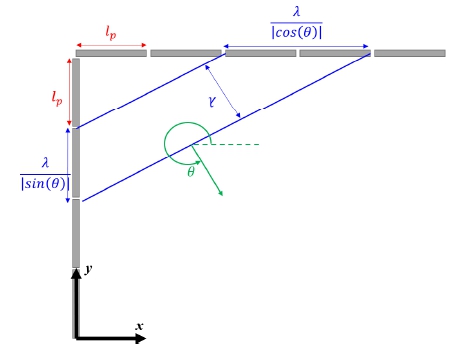
수조에서 다방향 불규칙파 생성은 다수의 규칙 경사파의 중첩을 통해 생성된다. 따라서 규칙 경사파에 대한 조파기 시계열의 생성은 다방향 불규칙파 생성의 기초가 된다. 먼저 Fig. 3과 같이 L type의 유한한 조파판으로 분할된 조파기를 고려한다. 조파판의 간격은 l_p이며 θ 방향으로 전진하는 규칙파를 생성하기 위한 단일 조파판의 조파기의 전달함수는 식 (11)과 같이 나타낼 수 있다.

Fig. 3

Wave generation system with segmented wave paddles

$\[ T{F}_{WM,3D}=\left\{\begin{array}{c}\frac{T{F}_{WM,2D}}{\sin \left(\theta \right)}\cos \left(\omega t+\frac{2\pi }{\lambda }{l}_p\left(i+0.5\right)\cos \left(\theta \right)\right) at x\\ \frac{T{F}_{WM,2D}}{\cos \left(\theta \right)}\cos \left(\mathit{\omega t}+\frac{2\pi }{\lambda }{l}_p\left(i+0.5\right)\sin \left(\theta \right)\right)at y\end{array}\right. \]$

(11)

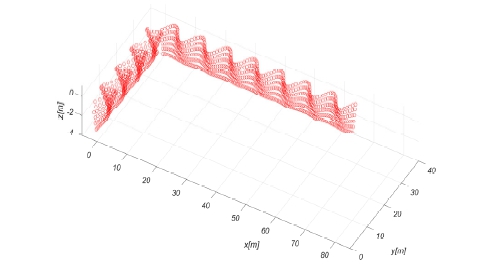
여기서 TF_WM,2D는 2차원 조파기의 전달함수를 의미하며 심해 공학수조의 전달함수에 대하여 Oh et al. (2022)에서 자세히 다루고 있다. i 는 기준 위치로부터 조파기의 순번을 의미한다. 식 (11)을 통하여 심해공학수조에 설치된 200개의 조파기에 고려하면 Fig. 4와 같은 조파판의 변위를 도출할 수 있다.

Fig. 4

Snapshot of wave paddle for regular oblique wave (T=2s)

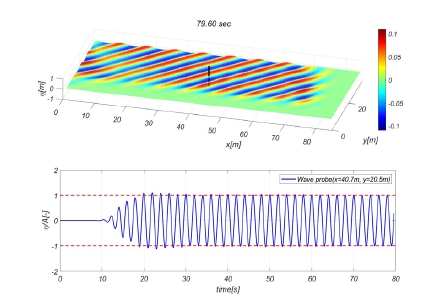
주기 1, 2, 3 그리고 4초를 가진 진폭 0.1 m의 규칙 경사파 시뮬레이션을 수행하였다. 파 방향은 –45 deg이며 시뮬레이션 주기는 60주기를 수행하였다. Fig. 5는 2초 주기의 규칙 경사파를 도시하였으며 목표 위치(x=40.5 m, y=20.7 m)에서의 목표 파고에 도달함을 확인할 수 있다.

Fig. 5

Example of regular oblique wave generation (T=2s)

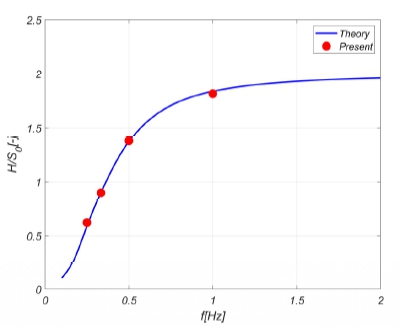
목표위치(x=40.5 m, y=20.7 m)에서 계산된 파 시계열의 조화해석을 통하여 도출된 전달함수와 이론적 전달함수를 비교하여 Fig. 6에 도시하였고 두 결과가 일치함을 확인하였다. 이를 통하여 경사파 생성 이론으로 도출된 식 (11)이 시뮬레이션으로 잘 구현됨을 알 수 있다.

Fig. 6

Comparison of transfer function of wave maker

3.2 Random phase method를 이용한 불규칙 경사파 생성

실해역의 해양파는 시간에 따라 임의로 변하며 여러 가지 방향으로 진행하는 다방향성을 가지고 있어 확률적 추정을 통하여 그 분포를 예측할 수 있다. 실제로 해상의 특성을 나타내는 유의파고(H_s) 그리고 첨두주기(T_p)를 통해 대상해역의 특성을 나타낼수 있는 스펙트럼을 정의할 수 있다. 본 연구에서는 불규칙 해상상태를 정의하기 위하여 식 (12)와 같은 JONSWAP spectrum을 사용하였다.

$\[ S_{\eta }\left(\omega \right)=A_{\gamma }\frac{5}{16}{H}_0^2\frac{{\omega }_p^4}{{\omega }^5}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{5}{4}{\left(\frac{\omega }{{\omega }_p}\right)}^{-4}\right){\gamma }^{\exp \left(-0.5{\left(\frac{\omega -{\omega }_p}{\sigma {\omega }_y}\right)}^2\right)} \]$

(12)

여기서 A_γ는 정규화 상수, γ는 peak shape parameter, σ는 spectral width parameter, ω_p는 peak 각주파수 그리고 ω는 파각주파수를 의미한다. 다방향분포를 정의하기 위한 방향스펙트럼은 식 (13)과 같이 파스펙트럼 S_η과 방향분포함수 D의 곱으로 표시된다.

$\[ S_{\eta }\left(\omega ,\theta \right)=D\left(\omega ,\theta \right)S_{\eta }\left(\omega \right) \]$

(13)

여기서 방향분포함수 D는 Mitsuyasu et al. (1975)가 제안한 형태인 식 (14)와 같이 표시되는데 s는 spreading parameter, Γ는 감마함수, θ₀는 주방향각 그리고 θ는 방향각을 의미한다.

$\[ D\left(\omega ,\theta \right)=\frac{2^{2s-1}}{\pi }\frac{{\Gamma }^2\left(s+1\right)}{\Gamma \left(2s+1\right)}{\mathrm{c}\mathrm{o}\mathrm{s}}^2\left(\frac{\theta -{\theta }_0}{2}\right) \]$

(14)

식 (12) 또는 (13)의 스펙트럼은 주파수 별 파의 에너지 분포를 나타내며 이를 시간영역의 신호를 생성하는 것이 필요하다. 본 연구에서는 불규칙파를 위한 조파판 변위 시계열 생성을 위해 random phase 방법을 활용하였다. Random phase 방법은 각 주파수 성분에 랜덤 위상을 할당하여 주파수 영역에서 시간영역으로 시계열을 생성하는 방법이다. 불규칙파를 위한 조파판 변위 시계열은 정현파의 합으로 가정할 수 있으므로 FFT를 통하여 불규칙한 시계열을 나타낼 수 있다. 따라서 FFT와 IFFT 알고리즘을 활용하면 빠르고 효율적으로 불규칙파를 위한 조파판 변위 시계열을 생성할 수 있다. 조파 시뮬레이션의 경우, 조파기 경계면의 속도가 필요하므로 계산된 조파판 변위 시계열로부터 유도된 속도 시계열을 이용하였다.

3.2.1 장파정 불규칙 경사파 생성

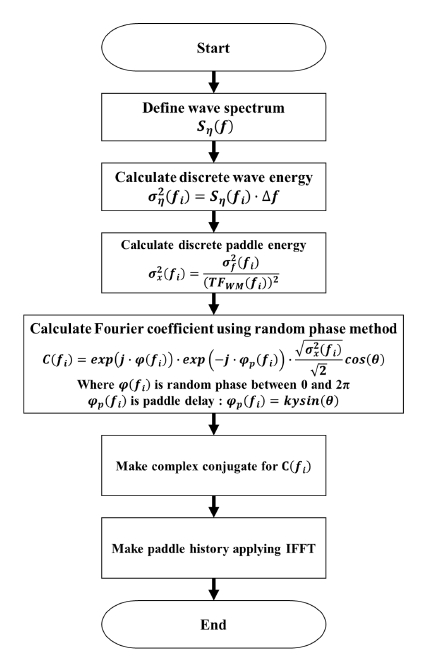
파성분의 방향이 동일한 장파정 불규칙 경사파(long crested oblique irregular waves)를 고려하고자 한다. 장파정 불규칙 경사파를 생성하기 위한 조파판 변위 시계열 생성 절차는 Fig. 7과 같이 나타낼 수 있다.

Fig. 7

Flow chart of generation of wave paddle signal for long crested irregular oblique waves

Fig. 7과 같은 절차를 통하여 목표 스펙트럼 S_η에 대한 조파판 변위 시계열을 생성할 수 있다. 해당 알고리즘의 검증을 위해 아래와 같은 Spectrum에 대하여 시뮬레이션을 수행하였다.

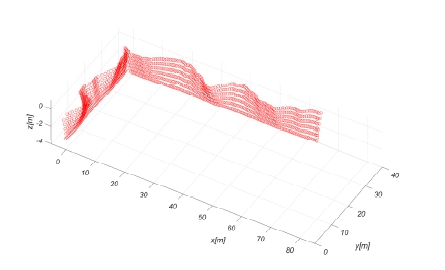
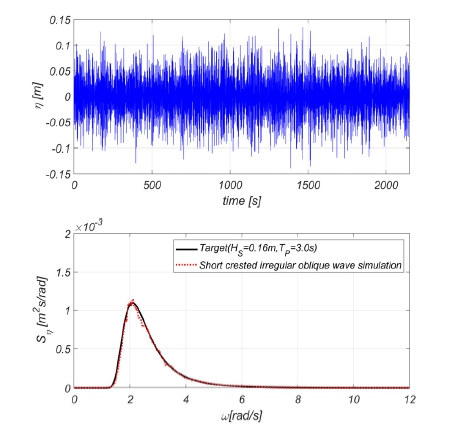
Fig. 7의 절차를 통해 심해공학수조에 설치된 200개의 조파판의 변위가 Fig. 8과 같이 계산된다. 조파판 변위를 반영한 조파시뮬레이션이 수행되었으며 조파면으로부터 불규칙파가 생성되어 소파면으로 전파됨을 Fig. 9에서 확인할 수 있다. 시뮬레이션 시간은 2,184초이며 목표지점(x=40.5 m, y=20.7 m)까지 파도가 도달되기 전 34초를 제외한 2,150초에 대하여 spectrum 해석을 수행하여 Fig. 10에 도시하였다. 조파판 변위 시계열을 통해 생성된 파 시계열의 스펙트럼과 목표 스펙트럼이 5% (ITTC, 2021)이내에서 잘 일치함을 알 수 있다.

Fig. 8

Snapshot of wave paddle for long crested irregular oblique waves (Hs=0.16 m, Tp=3.0 s)

Fig. 9

Simulation of long crested irregular oblique waves generation

Fig. 10

Wave time history and spectra of long crested irregular oblique waves at target point

3.2.2 다방향 불규칙파 생성

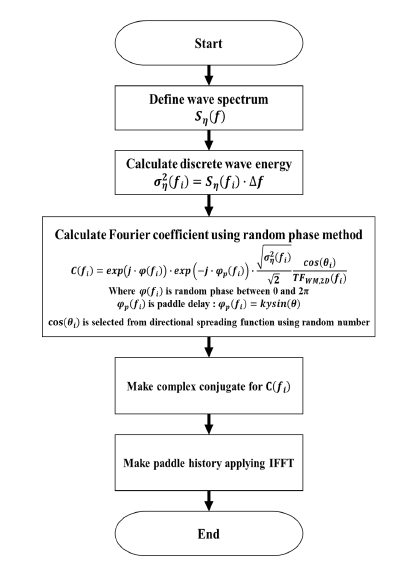
장파정 불규칙파와 달리 실해역의 파는 파성분의 방향의 분포가 존재하는 다방향 불규칙파이다. 다방향 불규칙파는 규칙파를 합성하는 방법에 따라 단일합성법(single summation method)과 이중합성법(double summation method)으로 구분된다. 이중합성법은 직관적이며 적용이 단순하지만 phase locking과 같은 현상이 발생할 수 있다. 따라서 이를 방지하기 위하여 단일합성법보다 많은 파성분의 분할이 요구된다 (Takayama et al., 1989). 본 연구에서는 단일합성법으로 조파판 변위 시계열을 생성하였으며 절차는 Fig. 11과 같다. Fig. 11과 같은 절차를 통하여 목표 스펙트럼S_η에 대한 조파판 변위 시계열를 생성할 수 있다. 해당 알고리즘의 검증을 위해 Table 2와 같은 Spectrum에 대하여 시뮬레이션을 수행하였다.

Fig. 11

Flow chart of generation of wave paddle signal for multi-directional irregular waves

Table 1.

Target spectrum for long crested irregular waves

Table 2.

Target spectrum for multi-directional irregular waves

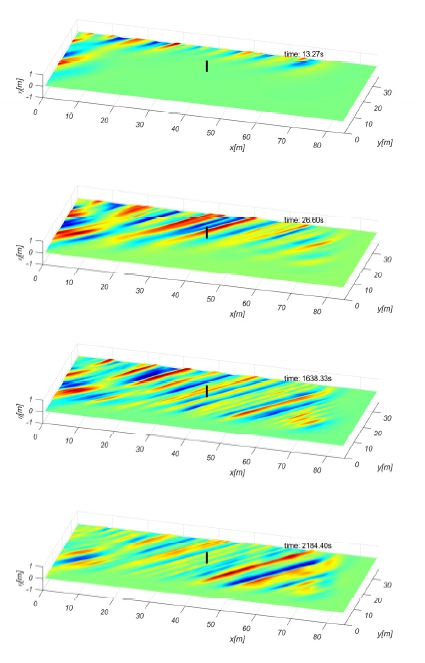
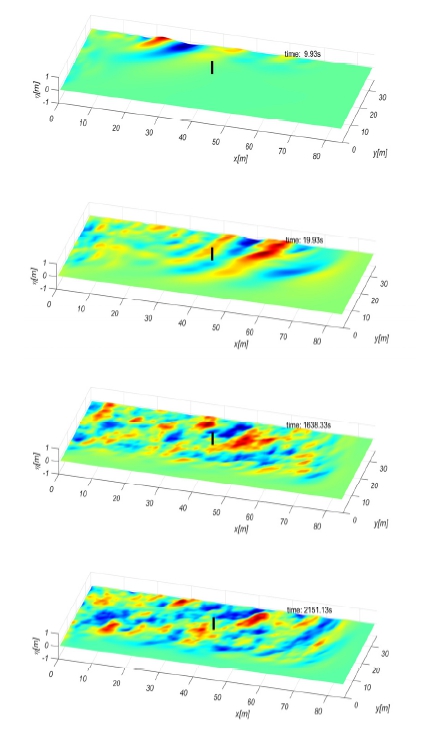
Fig. 11의 절차를 통해 심해공학수조에 설치된 200개의 조파판의 변위가 Fig. 12와 같이 계산된다. 조파판 변위를 반영한 조파 시뮬레이션이 수행되었으며 조파면으로부터 불규칙파가 생성되어 소파면으로 전파됨을 Fig. 13에서 확인할 수 있다.

Fig. 12

Snapshot of wave paddle for multi-directional irregular waves (Hs=0.16 m, Tp=3.0 s)

Fig. 13

Simulation of multi-directional irregular waves generation

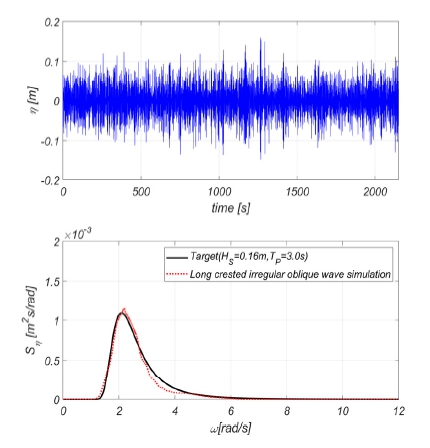
시뮬레이션 시간은 장파정 불규칙 경사파와 동일하며 2,184초이며 목표지점(x=40.5 m, y=20.7 m)까지 파도가 도달되기 전34초를 제외한 2,150초에 대하여 spectrum 해석을 수행하여 Fig. 14에 도시하였다.

Fig. 14

Wave time history and spectra of multi-directional irregular waves at target point

다방향 불규칙파의 조파판 변위 시계열을 통해 생성된 파 시계열의 스펙트럼과 목표 스펙트럼이 5 % (ITTC, 2021) 이내에서 잘 일치함을 알 수 있다. 하지만 다방향 불규칙파의 생성은 스펙트럼뿐만 아니라 방향분포 또한 잘 모사되었는지 확인이 필요하다. 방향분포를 추정하기 위해서는 3차원 파랑장이 반영되어야 한다. 따라서 이를 위해 다수의 위치의 파고 시계열의 상호상관성(cross corelation) 분석이 필요하다. 3.3장에서는 MLM(Maximum Likelyhood Method)에 대하여 논하며 본 시뮬레이션을 통해 도출된 시계열을 분석을 통해 방향분포를 살펴보고자 한다.

3.3. 다방향 불규칙파의 방향파 해석

3.3.1 Maximum Likelihood Method (MLM)

MLM은 다수 파고계에서 계측된 파 시계열을 기반하여 분산(variance) 오차가 최소화된 다방향 불규칙파의 방향분포를 추정하는 방법이며 식 (15)와 같이 유도된다 (Goda, 1985).

$\[ D\left(\omega ,\theta \right)=\kappa /\left[\sum _{m,n}^M {\Psi }^{-1}\left(\omega \right)\cdot \mathrm{e}\mathrm{x}\mathrm{p}\left(iK\left(x_n-x_m\right)\right)\right] \]$

(15)

여기서 Ψ는 상호스펙트럼(cross spectrum), κ는 정규화 상수(normalize constant), M은 파고계의 수, K는 파수 벡터(vector of wave number) 그리고 x는 파고계 위치를 의미한다. MLM의 경우, 파고계 배치에 민감하다고 알려져 있으며 Goda (1985)에 의하여 파고계 배치에 대한 가이드 라인이 다음과 같이 제시되어 있다. ① 어떤 쌍의 파고계도 파고계 사이의 거리가 동일하지 않아야 한다. ② 파고계 거리는 가능한 한 넓은 범위에서 균일하게 분포되어야 한다. ③ 한 쌍의 파고계 사이의 최소간격은 방향 분석을 수행할 구성 파 성분의 최소 길이의 절반 미만이어야 한다.

3.3.2 MLM 추정 코드 검증

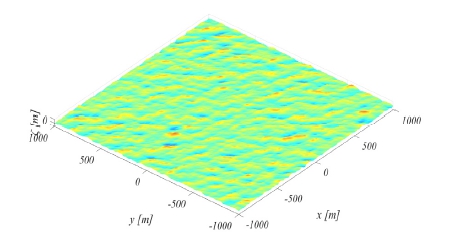
MLM 기반 방향파 추정 코드를 작성하였으며 이를 검증하였다. Table 3과 같은 다방향 불규칙를 단일합성법을 통하여 Fig. 15와 같이 생성하였다.

Table 3.

Target spectrum for multi-directional irregular waves

Fig. 15

Snapshot of wave field of multi-directional irregular waves

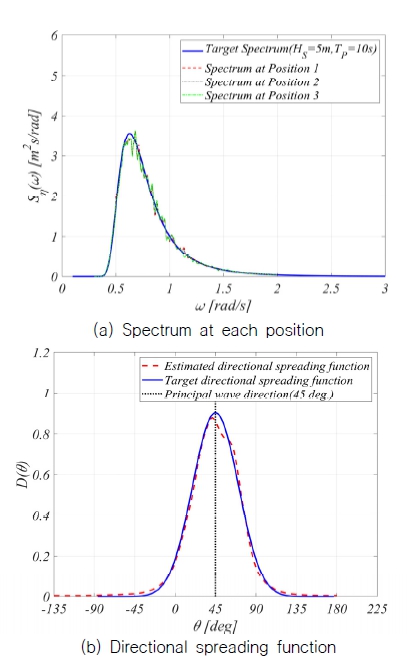
Goda (1985)의 가이드라인을 참조하여 3개의 지점(delta array)의 파 시계열을 선정하였으며 개발된 추정 코드를 통하여 방향파 분석을 수행하였고 이를 Fig. 16에 도시하였다. 추정코드를 통하여 3개 지점의 스펙트럼과 MLM으로 추정된 방향분 포함수가 목표값과 유사하게 추정되는 것을 알 수 있다.

Fig. 16

Frequency and directional wave spectra of random phase method

3.3.3 조파 시험을 통한 방향파 해석

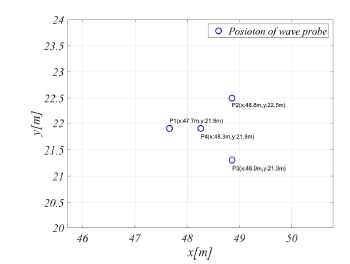
심해공학수조에는 3.2장에서 제시된 알고리즘과 동일한 방법으로 다방향 불규칙파가 생성된다 (Andersen and Figaard, 2014). 심해공학수조의 다방향 불규칙파 생성 시험을 수행하였다. Goda (1985)의 가이드라인을 참조하여 심해공학수조 중심에 Fig. 17과 같이 용량식 파고계(capacitance type wave probe) 4개를 star array 형태로 설치하였다. 계측신호를 수집하기 위한 데이터수집장치로 National Instruments사의 cDAQ가 사용되었고 Sampling rate는 100 Hz로 설정하였다.

Fig. 17

Wave probes at DOEB

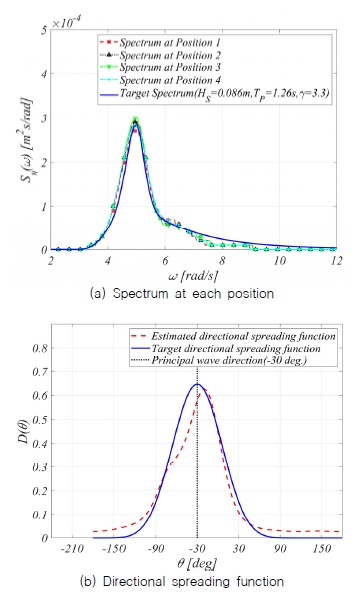
다방향 불규칙파는 Table 4와 같은 조건으로 Fig. 18과 같이 450초간 다방향파를 생성하였으며 설치된 파고계에서 파고를 계측하였다. 계측된 파 시계열을 개발된 추정코드를 통하여 방향파분석을 수행하였고 이를 Fig. 19에 도시하였다. 4개 지점의 스펙트럼이 목표 스펙트럼과 5% (ITTC, 2021) 이내에서 일치함을 확인할 수 있으며 MLM으로 추정된 방향분포함수 또한 파고계의 계측지점의 제한성과 수조의 소파영역에서의 반사와 같은 특성으로 인하여 목표값과 일부 차이가 발생하나 전반적인 방향분포함수가 목표값과 유사한 것을 확인할 수 있다. 일부 범위에서 목표값과 근소한 차이는 반복 시험을 포함한 교정 절차를 통해 목표하는 방향분포함수로 교정이 가능하다. 관련 절차 및 검증은 비용과 시간을 절약할 수 있는 수치수조의 조파 시뮬레이션을 통해 관련 사항을 기술하기로 한다.

Table 4.

Target spectrum for multi-directional irregular waves at DOEB

Fig. 18

Multi-directional irregular waves generation of DOEB

Fig. 19

Frequency and directional wave spectra of multi-directional irregular waves test at DOEB

3.3.4 조파 시뮬레이션의 방향파 해석 및 방향파 교정

상기 개발된 MLM 추정 코드를 통하여 3.2.2장에서 수행된 다방향파 불규칙파 시뮬레이션에 대하여 방향파 해석을 수행하였다.

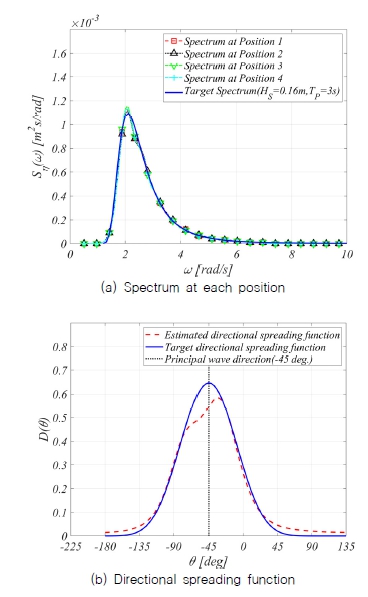
방향파 해석 수행을 위해 Goda (1985)의 가이드라인을 참조하여 Fig. 20과 같은 4개의 지점(star array)을 선정하였다. 조파시뮬레이션 결과를 통하여 방향파 분석을 수행하였고 이를 Fig. 21에 도시하였다. 4개 지점의 스펙트럼의 결과가 3.2.2장의 목표지점의 스펙트럼은 물론 목표 스펙트럼도 유사함을 확인하였다. 방향분포함수 또한 목표값과 유사한 분포로 추정된다. 이러한 결과를 통하여 다방향 불규칙파를 위한 조파판 변위 시계열 생성 알고리즘 또한 검증된 것으로 사료 된다.

Fig. 20

Positions of wave probes of simulation

Fig. 21

Frequency and directional wave spectra of multi-directional irregular waves simulation

방향분포함수의 경우, 수치감쇠영역의 반사파 또는 조파판의 모델링등과 같은 다양한 이유로 모형시험과 유사하게 일부영역에서 차이를 보인다.

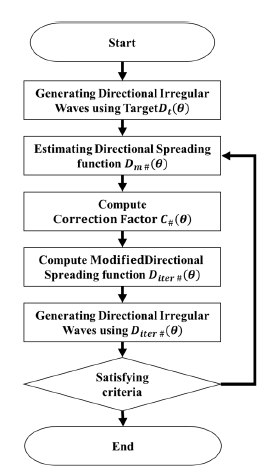
방향분포함수의 분포의 교정은 반복된 조파시험을 통해 목표하는 방향분포함수로 교정이 가능하다 (Schmittner et al., 2013). 교정 절차는 Fig. 22에 도시한 바와 같이 계측된 방향분포함수 D_m을 목표 방향분포함수 D_t의 비율로 정의되는 식 (16)과 같은 Correction factor C_i를 이용하여 입력 방향분포함수 D_iter를 도출한다. C_i를 통해 입력 방향분포함수 D_iter를 식 (17)과 같이 계산할 수 있다.

Fig. 22

Flow chart for directional spreading function correction

$\[ C_i\left(\theta \right)=\left\{\begin{array}{ll}{D}_t\left(\theta \right)/D_{m1}\left(\theta \right)& i=1\\ D_{iter i-1}\left(\theta \right)/D_{mi}\left(\theta \right)& i>1\end{array}\right. \]$

(16)

$\[ D_{iter i}\left(\theta \right)=\frac{\left(\prod _{k=1}^i C_k\left(\theta \right)\right)\cdot D_t\left(\theta \right)}{{\int }_0^{2\pi } \left(\prod _{k=1}^i C_k\left(\theta \right)\right)\cdot D_t\left(\theta \right)d\theta } \]$

(17)

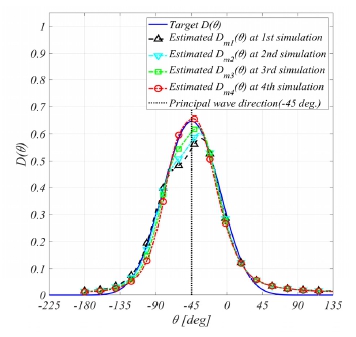
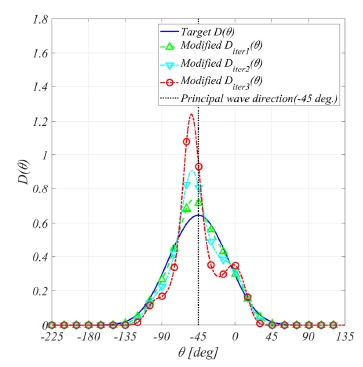
3.2.2장에서 수행된 방향분포함수의 분포 교정은 4번의 반복 조파 시뮬레이션을 통하여 교정을 확인하였다. 해당 방향파 분석은 Fig. 20과 동일한 위치에서 계산된 파 시계열을 통하여 수행되었다. Fig. 23은 각각의 각각 조파 시뮬레이션 이후 교정된 방향 분표함수를 도시하였다.

Fig. 23

Directional spreading function of iteration procedure

교정 횟수가 증가함에 따라 목표 방향분포함수에 수렴됨을 확인할 수 있다. Fig. 24는 교정 단계별 조파 시뮬레이션 이후 계산되어 입력된 방향분포함수를 도시하였다. Fig. 23에서 목표 방향스펙트럼과 차이가 나는 부분이 조정된 방향분포함수를 확인할 수 있다. 해당 절차를 통해 다방향 불규칙파의 방향분포를 교정할 수 있음을 확인할 수 있다. 모형수조에서도 다수의 반복이 필요하지만 해당 절차를 통하여 방향분포를 교정할 수 있는 가능성을 확인하였다.

Fig. 24

Input directional spreading function

4. 결 론

본 연구에서는 심해공학수조에서 활용하기 위한 다방향파 생성 및 분석을 위한 기초연구를 수행하였다. 3차원 경계요소법 기반 수치수조를 구현하여 조파기법 및 방향 스펙트럼 추정을 수행하였다. 이로부터 다음 결론을 얻을 수 있다.

1) 규칙 경사파를 포한한 다방향 불규칙파를 생성하기 위한 스네이크 조파기의 조파판의 변위 생성기법을 구현하였다. 해당 알고리즘에는 FFT와 IFFT를 변위 생성기법 연산에 사용하기 때문에 빠르고 효율적이다. 해당 생성기법으로 생성된 조파판의 변위를 이용하여 조파 시뮬레이션을 수행하였으며 목표 스펙트럼과 좋은 일치도를 통해 해당 생성기법의 타당성을 검증하였다.

2) 다방향파의 분석을 위해 MLM을 이용한 방향분포 추정코드를 개발하였고 단일합성법을 통해 생성된 파랑장을 추정하여 목표 방향분포함수와 동일한 방향분포함수를 추정함을 확인하였다.

3) 심해공학수조의 다방향파 모형시험을 수행하였고 개발된 추정코드를 이용하여 다방향파 해석을 수행하였다. 목표지점의 스펙트럼과 방향분포함수가 목표값과 유사한 결과를 확인하였으며 심해공학수조의 다방향 불규칙파 생성이 적절히 이루어짐을 확인하였다.

4) 다방향파의 불규칙파의 방향분포 교정 절차를 수립하였고 수치수조에서 해당 절차로 다방향 불규칙파의 방향분포를 교정하였다. 교정횟수가 증가할수록 추정 방향분포함수가 목표 방향분포함수에 수렴하는 결과를 확인하였다.

해당 연구로 확보된 다방향 불규칙파에 대한 조파기법 및 방향 스펙트럼 추정코드를 활용하여 모형시험에 활용할 예정이다.

Acknowledgments

본 연구는 선박해양플랜트연구소에서 지원하는 “심해용 복합해양 플랫폼 통합 성능평가 기술개발”(PES4760)의 결과물임을 밝히는 바입니다.

References

• Andersen, T.L. and Frigaard, P., 2014. Wave generation in physical models: Technical documentation for AwaSys 6. Department of Civil Engineering, Aalborg University. DCE Lecture notes No. 34.
• Goda, Y.. 1985. Random seas and design of maritime structures (1st edition). World Scientific Publishing.
• International Towing Tank Conference (ITTC), 2021, Laboratory Modelling of Waves (7.5-02-07-01.2), ITTC Recommended Procedures and Guidelines. International Towing Tank Conference.
• Jia, W., Liu, S., Li, J. and Fan, Y., 2020. A three-dimensional numerical model with an l-type wave-maker system for water wave simulations by the moving boundary method. Water, 12(1), pp.161 [https://doi.org/10.3390/w12010161]
• Lee, J.H., Choi, J.W., Yun, T.K. and Ha, M.K., 2005. Generation of real sea waves based on spectral nethod and wave direction analysis. Journal of the Society of Naval Architects of Korea, 42(3), pp.212-219. [https://doi.org/10.3744/SNAK.2005.42.3.212]
• Mitsuyasu, H., Tasai, F., Suhara, T., Mizuno, S., Ohkusu, M., Honda, T. and Rikiishi, K., 1975. Observations of the directional spectrum of ocean waves using a cloverleaf buoy. Journal of Physical Oceanography, 5(4), pp.750-760. [https://doi.org/10.1175/1520-0485(1975)005<0750:OOTDSO>2.0.CO;2]
• Oh, S., Cho, S.K., Jung, D. and Sung, H.G., 2018. Development and application of two-dimensional numerical tank using desingularized indirect boundary integral equation method. Journal of Ocean Engineering and Technology, 32(6), pp.447-457. [https://doi.org/10.26748/KSOE.2018.32.6.447]
• Oh, S., Jung, J.H. and Cho, S.K., 2020. Higher-order spectral method for regular and irregular wave simulations. Journal of Ocean Engineering and Technology, 34(6), pp.406-418. [https://doi.org/10.26748/KSOE.2020.052]
• Oh, S., Kim, E.S. and Jung, S., 2022. Development of meta model of transfer function for wavemaker of deep ocean engineering basin. Journal of Korean Navigation and Port Reserch, 46(6), pp.471-482.
• Schmittner, C.E., Scharnke, J., Pauw, W., van den Berg, J. and Hennig, J., 2013. New methods and insights in advanced and realistic basin wave modelling. OMAE 2013 - 32nd International Conference on Ocean, Offshore and Arctic Engineering. OMAE2013-11445. [https://doi.org/10.1115/OMAE2013-11445]
• Sung, H.G., Hong, S.Y. and Choi, H.S., 1997. A study on the boundary element method for numerical analysis of nonlinear free surface wave (1). Journal of the Society of Naval Architects of Korea, 34(4), pp.53-60.
• Takayama, T., 1982. Theoretical properties oblique waves generated by serpent-type wave makers. Rep. the Port and Harbor Research Institute, 21(2), pp.3-48.
• Takayama, T., Hiraishi, T. and Goda, Y., 1989. Comparison of single and double summation models for multi-directional wave generation. In Proc. International Association for Hydraulic Research XXIII Congress, Ottawa, Canada, August 21-25.
• van den Berg, J., 2011. Comparison of methods for short crested wave analysis. OMAE 2011 - 30th International Conference on Ocean, Offshore and Arctic Engineering. OMAE2011-49443. [https://doi.org/10.1115/OMAE2011-49443]