수중함 자유항주모형 개발 및 기본 성능 분석
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper describes the results of the development of the submarine Free Running Model (FRM). First, the goal of development was set based on the test conditions and the test environment, and the system was obtained accordingly. The target submarine, Joubert BB2 submarine, was selected with a scale of 18.35 in accordance with the development goal. In order to conduct a submarine FRM test underwater, where communication is impossible, the FRM must operate at least semi-autonomously. For this purpose, an Extended Kalman Filter (EKF) based underwater integrated navigation system and control system using a sailplane and an X-shaped sternplane were designed respectively. In addition, a ballast system was designed to enable the model to float to the water surface in case of an emergency. To verify its propulsion, navigation, and control performance, the FRM tests were conducted in both indoor and outdoor basins. As a result, the relationship between propeller RPM and vehicle speed was derived, and it was confirmed that the navigation and control performance met the target value.
Keywords:
Submarine free running model, Propulsion performance, Navigation performance, Depth control performance, Way-points tracking performance키워드:
수중함 자유항주모형, 추진 성능, 항법 성능, 심도 제어 성능, 경로점 추종 성능1. 서 론
수중함은 대표적인 해군의 핵심 전력으로 크고 작은 전쟁에서 그 전략적 중요성이 입증된 바 있어 각국은 고성능의 수중함 개발에 천문학적인 비용을 투자하고 있다. 수중함의 조종성능은 작전 범위나 운용 효과도에 영향을 미칠 뿐만 아니라 승조원의 안전과도 밀접한 관련이 있는 성능지표 중 하나이기 때문에, 함 설계 단계에서부터 실선의 조종성능을 정확하게 추정하기 위한 다양한 연구들이 수행되었다. 수중함 조종성능 추정에는 일반적으로 수중함 조종운동 시뮬레이션이 사용된다. 조종운동 시뮬레이션을 위한 대표적인 수학모델은 Gertler and Hagen (1967)과 Feldman (1979)에 의해 제안되었으며, 이 수학모델은 수중함에 작용하는 동유체력을 유체력계수(hydrodynamic coefficients)와 상태변수로 이루어진 다항식 형태로 모델링했다는 특징이 있다.
수중함은 사령탑 및 부가물에서의 유동 박리 현상과 회전하는 추진기에 의한 유동장 교란 등의 영향이 매우 강하게 작용하여 복잡한 6자유도 비정상(unsteady) 운동을 하므로 일반적으로 해석적 방법보다는 모형시험을 통해 유체력계수를 도출하게 된다(Shen and Hess, 2010). 유체력계수를 정밀 도출하기 위한 다양한 시험기법이 연구되었으며, 평면운동장치(Planar Motion Mechanism, PMM)시험과 회전팔시험, 원추형시험 등의 구속모형시험기법을 주로 사용해왔다 (Feldman, 1987; Rhee et al., 2000; Kim et al., 2012; Park et al., 2020). 최근에는 CFD를 활용한 수치 수조 구속모형시험 해석에 관한 연구도 수행되고 있다(Toxopeus et al., 2012; Sung and Park, 2015; Cho et al., 2020). 그러나 구속모형시험은 기구적인 한계로 인해 다축이 연성된 기동을 모형에 인가하여 시험하는 것이 어렵기 때문에 모든 유체력계수를 구속모형시험을 통해 도출하는 것은 현실적으로 불가능하다. 또한 수중함의 작전 범위가 점차 확대되어 복잡한 기동이 요구됨에 따라 전통적인 구속모형시험 기반의 조종운동 모델이 유효한 범위를 넘어서는 구간에 대한 예측 필요성이 점차 중요해지고 있다. 이러한 이유로 미국, 영국과 같은 선진국들은 수중함 실선 조종성능을 비교적 가장 정확하게 예측할 수 있다고 알려진 자유항주모형시험을 조종성능 예측과 운동모델 검증 및 보완에 활용하고 있다 (Kimber and Crossland, 2008; Shen and Hess, 2010; Kimber, 2011; Pfitsch et al., 2016).
자유항주모형시험은 자체추진, 운동계측센서, 자동조종장치(autopilot) 등을 탑재한 축소모형을 이용하는 시험기법이다. 구속모형시험과 마찬가지로 형상 변경 시 재시험이 필요하거나 척도효과 고려가 어렵다는 모형시험 고유의 단점에서 자유롭기 어렵지만, 선회나 지그재그와 같은 조종시험을 통해 조종성능을 직접적으로 평가할 수 있다는 장점이 있다. 또한 실제 수중함과 유사한 6자유도 기동을 모사할 수 있기 때문에 유도조종 알고리듬 기법 개발, 함 운용교본 작성 및 검증, 안전운항영역(Safety Operational Envelope, SOE) 분석 등 수중함 운용 전반에 걸쳐 다양한 분야에 활용할 수 있으며, 시험에서 얻은 데이터를 활용하여 조종운동 모델을 보완할 수 있다.
본 논문은 국방과학연구소에서 수중함 조종운동 모델 정밀화기술 연구를 목적으로 개발한 수중함 자유항주모형 개발에 관한 내용을 수록하고 있다. 2장에서는 수중함 자유항주모형 개발 목표와 함형 및 제원 선정 결과, 밸러스트 시스템을 포함하는 시스템 구성, 그리고 항법 알고리듬과 제어 알고리듬 설계 결과를 수록하고 있다. 3장에서는 설계를 바탕으로 제작한 수중함 자유항주모형의 추진, 항법, 그리고 제어 성능을 분석한 결과를 수록하고 있다.
2. 수중함 자유항주모형 개발
2.1 개발 목표
본 연구에서 수중함 자유항주모형(Free Running Model, FRM)은 조종운동 모델 정밀화를 위한 자유항주모형시험 데이터 확보와 조종성능 평가를 위한 자유항주모형 조종시험 수행 기법 연구, 자동조종 알고리듬 검증 등의 목적에 의해 개발되었다. 이러한 목적에 따라 개발 목표는 다음과 같다.
먼저 함형은 우수한 조종성능을 가진 공개된 함형이어야 한다. 넓은 기동 범위에 대한 운동모델 정밀화 기술을 연구하기 위해서는 모형의 조종성능이 뛰어나야 한다. 또한 함형이 대중에 공개되어 관련 해석이나 시험 데이터를 확보할 수 있다면 획득한 기술에 대한 검증이 수월하게 이루어질 수 있다.
다음으로 자유항주모형은 실선과의 상사를 최대한 만족할 수 있어야 한다. 모형시험을 통해 실선의 조종성능을 예측하기 위해서는 실선과의 기하학적 상사와 역학적 상사를 만족해야 한다. 또한 획득한 데이터의 신뢰도를 확보하고 안전하게 시험을 진행할 수 있도록 자유항주모형은 적절한 항법 및 제어 성능을 가져야 한다. 탑재 센서의 사양들과 시험장 크기에 따른 안전 범위 등을 고려하여 항법 성능 기준은 한 번의 주행에 대하여 1% 미만의 궤적 오차로 설정하였으며, 심도 제어 성능 기준은 심도 정상상태 오차를 기준으로 모형 직경의 0.2배 이내로 설정하였다.
자유항주모형은 또한 주어진 시험장에서 선회시험이나 지그재그 시험 등의 조종시험이 가능해야 하며, 이때 시험조건 충족을 위한 가속, 심도 변경 구간 등이 고려되어야 한다. 자유항주모형시험을 통해 획득한 데이터의 신뢰도 확보를 위해서는 외란의 영향을 최대한 배제할 수 있어야 하며, 이를 위해 Figs. 1~2와 같이 두 곳의 수조 환경의 시험장을 확보하였다. 선박해양플랜트연구소(KRISO)의 심해공학수조의 경우 조파기 등의 장비를 제외한 시험 가용 영역은 길이 80 m, 폭 34 m, 수심 12 m이며, 국방과학연구소의 다목적 수상/수중 시험시설의 시험 가용 영역은 심해 공학수조와 유사하다.
마지막으로 자유항주모형은 긴급부상 시험을 위한 밸러스트시스템을 갖춰야 한다. 수중함 안전운항영역 작성을 위해서는 긴급부상 모델링이 필수적이고, 이를 위해 자유항주모형 긴급부상시험을 수행하여 긴급부상 거동의 특성을 파악하고자 한다.
이와 같은 개발 목표들을 달성하기 위해 함형과 제원을 선정하고 시스템 구성과 운용 알고리듬을 설계하였다.
2.2 함형 및 제원 선정
설계 목표를 고려하여 MARIN에서 일반에 공개한 BB2 형상과 S7371R 추진기를 선정하였다 (Overpelt et al., 2015). 해당 함형은 모형시험과 전산유체역학해석 등 다양한 선행연구가 이루어진 바 있다 (Cho et al., 2020; Kim et al., 2022; Kwon et al., 2022). BB2 형상은 기존의 수중함들과 비교했을 때 길이 대 높이 비(L/D)가 작아 선회성능이 뛰어날 것으로 판단되었다. 또한 해당 함형은 X형 함미타가 배치된 것이 특징인데, 이는 조종성능 측면에서 유리하게 작용한다 (Renilson, 2015; Dubbioso et al., 2017).
제원 선정을 위해서는 실선과의 상사, 그리고 주어진 시험장에서의 시험 가능성을 종합적으로 고려해야 한다. 먼저 자유항주 모형의 역학적 상사를 위해 고려해야 하는 무차원수를 살펴보면 Froude 수와 Reynolds 수, 그리고 Strouhal 수가 있다. Froude 수는 중력에 의한 정유체력과 관성력 간의 비율을 의미하며, Reynolds 수는 점성력과 관성력 간의 비율을, 그리고 Strouhal 수는 비정상(unsteady) 힘과 모멘트의 상사를 의미한다. Froude 수와 Reynolds 수는 동시에 만족할 수 없으므로 일반적으로 Froude 수와 Strouhal 수를 상사 시키고, Reynolds 척도 효과(scale effect)를 최소화하기 위해 시험 설비를 고려하여 가능한 큰 크기의 제원을 선정하며, 난류촉진장치를 통해 난류 조건을 만족시킬 수 있도록 한다 (Gertler, 1950; Shen and Hess, 2010).
본 연구에서는 주어진 시험장에서 시험이 가능한 제원을 역으로 산출하여 가능한 큰 크기의 제원을 도출하였다. 최소 Reynolds 수로는 유동 천이영역을 넘어서기 위해 길이 기준 5 X 106, 폭 기준 0.6 X 106 이상이 되도록 하였고 (Schoenherr, 1932; Lamont, 1982), 난류촉진장치를 선체와 부가물 전방에 부착하여 난류 조건을 만족시킬 수 있도록 하였다. 선회에 필요한 공간은 선행연구 (Overpelt et al., 2015)에 따라 모형 길이의 8.5배로 설정했으며, 간략한 1자유도 시뮬레이션을 통해 가/감속에 필요한 길이를 모형 길이의 10배로 가정하였다. 수평면 마진은 모형 길이의 2배로 설정하였으며, 수심은 실선 스케일에서 최대 200 m를 모사하도록 기준을 설정하였다.
설정된 제약조건에 따라 모형 길이를 산출해보면 3.4 m 이상 3.9 m 이하로 도출된다. 선행연구 (Overpelt et al., 2015)에서 사용한 모형의 길이가 3.826 m로 유사한 수준이므로 추후 모형시험 결과 비교분석이 용이하도록 본 연구에서도 모형 길이를 3.826 m로 설정하였다. 이때 모형의 최대 전진속력 1.8 m/s(실선기준 15 kts), 15 ℃ 청수에 대하여 길이 기준 Reynolds 수는 약 6 X 106이다.
2.3 시스템 구성
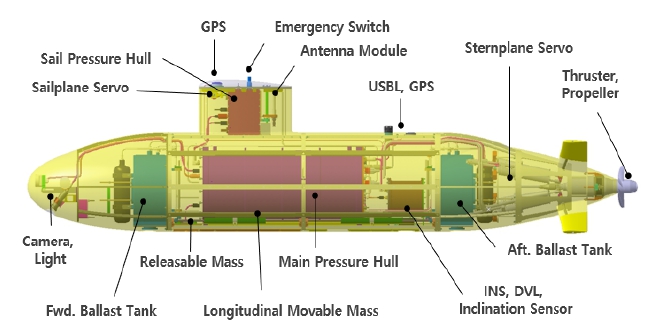
수중함 자유항주모형 시스템 구성은 Fig. 3과 같다. 그림의 가 독성을 위해 부력재는 제외하였으며, 실제 모형에는 빈 공간 대부분에 부력재가 탑재된다. 선체 구성은 장비들을 지지하는 프레임에 압력용기 및 기타 장비들을 배치하는 방식을 채택하였다. 이러한 구성은 장비 대부분을 압력선체 내부에 구성하는 방식과 비교할 때 수밀 커넥터와 부력재가 더 많이 요구된다는 단점이 있긴 하지만 구성이 단순하고 제작비용이 상대적으로 저렴하며 유지보수 및 점검이 용이하다는 장점이 있다.
압력용기는 크게 메인압력용기와 항법압력용기, 그리고 사령탑압력용기 세 가지로 구분된다. 먼저 메인압력용기는 부력의 대부분을 차지하기 때문에 목표하는 부력중심 근처에 배치하였으며, 내부에는 연산 장비들과 배터리, 전원분배기, 밸브 등이 탑재된다. 메인압력용기 상부와 하부에는 두 개의 압력센서를 장착하여 심도 계측에 이용하였다. 항법압력용기에는 관성항법시스템(Inertial Navigation System, INS)과 기울기센서가 탑재되며, 항법압력용기 바로 아래에 속도 계측을 위한 도플러 속도계(Doppler Velocity Logger, DVL)를 배치함으로써 항법 연산 시 좌표변환의 번거로움을 최소화하고자 하였다. GPS 수신기는 사령탑과 갑판에 각각 한 개씩 탑재하였으며, 수신기가 물 밖으로 노출될 때 계측된 위치 신호는 항법압력용기 내에 있는 INS로 직접 입력된다. 사령탑 압력용기에는 통신을 위한 모듈과 함수타 구동기, 장비 점검을 위한 포트와 비상 스위치를 배치하였다. 안테나는 수중함 양강 마스트와 유사하게 사령탑 내부에 배치되어 필요시에만 선체 외부로 전개될 수 있도록 하였다.
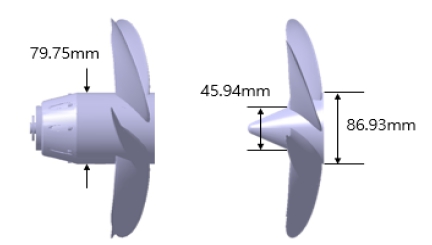
추진전동기는 협소한 함미 공간을 고려하여 일체형으로 배치하였다. 전동기 최대회전수 1200 RPM과 전동기출력 2.2 kW 사양을 고려하여 Tecnadyne사의 Model 2020에서 덕트를 제거하고 프로펠러를 교체하였다. Model 2020은 수심 850 m까지 운용이 가능하고 2.5 kW 출력의 BLDC 모터가 탑재되었으며, RPM 피드백을 위한 엔코더가 탑재되어있다. 상용 일체형 추진기를 활용함에 따라 선행연구와 추진기 허브 형상에 차이가 있다. Fig. 4는 추진기 형상을 비교한 그림이며, 왼쪽 추진기가 본 연구에서 사용한 추진기 형상이고, 오른쪽이 선행연구 (Overpelt et al., 2015)의 추진기 형상이다. Model 2020의 경우 추진기 모터에 부착된 맴브레인 내부에 내장된 마그네틱 고정자와 프로펠러 허브 내부에 장착된 마그네틱이 상호 동일 극성에 의한 반발 작용으로 회전하는 구조이다. 이로 인해 선행연구 대비하여 허브가 두껍다는 특징이 있다. 함미타 구동기는 4개의 함미타를 각각 구동할 수 있도록 설계하였으며, 함미 공간이 협소하기 때문에 수중용 선형모터를 활용하였다. 최대 각변위는 ±40°이며, 최대 각속도는 ±45 °/s이다.
수상/수중 상태 변환 및 긴급부상 시험 등을 목적으로 함수와 함미에 밸러스트 시스템이 배치되었으며, 비상시 대응 방안 중 하나로 밸러스트 시스템을 활용하였다. 육상 제어콘솔에서 송신하는 비상 신호는 함 갑판에 배치된 USBL(Ultra Short Base Line)을 통해 수신할 수 있으며, 압력용기에 배치된 누수센서를 통해 누수가 발생할 시에도 비상로직이 운용된다. 또한 투하가 가능한 무게 추와 전자석을 함저에 배치하여 전원이 차단되었을 때 무게추가 투하되어 모형이 부상할 수 있도록 설계하였다.
실선과의 관성량 상사를 위해 이동식 추와 부력재가 각각 모형 상/하부에 배치되었으며, 모형 유실 방지를 위해 약간의 양성 부력을 갖도록 중량 설계하였다. 본 연구에서 사용된 수중함 자유항주모형의 제원은 Table 1에 나타내었다. 실선과 Froude 수, Strouhal 수 상사를 만족하도록 하였으며, 질량과 부력, 무게중심, 부력중심, 그리고 관성모멘트는 3차원 모델을 통해 계산한 값이다.
2.4 밸러스트 시스템
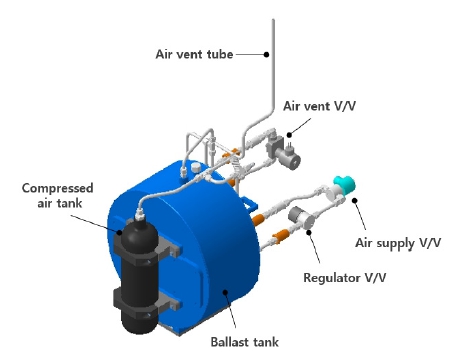
밸러스트 시스템은 주부력탱크(Main Ballast Tank, MBT)와 압축공기를 보관하고 있는 압축공기탱크, 그리고 주부력탱크 공 기 배출과 공급을 위한 밸브 등으로 구성된다. 함수와 함미 주부력탱크 용량은 각각 수중함 수상배수량의 약 5 %로 동일하다. 밸러스트 시스템 구성은 Fig. 5와 같다.
실선과 유사하게 수상 상태일 때 주부력탱크 내부는 공기로 가득 차 있으며, 잠항을 위해서는 공기 배출 밸브를 열어 주부력 탱크 내에 공기가 배출되고 평형수가 유입될 수 있도록 한다. 비상 대응 또는 긴급부상 시험 등을 위해 긴급부상하기 위해서는 공기 공급 밸브를 열어 압축공기를 통해 주부력탱크 내의 평형수를 밀어낸다. 수상 상태는 수선면이 갑판 아래에 위치하며, 수상 상태일 때의 수선면 위의 부피는 주부력탱크의 총 용량과 설계된 양성부력에 해당하는 부피의 합과 같다. 수중상태에서 수선면은 모형이 양성부력으로 설계되었기 때문에 사령탑 상부에 걸치게 된다. Figs. 6~7은 각각 수상/수중상태를 나타낸다.
2.5 항법 알고리듬
수중함 자유항주모형 항법은 INS와 DVL, GPS, 그리고 심도센서와 기울기 센서 계측값을 활용한 수중 복합항법 알고리듬을 사용하였다. 본 연구에서 사용한 주요 센서들의 사양은 Table 2와 같다.
본 연구에서 선정한 INS는 GPS 신호를 융합하여 위치와 속도를 계산해주는 알고리듬이 내장되어있지만, DVL이나 심도 센서 계측값을 내부적으로 융합하는 것은 불가능했다. 이러한 이유로 INS의 항법 연산 결과가 아닌 INS 내에 있는 가속도계와 자이로 계측값을 항법에 직접 사용하였다.
센서 계측 신호의 통합에는 일반적으로 수중운동체 항법 시스템에 활용되는 약결합(loosely coupled) 방식의 확장칼만필터를 활용하였다 (Park et al., 2014; Karmozdi et al., 2020; Lee, 2022). 칼만필터의 전파(propagation) 단계에서 운동학을 기반으로 가속도계와 자이로 계측값을 활용하여 갱신하고, 계측값 갱신(measurement update) 단계에 심도와 자세, 그리고 속도 계측값을 사용하였다. 수중함 자유항주모형의 운용 시간은 10분 내외로 짧고 가로세로 200 m 이내의 좁은 범위에서 운용되므로 임의의 위경도에 고정된 NED 좌표계를 관성좌표계로 가정하였다(Fossen, 2011). 필터 설계에 사용한 시스템 상태방정식과 출력 방정식은 다음과 같다.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
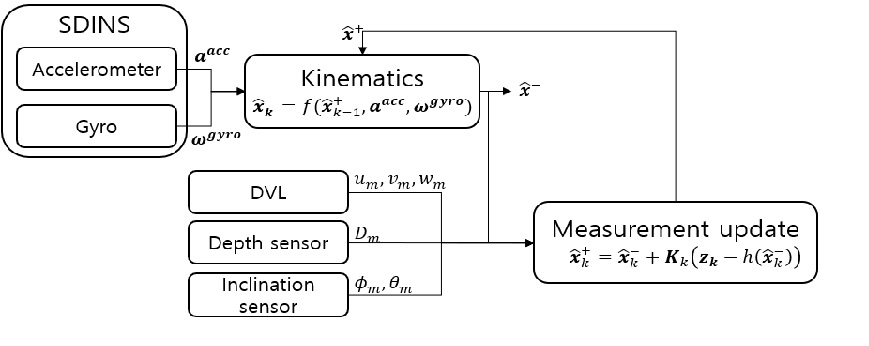
상태변수 x는 관성좌표계 상에서의 위치벡터 η1=[x y z]T와 3축 오일러 자세각 η2=[ϕ θ ψ]T, 3축 선형 속도벡터 v1=[u v w]T로 이루어진 벡터이다. 시스템 입력변수 u는 가속도 계측값 aacc과 자이로 계측값 ωgyro으로 이루어진 벡터이다. 출력변수 z는 심도 계측값 Dm과 횡동요각 계측값 ϕm, 종동요각 계측값 θm, 그리고 3축 속도 계측값으로 이루어진 벡터이다. f와 h는 각각 시스템 상태방정식과 출력방정식을 의미하며, w와 v는 각각 평균이 0이고 임의의 공분산값을 갖는 시스템 백색잡음 벡터와 계측 백색잡음 벡터이다. 본 연구에서 사용한 알고리듬은 Fig. 8과 같다.
관성항법에서 초기값 정렬의 정확도는 항법 성능을 결정짓는 매우 중요한 요소 중 하나이다. 특히 선수각의 경우 자이로 계측값을 통해 간접적으로 추정되기 때문에 가관측성이 다른 상태변수에 비해 매우 낮아 초기 정렬오차가 그대로 누적된다. 선수각정렬방법으로는 모형 내에 각기 다른 위치에 고정된 두 개 이상의 GPS 신호를 이용하는 방법과 모형이 직진할 때 단일 GPS 신호의 변화량을 이용하는 방법, 그리고 별도의 치구를 활용하는 전달정렬 방법이 있다. 수중함 자유항주모형은 GPS 수신기가 길이 방향으로 두 개가 설치되어있지만, 수중상태인 경우 함미부 수신기가 수면 아래에 잠기게 된다. 또한 시험장 공간이 한정되어 단일 GPS 신호의 변화량을 이용하는 경우 본 시험을 진행할 공간이 축소되는 문제가 있었으며, 실내수조의 경우 GPS 신호를 활용하기 어려웠다. 따라서 본 연구에서는 전달정렬 방식을 사용하였다. 전달정렬을 위한 정렬용 치구는 시험장 내에 고정된 위치에 설치되며 모형을 함수와 함미부에서 동시에 고정하여 치구와 모형의 방위가 일치할 수 있도록 제작되었다.
2.6 제어기 설계
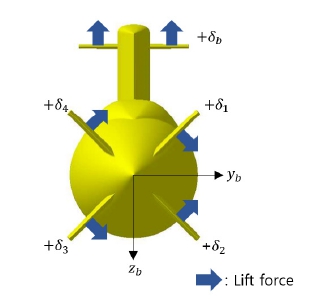
본 연구에서는 PID 제어기를 사용하여 자세 제어기를 설계하였다. 제어기 설계에 사용한 좌표계와 기호, 운동방정식은 Gertler and Hagen (1967)을 따른다. 다만 제어판 각도 정의와 제어력과 관련된 항들은 X형 함미타에 관한 연구인 Thune(2015)의 내용을 차용하였다. 대상 함형의 제어판은 개별 구동되는 함미타 4개와 하나의 구동기에 의해 좌/우현이 한꺼번에 구동되는 함수타 1개로 구성된다. Fig. 9는 본 연구에서 정의한 제어판 번호와 각도를 나타낸다. 함미타는 우현 상부 타부터 좌현 상부 타까지 시계방향으로 번호를 정의하였고 함수타는 아래첨자 b를 사용하여 정의한다. 함이 전진하고 있을 때 제어판에 의한 양력의 방향이 Fig. 9와 같은 경우 양의 타각으로 정의한다.
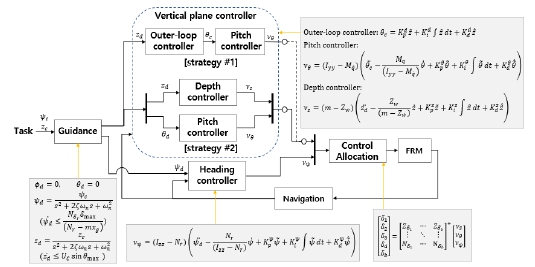
본 연구에서 설계한 제어 시스템은 Fig. 10과 같다. 먼저 주어진 임무로부터 침로 ψc와 심도 zc 명령이 입력되고, 과도한 제어명령이 인가되는 것을 방지하기 위해 2차 시스템의 형태로 추종침로 ψd와 심도 zd를 생성하였다. 추종 침로와 심도는 수중함의 동역학으로 충분히 추종할 수 있도록 변화율을 제한하였다. Fig. 10의 유도법칙에서 U는 함속, θmax는 최대 허용 종동요각, δmax 는 최대타각, Nr과 Nδr은 선수동요방향 유체력계수, ζ는 감쇠비, ωn은 고유주파수를 의미한다.
먼저 수평면 제어기 설계를 위해 수중함 선수각동요 방향 운동모델을 선형화하고 의사(pseudo) 선수동요 제어력 νψ을 계산한다. 여기서 Kpψ, Kiψ, Kdψ는 각각 비례, 적분, 미분 제어이득, 위첨자 ~는 현재 상태값과 추종 유도값의 차이를 의미한다.
수직면 제어기 또한 수평면 제어기와 마찬가지로 선형 운동모델을 기반으로 의사 상하동요 제어력 νz와 의사 종동요 제어모멘트 νθ를 계산하도록 설계하였다. 수평면 제어기와는 다르게 두 가지 제어전략을 사용하였는데, 첫 번째 전략은 이중루프 구조로 종동요각 변화를 통해 심도를 변경하는 제어전략이고, 두 번째 전략은 함수타와 함미타를 각각 심도 제어와 종동요각 제어에 사용하는 제어전략이다. 이중루프 구조 제어전략은 빠른 심도 변경이 가능하다는 장점이 있어 급격한 심도 변화가 요구될 때 사용되며, 함수/함미타의 역할을 분리하는 두 번째 제어전략은 심도변경 속도가 느려 주로 트림과 심도를 유지한 채 주행할 때 사용된다. 수평/수직면 제어기에서 제어이득은 사전에 구축해놓은 구속모형시험 결과 기반 6자유도 조종운동 시뮬레이션을 통해 초깃값과 범위를 선정하고, 자유항주모형시험을 수행하며 값을 보정하여 사용하였다.
대상 함형은 제어에 사용하는 제어판의 개수가 제어하고자 하는 의사 제어력 및 제어모멘트의 수보다 많으므로, 앞서 계산한 의사 제어력과 제어모멘트를 각각의 타에 할당하는 방법은 무수히 많다. 따라서 본 연구에서는 수식 6과 같이 의사역행렬(pseudo inverse) 기법을 이용하여 최적 제어력 할당(control allocation)을 수행하였다. 두 번째 제어전략에 대한 제어력 할당은 수식 6의 행렬식을 함수타와 함미타 각각에 대해 분리하여 수행하였다.
| (6) |
3. 수중함 자유항주모형 성능 분석
앞선 2절의 설계 결과를 바탕으로 수중함 자유항주모형을 제작하고, 기본적인 성능을 분석하여 목표했던 설계 기준치를 만족하는지 시험을 통해 확인하였다.
3.1 추진성능 분석
추진성능 분석을 위해 자유수면효과가 거의 없는 심도에서 추진기 RPM을 변화시켜가며 RPM에 따른 함속을 계측하였다. 시험을 수행한 심도는 심도 대비 직경(H/D) 5.19이며, 함속은 실선기준 6.0, 8.3, 10.0, 12.5 kts이다. 실선 기준 12.5 kts 케이스의 경우 길이 기준 Reynolds 수가 5.01X106이고 직경 기준 Reynolds 수가 0.76X106으로 제원 설정 시 목표했던 수치를 만족한다.
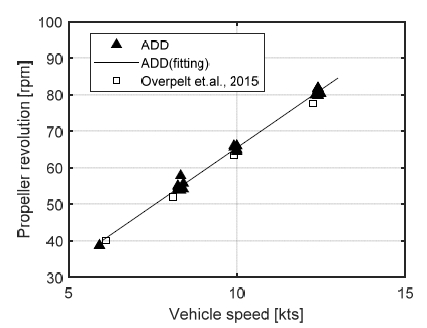
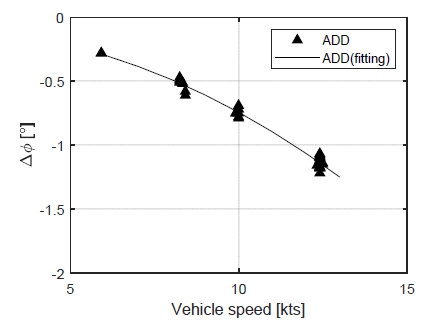
추진시험 결과는 Figs. 11~12와 같다. Fig. 11은 함속과 프로펠러 rpm의 관계를 나타내며, Fig. 12는 함속에 따른 횡동요각의 정지 상태 대비 변화량을 나타낸다.
ADD로 표시한 삼각형 표식이 본 연구 결과이고, 사각형 표식은 선행연구 결과이다. 횡동요각의 경우 선행연구에서는 결과를 제시하지 않아 본 연구 결과만을 나타내었다. 두 그래프 모두 선행연구와의 비교를 위해, 스케일을 이용하여 실선 기준으로 환산한 값을 나타내었다. 실선의 속도와 rpm 및 횡동요각의 관계를 추정하기 위해서는 모형선과 실선 간의 마찰저항 차이 보정 등의 과정이 추가적으로 필요하다. 함속과 프로펠러 rpm은 선형의 관계를 보이는 것을 확인할 수 있으며, 선행연구와도 유사한 결과를 보였다. 시험 결과를 통해 실선 스케일에서의 함속과 프로펠러 rpm 관계식을 도출해보면 다음과 같다. 이때 결정계수는 0.9998이다.
| (7) |
여기서 u는 전진속도를 의미한다. 식 7을 통해 중립 운항 타각 시험을 비롯한 조종성능 평가를 위한 시험에서 프로펠러 rpm을 결정할 수 있다.
Fig. 12를 살펴보면, 함속이 증가함에 따라 횡동요각 변화량이 커지는 것을 확인할 수 있다. 이는 프로펠러 회전에 의한 반작용 토크의 크기 변화에 따른 것이다. 모형이 전진할 때 프로펠러는 함미에서 볼 때 시계방향으로 회전하며, 프로펠러 회전에 대한 반작용 토크가 선체에 작용한다. 높은 함속에서 추진기 회전수가 증가할수록 반작용 토크가 증가하게 되며, 이러한 반작용 토크는 정상상태에 도달했을 때 정유체모멘트와 평형을 이룬다. 이러한 평형 관계를 통해 프로펠러 반작용 모멘트를 역으로 모델링할 수 있다.
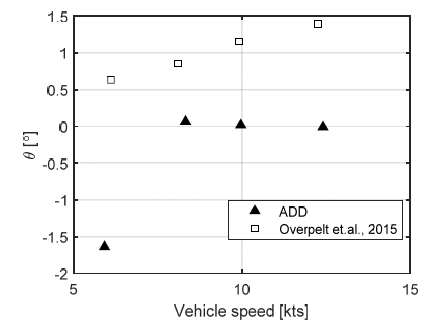
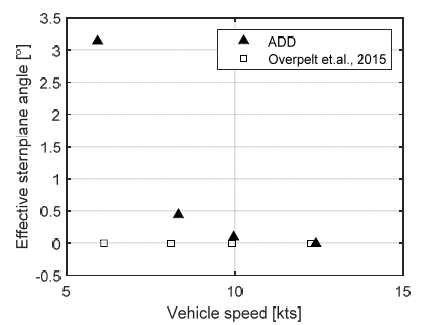
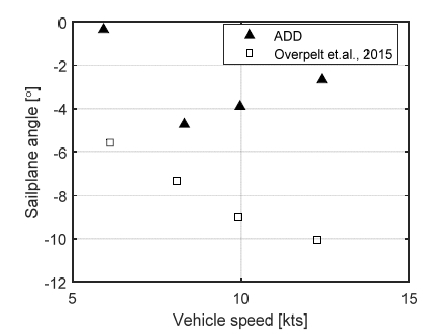
Figs. 13~15는 추진시험 시 계측한 종동요각과 유효함미타각, 그리고 함수타각의 반복시험 평균값을 나타낸다. 앞선 결과와 마찬가지로 선행연구와의 비교를 위해 스케일을 이용하여 실선 기준으로 환산한 값을 나타내었다. 선행연구와는 제어전략과 정유체적 특성이 달라서 프로펠러 rpm 결과와는 다르게 상이한 결과를 얻을 수 있었다. 선행연구는 함미타를 사용하지 않고 함수타와 종동요각을 통해 평형을 유지하는 전략을 사용했기 때문에 본 연구 대비 종동요각과 함수타각이 크게 나타났다. 본 연구에서는 6.0 kts 케이스를 제외한 나머지 케이스에서 함수/함미타 역할을 각각 심도제어와 종동요각 제어로 분리하는 제어전략을 사용하여 Fig. 13과 같이 종동요각을 0도로 유지한 채 전진하는 것이 가능했다. 이러한 경우 수직속도 성분을 0으로 유지할 수 있어 향후 동유체력 모델링 관점에서 유리하다. 다만 6.0 kts 케이스에서는 함속이 낮아 함수타만으로는 제어력이 부족했고, 이로 인해 이중루프 구조의 제어전략을 사용하여 시험을 수행하였다.
자유항주모형의 선체는 양성부력에 의해 상승하려는 힘과 무게중심보다 높은 갑판과 사령탑에 의해 선수를 들어 올리는 방향으로 양의 종동요 모멘트를 받게 된다. 따라서 이들을 상쇄하기 위해 Figs. 14~15와 같이 함미타는 음의 종동요 모멘트를 발생시키는 양의 타각을 가지며 함수타는 모형을 가라앉히려는 힘을 발생시키는 음의 타각을 갖는다.
3.2 항법 성능 분석
수중함 자유항주모형은 매 시험 정렬용 치구에서 출발하고 시험 종료 후 정렬용 치구로 복귀하였다. 복귀가 완료된 시점에 항법 위치와 실제 정렬용 치구 위치를 비교하여 모형의 항법 성능을 분석하였다. 직진과 선회를 포함하는 임의의 경로로 150 m이상 주행한 후 주행거리 대비 끝점 오차 분석 결과를 Table 3에 나타내었다. MWUTF는 국방과학연구소 다목적 수중/수상 시험시설에서 수행한 결과이고, DOEB는 KRISO 심해공학수조에서의 결과이다.
두 시험장 모두 끝점오차 비율이 평균 1 % 이내로 목표했던 성능을 만족함을 확인할 수 있었다. 두 시험장의 결과를 비교해보면 심해공학수조에서의 오차가 더 크게 나타났는데, 이는 심해공학수조의 바닥 철판에서의 DVL 신호 난반사의 영향으로 파악되었다. DVL 신호 노이즈 감소를 위해 심해공학수조 바닥에 난반사를 저감시키는 처리를 했지만, 처리가 되지 않은 일부 구간을 지날 때 DVL 신호 노이즈가 증가하는 현상이 확인되었다.
3.3 제어 성능 분석
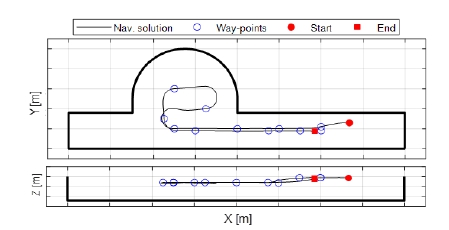
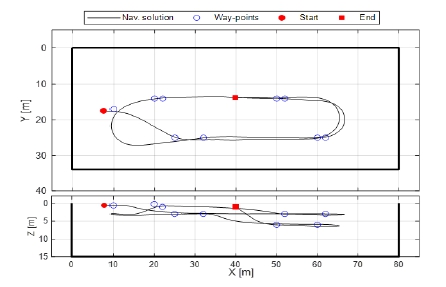
제어 성능 분석을 위하여 경로점 추종 제어를 수행하였다. 추진시험 때와 마찬가지로 실선 기준 함속 6.0, 8.3, 10.0, 12.5 kts에서 수행했으며, 경로점들의 심도는 모형 기준 1 m~3.5 m로 설정하였다. Figs. 16~17은 두 시험장에서의 경로점 추종 제어 결과 예시를 보여준다. 상단의 그래프는 X-Y 평면 궤적이며, 하단의 그래프는 X-Z 평면 궤적을 나타낸다. Table 4는 함속과 심도 명령에 따른 정상상태 심도 추종 오차를 나타낸다.
Fig. 16과 Fig. 17을 보면 수중함 자유항주모형이 수평면과 수직면 모두 우수한 경로점 추종 성능을 보였다. 정상상태 심도 추종 오차를 살펴보면 함속과 심도에 따라 차이가 있지만, 0.07 m (0.12D) 이내로 제어할 수 있었다. 함속이 빠를수록 심도 추종 오차가 작은 경향을 보였는데, 이는 함속 증가에 따른 타 제어력 증가의 영향으로 파악된다. 또한 심도가 얕아질수록 심도 추종 오차가 증가하는 경향을 보였는데, 이는 자유수면과 가까워질수록 자유수면에 의한 흡인력(suction force)이 작용하여 정상상태 오차를 키우는 것으로 파악된다.
4. 결 론
본 연구에서는 수중함 자유항주모형 개발 결과와 기본적인 성능을 분석한 내용을 수록하고 있다. 기본성능으로써 추진 성능과 항법 성능, 그리고 제어 성능을 분석하였으며, 설계 목표를 모두 만족함을 확인하였다. 향후 수중함 자유항주모형을 이용한 조종시험과 과도기동시험 결과를 분석하여, 실선의 조종성능을 추정하고 운동모델을 정밀화할 예정이다.
수중함 자유항주모형시험은 높은 기술력을 요하는 시험기법으로 세계적으로 수행 가능한 국가가 매우 적으며, 국내에는 시험기법 확보가 완료되지 않았다. 따라서 그동안 국내 건조 수중함의 자유항주모형시험은 국내에서 수행된 바 없는 실정이다. 본 연구를 통해 앞으로 건조될 수중함은 국내에서 자유항주모형시험 수행이 가능할 것으로 기대한다.
Acknowledgments
이 논문은 2020년 정부의 재원으로 수행된 연구 결과임
References
-
Cho, Y.J., Seok, W., Cheon, K.H. and Rhee, S.H., 2020. Maneuvering simulation of an X-plane submarine using computational fluid dynamics. International Journal of Naval Architecture and Ocean Engineering, 12, pp.843-855.
[https://doi.org/10.1016/j.ijnaoe.2020.10.001]

-
Dubbioso, G., Broglia, R. and Zaghi, S., 2017. CFD analysis of turning abilities of a submarine model. Ocean Engineering, 129, pp.459-479.
[https://doi.org/10.1016/j.oceaneng.2016.10.046]

-
Feldman, J., 1979. DTNSRDC Revised Standard Submarine Equation of Motion. David W. Taylor Naval Ship R&D Center Report No DTNSRDC SPD-0393-09.
[https://doi.org/10.21236/ADA071804]

- Feldman, J., 1987. Straightline and rotating arm captive-model experiments to investigate the stability and control characteristics of submarine and other submerged vehicles, David W. Taylor Naval Ship R&D Center Report No DTRC/SHD-0393-20.
-
Fossen, T.I., 2011. Handbook of marine craft hydrodynamics and motion control. John Wiley & Sons Ltd.
[https://doi.org/10.1002/9781119994138]

- Gertler, M., 1950, Resistance experiments on a systematic series of streamlined bodies of revolution for application to the design of high-speed submarines. David Taylor Model Basin. Report C-297.
-
Gertler, M. and Hagen, G. R., 1967. Standard Equations of Motion for Submarine Simulation, Naval Ship Research and Development Center Report No 2510.
[https://doi.org/10.21236/AD0653861]

-
Karmozdi, A., Hashemi, M., Salarieh, H. and Alasty, A., 2020. INS-DVL Navigation Improvement Using Rotational Motion Dynamic Model of AUV. IEEE Sensors Journal, 20(23), pp.14329-14336.
[https://doi.org/10.1109/JSEN.2020.3007929]

-
Kim, D., Lee, G.J., Kwon, C.S., Kim, Y.G., Park, J. and Jun, B. 2022. Added mass of submerged bodies obtained by forced oscillation tests and numerical calculations of potential flow. Journal of the Society of Naval Architects of Korea, 59(4), pp.214-224.
[https://doi.org/10.3744/SNAK.2022.59.4.214]

-
Kim, Y.G., Yun, K.H., Kim, S.Y. and Kim, D.J., 2012. Captive model test of submerged body using CPMC. Journal of the Society of Naval Architecture of Korea, 49(4), pp.296-303.
[https://doi.org/10.3744/SNAK.2012.49.4.296]

-
Kimber, N., 2011. Submarine manoeuvring: correlating simulation with model tests and full scale trials. The Royal Institution of Naval Architects Warship 2011: Naval Submarines and UUVs, Bath, The United Kingdom, 29-30, June 2011.
[https://doi.org/10.3940/rina.ws.2011.07]

-
Kimber, N., and Crossland, P., 2008. Advances in experimental techniques for understanding the manoeuvring performance of submarines. The Royal Institution of Naval Architects Warship 2008: Naval Submarines 9, Glasgow, The United Kingdom, 10-11, June 2008.
[https://doi.org/10.3940/rina.ws.2008.03]

-
Kwon, C., Kim, D., Yun, K. and Kim, Y., 2022. A captive model test on hydrodynamic force and neutral level flight of BB2 submarine in straight operation at near free surface with different depths. Journal of the Society of Naval Architects of Korea, 59(5), pp.288-295.
[https://doi.org/10.3744/SNAK.2022.59.5.288]

-
Lamont, P.J., 1982. Pressures around an inclined ogive cylinder with laminar, Transitional, or Turbulent Separation, AIAA Journal, 20, pp.1492-1499.
[https://doi.org/10.2514/3.51212]

-
Lee, J., 2022. Development of underwater integrated navigation based way-points tracking and fault tolerant control for a submarine free-running model in ocean engineering basin. Journal of Institute of Control, Robotics and Systems, 28(5), pp.459-467.
[https://doi.org/10.5302/J.ICROS.2022.22.0019]

- Overpelt, B., Nienhuis, B. and Anderson, B., 2015. Free running manoeuvring model tests on a modern generic SSK class submarine(BB2). In Pacific International Maritime Conference. Sydney, Australia, 6-8 October 2015.
-
Park, J.Y., Rhee, S.H., Lee, S., Yoon, H.K., Seo, J., Lee, P.Y., Kim, H.S. and Lee, H., 2020. Study on the estimation of autonomous underwater vehicle’s maneuverability using vertical planar motion mechanism test in self-propelled condition. Journal of the Society of Naval Architects of Korea, 57(5), pp.287-296.
[https://doi.org/10.3744/SNAK.2020.57.5.287]

-
Park, Y., Kang, C., Lee, D.H. and Park, C.G., 2014. Reduced error model for integrated navigation of unmanned autonomous underwater vehicle. Journal of Institute of Control, Robotics and Systems, 20(5), pp.584-591.
[https://doi.org/10.5302/J.ICROS.2014.13.1973]

-
Pfitsch, D., Gordon, B., Rice, J. and Cubbage, S., 2016. Development and deployment of autonomous scale submarine models for hydrodynamic testing of U.S. Navy Submarine Maneuvering Characteristics. MTS/IEEE Oceans 2016 conference, Monterey, United States of America, 19-23 September 2016.
[https://doi.org/10.1109/OCEANS.2016.7761068]

-
Renilson, M, 2015. Submarine hydrodynamics. Springer.
[https://doi.org/10.1007/978-3-319-16184-6]

- Rhee, K.P., Yoon, H.K., Sung Y.J., Kim, S.H. and Kang, J.N., 2000. An experimental study on hydrodynamic coefficients of submerged body using planar motion mechanism and coning motion device. International Workshop on Ship Maneuverability, pp.1-20.
- Schoenherr, K.E., 1932. Resistance of flat surfaces moving through a fluid. SNAME Transactions, 40.
-
Shen, Y.T. and Hess, D.E., 2010. An experimental method to satisfy dynamic similarity requirements for model submarine maneuvers. Journal of Ship Research, 54(3), pp.149-160.
[https://doi.org/10.5957/jsr.2010.54.3.149]

-
Sung, Y.J. and Park, S. 2015. Prediction of ship manoeuvring performance based on virtual captive model tests. Journal of the Society of Naval Architects of Korea, 52(5), pp.407-417.
[https://doi.org/10.3744/SNAK.2015.52.5.407]

- Thune, S., 2015. Simulation of submarine manoeuvring. Royal Institute of Technology, Sweden.
-
Toxopeus, S., Atsavapranee, P., Wolf, E., Daum, S., Pattenden, R., Widjaja, R., Zhang, J.T. and Gerber, A., 2012. Collaborative CFD exercise for a submarine in a steady turn, 31th International Conference on Offshore Mechanics and Arctic Engineering, Rio de Janeiro, Brazil, 2012.
[https://doi.org/10.1115/OMAE2012-83573]