다중 선박의 상태추정을 위한 Multiple PDAF 알고리즘

1. 서 론

다중 대상 추적(MTT, Multiple-Target Tracking)은 자율 시스템이 주변을 인식하고 이해할 수 있도록 하므로 자율 주행 및 운항에서 중요한 문제이다. 최근 MTT는 자율주행차, 드론, 자율운항 선박 및 로봇 공학을 포함한 광범위한 자율 시스템 분야에 활발히 연구되고 있다. 자율운항 선박에서 MTT는 부표, 바위 및 기타 위험과 같은 장애물뿐만 아니라 다른 선박을 탐지하고 추적하는 것을 포함한다. 또한, 선박 항로 모니터링, 위험 선박 탐지, 선박이 환경에 미치는 영향 평가와 같은 다양한 해양 교통 통제 및 감시 시스템에 사용되고, MTT의 개발은 여러 선박의 상태를 동시에 추정할 수 있으므로 주변 상황 인식 및 모니터링 관점에서 유용하다.

MTT 정보는 자율운항선박이 안전하고 효율적인 경로를 계획하고 실행하며 충돌을 방지하고 연료 소비를 최적화하는 데 유용하다. 자율운항 선박에서 MTT를 수행하기 위해 레이더 같은 센서의 신뢰성과 정확성뿐만 아니라 선박자동식별장치(AIS, Automatic Identification System) 및 해상교통관제시스템(VTS, Vessel Traffic Service System)데이터를 통합하는 필요성이 제기되고 있다.

이러한 다중 물체 추적을 위한 알고리즘으로는 준 최적 베이지안 모델의 확률적 데이터 연관 필터(PDAF, Probabilistic Data Association Filter)와 결합 확률적 데이터 연관 필터(JPDAF, Joint-Probabilistic Data Association Filter)가 있으며, 이는 센서로부터 측정된 값을 객체에 연관시키고 시간이 지남에 따라 식별된 객체를 유지하기 위한 확률론적 구조를 제공한다(Bar-Shalom et al., 2009).

관련한 연구로는 ARPA 레이더와 AIS 데이터를 융합한 무향 칼만 필터 기반(UKF, Unscented Kalman Filter) PDAF 연구(Han et al., 2023;Fortmann et al., 1983)가 있으며, 이는 레이더 데이터를 이용하여 비주기적으로 전송되는 AIS 데이터를 보완하는 센서 융합 기법이지만 단일객체만을 추적하는 한계가 있다. 또한, JPDAF 기반으로 기존의 운동 정보(위치, 속도, 가속도) 외 EO/IR(Electro – Optics/InfraRed) 영상 센서로부터 얻은 표적의 형상 정보의 유사도가 일정 값 이상이면 객체와 연관 지어 유효화 행렬의 경우의 수를 줄여주는 연구가 진행되었으며, 항적 관리 알고리즘이 추가되어 다중 객체 추적에 정확도를 높였다(Kim et al., 2016).

또한, 시스템 모델을 CV(Constant Velocity)와 CA(Constant Acceleration)를 동시에 사용하여 다중 시스템 모델을 갖는 상호작용 다중모델 필터(IMM, Interacting Multiple Model)를 PDAF에 접목해 클러터(clutter) 환경에서 다양한 동역학 시스템을 가진 객체의 상태 추정값의 정확성을 높이는 기술도 개발되고 있다(Liu et al., 2022). 하지만 PDAF는 단일객체만을 추적한다는 한계가 있으며(Habtemariam et al., 2011), JPDAF는 유효 측정치가 많을수록 사건 행렬(event matrix)의 경우의 수가 기하급수적으로 많아져 실시간으로 사용하기에 무리가 있다. 이를 보완하기 위해 연관 사건의 주변 확률(the marginal probability)을 트리구조 형태인 신뢰 전파(LBP, Loopy Belief Propagation) 알고리즘을 사용하여 기하급수적인 계산을 줄인 기법이 있으며(Rutten et al., 2014; Williams et al., 2012), 관찰 객체의 수를 안다고 가정한 뒤 k-평균(k-means) 알고리즘을 통해 측정값들을 군집화(clustering) 한 다음 유효 측정값들의 중앙값(centroid measurement)만을 사용하여 사건 행렬의 행을 줄인 EC-JPDAF 기법도 존재한다(Fowdur et al., 2021). 또한, 여러 연관 가설(association hypothesis) 중에 비용을 고려하여 순위를 정해 최적의 값을 찾는 Murty's 방법이 개발되고 있다.

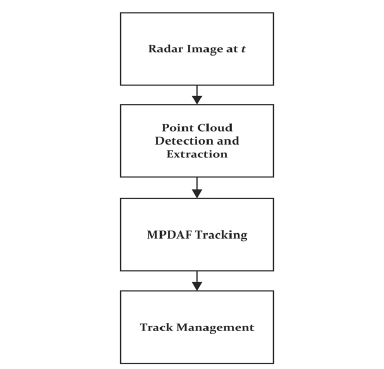
본 연구는 단일객체 추적 알고리즘인 PDAF를 병렬적으로 처리하는 방식인 MPDAF를 제안한다. MPDAF는 PDAF보다 복잡하고 유연한 확률적 데이터 연결 체계를 통합하여 PDAF의 기능을 확장한다. 이를 통해 센서 구역이 중복되고 센서 고장 및 센서 측정이 모호하고 복잡한 상황에서 여러 객체를 정확하게 추적할 수 있다. 또한, JPDAF의 기하급수적인 경우의 수를 고려하지 않으며, 단일객체 추적으로 제한되었던 PDAF의 단점도 보완하고 적은 양의 계산 부하로 다중 객체를 추적할 수 있다. 본 논문에 사용된 데이터는 독일 항공우주 센터(DLR)에서 제공한 레이더 데이터 세트와 각 데이터 세트 표적들의 AIS 데이터를 활용 하였으며, 실험 수행의 모식도는 Fig. 1과 같다. 실험의 요약으로는 시간 t 순간에서 레이더 이미지 데이터의 포인트 클라우드(point cloud)를 탐지 및 추출 후 제안한 알고리즘 MPDAF와 항적 관리를 적용하여 다중 객체의 궤적을 추정한다.

Fig. 1

Flowchart of the proposed multiple target tracking algorithm

본 논문의 구성은 2절에서 실험에 사용된 데이터 세트인 레이더 데이터와 AIS에 대한 설명과 제안한 MPDAF, 항적 관리 알고리즘에 관해 설명하며, 3절에서는 수행된 실험결과를 분석하고, 4절에서는 결론으로 마무리한다.

2. 본 론

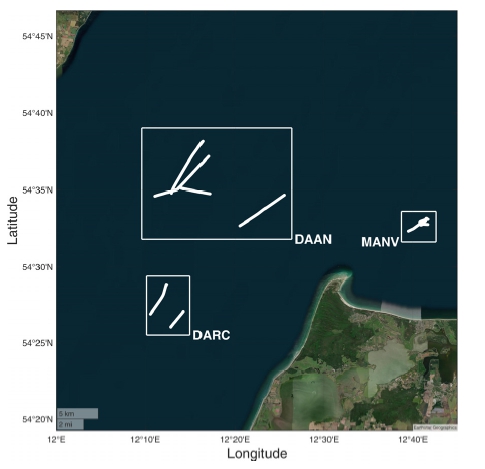
이 장에서는 DLR에서 제공받은 세 가지 레이더 이미지 데이터 세트와 AIS에 관해 설명한다. 또한, 제안된 알고리즘의 순서도와 과정을 설명하면서 사용된 매개변수를 정의하며, 선박의 2차원 운동에 관한 시스템 모델과 측정 모델에 대한 매개변수를 정의한다. 또한, 객체의 측정값이 일정 기준치 이상 측정되지 않거나 상태 오차 공분산 값이 설정된 값 이상이 되었을 때 그 객체의 궤적을 제거하는 항적 관리에 관해 설명한다. Fig. 2는 발트해 부근에서 받은 선박들의 AIS데이터의 궤적을 위성사진으로 나타낸 것이다.

Fig. 2

The AIS trajectories of each ships near the Baltic Sea

2.1 데이터 세트

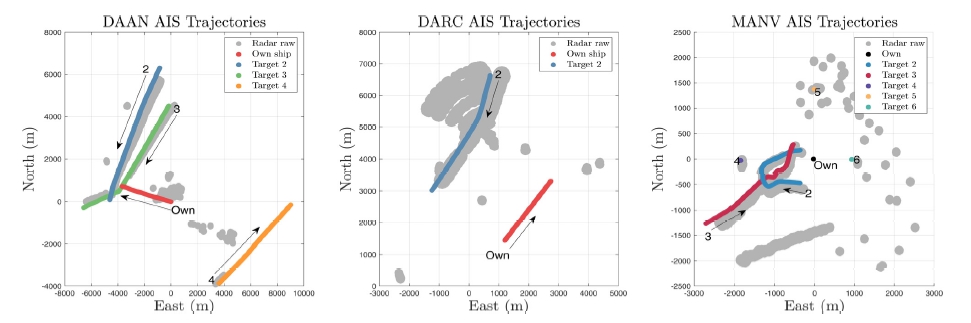
본 실험 데이터 세트는 레이더(X-band) 의 이미지를 여러 처리방식을 거쳐 받았으며(Vivone et al., 2019), 레이더 데이터 세트의 이름은 각각 DAAN(Data Association with Aids to Navigation), 레이더 비컨 (RACON)을 기반으로 측정한 DARC(Data Association with RACON), MANV(Manoeuvres)(Fowdur et al., 2019)고, 포함된 정보는 Table 1과 같다. 또한, 레이더 이미지의 해상도는 MANV의 경우 픽셀은 6 m의 해상도이며 다른 두 데이터 세트는 11 m의 해상도를 가진다. Table 2에는 각 데이터 세트의 동적 표적의 길이와 너비를 나타낸다. Fig. 3는 데이터 세트별 궤적(AIS 및 탐지된 레이더 측정값)을 나타내었다.

Table 1

Summary of the datasets

Table 2

Dimensions of vessels for the different datasets

Fig. 3

Trajectory(coloured) description of data sets including radar data(gray dots)

실험 데이터 세트는 X-band 레이더의 화면을 1 Hz 주기로 측정하였고 무작위 데이터가 손실됐음을 Table 1 Frame의 전체 개수와 Duration[s]의 항목에서 확인할 수 있다. 각 레이더 이미지는 시간 순차적으로 처리되었으며 과정은 다음과 같다.

(a) 각 이미지의 인터페이스 정보 제거 후 레이더 이미지를 회색조(grayscale)로 변환.

(b) 임곗값보다 낮은 blob들을 제거. 이 과정에서 클러터(clutter)를 줄임.

(c) 헤시안 판정법(Determinant of Hessians, DoH)을 이용한 blob 탐지 알고리즘 적용.

(d) 추출된 blob의 거리[m], 베어링(bearing [rad])을 저장 후 ENU(East North Up) 좌표계로 변환.

AIS 데이터는 선속에 따라 전송되는 주기가 달라진다. 선속이 빠르면 주기가 짧아지고, 느려지면 주기가 길어지는 특성이 있다. AIS 데이터는 선형적으로 보간하여 레이더 이미지 데이터 주기와 맞춘 1 Hz 주기를 갖는다. 실험에 사용한 AIS 데이터로는 위치, COG(Course Over Ground), SOG(Speed Over Ground), 헤딩 각이며, 위치(위도 [°], 경도 [°]) 값은 각각 East[m], North[m] 으로 변환하였다.

2.2 Proposed Multiple Probabilistic Data Association Filter (MPDAF)

MPDAF는 PDAF와 마찬가지로 허위 측정치가 발생하는 환경 혹은 객체가 탐지되지 않았을 때의 환경에서 객체를 추적하기 위한 확률적 데이터 연관 방법이며 (Kim, 2012) 단일객체가 아닌 다중 객체를 위해 사용된다. 한 표적의 측정치는 1개를 초과할 수 없으며, 표적은 때에 따라 측정되지 않을 수 있다고 가정한다. 또한, MPDAF는 PDAF 알고리즘을 객체 수마다 독립적으로 시행한 알고리즘으로 더욱 복잡하고 유연한 확률적 데이터 연결 체계를 통합하여 PDAF의 기능을 확장한다.

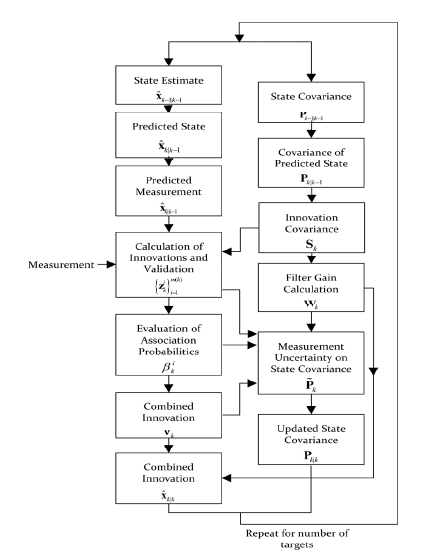
이를 통해 센서 측정 값이 중복되고 센서 고장 및 센서 측정이 모호한 복잡한 상황에서 여러 객체를 정확하게 추적할 수 있다. 비록 PDAF 알고리즘보다 계산량이 많지만, 여러 객체의 측정값에 대한 불확실성을 해소하기 위해 적합한 기법이다. MPDAF의 구조는 칼만 필터를 기반으로 하고, 객체의 시스템 모델 혹은 측정 모델이 비선형이면 확장 칼만 필터(EKF, Extended Kalman Filter), 무향 칼만 필터 등을 적용할 수 있다. 제안된 MPDAF는 칼만 필터 구조에 gating 단계와 data association 단계가 추가되며 순서도는 다음 Fig. 4와 같다.

Fig. 4

MPDAF flow chart

2.3 Prediction 단계

Prediction 단계의 기본 프레임은 표준 칼만 필터와 유사하며 본 연구에서 모든 객체의 시스템 모델 행렬(F, system model matrix)은 CV 모델을 적용하였고, 측정 모델 행렬(H, measurement model matrix)은 처리된 레이더 이미지 측정값의 x(East[m]), y(North[m]) 만을 측정하는 것으로 고려하였으며 다음과 같다.

$\[ {\mathrm{F}}_{\mathrm{k}}=\left[\begin{array}{cccc}1& 0& \mathrm{T}& 0\\ 0& 1& 0& \mathrm{T}\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right],{\mathrm{H}}_{\mathrm{k}}=\left[\begin{array}{c}1\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\\ 0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}1\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}0\end{array}\right] \]$

(1)

샘플링 주기 T는 데이터 전송 주기와 맞추기 위해 1 초[s]로 설정했고, 상태변수 x_k는 선박의 2차원 위치와 속도를 의미하는 $$ \left[\begin{array}{c}x\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}y\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\dot{\mathrm{x}}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\dot{\mathrm{y}}\end{array}\right]$$으로 정의하였으며, 추적하고자 하는 표적의 초기 상태변수 x₀는 각 표적의 초기 AIS 데이터로 초기화했다. SOG와 COG 같은 경우 각각 단위 변환 후 초기 상태변수에 입력되었다. 다음 식은 AIS 데이터를 통해 초기화된 상태변수에 관한 식이다.

$\[ x= East of the AIS \]$

(2)

$\[ x= East of the AIS \]$

(3)

$\[ \dot{x}=SOG\cdot cos\left(COG\right) \]$

(4)

$\[ \dot{y}=SOG\cdot sin\left(COG\right) \]$

(5)

Table 3은 표준 칼만 필터의 prediction 단계가 요약되어 있고, 식 (2)-(5)를 통해 초기 상태변수 값을 입력하여 prediction 단계를 진행한다. 초기 오차 공분산 P₀과 시스템 잡음 공분산 Q_k-1는 3절에 정의되어 있다.

Table 3

The prediction algorithm of Kalman filter

2.4 Gating 단계

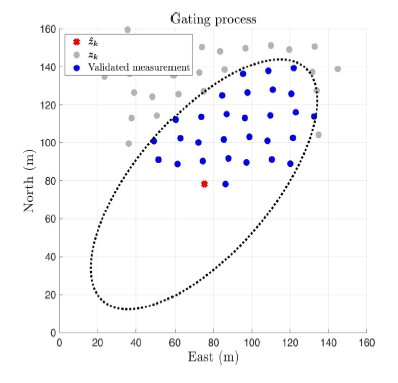
MPDAF를 사용하는 환경은 측정치가 많을 때 특정 측정치의 최대 연관 확률을 계산할 때 쓰인다. 이때 모든 측정치를 사용하게 되면 시간 복잡도가 기하급수적으로 커지기 때문에 gating 단계에서 측정값들이 걸러지게 된다. Gating 단계는 예측된 측정치 $$ {\widehat{\text{z}}}_{\text{k}}$$와 레이더의 모든 측정치 z_k의 마할라노비스거리(mahalanobis distance)M_k를 일정 임계치(threshold)와 비교하여 이를 만족하는 유효 측정치(validated measurement) 이외의 측정치를 제거한다.

$\[ {\mathbf{M}}_{\mathrm{k}}={\left(\mathbf{z}-{\widehat{\mathbf{z}}}_{\mathrm{k}\mid \mathrm{k}-1}\right)}^{\mathrm{T}}{\mathbf{S}}_{\mathrm{k}}^{-1}\left(\mathbf{z}-{\widehat{\mathbf{z}}}_{\mathrm{k}\mid \mathrm{k}-1}\right) \]$

(6)

$\[ {\mathbf{M}}_{\mathrm{k}}\le \mathrm{\gamma } \]$

(7)

Fig. 5처럼 회색 점의 미가공 레이더(raw radar) 데이터가 식 (7)를 만족할 때, 유효 측정치로 간주하며 만족하지 못한 데이터들은 측정치에서 제외되며, 파란색의 유효 측정치만을 MPDAF의 update 단계에서 사용한다.

Fig. 5

Gating process. Validated measurements are selected (blue dot), remove measurements other than validated measurements(gray dot).

2.5 Data Association 단계

Data association 단계에서는 유효 측정치들의 가능도 비 $$ {\mathcal{L}}_k^i$$(likelihood ratio)를 이용하여 어느 유효 측정치가 실제 측정치와 유사한지에 대한 연관확률을 계산한다.

$\[ {\beta }_k^i=\left\{\begin{array}{cc}\frac{L_k^i}{1-P_D{P}_G+\sum _{j=1}^{m_k} L_k^j},& \hspace{0.25em}i=1,\dots ,m_k\\ \frac{1-P_D{P}_G}{1-P_D{P}_G+\sum _{j=1}^{m_k} L_k^j},& i=0\end{array}\right. \]$

(8)

식 (8)에서 분모는 정규화를 하기 위한 항이며, P_D는 객체가 탐지될 확률, P_G는 만약 객체가 탐지됐을 때, 실제 측정값이 게이트 안에 있을 확률이다. m_k는 유효 측정치의 개수이며, 만약 i = 0일 때, gating 단계를 만족하는 측정치가 없고, 객체가 탐지되지 않을 경우이며 이는 모두 확률적으로 표현된다.

$\[ L_k^i=\frac{N\left({\mathbf{z}}_{\mathrm{k}}^{\mathrm{i}};{\widehat{\mathbf{z}}}_{\mathrm{k}\mid \mathrm{k}-1},{\mathbf{S}}_{\mathrm{k}}\right){\mathrm{P}}_{\mathrm{D}}}{\lambda } \]$

(9)

식 (9)에서 λ는 유효영역 부피 V_k당 유효 측정치 m_k의 개수. 즉, 공간 밀도이며 푸아송 분포를 따른다. 본 실험에서는 밀도 값을 따로 입력하지 않고, 다음 식을 사용했다.

$\[ \lambda =\frac{m_k}{{\mathit{V}}_k} \]$

(10)

$\[ V_k=c_{n_z}{\left|\gamma {\mathbf{S}}_{\mathrm{k}}\right|}^{1/2}={\mathrm{c}}_{{\mathrm{n}}_{\mathrm{z}}}{\gamma }^{{\mathrm{n}}_{\mathrm{z}}/2}{\left|{\mathbf{S}}_{\mathrm{k}}\right|}^{1/2} \]$

(11)

n_z는 DOF(Degree of Freedom)이며, 본 실험에서는 2차원으로 가정했다. V_k는 n_z차원에서 유효영역의 부피를 의미한다. 유효영역 γ는 카이제곱 분포의 역 누적분포 함수를 이용하여 설정한다. 상수 c_nz는 n_z에 따라 달라지며 Table 4와 같다.

Table 4

Constant cnz for each DOF

2.6 Update 단계

이 단계에서는 앞에서 구한 연관확률 $$ {\beta }_k^i$$로 인해 기존 표준 칼만 필터와는 다른 구조를 가지며, 다음 Table 5와 같다.

Table 5

The update algorithm of the PDAF

사후 오차 공분산 P_klk에서 측정값이 없을 확률인 β⁰가 1일 때 공분산은 해당 시간에서 측정치를 이용하여 update를 하지 않는다. β⁰가 1이 아닌 경우 공분산 $$ {\mathbf{P}}_{\mathrm{k}\mid \mathrm{k}}^{\mathrm{c}}$$로 인해 사후 오차 공분산이 update 하며, 나머지 공분산 $$ {\stackrel{\mathrm{~}}{\text{P}}}_{\text{k}}$$는 유효 측정값 중 어떤 값이 실제 측정값인지 알 수 없으므로 사후 오차 공분산 값을 증가시키는 항이다.

2.7 다중표적 항적 관리

해당 알고리즘은 객체가 센서의 측정 범위를 벗어나도 상태추정을 반복하여 계산적인 측면에서 불리하다. 그 때문에 본 연구에서 각 객체의 유효 측정치가 일정 횟수 탐지되지 않거나 객체의 유효영역이 오차 공분산에 의해 임계치보다 커지게 되면 해당 객체의 상태추정을 정지하도록 수행했다. 예로, Fig. 6(a)에서 target 4 는 레이더 탐지 거리에서 벗어나기 때문에 제안한 항적 관리 알고리즘을 적용하여, 추적을 중단하였다.

Fig. 6

The left column shows estimated trajectories(coloured), radar raw data and validated measurements(yellow dots and the right column shows error value of the estimated trajectory.

3. 실험결과

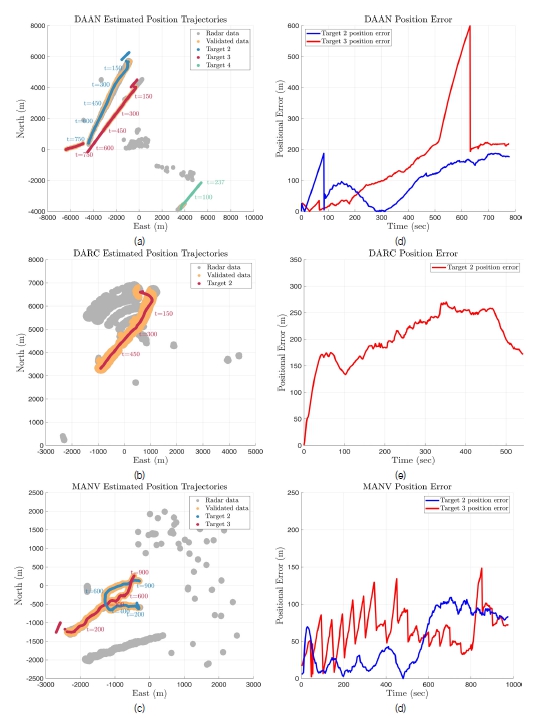
본 연구에서는 레이더 이미지를 통해 여러 대 선박의 위치, 속도를 MPDAF를 이용하여 추정하였으며, 항적 관리를 통해 특정 조건을 만족하는 객체를 실험 중 제외하였다. 실험 결과는 Fig. 6(a),(b),(c)와 같고, 알고리즘의 평가를 위해 위치 오차를 Fig. 6(d),(e),(f)와 같이 그래프로 나타냈다. 실험에서는 모든 데이터 세트의 정적 장애물과 자선(own ship)의 상태는 추정하지 않고, 동적 표적의 상태추정을 수행하였다. 실험에서 사용된 매개변수의 값은 Table 6과 같고, 측정 잡음 공분산 R_k과 공정 잡음 공분산 Q_k은 데이터 세트마다 최적값이 달라진다. 각각의 잡음 공분산 값들은 반복적인 실험을 통해 Table 6과 같이 설정하였다.

Table 6

The definition of parameters and initial value

Fig. 6(a)의 target 4는 레이더 최대 탐지 반경을 벗어남에 따라, 약 237초부터 상태추정을 하지 않는 것을 확인할 수 있으며, 이는 항적 관리 알고리즘이 잘 적용됐다는 것을 알 수 있다. Fig. 6(a) target 3의 경우 약 500초부터 630초까지 레이더 데이터의 손실로 인해 prediction 단계의 프로세스 모델에 비중을 두기 때문에 항적을 계산함에 따라, 위치 오차가 증가하는 것을 확인할 수 있고, 레이더 신호가 회복된 630초 이후에는 위치 오차가 감소하는 것을 확인할 수 있다. target 2의 초기 오차값이 큰 이유는 초기 AIS값을 받아 상태추정을 하고 있지만, 레이더의 제한된 최대 측정 거리로 인해 레이더 값이 할당되지 못한 것이 원인이며, 이후 약 100초에는 레이더 측정값이 gating 단계를 만족하여 안정적인 위치 추정 성능을 보여주고 있다.

데이터 DARC는 레이더 비컨을 이용했기 때문에 허위 측정치(clutter)가 다른 데이터 세트보다 많지만 Fig. 6(b)를 통해 안정적인 위치 추정 성능을 확인할 수 있다. 오차는 다소 높은 것을 확인할 수 있는데 이는 데이터 세트 처리 과정의 영향으로 보인다. 또한, DAAN과 DARC의 target 2는 다른 물체와 달리 길이와 폭이 상대적으로 길어 AIS 안테나의 위치가 선박 중앙에 설치되지 않아 위치 오차가 발생하는 것으로 예상된다.

Fig. 6(c)를 보면 target 2, 3 외에도 회색 점이 연속되는 다른 물체가 측정된 것을 확인할 수 있는데 이는 AIS 장치가 설치되지 않은 다른 소형선으로 보인다. MANV의 경우 여러 객체 중 움직이는 객체에 초점을 두었으며 객체가 약 400초에서 500초 사이에 두 객체의 궤적이 서로 교차하게 되는데 적절한 잡음 공분산 값으로 위치 추정이 정확한 것을 확인할 수 있다. 또한, MANV의 오차 그래프를 보게 되면 다른 두 데이터 세트와 다르게 상대적으로 낮은 오차값을 보이는데 이는 MANV에 사용된 두 객체 선체의 길이와 폭이 작고, 레이더의 해상도가 정밀하기 때문이다. 또한, 약 400초 구간과 800초 구간에서 오차값이 급격하게 올라가는 것을 확인할 수 있으며, 이는 두 타선 객체가 겹치게 될 때인 것을 알 수 있다.

4. 결 론

본 논문은 해상환경에서 획득한 레이더 데이터 세트를 이용하여 제안한 다중물체추적 알고리즘인 MPDAF를 적용하였고, 특정 조건을 만족하는 객체의 궤적을 제거하는 항적관리 알고리즘도 적용하였다. 제안된 알고리즘은 AIS를 활용하여 MPDAF의 초기 상태변수로 사용하였으며, 추적 오차는 객체의 크기, 궤적의 겹침에 따라 달라짐을 확인했다. 추가로 Fig. 3에서 확인할 수 있듯이 AIS 경로와 레이더 데이터값의 약간의 편차가 있으며, 이는 오차에도 영향을 주는 것으로 판단된다. 향후 이러한 오차를 줄이기 위해 시스템 모델을 등속운동 모델을 고려할 뿐 아니라 CT(Coordinated Turn) 모델도 동시에 고려하는 상호작용 다중모델 필터를 사용할 예정이며, AIS값을 초기에만 입력하는 것이 아닌 AIS/레이더 다중센서 퓨전을 통해 알고리즘을 개발할 예정이다.

Acknowledgments

이 논문은 2023년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원(P0017006, 2023년 산업혁신인재성장지원사업) 및 해양수산부 재원으로 해양수산과학기술진흥원의 지원(1525014528, "스마트항만-자율운항선박 연계기술 개발")을 받아 수행된 연구임.

References

• Bar-Shalom, Y., Daum, F. and Huang, H., 2009. The probabilistic data association filter. IEEE Control Systems Magazine, pp.82-91. [https://doi.org/10.1109/MCS.2009.934469]
• Fortmann, T., Bar-Shalom, Y. and Scheffe, M., 1983. Sonar tracking of multiple targets using joint probabilistic data association. IEEE Journal of Oceanic Engineering, 8(3), pp.173-184. [https://doi.org/10.1109/JOE.1983.1145560]
• Fowdur, J.S., Baum, M. and Heymann, F., 2019. A marine radar dataset for multiple extended target tracking. 1st Maritime Situational Awareness Workshop (MSAW 2019), Italy, Lerici (La Spezia), 08-10 October 2019.
• Fowdur, J.S., Baum, M. and Heymann, F., 2021. Real-world marine radar datasets for evaluating target tracking methods. Sensors, 21(14), pp.4641. [https://doi.org/10.3390/s21144641]
• Habtemariam, B.K., Tharmarasa, R., Kirubarajan, T., Grimmett, D. and Wakayama, C., 2011. Multiple detection probabilistic data association filter for multistatic target tracking. 14th International Conference on Information Fusion, Chicago, IL, USA, pp.1-6.
• Han, C.W., Lee, S.W. and Jin, E.S., 2023. Tracking of ARPA radar signals based on UK-PDAF and fusion with AIS data. Journal of Ocean Engineering and Technology, 37(1), pp.38-48. [https://doi.org/10.26748/KSOE.2022.046]
• Kim, E.S., 2012. Fast algorithm of multi-target tracking using multi-model and probabilistic data association. M.E., Hanyang University, pp.21-43.
• Kim, S.J., Jung, Y.H., Kang, J.W. and Yoon, J.H., 2016. Multiple target tracking using target feature information. Journal of Korean Multimedia Society, 19(5), pp.890-900. [https://doi.org/10.9717/kmms.2016.19.5.890]
• Liu, Z., Fang, Y., Zhang, L., Li, J. and Hu, J., 2022. A robust videoSAR single target tracker by integrating correlation filter and IMM-PDAF. IEEE Geoscience and Remote Sensing Letters, 19, pp.1-5. [https://doi.org/10.1109/LGRS.2022.3206835]
• Rutten, M., Willams, J., Gordon, N., Jah, M., Baldwin, J. and Stauch, J., 2014. A comparison of JPDA and belief propagation for data association in SSA. Advanced Maui Optical and Space Surveillance Technologies Conference, 9-12.
• Vivone, G., Braca, P., Granström, K., Natale, A. and Chanussot, J., 2019. Converted measurements Bayesian extended target tracking applied to X-band marine radar data. Journal of Advances in Information Fusion. pp.189-210.
• Williams, J. and Lau, R., 2012. Approximate evaluation of marginal association probabilities with belief propagation. IEEE Transactions on Aerospace and Electronic Systems. 50(4), pp.2942-2959. [https://doi.org/10.1109/TAES.2014.120568]