받음각을 갖는 3차원 캐비테이터에서 발생하는 비축대칭 초공동 유동해석
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this study, morphological and hydrodynamic characteristics of the non-axisymmetric supercavity generated behind a disk-shaped cavitator were examined. By extending the previous study on axisymmetric supercavitating flow based on a boundary element method, hydrodynamic forces acting under the angle of attack condition of 0 to 30 °and shape characteristics of the supercavity were analyzed. The results revealed that increasing the angle of attack by 30 °reduced the length and width of the cavity by about 15% and the volume by about 40 %. An empirical formula that can quantitatively estimate the geometrical characteristics and change of the cavity was derived. It is expected that this method can be used to evaluate the shape information and force characteristics of the supercavity for the control of the vehicle in a very short time compared to the viscous analysis in the initial design stage of the supercavity underwater vehicle.
Keywords:
Inviscid flow, Boundary element method, Cavitator, Supercavitation키워드:
비점성 유동, 경계요소법, 캐비테이터, 초공동1. 서 론
2009년부터 시작된 국내의 초공동(supercavitation)을 이용한 수중 운동체의 고속화 기술은 초공동의 현상학적 특성과 유동학적특성을 규명하기 위한 이론 및 실험연구를 중심으로 이루어져 왔다. 실험연구의 경우 자연 공동보다 상대적으로 저속에서 캐비테이터 후방에 압축가스를 분사할 때 발생하는 환기 초공동(ventilated supercavitation) 또는 인공 초공동(artificial supercavitation)에 대해 집중적으로 연구되어왔다. Ahn et al. (2015, 2021)은 캐비테이션 터널 실험을 통해 공기를 분사하여 낮은 속도에서 인공 공동을 발달시키는 연구를 수행하였으며, 공기 분사의 증감에 따른 공동의 생성과 소멸 과정의 물리적 특성을 규명하였다. Jeong et al. (2019)은 캐비테이터 후방에 위치한 몸체의 형상을 변화시켜가며 실험하였고 전두부의 형상이 초공동의 최초 발생 시점과 적정 분사량에 영향을 미치며, 후두부의 형상은 초공동의 발달과 항력 특성에 큰 영향을 미친다는 것을 밝혔다. 수치해석 연구의 경우 초고속 상태에서 발생하는 자연 초공동 유동 현상을 상대적으로 매우 빠른 시간에 해석하는 장점이 있는 비점성 유동 기반의 경계요소법(Boundary Element Mehod, BEM)을 중심으로 개발되었다. Kim et al. (2013)은 다양한 형상의 2차원 및 3차원 축대칭 캐비테이터에서 발생하는 초공동 해석법을 개발하였으며, Park et al. (2018), Hwang et al. (2021)은 몸체의 영향을 고려한 2차원 및 3차원 수중 운동체에서 발생하는 초공동 해석법을 개발하였다. 대부분의 선행 연구들은 축대칭 캐비테이터가 받음각이 없는 균일 유동장 상태에서 이동할 때 발생하는 초공동 유동을 대상으로 수행되었다.
실제 초공동 수중 운동체는 공동에 둘러싸여 부력을 상실하기 때문에 몸체 전방에 위치한 캐비테이터와 후방의 제어핀 받음각을 변화시켜 양력 및 항력을 변화시키고 이를 조절하여 자세와 심도를 제어한다. 따라서 캐비테이터의 받음각 변화에 따른 초공동의 기하학적 특성과 작용하는 유체력을 정확하게 평가하는 것이 중요하다. 특히 캐비테이터에서 발생한 공동이 중력장 효과로 인해 비대칭 형상으로 발생하면 운동체 후방 몸체의 일부가 물과 접촉하면서 플래닝 현상이 발생하고 비대칭적으로 공동 밖 유동에 노출되는 제어핀에는 제어력의 불균형이 발생한다. Kiceniuk (1954)는 캐비테이터의 받음각을 변화시켜 계측한 실험연구를 통해 변화하는 유체력의 일반적 특성을 밝힌 바 있지만, 초공동의 형상 변화에 대한 정보를 제시하지는 못하였다. Semenenko (2001)는 축대칭 공동에 작용하는 양력과 중력을 운동량 정리로 계산하여 공동의 중심선 변화를 예측할 수 있는 경험식을 제시하였지만, 초공동의 전체 형상 변화에 대한 정보는 알 수 없다. Lee et al. (2019)은 정적 받음각을 갖는 초공동 운동체의 환기 초공동 활주 특성과 작용하는 유체력을 계측하여 동적 활주력을 도출한 바 있으며, Yi et al. (2021)은 원형 캐비테이터의 받음각변화에 따른 환기초공동의 형상을 계측하고 Logvinovich의 모델링과 비교하여 공동 상·하단의 형상 특성은 양·음의 받음각에 따라 달라진다는 것을 검증하였다. 본 연구에서는 기존의 축 대칭 비점성 경계요소법 계산을 확장하여 받음각을 갖는 3차원 원판형 캐비테이터를 대상으로 0~30 °의 받음각 변화 조건에서 발생하는 자연 초공동을 해석하고 작용하는 유체력과 초공동의 형상 특성을 해석하였다.
2. 수치해석 방법
2.1 지배 방정식 및 경계 조건
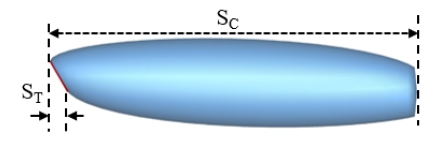
Fig. 1은 받음각을 갖는 캐비테이터의 초공동 해석에 사용된 모델로 원판형 캐비테이터(ST)와 캐비테이터에서 발생하는 공동 영역(SC)으로 구성된다.
유동 영역의 지배 방정식은 다음 식 (1)인 라플라스 방정식이며, 경계 조건은 식 (2)~(6) 순서로 비 침투조건, 무한 원방 조건, 운동학적 경계 조건, 동역학적 경계 조건 및 공동의 공동마감 조건이다.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
이때 φ는 교란 속도 포텐셜, 은 경계면에서 유체영역으로 향하는 법선벡터, Φ는 유동장의 전체 속도 포텐셜, 는 유동장의 전체 속도, 는 유입 유동의 속도이며, 는 계산 위치 좌표이다. 또한 는 생성된 공동의 형상 함수, p는 공동의 내부압력, pv는 유체 증기압, tc는 공동의 두께이고, 는 각 공동이 마감되는 끝단의 위치 벡터이다.
2.2 적분 방정식
경계면에서 라플라스 방정식을 충족하는 속도 포텐셜은 Green 정리를 만족하며, 경계면에 다이폴(dipole)과 소스(source)를 분포하면 식 (7)과 같이 정리된다. 이때 다이폴은 몸체와 공동경계면 전체에 분포하여 계산 영역을 구성하고 소스는 공동 표면에 분포시켜 공동 형상을 수렴시키는 계산에 사용하게 된다. 여기서 μ는 다이폴 세기, q는 소스 세기, G는 Green 함수이며, r은 제어점에서 특이점까지의 거리이며, SA는 전체 계산 영역을 SC는 공동영역을 의미한다.
| (7) |
동력학적 경계 조건인 식 (5)는 공동 표면에서의 접선방향 속도벡터(Vt)의 크기가 일정하다는 조건으로 변환된다. 이를 통하여 공동 표면의 전체 속도 포텐셜은 식 (8)로 나타낼 수 있으며, 다이폴의 변화가 공동 표면의 유동 방향 접선 길이에 비례함을 의미한다. 여기서 는 공동의 생성 위치를 의미한다.
| (8) |
공동마감 조건인 식 (6)의 경우, 공동의 모양은 소스의 세기에만 관련이 있고, 공동이 유한한 길이를 가지기 위하여 공동에 분포된 소스의 적분이 0이 되는 식 (9)로 표현이 가능하다. 이때 수식의 L은 공동의 생성 위치에서 마감 지점까지 공동 표면 유동의 접선방향 길이이다.
| (9) |
2.3 적분 방정식의 이산화
적분 방정식인 식 (7)을 이산화하면 식 (10)과 같이 표현되며, 전체 영역을 계산함으로써 각 패널에서의 유기 속도 포텐셜을 계산할 수 있다. 이때 NA, NC는 각각 전체와 공동에 분포된 패널의 개수를 의미한다.
| (10) |
공동 표면의 동역학적 경계 조건인 식 (8)은 식 (11)로 이산화 가능하며, 식 (12)는 각 공동의 생성 위치에서부터 각 계산지점까지의 공동의 유동 접선방향 길이를 의미한다. 이때 sk는 공동패널의 유동 접선방향 길이를 의미하고, NC.M.P는 공동의 생성되는 패널의 번호를 의미한다.
| (11) |
| (12) |
공동마감 조건인 식 (9)는 이산화하면 식 (13)으로 표현된다. 본 수치해석의 공동마감 조건은 공동의 생성 위치 혹은 회전 방향마다 조건을 적용하지 않으며, 전체 공동 표면을 하나의 식으로 계산하였다.
| (13) |
3. 수치해석 결과 및 분석
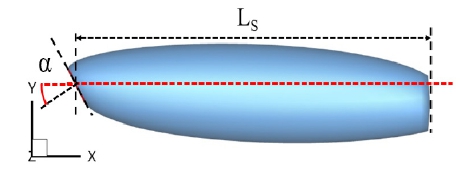
원판형 캐비테이터가 일정 받음각을 갖는 상태에서 발생하는 비축대칭 초공동 유동을 해석하기 위해 사용된 좌표계와 특성 파라미터는 Fig. 2와 같다. 캐비테이터의 받음각(α)은 Fig. 2와 같이 운동체의 축 중심선과 xz평면 사이의 각도이며, z축을 기준으로 반 시계 방향을 양의 값으로 정의하였다. 공동의 길이(Ls), 두께(Ds) 및 반경(Rs)은 캐비테이터의 중심을 기준으로 정의하였다(Table 1). 여기서 공동의 형상 정보와 작용하는 유체력은 캐비테이터의 직경(DC)으로 무차원하였다. Fig. 2와 같은 받음각을 갖는 캐비테이터에서 발생하는 초공동은 y축 방향으로 비대칭적으로 발생한다. 따라서 공동 반경을 y+방향 RS_Y+와 –방향의 반경 RS_Y-로 구분하여 정의하였으며, 두 반경의 합을 y축 공동 두께 DS_Y로 정의하였다.
3.1 받음각 변화에 따른 양력과 항력 변화
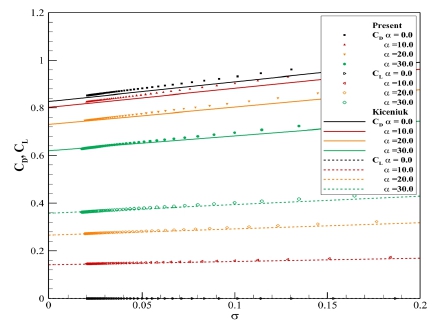
초공동이 성장하여 수중 운동체 전체를 감싸게 되면 모든 유체력은 캐비테이터에 집중되고 자세제어에 사용되기 때문에 초공동 운동체 해석에 있어 캐비테이터에 작용하는 유체력을 정확하게 추정하는 것은 매우 중요하다. 유체력을 평가하기 위하여 캐비테이터 받음각을 변화시키며 계산하였으며, 운용환경을 고려하여 받음각이 0, 10, 20, 30도인 경우를 선정하였다. Fig. 3은 공동수 변화에 따른 양력과 항력 계산 결과를 보여준다. 해석 결과의 비교, 검증을 위해 Kiceniuk (1954)의 식 (14)와 식 (15)를 실선과 점선으로 함께 표시하였으며, 이 경험식은 캐비테이터의 받음각(α)이 50 °보다 작을 때 실험과 잘 일치하는 것으로 알려져있다. 수식에서 사용한 CD0는 Garabedian (1956)의 해석해 0.827을 사용하였다. 여기서, 공동수는 식 (16)으로 정의하며, P∞는 유입 유동의 압력, Pv는 유체 증기압이다. 전체적으로 공동수가 낮아질수록 양력계수와 항력계수 모두 선형적으로 작아지는 것을 확인할 수 있으며, 경험식과 비교하면 공동수가 큰 영역에서 다소 차이가 있지만, 공동수가 작아질수록, 즉 이동 속도가 빨라져 공동이 충분히 성장하여 초공동이 되는 영역에서는 차이가 작으며, 캐비테이터의 받음각의 변화에 따른 양력계수와 항력계수의 변화가 잘 일치함을 확인할 수 있다.
| (14) |
| (15) |
| (16) |
3.2 받음각 변화에 따른 초공동 길이 및 두께의 변화
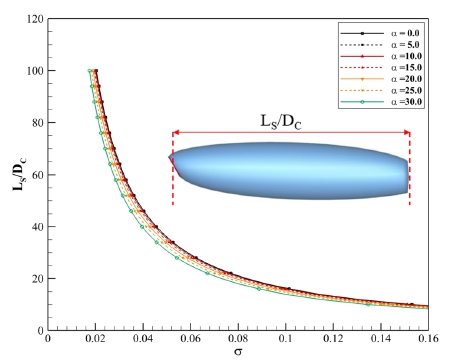
공동 길이 변화의 특성을 파악하기 위하여, 다양한 속도 조건에서 캐비테이터의 받음각을 0도에서부터 30도까지 5도 간격으로 변화시켜가며 공동 길이를 계산한 결과를 Fig. 4에 나타내었다. 동일 받음각 조건에서 공동수가 작아질수록 공동 길이가 커지며, 동일 공동수 조건에서 받음각이 커지면 공동 길이는 짧아지는 것을 확인할 수 있다. 그 차이는 초공동이 크게 발달하는 낮은 공동수 영역에서 더욱 크게 나타난다.
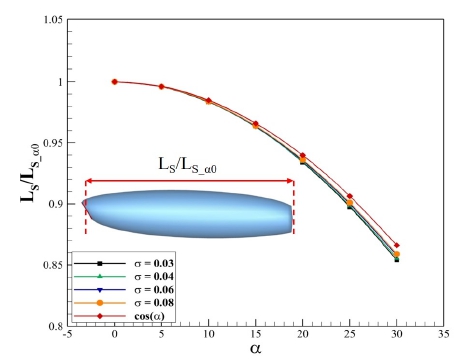
Fig. 5는 Fig. 4에 나타낸 계산 결과 중 특정 공동수의 결과들을 선정하여 나타내었다. 캐비테이터 직경(DC)이 아닌 LS_α0로 무차원화 하였으며, 받음각의 xy 평면 투영 성분인 cos(α)와 비교하였다. 여기서 LS_α0는 동일한 공동수에서 캐비테이터의 받음각이 0도일 때의 공동 길이이며 이를 기준 길이로 정의하였다. Fig. 5의 무차원화된 공동 길이(LS/LS_α0)는 캐비테이터의 받음각이 커질수록 cos(α)와 차이가 발생하지만, 공동수에 상관없이 cos(α)와 근사한 결과를 보여준다. 이는 캐비테이터에 작용하는 양력계수와 항력계수와 같이 공동 길이 또한 공동수와 캐비테이터의 받음각에 대한 함수로 간단히 표현할 수 있음을 의미하며, 이는 식(17)과 같이 나타낼 수 있다. Table 2는 계산된 공동 길이와 식(17)의 상대 백분율 오차값이며, 받음각의 크기와 공동수에 상관없이 잘 일치하는 것을 확인할 수 있다.
| (17) |
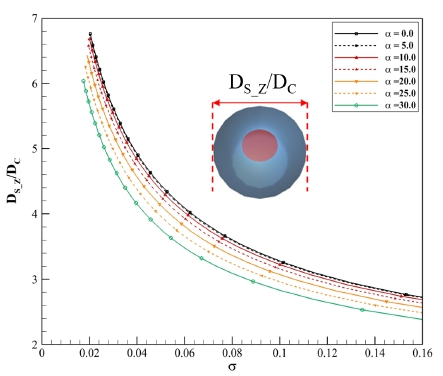
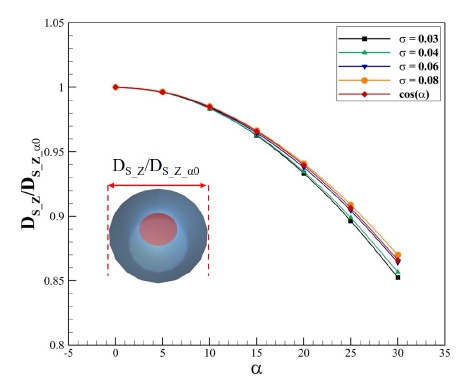
캐비테이터 받음각의 변화에 따른 공동의 z축 방향 두께 변화의 특성을 파악하기 위하여, 다양한 속도 조건에서 캐비테이터의 받음각을 0도에서부터 30도까지 5도 간격으로 변화시켜가며 계산하였고 그 결과를 Fig. 6에 나타내었다. 여기서 z축 두께는 전체 공동 형상에서 z축 방향의 최대 두께이며, 이해를 돕기 위하여 축 방향 형상을 함께 표시하였다. 동일 받음각 조건에서 공동수가 작아지면 초공동의 직경이 커지며, 동일 공동수 조건에서 받음각이 커질수록 공동의 직경은 감소한다. 공동 길이의 경우와 유사하게 변화를 정량적으로 평가할 수 있다. Fig. 7은 Fig. 6의 계산 결과 중 특정 공동수의 결과를 DS_Z_α0로 무차원화한 결과이다. 공동수에 따라서 다소 차이가 있지만, 캐비테이터의 받음각 변화에 따라서 cos(α)와 유사한 값을 갖는다는 것을 알 수 있다. DS_Z_α0는 동일한 공동수에서 받음각이 0도인 경우의 발생하는 공동의 z축 방향 두께이며, ‘z 축 방향 기준 두께’로 명명한다.
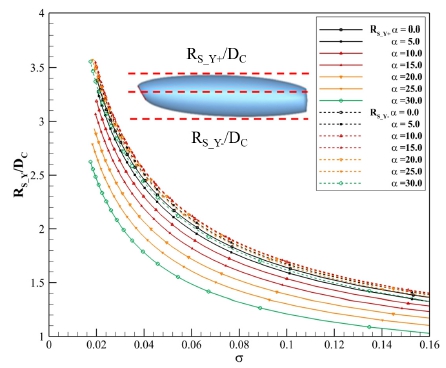
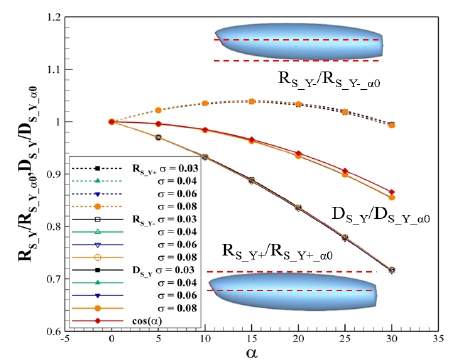
공동의 y축 방향 두께 변화를 파악하기 위하여 마찬가지로 캐테이터의 받음각을 0도에서부터 30도까지 5도 간격으로 변화시켜가며 계산하여 Fig. 8에 x축을 공동수로 하여 나타내었으며, y축에 y+ 방향과 y- 방향의 공동 최대 반경을 나타내었다. y+방향의 반경(RS_Y+)의 경우 캐비테이터의 받음각이 증가함에 따라 감소하며, 공동수가 작아질수록 커진다. 이는 공동 길이 및 z축 방향의 두께와 동일 경향이며, z축 방향 공동 두께와 감소량의 크기가 거의 같다. y-방향 반경(RS_Y-)의 경우 변화 초기에 캐비테이터의 받음각이 증가함에 따라서 그 값이 감소하지 않고 증가하지만, 점차 증가량의 추세가 감소하며, 받음각 15도에서 최대 반경을 가진 후 감소한다는 것을 알 수 있다. 결과적으로 캐비테이터의 받음각이 30도에 이르면 받음각이 0도인 경우와 그 값이 거의 같게 된다. Fig. 9는 Fig. 8의 특정 공동수의 반경(RS_Y±) 및 y축 방향 직경(DS_Y)을 각각 RS_Y+_α0, RS_Y-_α0 그리고 DS_Y_α0로 무차원화한 결과이며, cos(α)의 값과 비교하여 나타내었다. 이때 무차원화에 사용한 요소는 각각 ‘y+ 방향 기준 반경’, ‘y- 방향 기준 반경’ 그리고 ‘y 축 방향 기준 두께’로 명명하였으며, 같은 공동수에서 캐비테이터 받음각이 0도인 경우의 발생하는 공동 반경 및 두께이다.
Fig. 9에 나타낸 초공동 반경의 경우 앞서 서술한 바와 같이 RS_Y-의 경우 공동수에 상관없이 캐비테이터 받음각 15도에서 최대치를 가지며, RS_Y+의 경우 z축의 경우와의 경향성은 같으나 그 변화가 크게 나타난다. 두 결과는 캐비테이터 받음각에 따라 다른 경향성이 있는 것처럼 보이나, y축 방향의 두께(DS_Y)를 살펴보면 공동 두께 및 반경 변화의 경향성을 쉽게 이해할 수 있다. 캐비테이터에서 발생한 양력으로 인하여 공동이 전체적으로 y- 방향으로 이동하여 편중되기 때문에 각 반경의 크기와 위치가 변화하였을 뿐이며 받음각의 변화에 따른 y축 방향의 공동의 두께(DS_Y) 변화는 z축 방향 두께(DS_Z) 변화와 동일하게 cos(α)와 유사하다는 것을 알 수 있다. y축과 z축에 대한 변화를 종합하면 y축 방향의 경우 중심선의 변화를 직접적으로 받기에 반경 변화를 정의하기 힘들지만, 전체적인 공동 두께 변화는 중심선 변화에 상관없이 동일 경향을 보인다. 따라서 받음각에 따른 중심선 변화에 상관없이 초공동의 두께(DS)는 공동수와 캐비테이터 받음각을 이용하여 식 (18)과 같이 정리할 수 있다.
| (18) |
3.3 받음각 변화에 따른 초공동 체적의 변화
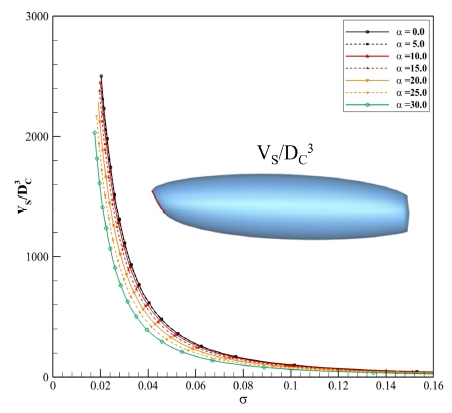
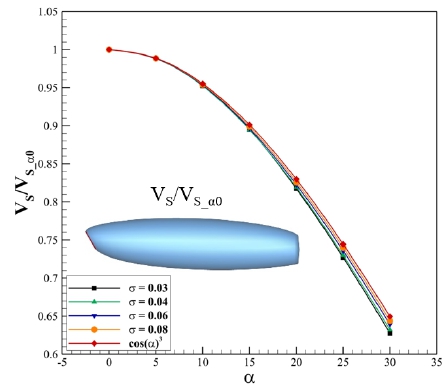
다양한 속도 조건에서 캐비테이터 받음각의 변화에 따른 공동의 체적변화를 계산하여 Fig. 10에 나타내었으며, 앞선 경우와 마찬가지로 캐비테이터의 받음각은 0도에서 30도까지 5도 간격으로 계산하였다. 동일 공동수 조건에서 받음각이 커질수록 공동의 체적이 감소하는 것을 확인할 수 있다. Fig. 11은 Fig. 10의 결과 중 특정 공동수 조건에 대한 결과를 받음각 0도 상태의 체적(VS_α0)으로 무차원화한 결과이며 캐비테이터의 받음각이 증가함에 따라 식 (19)와 같이 cos(α)3의 비율로 줄어든다는 것을 알 수 있다. 이와 같은 결과는 공동의 길이 및 공동의 최대 직경과 같이 일반적인 위치에서 공동의 표면 또한 기준을 가지고 cos(α)의 비율로 변화함을 의미한다.
| (19) |
3.4 받음각 변화에 따른 초공동 중심선의 변화
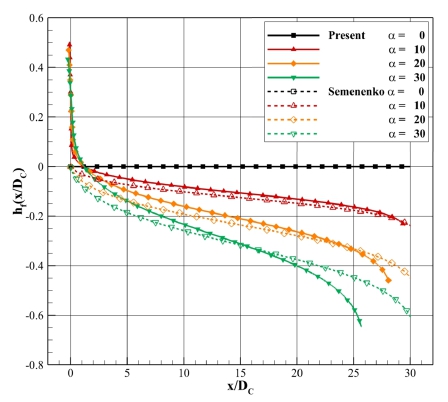
공동 형상의 거동을 파악하기 위한 지표로 공동의 중심선 변화를 이용하였다. 캐비테이터에서 발생한 양력이 유동을 변화시키는데, 이를 운동량으로 정리하여 공동의 중심선을 계산할 수 있는 Semenenko (2001)의 식 (20)을 사용하여 비교하였다. 이때 R(s)는 공동 반경 함수이며, 본 수치해석의 받음각이 없고, 초공동의 길이가 캐비테이터 직경의 30배일 때 계산되는 공동의 형상을 이용하였다. 식 (20)에 사용하는 양력은 식 (21)을 이용하여 본 수치해석에서 계산되는 항력계수로 구하였고, 이때 적용되는 캐비테이터의 받음각은 0, 10, 20, 30도를 사용하였다. 본 수치해석의 계산 결과는 동일 공동수 조건에서 캐비테이터의 받음각을 변화시켜가며 계산하였다. 중심선의 형상을 Fig. 12에 나타내었으며, 계산된 주요 계산 결과를 Table 3에 나타내었다. 이때 hf는 중심선의 위치로서 공동 중심선이 x축에서 이동한 변화량을 나타내며, 캐비테이터의 직경으로 무차원화 되어있다. 일반적으로 공동 상, 하면의 중심을 공동 중심선이라 정의한다. 그러나 받음각이 있는 경우 공동 상, 하면의 시작점이 다르기 때문에 캐비테이터에 걸쳐있는 공동은 캐비테이터 면과의 중심을 공동 중심선으로 정의하였다.
| (20) |
| (21) |
공통된 경향성으로는 캐비테이터 받음각이 커짐에 따라서 전체 영역에서 중심선의 변화량은 받음각에 비례하여 점차 증가한다. 또한, 중심선의 기울기가 공동의 단면적이 작은 시작과 끝에서 크며, 공동의 단면적이 큰 중심부에서는 비교적 작다. 식 (20)에서도 중심선의 기울기가 공동의 단면적에 반비례하는 것을 확인할 수 있다. 본 수치해석의 결과가 운동량 정리와 잘 일치하며, 공동 형상 변화에 유의미한 결과를 가짐을 알 수 있다. 받음각이 작을 때는 유사한 결과를 가지지만, 받음각이 커질수록 계산 간의 차는 커진다. 본 해석법의 경우 공동의 길이가 점차 짧아지고 중심선의 최대 변화량이 커지는 것이 보인다. 이는 Semenenko의 경우 받음각에 따른 캐비테이터의 변화와 공동 형상의 변화를 고려하지 않기 때문이다. 또한, 공동 전방에서 공동이 캐비테이터에 걸쳐 존재하기 때문에 중심선이 x축 아래가 아닌 위에 존재하지만, 짧은 구간에서 급격히 감소하여 x/DC가 약 1.1인 지점에서 중심선의 변화량은 0이 된다. 받음각의 존재로 더욱 얇게 형성된 공동은 더 큰 기울기를 가지며 변화하며, 이러한 기울기의 증가는 공동 길이에 따라서 누적되어 공동의 절반에서 두 결과의 중심선이 동일 변화량을 가지고, 공동의 끝에서 본 수치해석의 최대 변화량이 더 큰 값을 가진다.
3.5 받음각 변화에 따른 초공동의 비대칭성
Fig. 13은 캐비테이터의 받음각의 변화에 따른 초공동의 전체적인 형상 변화와 비대칭성을 살펴보기 위해 받음각이 0, 30도이고 공동수가 σ = 0.0202인 경우를 계산하여 표시하였다. 캐비테이터로부터 일정 거리마다 공동의 단면을 순서대로 나타내었으며, 캐비테이터의 정면 형상도 같이 나타내었다. 받음각이 α=0°인 경우 공동 길이는 LS/DC=100이며, α=30°인 경우는 LS/DC=84.8로 초공동의 길이는 약 15%, 부피는 약 40% 감소하며, 초공동의 중심선이 -y 방향으로 이동하는 것을 확인할 수 있다. 초공동 수중 운동체의 제어성능에서 이러한 공동의 형상 변화는 매우 중요한 요소이다. 짧고 비대칭적 초공동의 발생으로 인한 공동면이 몸체와 접촉하게 되는 플래닝 현상이 발생할 가능성이 커지게 되며, 제어핀의 접수 면적 또한 변화하게 되어 작용하는 유체력이 변화하고 토크가 발생한다.
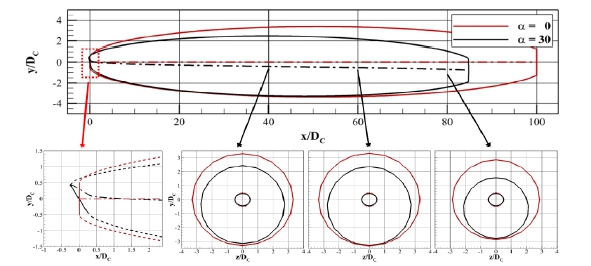
Cavity outline and mid-line denoted by horizontal and vertical section at cavitation number = 0.0202
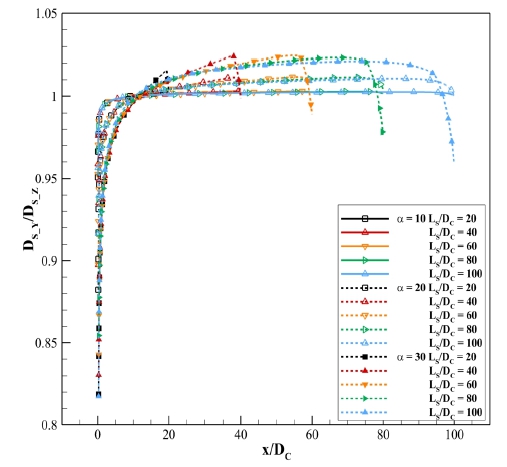
받음각이 존재하는 경우 각 위치에서 공동의 단면은 타원 형상을 가진다. 이를 정밀하게 파악하기 위하여, Fig. 14에 다양한 조건에서 계산된 공동의 y축 직경(DS_Y)을 z축 직경(DS_z)으로 무차원하여 비대칭비로 정의하였다. 전체적으로 공동 길이에 상관없이 캐비테이터의 받음각이 같을 때 동일 x/DC 위치에서 동일 비대칭비를 가진다. 또한 비대칭비의 변화량은 받음각의 크기에 비례하여 증가하며, 공동 길이 및 받음각에 상관없이 캐비테이터 인근에서 1보다 작은 값을 가지고, x/DC가 약 11인 지점에서 직경비 1을 가지며, 이후 1보다 큰 값을 가진다. 이러한 결과는 공동 단면형상이 캐비테이터의 인근에서는 캐비테이터의 기울어진 형상에 영향을 받아 z축 방향으로 길고 y축으로 짧지만, 급격하게 캐비테이터 정면 형상의 영향이 작아지며 다른 요인으로 인하여 y축으로 길어지는 것을 의미한다.
4. 결 론
본 연구는 비점성 유동 경계요소법에 기반한 축대칭 초공동 유동 해석법을 확장하여 3차원 초공동 유동을 계산하였다. 특히 다양한 받음각에서 원판형 캐비테이터에서 발생하는 유체력과 공동의 기하학적 특성을 파악하기 위한 목적으로 수행되었다.
받음각 변화에 따라 캐비티이터에 작용하는 유체력 및 공동 중심선 변화는 기존 실험 및 동역학 계산 결과와 비교하여 정량적으로 평가하였으며 잘 일치함을 확인하였다. 다양한 속도 조건과 받음각의 변화에 따른 공동의 기하학적 형상 변화를 분석하였다. 이를 통해 동일 공동수 조건에서 받음각을 갖는 경우 공동이 크기는 작아지며, 받음각이 커질수록 변화량이 일정 규칙성을 가지며 커진다는 것을 확인하였다. 받음각이 30도일 경우 공동의 길이와 폭이 약 15 %, 부피는 약 40 %까지 감소하며, 공동의 기하학적 특징과 변화량을 정량적으로 추정할 수 있는 경험식을 도출하였다. 공동의 중심선은 캐비테이터에서 발생하는 양력과 반대 방향으로 이동하며 그 변화량은 캐비테이터의 받음각에 비례하고 받음각이 클수록 공동 단면의 비대칭성이 커짐을 확인하였다. 본 연구에 사용된 해석 방법은 초공동 수중 운동체의 초기 설계 단계에서 점성해석법과 비교하여 매우 짧은 시간에 운동체제어를 위해 필요한 초공동의 형상 정보와 유체력 특성을 파악하는데 활용할 수 있을 것으로 기대한다.
Acknowledgments
본 연구는 과학기술정보통신부의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(RS-2023-00208512).
References
-
Ahn, B.K., Jung, S.W., Kim, J.H., Jung, Y.R. and Kim, S.B. 2015. Experimental study on artificial super cavitation of the high speed torpedo. Journal of the Korea Institute of Military Science and Technology, 18(3), pp.300-308.
[https://doi.org/10.9766/KIMST.2015.18.3.300]

-
Ahn, B.K., Kim, K.S., Jeong, S.W. and Yoon, H.G., 2021. An experimental study on multi-injected artificial supercavitation. Journal of the Society of Naval Architects of Korea, 58(1), pp.24-31.
[https://doi.org/10.3744/SNAK.2021.58.1.024]

-
Garabedian, P.R. 1956. Calculation of axially symmetric cavities and jets. Pacific Journal of Mathematics, 6(4), pp.611-684.
[https://doi.org/10.2140/pjm.1956.6.611]

-
Hwang, D.G., Ahn, B.K., Park, J.H., Jeon, Y.H. and Hwang, J.H. 2021. Numerical analysis of the supercavitating underwater vehicle according to different shapes and depth conditions using a VP-BEM method. Journal of the Korea Institute of Military Science and Technology, 24(2), pp.237-244.
[https://doi.org/10.9766/KIMST.2021.24.2.237]

-
Jeong, S.W., Park, S.T. and Ahn, B.K., 2019. An experimental study on artificial supercavitation generated by different combinations of the cavitator and body. Journal of the Society of Naval Architects of Korea, 56(4), pp.327-334.
[https://doi.org/10.3744/SNAK.2019.56.4.327]

- Kiceniuk, T. 1954. An experimental study of the hydrodynamic forces acting on a family of cavity-producing conical bodies of revolution inclined to the flow. Report_No_E-12-17.
-
Kim, J.H., Jang, H.G., Ahn, B.K. and Lee, C.S. 2013. A numerical analysis of the supercavitating flow around three-dimensional axisymmetric cavitators. Journal of the Society of Naval Architects of Korea, 50(3), pp.160-166.
[https://doi.org/10.3744/SNAK.2013.50.3.160]

-
Lee, J.H., Paik, B.G., Kim, K.Y., Kim, M.J., Kim, S. and Lee, S.J. 2019. Experimental study on supercavitated body with static angle-of-attack. Journal of the Society of Naval Architects of Korea, 56(6), pp.541-549.
[https://doi.org/10.3744/SNAK.2019.56.6.541]

-
Park, H.J., Kim, J.H. and Ahn, B.K., 2018. Numerical analysis of axisymmetric supercavitating underwater vehicle with the variation of shape parameters. Journal of the Society of Naval Architects of Korea, 55(6), pp.482-489.
[https://doi.org/10.3744/SNAK.2018.55.6.482]

- Semenenko, V.N. 2001. Artificial supercavitation. physics and calculation. Ukrainian Academy of Sciences Kiev Inst of Hydromechanics.
- Yi, J.J., Kim, M.J., Paik, B.G. and Kim, K.C. 2021. The prediction of ventilated supercavitation shapes according to the angle of attack of a circular cavitator. Journal of the Korean Society of Visualization, 19(3), pp.22-30.