[ Research Paper ]

Journal of the Society of Naval Architects of Korea - Vol. 60, No. 4, pp.213-221

ISSN: 1225-1143 (Print) 2287-7355 (Online)

Print publication date 20 Aug 2023

Received 15 Feb 2023 Revised 18 Apr 2023 Accepted 18 May 2023

DOI: https://doi.org/10.3744/SNAK.2023.60.4.213

독립형 LNG 화물창의 공학적 결함 평가

서재훈¹ ; 박규식² ; 차인환³ ; 정준모¹^{, †}

1인하대학교 조선해양공학과
2포스코 철강솔루션연구소
3(주)현대미포조선 구조설계부

Engineering Critical Assessement for an Independent Type-B LNG Cargo Tank

Jae Hoon Seo¹ ; Kyu-Sik Park² ; Inhwan Cha³ ; Joonmo Choung¹^{, †}

1Department of Naval Architecture and Ocean Engineering, Inha University
2Steel Solution R&D Center, POSCO
3Hull Initial Design Department, Hyundai Mipo Dockyard Co., Ltd. (GRC)

Correspondence to: ^†Joonmo Choung, heroeswise2@gmail.com

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

The demand for Liquefied Natural Gas (LNG) carriers and LNG-fueled ships has significantly increased in recent years due to the sulfur-oxide emission regulations by the International Maritime Organization (IMO). The main goal of this paper is to introduce the process for the Engineering Critical Assessment (ECA) of IMO independent type-B cargo tanks made from 9% nickel alloy. A methodology proposed by the British Standard was used to conduct ECA for any structure with initial flaws. Based on this standard, a Matlab code was developed to perform ECA. Coarse mesh Finite Element Analysis (FEA) was performed on an independent type-B LNG cargo tank with a capacity of 15,000 m³. The location with the highest development of maximum principal stress was identified at the bottom of the cargo tank. Fine mesh FEA was performed to obtain the stress range required for ECA. The dynamic cargo tank loads used for FEA were determined using some ship rules presented by Det Norske Veritas. As a result of performing a 20-year long-term crack propagation analysis with a semi-elliptical surface crack, the fracture-to-yield ratio exceeded the Fracture Assessment Line (FAL) and some structural reinforcement was necessary. Performing a 15-day short-term crack propagation analysis, the fracture-to-yield ratio remained within the FAL, and no significant LNG leaks were expected. This paper is believed to provide a guide for performing ECA of LNG cargo tanks in the future by providing the basic theory and application sample necessary to perform ECA.

Keywords:

LNG, Independent type-B tank, ECA, Stress intensity factor, Crack growth rate

키워드:

액화천연가스, 독립 B형 화물창, 공학적 결함 평가, 응력 확대 계수, 균열 진전 속도

1. 서 론

기존의 석탄이나 석유를 대신하여 비교적 청정에너지로서 액화 천연가스(Liquified Natural Gas, LNG)가 주목받고 있다. 기존의 LNG 운반선뿐만 아니라 LNG를 연료로 사용하는 선박(LNG 추진선)의 요구도 점차 증가하고 있다. 이러한 LNG는 영하 160도 미만에서 끊는점(boiling point)을 가지기 때문에, 스테인리스강, 9% 니켈 합금강, 고망간강 등이 주로 적용되고 있다. 국제해사기구(International Maritime Organization, IMO)는 다양한 유형의 LNG 화물창을 분류하고 있다 (MSC, 2016). 이러한 화물창 중에서 B형 독립 화물창(independent type-B tank)은 내부 보강재를 포함하는 1차 방벽이 화물을 저장하는 역할을 수행한다. B형 독립 화물창은 파손 전 누출(leak before failure)을 전제로 설계되어야 한다. 따라서 장기간 운항으로 인한 초기 작은 균열의 전파가 안정적인지 여부 및 관통 균열 발생 후 단기간 운항으로 인한 취성 파괴(brittle fracture) 발생 여부에 대한 검증이 필요하다. B형 독립 화물창은 많은 내부 보강재로 용접되므로 작은 초기 결함의 가능성을 무시할 수 없다. 이러한 초기 결함은 반복적인 내부 유체력과 선체 운동으로 인한 관성력에 의하여 피로 파괴뿐만 아니라 균열의 성장에 대한 안전도가 담보되어야 한다.

Lee et al. (2021)은 임계 응력 확대 계수(threshold stress intensity factor)를 좀 더 정밀하게 추정하는 연구를 수행한 바 있다. Park and Choi (2021)은 LNG 화물창의 크기를 생애 주기에 맞추어 설계하는 방법을 제시한 바 있다. Song (2022)은 LNG 화물창의 기계적 물성 및 단열 성능에 대한 연구를 수행한 바 있다.

Kim et al. (2010)은 LNG 저장용 9 % 니켈 합금강의 저온 균열 진전 특성에 대하여 실험적 연구를 수행한 바 있다. 3가지 LNG 화물창 소재(알루미늄, 9 % 니켈 합급강, 스테인리스강)에 대한 실험적 연구를 통하여 초저온 균열 진전 특성을 제시한 바 있다 (Lee et al., 2013). Kim et al. (2017)은 균열 진전 시험을 통하여 균열 진전 선도를 얻은 후 맞대기 용접 시편에 대하여 균열 진전 시험 및 British Standard Institution (BSI, 2019)에 의거하여 피로 수명을 평가하였다. 그들은 BSI가 시험 결과에 비하여 상당히 보수적인 결과를 제시하는 것을 확인하였다.

BSI (2019)는 파괴 역학에 기반한 공학적 결함 평가 기법을 제시하고 있으며, 이를 ECA (Engineering Critical Assessment)라 한다. Kang et al. (2015)는 BSI의 공학적 결함 평가 기법을 적용할 수 있는 소프트웨어를 개발하였고, 이를 앵커 파일(anchor pile)에 적용시킨 바 있다. Kim and Shafiqul (2021)도 BSI (2019)을 준용하여 공학적 결함 평가 기법을 적용할 수 있는 소프트웨어를 개발하였고 이를 활용하여 LNG 운반선 B형 화물창의 균열 진전 해석을 수행한 바 있다. 그러나 이 연구에서는 10^-8 확률 수준의 하중을 균열 진전 해석에 적용함으로써 DNVGL (2017a)에서 권고하는 확률 수준과는 큰 차이를 보였다.

본 연구에서는 매트랩(matlab)을 이용하여 BSI (2019)에 의거한 코드를 개발하였다. 이 코드에 적용된 기초적인 이론에 대하여 소개하였다. 이 코드를 이용하여 9 % 니켈강으로 제작된 독립형 B형 화물창의 ECA를 수행하였다.

2. 이론적 배경

2.1 파손 평가 선도

파손 평가선

용접 부재에 균열이 존재하는 경우 작은 하중에서도 단면적의 부족으로 인하여 파단(fracture)할 수도 있으며 단면적이 부족하지 않더라도 큰 하중이 작용하여 항복(yielding)할 수도 있다. 여기서 BSI (2019)은 이러한 두 가지 가능성의 임계선 제시한 바 있으며, 이를 파손 평가선(failure assessment line, FAL)이라 정의한다. FAL을 결정하는 변수를 각각 파단비(fracture ratio) 및 항복비(yield ratio)라 정의하며 K_r 및 L_r의 기호를 사용한다. 파손 평가 선도(Failure Assessment Diagram, FAD)는 임계선인 FAL과 균열의 성장에 따른 실제 파단비 및 실제 응력비의 변화를 도시한 선도이다.

BS는 일축 인장 시험 결과의 보유 여부 및 루더의 항복 평탄부(Lüders yield plateau)의 유무에 따라 다양한 FAL을 제공한다. 설계 단계에서는 화물창 재료의 일축 인장 시험 결과를 보유하지 않은 경우가 많다. 또한 9 % 니켈강과 같은 초저온 소재의 일축 인장 시험 결과에는 통상 항복 평탄부가 존재하지 않는다. 즉, 일축 인장 시험 결과를 보유하지 않은 경우 및 루더의 평탄부가 없는 소재의 경우 식 (1)을 이용하여 FAL을 도시할 수 있다. 즉, 파단비는 항복비의 함수로 표현된다. 식 (1)에 사용된 계수는 식 (2)-(3)을 기반으로 결정된다. 항복비의 최댓값은 식 (4)를 이용하여 결정된다.

K r L r = 1 + 12 L r 2 - 0.5 0.3 + 0.7 e - μ L r 6 f o r L r ≦ 1 K L r (1) L r (N - 1) / 2 N f o r 1 < L r < L r m a x 0 f o r L r ≧ L r m a x

(1)

μ = m i n 0.001 E σ Y 0.6

(2)

N = 0.3 1 - σ Y σ U

(3)

L r m a x = σ Y + σ U 2 σ Y

(4)

K_r : fracture ratio

L_r : yield ratio

σ_Y : engineering yield strength

σ_U : engineering tensile strength

E : elastic modulus

파단비와 항복비

파단비는 식 (5)와 같이 구조물에서 발생한 일차 응력 확대 계수(primary stress intensity factor) $K I p$ 와 이차 응력 확대 계수(secondary stress intensity factor) $K I s$ 의 합과 파괴 인성(fracture toughness) K_mat과의 비율을 의미한다. 파단비를 결정하기 위해서는 소성 수정 계수(plastic correction factor) V 또는 소성 교호 계수(plastic interaction factor) ρ를 선택적으로 적용 할 수 있다. 본 논문에서는 소성 수정 계수를 식 (6)에 제시하였다.

반면, 식 (7)의 항복비는 구조물에 작용하는 기준 응력 σ_ref과 항복 강도 σ_Y와의 비율을 의미한다. 원론적으로 항복비는 구조물에 작용하는 하중과 잔여 항복 강도(균열 α를 제외한 잔여 단면적과 항복 강도의 곱)의 비율을 의미한다. 따라서 순수 인장력이 작용할 경우와 굽힘과 인장이 동시에 작용할 경우를 분리해서 기준 응력을 결정해야 한다.

K r = K I p + V K I s K m a t K I p + K I s K m a t + ρ

(5)

V = m i n 1 + 0.2 L r + 0.02 K I s L r K I p 1 + 2 L r, 3.1 - 2 L r f o r L r ≦ 1.05 0.4 f o r L r > 1.05

(6)

L r = σ r e f σ Y

(7)

$K I p$ : primary stress intensity factor

$K I s$ : secondary stress intensity factor

K_mat : fracture toughness

V : plasticity correction factor

ρ : plasticity interaction factor

σ_ref : reference stress

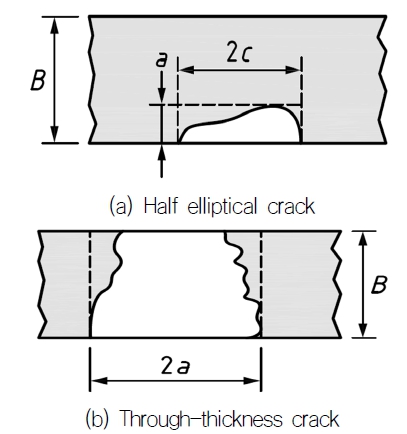
반타원 표면 균열의 경우(Fig. 1(a) 참조), 막응력(membrane stress) 및 굽힘 응력(bending stress)이 동시에 작용할 때 식 (8)을 적용하여 기준 응력을 구할 수 있으며, 막응력에 비하여 굽힘 응력이 상대적으로 작을 경우 식 (9)를 이용한다. 식 (8) 및 식(9)의 기준 응력을 결정하기 위해서, 막응력 P_m 및 굽힘 응력 P_b를 결정해야 한다. 이 응력은 최종 한계 상태(ultimate limit state, ULS)에 상응하는 극한 하중에 의하여 실제 구조물에 발생한 응력을 의미한다 (DNVGL, 2017b). 통상 ULS 응력은 수계산 또는 유한 요소 해석(Finite Element Analysis, FEA)을 통하여 산정된다. Fig. 1(b)와 같은 관통 균열의 경우, 식 (10)을 이용하여 기준 응력을 결정할 수 있다. 식 (11)의 α″ 는 잔여 단면적 계수이다.

Fig. 1

Types of cracks (BSI, 2019)

σ r e f = P b + P b 2 + 9 P m 2 1 - a'' 2 3 1 - a'' 2

(8)

σ r e f = P b + 3 P m a'' + P b + 3 P m a'' 2 + 9 P m 2 1 - a'' 2 3 1 - a'' 2

(9)

σ r e f = P b + P b 2 + 9 P m 2 1 - a'' 2 3 1 - a'' 2

(10)

a'' = a / B 1 + (B / c) for W ≧ 2 (c + B) (a / B) (2 c / W) for W < 2 (c + B)

(11)

P_m : membrane stress corresponding to ULS load

P_b : primary stress corresponding to ULS load

α : crack depth

2c : crack length

W : plate width

B : plate thickness

2.2 Paris 법칙과 균열 성장

균열 성장 속도

Paris 공식이라 불리는 균열 성장률(dα/dN)은 식 (12)과 같다. 식 (13)의 응력 확대 계수 범위 △K는 기하학적 형상, 하중 크기, 균열 형상 등의 함수이다. △K가 임계 응력 확대 계수 범위 △K₀보다 작을 경우 균열은 성장하지 않는다(da/dN = 0). 반면 △K가 소재의 평면 변형률 파괴 인성 K_mat보다 커지면 불안정한 균열의 성장으로 인하여 균열의 진전보다는 급격한 찢김 현상(brittle fracture)이 발생하는 것으로 간주된다 (Dowling et al., 2020). 즉 식 (12)는 △K₀ < △K < K_mat 구간에서 유효하다. 식 (13)을 식 (12)에 대입하여 적분하면 식 (14)를 얻을 수 있다. 즉 식 (14)에 대한 적분을 통하여 균열의 성장을 구할 수 있다. 응력 확대 계수 범위는 Y△σ에 의존하는데 Y△σ는 일차 응력 범위(primary stress range) 및 이차 응력(secondary stress)에 각종 계수를 곱하여 결정된다. 일차 응력 범위는 주로 변동 하중에 기인하며, 이차 응력은 정적인 열하중 또는 잔류 응력에 기인한다. 일차 응력 범위 및 이차 응력 범위는 각각 식 (16) 및 식 (17)에 의해 결정된다.

d a / d N = A Δ K m

(12)

Δ K = Y Δ σ π a

(13)

∫ a i a f 1 Y m π a m / 2 d a = A Δ σ m N

(14)

Y Δ σ = Y Δ σ p + Y σ s

(15)

Y Δ σ p = f w M m Δ P m + M b Δ P b

(16)

Y σ s = M m Q m + M b Q b

(17)

반타원 표면 균열

식 (16)에 사용된 f_w는 식 (18)을 이용하여 구할 수 있다. 식 (16)-(17)의 M_m는 식 (19)을 이용하여 구할 수 있다. 식 (19)의 계수들은 식 (20)-(25)를 이용하여 결정할 수 있다. 식 (17)의 M_b는 식 (26)을 이용하여 결정될 수 있다. 식 (26)의 계수항은 식 (27)-(30)을 통하여 구할 수 있다.

f w = s e c π c W a B

(18)

M m = M 1 + M 2 a / B 2 + M 3 a / B 4 g f θ Φ

(19)

M 1 = 1.13 - 0.09 a / c f o r 0 < a / 2 c ≦ 0.5 c / a 1 + 0.04 c / a f o r 0.5 < a / 2 c ≦ 1

(20)

M 2 = 0.89 0.2 + a / c - 0.54 f o r 0 < a / 2 c ≦ 0.5 0.2 c / a 4 f o r 0.5 < a / 2 c ≦ 1

(21)

M 3 = 0.5 - 1 0.65 + a c - 14.0 1 - a c 24 f o r 0 < a 2 c ≦ 0.5 - 0.11 c a 4 f o r 0.5 < a 2 c ≦ 1

(22)

g = 1 + 0.1 + 0.35 a B 2 1 - sin ⁡ θ 2 f o r 0 < a 2 c ≦ 0.5 1 + 0.1 + 0.35 c a a B 2 1 - sin ⁡ θ 2 f o r 0.5 < a 2 c ≦ 1

(23)

f θ = a c 2 c o s 2 ⁡ θ + s i n 2 ⁡ θ 0.25 for 0 < a 2 c ≦ 0.5 c a 2 s i n 2 ⁡ θ + c o s 2 ⁡ θ 0.25 for 0.5 < a 2 c ≦ 1

(24)

Φ = 1 + 1.464 a c 1.65 for 0 < a 2 c ≦ 0.5 1 + 1.464 c a 1.65 for 0.5 < a 2 c ≦ 1

(25)

M b = H 1 + H 2 - H 1 s i n q ⁡ θ M m

(26)

H 1 = 1 - 0.34 a B - 0.11 a C a B 1 - 0.04 + 0.41 c a a B + f o r 0 < a 2 c ≦ 0.5 0.55 - 1.93 c a 0.75 + 1.38 c a 1.5 a B 2 f o r 0 < a 2 c ≦ 0.5

(27)

H 2 = 1 + G 1 a B + G 2 a B 2

(28)

G 1 = - 1.22 - 0.12 a c for 0 < a 2 c ≦ 0.5 - 2.11 + 0.77 c a for 0.5 < a 2 c ≦ 1

(29)

G 2 = 0.55 - 1.05 a c 0.75 + 0.47 a c 1.5 for 0 < a 2 c ≦ 0.5 0.55 - 0.72 c a 0.75 + 0.14 c a 1.5 for 0.5 < a 2 c ≦ 1

(30)

관통 균열

식 (16)에 사용된 f_w는 식 (31)을 이용하여 계산할 수 있다. 식 (16)의 M_m은 식 (32)을 이용하여 구할 수 있다.

f w = s e c ⁡ π c W

(31)

M m = 1 - 2 Z B

(32)

Z : position of through the thickness

3. IMO B형 LNG 화물창의 ECA

3.1 대상 선박 및 화물창

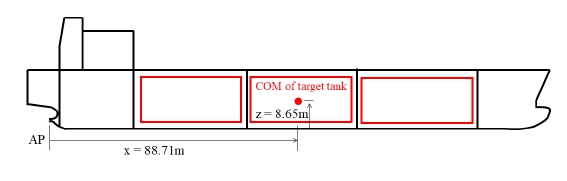
대상 선박은 수선간장 180 m의 중형급 선박으로 15,000 m³급 IMO B형 화물창을 3개 탑재하였다. 본 선박에 대한 주요 치수를 Table 1에 제시하였다. 선박의 원점(선미 수선 AP, 중심선 CL, 기선 BL)을 중심으로 화물창의 질량 중심(centre of mass, COM)은 길이 방향 88.71 m, 폭 방향 0 m, 수직 방향 8.65 m에 위치한다(Fig. 2 참조). 또한 선박의 회전 중심은 선박의 COM과 같다고 가정하였다.

Table 1.

Load cases for fatigue evaluation

Fig. 2

Location of the LNG cargo tank

3.2 하중 케이스

피로 한계 상태 평가를 위한 하중 조건은 선박의 운동에 따라 크게 8가지로 분류된다. 이를 정리하여 Table 2에 제시하였다. HSM(Head Sea Moment)은 전후동요, 상하동요, 종동요의 조합, FSM(Following Sea Moment)은 전후동요 및 종동요의 조합이다. BSP(Beam Sea Pressure) 및 BSR(Beam Sea Roll)은 좌우동요, 상하동요, 횡동요의 조합이다. OST(Oblique Sea Torsion)는 전후동요, 상하동요, 횡동요, 종동요의 조합이다. 각 하중 케이스의 번호 1 및 2는 응력 범위를 산출하기 위한 선체 운동의 방향성을 의미한다. 또한 각 하중 케이스의 P 및 S도 좌현과 우현을 의미하므로 선체 운동의 방향성을 의미한다.

Table 2.

Load cases for fatigue evaluation

선박에 작용하는 가속도 성분은 내항 해석 및 장기 가속도 해석을 통하여 직접 도출하거나, 선급 규칙에 의거하여 도출될 수 있다. 본 연구에서는 내항 해석 및 장기 가속도 분석을 통하여 질량 중심에서의 3자유도 가속도 성분(α_heave, α_roll, a_ptch)을 도출하였다. 선박의 원점(선미 수선 AP, 중심선 CL, 기선 BL)으로부터 측정된 좌표가 [x, y, z]인 위치에서의 가속도(α_X , α_Y, α_Z)는 식 (33)-(35)를 이용하여 산정된다 (DNVGL, 2017b). 여기에 사용된 계수를 하중 조합 계수(Load Combination Factor, LCF)라 한다. 즉 C_XG, C_YG, C_XS, C_XP, C_YS, C_XR, C_ZH, C_ZR, C_ZP를 L_CF라고 하며, 이는 참고 문헌 (DNV, 2017b)에 상세하게 제시되었다.

화물창 내부의 동압(dynamic pressure)은 식 (35)를 이용하여 계산될 수 있다 (DNVGL, 2017b).

a X = f β - C X G g s i n ⁡ ϕ + C X S a s u r g e + C X P a p t c h (z - R)

(33)

a Y = f β C Y G g s i n ⁡ θ + C Y S a s w a y - C Y R a r o l l (z - R)

(34)

a Z = f β C Z H a h e a v e + C Z R a r o l l - C Z P a p t c h (x - 0.45 L)

(35)

P l d = f c d ρ L N G a Z z 0 - z' + f u l l - l a X x 0 - x' + f u l l - t a Y y 0 - y'

(36)

f_β : Correction factors for incident waves

θ : Roll angle

ϕ : Pitch angle

R : Vertical coordinate of the ship rotation centre

f_cd : Factor for joint probability of occurrence of liquid cargo density and maximum sea state in 25 years design life

ρ_LNG : Density of LNG

x₀, y₀, z₀: Coordinate of the reference point of LNG tank

x′, y′, z′ : Coordinate of a point on the upper boundary of LNG tank

f_ull-l, f_ull-t : Longitudinal and transverse acceleration correction factors for the ullage space

L : Length of the ship defined as the distance on the summer load waterline

3.3 화물창 구조 해석

대상 LNG 화물창의 용적은 15,000 m³이며, 보강재 크기 기준의 유한 요소 해석 모델은 주로 셸 요소(shell element)를 이용하여 모델링 되었으며, 늑골과 보강재의 면재(face plate)는 보 요소(beam element)로 모델링 되었다. 화물창을 지지하는 초크(choke)는 갭 요소(gap element)를 이용하여 모델링 되었다. 초크는 독립형 화물창의 안정적인 지지력을 확보하기 위하여 사용되므로 갭 요소의 강성은 회물창의 강성에 비하여 상당히 크게 설정되었으며, 간극(gap)은 초기에 밀착된 것으로 간주하였다. 갭 요소를 사용할 경우 접촉 비선형으로 인하여 대칭 운동에 대하여 대칭의 응력이 발생하지 않는다. 그러나 DNVGL (2017a)에 의하면, Table 1에 보인 바와 같이 피로 해석을 위한 응력 범위를 2개의 독립적인 하중 케이스로부터 구할 수 있다. 따라서 접촉 비선형이 선형적 응력 범위의 산출에 영향을 미치지 않는다고 간주할 수 있다.

화물창 만재 조건(full load condition)이 평형수 조건(ballast condition)에 비하여 큰 응력을 유발하기 때문에 만재 조건에 상응하는 정하중을 고려하였다. 즉 화물창 자체의 자중에 의한 중력 가속도와 LNG로 인한 정압력을 우선적으로 고려하였다. 만재 조건에서의 동하중은 운동 기인 가속도와 동압력이 있으며, 이를 모두 적용하였다. 1단계 해석은 정하중만 부여하고, 2단계에서는 동하중(동압 및 운동 가속도)을 추가적으로 부여하였다.

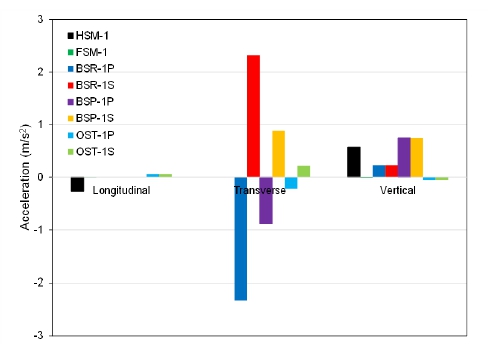
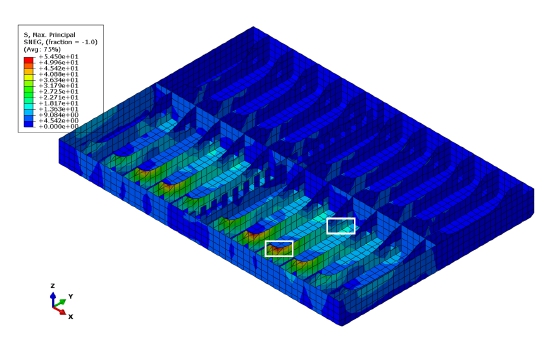
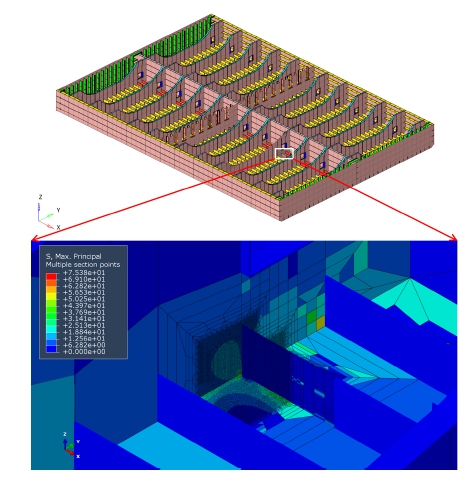
보강재 크기 유한 요소 해석 결과(최대 주응력)를 Fig. 4에 제시하였다. 모든 하중 케이스 중에서 BSR-1S에서 최대 주응력이 발생(Fig. 4 참조)하였으며, BSR-2S에서는 동일한 부분에 응력이 거의 발생하지 않았다. 최대 주응력은 횡 프레임에서 발생하였지만, 균열의 전파로 인한 누설에 대한 검토를 위하여 선저부에서 가장 높은 최대 주응력이 발생한 부분에 대하여 두께 크기 유한 요소 해석 모델을 생성하였다(Fig. 5 참조). 두께 크기 유한 요소 해석에서 얻은 BSR-1S 및 BSR-2S에 상응하는 관심 부위 최대 주응력은 각각 60.37 MPa 및 8.17 MPa이었다.

Fig. 3

Acceleration components by the load cases.

Fig. 4

Coarse mesh analysis results for BSR-1S

Fig. 5

Fine mesh analysis results for BSR-1S

3.4 균열 진전 해석

균열 진전 선도

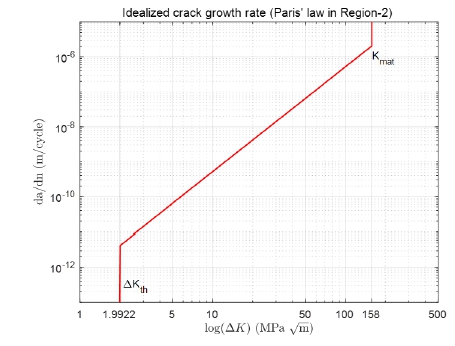
화물창 재료는 9 % 니켈 합금강이었으며, BSI (2019)가 요구하는 임계 응력 확대 계수 △K₀는 63 N/mm^3/2 및 파괴 인성 K_1c 는 4996.4 N/mm^3/2를 가정하였다. 절편 A와 기울기 m은 용접부의 노출 환경 및 하중비에 많은 영향을 받는다. BSI는 해양 환경에서는 이중 기울기에 상응하는 절편 A와 기울기 m 사용을 권고한다. 또한 보수적인 설계를 위하여 단일 기울기를 적용할 수도 있다. 본 연구에서는 보수적인 설계를 위하여 단일 기울기 m=3.0 및 A=5.21×10^-13 mm/cycle을 적용하였다. 이를 적용한 균열 진전 선도는 Fig. 6과 같다.

Fig. 6

Crack growth rate diagram

20년 장기 균열 진전 해석

본 연구에서는 화물창에 반타원 균열이 존재할 때 DNVGL (2017a)에 의거하여 초기 균열 크기를 결정하였다. 즉 맞대기 용접부 균열의 초기 전폭 2c는 5.0 mm였으며, 초기 깊이 a는 1.0 mm로 설정하였다. Fig. 5에서 얻은 최대 주응력을 우선 막 응력범위와 굽힘 응력 범위로 분리하여 Table 3에 정리하였다. 굽힘응력보다는 막 응력 성분이 지배적임을 확인할 수 있다.

Table 3.

Membrane and bending stresses

이 응력 범위는 1x10^-2 초과확률에 상응하는 하중에 의하여 생성된 응력 범위이므로 이를 특정한 확률 수준에 상응하는 응력 범위로 변환할 필요가 있다. Weibull 확률 밀도 함수(Probability Density Function, PDF)를 이용하여 이를 용이하게 결정할 수 있다. 즉 식 (37)를 이용하여 원하는 확률 수준에 상응하는 응력 범위를 도출할 수 있다. 여기서 n₀ 및 $Δ P m 0$ 는 각각 1x10^-2 확률 수준의 역수와 이에 상응하는 막응력 범위이다. 반면 n 및 △P_m 는 각각 원하는 확률 수준의 역수와 이에 상응하는 막응력 범위이다. 굽힘 응력 범위도 동일한 방법으로 도출이 가능하다. 본 연구에서 적용한 Weibull 형상 모수(shape parameter) h는 0.99였다.

Δ P m = Δ P m 0 1 - log ⁡ n log ⁡ n 0 1 h

(37)

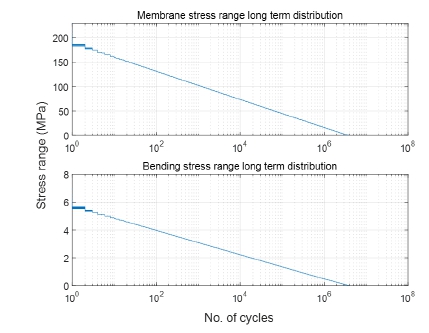
본 연구에서는 확률 수준을 200등분하여 그에 상응하는 응력범위를 도출하였다. 이를 Fig. 7에 제사하였다. 이 응력 범위 블록을 식 (16)에 대입함으로써 균열 진전 해석이 가능하다. 식 (16)에 응력 범위의 대입 순서에 따라 균열 진전에는 차이가 있을 수 있다. 예를 들어 초기 균열 상태에서 낮은 응력 범위 블록이 작용할 경우 임계 응력 확대 계수 범위보다 작은 응력 확대 계수가 산출되어 균열 진전에 전혀 영향을 미칠 수 없다. 반면 큰 응력 범위 블록이 작용할 경우 충분히 균열을 성장시킬 수 있으며 이후 작은 응력 범위가 작용할 경우에도 균열의 성장이 가능하다. 이러한 이유로 응력 범위의 작용 순서는 매우 중요하다. 큰 응력 범위 블록부터 작용시키는 방법, 응력 범위의 무작위 추출에 의한 방법, 블록별 응력 범위를 한 개씩 추출하여 작용시키는 방법 등 여러 가지 응력 작용 방법이 있을 수 있다. 본 연구에서는 큰 응력 범위 블록을 순차적으로 작용시키는 방법을 적용하였다.

Fig. 7

Membrane and bending stress range blocks for long-term crack growth analysis

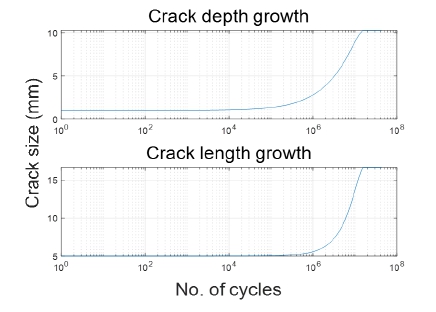
Fig. 8은 응력의 반복에 따른 균열 깊이 및 균열 길이의 성장을 나타낸다. 본 연구에서 계산된 파단비-항복비 궤적과 상용 프로그램 Crackwise (TWI, 2023)의 계산 결과가 거의 일치하는 것을 확인할 수 있다. 균열 깊이는 10⁵개 정도의 하중이 작용한 후 급격하게 성장하다가 10⁷개 이후에는 성장이 멈추는 것을 확인할 수 있다. 큰 응력 범위 블록부터 순차적으로 작용시켰기 때문에 잔여 응력 범위가 매우 작다.

Fig. 8

Crack growth curves from long-term crack growth analysis

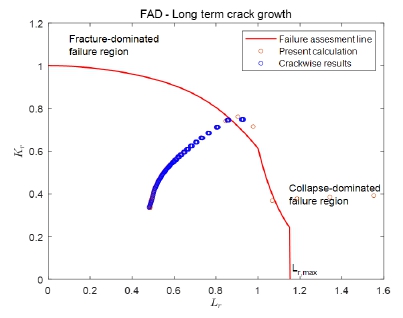
Fig. 9는 균열의 성장에 따른 FAD를 나타낸다. 균열 성장초기에는 파단비가 항복비보다 빠르게 증가하지만, 균열이 어느정도 성장한 후에는 항복비가 더 빠르게 증가하는 것을 확인할 수 있다. 최종적으로 계산된 파단비-항복비는 FAL를 벗어나기 때문에 추후 구조 보강에 따른 응력 범위의 감소가 필요할 것으로 사료된다.

Fig. 9

Path of fracture-yield ratios from long-term crack growth analysis

15일 단기 균열 진전 해석

Dowling et al. (2020)을 참고하여 초기 균열 α는 판의 두께 B (9 mm)와 동일하다고 가정하였다. 15일간의 응력 범위 분포는 Weibull PDF를 따른다고 가정하였으며, 15일간의 총 응력 범위 개수는 2x10⁵이었다. 또한 응력 범위의 확률 수준은 1x10^-2으로 장기 균열 진전 해석에서와 동일하였다.

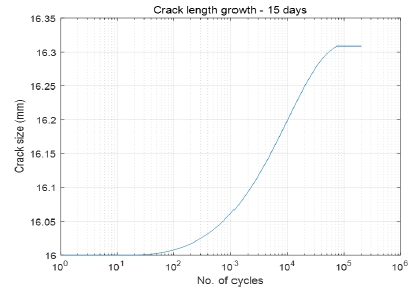
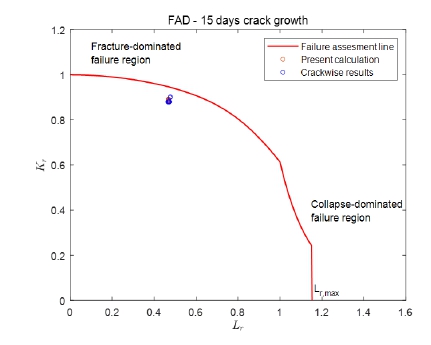
Figs. 10~11은 반복에 따른 균열의 성장과 FAD를 나타낸다. 파단비-항복비가 FAL 내부에 존재하므로, 급격한 균열의 성장이 발생하지 않을 것으로 추정할 수 있다. 15일 단기 균열 진정 해석의 경우에도 본 연구 계산 결과가 상용 프로그램 Crackwise (TWI, 2023)의 계산 결과와 거의 일치하는 것을 Fig. 11에서 확인할 수 있다. DNVGL (2017b)에 따른 누출량을 분석한 결과 15일간 52리터의 LNG가 누출될 수 있을 것으로 계산되었다.

Fig. 10

Crack growth curves from 15 days crack growth analysis

Fig. 11

Path of fracture-yield ratios from 15 days crack growth analysis

4. 결 론

BSI (2019)는 상당히 방대한 산업 규격이며, 많은 경험적 노하우가 담긴 규격이다. 따라서 BSI를 조선해양 설계 실무에 적용하기 위해서는 많은 선행 지식과 규격에 대한 이해가 필수적이다. 본 연구에서는 LNG를 저장 및 운송할 수 있는 B형 화물창의 균열 진전 안전도를 BSI에 의거하여 평가할 수 있도록 체계적으로 BSI의 방법론을 구체화하여 제시하였다.

본 논문에서는 구체적으로 다루지는 않았지만, 대상 선박의 운동 해석 및 장기 가속도 평가를 통하여 선체 COM에서의 장기가속도를 화물창의 하중을 얻는데 사용하였다. 화물창 하중 (동적 가속도 및 동적 화물 압력)은 DNVGL (2017a; 2017b)를 준용하였다.

B형 화물창의 종보강재 크기 유한 요소 해석을 실시하여 화물창 바닥에서 발생할 수 있는 가장 큰 응력 범위를 도출하였으며, 두께 크기 유한 요소 해석을 실시하여 막응력 범위 및 굽힘 응력범위를 도출하였다. 이 응력 범위를 자체적으로 개발한 균열 진전 해석 코드에 대입하여 B형 화물창의 장기 균열 진전 해석 및 15일 단기 균열 진전 해석을 실시하였다. 20년 장기 균열 진전해석으로부터 파단비-항복비 관계가 FAL을 초과하여 구조적인 보강이 요구됨을 확인하였다. 15일 단기 균열 진전 해석으로부터 급격한 균열의 성장이 발생하지 않음을 확인하였다.

향후 본 논문의 독자는 본 논문이 제시한 체계적인 방법론을 숙지하여 LNG 화물창 설계에 큰 도움이 되리라 사료된다. 본 논문에서는 가장 단순한 형태의 FAL을 적용하였지만, 향후 일축 인장 시험의 결과를 보유할 경우에도 균열 진전 평가를 수행할 수 있도록 코드의 개선이 필요하다.

Acknowledgments

본 결과물은 환경부의 재원으로 한국환경산업기술원의 플랜트연구사업의 지원(No. 146836) 및 해양수산부의 재원으로 해양수산과학기술진흥원(KIMST)의 지원(No. 202202103)을 받아 수행되었습니다.

References

British Standards Institution, 2019. Guide to methods for assessing the acceptability of flaws in metallic structures: British standard BS 7910:2019, Fourth edition. British Standards Institution, London.
DNVGL, 2017a. Liquefied gas carriers with independent prismatic tanks of type A and B.
DNVGL, 2017b. Rules for classification Ships Part 3 Chapter 4 Loads.
Dowling, N.E., Kampe, S.L. and Kral, M.V., 2020. Mechanical behavior of materials: engineering methods for deformation, fracture, and fatigue, Fifth edition, global edition. ed. Pearson, Harlow.
Kang, B.J., Kim, Y., Ryu, C.H., Ki, H.G., Park, S.G. and Oh, Y.T., 2015. Flaw assessment on an offshore structure using engineering criticality analysis. Journal of the Society of Naval Architects of Korea, 52(6), pp.435-443. [https://doi.org/10.3744/SNAK.2015.52.6.435]
Kim, B.I. and Shafiqul, I.M., 2021. Crack propagation analysis for IMO type-B independent tank with Liquefied Natural Gas carrier. Journal of the Korean Society of Marine Environment and Safety, 27(4), pp.529-537. [https://doi.org/10.7837/kosomes.2021.27.4.529]
Kim, H.S., Park, T.J., Lee, D.J., Shin, S.B. and Kim, M.H., 2017. A study on fatigue crack growth parameters for fatigue life assessment based on fracture mechanics. Journal of Welding and Joining, 35(1), pp.61-67. [https://doi.org/10.5781/JWJ.2017.35.1.61]
Kim, J.H., Shim, K.T., Kim, Y.K. and Ahn, B.W., 2010. Fatigue crack growth characteristics of 9% Ni steel welded joint for LNG storage tank at low temperature. Journal of Welding and Joining, 28(5), pp.45-50. [https://doi.org/10.5781/KWJS.2010.28.5.045]
Lee, J.S., You, W.H., Yoo, C.H., Kim, K.S. and Kim, Y., 2013. An experimental study on fatigue performance of cryogenic metallic materials for IMO type B tank. International Journal of Naval Architecture and Ocean Engineering, 5(4), pp.580-597. [https://doi.org/10.2478/IJNAOE-2013-0155]
Lee, W.-G., Gu, K.-H., Kim, C.-S. and Nam, K.-W., 2021. Reliability improvement of offshore structural steel F690 using surface crack nondamaging technology. Journal of Ocean Engineering and Technology, 35(5), pp.327-335. [https://doi.org/10.26748/KSOE.2021.022]
Maritime Safety Committee (MSC), 2016. International Code for the Construction and Equipment of Ships Carrying Liquefied Gases in Bulk (IGC Code), International Maritime Organization.
Park, E. and Choi, J., 2021. Greenhouse gas emission analysis by LNG fuel tank size through life cycle. Journal of Ocean Engineering and Technology, 35(6), pp.393-402. [https://doi.org/10.26748/KSOE.2021.071]
Song, H.-C., 2022. Assessment of cryogenic material properties of R-PUF used in the CCS of an LNG carrier. Journal of Ocean Engineering and Technology, 36(4), pp.231. [https://doi.org/10.26748/KSOE.2022.023]
TWI, 2023. CrackWISE. [WWW Document]. URL https://www.twisoftware.com/software/integrity-management-software/crackwise/, [Accessed 18 April 2023]

서 재 훈

박 규 식

차 인 환

정 준 모

Item	Dimension (m)
Length between perpendiculars	180.0
Moulded breadth	31.0
Moulded depth	20.2
Design draft	8.3

No	From	To	Remarks
1	HSM-1	HSM-2	Head sea moment
2	FSM-1	FSM-2	Following sea moment
3	BSP-1P	BSP-2P	Beam sea pressure from port side
4	BSP-1S	BSP-2S	Beam sea pressure from starboard side
5	BSR-1P	BSR-2P	Beam sea roll from port side
6	BSR-1S	BSR-2S	Beam sea roll from starboard side
7	OST-1P	OST-2P	Oblique sea torsion from port side
8	OST-1S	OST-2S	Oblique sea torsion from starboard side

Load case	Top layer stress	Bottom layer stress
BSR-1S	60.37	26.98
BSR-2S	0.00	83.80
△P_m	58.60
△P_b	1.77