[ Research Paper ]

Journal of the Society of Naval Architects of Korea - Vol. 60, No. 3, pp.202-211

ISSN: 1225-1143 (Print) 2287-7355 (Online)

Print publication date 20 Jun 2023

Received 07 Apr 2023 Revised 11 May 2023 Accepted 23 May 2023

DOI: https://doi.org/10.3744/SNAK.2023.60.3.202

조선소 병렬 기계 공정에서의 납기 지연 및 셋업 변경 최소화를 위한 강화학습 기반의 생산라인 투입순서 결정

남소현¹ ; 조영인¹ ; 우종훈¹^{, 2}^{, †}

1서울대학교 조선해양공학과
2서울대학교 해양시스템연구소

Reinforcement Learning for Minimizing Tardiness and Set-Up Change in Parallel Machine Scheduling Problems for Profile Shops in Shipyard

So-Hyun Nam¹ ; Young-In Cho¹ ; Jong Hun Woo¹^{, 2}^{, †}

1Department of Naval Architecture and Ocean Engineering, Seoul National University
2Research Institute of Marine Systems Engineering, Seoul National University

Correspondence to: ^†Jong Hun Woo, j.woo@snu.ac.kr

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

The profile shops in shipyards produce section steels required for block production of ships. Due to the limitations of shipyard’s production capacity, a considerable amount of work is already outsourced. In addition, the need to improve the productivity of the profile shops is growing because the production volume is expected to increase due to the recent boom in the shipbuilding industry. In this study, a scheduling optimization was conducted for a parallel welding line of the profile process, with the aim of minimizing tardiness and the number of set-up changes as objective functions to achieve productivity improvements. In particular, this study applied a dynamic scheduling method to determine the job sequence considering variability of processing time. A Markov decision process model was proposed for the job sequence problem, considering the trade-off relationship between two objective functions. Deep reinforcement learning was also used to learn the optimal scheduling policy. The developed algorithm was evaluated by comparing its performance with priority rules (SSPT, ATCS, MDD, COVERT rule) in test scenarios constructed by the sampling data. As a result, the proposed scheduling algorithms outperformed than the priority rules in terms of set-up ratio, tardiness, and makespan.

Keywords:

Reinforcement learning, Dynamic scheduling, Parallel machine scheduling problem, Tardiness, Set-up

키워드:

강화학습, 동적 스케줄링, 병렬 기계 스케줄링, 납기 지연, 셋업

1. 서 론

최근 조선소에서는 수주 호황에 따른 야드 내 작업 물량의 증가에 대처하기 위하여 생산 시스템의 생산성을 향상시키는 것이 중요한 문제가 되고 있다. 생산 시스템의 생산성 향상을 위한 방안으로는 생산 계획의 최적화, 새로운 설비의 투입, 추가적인 외주 작업 실시 등을 고려할 수 있다. 이 중 생산 계획의 최적화는 생산 시스템 내 불필요한 대기, 재고, 운반 등의 낭비 요소를 최소화함으로써 적은 비용으로 효율적인 생산성 개선이 가능하다. 조선 산업 분야에서는 유전 알고리즘을 이용한 탑재공장의 부하평준화 (Lee and Kim, 1995), 휴리스틱 알고리즘을 이용한 블록 적치장 운영계획의 최적화 (Son et al., 2014), Integer Linear Programming을 이용한 의장공장의 물량 할당 최적화 (Park and Kim, 2020) 등의 연구를 통해 생산성 향상을 달성하기 위한 노력이 이루어지고 있다.

조선소에 존재하는 다양한 생산 공정 중 형강공정은 각종 블록의 제작에 필요한 보강재를 생산하는 공정으로, 후행 공정에서 요구되는 물량을 적시에 공급하기 위해서는 효율적인 작업을 가능하게 하는 생산 계획의 수립이 중요하다. 형강공장에서 보강재는 web과 face의 용접을 통해 제작된다. 용접 공정에서는 보강재의 종굽힘변형을 방지하기 위한 목적으로 web의 상단부에 고주파 유도 가열을 수행하게 되는데, web과 face의 두께 및 폭을 기준으로 고주파 유도 가열의 온도와 위치가 결정되고 이에 따라 용접 라인의 set-up이 변경된다. 따라서 형강공정의 생산량 최대화는 동일한 스펙의 보강재들이 연속되도록 작업 순서를 계획하여 set-up 시간을 최소화함으로써 달성할 수 있다. 다만 각 보강재는 후행공정의 일정에 따라 납기일이 정해지기 때문에, 단순히 set-up을 최소화하는 것만 아니라 추가로 납기 준수의 관점에서 tardiness의 최소화도 고려해야 한다. 실제 현장에서는 set-up 시간 최소화를 위하여 같은 특성을 가지는 부재를 연이어 작업하기 위해 해당 부재가 입고될 때까지 의도적으로 용접 라인의 가동을 중지하기도 한다. 하지만 유휴 용접 라인이 있다는 것은 해당 시간 동안 입고가 되었음에도 작업이 되지 못하는 부재가 존재한다는 것을 의미하고, 대기 중인 부재의 납기 지연이 발생할 수 있다. 따라서 형강공정의 작업 순서 결정 문제는 trade-off 관계의 두 목적함수가 상존하는 다목적 최적화 문제가 된다.

일반적으로 형강공정에서 용접 작업은 작업시간에 있어 불확실성이 존재하게 된다. 이처럼 높은 변동성이 내재된 생산 시스템에 대해서는 사전에 수립한 계획을 그대로 적용하는 것보다 공정의 상황에 따라 적응적으로 계획을 수립하는 동적 스케줄링 방법론이 효과적이다. 우선순위규칙(dispatching rule)은 동적 스케줄링 방법론의 대표적인 예로, priority index에 따라 작업의 우선순위를 설정하여 실시간으로 작업 순서를 결정하는 것이 가능하다. 하지만 우선순위규칙은 생산 시스템의 형태나 조건에 따라 성능 변동이 크기 때문에, 단일 우선순위규칙을 적용하는 것만으로는 다양한 생산 환경에서 일관된 성능을 보장하는 것이 불가능하다.

본 연구에서는 set-up 변경과 tardiness의 최소화를 목적함수로 형강공정 내 병렬 용접 라인의 작업 순서 결정 문제에 대하여 공정의 상태에 따라 적절한 우선순위규칙을 적응적으로 선택할 수 있는 강화학습 기반의 동적 스케줄링 알고리즘을 제안한다. 이를 위하여 형강공정의 작업 순서 결정 문제를 상태와 보상에 set-up 변경과 tardiness의 최소화가 모두 고려된 MDP(Markov Decision Process)로 정의하고, 정의된 MDP로 에이전트가 상호작용하면서 최적 정책을 학습할 수 있도록 이산 사건 시뮬레이션 기반의 학습 환경을 구축한다. 최종적으로 학습에 사용된 계획 대상 블록의 수와 다르게 대상 블록의 수를 설정한 테스트 문제에서 단일 우선순위규칙만 적용하는 경우와의 비교를 통해 학습된 스케줄링 정책의 일반화 성능을 평가한다.

2. 선행연구

본 연구의 대상인 형강공정 내 용접 라인의 작업 순서 결정 문제는 큰 범주에서 병렬 기계 스케줄링 문제(parallel machine scheduling problem)로 일반화할 수 있다. 구체적으로 본 연구에서 다루는 병렬 기계 스케줄링 문제는 각 병렬 기계의 생산 능력이 동일하고, 기계에서의 작업시간에 확률적 변동이 존재하며, 작업 순서에 따라 일정한 set-up 시간을 갖는 문제이다. 이러한 병렬 기계 스케줄링 문제는 제조 시스템, 클라우드 컴퓨팅, 마이크로 컴퓨팅 등의 다양한 분야에 응용되기 때문에 그동안 병렬 기계에서의 작업 할당을 최적화하려는 연구들이 많이 수행되었다.

Kim et al. (2002)는 순서 의존적 set-up이 존재하는 병렬 기계 작업 문제에 대하여 total tardiness의 최소화를 목적함수로 lot을 고려하여 이웃해 탐색을 수행하는 simulated annealing 기반 스케줄링 알고리즘을 제안하였다. Chen and Chen (2009)는 variable neighborhood descent와 tabu search를 결합한 병렬 기계 스케줄링 알고리즘을 개발하였고, 납기 지연 작업의 수 최소화라는 목적함수를 고려하여 해의 탐색 범위를 줄이기 위한 4가지의 이웃해 구조를 제안하였다. Lee et al. (2013)의 연구에서는 total tardiness의 최소화를 목적함수로 순서 및 기계 의존적 set-up을 고려한 병렬 기계 스케줄링 문제를 다루었고, 스케줄링 알고리즘으로서 swap과 insertion 연산을 바탕으로 8가지 이웃해 탐색 전략을 정의하여 tabu search를 적용하였다. Chaudhry and Elbadawi (2017)은 total tardiness의 최소화를 목적함수로 갖는 병렬 기계 스케줄링 문제를 해결하기 위하여, 전체 작업의 처리 순서와 각 작업을 수행할 기계 정보로 chromosome을 구성하고 genetic algorithm을 적용하여 스케줄링을 수행하였다. Lee (2018)의 연구에서는 병렬 기계 시스템으로 모델링 되는 Acrylonitrile-Butadiene-Styrene plate 제작 공정의 스케줄링 문제에 대하여 total tardiness의 최소화를 위하여 두 단계로 구성된 스케줄링 알고리즘을 제안하였다. 해당 스케줄링 알고리즘은 먼저 ATCS_APD라는 우선순위규칙을 통해 초기 계획을 수립하고, iterated greedy 기반의 탐색 방법을 적용하여 초기 계획을 개선한다.

병렬 기계 스케줄링 문제에 강화학습 방법론을 적용하기 위한 연구도 많이 수행되고 있다. Zhang et al. (2007)의 연구에서는 Q-learning 알고리즘을 적용하여 강화학습 에이전트가 병렬 기계 생산 시스템 내 작업들의 완료 상태 및 납기 정보 그리고 각 기계의 작업 진행 상황 등의 정보를 입력받아 다섯 가지 우선순위규칙 중에서 mean weighted tardiness의 최소화를 위한 적절한 행동을 선택하도록 스케줄링 정책을 학습하였다. Zhang et al. (2012)은 상태 정보로서 병렬 기계 생산시스템 자체의 특성과 대상 작업들의 납기 관련 특성들을 포함하여 mean weighted tardiness의 최소화를 목적으로 하는 MDP 모델을 정의하였고 R-learning 알고리즘을 적용하여 작업 순서 결정을 위한 스케줄링 정책을 학습하였다. Paeng et al. (2021)의 연구에서는 DQN 알고리즘을 적용하여 에이전트가 total tardiness의 최소화를 목적으로 일정한 시간 간격마다 수행할 작업과 해당 작업을 할당할 기계를 선택하는 방식의 순서 의존적 set-up이 고려된 병렬 기계 스케줄링 알고리즘을 제안하였다. Julaiti et al. (2022)의 연구에서는 기계의 고장을 고려한 병렬 기계 스케줄링 문제를 생산 시스템의 통계적 정보에 기반하여 Partially Observable Markov Decision Process (POMDP)로 모델링하였다. 그리고 separate sampling 기법을 사용한 DDPG 알고리즘을 적용하여 에이전트가 세 가지 지표 (납기 지연 측면에서의 작업의 긴급도, 작업시간, 작업별 기계의 정상 작동시간 분포)에 대한 가중치를 조정하는 정책을 학습하도록 하였고, 학습된 정책을 기반으로 세 가지 지표를 가중합한 priority index를 생성하여 이에 따라 작업 순서를 결정하는 방식의 스케줄링 알고리즘을 제안하였다.

대부분의 선행연구에서는 실제 산업의 생산 시스템이 아닌 개념적인 문제만을 대상으로 스케줄링 알고리즘의 유효성을 확인하였다. 따라서 본 연구에서는 병렬 기계 문제로 모델링 할 수 있는 조선소 형강공정의 작업 순서 결정 문제에 대한 강화학습 기반의 스케줄링 알고리즘을 개발하여 실제 생산 시스템에서의 적용 가능성을 확인한다. 구체적으로 본 연구에서는 tardiness 최소화와 함께 생산량 향상을 위한 set-up 최소화를 동시에 달성하기 위하여, MDP 모델링에 있어 set-up과 tardiness 측면이 모두 고려된 보상과 상태 구조를 정의하고 이를 바탕으로 강화학습 기반의 다목적 동적 스케줄링 알고리즘을 제안한다.

3. 문제 정의

본 연구에서는 형강공정의 병렬 용접 라인에 대한 작업 투입순서 문제를 다루며, 목적함수로 tardiness와 set-up 변경 횟수의 최소화를 고려한다. 형강공정에서 보강재(section steel)는 web과 face라는 두 부재의 용접을 통해 제작되며, 보강재를 만들기 위한 web과 face는 크레인을 통해 세 개의 병렬 작업 라인 중 하나로 이동되어 배제 및 용접 공정을 수행한다. 최종적으로 용접이 완료된 보강재는 사상 공정을 수행하고 같은 블록에 속하는 보강재들은 파렛트 단위로 적치되어 반출된다.

가장 상위 개념인 블록에 대한 데이터 구조는 Table 1과 같다. 블록 집합 B = {B₁, ... , B_N}에 속하는 블록 B_i(i = 1, ..., N)은 n_i개의 보강재로 이루어져 있으며, 납기일 d_i를 가진다. 블록 B_i에 속하는 보강재의 집합을 S_i = {S_i1, ... , S_{in_i}}로 표현할 수 있고, 보강재 S_ij(j = 1, ... , n_i)는 동일한 부재의 개수인 n_ij, web과 face의 길이, 두께 정보인 θ_ij, 용접 두께인 ws_ij, 부재의 길이인 l_ij 를 속성으로 가진다. 실제 데이터의 예시는 Table 1에 나타냈다. 그 중 set-up 시간을 결정 짓는 θ_ij 는 4개의 실수형 자료의 벡터형태로 구성되어 있는데, 학습에서는 0부터 201 사이의 정수형으로 변환시켜 scalar 형태로 입력하였다.

Table 1

Data structure of profile shop in shipyard industry

본 연구에서 보강재의 작업은 동일한 생산 능력을 갖는 3개의 병렬 용접 라인 중 하나에서 수행된다고 가정한다. 보강재 S_ij에 대한 용접 공정 속도 v_ij는 보강재의 용접 두께 ws_ij에 의해 식 (1)으로 결정된다. 따라서 보강재 S_ij의 평균 작업시간은 식 (2) 와 같이 보강재의 길이 l_ij를 공정속도 v_ij로 나눈 결과가 된다.

하지만 실제 현장에서는 작업 시간에 있어 변동성이 존재하기 때문에, 본 연구에서는 식 (2)로 계산된 평균 작업 시간을 사용하여 식 (3)과 같이 정의한 균등분포(uniform distribution)에 따라 보강재 S_ij의 작업 시간이 확률적으로 결정된다고 가정한다.

v i j = 1200 - w s i j - 4.5 × 50 [m m / m i n]

(1)

p - i j = l i j v i j

(2)

p i j ∼ U 0.9 × p - i j, 1.1 × p - i j

(3)

형강공정의 용접 라인에 대하여 본 연구에서 추가적으로 가정한 사항은 다음과 같다. 용접 작업에 필요한 web과 face는 선행 공정에 해당하는 절단 공정이 완료된 상태로 용접 작업 전에 모두 준비되어 있다. 또한 각 용접 라인은 한 번에 하나의 보강재만 작업할 수 있다. 이때 용접 라인은 일주일 중 일요일을 제외한 6일 동안 가동되며, 하루 작업 가능 시간은 16시간이다. 그리고 각 용접 라인에서 연속해서 작업되는 두 보강재의 web과 face의 θ값이 다르면 set-up 변경이 이루어지며, set-up 시간은 작업 순서와 상관없이 5분이라고 가정한다. 위 가정 사항들을 정리하면 다음과 같다.

● 작업의 객체인 부재(web, face)는 작업 시작 전에 모두 준비되어 있음

● 각 용접 라인은 동일한 생산능력을 가짐

● 각 용접 라인은 한 번에 하나의 부재만 작업 가능함

● 작업은 하루 16시간씩 주 6일 작업함

● 두 보강재의 특성(θ)이 다르면 5분의 set-up 시간이 발생함

4. Markov Decision Process 모델링

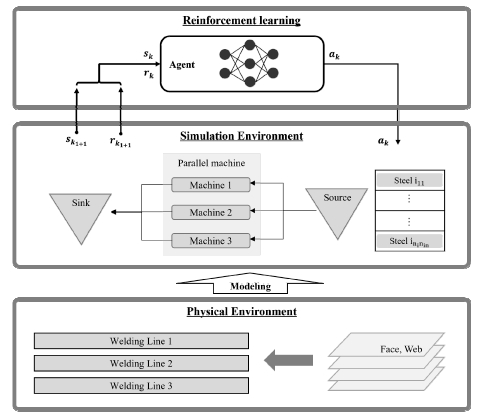
조선소의 형강공정에 대한 작업 순서 결정 문제에 강화학습 방법론을 적용하기 위해서는 주어진 문제를 MDP로 모델링 하여야 한다. MDP는 상태, 행동, 보상, 그리고 상태변환확률의 네 가지 요소로 에이전트와 환경의 상호작용을 정의한다. 본 연구에서는 각 용접 라인에서 보강재의 작업이 완료된 순간을 의사결정 시점으로 설정하여, 에이전트가 환경으로부터 해당 시점의 상태를 입력받아 행동을 결정하도록 한다. 그리고 학습 환경을 이산 사건 시뮬레이션 모델로 구현함으로써 환경에서는 에이전트가 선택한 행동을 바탕으로 상태변환확률 대신 시뮬레이션을 통해 다음 상태와 보상을 계산한다. 이러한 과정으로 에이전트는 샘플 데이터를 획득하고 학습 알고리즘을 통해 최적 정책을 학습한다. 형강공정 스케줄링 문제에 대한 전체적인 학습 프레임워크는 Fig. 1과 같다.

Fig. 1

Overall learning framework

4.1 상태

에이전트의 행동 결정의 기준이 되는 상태는 각 의사결정 시점 t에서의 작업이 미완료된 보강재와 각 용접 라인에 대한 정보를 기반으로 총 네 가지의 특성벡터로 구성된다. 그리고 대상 계획 기간이 달라져도 이미 학습된 에이전트의 적용이 가능하도록 상태의 크기가 블록의 개수와 독립적인 상태벡터를 정의했다.

첫 번째 특성벡터(f₁)는 set-up 횟수 최소화와 관련된 정보로서, 식 (4)와 같이 정의된다. 식 (4)는 현재 의사결정 시점에서 작업이 수행되지 않은 보강재 중 해당 시점에서 각 용접 라인의 set-up과 동일한 set-up을 갖는, 즉 set-up의 변경 없이 바로 작업이 가능한 보강재 개수의 전체 보강재 개수에 대한 비율이다. 이 값은 각 용접 라인마다 계산되기 때문에 첫 번째 특성벡터의 크기는 용접 라인의 수와 동일한 3이다.

두 번째(f₂) 및 세 번째(f₃) 특성벡터는 tardiness 최소화와 set-up 횟수 최소화와 관련하여, 작업 대기 중인 보강재에 대한 정보를 담고 있다. 두 번째 특성벡터는 작업 수행 시 용접 라인의 set-up 변경이 필요 없는 보강재들에 대하여 식 (5)와 같이 네 단계의 tardiness level에 속하는 보강재의 비율로 구성된다. 세 번째 특성벡터는 용접 라인의 set-up 변경이 요구되는 보강재들을 대상으로 동일한 방식으로 계산된다. 이때, 네 단계의 tardiness level은 의사결정 시점에서 작업 대기 중인 블록의 하루 작업 시간을 고려했을 때의 예상 지연 발생 정도로 구분하였다. 구체적으로 작업 시간의 변동성을 고려해도 지연이 발생하지 않는 경우(Level 1), 최대 작업 시간을 고려하면 지연이 발생하지만, 최소 작업 시간으로 작업될 경우에는 지연이 발생하지 않는 경우(Level 2), 아직 지연은 발생하지 않았지만, 최소 작업 시간으로 작업되어도 지연이 발생하는 경우(Level 3), 이미 지연이 발생한 경우(Level 4)로 tardiness level을 구분하였다. 두 번째 특성벡터와 세 번째 특성벡터의 크기는 tardiness level의 수와 동일한 4이다.

네 번째 특성벡터(f₄)는 작업 라인에 대한 일반적인 정보로서, 식 (6)과 같이 현재 의사결정 시점을 기준으로 각 용접 라인에 할당된 용접 작업의 남은 작업 시간으로 정의한다. 네 번째 특성벡터의 크기는 용접 라인의 수와 동일한 3이다.

f 1, k = N k N w I f L i n e k ’ s s e t — u p i s d e t e r m i n e d 1.0 O t h e r w i s e (I n i t i a l s t a t e) N k : t h e n u m b e r o f T — b a r s w h i c h h a v e t h e s a m e s e t — u p o f L i n e k' s s e t — u p N w : t h e n u m b e r o f T — b a r s w h i c h h a v e n o t b e e n w o r k e d y e t

(4)

f 23, g = N 23, g N w, 23 g = 1,2, 3,4, N 23, g : t h e n u m b e r o f T — b a r s w h i c h h a s t a r d i n e s s l e v e l g o f n o n — s e t u p (2) o r s e t — u p (3) N w, 23 : t h e n u m b e r o f T — b a r s w h i c h h a v e n o t b e e n w o r k e d y e t T a r d i n e s s l e v e l g = 1 i f d i - t ∈ max ⁡ r i j, + ∞ 2 i f d i - t ∈ (min ⁡ r i j, max ⁡ r i j] 3 i f d i - t ∈ (0, min ⁡ r i j] 4 i f d i - t ∈ (- ∞, 0] max ⁡ m i n r i j : m a x i m u m (m i n i m u m) r e m a i n i n g p r o c e s s i n g t i m e o f S i j t : c u r r e n t t i m e

(5)

f 4, k = r e m a i n i n g p r o c e s s i n g t i m e e x e p e c t e d p r o c e s s i n g t i m e 0 L i n e k i s w o r k i n g L i n e k i s i d l e, k = 1, 2, 3

(6)

s + p - i j

(7)

1 p - i j e x p m a x d i - p - i j - t, 0 k 1 p - e x p - s k 2 s p - : t o t a l a v e r a g e o f p r o c e s s i n g t i m e

(8)

4.2 행동

에이전트가 다음으로 작업할 보강재를 직접 선택하는 방식으로 행동을 정의할 경우, 가능한 행동 집합의 크기가 방대해지고, 의사결정이 진행됨에 따라 보강재의 수가 작업으로 인해 줄어들어 의사결정시점에 따라 가능한 행동 집합의 크기가 달라지는 문제가 발생한다. 따라서 에이전트의 행동은 tardiness 또는 set-up 최소화 문제를 풀기 위하여 고안된 대표적인 우선순위규칙 중 하나를 선택하는 것으로 정의된다. 구체적으로 전체 행동 집합을 SSPT, ATCS, MDD, 그리고 COVERT rule로 구성한다.

SSPT rule은 SPT(Shortest Processing Time) rule과 SST (Shortest Set-up Time) rule을 결합한 우선순위규칙으로, 식 (7)과 같이 set-up 시간(s, 5분)과 식 (2)에서 계산된 평균 작업 시간( $p - i j$ 을 더한 값이 낮을수록 높은 우선순위를 부여한다.

ATCS rule은 total weighted tardiness의 최소화를 목적으로 제안된 ATC(Apparent Tardiness Cost) rule을 set-up 최소화도 고려하도록 수정한 우선순위규칙이다. ATCS rule에서 priority index는 식 (8)과 같이 정의되며, 짧은 작업시간, 적은 slack time과 짧은 set-up 시간을 갖는 작업일수록 높은 우선순위를 부여한다. 본 연구에서 두 파라미터 k₁과 k₂의 값은 [1, 6] 범위 내 정수값으로 case study를 진행했을 때, 전체 보강재 개수 중 set-up이 발생하는 보강재 개수의 비율과 tardiness 측면에서 가장 좋은 결과를 나타낸 조합인 k₁ = 6, k₂ = 1로 설정한다.

MDD rule은 EDD(Earliest Due Date) rule과 SRPT(Shortest Remaining Processing Time) rule을 결합하여 만든 우선순위규칙으로, priority index는 식 (9)로 정의된다. MDD rule은 납기일 또는 남은 작업 시간을 고려한 작업 완료일이 빠른 작업일수록 높은 우선순위를 부여한다.

m a x d i, t + p - i j

(9)

COVERT rule은 식 (10)과 같이 priority index를 정의하여, 작업 시간이 짧고, 추정 대기 시간 대비 slack time의 비율이 작은 작업에 높은 우선순위를 부여한다. 본 연구에서 파라미터 k는 [1, 20]의 정수값으로 case study를 진행했을 때 mean tardiness가 가장 작은 결과를 보인 20으로 설정하였다.

1 p - i j m a x 1 - m a x d i - p - i j - t, 0 k p - i j, 0

(10)

4.3 보상

강화학습에서의 보상은 학습의 성능을 좌우하는 요소로, 목적함수와 직접적으로 연관된다. 본 연구에서 다루는 문제는 tardiness 최소화와 set-up 최소화라는 trade-off 관계의 두 목적함수를 고려하는 다목적 최적화 문제로, 보상은 tardiness 관점과 set-up 관점을 모두 포함하도록 정의되어야 한다.

첫 번째로 set-up 횟수 최소화 관점에서는 식 (11)과 같이 에이전트가 선택한 우선순위규칙에 따라 다음으로 작업할 보강재를 용접 라인에 투입하였을 때, 만약 set-up 변경이 발생하면 –0.1의 페널티를 부여하고, set-up 변경이 발생하지 않는다면 0의 보상을 준다. 두 번째로 tardiness 관점에서는 의사결정 시점 사이에 모든 보강재의 작업이 완료된 블록이 존재한다면, 해당 블록의 tardiness를 식 (12)와 같이 정의된 지수함수를 통해 [-1, 0] 범위 안으로 치환하고, 해당 값을 보상으로 할당한다. 즉, 납기일을 기준으로 보강재의 작업이 늦게 완료될수록 최대 페널티값인 –1에 가까운 보상을 할당한다. Reward₁은 보강재에 대한 보상이고, Reward₂는 보강재가 모여 만들어진 block에 대한 보상이므로 각 리워드의 발생 횟수는 Reward₁이 Reward₂ 대비 약 10배이다. 따라서 두 보상 간의 scaling을 위하여 Reward₁은 한 번 발생할 때마다 –1의 보상이 주어지는 Reward₂와 달리 10분의 1의 값인 -0.1로 설정하였다. 최종 보상은 식 (13)과 같이 두 보상의 합으로 계산된다.

R e w a r d 1 = - 0.1 i f s e t - u p c h a n g e o c c u r s 0 O t h e r w i s e

(11)

R e w a r d 2 = e - min ⁡ d i - C i - 1 d i : d u e d a t e o f i t h T - b a r C i : C o m p l e t i o n t i m e o f i t h T - b a r

(12)

T o t a l R e w a r d = R e w a r d 1 + R e w a r d 2

(13)

5. 학습 알고리즘

Schulman et al. (2017)의 연구에서 제안된 PPO(Proximal Policy Optimization) 알고리즘은 식 (14)과 같이 정의한 대리 손실함수(surrogate loss function) L(θ)을 최소화하여 최적의 정책을 학습하는 정책 기반 강화학습 알고리즘이다. PPO 알고리즘은 정책을 근사한 인공신경망의 가중치 θ를 업데이트 함에 있어 clip 함수를 도입함으로써 기존의 정책과 업데이트된 정책의 비율 r_t(θ)가 [1-ε, 1+ε]의 범위 안의 값을 갖도록 제한하여 과도하게 정책이 업데이트되는 것을 방지한다. A_t는 advantage 함수로서 TD error δ_t를 사용하여 식 (15)와 같이 정의되는 한계 누적 보상 기댓값 (marginal expected sum of rewards)을 계산한다.

L θ = E^t max ⁡ r t θ A^t, c l i p ⁡ r t θ, 1 - ϵ, 1 + ϵ A^t

(14)

A^t = δ t + γ λ δ t + 1 + ⋯ + γ λ T - t + 1 δ T - 1

(15)

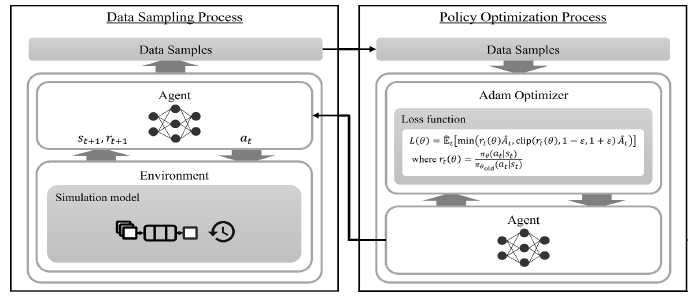
PPO 알고리즘을 기반으로 최적의 스케줄링 정책을 학습하는 전체적인 과정은 Fig. 2와 같다. 전체 과정은 샘플링 과정과 정책 최적화 과정의 두 가지 세부 과정으로 구성된다. 먼저 샘플링 과정에서는 앞서 4장에서 정의한 MDP에 따라 에이전트가 시뮬레이션 환경과 상호작용을 하면서 상태, 행동, 보상, 그리고 다음 상태의 네 가지 정보로 구성된 샘플 데이터를 획득한다. 그리고 정책 최적화 과정에서는 획득한 샘플들을 기반으로 PPO 알고리즘을 적용하여 식 (14)로 정의된 손실함수를 최소화하도록 정책을 근사한 인공신경망의 가중치를 업데이트한다. 이후 업데이트된 인공신경망으로 동일한 과정을 반복한다.

Fig. 2

Framework of PPO algorithm

6. 결과 분석

조선소의 현장 데이터를 분석한 결과, 형강공정에서는 1주 기준 약 80개의 블록에 대한 물량을 작업하며, 이는 평균 700개의 보강재에 해당한다. 따라서 에이전트의 학습 시나리오는 일주일 동안 작업 되는 물량에 해당하는 80개의 블록에 포함된 보강재의 작업 순서를 결정하는 문제로 설정했다. 그리고 학습된 정책의 일반화 성능을 위하여 본 연구에서는 조선소로부터 획득한 754개의 블록 데이터 중 80개의 블록을 매 에피소드마다 랜덤하게 샘플링하여 에이전트의 학습을 진행했다. 이때 각 블록의 납기일은 일요일을 제외하고 0~5 사이의 정수값으로 인코딩된 나머지 요일에서 랜덤으로 배정했다.

이후 강화학습 에이전트가 학습한 형강공정에 대한 작업 순서 결정 정책을 set-up ratio, tardiness, makespan의 세 가지 지표를 통해 평가했다. 첫 번째 평가 지표인 set-up ratio는 보강재의 전체 개수 대비 작업 시 용접 라인의 set-up 변경을 발생시킨 보강재의 비율로 정의한다. 본 연구의 목적함수 중 하나가 set-up의 최소화이기 때문에 set-up ratio가 작을수록 스케줄링 알고리즘의 성능이 좋음을 의미한다. 두 번째 평가 지표인 tardiness는 블록의 주어진 납기일과 해당 블록에 포함된 모든 보강재의 작업이 완료된 시점을 비교하였을 때 작업 완료가 지연된 일 수로 정의한다. 따라서 tardiness 값이 작을수록 납기 준수 관점에서 좋은 계획이다. 마지막 평가 지표인 makespan은 주어진 물량을 전부 작업하는 데 걸리는 시간으로 정의된다. Makespan이 짧을수록 동일 기간 내에 더 많은 보강재에 대한 용접 작업이 수행되었음을 의미하므로, 이는 단위 시간당 생산된 보강재의 수로 정의되는 throughput이 더 높음을 의미한다. 따라서 수립된 계획의 makespan이 짧을수록 형강공정에서 더 높은 생산량을 달성할 수 있다는 것을 의미한다.

학습 과정과 테스트 시나리오에 대한 설명은 Table 2와 같다. 학습 과정과 동일한 블록 80개에 대한 계획(테스트 시나리오 1)과 학습 과정 대비 장기간에 해당하는 블록 240개에 대한 계획(테스트 시나리오 2)의 두 가지 케이스를 설정한다. 학습 과정과 마찬가지로 총 754개의 블록 데이터에서 각 기간에 해당하는 블록의 개수만큼 랜덤으로 샘플링하여 테스트 문제를 구성하고, 알고리즘의 성능 비교는 이를 총 100번 반복하여 계산한 각 지표의 평균값을 기반으로 수행한다. 본 연구에서는 비교 대상 알고리즘으로 에이전트의 행동에 포함된 우선순위규칙 중 하나의 규칙만을 적용하는 알고리즘 그리고 임의로 우선순위규칙을 선택하여 작업 순서를 결정하는 알고리즘을 포함한다.

Table 2

Description of scenarios for training and testing

6.1 학습 결과

PPO 알고리즘에서 에이전트가 학습할 정책은 인공신경망으로 모델링 되며, 본 연구에서는 총 5개의 완전 연결계층(fully connected-layer)으로 인공신경망을 구성한다. 입력층은 상태벡터의 크기와 동일한 14개의 노드를 갖고 세 개의 은닉층은 차례대로 각각 512개, 512개, 256개의 노드를 갖는다. 마지막으로 출력층은 전체 행동의 수와 동일한 4개의 노드를 갖는다. 이때 마지막 출력층을 제외한 첫 번째에서 네 번째 층은 모두 활성 함수로 ReLU(Rectified Linear Unit)함수를 사용한다.

본 연구에서 에이전트의 학습에 사용한 PPO 알고리즘의 하이퍼파라미터는 Table 3과 같다. 에이전트는 전체 10,000번의 에피소드에서 학습을 수행한다. 이때 각 에피소드에서의 학습은 에이전트가 환경과 상호작용을 통해 50개의 샘플을 획득할 때마다 수행되며, 해당 샘플을 기반으로 5번의 연속적인 가중치 업데이트가 이루어진다. 가중치 업데이트 시 손실함수 값은 clipping parameter ε, discount ratio γ, GAE parameter λ를 각각 0.2, 0.98, 0.95로 설정하여 계산되며, 최적화 알고리즘으로는 learning rate를 0.0005로 설정한 Adam 알고리즘을 적용한다.

Table 3

Hyper-parameters in the learning rate

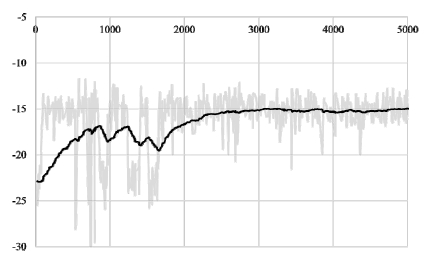
에이전트의 학습이 진행됨에 따른 각 에피소드 별 누적 보상의 그래프는 Fig. 3와 같다. 학습 초기에 누적 보상이 -20에서 -15사이에서 변동하다가 약 3,000 에피소드 이후에는 대략 -15로 수렴한 것을 볼 수 있다. 즉 set-up과 tardiness를 감소시키는 방향으로 스케줄링 정책이 학습되는 것을 확인할 수 있다.

Fig. 3

Graph of cumulative rewards

6.2 테스트 시나리오 1

테스트 시나리오 1에서는 학습 과정과 동일하게 블록 80개에 대하여 테스트를 진행하였다.

Set-up ratio 관점에서의 결과는 Table 4와 같다. 테스트 시나리오 1과는 달리, 더 짧은 기간에 대해서는 강화학습이 SSPT보다 set-up 관점에서 더 좋은 결과를 나타냈다. 강화학습 다음으로는, set-up을 고려한 dispatching rule인 SSPT와 ATCS가 set-up 비율 40% 이하의 값을 나타냈다. 반면 MDD rule의 경우 약 90%의 set-up 비율로, 10개 중 9개의 작업에서 set-up이 발생했다.

Table 4

Result of Set-up ratio (scenario 1)

Tardiness 관점에서의 테스트 시나리오 1의 결과는 Table 5와 같다. 강화학습으로 학습한 모델에 따라 투입순서를 결정한 경우, 평균 0.03시간, 약 2분의 지연이 나타났다. 반면 set-up 비율에서 강화학습 다음으로 낮은 값을 보였던 SSPT rule의 경우 평균 7.9시간의 납기 지연이 발생하는 것을 확인할 수 있었다.

Table 5

Result of tardiness (scenario 1)

1주치 물량에 대하여 강화학습으로 학습한 모델과 학습에서 행동으로 선택되었던 dispatching rule을 이용하여 makespan을 측정한 결과는 Table 6과 같다. 일주일, 즉 6일에 해당하는 물량에 대하여 강화학습으로 학습한 모델을 이용하여 투입순서를 결정하였을 때 평균 3.07일안에 모든 강재에 대한 작업이 수행되는 것을 확인할 수 있었다. 다음으로는 SSPT rule, ATCS rule이 짧은 makespan 값을 가지는 것을 확인할 수 있었다. 반면 COVERT rule과 MDD rule은 네 개의 dispatching rule을 무작위로 적용하여 투입순서를 결정한 Random 케이스보다 더 긴 makespan 값이 측정되었다. 특히 MDD rule의 경우 전체 작업 중 90%의 작업에서 set-up 시간을 고려했기 때문에 가장 긴 makespan을 가진 것으로 판단된다.

Table 6

Result of makespan (scenario 1)

학습과 동일하게 1주치 물량, 블록 80개에 대하여 학습한 모델, 그리고 강화학습에 있어서 행동으로 정의되었던 네 개의 dispatching rule, 마지막으로 네 가지 dispatching rule을 무작위로 사용한 Random 케이스에 대하여 테스트 한 결과, makespan 지표를 제외한 set-up 비율, tardiness 지표에서는 강화학습으로 학습한 모델이 가장 좋은 결과를 나타내었다. 다만 makespan 지표에서 가장 좋은 결과를 보였던 SSPT rule의 경우, set-up 비율에서는 강화학습 다음으로 낮은 set-up 비율 값을 나타냈지만, 납기 지연에서는 네 가지 dispatching rule 중 가장 큰 값을 보였다.

6.3 테스트 시나리오 2

테스트 시나리오 2에서는 학습 과정보다 긴 계획 범위를 갖는 3주치 물량에 해당하는 블록 240개에 대한 투입순서 결정에 대하여 테스트를 진행하였다. 에이전트의 상태와 행동의 크기가 블록의 개수와 독립적이기 때문에 블록의 개수를 달리하여 이미 학 습된 모델을 적용할 수 있었다. 본 연구에서 제안한 MDP 모델은 블록의 개수와 독립적인 방식으로 상태와 행동을 정의하기 때문에 테스트 단계에서 블록 개수가 달라져도 이미 학습된 모델의 적용이 가능했다.

Set-up ratio에 대하여 강화학습 방법으로 학습한 모델을 통해 테스트한 결과와 각 dispatching rule에 의해 테스트 한 결과는 Table 7과 같다. 테스트 시나리오 1과 달리, dispatching rule 중 SSPT가 가장 작은 Set-up Ratio 결과를 보였으며, 강화학습으로 학습한 모델이 24.4%로 두 번째로 좋은 결과를 나타냈다. 반면 COVERT, MDD rule의 경우에는 전체 작업 중 절반에서 set-up이 발생하는 것을 확인할 수 있었고, 테스트 시나리오 1과 마찬가지로 투입순서를 MDD rule을 사용하여 결정한 결과, 10개 중 9개의 강재의 작업에서 set-up이 발생하는 것을 확인할 수 있었다.

Table 7

Result of set-up ratio (scenario 2)

납기 지연 측면에서 학습한 모델과 각 우선순위규칙만을 적용한 결과는 Table 8과 같다. 테스트 시나리오 1과 유사하게 강화학습으로 학습한 모델이 평균 0.02 시간의 가장 작은 tardiness 값을 나타냈고, 다음으로 ATCS rule, 그리고 COVERT rule이 작은 tardiness 값을 가졌다. 반면 SSPT rule의 경우 평균 하루 이상의 납기 지연을 나타냈다.

Table 8

Result of tardiness (scenario 2)

Makespan에 대하여 테스트 한 결과는 Table 9와 같다. 일주일 중 일요일을 제외한 작업 일정을 고려했을 때, 총 20일에 해당하는 작업 물량을 소화하는 데 필요한 기간은 SSPT rule이 가장 짧은 11일을 나타냈다. 강화학습으로 학습한 모델은 다음으로 짧은 11.54일을 보였지만 MDD rule의 경우 모든 물량을 작업하기 위해서는 평균 15일이 필요한 것으로 나타났다. 테스트 시나리오 1과 마찬가지로 set-up 시간을 고려했기 때문에 다른 우선순위규칙 대비 긴 makespan을 가진 것으로 판단된다.

Table 9

Result of makespan (scenario 2)

학습 단계와 달리, 투입순서를 결정해야 하는 블록의 개수를 세 배로 늘려 테스트를 진행한 결과, 학습과 동일한 물량을 테스트하였을 때와 유사한 결과를 나타냈다. set-up 비율과 makespan 지표에서는 SSPT가 가장 낮은 값을 보였으며, 강화학습으로 학습한 모델이 그다음으로 좋은 결과를 보였다. 납기 지연 측면에서는 강화학습으로 학습한 모델을 적용한 결과가 가장 좋은 결과를 보였으며, 타 지표에서 가장 좋은 결과를 보였던 SSPT rule의 경우 각 의사결정 시점마다 랜덤하게 dispatching rule을 선택하여 적용한 결과보다 약 5배에 해당하는 평균 26시간의 납기 지연이 발생하는 것을 확인할 수 있었다. 따라서 모든 지표를 종합적으로 고려하였을 때. 강화학습으로 학습한 모델이 납기 지연과 set-up 시간 최소화(makespan 최소화)라는 두 가지 목적을 가장 효과적으로 달성할 수 있음을 확인하였다.

7. 결 론

본 연구에서는 조선소 형강공정에서의 생산성 향상을 달성하기위한 방안으로서, 작업 시간에 있어서 변동성이 존재하는 형강공정 내 병렬 용접 라인에 대하여 보강재의 작업 순서를 결정하는 강화학습 기반의 동적 스케줄링 알고리즘을 개발하였다. 이때, 생산성 향상은 생산량 최대화와 지연 최소화라는 두 가지 측면에서 고려하였고, 각각은 다시 set-up 최소화와 tardiness 최소화라는 구체적인 목적함수로 정의하였다. 그리고 강화학습 방법론을 기반으로 두 목적을 달성할 수 있는 스케줄링 정책의 학습을 위해서 형강공정의 작업 순서 결정 문제에 대하여 trade-off 관계의 두 목적함수를 모두 고려할 수 있는 MDP 모델을 제안하였다.

개발된 알고리즘은 작업 물량이 다른 두 개의 테스트 시나리오에 대하여 우선순위규칙과의 비교를 통해 성능을 평가하였다. 결과적으로 set-up ratio, tardiness, 그리고 makespan의 세 가지 평가 지표를 종합적으로 고려했을 때, 에이전트가 학습한 스케줄링 정책이 단순히 하나의 우선순위규칙만 적용하는 것보다 생산량 최대화와 지연 최소화의 관점에서 더 좋은 성능을 보였다. 즉, 본 연구에서 제안한 MDP 모델이 set-up 최소화와 tardiness 최소화라는 두 목적함수가 적절히 균형을 이루도록 하고, 형강공정의 변화하는 상태에 따라 적응적으로 우선순위규칙을 선택하는 정책을 학습하는 것이 더욱 효과적임을 확인하였다.

다만, 본 연구에서는 모든 보강재에 대한 작업이 바로 가능하다는 가정하에 모든 작업 물량에 대한 정보가 주어진 상태에서 에이전트가 작업 순서를 결정하였다. 추후 연구에서는 작업 준비에 있어서 변동성을 고려하도록 알고리즘을 확장할 계획이다. 즉 형강공정에서는 용접 공정에 앞서 보강재를 구성하는 web과 face 강재에 대한 절단 공정이 수행되는데, 이를 확률적 분포에 따라 용접 공정에 보강재의 작업이 도착하는 형태로 모델링하여 학습 및 테스트를 진행할 예정이다. 또한 본 연구에서는 set-up 최소화와 tardiness 최소화에 해당하는 보상에 대한 가중치를 하나의 값으로 고정하고 학습을 수행하였는데, 향후에는 두 목적함수의 다양한 가중치 조합에 대하여 최적의 의사결정을 내릴 수 있도록 스케줄링 알고리즘을 개선하는 방향으로 연구를 진행할 계획이다.

Nomenclature


Bi :	블록 i (i = 1, ..., N)
n_i :	블록 i에 속한 보강재의 개수
d_i :	블록 i의 납기일 (i = 1, ..., N)
S_i_j :	블록 i에 속한 j번째 보강재(j = 1, ..., ni)
n_ij :	보강재 S_ij와 identical한 보강재의 개수
θ_ij :	보강재 S_ij의 web, face 정보
w_sij :	보강재 S_ij의 용접 두께
l_ij :	보강재 S_ij의 용접 길이
v_ij :	보강재 S_ij의 용접 속도
p_ij :	보강재 S_ij의 용접 시간

Acknowledgments

본 연구는 국방과학연구소 선도형 핵심 기술 (응용연구) 사업의 자체 개발 이산 사건 시뮬레이션 방법에 의한 소티 생성률 산출 기술 개발 및 검증 과제의 도움을 받아 수행되었습니다.

References

Chaudhry, I.A. and Elbadawi, I.A., 2017. Minimisation of total tardiness for identical parallel machine scheduling using genetic algorithm. Sādhanā, 42(1), pp.11-21. [https://doi.org/10.1007/s12046-016-0575-7]
Chen, C.L. and Chen, C.L., 2009. Hybrid metaheuristics for unrelated parallel machine scheduling with sequence-dependent setup times. The International Journal of Advanced Manufacturing Technology, 43(1), pp.161-169. [https://doi.org/10.1007/s00170-008-1692-1]
Julaiti, J., Oh, S.C., Das, D. and Kumara, S., 2022. Stochastic parallel machine scheduling using reinforcement learning. Journal of Advanced Manufacturing and Processing, 4(4), pp.e10119. [https://doi.org/10.1002/amp2.10119]
Kim, D.W., Kim, K.H., Jang, W. and Chen, F.F., 2002. Unrelated parallel machine scheduling with setup times using simulated annealing. Robotics and Computer-Integrated Manufacturing, 18(3-4), pp.223-231. [https://doi.org/10.1016/S0736-5845(02)00013-3]
Lee, C.H., 2018. A dispatching rule and a random iterated greedy metaheuristic for identical parallel machine scheduling to minimize total tardiness. International journal of production research, 56(6), pp.2292-2308. [https://doi.org/10.1080/00207543.2017.1374571]
Lee, J.H., Yu, J.M. and Lee, D.H., 2013. A tabu search algorithm for unrelated parallel machine scheduling with sequence-and machine-dependent setups: minimizing total tardiness. The International Journal of Advanced Manufacturing Technology, 69(9), pp.2081-2089. [https://doi.org/10.1007/s00170-013-5192-6]
Lee, J.W. and Kim, H.J., 1995. Erection process planning & scheduling using genetic algorithm. Journal of the Society of Naval Architects of Korea, 32(1), pp.9-16.
Paeng, B., Park, I.B. and Park, J., 2021. Deep reinforcement learning for minimizing tardiness in parallel machine scheduling with sequence dependent family setups. IEEE Access, 9, pp.101390-101401. [https://doi.org/10.1109/ACCESS.2021.3097254]
Park, J.K. and Kim, M.K., 2020. Optimization of quantity allocation using integer linear programming in shipbuilding industry. Journal of the Society of Naval Architects of Korea, 57(1), pp.45-51. [https://doi.org/10.3744/SNAK.2020.57.1.045]
Schulman, J., Wolski, F., Dhariwal, P., Radford, A. and Klimov, O., 2017. Proximal policy optimization algorithms. arXiv preprint arXiv:1707.06347, .
Son, J.R., Suh, H.W. and Ha, B.H, 2014. A heuristic algorithm for block storage planning in shipbuilding. Journal of the Society of Naval Architects of Korea, 51(3), pp.239-245. [https://doi.org/10.3744/SNAK.2014.51.3.239]
Zhang, Z., Zheng, L., Li, N., Wang, W., Zhong, S. and Hu, K., 2012. Minimizing mean weighted tardiness in unrelated parallel machine scheduling with reinforcement learning. Computers & operations research, 39(7), pp.1315-1324. [https://doi.org/10.1016/j.cor.2011.07.019]
Zhang, Z., Zheng, L. and Weng, M. X., 2007. Dynamic parallel machine scheduling with mean weighted tardiness objective by Q-Learning. The International Journal of Advanced Manufacturing Technology, 34(9), pp.968-980. [https://doi.org/10.1007/s00170-006-0662-8]

남 소 현

조 영 인

우 종 훈

Block	Section steel	Characteristics
B_i	S_i1	$n i 1, θ i 1, w s i 1, l i 1, v i 1, p - i 1 n i 1 = 5 E A, θ i 1 = 200,15,150,15 m m, w s i 1 = 4.5 m m, l i 1 = 8,800 m m, v i 1 = 1,100 m m / m i n, p - i 1 = 8 m i n$
	S_i2	$n i 2, θ i 2, w s i 2, l i 2, v i 2, p - i 2$
	…
	S_ij	$n i j, θ i j, w s i j, l i j, v i j, p - i j$

Scenario	Number of blocks
Training	80
Test scenario 1	80
Test scenario 2	240

Hyper-parameters	Value
Number of episodes E	10,000
Running horizon T	50
Optimization epoch K	5
Clipping parameter ε	0.2
Discount ratio γ	0.98
GAE parameter λ	0.95
Learning rate α	0.0005

Dispatching rule	Set-up ratio [%]
Reinforcement learning	21.3
SSPT	23.5
ATCS	31.8
COVERT	48.1
Random	49.1
MDD	90.0

Dispatching rule	Tardiness [hour]
Reinforcement learning	0.03
ATCS	0.04
COVERT	0.13
MDD	1.28
SSPT	1.68
Random	7.90

Dispatching rule	Makespan [day]
Reinforcement learning	3.07
SSPT	3.13
ATCS	3.35
Random	3.43
COVERT	3.52
MDD	4.00