Bagnold 충격수를 고려한 압축 팽창하는 갇힌 공기에 미치는 축척비 효과에 대한 상사 해석


This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
A developed code based on the unified conservation laws of incompressible/compressible fluids is applied to analyze similarity in pressure oscillations caused by pulsating air pockets in sloshing tanks. It is shown that the nondimensional time histories of pressure show good agreements under Froude and geometric similarities, provided that there are no pulsating entrapped air pockets. However, the nondimesional period of pressure oscillation due to the pulsating air pocket becomes longer as the size of the sloshing tank increases. The discrepancy in the nondimensional period is attributed to the compressibility bias of the entrapped air. To get rid of the compressibility bias, the ullage pressure in a sloshing tank is adjusted based on the Bagnold’s impact number. The variation in the period of pressure oscillation according to the ullage pressure is explained based on the spring-mass system. It is shown that the nondimensional period of pressure oscillation is virtually constant when the ullage pressure is adjusted based on the Bagnold’s impact number, regardless of tank size. It is found that the Bagold’s impact number should be the same, if the time history of pressure is important while an entrapped air pocket pulsates.
Keywords:
Bagnold’s impact number, Entrapped air pocket, Compressiblity bias, Similarity, Ullage pressure키워드:
Bagnold 충격수, 갇힌 공기, 압축성 왜곡, 상사, 얼리지 압력1. 서 론
슬로싱이나 해양구조물에 파가 부딪히는 경우와 같은 급격한 자유표면 유동에서 기체가 액체나 고체벽에 의해 고립되는 경우 유동의 Mach 수와 관계없이 갇힌 기체의 빠른 압축 팽창이 발생한다. 갇힌 기체의 압축 팽창은 주위 액체의 압력장을 변화시켜 구조물에 급격히 진동하는 유체력을 발생시킨다. 이러한 압력 진동 해석을 위해서는 액체와 기체의 대부분의 영역에서 유동이 비압축성이어도 갇힌 공기의 압축성 효과가 반드시 고려되어야 한다.
압축성 유동 해석에서 흔히 사용되는 밀도 기반 기법은 Mach 수가 낮은 경우 밀도-압력 관계식에 발생하는 수치적 경직성으로 인해 수렴에 어려움이 발생한다. 이러한 어려움을 피하고자 압축성 유동해석에 압력 기반 기법을 적용하려는 연구들이 진행 되어 왔다 (Wei et al., 2021; Sun et al., 2019). Luo et al. (2016)은 입자법에서 비압축성 및 압축성 유체에 대해 동일한 지배방정식을 적용하고 기체의 밀도를 polytropic 관계식을 이용하여 계산함으로써 에너지 방정식을 비연성 시키는 기법을 제안하였다. Shin (2020)은 격자 기반에서 비압축성/압축성 통합보존식에 대한 압력 기반 해석 기법을 개발하였다. 개발된 코드는 갇힌 관 안에서 압축 팽창하는 공기에 의한 물의 진동이나 탱크 내부 물의 자유 낙하 과정에서 탱크 바닥과 물 사이 갇힌 공기의 압축 팽창에 대한 다른 계산 결과들과의 비교를 통해 검증되었다. 액체와 고체 벽에 갇힌 기체의 압축 팽창이 짧은 주기로 인해 거의 등엔트로피 과정임을 보고하였으며 (Shin, 2019), 슬로싱 탱크 내부 갇힌 공기의 압축 팽창에 의한 압력 진동에 대한 Lugni et al. (2010)의 실험 결과와 비교하여 통합보존식 해석 결과가 좋은 일치를 보임을 보고하였다 (Shin, 2021).
슬로싱에 대한 모형 시험의 경우 탱크 크기 차이에도 불구하고 유체의 관성력과 중력의 비를 상사시키기 위해 Froude 수를 동일하게 한다. 그러나 대부분의 실험에서 탱크 내부 기체의 기준 압력은 탱크 크기에 관계없이 대기압으로 고정한다. 이러한 경우 갇힌 공기 주위 유체의 질량은 탱크 크기에 따라 급격히 변하지만 갇힌 공기의 강성은 비례해서 변하지 않기 때문에 압축성 왜곡이 발생한다. Lafeber et al. (2012)은 크기가 다른 수조에서 수면파가 수직 벽면과 충돌하는 과정에 갇힌 공기의 압축 팽창에 의한 압력 진동을 계측하였다. Froude 상사가 성립하도록 입사파의 조건을 조절하고 계측된 압력과 시간을 무차원하여 비교하였으나 수조의 크기가 큰 경우 무차원화된 압력 진동의 주기가 확연히 길어짐을 보고하였고 그 원인으로서 갇힌 공기의 압축성 왜곡을 지목하였다.
본 연구에서는 슬로싱 탱크 내부 갇힌 공기의 압축 팽창에 대해 검증된 통합보존식 해석 코드를 이용하여 탱크 크기에 따른 압력 진동의 상사에 대한 해석이 수행되었다. 기하학적 상사 및 Froude 상사가 성립하는 경우, 갇힌 공기에 의한 압축 팽창 현상의 발생 유무에 따른 무차원화된 압력의 시간 변화에 대한 상사가 검토되었다. Bagnold 충격수 (Bagnold, 1939)에 기초하여 공기의 압축 팽창 과정에서 발생하는 압력 진동 주기의 불일치가 갇힌 기체의 압축성 왜곡에 기인함을 설명하였다. Bagnold 충격수를 고려하여 탱크 내부 기준 압력, 즉 얼리지 압력을 조절한 계산을 수행하고 무차원화된 압력의 시간 변화에 대한 상사를 해석하였다.
2. 비압축성/압축성 통합보존식 해석 기법
본 연구에서 사용된 비압축성/압축성 통합보존식에 대한 압력 기반 기법은 Shin (2020)에 자세히 소개되어 있다. 지배방정식은 Newtonian 유체에 대한 질량 및 운동량 보존식이다. 질량 보존식은 수송정리에 물리량을 질량으로 대입하여 구해지며 밀도에 대한 어떠한 가정도 적용하지 않는다.
| (1) |
여기서 ρ는 밀도, ui는 속도 벡터이다.
수송정리에 물리량을 운동량으로 대입하면 밀도에 대한 가정을 사용하지 않아도 질량 보존식을 소거함으로써 속도의 전미분 항을 비압축성의 경우와 동일하게 얻는다. 다만 압축성 유체의 조성관계식(constitutive equation)에는 속도장의 발산(divergence) 항에 이차 점성계수 λ가 곱해진 항이 추가된다. 그러나 이차 점성계수 λ의 불확실성과 그 영향의 미미함으로 인해 최근의 아음속 압축성 유동 해석에서 λ는 흔히 영으로 간주 된다 (Luo et al., 2016). 이러한 경우 운동량 보존식은 비압축성 유체의 경우와 동일하다.
| (2) |
여기서 p는 압력, μ는 점성계수, gi는 중력가속도 벡터이다.
유동 영역을 비압축성과 압축성 영역으로 구분하기 위해 CLSVOF법 (Kwakkela et al., 2013; Yokoi, 2013)을 연성시켜 매질 경계면을 포착하였다.
| (3) |
여기서 α는 지시 함수(indicator function)이다 (Denner et al., 2018).
본 연구에서 압축성 영역의 밀도가 변수이기 때문에 밀도에 대한 식이 추가되지 않으면 문제가 닫히지 않는다. 비압축성 영역에서는 밀도를 초기치 ρo로 고정하고 압축성 영역에서는 압력이 갱신될 때마다 polytropic 관계식을 사용하여 밀도를 계산한다.
| (4) |
| (5) |
여기서 ρref와 pref는 기체의 기준 상태에서의 밀도와 압력이고 n는 polytropic 지수로서 기체의 압축 팽창이 등엔트로피 과정이면 비열비 γ이고 등온 과정이면 1이다. 본 연구에서는 기체 영역에서 계산되는 압력으로부터 식 (5)에서 기체의 밀도를 계산하기 때문에 기체가 거의 비압축성에 가까운 거동을 하는 경우에도 수치적 경직성에 따른 어려움이 전혀 발생하지 않는다.
압축성 영역을 포함한 전 유동 영역에서 압력 계산을 위한 Poisson 방정식을 얻기 위하여 fractional step 기법(Liu and Pletcher, 2007)이 적용되었다. 운동량 보존식 (2)에서 압력 기울기를 제외하고 중간 단계 속도 벡터 ui*를 계산하고 다음 단계에서의 압력 기울기 ∂pn+1/∂xi가 더해진 속도 벡터 uin+1이 질량 보존식을 만족하도록 요구하면 압력에 대한 Poisson 방정식이 다음과 같이 얻어진다. 이 과정에서 기체의 압축성 효과는 Poisson 방정식의 생성항에 포함된다.
| (6) |
| (7) |
| (8) |
압축성 영역에서 밀도의 전미분이 영이 아니기 때문에 식 (8)의 생성항은 압력이 갱신될 때마다 다시 계산되어야 한다. 이 과정에서 밀도의 시간 미분 항에 대해 압력의 시간 미분 항과의 관계식이 유도되고 이 항을 이항시켜 Poisson 행렬에 반영하면 압력 Poisson 행렬의 대각 요소의 절대치가 증가하기 때문에 압력장의 수렴성이 향상된다 (Shin, 2020).
지배방정식은 조밀도가 조절된 배후 Cartesian 격자계에서 이산화 되었다. 시간 전진에 대한 안정성 확보를 위해 매 시간 단계마다 국소 Courant 수의 최대치가 일정한 값이 되도록 시간 간격 ∆t가 조절되었다. 이러한 방법은 본 연구에서와 같이 안정성 확보를 위한 시간 간격 ∆t에 대한 요구가 계산 과정 동안 대단히 크게 변화하는 경우 중요한 장점을 제공한다. 대류항 계산에는 5차의 WENO 기법 (Wang et al., 2018; Zhu and Qiu, 2016)이 적용되었으며 점성항 계산에는 2차의 중앙차분이 적용되었다. 매질 경계면에서 발생하는 비물리적인 압력 진동을 억제하기 위해 밀도의 역수를 가중치로 하는 요소 평균 밀도가 계산되었다(Shin, 2020).
3. 슬로싱 탱크 크기에 따른 공기 완충 효과 특성
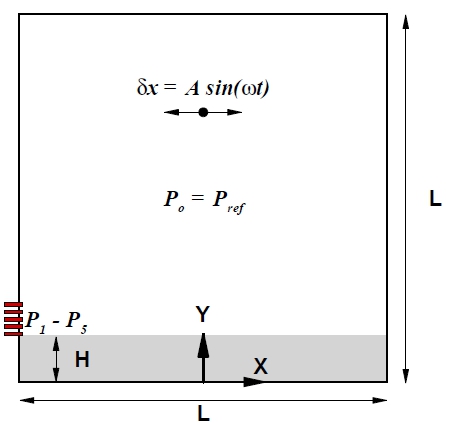
개발된 비압축성/압축성 통합보존식 해석 코드를 이용하여 슬로싱 탱크 크기에 따른 공기 완충 효과 특성이 해석되었다. Fig. 1은 이 문제에 대한 개략도이다. 이 문제에 대해서는 슬로싱 유동 중 갇힌 공기의 압축 팽창에 의한 압력 진동에 대한 실험 결과 (Lugni et al., 2010)와 여러 계산 결과들이 보고되어 있다. 탱크는 폭과 높이가 모두 L인 정사각형 탱크이며 탱크 내부에 수심 H의 물이 채워져 있으며 물 위의 기체는 공기이다.
탱크의 길이 L은 0.5, 0.75, 1, 1.5, 2 m 등으로 변화시켰으며 모든 경우에 H/L은 0.125로 주어졌다. 탱크는 진폭 A, 각속도 ω로 Asin(ωt)의 좌우동요를 하며 A/L = 0.03이다. Froude 상사를 만족시키기 위해 Aω/(gH)1/2가 0.1064가 되도록 각속도 ω를 조절하였다. 좌표계의 원점은 탱크 바닥의 중앙에 위치한다. 탱크의 좌측 벽면에 바닥으로부터 높이 Y/L이 0.13, 0.15, 0.17, 0,19, 0.21인 위치에서 압력의 시간 변화가 기록되었다.
중력가속도 g는 9.81 m/s2으로 주어졌다. 물의 밀도 ρ는 1000 kg/m3으로 고정되었다. 공기의 경우 초기 밀도는 1.2 kg/m3로 주어졌으며 이후 계산되는 압력으로부터 polytropic 관계식을 사용하여 계산되었다. 기체의 거동은 비열비 γ가 1.4인 등엔트로피 과정이 가정되었다 (Shin, 2019). 동점성계수 ν는 물과 공기에서 각각 1×10-6, 1.5×10-5 m2/s로 주어졌다. 탱크 내부에 400×400개의 격자가 배치되었으며 시간 간격 ∆t는 국소 Courant 수의 최대치가 0.5가 되도록 매 시간 단계마다 조절되었다.
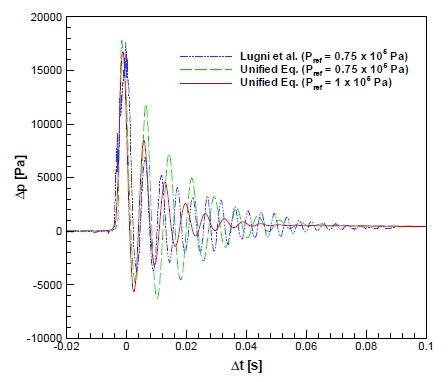
얼리지 압력 Pref은 1×105 Pa을 기준으로 하고 다음 절에서 설명되듯이 Bagnold 충격수를 고려하여 0.5×105 ~ 2×105 Pa로 변화시킨 경우에 대한 계산 결과도 비교하였다. 탱크 크기 L이 1 m 인 경우는 Lugni et al. (2010)의 슬로싱 탱크 내부 갇힌 공기의 압축 팽창에 대한 실험 결과가 보고된 경우와 얼리지 압력을 제외한 모든 조건이 동일하다. Fig. 2는 얼리지 압력이 0.75×105 Pa인 경우에 대한 실험 결과 (Lugni et al., 2010)와 통합보존식 해석 코드를 이용한 계산 결과 (Shin, 2021) 및 본 연구에서 기준 압력으로 고려되는 1×105 Pa인 경우에 대해 Y/L = 0.19에서 계산된 압력의 시간 변화에 대한 비교를 보여준다. 얼리지 압력이 다른 두 계산의 경우 계산된 압력 진동 주기에 차이가 있음을 관찰할 수 있다. 본 연구에서 사용된 통합보존식 해석 코드의 격자나 시간 간격 등의 수치 인자에 대한 수렴성은 Shin (2020)에 자세히 보고되어 있으며, Shin (2021)에서는 본 연구와 유사한 슬로싱 유동에서 갇힌 공기의 압축 팽창에 대한 격자 수렴성이 보고되었다. 시간 간격의 경우 기체 영역에서 국소 Courant 수 제한 만족을 위해 요구되는 시간 간격이 대단히 작아서 한 주기의 압력 진동 동안 300회 이상의 시간 단계가 포함됨이 보고되었다.
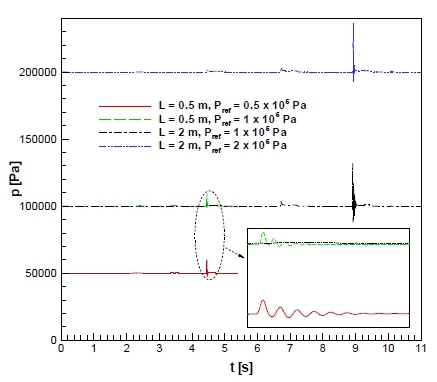
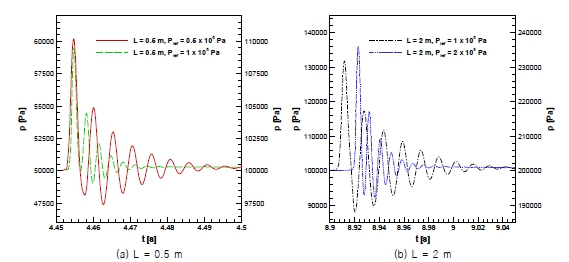
Fig. 3은 탱크 크기가 0.5 m와 2 m인 경우에 대해 Froude 상사만 성립하고 얼리지 압력은 1×105 Pa로 고정한 경우와 Bagnold 충격수가 일치하도록 얼리지 압력을 변화 시킨 경우들에 대해 Y/L = 0.19에서 계산된 압력의 시간 변화를 보여준다. 수심 H, 좌우동요 진폭 A, 압력 계측점 위치 등은 기하학적 상사가 성립하도록 결정되며, Froude 상사는 Aω/(gH)1/2가 0.1064가 되도록 좌우동요 주기 ω를 탱크 크기에 따라 조절하여 성립시킨다. Bagnold 충격수를 고려하여 얼리지 압력을 조절하는 경우 다음 절에서 설명되듯이 얼리지 압력이 탱크 크기에 비례해서 커져야 하므로 각각의 탱크에서 얼리지 압력을 0.5×105 Pa 또는 2×105 Pa로 변화시켰다. 그림에서 큰 압력 진동이 발생하는 시간이 슬로싱 유동에서 공기가 갇히면서 압축 팽창하는 시간이다.
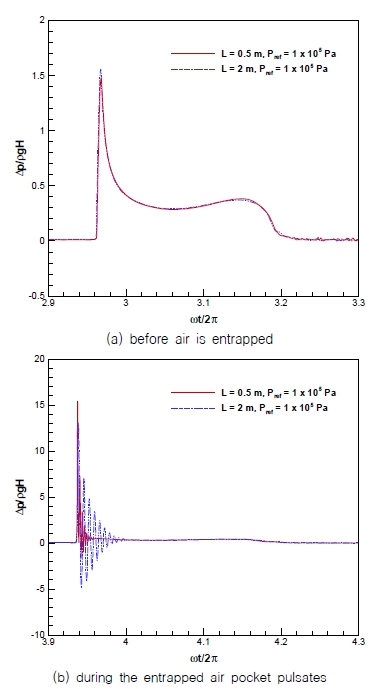
Fig. 4는 탱크의 크기 L이 0.5와 2 m인 경우 얼리지 압력을 1×105 Pa로 동일하게 하여 Y/L = 0.19에서 계산된 무차원화된 시간에 따른 압력 변화 비교를 보여준다. 시간 t에 대해서는 탱크의 좌우동요 주기 ω를 이용하여 ωt/2π로 무차원화 하였다. 이 경우 시간 축에서 1의 간격은 탱크의 크기와 관계없이 좌우동요가 1회 완료되는 시간 간격에 해당한다. 압력의 경우 압력 변화량 ∆p를 정지 상태에서 탱크 바닥에 작용하는 정수력학적 압력 ρgH로 무차원화 하였다. Fig. 4(a)의 경우는 갇힌 공기의 압축 팽창이 시작되기 직전 주기로서 기하학적 상사와 Froude 상사가 성립하는 경우 무차원화된 압력의 시간 변화가 좋은 일치를 보임을 확인할 수 있다. Fig. 4(b)는 Fig. 4(a)에 비해 좌우동요가 한 주기 더 진행되어 탱크 벽에 물이 충돌하는 과정에서 공기가 갇히면서 압축 팽창이 발생하는 시간 동안의 비교이다. Fig. 4(a)와 동일하게 시간 및 압력 변화량을 무차원화 하였으나 갇힌 공기의 압축 팽창이 발생하면 압력 진동 주기에 확연한 차이가 발생하며 큰 탱크에서 무차원화된 압력 진동 주기가 훨씬 길어진다. 이러한 계산 결과는 Lafeber et al. (2012)의 크기가 다른 수조에서 Froude 상사가 만족되도록 조파기를 조절한 수면파-수직벽 충돌 실험에서 계측된 무차원화된 압력 진동 비교 결과와 부합한다.
4. Bagnold 충격수를 고려한 얼리지 압력 조절
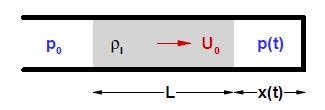
모형의 크기에 따라 Froude 상사가 성립하더라도 갇힌 공기의 압축 팽창이 발생하면 무차원화된 압력 진동 주기에 차이가 발생하는 원인은 압축성 왜곡이 발생하기 때문으로 생각되고 있다 (Lafeber et al., 2012). 가두어진 공기의 압축성 왜곡은 Fig. 5에 보인 Bagnold의 1차원 피스톤 모형으로 설명될 수 있다. 이 문제에서는 초기에 길이 xo의 기체가 실린더 벽에 가두어져 있으며 길이 L의 액체에 의해 밀리면서 압축 팽창이 시작된다. 기체의 초기 압력은 액체 외부의 고정된 압력 po와 동일하다. 액체의 밀도는 ρl로 고정되어 있으며 초기 속도 Uo로 기체를 압축시킨다. 이 문제에서 기체는 준평형 상태로 가정되어 기체 내부 압력의 공간상 변화는 무시된다. 무차원화된 시간 t* = Uot/xo에 대한 무차원화된 압력 p* = p/po는 다음과 같이 정의되는 Bagnold 충격수(impact number) S에 의해 결정된다.
| (9) |
충격수가 큰 경우는 기체의 압축 팽창에 따른 위치 에너지에 비해 액체의 운동 에너지가 지배적인 경우로서 급격한 충돌에 해당한다. 크기가 다른 슬로싱 탱크에서 Froude 상사가 성립하는 경우 갇힌 기체 주위의 자유표면이 축척비 대로 유사하게 형성된다면 L/xo은 유사한 값이 유지될 수 있다. 그러나 Froude 상사가 성립하는 경우 ρlUo2는 탱크 크기에 비례하여 커진다. 따라서 슬로싱 탱크의 얼리지 압력에 해당하는 po가 탱크 크기에 관계 없이 일정한 경우에는 탱크 크기에 비례해서 충격수가 커진다. 충격수가 크면 액체의 운동 에너지가 기체의 위치 에너지에 비해 지배적이며 진동 주기는 길어진다. Froude 상사가 성립하는 경우 ρlUo2/po를 일정하게 하기 위해서는 얼리지 압력을 탱크 크기에 비례해서 조절하여야만 동일한 충격수를 유지할 수 있다.
얼리지 압력의 감소는 polytropic 관계식 (5)로부터 동일한 밀도 변화에 의해 발생하는 압력 변화량의 감소를 의미하며 이는 질량-스프링 계에서 강성의 감소를 의미한다. 작은 탱크에서 얼리지 압력의 감소는 주위 액체의 부가질량 감소에 비례하여 갇힌 기체의 강성을 낮추는 효과를 가져옴으로써 작은 모형에서의 압력 진동 주기의 감소를 방지할 수 있다.
탱크 크기에 따라 Bagnold 충격수를 고려하여 얼리지 압력을 조절한 경우에 대한 계산을 수행하였다. 전절의 경우와 동일하게 탱크 크기의 변화에도 기하학적 상사 및 Froude 상사가 만족되도록 조건들을 유지하였으며 추가적으로 얼리지 압력만 탱크 크기에 비례해서 조절하였다.
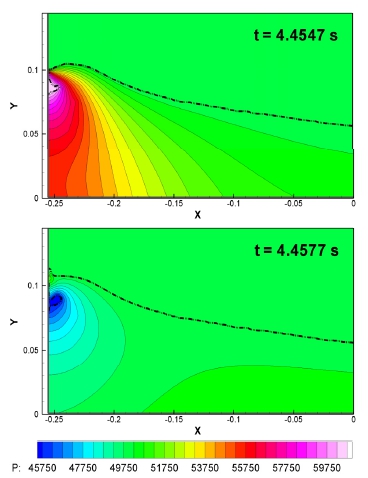
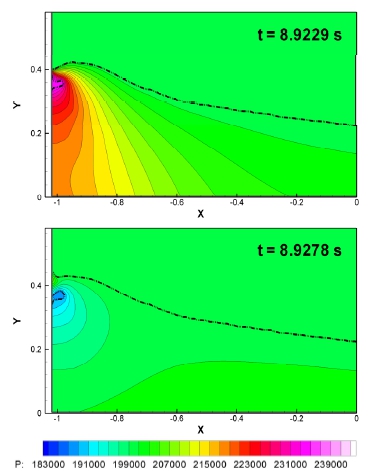
Fig. 6-7은 탱크 크기 L = 0.5, 2 m에 대해 얼리지 압력 Pref = 0.5×105, 2×105 Pa 로 조절한 경우 갇힌 공기 주위의 압력 분포를 보여준다. 위의 그림은 갇힌 공기가 압축되면서 압력 최대치가 발생하는 순간의 압력장이며 아래 그림은 압축된 공기가 팽창하면서 압력의 최소치가 발생하는 순간의 압력장이다. 갇힌 공기 내부 압력은 시간에 따라 급격히 변하지만 공기의 밀도가 물에 비해 대단히 작아서 갇힌 공기 내부 압력의 공간상 변화는 미미함을 관찰할 수 있다. 그러나 갇힌 공기의 압축 팽창은 주위 물의 압력도 급격히 변화시킨다. 물의 밀도가 크기 때문에 물에서의 압력 기울기는 대단히 가파르다. 외부 공기와 접하는 자유표면 방향으로는 시간에 따라 변화가 없이 얼리지 압력이 회복되도록 급격한 압력 기울기가 발생함을 관찰할 수 있다. 탱크의 크기나 얼리지 압력은 4배 차이가 나지만 갇힌 공기와 주위 자유표면 형상이나 압력장의 특성이 거의 유사함을 관찰할 수 있다.
Fig. 8은 탱크 크기 L = 0.5, 1, 2 m에서 얼리지 압력 Pref = 0.5×105, 1×105, 2×105 Pa인 경우에 대해 갇힌 공기의 첫 번째 최대 팽창이 발생하는 순간의 자유표면들의 비교를 보여준다. 탱크의 크기와 무관하게 축척비에 따라 거의 유사한 형태가 유지됨을 관찰할 수 있다.
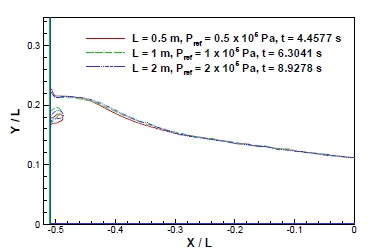
Comparison of calculated free surface at the moment the entrapped air pocket expands; L = 0.5, 1, 2 m, Pref = 0.5×105, 1×105, 2×105 Pa
Fig. 9는 탱크 크기 L = 0.5, 2 m의 경우에 대해 얼리지 압력만 Bagnold 충격수를 고려하여 변화시킨 경우에 계산된 압력의 시간 변화 비교를 보여준다. L = 0.5 m의 경우 기준치 Pref = 1×105 Pa 에서 Pref = 0.5×105 Pa로 낮아지면서 압력 진동 주기가 확연히 길어진다. 반대로 L = 2 m의 경우 기준치 Pref = 1×105 Pa 에서 Pref = 2×105 Pa로 높아지면서 압력 진동 주기가 짧아진다.
Fig. 10은 탱크 크기 L = 0.5, 2 m에서 얼리지 압력을 Pref = 0.5×105, 2×105 Pa로 변화시킨 경우에 대해 Y/L = 0.19에서 계산된 압력의 시간 변화를 무차원화하여 비교한 결과를 보여준다. 기하학적 상사와 Froude 상사는 만족시켰으나 얼리지 압력을 1×105 Pa로 고정했던 Fig. 4(b)와 달리 가두어진 공기의 압축 팽창이 발생하는 시간 동안에도 무차원화된 압력의 시간 변화가 거의 유사함을 확인할 수 있다.
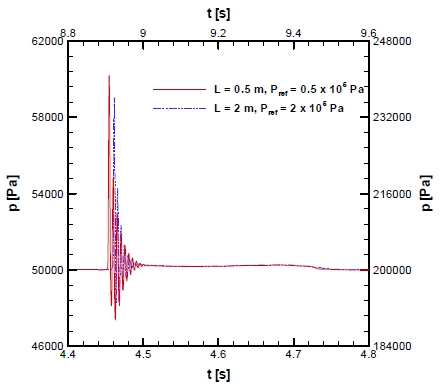
Comparison of time histories of pressure at Y/L = 0.19; L = 0.5 m, Pref = 0.5×105 Pa and L = 2 m, Pref = 2×105 Pa
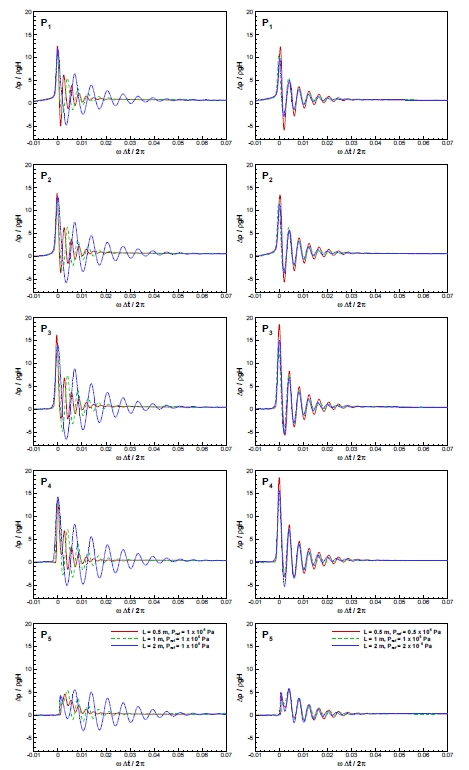
Fig. 11은 탱크 크기 L = 0.5, 1, 2 m의 경우에 대해 얼리지 압력을 1×105 Pa로 고정한 경우(좌측)와 탱크 크기에 따라 0.5×105, 1×105, 2×105 Pa로 변화시킨 경우(우측)에 대해 Y/L = 0.13, 0.15, 0.17, 0.19, 0.21의 5개의 압력 계측점에서 계산된 압력의 시간 변화의 비교를 보여준다. 가로축은 첫 번째 압력 최대치가 발생하는 시점으로부터의 경과 시간 ∆t에 대해 탱크의 좌우동요 주기 ω를 이용하여 ω∆t/2π로 무차원화하였으며 세로축은 압력 변화량 ∆p를 정지 상태에서 탱크 바닥에 작용하는 정수력학적 압력 ρgH로 무차원화하였다. 얼리지 압력을 1×105 Pa로 고정한 경우 압력 계측점에서 계산된 무차원화된 압력의 시간 변화가 5개의 계측점 모두에서 탱크의 크기가 커지면 압력 진동 주기가 확연히 길어졌다. 그러나 얼리지 압력을 Bagnold 충격수를 고려하여 탱크 크기에 비례해서 조절한 경우는 모든 압력 계측점에서 거의 일치하는 결과를 보인다.
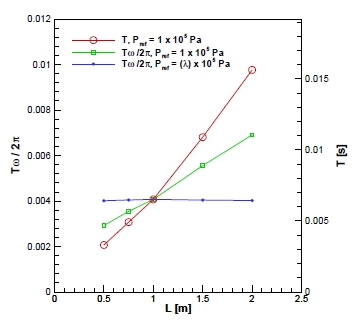
Fig. 12와 Table 1은 탱크 크기에 따라 계산된 압력 진동 주기의 변화를 보여준다. 탱크 크기 L = 0.5, 0.75, 1, 1.5, 2 m의 경우에 대해 얼리지 압력을 1×105 Pa로 고정한 경우와 Bagnold 충격수를 고려하여 탱크 크기에 따라 얼리지 압력을 변화시킨 경우를 비교하였다. 적색 원은 얼리지 압력을 1×105 Pa로 고정한 경우 계산된 진동 주기를 실제 초 단위(우측 축)로 비교한 결과이며 녹색 사각형은 주기 T를 Tω/2π(좌측 축)로 무차원화하여 비교한 결과이다. 청색 마름모는 얼리지 압력을 Bagnold 충격수를 고려하여 변화시킨 경우 계산된 주기를 무차원화하여 비교한 결과이다. 얼리지 압력을 고정한 경우 압력 진동 주기는 탱크 크기에 따라 0.0033 s에서 0.0156 s까지 약 4.7배의 변화가 발생하였으며 무차원화한 경우도 약 2.4배의 차이가 나타났다. 그러나 얼리지 압력을 변화시키고 계산된 진동 주기를 무차원화한 경우에는 0.00402 ~ 0.00408의 범위 내의 주기가 예측되어 변화 폭이 약 1.5% 이내 임을 확인하였다.
5. 결 론
슬로싱 탱크 내부 갇힌 공기의 압축 팽창에 대한 실험 결과와의 비교를 통해 검증된 비압축성/압축성 통합보존식 해석 코드를 이용하여 탱크 크기에 따른 압력 진동 주기에 대한 상사가 해석되었다.
기하학적 상사와 Forude 상사가 성립하는 경우 무차원화된 압력의 시간 변화는 공기가 갇히면서 압축 팽창하기 전까지는 탱크 크기에 무관하게 일치하였다.
얼리지 압력을 고정한 경우에는 갇힌 공기의 압축 팽창이 발생하면 무차원화된 압력 진동 주기가 탱크 크기가 커짐에 따라 길어짐을 확인하였으며 그 이유는 갇힌 기체의 강성이 주위 액체에 의한 부가질량 증가에 비례해서 증가하지 않기 때문으로 해석되었다.
슬로싱 탱크 크기가 4배 차이가 나는 경우 Froude 상사가 만족되어도 얼리지 압력을 고정한 경우는 약 2.4배의 무차원화된 압력 진동 주기의 차이가 발생하였으나 Bagnold 충격수를 고려하여 얼리지 압력을 변화시킨 경우에는 그 차이가 1.5% 이내 임을 확인하였다.
갇힌 공기의 압축 팽창이 발생하는 동안 압력의 시간 변화가 중요한 경우에는 기하학적 상사와 Froude 상사 외에도 Bagnold 충격수에 대한 고려가 필요함을 확인하였다.
Acknowledgments
이 논문은 부경대학교 자율창의학술연구비(2023년)에 의하여 연구되었음.
References
-
Bagnold, R., 1939. Interim report on wave-pressure research. Journal of the Institution of Civil Engineers, 12, pp.202-226.
[https://doi.org/10.1680/ijoti.1939.14539]

-
Denner, F. Xiao, C.N. and Wachem, B.G.M., 2018. Pressure-based algorithm for compressible interfacial flows with acoustically-conservative interface discretization. Journal of Computational Physics, 367, pp.192-234.
[https://doi.org/10.1016/j.jcp.2018.04.028]

-
Kwakkela, M. Breugema, W.P. and Boersma, B.J., 2013. Extension of a CLSVOF method for droplet-laden flows with a coalescence/breakup model. Journal of Computational Physics, 253, pp.166-188.
[https://doi.org/10.1016/j.jcp.2013.07.005]

- Lafeber, W. Brosset, L. and Bogaert, H., 2012. Comparison of wave impact tests at large and full scale: results from the sloshel project. Proceedings of the Twenty-second International Offshore and Polar Engineering Conference, Rhodes, Greece, 17-22 June 2012.
-
Liu, K. and Pletcher, R.H., 2007. A fractional step method for solving the compressible Navier-Stokes equations. Journal of Computational Physics, 226(2), pp.1930-1951.
[https://doi.org/10.1016/j.jcp.2007.06.026]

-
Lugni, C. Brocchini, M. and Faltinsen, O.M., 2010. Evolution of the air cavity during a depressurized wave impact. II. The dynamic field. Physics of Fluids, 22, 056102.
[https://doi.org/10.1063/1.3409491]

-
Luo, M. Koh, C.G. Bai, W. and Gao, M., 2016. A particle method for two-phase flows with compressible air pocket. International Journal for Numerical Methods in Engineering, 108(7), pp.695-721.
[https://doi.org/10.1002/nme.5230]

-
Shin, S., 2019. Variation in air cushion effects caused by isentropic and isothermal processes of entrapped air in incompressible free surface flows. Journal of Computational Fluids Engineering, 24(3), pp.76-83.
[https://doi.org/10.6112/kscfe.2019.24.3.076]

-
Shin, S., 2020. Simulation of compressibility of entrapped air in an incompressible free surface flow using a pressure-based method for unified equations. International Journal for Numerical Methods in Fluids, 92(10), pp.1274-1289.
[https://doi.org/10.1002/fld.4827]

-
Shin, S., 2021. Simulation of a pulsating air pocket in a sloshing tank using unified conservation laws and HCIB method. Journal of the Society of Naval Architects of Korea, 58(5), pp.271-280.
[https://doi.org/10.3744/SNAK.2021.58.5.271]

-
Sun, H. Sun, Z. Liang, S. and Zhao, X., 2019. Numerical study of air compressibility effects in breaking wave impacts using a CIP-based model. Ocean Engineering, 174, pp.159-168.
[https://doi.org/10.1016/j.oceaneng.2019.01.050]

-
Wang, B.S. Li, P. Gao, Z. and Don, W.S., 2018. An improved fifth order alternative WENO-Z finite difference scheme for hyperbolic conservation laws. Journal of Computational Physics, 374, pp.469-477.
[https://doi.org/10.1016/j.jcp.2018.07.052]

-
Wei, Z. Jiang, Q. and Nie, S., 2021. A pressure‐based numerical scheme for compressible–incompressible two‐phase flows. International Journal for Numerical Methods in Fluids, 93(11), pp.3215-3230.
[https://doi.org/10.1002/fld.5029]

-
Yokoi, K., 2013. A practical numerical framework for free surface flows based on CLSVOF method, multi-moment methods and density-scaled CSF model: numerical simulations of droplet splashing. Journal of Computational Physics, 232, pp.252-271.
[https://doi.org/10.1016/j.jcp.2012.08.034]

-
Zhu, J. and Qiu, J., 2016. A new fifth order finite difference WENO scheme for solving hyperbolic conservation laws. Journal of Computational Physics, 318, pp.110-121.
[https://doi.org/10.1016/j.jcp.2016.05.010]