구동기 비선형 모델을 이용한 워터제트 추진 무인수상정의 조이스틱기반 이접안 제어 알고리즘
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Unmanned Surface Vehicle (USV)’s berthing and unberthing is the most difficult maneuvering tasks and have the highest risk of accidents. In this paper, we designed a berthing/unberthing control algorithm given human joystick command for an USV equipped with a waterjet and a bow thruster. The berthing and unberthing maneuvers are performed remotely by a joystick operator at the Ground Control Center (GCC) where the status of USV and environmental situation can be monitored. We interpret the human joystick commands into USV’s desired speed, yaw rate, and heading angle commands. next, we developed a control algorithm for the desired target values of MIMO actuators (engine speed, bucket step, nozzle angle, and bow thruster state) to follow the interpreted commands. The validity of the control algorithm is confirmed through simulations and sea trials at Gwang Am port.
Keywords:
Warterjet, Unmanned Surface Vehicle(USV), Berthing and unberthing, Multi Input Multi Output(MIMO), Remote control키워드:
워터제트, 무인수상정, 이접안, 다중 입력 다중 출력, 원격 조종1. 서 론
최근 자율운항 무인선을 통한 실질적인 운용 소요가 증가하고 있다. 또한 항만 물동량 증가로 인해 운항하는 선박이 증가하는 추세이다. 이에 따라 많은 선박이 제한된 항만 내에서 이접안을 하고 있는데, 무인선도 이러한 복잡한 항만 환경에서 안전하게 이접안 할 필요가 있다. 최근 이러한 문제에 대한 대책으로 자율 이접안이나, 선박 운항자가 항만에 설치되어 있는 선박과 부두와의 거리정보 센서와 원격 조종기를 이용하여 이접안을 수행하는 시스템에 대한 연구 (Yamato et al., 1992; Hasegawa and Kitera, 1993; Im and Hasegawa, 2002)가 활발히 진행되고 있다.
선박의 이접안은 전체 항해 중 난이도가 높은 항해로 사고 위험도도 가장 높아 선장의 오랜 경험과 높은 숙련도를 요구하는 조종이다. 따라서 대부분의 선박은 경험 많은 도선사와 예선의 도움을 받아 이접안하고 있다. 그러나 예선 사용 비용이 크므로 일부 선박들은 경비를 줄이기 위하여 쓰러스터 같은 보조 장치를 장착하고 이를 활용하여 자력으로 이접안하기도 한다. 선원이 승선하지 않은 무인수상정에 있어서 이접안 조종은 원격/자율제어로 수행해야 하므로 더욱 어려운 문제라고 할 수 있다.
본 연구에서는 워터제트 추진기와 선수 추진기를 장착한 무인수상정의 원격 이접안 조종을 위한 MIMO(Multi Input Multi Output) 제어기를 개발하였다. 기존의 MIMO 시스템에 대한 비선형 제어 알고리즘을 이용한 연구로는 Slotine and Li, 1991; Fossen, 1999; Fossen, 2002가 있다. 비선형 (Slotine and Li, 1991) 제어의 장점은 선박에 작용하는 비선형 유체력을 효과적으로 상쇄하여 정밀한 제어가 가능하다는 점이지만, 실제 선박에 작용하는 비선형 유체력을 정확히 모델링하는 어려움 때문에 실제 효과는 많지 않을 수 있다. 따라서 통상 PID(Proportional Intergral and Derivative) 제어를 사용하거나, 알고리즘에 외란 관측기 (Aschemann et al., 2016)와 같은 외란 보상 알고리즘들을 추가하여 실제 선박제어에 적용할 수 있다.
조이스틱을 이용한 선박의 이접안 제어에 대해 프로펠러와 타를 가지는 선박을 이용해 수행된 연구 (Hong et al., 2007)가 있다.
무인수상정을 원격으로 제어하기 위해 조이스틱을 사용하여 무인수상정 운용자가 원하는 전진 방향 속도(u), 횡 방향 속도(v), 선회 각속도(r), 선수 각(heading)을 명령할 수 있도록 하였다. PID 제어를 기반으로 하고 워터제트 추진 구동기의 비선형 추력 모델을 이용한 제어기를 설계하였다. 설계된 제어기가 속도 및 선수 각을 유지할 수 있도록 알고리즘을 구성하였고, MATLAB과 Unity 시뮬레이션 프로그램을 통해 실제 무인수상정에서의 동작을 예측하고 분석하여 알고리즘을 사전 검증하였다. 그 후 실제 무인수상정에 적용하여 검증하였다.
2. 무인수상정 구동부 시스템
2.1 무인수상정 구조
본 연구에 사용된 무인선은 선박해양플랜트연구소(KRISO)의 아라곤 3호이다. 주 추진기는 워터제트이며, 보조 추진기로 선수의 방향을 제어할 수 있는 선수 추진기가 탑재되어있다. 제어할 수 있는 구동부는 워터제트 이중역전버켓과 노즐각, 엔진 RPM, 선수 추진기의 ON/OFF가 있다. 아라곤 3호의 사양은 Table 1과 같고 무인수상정의 실제 모습은 Fig. 1과 같다. 워터제트 구동부의 버켓과 노즐, 선수 추진기는 Fig. 2와 같이 구성되어 있다.
아라곤 3호의 모델 특성은 선박해양플랜트연구소에서 다음과 같은 실험을 통해 도출하였다. 우선 버켓 시험은 RPM을 고정한 뒤, 각각의 버켓 단수에 따른 추력과 노즐 각에 따른 속도 및 선회 각속도 계측을 하였다. 선수 추진기의 경우, 양쪽으로 번갈아 가며 구동시켜 선회 각속도를 계측하였다. 또한 지그재그 및 선회시험 등을 통해 구동부의 추력에 대한 선박의 동역학적 모델을 도출하였다.
2.2 무인수상정 워터제트 구동부
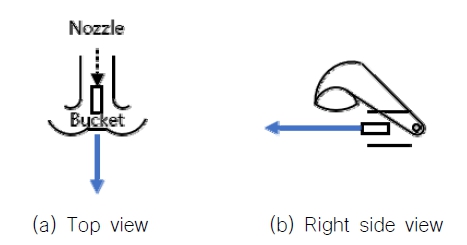
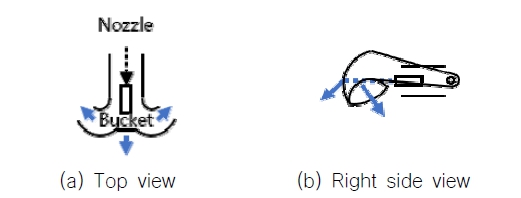
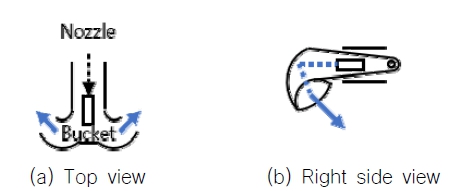
아라곤 3호의 경우, 워터제트 이중역전버켓의 단수에 따라 추력의 방향과 낼 수 있는 범위가 변화하게 된다. 워터제트의 출력 구조는 Figs. 3-5와 같다. 아라곤 3호의 버켓 단수의 경우 1 ~ 19단으로 나뉘어 있다. 19단은 완전히 열린 상태 10단은 중립 상태이고, 1단은 완전히 닫힌 상태이다. Fig. 3은 19단의 예시로 완전히 열린 상태에서의 출력을 도식화 한 것이다. 버켓이 완전히 열린 경우, 엔진의 프로펠러를 통해 노즐로 나온 물줄기가 온전히 배를 앞으로 미는 힘으로 작용한다. Fig. 4는 10단의 예시로 중립 상태에서의 출력을 도식화 한 것이다. 버켓이 중립 상태일 경우 버켓에 의해 물줄기가 세 갈래로 나뉘고 힘의 평형을 이루게 되어 0N의 추력을 가지게 된다. Fig. 5는 1단의 예시로 완전히 닫힌 상태에서의 출력을 도식화 한 것이다. 버켓이 완전히 닫힌 경우, 출력된 물줄기가 모두 버켓을 통해 방향이 바뀌어 후진 방향으로 추력을 가지게 된다. 아라곤 3호의 이중역전버켓의 단수(step)와 엔진 RPM에 따른 각각의 추력(TP)은 ‘5.1 전진 방향 속도 제어기 구조’의 Fig. 12를 참고한다.
노즐의 각도를 변경하면 물줄기의 방향이 바뀌게 된다. 바뀐 물줄기의 방향은 선박 추력의 방향을 바꾸게 되고 회전 모멘트를 발생시킨다. 때문에, 노즐의 각도는 선수가 회전할 수 있도록 하여 선수 각속도와 선수 각을 제어할 수 있도록 한다.
2.3 워터제트 구동부 추력 모델
아라곤 3호의 모델 특성은 선박해양플랜트연구소에서 다음과 같은 실험을 통해 도출하였다. 우선 버켓 시험은 RPM을 고정한 뒤, 각각의 버켓 단수에 따른 추력과 노즐 각에 따른 속도 및 선회 각속도 계측을 하였다. 선수 추진기의 경우, 양쪽으로 번갈아 가며 구동시켜 선회 각속도를 계측하였다. 또한 지그재그 및 선회시험 등을 통해 구동부의 추력에 대한 선박의 동역학적 모델을 도출하였다.
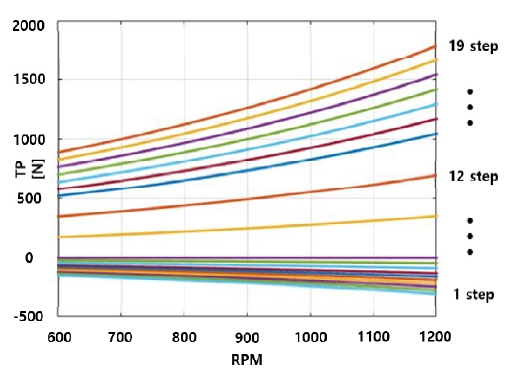
그 결과 엔진 RPM에 의한 추력(TP_RPM)은 식 (1)과 같이 도출되었다. Table 2는 버켓 단수에 따른 추력 비율(Ratiobk_step)이다. 워터제트에 의한 최종 추력(TP)은 식 (2)와 같이 TP_RPM와 Ratiobk_step를 곱한 결과이다. 이 최종 추력 TP의 식을 이용해 각 단수에서의 RPM - TP 그래프를 나타낸 것이 Fig. 6이다.
| (1) |
| (2) |
3. 선박 비선형 운동 방정식
제어 알고리즘 설계 시 알고리즘 성능 실험에 앞서 시뮬레이션으로 알고리즘을 검증하기 위해 무인수상정의 비선형 운동 방정식을 도출하였다 (Yoon and Kim, 2005; Won et al., 2006; Hong et al., 2007).
시뮬레이션 검증 없이 제어 알고리즘을 바로 실선에 구현 실험하는 것은 많은 시행착오 및 실험 시간을 요하므로 시뮬레이션 과정은 필수적이다.
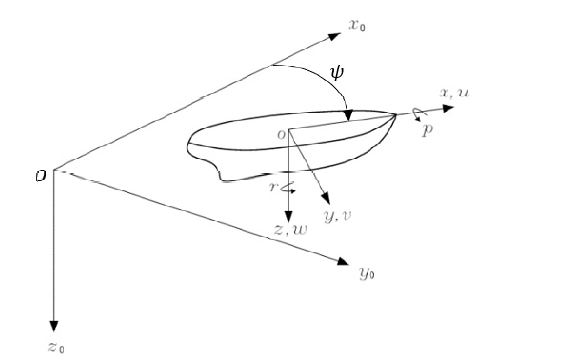
선박의 운동 방정식 기술을 위한 좌표계는 Fig. 7와 같이 정의한다. 선박은 일반적으로 6자유도 운동을 하지만 이접안 문제에서는 간단하게 3자유도 운동으로 선박의 Surge, Sway 그리고 Yaw 운동만을 고려해도 충분하다. 이러한 경우, 전진 방향 속도와 횡 방향 속도, 각속도는 식 (3) ~ (5), 추력기에 의한 미분방정 식 및 관성 모멘트는 식 (6) ~ (8)과 같이 나타낼 수 있다. 식 (3), (4) 및 (5)는 모든 선박에 적용될 수 있는 운동 방정식이며, 식 (6), (7) 및 (8)은 동역학 방정식이다. 여기서 x0, y0, z0는 Surge, Sway와 Yaw 방향의 공간 변위 좌표계이다. 또한 u, v, r은 같은 방향의 공간 속도 좌표계이다. Ψ는 선박의 선수 각이다.
| (3) |
| (4) |
| (5) |
위와 같은 좌표계 정의에 의하여, 선박 동역학 방정식은 다음 식 (6) ~ (8)과 같다. 여기서 XH, YH, NH는 선체 주위의 유체에 의해 작용하는 유체력이다. XR, YR, NR은 노즐 각(δ)의 변화로 인해 발생하는 워터제트에 의한 각 방향으로의 힘 또는 모멘트이다. 또한 XP는 주 추진기인 워터제트에 의한 힘이며, YT, NT는 선수 추력기에 의한 힘을 의미한다. 여기서 m은 선박의 질량, Izz는 선박의 z축에 대한 관성 모멘트 그리고 xG는 선박의 무게중심으로부터의 x축 거리이다.
| (6) |
| (7) |
| (8) |
4. 무인수상정 제어 시스템 구조
4.1 조이스틱 명령
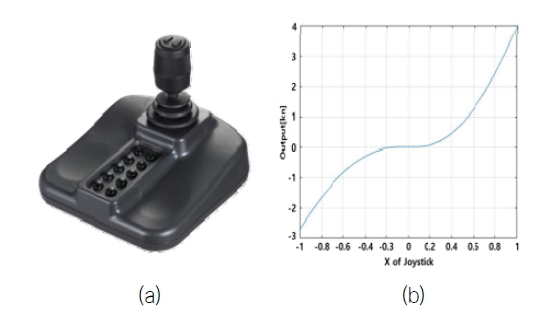
본 연구에서 사용한 조이스틱은 Fig. 8(a)와 같다. 여기서 X는 전진 방향(surge) 명령, Y는 횡 방향(sway) 명령이고, Z는 선회방향(yaw) 회전 명령을 줄 수 있다.
조이스틱 명령의 경우, -1024~1023으로 출력되는 값을 –1~1로 정규화 하였다. 그 후, 중립의 위치에서 사람의 손 떨림 및 노이즈를 방지하기 위해 deadzone을 설정하였다. –0.1~0.1(10%)의 값에 대하여 deadzone으로써 0의 값으로 인식하도록 하였다. 또한 배의 진행 방향에 대한 조이스틱 X 방향 값의 경우, 저속 구간에서의 제어를 용이하도록 하기 위해 2차식을 이용하여 Fig. 8(b)와 같이 저속 구간에 대한 조이스틱 명령 감도를 감소시켰다. 추력 모델을 기반으로 최대 전진 속도는 4 knots, 최대 후진 속도는 –2.72 knots으로 설정하였다. 실제 제어 시 최대 후진 속도는 –2 knots까지만 제어된다.
또한, 횡 방향의 경우, 아라곤 3호의 선수 추진기 특성상 ON/OFF와 방향 제어만이 가능하기 때문에, 조이스틱 Y 방향 값의 경우, 음의 값일 때 선박의 좌측 방향, 양의 값일 때 우측 방향으로 추력이 생기도록 설정하였다. 횡 방향 deadzone은 –0.5 ~ 0.5(50%)로 설정하였다.
4.2 조이스틱 무인수상정 제어 개념
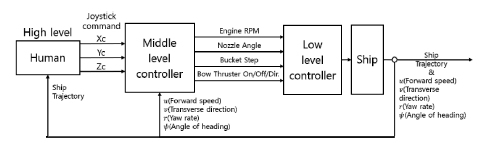
아라곤 3호의 제어 시스템 구조의 경우, Fig. 9와 같다. 무인수상정 운용자가 관제소에서 무인수상정의 위치와 속도(u, v, r), 선수 각(heading angle, Ψ) 상태를 확인하며 조이스틱을 통해 속도에 대한 제어 명령을 무인수상정으로 전송한다. 무인수상정에서 제어 명령을 받으면 구동부 제어 알고리즘을 통해 모델기반의 PID 제어를 거쳐 출력해야 할 구동기 명령 값을 계산한다. 그 후 각각의 구동부(엔진 RPM, 노즐 각, 버켓 단수, 선수 추진기)에 목표 제어 명령 값을 보내 제어한다.
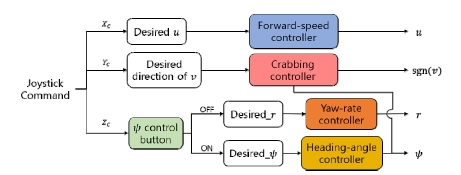
조이스틱 명령에 u, v, r, Ψ의 제어는 Fig. 10과 같이 이루어진다. 조이스틱의 X축 방향으로의 명령은 Fig. 8의 (b)와 같이 변환되어 목표 전진 방향 속도(udes)가 되고, Fig. 11의 forward-speed controller를 거쳐 명령 된 전진 방향 속도를 유지하게 된다.
조이스틱 Y 값에 의하여 방향에 대한 명령 값(desired direction of v)이 입력되면, Crabbing controller를 거쳐 원하는 방향으로의 횡 방향 제어가 이루어지게 된다.
조이스틱 Z축 회전 방향으로의 명령은 선수 각속도와 선수 각 제어로 두 가지 명령으로 구분할 수 있다. 선수 각 제어 활성 버튼(Ψ control button)이 off 상태일 경우 목표 선수 각속도에 대한 명령이 된다. 반대로 버튼이 on 상태일 경우 목표 선수 각에 대한 명령이 된다. 조이스틱 Z 값에 의해 선수 각속도에 대한 명령 값(desired r)이 입력되면, yaw-rate 제어기를 거쳐 명령된 선수 각속도를 유지하게 된다. 선수 각속도에 대한 명령 값(Ψdes)이 입력되면, heading-angle 제어기를 거쳐 명령 된 선수 각을 유지하게 된다.
5. 무인선 제어기 알고리즘
5.1 전진 방향 속도 제어기 구조
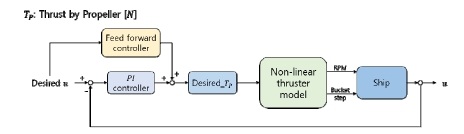
전진 방향 속도 제어기의 경우 Fig. 11의 개념도와 같이 동작한다. 목표 전진 방향 속도(udes)가 입력되면, 식 (9)를 통해 PI 제어기에 의한 계산 값과 feed forward 제어기에 의한 추력 계산 값(TP_ff)을 합하여 목표 추력(TP_des)으로 변환한다. 목표 추력은 비선형 추력 모델을 이용한 제어 알고리즘(Fig. 12)을 거쳐 목표 버켓 단수와 RPM을 정한다. 계산된 버켓 단수와 RPM을 무인수상정에 명령한다.
| (9) |
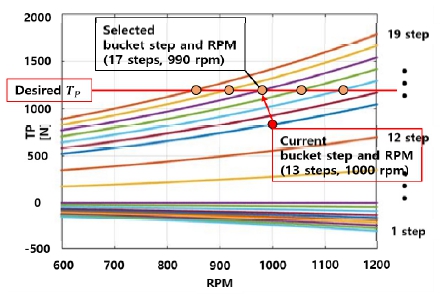
비선형 추력 모델을 이용한 제어 알고리즘에서의 목표 추력에 대한 목표 버켓 단수와 RPM을 정하는 방법은 다음과 같다. 우선, 식 (12)의 계산을 통해 모든 버켓 단수에 대해 목표 추력을 가지는 RPM 해를 구한다. 도출된 해들 중 현재 RPM에 대해 가장 변화가 적은 RPM을 가지는 해를 찾아 목표 버켓 단수와 목표 RPM(RPMdes)으로 지정한다.
Table 2의 버켓 단수에 따른 추력 비율(Ratiobk_step)과 RPM에 의한 추력 식 (1)을 곱하여 추력(TP) 식 (2)를 구한다.
식 (2)를 이용하여 RPM의 해(RPMdes)를 구하는 식 (12)를 도출하였다.
| (12) |
무인수상정의 최저 RPM은 600 rpm 이고, 최대 1200 rpm 까지만 사용할 수 있다. 이때 각 버켓 단수에 따른 600~1200 rpm에서의 추력 그래프의 변화율이 각각 다르다. 이로 인해 해가 없는 구간이 생기게 된다. 이렇게 발생된 해가 없는 추력 구간(-21N<TP<0N), (0N<TP<174N)에 대해서는 다음과 같이 구현하였다. 우선 목표 추력이 (-21N<TP<0N) 구간일 경우 다음과 같다. 절댓값 기준 현재 무인수상정의 추력이 목표 추력보다 작을 경우, 버켓을 중립 단수인 10단으로 명령하고 현재의 RPM을 유지한다. 목표 추력보다 클 경우 9단 그리고 최저 RPM인 600 rpm을 명령한다. 목표 추력이 (0N<TP<174N)인 경우 현재 추력과 목표 추력의 오차가 87N 미만인 경우, 현 상태를 유지한다. 오차가 87N 이상일 경우 현재 무인수상정의 추력이 목표 추력보다 작을 경우, 버켓을 10단으로 명령하고 현재의 RPM을 유지한다. 목표 추력보다 클 경우, 11단으로 명령하고 최저 RPM인 600 rpm을 명령한다.
구현된 제어 알고리즘의 기본 구조는 PID 제어를 기반으로 하고 있다. 무인수상정에 갑작스러운 속도 변화를 명령으로 내리게 되면, 속도 오차 값이 누적되어 원하는 속도까지 도달하게 된다. 이때 feed forward 제어 알고리즘을 사용할 경우, 목표로 하는 속도에 근접한 상태까지 빠르게 도달하기 때문에 제어의 반응 속도가 증가하게 된다. 이러한 이유로 인해 실험에 사용한 제어 알고리즘에 feed forward 제어기를 적용하였다.
우선, feed forward 제어기 그래프를 만들기 위해 실험에 사용된 아라곤 3호의 모델을 이용하여 무인수상정이 전진 방향으로 정상상태에서의 속도와 추력의 상관관계 표인 Table 3를 구하였다. 조이스틱의 제한 속도인 4 knots에 비해 더 높은 5 knots까지 속도가 높아지기 때문에 5 knots까지 구하였다. 이 표를 이용하여 선형 보간법을 적용하면, 속도에 대한 추력 값을 구할 수 있다.
5.2 선수 각속도 제어기 구조
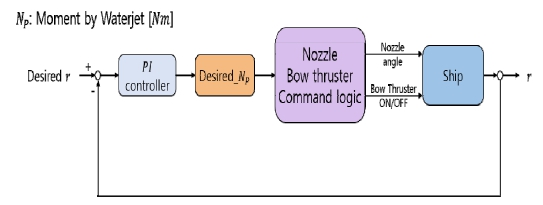
선수 각속도 제어기의 경우 Fig. 13와 같이 동작한다. 목표 선수 각속도(rdes)가 입력되면, PI 제어기 식 (13)을 통해 목표 회전 모멘트(NP_des)를 계산한다. 목표 회전 모멘트의 값은 노즐과 선수 추진기 명령 로직을 거쳐 무인수상정의 노즐 각과 선수 추진기의 동작을 제어하여 선수 각속도를 제어한다. 명령 로직은 다음과 같다.
우선 버켓 단수가 4~9단 사이일 경우, 목표 회전 모멘트에서 선수 추진기의 추력인 255N 만큼 빼준다. 그 후, 회전해야 할 방향에 맞추어 선수 추진기를 동작시킨다. 그 외의 단수에 있을 경우는 위의 과정을 거치지 않는다.
목표 회전 모멘트와 현재 회전 모멘트를 식 (14)에 대입하여 목표 노즐 각(Nades)으로 변환한 뒤 노즐 각에 명령을 내려 제어한다. 노즐 각의 범위는 –30°~30°의 범위를 가지기 때문에 식 (14)의 Nades의 계산 결과 –30° 이하의 경우 –30°, 30° 이상의 경우 30°가 되도록 하였다.
| (13) |
| (14) |
| (15) |
5.3 선수 각 제어기 구조
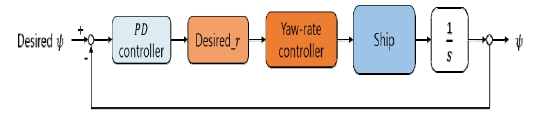
선수 각 제어기의 경우 2중 루프 제어를 활용하였다. 선수 각 제어기는 Fig. 14와 같이 동작한다. 목표 선수 각(Ψdes)이 입력되면, PD 제어기 식 (15)를 통해 목표 회전 각속도를 구해 무인수상정에 대해 yaw-rate 제어를 진행한다. 노즐 각과 선수 추진기를 제어하여 선수 각 회전 속도가 제어된다. 선수가 움직이며 적분 되어 선수 각이 제어된다.
5.4 횡 방향 제어기 구조
횡 방향 제어기에서 주로 사용되는 선수 추진기의 경우, 추진기 특성상 RPM 조절이 불가능하여 ON/OFF와 방향만을 제어할 수 있다. 또한 연속으로 동작시킬 경우, 선수 추진기에 무리가 가기 때문에 구동이 필요할 때는 1초 간격으로 ON/OFF를 반복하도록 하였다. 선수 추진기가 동작하게 되면 회전 모멘트가 생기기 때문에 회전하게 된다. 이를 방지하기 위해 동시에 노즐 각을 제어하여 선수 각이 오차범위 내에서 유지되도록 하였다.
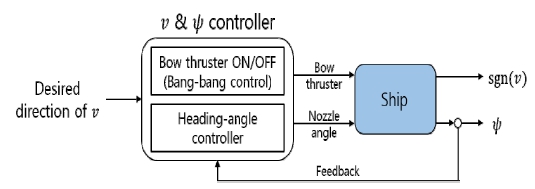
횡 방향 제어기는 Fig. 15와 같이 동작한다. 우선 좌/우 횡 방향에 대한 제어 목표 값이 입력되면 횡 방향과 선수 각 제어기 로직(Nozzle & Bow thruster Command logic)을 거치게 된다. 이 로직에서는 선수 추진기에 대한 방향과 ON/OFF 제어와 선수 각 제어기를 거치게 된다. 이러한 로직을 거쳐 결정된 선수 추진기와 노즐 각에 대한 명령을 내려 횡 방향과 선수 각에 대해 제어한다.
5.5 알고리즘 시뮬레이션
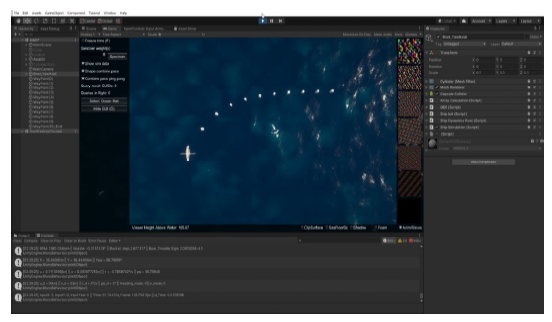
알고리즘을 구상하는 단계에 Matlab을 사용해 무인수상정의 역학 모델과 구동부 모델을 적용하였다. 스텝 입력을 통해 무인수상정의 안정화 상태에서의 추력과 속도 그리고 구동부의 안정성을 테스트하였다. 그 후 C#을 기반으로 이루어진 3D 및 2D의 개발 환경을 제공하는 게임 엔진인 Unity 실시간 시뮬레이션 프로그램을 사용해 무인수상정의 3D 모델에 알고리즘을 적용하였으며, input system 기능을 이용하여 조이스틱 입력을 실시간으로 받아들여 명령에 대한 실제 무인수상정의 실제 움직임에 대한 시뮬레이션을 진행 및 분석하였다. 이 과정을 거쳐 제어 이득과 불안정한 부분들을 사전에 보완하였다. Fig. 16은 Unity 실시간 시뮬레이션 화면이다.
6. 실험 결과
6.1 실험 방법
워터제트 기반 무인선 이접안 시험은 선박해양플랜트연구소(KRISO)의 주도하에 실행되었으며, 경남 광암항에서 수행되었다.
실해역에서의 제어 알고리즘 시험은 관제소에서 관제시스템의 전자해도를 통해 아라곤 3호의 위치와 속도 등을 확인하며, 조이스틱을 이용한 원격 조종 이접안 알고리즘의 작동과 구동부의 안정화가 제대로 이루어졌는지에 대해 관찰하였다. 무인수상정 제어에 사용되는 탑재프로그램에는 MFC와 C++ 프로그램이 사용되었다.
6.2 스텝 입력 제어 실험
스텝 입력에 대한 제어 실험은 전진 방향 속도(u), 선수 각속도(r), 선수 각(Ψ) 제어와 횡 방향 제어(Crabbing) 실험을 하였다. 이 실험은 제어 이득을 선정하기 위하여 진행되었다. 제어 실험을 통해 선정한 제어 이득은 Table 4와 같다.
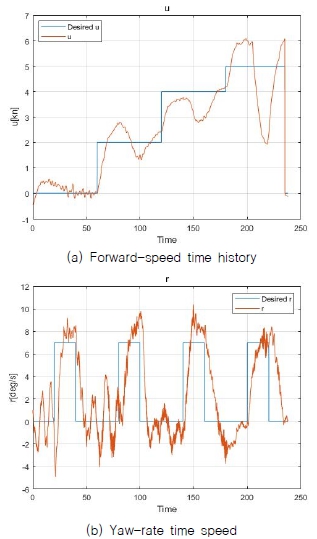
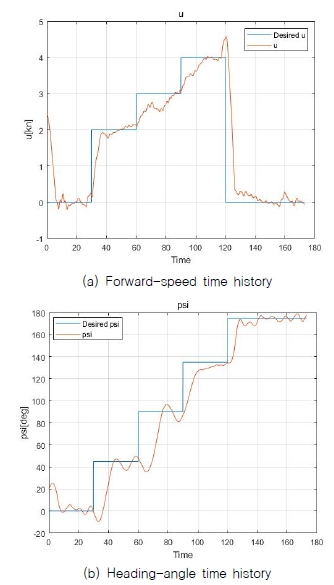
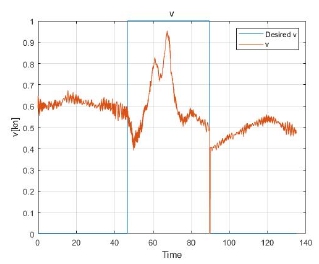
Fig. 17의 (a)와 (b)는 각각 스텝 입력에 대한 u와 r제어 실험 결과이다. 선수 방향 속도(u)와 선수 각속도(r)에 대한 입력을 스텝 입력으로 주어 반응을 확인하였다. 그 결과 r의 스텝 입력에 의해 무인수상정이 회전하게 될 때 무인수상정의 추력 구조상 u의 제어 값이 순간 낮아지는 것을 확인할 수 있었다. 또한 r의 경우, 약 2°/s의 오차 범위를 가지는 것을 확인하였다. Fig. 18의 (a)와 (b)는 각각 스텝 입력에 대한 u와 Ψ제어 실험 결과이다. 선수 각(Ψ)의 경우 전체적으로 최대 10의 오차 범위로 제어되는 것을 확인하였다. Fig. 19는 스텝 입력에 대한 Crabbing(v) 제어 실험 결과이다. v제어의 입력은 방향과 방향에 대한 제어의 ON/OFF 명령으로 –0.5~0.5 사이에서는 제어기가 동작하지 않는다. 실험 결과 v의 입력이 0인 상태에서는v제어가 동작하지 않기 때문에 외력에 또는 노즐 각도에 의한 추력에 의해 약 0.6 knots의 속도를 유지하고 있다. Idle 상태인 0.6 knots에서 조이스틱 입력이 +1이 되는 순간부터 양의 방향으로 속도가 약 0.35 knots 증가하여 약 0.95 knots와 원하는 방향으로의 제어가 되는 것을 확인할 수 있다. 만약 조이스틱 입력이 –1로 방향이 반대일 경우는 idle 상태인 0.6 knots의 속도가 약 0.25 knots로 감소할 것으로 보인다. 이러한 결과는 탑재된 선수 추력기의 장시간 가동 시 브러쉬 고장 문제로 인해 발생하였다.
또한 무인수상정의 경우 느린 동역학적 특성으로 인해 제어에 대한 반응이 느린 것을 확인할 수 있었다.
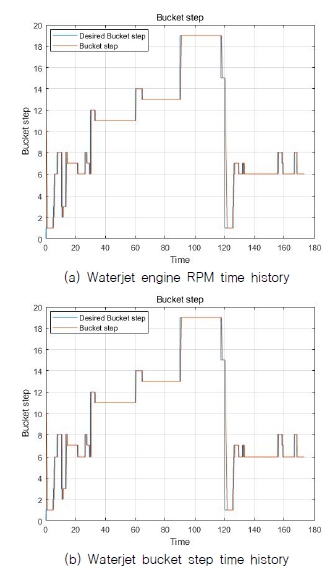
Fig. 20은 시험 도중 무인수상정의 (a)RPM과 (b)버켓 단수의 반응을 나타낸 그래프이다. 순간적인 RPM의 변화가 크지 않고 버켓 단수 또한 자주 변화하지 않는 것을 보여주어 안정적인 것을 확인할 수 있었다.
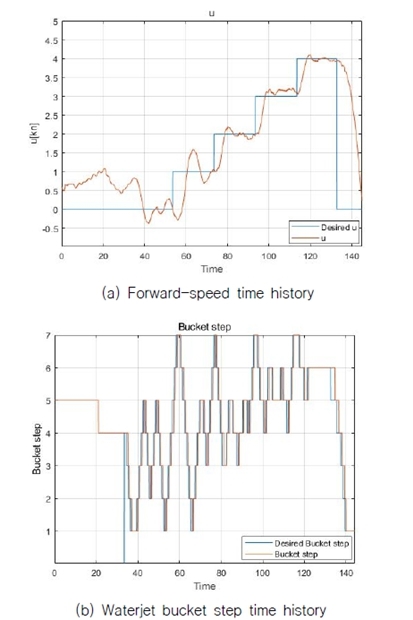
Fig. 21은 추력 모델을 사용하지 않은 일반적인 PI 제어를 이용하여 전진 방향 속도에 대한 스텝 이력 실험 결과이다. 이 실험에서의 버켓 스텝의 구동 범위는 1 ~ 7단으로 4단에서 중립을 가진다.
Fig. 21의 (b) 무인수상정의 속도를 유지하기 위해서 버켓 스텝의 열림과 닫힘이 반복하며 불안정한 모습을 보여주었다. 반면, 추력 모델을 이용하여 제어기를 구현한 결과, Fig. 20의 (b)와 같이 안정적인 버켓 상태를 유지하며 목표 속도를 유지하는 것을 확인할 수 있다.
Fig. 17의 (a) 선수 방향 속도 실험 당시 (b) 선수 각속도에 대한 스텝 입력 실험을 동시에 진행하였다. 때문에, Fig. 17의 (a) 그래프에서 선수 각속도가 입력되는 시간에 선수 방향 속도가 목표값을 제대로 구현하지 못하는 것을 확인할 수 있다. 하지만 Fig. 21의 (a) 실험 당시에는 선수 각속도 실험을 동시에 진행하지 않았기 때문에 더 안정적으로 전진 방향 속도가 유지되는 것을 확인할 수 있다.
6.3 조이스틱 원격 제어
앞선 스텝 입력 제어 실험을 통해 선정된 제어 이득을 적용하여 실제 조이스틱 명령을 통해 원격 접안 및 이안을 시도하였다.
관제소에서 관제시스템의 전자해도를 통해 무인수상정의 위치와 속도, 방향을 파악하였다. 조이스틱을 통해 수동으로 원격 제어를 하며 무인수상정의 카메라를 통해 주변을 확인하고 계류장에 안전하게 접안 및 이안하는 실험을 진행하였다.
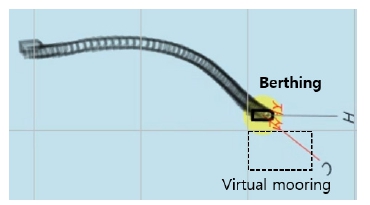
Fig. 22는 가상의 계류장에 대해 조이스틱을 이용해 실제 무인수상정을 접안하는 과정의 경로이다. 접안의 경우 계류장에서 거리가 약 40 m 떨어진 지점 전까지는 조이스틱 명령 최대 속도인 약 4 knots로 이동하였다. 그 후 계류장과 약 40 m 정도의 거리로 가까워졌을 때 점점 속도를 낮추며 선수를 회전시켜 계류장을 바라보고 이동하였다. 계류장과 약 16 m의 거리가 남았을 때부터 서서히 계류장과 수평 방향이 되도록 선수를 회전시키며 접근하였다. 계류장에 도착할 때 계류장과 수평을 이루고 정지하여 안전하게 접안하였다.
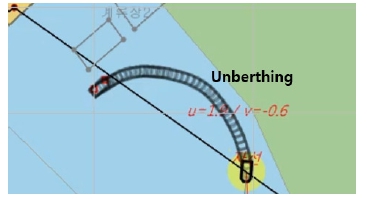
Fig. 23은 조이스틱을 이용해 실제 계류장에 대해 실제 무인 수상정을 이안하는 과정의 경로를 해도에서 기록한 것이다. 이안의 경우 대체로 4 knots의 명령을 주며 동시에 최대 회전 속도 명령 값인 6 degree/s를 주며 우회전을 하며 해안을 따라 빠져나왔다.
7. 결 론
본 시스템이 적용되는 워터제트 무인수상정의 경우 단일 워터제트 및 선수 추진기를 갖는다. 실측 실험 결과로부터 무인수상정의 동역학 모델을 구하여 시뮬레이션에 사용하였다. Matlab과 C# 기반의 Unity를 사용하여 제어 알고리즘에 대한 시뮬레이션을 진행하였다. 이를 기반으로 조이스틱의 X 방향은 전진 방향 속도(u), Y방향은 횡 방향 속도(v), Z축은 선수 각속도(r), 선수 각(Ψ)로 변환하여, 4개의 입력에 대해 총 4개의 엔진 속도, 버켓 단수, 노즐 각, 선수 추진기의 동작 여부 및 방향에 대한 출력을 가지는 MIMO(Multi Input Multi Output) 시스템에 PID 및 feed forward 제어 알고리즘을 설계하였다. 이 제어 알고리즘에서는, 시뮬레이션에 사용된 무인수상정의 구동부 모델을 이용하여 제어 알고리즘을 구성하였다.
본 연구를 통해 개발된 무인수상정의 모델을 이용한 제어기의 경우 엔진 속도, 버켓 단수 등에 대하여 직접 PI 제어하는 것에 비해 구동부의 안정성이 확연하게 좋아지는 것을 확인할 수 있었다. 그러나 본 연구에 사용된 무인수상정의 선수 추진기의 모터가 연속으로 동작시킬 수 있는 시간이 매우 짧아 원하는 선회 관련 제어를 하는 것에 있어 다소 미흡한 결과를 보여주었다. 특히, 이접안 시 선속이 느린 상태에서, 위터제트 노즐 각에 의한 회전 모멘트가 미약하다. 이 경우, 선수 추진기의 동작시간을 늘릴 수 있다면 좀 더 향상된 선회 성능을 보여줄 것이다. 그러나 여러번의 실험 결과 조이스틱을 이용한 원격 수동 제어 실험에서 극단적인 상황이 아닌 경우에는 큰 문제가 발생하지는 않았다.
추후 연구에서는 선수 추진기를 Brushless Direct Current (BLDC) 모터로 변경하는 것과 같은 하드웨어적 문제 해결이 필요하다.
Acknowledgments
본 논문은 중소벤처기업부의 재원으로 국가연구개발사업인 “해양수산재해 탐지용 무인선 실증”(1425157873) 및 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구(P0008473)입니다.
References
-
Aschemann, H., Wirtensohn, S. and Reuter, J., 2016. Nonlinear observer-based ship control and disturbance compensation. IFAC-Papers Online, 49(23), pp.297-302.
[https://doi.org/10.1016/j.ifacol.2016.10.358]

- Fossen, T., 1999. Guidance and control of ocean vehicles. Ph.D. University of Trondheim.
- Fossen, T.I., 2002. Marine Control Systems. Marine Cybernetics: Trondhiem.
- Hasegawa, K., and Kitera, K., 1993. Automatic berthing control system using network and knowledge-base. Journal of Kansai Society of Naval Architecture of Japan, 220, pp.135-143.
-
Hong, S.K., Jung, Y.H., Won, M.C. and Kim, S.Y., 2007. Development of control algorithm for ship berthing and unberthing systems using a joystick. Journal of Korean Navigation and Port Research, 31(5), pp.325-332.
[https://doi.org/10.5394/KINPR.2007.31.5.325]

- Im, N.K. and Hasegawa, K., 2002. Motion identification using neural networks and its application to automatic ship. Journal of Ship and Ocean Technology, 6(1), pp.16-26.
- Slotine, J.J.E. and Li, W., 1991. Applied nonlinear control. Englewood Cliffs, NJ: Prentice Hall.
- Won, M.C., Hong, S.K., Jung, Y.H., Kim, S.Y., Son, N.S. and Yoon, H.G., 2006. Development of nonlinear control algorithm for automatic berthing of ships. Proceedings of the Korea Committee for Ocean Resources and Engineering Conference, Korean Society of Ocean Engineers, 2006. pp.359-362.
-
Yamato, H., Koyama, T. and Nakagawa, T., 1992. Automatic berthing using the expert system. IFAC Proceedings Volumes, 25(3), pp.173-184.
[https://doi.org/10.1016/S1474-6670(17)50288-8]

-
Yoon, H.K., and Kim, S.Y., 2005. A study on the model test scheme for establishing the mathematical model of hydrodynamic force and moment acting on a slowly moving ship. Journal of the Society of Naval Architects of Korea, 42(2), pp.98-104.
[https://doi.org/10.3744/SNAK.2005.42.2.098]