국제해상충돌예방규칙을 고려한 Event Triggered NMPC 기반의 선박 충돌 회피 알고리즘

1. 서 론

항만 인근 해안은 정박 중인 선박들과 운항 중인 선박들로 복잡하며 이로 인한 선박 충돌사고 위험도가 높다. 선박 충돌사고는 환경오염, 인명피해 그리고 경제적 손실을 유발할 수 있다. 선박 충돌사고의 약 75%는 사람의 과실과 같은 인적 요인에 의해 발생하고 있으며 (Allianz global Corporate & Specialty, 2022), 인적 요인에 의한 선박사고를 최소화하기 위해 자율운항 선박의 충돌 회피에 관한 기술 연구가 활발히 진행 중이다.

선박의 충돌 회피는 해상에 정박 중인 선박(정적 장애물)에 대한 충돌 회피와 운항 중인 선박(동적 장애물)에 대한 충돌 회피로 구분하여 고려할 수 있다. 정박 중인 선박은 조류의 영향으로 앵커링 한 지점을 기준으로 일정한 영역을 정박 영역으로 보고, 이 영역 내에 선박이 정박하고 있다고 가정할 수 있다. 이러한 정박 영역은 선박의 길이, 톤수, 정박지의 해저 토양의 상태에 따라 달라진다. 정박 중인 선박에 대해 충돌 회피 기동은 따로 규정하고 있지 않지만, 운항 중인 선박에 대한 충돌 회피와 관련해서는 국제해사기구 (IMO: International Maritime Organization)에서 국제해상충돌예방규칙(COLREGs: international regulation for preventing collisions at sea)을 규정하였으며 자율운항 선박도 이러한 규정을 준수하여 충돌 회피 기동을 해야 한다.

NMPC(Nonlinear Model Predictive Control)는 모델 기반 예측 제어로 비선형 동역학 모델에 대한 동적 매개변수 계수의 값을 기반으로 구속조건에 대하여 일정 시간(prediction horizon time)동안 예측하고 최적화 계산을 한다는 점에서 충돌 회피 기동 수행에 유리하다. 또한, 최적화 과정을 통해 얻은 제어입력을 기반으로 기동하기 때문에 목적함수를 적절히 설정할 경우 연료 소비를 최소화하며 친환경과 경제성을 추구할 수 있다.

관련한 연구로 NMPC를 통한 경로점 및 궤적 제어와 제약조건을 고려한 고정 장애물 및 동적 장애물에 대한 회피 기동에 관한 시뮬레이션 연구가 (Xue et al., 2021; Sandeepkumar et al., 2022) 진행되었으며, NMPC를 기반으로 복잡한 수역에서 COLREGs를 준수하는 선박의 충돌 회피 기동 (Yuan and Gao, 2022)과 충돌 조우 상황에서 COLREGs 규정을 준수하지 않는 선박에 대해 예외 상황을 판단하고 이에 따른 충돌 회피 기동을 하는 연구 (Eriksen et al., 2020)가 진행되었다. 또한, Liu et al. (2022)는 NMPC를 통해 최적화 문제에 대한 계산 부담을 줄이기 위해, 정박 중인 선박에 대한 event- triggered-based NMPC 방법을 제안하였고, 이를 통해 다중선박의 충돌 회피 및 궤적 추적을 시뮬레이션을 통해 검증하였다. Gonzalez-Garcia et al. (2022)는 LiDAR 센서를 통해 장애물을 감지하고 이에 따른 비선형 모델 예측제어 기반 경로 추종 및 충돌 회피에 대해 시뮬레이션 및 실제 소형 선박 모델의 실험을 통해 검증하였다.

본 연구에서는 운항 중인 선박에 대해 clutter 환경에서 RADAR 센서를 통해 얻은 데이터에 기반하여 PDAF (Probabilistic Data Association Filter) 알고리즘을 이용하여 타선의 위치를 추정하고 이를 기반으로 충돌 위험도를 판단한다. 충돌 위험도가 감지되었을 경우, 기하학적으로 COLREGs 규정을 준수하는 경로점을 계산하고, event-trigger NMPC를 통해 충돌 회피 기동하는 것을 목표로 하였으며, 이를 MATLAB 시뮬레이션을 통해 검증하였다.

이에 본문 2장과 3장에서 IMO에서 규정한 COLREGs 규정과 충돌 위험　판단을 위한 충돌 위험도 내용을 요약하고 4장에서는 NMPC를 통한 동적 장애물 회피 방법, 5장은 PDAF 알고리즘을 통한 선박의 위치 추정 알고리즘, 6장과 7장에서 본 연구에서 얻은 결과를 정리하고 결론을 정리하였다.

2. COLREGs Rules

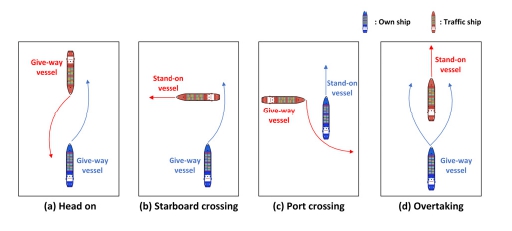
IMO는 1972년 해상 충돌 방지를 위한 국제 해상 충돌 방지 규정(COLREGs)을 발표했다. COLREGs는 국제적으로 통용되는 충돌방지규칙일 뿐만 아니라 해상에서 선박이 지켜야 할 운용규칙으로서 충돌상황에 따른 회피 기동을 규정하고 있다. COLREGs 규정의 내용은 다음과 같다. 충돌 회피 조작의 단계는 충돌 위험도를 판단하고 조우 상황을 판단하여 조우 상황을 제13조 또는 제15조의 규정에 따라 분류하고 규정에 따라 유지 선박과 회피 선박의 역할에 따라 충돌 회피를 수행한다. COLREGs 규정(Part B. 제16조~17조)에 대한 충돌 조우 상황에 따른 자선과 타선의 충돌 회피 기동에 대한 의무에 관한 내용은 Fig. 1을 통해 알 수 있다.

Fig. 1

Classification of collision situations based on COLREGs rules

3. 충돌 위험 판단 지표

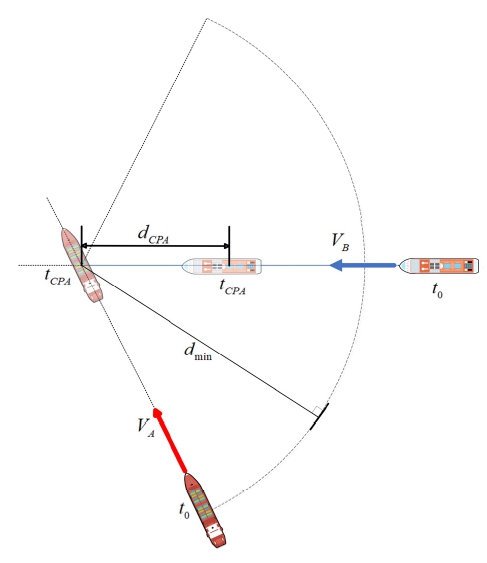
충돌 회피 기동을 시행하기 전에 먼저 선박의 충돌 위험성을 판단해야 한다. 이에 대해 Fig. 2와 같이 Closest Point of Approach (CPA)와 타선과의 상대 거리 기준을 활용하여 충돌 위험성을 판단할 수 있다. (Kuwata et al., 2014; Kang et al., 2019; Xie et al., 2019). 자선과 타선의 위치벡터와 속도벡터를 통해 TCPA(Time Closest Point Approach, t_cpa)와 DCPA(Distance Closest Point Approach, d_cpa)를 구하며, 이를 통해 충돌 위험도를 판단한다. DCPA는 자선과 타선이 가장 가까워지는 시점의 거리이며, 이때의 시간을 TCPA로 정의한다.

Fig. 2

Conceptual diagram of TCPA and DCPA

자선과 타선의 위치벡터는 각각 $$ {\overrightarrow{p}}_A$$, $$ {\overrightarrow{p}}_B$$이고, 속도벡터는 $$ {\overrightarrow{v}}_A$$, $$ {\overrightarrow{v}}_B$$이다. 식 (1), (2)를 통해 t_cpa와 d_cpa를 구할 수 있으며, 항만 및 해역에서 규정한 T_cpa와 D_cpa값 이내일 때 충돌 조우 상황으로 판단한다. 또한, 선박 충돌 안전반경인 D_th (=d_min)을 고려하여, 식 (3)에서 자선에서 바라본 타선의 위치벡터의 크기 R을 구하고, R이 D_th보다 작거나 같을 때 충돌 위험이 있다고 규정한다. 그리고 최종적으로 식 (4)를 만족하는 경우 충돌 위험도가 있다고 판단하여 COLREGs 규정을 준수하여 충돌 회피 기동을 하도록 한다.

4. Event-triggered NMPC algorithm

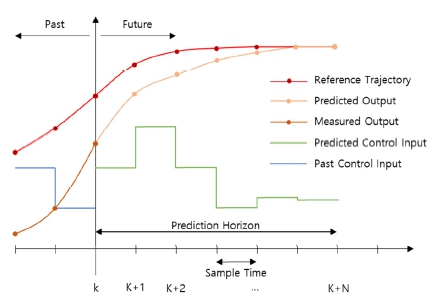
MPC는 모델을 기반으로 Fig. 3 같이 k시점부터 예측 시점(Prediction horizon, N) 후에 해당하는 k+N 시점까지 제약조건에 해당하는 Inequality constraint g₁(w)과 equality constraint g₂(w)를 만족하도록 하는 상태변수와 제어입력에 대한 cost의 합에 해당하는 목적함수(object function, J_N(x₀, u))를 최소화하도록 제어입력을 산출한다.

Fig. 3

Model Prediction Control (MPC) conceptual diagram

MPC에서 최종적으로 얻은 제어입력에서 k시점 해당하는 값만 사용하며 다음 스텝에서 다시 제약조건을 만족하며 예측 시점 N번 만큼에 해당하는 목적함수를 최소로 하는 제어입력을 구하는 과정들을 반복계산하며 모델을 최적 제어한다.

식 (5)에서 x_u, x_r는 상태변수 및 Reference 상태변수 u, u_r은 제어입력 및 Reference 제어입력을 의미한다. Q_MPC, R_MPC은 양준정부호 (Positive semi-definite) 가중치 행렬을 의미한다. 식 (6)은 각각의 예측 시점의 Cost function의 값들을 합한 목적함수이며, 식 (7)과 (8)의 제약조건을 만족하는 제어입력을 계산한다. 식 (9)의 f()는 무인 선박의 비선형 동역학 모델을 의미한다.

평상시에는 전역 경로 점을 reference로 하여 NMPC에서 계산된 제어입력을 바탕으로 경로 추종(trajectory following)을 진행한다. 자선에 장착된 RADAR를 이용하여 PDAF 알고리즘을 적용하여 타선의 위치 및 속도를 추정하고 이를 바탕으로 충돌 위험이 있다고 판단되는 경우, COLREGs 준수를 위해 자선과 타선의 안전반경을 고려한 원에 대해 자선을 기준으로 우현에 있는 접점을 기하학적으로 찾는 방법 (Niu et al., 2017)으로 회피한다.

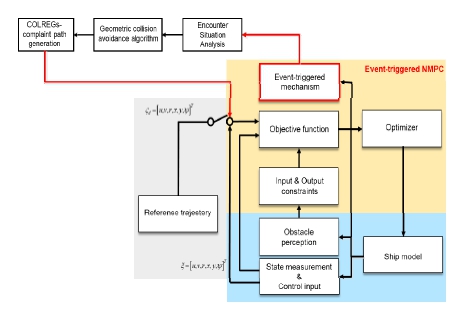
충돌 회피 상황에서, 기하학적으로 찾은 경로점을 끝까지 추종하지 않고, 우현의 경로점을 중심으로 특정 반경에 들어왔을 경우 또는 충돌 위험이 해제된 경우, 다시 전역 경로점을 추종하도록 하는 event-trigger 방식을 적용하였다. Fig. 4는 기하학적 방식으로 COLREGs를 충족하는 타선의 우현의 경로점을 찾아 회피하는 event-trigger NMPC 알고리즘에 대한 다이어그램이다.

Fig. 4

Proposed event-triggered NMPC algorithm flow chart

4.1 무인 선박 동역학 모델

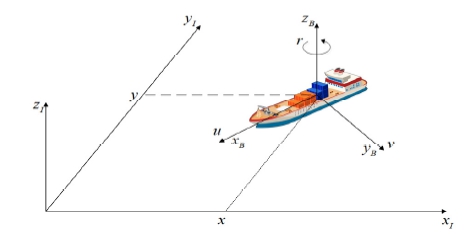
본 연구에서 사용한 무인 선박 동역학 모델은 surge, sway, heave, roll, pitch, yaw의 6 자유도 모델을 아래와 같은 가정을 통해, Fig. 5와 같이 3 자유도 모델로 근사화하여 사용한다.

Fig. 5

Unmanned ship model used in NMPC

1. 바람과 해류에 의한 heave, roll, pitch 운동은 무시한다.

2. 관성(inertia), 부가 질량(added mass), 유체역학적 감쇠(hydrodynamic damping) 행렬들은 대각 행렬이다.

3. 제어 변수는 surge force와 yaw moment이다.

선박 모델에 대한 3 자유도(surge, sway, yaw) 동역학 식은 식 (12) ~ (14)와 같으며, 이에 따른 동역학 계수는 Table 1과 같다 (Abdelaal et al., 2018).

$\[ \dot{x}=ucos\left(\phi \right)-vsin\left(\phi \right) \]$

(11)

$\[ \dot{y}=ucos\left(\phi \right)+vsin\left(\phi \right) \]$

(12)

$\[ \dot{\phi }=r \]$

(13)

$\[ \dot{u}=\frac{m_2}{m_1}vr-\frac{d_1}{m_1}u+\frac{1}{m_1}{\tau }_u \]$

(14)

$\[ \dot{v}=\frac{m_1}{m_2}ur-\frac{d_2}{m_2}v \]$

(15)

$\[ \dot{r}=\frac{\left(m_1-m_2\right)}{m_3}uv-\frac{d_3}{m_3}u+\frac{1}{m_3}{\tau }_r \]$

(16)

Table 1

3-DOF USV parameter

4.2 이동하는 타선과의 장애물 제약조건

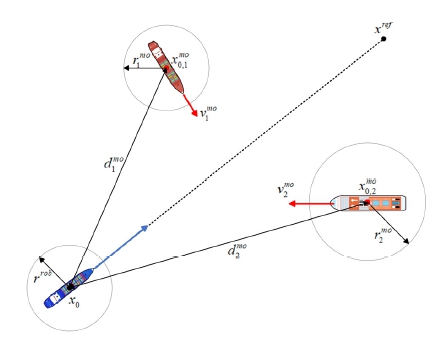
Fig. 6과 같은 상황에서, 자선은 타선과의 충돌을 회피하기 위해 자선의 안전반경과 타선의 안전 영역을 고려하여 충돌하지 않을 물리적 조건에 대해 고려해야 한다.

Fig. 6

NMPC dynamic obstacle constraints

x_k, y_k는 자선의 수평 위치, $$ x_i^{mo}$$, $$ y_i^{mo}$$는 이동하는 타선의 수평 위치에 해당하며, $$ r^{own}$$은 자선의 안전반경 $$ r_i^{mo}$$는 타선의 안전반경에 해당한다. 식 (17)은 상대 선박의 위치벡터에 해당하며, 상대 선박은 등속운동 모델로 가정하고 초기 속도($$ v_i^{mo}$$) 및 각도 ($$ {\theta }_i^{mo}$$)를 통해 시간에 따른 위치벡터를 식 (18)과 같이 나타냈다. 식 (19)는 자선과 타선 사이의 거리를 나타내며, 식 (20)은 이동하는 타선과의 충돌이 일어나지 않은 조건을 의미하며 S_b는 추가적인 안전 경계를 의미한다. 최종적으로 식 (21)과 같은 inequality constraint를 NMPC에서 고려하여 계산하였다.

$\[ x_{\mathrm{0,1}}^{mo}={\left[x_{\mathrm{0,1}}^{mo},y_{\mathrm{0,1}}^{mo}\right]}^T,x_{\mathrm{0,2}}^{mo}={\left[x_{\mathrm{0,2}}^{mo},y_{\mathrm{0,2}}^{mo}\right]}^T \]$

(17)

$\[ \begin{array}{l}{x}_{0,i}^{mo}=\left[\begin{array}{c}{x}_{k,i}^{mo}\\ y_{k,i}^{mo}\end{array}\right]=\left[\begin{array}{c}{x}_{0,i}^{mo}\\ y_{0,i}^{mo}\end{array}\right]+T_s\left[\begin{array}{c}{v}_i^{mo}\mathrm{c}\mathrm{o}\mathrm{s}\left({\theta }_i^{mo}\right)\\ v_i^{mo}\mathrm{s}\mathrm{i}\mathrm{n}\left({\theta }_i^{mo}\right)\end{array}\right]\\ \mathrm{f}\mathrm{o}\mathrm{r} all k=0,\dots ,N-1 \mathrm{a}\mathrm{n}\mathrm{d} i=0,\dots ,n_{mo}\end{array} \]$

(18)

$\[ d_{k,i}^{mo}=\sqrt{{\left(x_k-x_i^{mo}\right)}^2+{\left(y_k-y_i^{mo}\right)}^2} \]$

(19)

$\[ d_{k,i}^{mo}\ge r^{own}+r_i^{mo}+S_b \]$

(20)

$\[ g^{mo}\left(k,i\right)=-d_{k,i}^{mo}+r^{own}+r_i^{mo}+S_b\ge 0 \]$

(21)

4.3 COLREGs를 충족하는 기하학적 경로점 생성

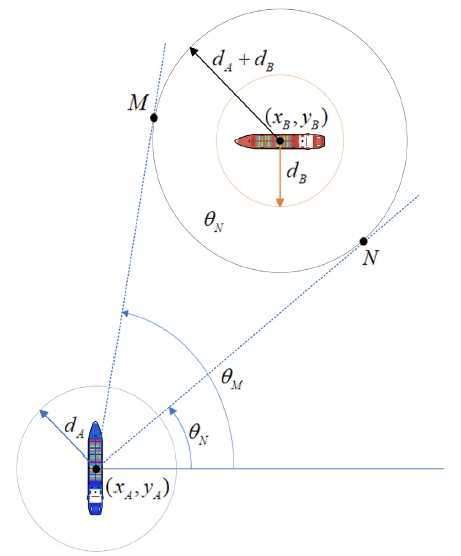
NMPC에서 타선에 대한 제약조건을 고려함으로써 선박의 충돌 회피를 할 수 있으나, COLREGs 규정을 만족하게 하도록 기하학적 충돌 회피 방법을 추가로 고려하였다. COLREGs 규정을 준수하기 위해, 충돌 조우 상황 시 자선을 기준으로 타선에 대해 우현으로 회피 기동을 해야 한다. 이러한 부분에 있어 충돌 위험이 판단되었을 때, 자선과 타선의 안전 영역을 고려하여 기하학적으로 자선을 기준으로 자선과 타선의 안전 영역을 고려한 원에 접하는 점들에서 오른쪽 점(right-side tangent point)에 해당하는 점을 Fig. 7과 같이 계산하였다. 여기서 자선의 수평 위치는 x_A, y_A이고 타선의 수평 위치는 x_B, y_B이며, 자선과 타선의 안전반경은 각각 d_A, d_B이다. 또한, 자선의 우현을 기준으로 타선의 안전반경의 접점을 M, N으로 나타내고 자선의 우현을 기준으로 접점까지의 각도를 θ_M, θ_N으로 정의하였다.

Fig. 7

Principles of generating geometric waypoints that satisfy COLREGs

$\[ {\left(x-x_B\right)}^2+{\left(y-y_B\right)}^2={\left(d_A+d_B\right)}^2 \]$

(22)

$\[ \left(y-y_B\right)\left(y-y_A\right)=-\left(x-x_B\right)\left(x-x_A\right) \]$

(23)

식 (22)는 타선을 기준으로 자선과 타선의 안전반경을 고려한 원의 방정식에 해당하며, 식 (23)은 자선과 타선의 수직이 되는 조건이다. 따라서 식 (22)와 (23)을 연립하면, 타선을 기준으로 자선과 타선의 안전반경을 고려한 원의 접점의 좌표 M(x_M, y_M), N(x_N, y_N)을 구할 수 있다.

$\[ \Delta \theta ={\theta }_M-{\theta }_N \]$

(24)

(25)

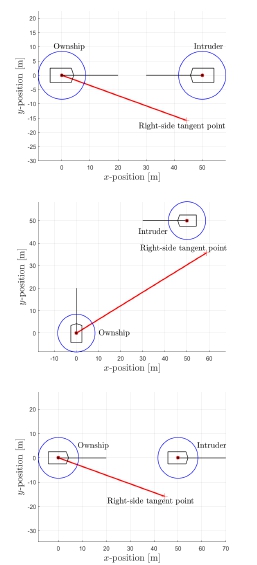
식 (24)와 (25)의 조건을 충족하는 점을 찾으면 자선을 기준으로 우현 방향의 오른쪽 접점에 해당하는 N을 구할 수 있다. Fig. 8은 COLREGs 규정에서 규정한 충돌 조우 상황에 대항하는 head on, starboard crossing 및 overtaking에 대하여 오른쪽 접선 점을 구한 결과이다. 3장에서 언급된 방식대로 충돌 위험이 탐지된 경우, 기하학적으로 계산된 우현 방향의 N을 새로운 경로점으로 NMPC에 입력하게 되며, 이를 통해 COLREGs를 충족하게 된다. 여기서, 자선이 N 경로점을 끝까지 추종하기보다는 COLREGs를 만족하기 위함이므로, N 경로점을 중심으로 특정 반경 내에 선박이 도달하였거나, 충돌 위험도가 해제되었을 경우는, 기존의 전역 경로점을 다시 추종하도록 NMPC가 운용된다.

Fig. 8

Example of creating geometric waypoints that satisfy COLREGs (head on, starboard crossing and overtaking)

5. PDAF 알고리즘

PDAF 알고리즘은 클러터 등에 의해 허위 측정치가 발생하는 상황과 표적이 탐지되지 않았을 때의 상황에서 적절하게 단일 표적을 추적하기 위해 유효한 측정값들의 확률 데이터 연관을 계산하는 방법이며, 주로 RADAR를 사용하여 객체를 탐지할 때 쓰인다. PDAF는 연관 확률을 계산하고, 표적이 될 가장 가능성이 큰 측정값을 선택한다. 연관 확률은 베이지안 정보로서 PDAF 추적 알고리즘에서 사용되며 측정값의 불확실성을 나타낸다. PDAF의 목적으로는 추정하고자 하는 상태변수의 최소 평균 제곱 오차(Minimum Mean Square Error, MMSE)값을 구하는 것이다. (Yaakov et al., 2009)

5.1 PDAF 방법

PDAF를 적용하기 위해서는 몇 가지 가정을 해야 한다. 표적의 탐지는 시간에 대해 독립적으로 발생하는 확률 P_D를 갖는다. 즉, 표적은 항상 탐지되는 것은 아니며, 표적의 true 측정값이 유효 영역 안에 있을 확률 P_G를 갖는다 (Kim, 2012).

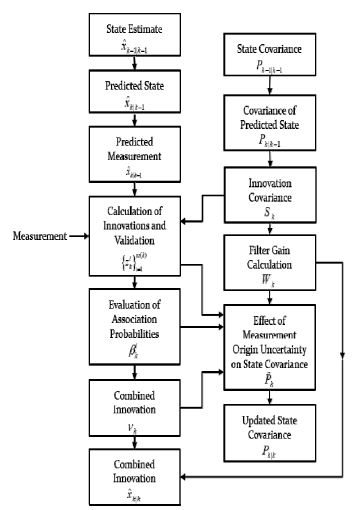
PDAF 방법은 단일 표적을 추적하는 suboptimal 베이지안 데이터 연관 방법으로, 구조적으로는 칼만 필터를 기반으로 하며, 몇 가지 단계가 추가된 구조이다 (Kang, 1994). 만약 시스템모델 혹은 측정 모델이 비선형이면 확장칼만필터(extended Kalman filter)를 기반으로 한다. 추가된 단계로는 유효범위 안에 유효 측정값을 찾는 gating 단계와 gating 된 모든 측정값 각각이 표적의 측정값이 될 가능성인 사후 연관 확률인 $$ {\beta }_0^i$$를 구하는 단계가 있다. PDAF의 단계의 순서로는 Fig. 9와 같다.

Fig. 9

The PDAF algorithm flow chart

5.2 클러터 생성

클러터의 특징으로는 유효 영역에서는 균일한 분포를 가지며 클러터가 포함된 측정값들은 서로 시간에 대해 독립적 (i.i.d.: Independent and Identically Distributed)이다. 클러터의 개수는 푸아송 분포(Poisson distribution), 즉 밀도 λ를 갖는 푸아송 과정을 따르며 클러터의 수학적 표현은 다음과 같다.

$\[ \begin{array}{cc}\lambda =\frac{m_k}{V_k},& m_k\sim Pois\left(\lambda \right)\end{array} \]$

(26)

$\[ V_k=c_{n_z}{\left|\gamma S_k\right|}^{1/2}=c_{n_z}{\gamma }^{n_z/2}{\left|S_k\right|}^{1/2} \]$

(27)

여기서 m_k는 클러터의 개수, n_z는 DOF(Degree of Freedom)이며, V_k는 n_z차원에서 유효 영역의 부피를 의미한다. 유효 영역 γ는 카이제곱 분포의 역 누적분포 함수를 이용하여 설정한다. 상수 $$ c_{n_z}$$는 n_z에 따라 달라지며 Table 2와 같다.

Table 2

Constant cnz for each DOF

본 실험에서 DOF는 이며, 표적이 유효 영역 안에 측정될 확률값 P_G는 0.99로 유효 영역 γ가 9.21이다.

5.4 Gating 단계

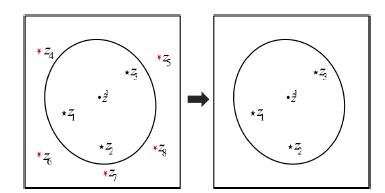
Gating 단계에서는 표적의 예측된 측정치 $$ {\widehat{\mathit{z}}}_k$$와 센서로 측정된 모든 측정치 z_k(클러터 및 예측된 표적값)의 제곱 Mahalanobis distance(M_k)를 비교하여 유효범위 안에 모든 측정값을 표적의 유효 측정값들로 선택하는 단계이고 수식은 다음과 같으며, Fig. 10에 묘사되어 있다.

Fig. 10

Gating process describe

$\[ M_k={\left(z-{\widehat{z}}_{k\mid k-1}\right)}^T{S}_k^{-1}\left(z-{\widehat{z}}_{k\mid k-1}\right) \]$

(36)

$\[ M_k\le \gamma \]$

(37)

Fig. 10에서 식(37)을 만족하는 값들 만 원 안에 남게 되고, 원 밖에 있는 값들은 제거된다.

5.7 시뮬레이션 결과

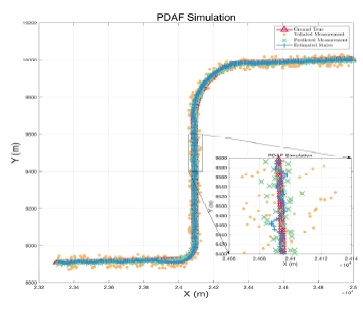
PDAF 알고리즘만을 검증하기 위해 시스템 모델을 등속운동 모델로 가정하고 측정 모델은 위치 x, y만을 측정하는 선형 모델로 설정했다. 측정되는 객체는 자선이며, 클러터는 자선의 진 측정치를 기준으로 30 m × 30 m 넓이에서 균일하게 생성했다. 표본 시간 T_s는 1초이며 총 실험 시간은 50초이다. PDAF 알고리즘을 검증하기 위한 설정된 매개변수는 Table 3에서 확인할 수 있으며, 시뮬레이션 결과는 그림 Fig. 11에서 임의로 생성한 경로(ground true)와 추정한 위치(estimated states)를 확인 할 수 있다.

Table 3

Parameters used in the PDAF simulation

Fig. 11

Results of the PDAF algorithm

위의 결과로 많은 클러터가 발생하여 자선의 위치 측정에 방해가 있음에도 불구하고 PDAF 알고리즘은 단일 객체 추적에 준수한 성능을 지녔다는 것을 알 수 있다. 또한, 평균 제곱근 오차(root mean square error)를 통해 수치적으로도 안정된 수치를 보인다.

6. 시뮬레이션 결과

제안한 알고리즘을 검증하기 위해 시뮬레이션은 2.8 GHz i7 프로세서에서 MATLAB R2021a를 활용하였으며, NMPC 알고리즘은 CasADi framework/IPOPT solver (v3.5.5 for MATLAB)를 사용하였다. 시뮬레이션에 T_s = 0.1로 설정하였으며, 자선과 타선이 등속운동 모델로 head-on, crossing, overtaking의 충돌상황에 대해 시뮬레이션이 진행했다. 시뮬레이션에 사용된 주요 파라미터는 Table 5와 같다.

Table 4

RMSEs value of location x, y

Table 5

Parameters of the simulation

NMPC 알고리즘을 통해 자선은 전역 경로점을 추종하는 중에 자선에 장착된 RADAR에서 얻은 데이터를 활용하여 PDAF 알고리즘으로 타선의 위치와 속도를 추정하고, 이를 활용하여 3장에서 언급된 방법으로 위험도를 탐지한다. 충돌 위험이 탐지된 경우, 4, 3장에서 언급된 COLREGs를 충족하는 기하학적 경로점 생성 방식으로 새로운 경로점을 적용하는 event-triggered NMPC 알고리즘을 적용하였다. 기하학점 경로점의 특정 반경 안에 자선이 진입하거나, 또는 충돌 위험도가 해제된 경우, 원래의 전역 경로점을 추종하도록 NMPC를 설계하였다.

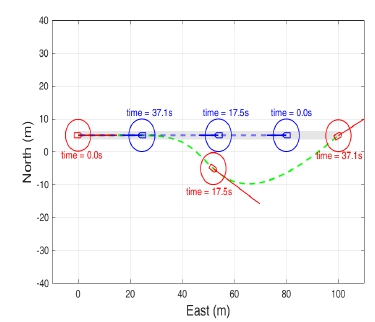
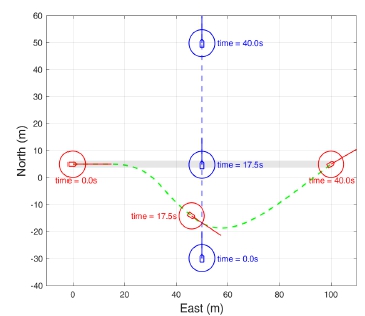
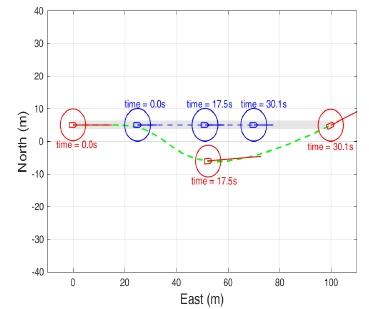
Figs. 12-14는 각각 head on, crossing, overtaking 상황에서 PDAF를 통해 추정된 타선의 위치를 추정하고 event-triggered geometric 기반 충돌 회피 알고리즘 적용하여, CORLEGs를 충족하면서 충돌 회피 기동을 하는 것을 확인할 수 있다.

Fig. 12

Head-on simulation

Fig. 13

Crossing simulation

Fig. 14

Overtaking simulation

7. 결론 및 향후 계획

본 논문은 head on, crossing, overtaking 상황에서 자선에 장착된 RADAR에서 얻은 데이터를 기반으로 PDAF 알고리즘을 통해 하나의 동적 선박의 위치와 속도를 추정하고, 추정된 값을 통해 충돌 위험도를 계산 후 event-triggered NMPC 알고리즘 기반으로 COLREGs를 충족하는 충돌 회피 알고리즘을 제안하였다, 그리고 이를 MATLAB 시뮬레이션을 통해 검증하였다. 추후 연구에서는 2척 이상의 선박들에 대한 상태 추정과 충돌 회피 알고리즘 검증을 추가적으로 진행할 예정이며, 시험분석 또는 해석적으로 선박의 동역학 파라미터를 구하고 이를 적용하여 실시간으로 동적 선박에 대한 회피 실험을 실 해역에서 수행할 예정이다.

Acknowledgments

이 논문은 2023년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원과 2023년도 정부(해양수산부) 재원으로 해양수산과학기술진흥원의 지원을 받아 수행된 연구임.((P0017006, 2023년 산업혁신인재성장지원사업), (1525014528, "스마트항만-자율운항선박 연계기술 개발"))

References

• Abdelaal, M., Fränzle, M. and Hahn, A., 2018. Nonlinear model predictive control for trajectory tracking and collision avoidance of underactuated vessels with disturbances. Ocean Engineeing. 160, pp.168–180. [https://doi.org/10.1016/j.oceaneng.2018.04.026]
• Allianz global Corporate & Specialty (Allianz), 2022, Safety and shipping review 2022: An annual review of trends nd developments in shipping losses and safety: Allianz.
• Eriksen, B.-O.H., Bitar, G., Breivik, M. and Lekkas, A.M., 2020. Hybrid collision avoidance for ASVs compliant with COLREGs rules 8 and 13–17. Fronttiers Robotic AI 7, 11. [https://doi.org/10.3389/frobt.2020.00011]
• Yaakov, B.S., Fred, D. and Jim, H., The probabilistic data association filter, IEEE Control Systems Magazine, 2009, pp.82-91. [https://doi.org/10.1109/MCS.2009.934469]
• Gonzalez-Garcia, A., Collado-Gonzalez, I., Cuan-Urquizo, R., Sotelo, C., Sotelo, D. and Castañeda, H., 2022. Path-following and LiDAR-based obstacle avoidance via NMPC for an autonomous surface vehicle. Ocean Engineeing. 266, 112900. [https://doi.org/10.1016/j.oceaneng.2022.112900]
• Kang, D.I., Design of underwater target tracking filter, Kyungpook National University, 1994, pp.10-21.
• Kang, L., Lu, Z., Meng, Q., Gao, S. and Wang, F., 2019. Maritime simulator based determination of minimum DCPA and TCPA in head-on ship-to-ship collision avoidance in confined waters. Transportmetrica A: transport science 15, pp.1124–1144. [https://doi.org/10.1080/23249935.2019.1567617]
• Kim, E.S., Fast algorithm of multi-target tracking using multi-model and probabilitstic data association, Hanyang University, 2012, pp.21-43.
• Kuwata, Y., Wolf, M.T., Zarzhitsky, D. and Huntsberger, T.L., 2014. Safe maritime autonomous navigation with COLREGS, using velocity obstacles. IEEE Journal of Ocean. Engineering. 39, pp.110–119. [https://doi.org/10.1109/JOE.2013.2254214]
• Liu, C., Hu, Q., Wang, X. and Yin, J., 2022. Event-triggered-based nonlinear model predictive control for trajectory tracking of underactuated ship with multi-obstacle avoidance. Ocean Engineeing. 253, 111278. [https://doi.org/10.1016/j.oceaneng.2022.111278]
• Niu, H., Savvaris, A. and Tsourdos, A., 2017. USV geometric collision avoidance algorithm for multiple marine vehicles, Presented at the OCEANS 2017 - Anchorage, pp.1–10.
• Sandeepkumar, R., Rajendran, S., Mohan, R. and Pascoal, A., 2022. A unified ship manoeuvring model with a nonlinear model predictive controller for path following in regular waves. Ocean Engineeing. 243, 110165. [https://doi.org/10.1016/j.oceaneng.2021.110165]
• Xie, S., Chu, X., Zheng, M. and Liu, C., 2019. Ship predictive collision avoidance method based on an improved beetle antennae search algorithm. Ocean Engineeing. 192, 106542. [https://doi.org/10.1016/j.oceaneng.2019.106542]
• Xue, Y., Wang, X., Liu, Y. and Xue, G., 2021. Real-time nonlinear model predictive control of unmanned surface vehicles for trajectory tracking and collision avoidance presented at the 2021 7th International Conference on Mechatronics and Robotics Engineering, pp.150–155. [https://doi.org/10.1109/ICMRE51691.2021.9384818]
• Yuan, W. and Gao, P., 2022. Model predictive control-based collision avoidance for autonomous surface vehicles in congested inland waters. Mathematical Problems in Engineering. 2022, pp.1–15. [https://doi.org/10.1155/2022/7584489]