합성곱 신경망과 복셀화를 활용한 선박 저항 성능 예측
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The prediction of ship resistance performance is typically obtained by Computational Fluid Dynamics (CFD) simulations or model tests in towing tank. However, these methods are both costly and time-consuming, so hull-form designers use statistical methods for a quick feed-back during the early design stage. It is well known that results from statistical methods are often less accurate compared to those from CFD simulations or model tests. To overcome this problem, this study suggests a new approach using a Convolution Neural Network (CNN) with voxelized hull-form data. By converting the original Computer Aided Design (CAD) data into three dimensional voxels, the CNN is able to abstract the hull-form data, focusing only on important features. For the verification, suggested method in this study was compared to a parametric method that uses hull parameters such as length overall and block coefficient as inputs. The results showed that the use of voxelized data significantly improves resistance performance prediction accuracy, compared to the parametric approach.
Keywords:
Convolutional neural network, Voxelization, Deep learning, Computational fluid dynamics, Resistance performance키워드:
합성곱 신경망, 복셀화, 딥러닝, 전산유체역학, 저항 성능1. 서 론
일반적으로 선박의 최종 선형 도출 과정은 다음과 같다. 먼저, 다양한 선형 설계안을 만들고 이들을 대상으로 Reynolds Averaged Navier-Stokes (RANS) 방정식 기반의 수치해석을 수행하여 유체역학적 성능을 확인한다. 그 결과를 토대로 모형시험을 수행할 설계안을 선정하고, 모형시험을 통해 목표 성능이 달성되는지 확인한 후 최종 선형이 결정된다. 수치해석에 소요되는 시간과 비용은 CPU 코어수와 같은 전산 자원의 규모에 직접적인 영향을 받는다. 국내 대형조선소 3사는 기 확보된 대규모 전산 자원을 최대한 활용하여 수치해석에 소요되는 시간을 최소화하고 주어진 일정 내에서 가급적 많은 설계안 들이 검토되는 전략을 활용하고 있다. 반면, 충분한 전산 자원이 구비되어 있지 않은 중/소형 조선소의 경우, 다양한 선형 설계안을 평가하는데 여전히 많은 시간과 노력이 요구되는 실정이다. 따라서 선형의 초기 설계 단계에서 선박의 저항 성능이 빠르고 정도 높게 추정되는 방법론이 개발된다면 이는 설계 비용과 시간의 절감 측면에서 유용하게 활용될 수 있다.
한편, 최근 Information Technology (IT)분야의 비약적인 발전을 바탕으로 딥러닝(deep learning) 기법을 활용한 연구도 활발하게 이루어지고 있다 (LeCun et al., 2015). 머신 러닝(Machine learning) 기법 중 하나인 딥러닝 기법은 컴퓨터 시스템이 명시적 지시 없이 자동으로 작업을 수행하고, 예측이나 결정을 내리기 위한 수학적 모델을 구축하는 통계적인 방법이다. 최근 몇 년 동안, 딥러닝 기법은 음성 인식, 객체 분류, 자연어 처리와 같이 복잡하고 다양한 형태의 데이터 세트를 학습하기 위한 용도로 활용되어져 왔다 (Wason, 2018). 조선·해양 분야에서도 딥러닝 기법이 여러 연구에 적용된 바 있는데 대표적인 연구 사례로, 파도의 높이 예측, 선박의 풍하중 계산, 해양 플랫폼의 손상 감지, 연료 소비량 예측, 선박 탐지 등이 있다 (Panda, 2021). 뿐만 아니라 Beşikçi et al. (2016)은 선박의 속도, 분당 회전수 등을 인공신경망의 입력값으로 활용해 연료 소비량을 예측했다. Zhao et al. (2019) 은 임베디드(Embedded) 딥러닝 기법을 활용해 선박 탐지 및 인식에 관한 연구를 수행했고, Choi et al. (2019)은 극지방 얼음의 농도 예측에 인공신경망을 활용한 바 있다. 앞서 언급한 조선·해양 분야와 관련된 다양한 연구 주제 외에도 특히, 선박의 성능 예측과 관련하여 딥러닝 기법을 활용하는 연구들도 활발히 진행되어져 왔다. Grabowska and Szczuko (2015)는 선박의 저항 성능에 영향을 끼치는 요소들을 매개변수로 활용해 인공신경망으로 정수 중 저항성능을 예측했다. Kim and Park (2015)은 선박의 저항, 자항 요소 추정을 위해 파라메트릭(Parametric) 신경망 구성 방법을 제안하였다. 그리고 Kim et al. (2022b)은 CFD 해석을 통해 얻은 압력 분포, 파동 프로파일 및 후류 프로파일 이미지를 합성곱 신경망(Convolutional Neural Network, CNN)의 입력값으로 활용해 저항 성능을 예측하는 연구를 수행하였다. 또한 Kim et al. (2022a)은 선박의 오프셋을 입력값으로 사용하여 선박의 잉여저항계수가 추정되는 합성곱 신경망 기반의 방법을 제안하였다.
인공신경망을 이용하여 선박의 저항 성능을 정도 높게 예측하기 위해서는, 선박의 제원뿐만 아니라 CAD 기반의 형상 정보도 입력자료로 활용하는 것이 유리하다. 또한 선체 표면의 압력장 분포와 같은 이미지를 활용하는 연구의 경우, 해석에 사용된 수치해석 기법에 대한 신뢰성 검증과 더불어, 수치해석 시 저항값 이외에 특정 이미지를 추가적으로 산출, 저장하는 단계가 필요하다. 본 연구에서는 합성곱 신경망의 입력값으로 복셀화된 선형 데이터를 활용하여 선박의 저항 성능을 예측하는 방법을 제안하고자 한다. 즉, 선형을 복셀로 변환시킨 형상정보 데이터, 저항성능에 영향을 줄 수 있는 대표적인 부가정보 데이터 그리고 해당 선형별 저항 데이터를 구축, 학습시킨 후 임의의 선형에 대한 저항값을 예측, 비교하여 예측 정확도를 확인하는 연구를 수행하였다. 제2장에서는 본 연구에서 제안하는 딥러닝 모델을 포함한 방법론에 대하여, 3장에서는 딥러닝 모델의 학습에 사용된 데이터에 대하여, 4장에서는 제안된 방법론과 다른 방법론과의 비교 결과에 대하여 논의한다. 마지막으로, 5장에서는 본 연구의 결론 및 향후 연구를 다루고자 한다.
2. 딥러닝 모델
2.1 딥러닝 모델 개요
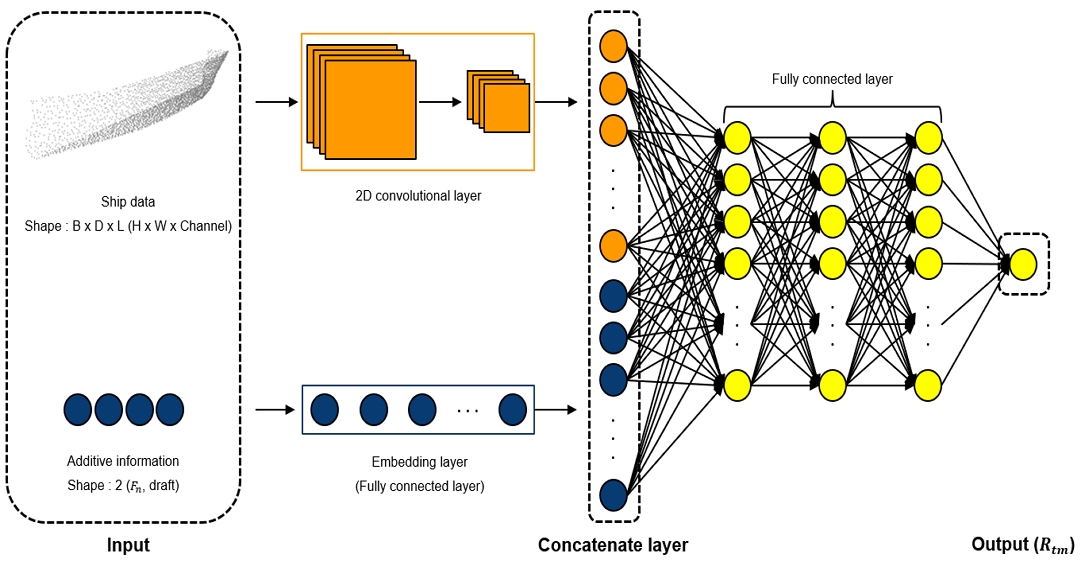
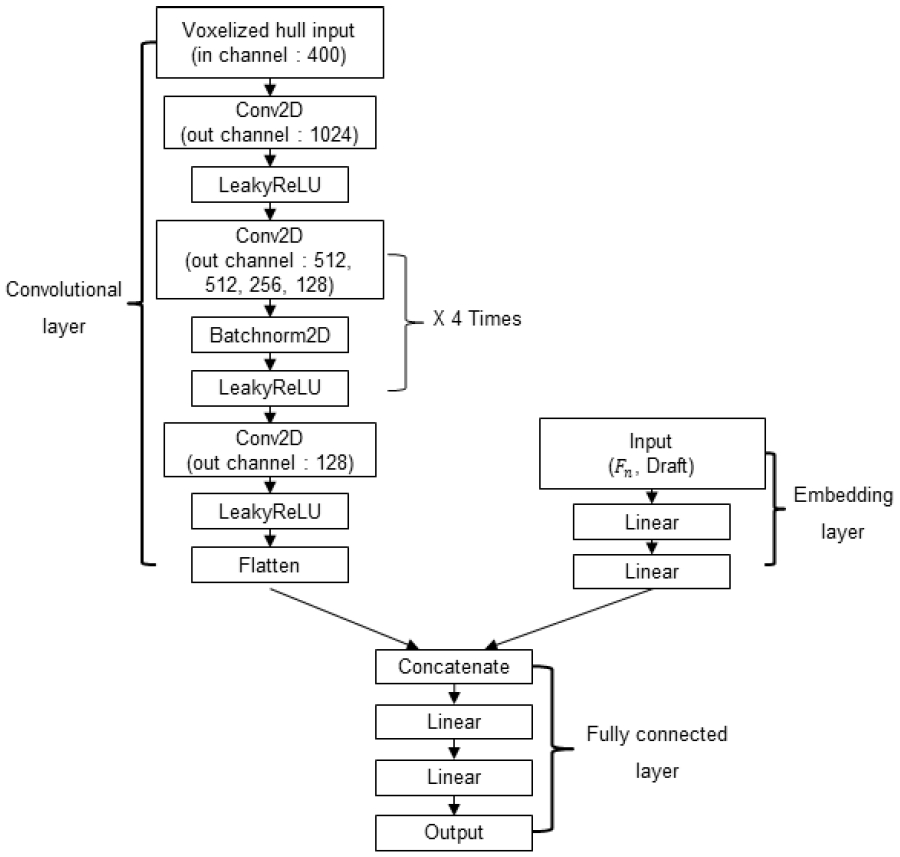
본 연구에서 제안하는 딥러닝 모델의 핵심은 3D CAD 데이터 형태의 선형을 복셀화하여 인공신경망 활용에 유리한 형태로 변환한 점과 저항 성능에 영향을 미칠 수 있는 부가 정보를 임베딩 기법을 통해 딥러닝 모델에 적용한 점으로 나눌 수 있으며 이를 Fig. 1에 간략하게 도시하였다. 본 연구의 딥러닝 모델에서 선박의 형상(input)은 합성곱 층(2D convolutional layer)을 이용해 학습하며 Froude number(이하, Fn), 흘수(이하, Draft)와 같이 저항 성능과 상관관계가 있는 부가 정보(input)는 임베딩 층(embedding layer)을 통해 학습한다. 이렇게 별개로 학습되어진 선박의 형상과 부가 정보는 완전연결층(fully connected layer)을 거치면서 취합되고 모형선의 전저항(output)과 연관되도록 구성되었다. 특히, Fig. 1과 같이 여러 종류의 유사한 입력값을 가지는 인공신경망 모델을 다중 입력 모델(multi-input model)이라 한다.
2.2 합성곱 신경망
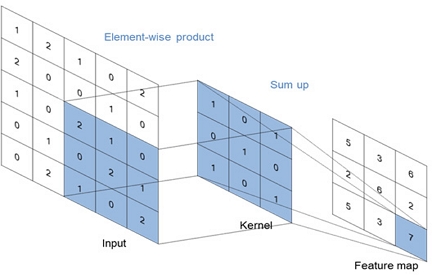
합성곱 신경망이란 대뇌의 시각피질 구조를 모방하여 만든 방법론으로 이미지 또는 영상 처리에 주로 활용된다. 합성곱 신경망을 딥러닝 기법 연구에 활용할 때 통상적으로 합성곱(convolution) 연산, 활성화 함수(activation function), 풀링(pooling) 연산을 순서대로 반복 배치해 깊은(deep) 인공신경망을 구성하고 마지막에 완전연결층을 통해 분류 또는 회귀를 수행한다 (Krizhevsky et al., 2017). 이때, 합성곱 연산은 이미지 또는 영상의 특징을 추출하는 역할을 한다. 즉, Fig. 2와 같이 커널(kernel)이라는 n x m 크기의 행렬을 활용해 높이 x 너비 크기의 이미지를 처음부터 끝까지 훑으면서 겹쳐지는 부분의 각 이미지와 커널의 원소값을 곱하고 이를 모두 합한 값을 출력으로 정의한다.
본 연구에서 선박의 형상은 복셀화를 통해 이미지와 같이 다중 채널을 가지는 행렬의 형태로 표현되고, 합성곱 신경망을 통해 학습된다. 선형의 복셀화는 추후 3장 데이터 구성에서 자세히 기술하고자 한다.
2.3 임베딩
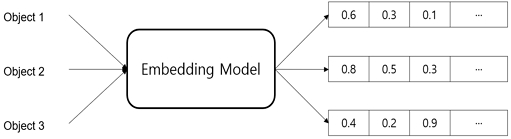
임베딩은 주로 자연어 처리 분야에서 활용되는 기법으로 단어, 문장, 숫자 같은 변수를 벡터로 표현하는 방법을 의미한다. 특히, 단어나 문장을 표현하는 문자열 자료형을 가진 데이터는 딥러닝 모델에 사용되는 벡터로 표현하기 힘들기 때문에 임베딩 기법을 활용해 특정 값을 지니는 벡터로 변환한 후 딥러닝 모델에 적용한다. 이 때문에 자연어처리 분야에서는 워드 임베딩(word embedding)이라는 표현이 사용된다. 숫자 데이터의 경우에도 데이터의 값 자체를 벡터화하여 인공신경망에 그대로 적용하게 되면 해당 벡터가 갖는 차원이 한정되기 때문에 해당값이 딥러닝 모델의 출력값에 직접적인 영향을 줄 수 있다. 따라서 이를 해결하기 위해 임베딩 기법의 활용이 필요하다. Pytorch (Paszke et al., 2019) 같은 딥러닝 프레임워크에서 임베딩 모듈을 지원하며, 임베딩 과정의 예시를 Fig. 3에 나타내었다. 딥러닝 프레임워크에서 제공하는 임베딩 함수는 주로 자연어처리에 초점이 맞춰져 있기 때문에 Fn, Draft, 선속 등과 같은 실수 데이터의 입력에 그대로 적용되기 어렵다.
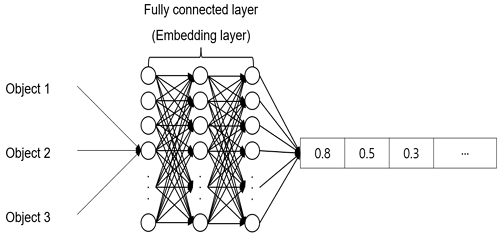
따라서 본 연구에서는 인공신경망의 기초가 되는 완전연결층을 활용해 부가 정보(Fn, draft)가 학습에 활용되도록 구현했다. Fig. 4에는 완전연결층을 적용한 임베딩 과정을 도시하였다. 부가 정보는 완전연결층을 통해 손실 함수가 최소화되는 방향으로 학습되며, 이후 학습된 부가 정보는 합성곱 신경망을 통해 차원이 축소된 선형 정보와 결합된다. 완전연결층을 활용해 딥러닝 프레임워크에서 지원하는 임베딩 함수로 대체함으로써 실수형태의 데이터를 원하는 차원으로 벡터화하였다.
3. 데이터 구성
3.1 데이터 개요
본 연구에서 딥러닝 모델의 입력값으로 사용되는 학습 데이터는 복셀화된 선박의 형상 데이터, 부가 정보(Fn, Draft) 데이터이고, 출력값은 모형선의 전저항(RTM) 데이터로 총 세 가지이며 이를 Table 1에 나타내었다. 입력값과 출력값의 결정에 관한 내용은 4장에 상세히 기술하였다.
3.2 선형 데이터의 복셀화
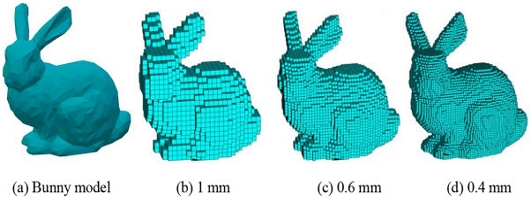
복셀(voxel)이란 volume과 pixel의 합성어로 픽셀을 3D로 구현한 것이다. 3차원 기하학적 형상 정보를 정규 격자 내 픽셀 단위로 표현한 것으로써, 이런 형태로 변환하는 과정을 복셀화(voxelization)라고 한다. 복셀화는 주로 의료영상 처리 분야에서 많이 활용되며, 3차원 오브젝트의 내부 정보를 묘사하거나 3차원 오브젝트를 행렬 형태로 변환할 때 유용하다. Fig. 5는 복셀화의 예시를 나타낸 것으로 복셀화된 결과는 사용자가 정의한 해상도에 따라 상이한 형태를 띄게 된다.
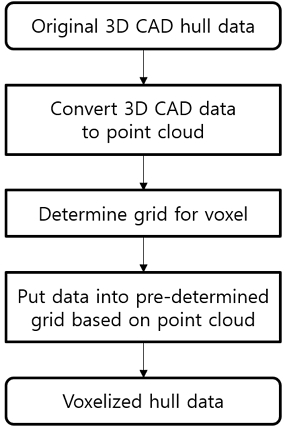
조선·해양 분야에서도 복셀화를 활용한 연구가 진행된 사례가 있는데 Janßen et al. (2015)은 수치해석을 위해 구성된 격자에 삼각형 표면 메쉬를 매핑하는 복셀화 방법을 제안한 바 있다. 본 연구에서 복셀화는 선체 형상을 길이 x 폭 x 깊이의 3차원 텐서로 표현하기 위해 적용하였으며, 이러한 표현법은 선박의 공간적 특징을 추출하기에 용이하므로 결과적으로 합성곱 신경망의 입력 데이터로 적용하기에 유리한 측면이 있다. 3차원 선형 정보의 복셀화를 위해 본 연구에서 적용한 라이브러리는 Open3D (Zhou et al., 2020)이다. Fig. 6은 선체 형상을 복셀화하는 과정을 도식화한 것이다. 먼저, CAD 자료 기반의 형상을 포인트 클라우드로 변환시키고 이를 사전에 크기가 결정된 3차원 격자에 대입시켜 격자 셀들의 포인트 포함 여부를 기준으로 1 또는 0의 값이 할당되도록 절차를 구성하였다.
3.3 부가 정보 데이터
앞서 언급한 바와 같이 임베딩을 통한 딥러닝 모델의 학습에 사용된 두 가지 부가 정보 데이터는 Fn와 Draft이다. 오프셋 데이터를 합성곱 신경망의 입력 데이터로 활용하여 선박의 잉여 저항을 예측한 연구 (Kim et al., 2022a)에서는 부가 정보로 선박의 주요 제원에 해당되는 길이-폭비(L/B), 폭-흘수비(B/T), 길이-흘수비(L/T), 선수벌브-선박길이비(BulbL/LBP), Fn 등이 사용되었다. 하지만 본 연구에서는 복셀화를 통해 선박의 형상적 특성이 묘사될 수 있다고 판단했기 때문에 선박의 기본 제원 정보 이외에 저항 성능과 직접적인 연관성이 있는 2가지 정보만을 활용하였다.
공개 선형인 KCS(KRISO Container Ship)의 원본 CAD 데이터와 이를 복셀화시킨 결과를 Fig. 7에 함께 도시하였다.
3.4 저항 데이터 산출 및 검증
본 연구에서 학습데이터 확보를 위해 필요한 선박의 저항 성능 데이터는 상용 유체 해석 프로그램인 STAR-CCM+(Ver. 15.06)를 활용하여 산출하였다. STAR-CCM+는 대형 조선소 및 조선·해양 관련 연구기관 등에서 선형과 프로펠러의 설계, 성능 추정 시 많이 사용되는 상업용 S/W이다. 그런데 수치해석을 이용해 다양한 선형의 저항 성능 데이터를 확보하기에 앞서 수치해석 기법의 신뢰성 검증이 선행되어야 한다고 판단하였다. 이를 위해 선형 정보와 모형시험 결과가 공개되어 있는 KCS를 대상선으로 선정하였다. 수치해석은 RANS방법을 기반으로 자유수면이 고려되는 비정상해석(unsteady simulation)이 수행되었으며 기본적인 수치해석기법은 Table 2에 정리하였다.
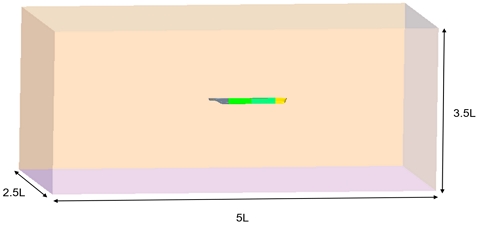
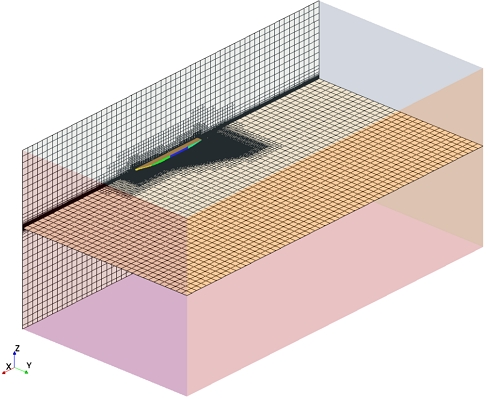
수치해석 시 사용된 계산 영역은 Fig. 8에 나타내었다. 도시된 계산 영역은 모형선의 길이(L)로 무차원화하였고, X(선박의 길이방향), Y(선박의 폭방향), Z(수심 방향) 방향으로 각각 5L, 2.5L, 3.5L의 크기를 가지고 있다. 또한 수치해석 시 계산시간의 단축을 위해 선박의 반 폭만 해석하였고 해석 결과로부터 산출된 저항을 2배 하여 해당 모형선의 전저항(RTM)을 얻었다.
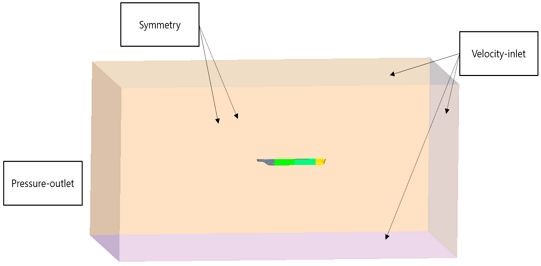
경계조건은 Fig. 9에 나타낸 바와 같이 선박의 전방면, 상부면, 하부면에는 속도유입 경계조건(velocity-inlet)을, 후방면은 압력유출 경계조건(pressure-outlet)을 부과하였고, 양쪽 측면에는 대칭경계조건(symmetry)을 각각 적용시켰다.
Fig. 10에 나타낸 바와 같이 비정렬 격자계가 구성되었으며 자유수면의 사실적인 모사를 위해 수선면 근처의 격자계는 조밀하게 분포시켰다. 시간 간격(time step)은 0.025초로 설정하고 대상 선박의 저항이 충분히 수렴되었다고 판단되는 80초까지 수치 해석이 진행되었다. 모형선의 전저항(RTM)은 계산 종료 시점을 기준으로 마지막 10초간 얻어진 전저항 데이터를 평균하여 산출하였다.
Table 3에는 KCS 선형을 대상으로 수치 해석과 모형 시험에서 각각 산출된 모형선의 전저항(RTM), 전저항계수(CTM)를 비교하였다. 모형시험 결과는 Feng et al. (2020)의 논문을 참고하였으며 선속, 24Knots 조건에서 수치해석과 모형시험으로부터 도출된 전저항계수(CTM)의 차이는 0.1% 이내임을 확인할 수 있었다. 이로부터 딥러닝 학습용 데이터 생성을 위한 수치해석 기법의 신뢰성이 확보되었다고 판단하였다.
3.5 입·출력 데이터 수집
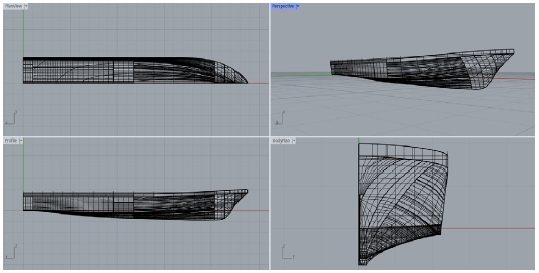
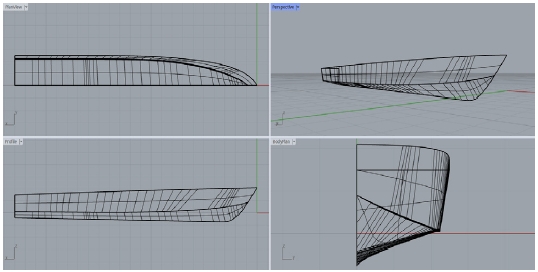
본 연구에서 정의된 선종은 순찰선, 조사선, 컨테이너선, 탱커 등으로 Orca3D 소프트웨어를 활용해 선형을 생성하였다. Orca3D는 Rhino3D라는 CAD S/W의 plug-in 모듈로 선형 설계와 페어링(fairing), 유체정역학(hydrostatics), 비손상 복원성(intact stability) 해석이 가능하고 특히, 사용자는 선종 및 주요 치수 값의 입력을 통해 선형을 용이하게 생성시킬 수 있다. Fig. 11에는 순찰선의 기준 선형을, Fig. 12에는 Orca3D를 활용해 복원한 순찰선 선형을 나타내었다. 본 연구에서는 선종별로 정의된 기준 선형을 기반으로 선박의 길이, 폭, 높이에 변화를 주면서 여러 선형을 생성했다. 이때, 변형 범위는 선종 별로 기준 선형의 제원을 고려하여 결정하였으며 컨테이너선, 순찰선, 조사선을 대상으로 각각 196개, 12개, 12개 등 총 220개의 선형 데이터를 생성하였다. 추가로, 탱커 선형의 경우 선박의 배수량 변경을 통해 21개의 선형 데이터를 정의하였다. 따라서 본 연구에서는 총 241개의 선형 데이터가 활용되었으며, 각 선종별 선속, 길이, 폭, 높이의 최대/최소값 등 선형의 변화 범위는 Table 4에 나타내었다.
수치해석은 모형선 축척에서 수행되었으며, 컨테이너선은 31.599, 탱커는 17.400, 순찰선 및 조사선은 5.950의 축척비(Scale ratio)를 각각 가진다. 본 연구에서 제안하는 방법이 고정된 선속에서 제원만 변화되는 상황과 선속 및 제원이 함께 변화되는 상황 모두에서 신뢰할만한 결과를 도출하는지 확인하고자 컨테이너선은 모두 24Knots로 선속을 고정시킨 반면, 순찰선, 조사선 및 탱커는 저속영역에서 고속영역까지 선속의 변화를 고려하였다. 또한 결과의 신뢰성을 위해 복셀화된 선형 및 부가정보-저항 쌍 데이터의 수가 유사한 수준이 되도록 생성하였다. 즉, 컨테이너선의 경우 196개의 쌍 데이터를 확보하였고, 탱커, 순찰선, 조사선은 각각 85개, 48개, 48개 등 총 181개의 쌍 데이터를 확보하였다.
4. 비교 시험
본 연구에서 제안하는 복셀화 된 선형 정보를 합성곱 신경망의 입력으로 활용하는 방법론과 기존의 매개변수 표현법을 사용하는 방법론 간의 예측 정확도를 비교하는 연구를 수행하였다. 그리고 두 방법론 간의 우열을 판단하기 위한 값으로 결정계수(R2)를 정의하였다. 결정계수는 회귀 모델에서 독립변수(딥러닝 모델의 예측값)가 종속변수(수치해석을 통해 얻은 관측값)를 얼마만큼 설명해 주는지를 나타내는 지표이며, 결정계수의 값은 통상 0에서 1사이의 값을 가진다. 이때, 값이 0에 가까울수록 회귀식의 정확도가 낮고, 1에 가까울수록 정확도가 높다는 것을 의미한다. 결정계수의 정의는 식 (1)에 나타내었으며 SST(Total sum of squares)는 관측값에서 관측값의 평균을 뺀 값들의 제곱 합이며 SSR(Residual sum of squares)은 관측값에서 예측값을 뺀 값인 잔차(residual)의 제곱 합을 의미한다.
| (1) |
4.1 저항 예측 모델
Fig. 13에는 본 연구에서 활용한 신경망의 구조를 나타내었다. 신경망의 입력값은 앞서 기술한 바와 같이 선형과 부가 정보로 구성된다. 복셀화와 합성곱 신경망을 활용해 선형 특징을 추출하고, 부가 정보는 두 개의 선형층(linear)을 거쳐 선박의 형상 정보와 결합층(concatenate layer)에서 합쳐진다. 완전연결층의 각 사이에는 ReLU(Rectified Linear Unit) 활성화 함수를 사용하였다. 또한 임베딩 층과 완전연결층의 가장 마지막 단계에는 예측 값을 0에서 1 사이로 반환하는 Sigmoid 활성화 함수를 사용했다. Fig. 13의 합성곱 신경망에서 2D 합성곱 신경망 사이에 존재하는 활성화 함수인 LeakyReLU(Leaky Rectified Linear Unit)는 앞서 언급한 ReLU 함수와 유사하지만 입력값이 0 이하이면 사전에 정의된 양의 기울기를 사용하는 일차 함수의 해당 값으로 반환하고, 0 이상이면 그대로 반환하도록 정의되어 있다. Fig. 13의 또 다른 활성화 함수인 Batchnorm2D는 각 배치 단위별로 입력 데이터가 다양한 분포를 가지더라도 이들 데이터의 평균과 분산을 이용해 정규화시키는 역할을 한다. 회귀 문제에서 주로 사용되는 평균제곱오차(Mean Square Error, MSE)를 활용하여 손실함수를 정의하였다. 평균제곱오차란 예측값과 관측값의 차이 즉, 오차를 제곱해 평균으로 나눈 값이다. 손실함수를 통해 전체 인공신경망 모델을 평가하고 최적화 기법을 통해 학습한다. 최적화는 경사 하강법 기반의 연산(Adam optimizer)을 통해 수행되었다. 신경망 모델의 출력 값은 최대-최소 역정규화를 통해 저항 값으로 변환하였다. 신경망의 학습 시 사용된 초모수(hyper parameter)는 Table 5에 나타내었다.
수치해석을 통해 수집한 선체 및 부가정보-저항 쌍 데이터를 70%, 20%, 10%의 비율로 학습, 검증, 테스트 데이터로 각각 구분하였다. 제안된 인공신경망으로 1회 학습 수행 시 약 600초의 시간이 소요되었으며, 이때 CPU는 AMD Ryzen 9 3900X 12-Core Processor, GPU는 NVIDIA GeForce RTX 2080 Ti x 2, RAM은 64GB 사양을 가지는 서버를 사용하였다.
4.2 방법론 비교
본 연구에서 제안하는 복셀화 기반의 방법론과 기존의 매개변수 표현법을 사용하는 방법론으로부터 각각 도출된 저항성능 예측 결과를 비교하였다. 매개변수 표현법은 선박의 형상을 숫자 지표로 나타내기 때문에 선박의 형상을 나타낼 수 있는 적절한 매개변수의 선정이 중요하다. 본 연구에서는 앞선 연구들을 참조하여 매개변수들을 결정하였으며 이를 Table 6에 나타내었다. 또한, Table 7에는 매개변수를 통한 저항 성능 예측 모델에 활용한 초모수를 나열하였다.
예측 정확도 비교를 위해 각 방법론 별로 10회 새롭게 학습하였으며, Fig. 14는 각 방법론 별로 산출된 결정계수 값을 나타낸다. 본 연구에서 제안된 방법으로 도출된 결과 중 가장 예측 성능이 우수한 경우의 결정계수는 0.996이었고, 매개변수 기반 방법을 이용하여 도출한 결과 중 가장 높은 결정계수는 0.871이었다. Table 8에는 10번의 학습 시 방법론 별로 산출된 결정계수 값을 모두 나타내었다. 본 연구에서 제안한 방법론으로부터 도출된 결정계수는 매개변수 기반의 방법으로 얻은 결정계수에 비해 전체적으로 우수한 결과를 보이고 있으며, 각 학습 회차 간의 편차도 적었음을 확인할 수 있었다. 이로부터 본 연구에서 제안한 방법이 일관성 및 안정성 측면에서 장점이 있다고 판단된다.
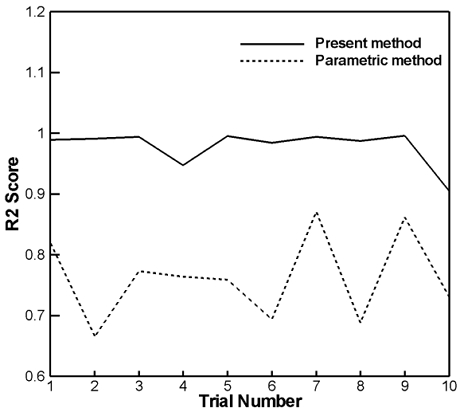
Comparison of R2 scores in presented method deep learning model and parameter-based deep learning model
본 연구에서 제안한 방법과 매개변수 표현 방법으로부터 산출된 결과 중 가장 높은 결정계수 값을 보였던 경우의 일부 결과를 Table 9에 각각 나타내었다. Table 9의 관측값(Observation)은 수치해석을 통해 산출한 모형선의 전저항(RTM)을 의미한다. 수치해석을 통해 수집된 총 377개의 선형 및 부가정보-저항 쌍 데이터 중 10%에 해당하는 테스트 데이터 37개 중 12개의 데이터를 무작위로 선택하여 나타낸 것이다. 비교 결과, 선박의 크기에 따라 두 방법론 간의 예측 경향은 차이를 보였다. 본 연구에서 제안한 기법의 경우 선박의 크기에 상관없이 관측값과의 차이가 일정한 수준 이내로 관찰되는 반면, 매개변수 기반의 방법은 대상 선박의 크기에 따라 오차 수준의 편차가 컸다. 또한 고정된 선속에서 선형의 변화만 고려된 컨테이너선의 경우, 본 연구에서 제안된 기법으로부터 산출된 오차가 매개변수 기반의 방법으로부터 산출된 오차보다 적었다. 통상적으로 선형 설계 시 목표 선속에서 선형을 변경해가면서 최적 선형을 도출하는데, 그런 측면에서 본 연구에서 제안하고자 하는 합성곱 신경망과 복셀화를 활용한 방법이 매개변수 기반 방법보다 유리한 측면이 있다고 판단된다.
5. 결 론
본 연구에서는 수치해석과 유사한 수준의 정확도를 유지하면서도 통계 모델과 같이 짧은 시간 내에 선박의 저항 성능이 예측 가능한 인공신경망 기반의 방법론을 제안하고자 하였다. 즉, 선형의 복셀화와 합성곱 신경망을 활용하여 선체의 형상적 특징이 효과적으로 학습될 수 있도록 유도하였다. 본 연구에서 제안하는 방법론의 성능 및 적용 가능성을 확인하고자 기존의 매개변수 기반 방법론으로부터 도출된 저항성능 예측 결과와 비교하였다. 두 모델의 학습, 검증, 테스트를 위하여 다수의 수치해석이 먼저 수행하였으며 이를 통해 선체 및 부가정보-저항 쌍 데이터를 확보하였다. 방법론의 예측 성능을 판단하는 지표로는 결정계수가 정의되었으며, 제안된 방법론과 기존의 매개변수 기반 방법론에서 도출된 가장 높은 결정계수의 값은 각각 0.996, 0.871이었다.
통계 데이터 기반의 회귀 모델을 평가할 때 적용하는 통상적인 기준에서는 두 방법론 모두 허용 가능한 수준의 정확도를 보여주었지만 제안된 방법론의 결정계수 값이 약 0.125 더 높았다. 방법론 간의 비교를 통해 확인된 향상된 예측 성능은 다양한 대안을 탐색해야 하는 선박의 초기 설계 단계에서 그 활용도가 높을 것으로 판단된다. 물론, 데이터 수와 품질이 결과에 큰 영향을 미칠 수 있는 인공신경망의 특성상 신뢰성 높은 데이터의 수집이 지속적으로 요구된다. 이를 위해 다양한 선형 및 선속에서 관련 데이터를 계속하여 확보해 나갈 계획이며, 이를 축적, 학습에 활용한다면 더욱 향상된 예측 정확도와 강건성(robustness)을 갖는 모델로 개선될 가능성이 있다고 판단된다.
또한 계획 중인 향후 연구로 선종에 따른 예측 성능의 변동성을 줄이기 위하여 다중 작업(multi-task) 데이터에 특화된 메타러닝(meta-learning)기법을 활용하는 연구와 노드(node)와 간선(edge)들로 선체를 표현하는 그래프 신경망(Graph Neural Networks, GNN)기반의 방법론과 본 연구에서 제안한 방법론 간의 비교 연구 등이 있다.
Acknowledgments
이 논문은 2022년도 정부(교육부)의 재원으로 한국연구재단 기초연구사업의 지원을 받아 수행된 연구임(No.2020R1G1A1014172).
References
-
Beşikçi, E.B., Arslan, O., Turan, O. and Ölçer, A.I., 2016. An artificial neural network based decision support system for energy efficient ship operations. Computers & Operations Research, 66, pp.393-401.
[https://doi.org/10.1016/j.cor.2015.04.004]

-
Choi, M.J., De Silva, L.W. A. and Yamaguchi, H., 2019. Artificial neural network for the short-term prediction of Arctic sea ice concentration. Remote Sensing, 11(9), pp.1071.
[https://doi.org/10.3390/rs11091071]

-
Feng, D., Ye, B., Zhang, Z. and Wang, X., 2020. Numerical simulation of the ship resistance of KCS in different water depths for model-scale and Full-scale. Journal of marine science and engineering, 8, pp.745
[https://doi.org/10.3390/jmse8100745]

-
Grabowska, K. and Szczuko, P., 2015,. Ship resistance prediction with artificial neural networks. In 2015 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA), Poznan, Poland, 28 December 2015.
[https://doi.org/10.1109/SPA.2015.7365154]

-
Janßen, C.F., Koliha, N. and Rung, T., 2015. A fast and rigorously parallel surface voxelization technique for GPU-accelerated CFD simulations. Communications in Computational Physics, 17(5), pp.1246-1270.
[https://doi.org/10.4208/cicp.2014.m414]

-
Kim, Y.C., Kim, K.S., Hwang, S.H., and Yeon, S. M., 2022a. Prediction of Residual Resistance Coefficient of Ships using Convolutional Neural Network. Journal of the Society of Naval Architects of Korea, 59(4), pp.243-250.
[https://doi.org/10.3744/SNAK.2022.59.4.243]

-
Kim, H.C. and Park, H.G., 2015. Practical application of neural networks for prediction of ship's performance factors. Journal of Ocean Engineering and Technology, 29(2), pp.111-119.
[https://doi.org/10.5574/KSOE.2015.29.2.111]

-
Kim, J.H., Roh, M.I., Kim, K.S., Yeo, I.C., Oh, M.J., Nam, J.W., Lee, S.H. and Jang, Y.H., 2022b. Prediction of the superiority of the hydrodynamic performance of hull forms using deep learning. International Journal of Naval Architecture and Ocean Engineering, 100490.
[https://doi.org/10.1016/j.ijnaoe.2022.100490]

-
Krizhevsky, A., Sutskever, I. and Hinton, G. E., 2017. Imagenet classification with deep convolutional neural networks. Communications of the ACM, 60(6), pp.84-90.
[https://doi.org/10.1145/3065386]

-
LeCun, Y., Bengio, Y, and Hinton, G., 2015. Deep learning. Nature, 521(7553), pp.436-444.
[https://doi.org/10.1038/nature14539]

- Panda, J.P., 2021. Machine Learning for Naval Architecture. Ocean and Marine Engineering. arXiv preprint arXiv:2109.05574, .
- Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., Killeen, T., Lin, Z., Gimelshein, N., Antiga, L., Desmaison, A., Kopf, A., Yang, E., DeVito, Z., Raison, M., Tejani, A., Chilamkurthy, S., Steiner, B., Fang, L., Bai, J. and Chintala, S., 2019. Pytorch: An imperative style, high-performance deep learning library. Advances in neural information processing systems, 32.
-
Wason, R., 2018. Deep learning: Evolution and expansion. Cognitive Systems Research, 52, pp.701-708.
[https://doi.org/10.1016/j.cogsys.2018.08.023]

-
Zhao, H., Zhang, W., Sun, H. and Xue, B., 2019. Embedded deep learning for ship detection and recognition. Future Internet, 11(2), pp.53.
[https://doi.org/10.3390/fi11020053]

-
Zhou, Y., Lu, H., Wang, G., Wang, J. and Li, W., 2020. Voxelization modelling based finite element simulation and process parameter optimization for Fused Filament Fabrication. Materials & Design, 187, 108409.
[https://doi.org/10.1016/j.matdes.2019.108409]