[ Article ]

Journal of the Society of Naval Architects of Korea - Vol. 59, No. 1, pp.55-63

ISSN: 1225-1143 (Print) 2287-7355 (Online)

Print publication date 20 Feb 2022

Received 20 Oct 2021 Revised 22 Dec 2021 Accepted 09 Jan 2022

DOI: https://doi.org/10.3744/SNAK.2022.59.1.55

좌초선의 이초 계획 수립을 위한 정적 평형 기반의 자세 계산 방법

이우용¹ ; 함승호¹^{, †}

; 구남국²

1창원대학교 조선해양공학과
2동의대학교 조선해양공학과

A Calculation Method of the Ship’s Posture Based on the Static Equilibrium for the Refloating Plan of the Stranded Ship

Woo-yong Lee¹ ; Seung-Ho Ham¹^{, †}

; Namkug Ku²

1Department of Naval Architecture and Marine Engineering, Changwon National University
2Department of Naval Architecture and Ocean Engineering, Dong-eui University

Correspondence to: ^†Seung-Ho Ham, shham@changwon.ac.kr

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

A stranded ship means a ship which is stuck on a rock or a seabed, and cannot move by itself. The lightening plan is required to refloat the stranded ship. For this, we have to understand the forces and moments acting on the ship, which is composed of the gravity, buoyancy, and reaction force due to the touched area below the ship. This study defines those forces and moments, and proposed the calculation method to find the posture based on the static equilibrium. It is divided by two steps. In the first step, the magnitude and position of the reaction force are obtained based on the known information such as initial trim angle and draft of the ship. In the second step, the reaction force and the posture is calculated due to the three cases such as addition, reduction, and movement of the cargo. It is applied to three examples in order to calculate the reaction force, and the trim angle due to changes of the cargo. As a results, we successfully obtain the magnitudes and positions of forces acting on the stranded ship and to check the posture of the stranded ship.

Keywords:

Stranded, Refloating, Static equilibrium, Reaction force, Freeing force

키워드:

좌초, 이초, 정적 평형, 지면반력, 이초력

1. 서 론

연안에서의 급격한 해상 상태 변화와 항해사 조종 미숙 등의 이유로 선박이 부두나 암석에 걸려서 움직이지 않거나 파손되는 상황이 빈번하게 발생하고 있다. 최근 Fig. 1의 사진과 같이 수에즈 운하에서 발생한 에버그린 마린(Evergreen Marine)사의 에버기븐(Ever Given)호의 좌초를 대표적인 예로 들 수 있다.

Fig. 1

Ever Given stranded in Suez Canal (URL : https://www.bbc.com)

이처럼 선박의 선저가 비의도적으로 육지에 닿게 되어 선박이 운용할 수 없는 상태에 놓이게 되는 것을 좌초라고 한다. 선박이 좌초될 경우 Fig. 2과 같이 선체가 정수 중 상태일 때보다 육상으로 많이 드러나게 된다.

Fig. 2

Stranding of general cargo ship Lysblink Seaways (URL : https://www.gcaptain.com)

좌초선을 접촉된 육지로부터 안전한 수역으로 구조하는 것을 이초라 한다. 앞서 언급한 것과 같이 좌초될 경우 선박의 선체가 수면 위로 드러나게 되는데, 이때 수면 위로 드러난 부피만큼의 부력의 손실이 생겨나고, 손실된 부력의 크기만큼 지면반력이 발생하게 된다. 좌초선을 이초하기 위해서는 스스로 배를 띄우거나 지면반력의 크기를 최소화시켜야 한다. 이를 위해 좌초선의 중량과 좌초선에 작용하는 부력, 지면반력의 크기를 계산하고, 선박 내 화물 제거 및 이동 또는 외부에서 화물을 추가하는 이초 계획 수립이 필요하다 (Varsami et al., 2012).

좌초된 선박을 이초하는 프로그램으로 Hebert-ABS에서 개발한 HECSALV와 HECSALV를 미군 사용에 적합하도록 변형한 POSSE가 대표적이다. 이러한 이초 프로그램은 국내 도입 및 적용하기에 큰 비용이 발생하게 되어 어려움이 따르고 있다. 현재 국내 연안에서도 좌초 사고가 빈번히 발생하고 있음에도 국내에서 이초에 대한 연구는 미흡한 실정이며, 쉽게 사용 가능한 이초 프로그램의 개발 사례도 없다. 한편, Lee (2014), Byun et al. (2001), Bartholomew (1992), Choi et al. (2000), Ham et al. (2015) 등에서 좌초선 인양과 관련된 연구들이 수행되었지만, 이초에 대한 역학적인 이론이나 자세 변화 등은 다루지 않았다. 따라서 본 연구에서는 좌초선에 작용하는 힘에 대해서 분석하고, 선박 내 화물의 변화를 통한 이초 계획을 수립함으로써 좌초선 이초 가능성을 확인하였다.

2. 정적 평형을 고려한 이초 해석 방법

2.1 좌초선에 작용하는 힘 분석

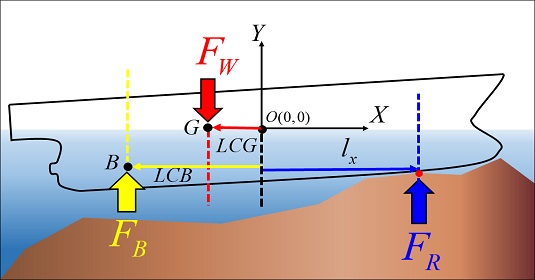
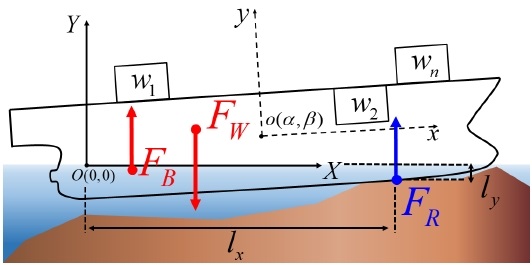
좌초선에 작용하는 힘은 선박의 중량(F_W), 부력(F_B), 그리고 선박이 좌초되면서 손실된 부력의 크기만큼의 지면반력(F_R)이 추가로 작용한다. 선박에 작용하는 힘은 Fig. 3에 표시하였으며 각 힘이 작용하는 위치는 LCG, LCB로 정의하며, 지면반력이 작용하는 위치와 global 좌표계의 원점 사이의 거리는 l_x로 정의한다.

Fig. 3

Forces and acting points on a stranded ship

좌초되지 않은 상태의 선박이 정적 평형을 이루기 위해서는 선박의 중량과 부력에 의한 힘 평형 방정식(식 (1))과 모멘트 평형 방정식(식 (2))을 만족하여야 한다 (Beer et al., 2016).

∑ F = - F W + F B = 0

(1)

∑ M = F W • L C G + F B • L C B = 0

(2)

하지만 좌초선의 경우 지면반력(F_R)이 추가되어 세 힘에 대한 힘과 모멘트 평형 방정식(식 (3), (4))를 만족해야 한다.

∑ F = - F W + F B + F R = 0

(3)

∑ M = F W • L C G + F B • L C B + F R • l x = 0

(4)

좌초선의 지면반력과 마찰계수(μ)를 통해 이초에 필요한 힘을 구할 수 있는데 이를 이초력(Freeing force: F_Free)이라 한다(Wilkins, 2021). 암초에 좌초된 경우 이초에 필요한 이초력의 크기는 아래의 식 (5)와 같다.

F F r e e = 1.12 μ F R

(5)

좌초선의 이초를 위해서는 지면반력(F_R)의 크기를 감소시켜 인양 시 이초력을 감소시켜야 한다. 만약 지면반력이 0일 경우 좌초선은 자력으로 부양이 가능하며, 스스로 좌초 상황에서 벗어날 수 있다.

2.2 이초 해석 과정

좌초 초기에 지면반력의 크기는 주어져 있지 않기 때문에 지면반력을 계산해야 한다. 선박이 좌초된 상태에서는 움직이지 않기 때문에 평형 방정식을 통해 지면반력의 크기와 작용점을 계산한다. 이후에는 지면반력을 줄이기 위해 화물을 이동시키거나 제거하고, 화물을 적재하여 발생하는 트림에 의한 이득이 침하량보다 클 경우에는 추가하기도 한다. 화물의 변화가 발생하면 선박의 무게 중심 위치가 변경되고, 이에 따라 자세가 변경되며 새로운 평형 자세를 찾게 되는데 이 과정에서 부력과 부력중심, 지면반력의 크기 또한 함께 변경된다.

본 연구에서는 이초 해석 과정을 크게 두 단계로 나누었다. 첫 번째 단계(Step 1)에서는 현재 좌초선의 상태를 기반으로 미지수인 초기 지면반력을 계산하고, 두 번째 단계(Step 2)에서는 선박 내 화물의 이동, 제거, 추가에 따른 선박의 자세와 지면반력의 변화를 계산하였다. 이어지는 절에서는 2차원 선박을 예시로 하여 각각의 단계를 상세히 설명한다.

2.3 [Step 1] 초기 지면반력 계산

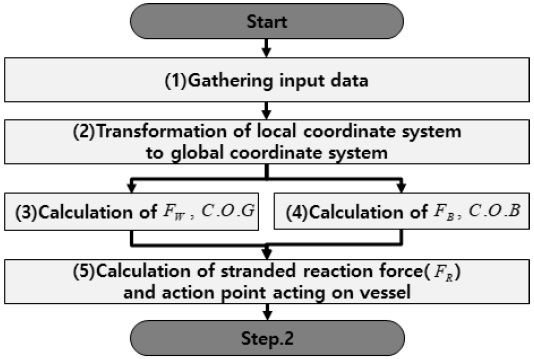
좌초선의 초기 지면반력을 계산하기 위한 세부 절차는 Fig. 4와 같다.

Fig. 4

Detailed procedure of the Step 1

첫 번째 단계는 입력 정보 수집이다(Fig. 4의 (1)). 좌초선의 현 상태를 기준으로 다음과 같은 입력 정보가 필요하다(Table 1).

Table 1

Input data for step 1

두 번째로 선박 형상을 사용하여 좌표 변환을 수행한다(Fig. 4의 (2)). Global 좌표계의 원점을 설정하고, 선박이 떨어져 있는 위치를 위치(α, β)로 정의하였다. 선박에 고정된 local 좌표계를 설정하고, 선박의 종경사각(θ)을 사용하여 선형을 구성하고 있는 각 점의 회전 변환과 평행 이동(식 (6))을 통해 global 좌표계에서의 위치를 계산한다. 이때 x_n, y_n은 선박의 hullform의 입력 좌표, x′_n,y′_n은 변환된 hullform의 좌표로 정의한다.

x n' y n' = α β + c o s θ - s i n θ s i n θ c o s θ x n y n

(6)

세 번째로 좌초선의 선박의 중량(F_W)과 선박의 중량 작용점(C.O.G) 계산을 수행한다(Fig. 4의 (3)). 좌초선의 중량은 좌초선의 LWT와 모든 화물의 중량을 더하여 구한다(식 (7)). 무게 중심은 LWT의 무게중심과 각 화물의 무게 중심을 이용하여 무게 중심계산식(식 (8))을 이용하여 계산한다.

F W = w L W T + ∑ i = 1 n w i

(7)

L C G = w L W T • L C G L W T + ∑ i = 1 n w i • x w i F W V C G = w L W T • V C G L W T + ∑ i = 1 n w i • y w i F W C . O . G = L C G, V C G

(8)

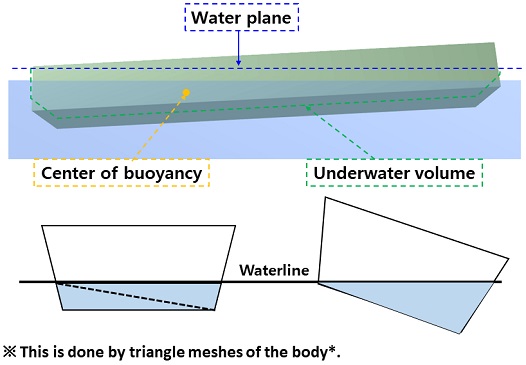
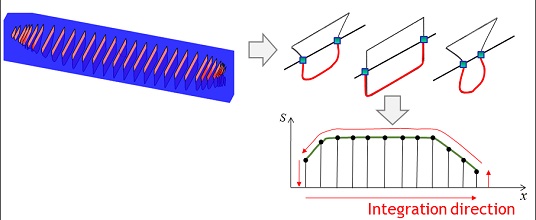
네 번째로 좌초선에 작용하는 부력(F_B)과 부력의 작용점(C.O.B)을 계산한다(Fig. 4의 (4)). 좌초선의 부력은 여러 방법을 통하여 계산된다. 삼각 메쉬로 구성된 형상과 수면의 교차 계산을 통해 직접 부피와 중심을 계산하는 방법 1(Fig. 5)과 offset table에 주어진 선형 정보를 기반으로 길이 방향으로 적분을 통해 부피와 중심을 계산하는 방법 2(Fig. 6)가 있다. 본 연구에서는 방법 1, 2를 상황에 따라 적절히 사용하여 부피와 중심을 계산하였다.

Fig. 5

Polyhedron integral method

Fig. 6

Offset table method

Step 1의 마지막으로 지면반력(F_R)의 크기와 작용점(l_x, l_y)을 계산한다 (Fig. 4의 (5)).은 앞서 계산한 선박의 중량(F_W)과 부력, 각 힘의 작용점들을 바탕으로 계산한다. 힘 평형 방정식 (식 (9))을 이용하여 좌초선의 지면반력의 크기를 계산하고, 식 (2)를 변형한 식 (10)을 이용하여 지면반력의 작용점을 계산한다. Fig. 7은 Step 1을 통해 계산된 좌초선에 작용하는 힘과 작용점, 좌초선의 자세를 나타낸다.

Fig. 7

Calculated force and acting point on stranded ship

F R = F W + F B

(9)

l x = F W • L C G - F B • L C B F R l y = F W • V C G - F B • V C B F R

(10)

2.4 [Step 2] 화물 이동에 따른 지면반력의 변화와 선박 자세 변화 계산

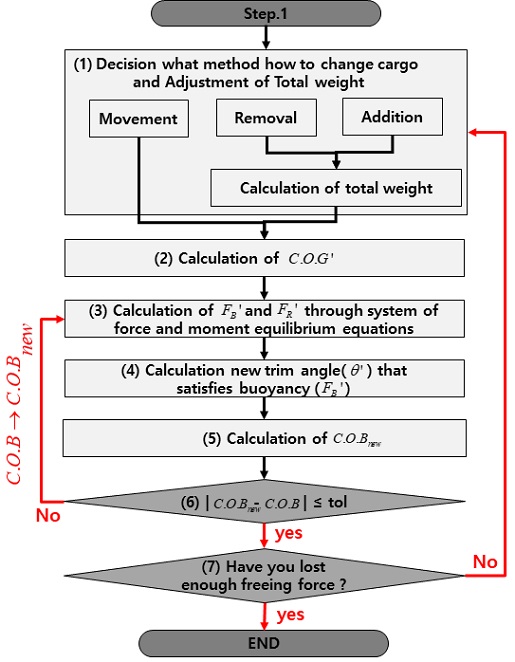
Step 1 과정에서 획득한 입력 정보를 바탕으로 좌초선의 중량, 부력, 지면반력의 크기와 각 힘의 작용점을 계산하였다. 이후 Step 2 에서는 화물의 이동, 제거, 또는 추가에 따른 선박의 자세와 지면반력의 크기를 계산한다. 선박의 무게 중심 변경에 따라 자세와 부력, 지면반력의 크기가 동시에 변경되기 때문에 평형 자세를 찾기 위해 반복법(iteration)을 사용하였다. 이에 대한 세부 절차는 Fig. 8과 같다.

Fig. 8

Detailed procedure of the Step 2

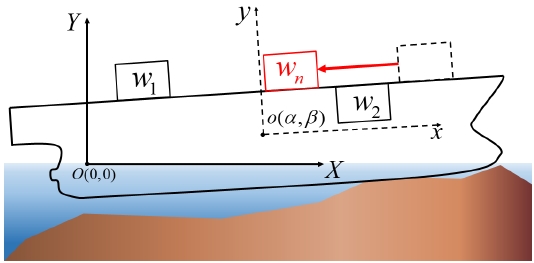
Step 2의 첫 번째는 중량 조정 단계이다(Fig. 8의 (1)). 중량 조정은 좌초선 내 화물의 이동(movement), 제거(removal)와 외부로부터 화물을 추가(addition)하는 세 방법을 이용하였다. 화물 이동은 좌초선의 중량 변화가 없다. 화물 제거와 추가의 경우 좌초선의 중량을 새로 계산한다. Fig. 9는 화물의 이동을 나타낸다.

Fig. 9

Movement of the cargo in the stranded ship

두 번째로는 새로 계산된 선박의 중량(F_{W_new})을 바탕으로 식 (9)를 사용하여 좌초선에 작용하는 중량의 작용점(C.O.G′)을 다시 계산한다(Fig. 8의 (2)).

세 번째로 새로 계산된 좌초선의 중량과 작용점을 이용하여 힘 평형 방정식(식 (1))과 모멘트 평형 방정식(식 (2))을 연립한 식 (11)과 (12)을 이용하여 화물의 변화로 인해 변경된 부력(F_B′)과 지면반력(F_R′)을 계산한다(Fig. 8의 (3)). 이때 좌초선의 지면반력 작용점은 변화하지 않으며, 좌초선의 부력의 작용점은 기존의 부력 작용점(C.O.B)과 동일하다고 가정한다.

F B' = L C G' - l x L C B - l x F W_n e w

(11)

F R' = L C G' - L C B l x - L C B F W_n e w

(12)

네 번째로 변경된 부력을 만족하는 선박의 자세를 계산한다(Fig. 8의 (4)). 선박은 좌초된 지점을 기준으로 경사 하게 되며 이때 식 (11)에서 구한 부력이 되도록 종경사각(θ′)을 변경한다. 해석적으로는 해를 구하기 어려우므로 수치적으로 반복 계산을 통해 오차가 0이 되는 θ′를 구해야 한다.

다섯 번째로 종경사각(θ′) 만큼 변화한 좌초선에 작용하는 부력의 작용점(C.O.B_new)을 새로 계산한다(Fig. 8의 (5)).

여섯 번째로 기존 부력의 작용점(C.O.B)과 새롭게 계산된 부력의 작용점(C.O.B_new)을 비교한다(Fig. 8의 (6)). 두 값의 차이가 tol 값보다 작을 때까지 반복 계산을 한다(식 (13)).

C . O . B n e w - C . O . B ≤ t o l

(13)

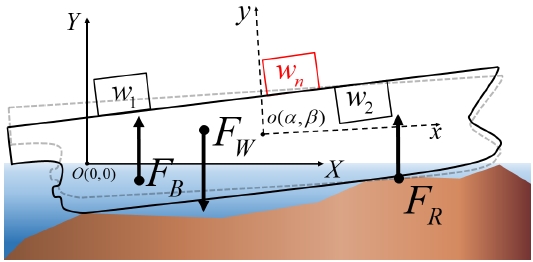
만약 오차가 tol 보다 클 경우, 새로 계산된 부력의 작용점을 Fig. 8의 (3) 과정의 부력의 작용점(C.O.B)으로 재설정하여 식 (13)을 만족할때까지 Fig. 8의 (3)~(5)의 과정을 반복한다. 만약 식 (13)을 만족할 경우, 그때의 중량(FW_new), 부력(F_B′), 지면반력(F_R′)과 각 힘의 작용점 C.O.G′, C.O.B_new를 좌초선에 작용하는 힘과 작용점으로 설정한다. 중량 조정에 의해서 변경된 좌초선의 자세와 작용하는 힘은 Fig. 10과 같다.

Fig. 10

Changes in the attitude of the stranded ship due to changes in cargo location.

마지막으로 충분한 이초력이 확보되었는지 확인한다(Fig. 8의 (7)). 지면반력에 의해서 계산된 이초력이 이초를 하는데 충분히 감소하였을 경우 해당 중량 조정 방법을 이초 계획으로 확정하며, 만약 이초력이 충분히 감소하지 않았을 경우 중량 조정 단계(Fig. 8의 (1))로 돌아가 이초가 가능할 때까지 화물을 조정한다.

3. 이초 해석 적용

3장에서는 3가지 선형에 대해 좌초 상황을 가정하였다. 3.1과 3.2에서는 직사각형 바지선과 사다리꼴 형상 선박에 대하여 2장에서 제안한 이초 해석 과정을 적용하고 결과를 검증하였다. 3.3에서는 6,300 TEU container ship에 이초 해석을 적용하였다.

3.1 직사각형 바지선

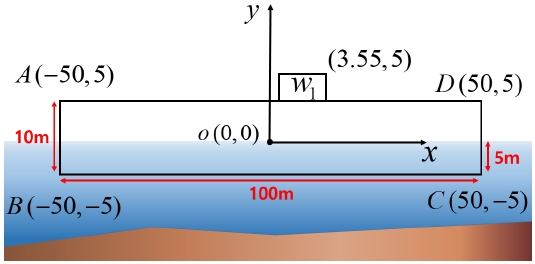
Fig. 11과 같은 직사각형 형상의 바지선에 이초 해석의 초기 지면반력 계산을 실행한다(Fig. 4). Step 1의 첫 번째 단계로 바지선의 좌초 시 수집된 입력 정보는 Table 2와 같다.

Fig. 11

State before the barge is stranded

Table 2

Input data of a barge

두 번째로 초기 지면반력을 계산하기 위하여 local 좌표계 상의 선박의 형상 좌표들을 종경사각(1°)과 global 좌표계 상에서 선박이 떨어져 있는 위치(0, 0.5) 값을 이용하여 global 좌표계로 변환하여 준다(Fig. 4-(2)). 좌표계 변환을 통하여 local 좌표계에서 global 좌표계로 변환된 선박의 형상은 Table 3과 같다.

Table 3

Transform the hullform from local coordinate system to the global coordinate system

세 번째로 좌초선의 변환된 형상과 cargo의 중량과 작용점을 바탕으로 바지선에 작용하는 중량과 작용점을 계산한다. 네 번째로 부력과 부력의 작용점을 계산하여 Table 4에 나타내었다.

Table 4

Weight, buoyancy and acting points on a barge

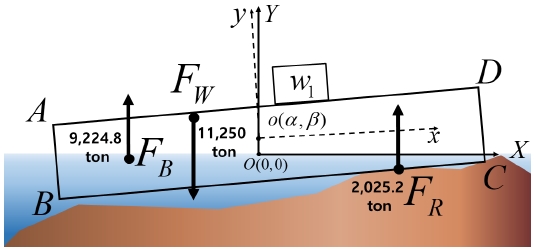
Step 1의 마지막 과정으로 최종 계산된 바지선의 지면반력과 지면반력 작용점은 Table 5와 같다. Table 4,5의 결과를 힘과 모멘트 평형식에 대입하여 정확하게 힘과 모멘트 평형을 이룬 것을 검증하였다. 그리고, 그때의 바지선의 자세는 Fig. 12와 같다.

Table 5

Calculation result of Step 1 of the stranded ship using program

Fig. 12

Forces and acting points on the stranded ship

Step 2의 첫 번째로 좌초선의 화물 조정 방법 중 화물 이동을 선택하였다. 좌초선의 화물은 local 좌표계 기준으로 (-50, 0) 위치로 이동하였다. 화물을 이동할 경우 좌초선에 작용하는 중량의 크기는 변화하지 않는다.

두 번째 과정으로 좌초선의 중량 작용점의 계산한다. 이때 좌초선의 중량과 그 작용점은 Table 6과 같다.

Table 6

The center of gravity of the barge changed due to cargo movement

세 번째로 화물 조정에 의해 변화한 새로운 부력(F_B′)과 지면반력(F_R′)을 계산한다. 계산된 힘의 크기는 Table 7과 같다.

Table 7

The newly calculated value of buoyancy and reaction force

네 번째로 새로운 부력을 만족하는 종경사각(θ′)을 계산한다. 좌초선의 종경사각은 Table 8과 같다.

Table 8

The size of trim angle that satisfies the new buoyancy

다섯 번째로 변화된 선박의 자세에 대한 부력의 작용점을 계산한다. 새로 계산된 부력의 작용점은 Table 9와 같다.

Table 9

The center of buoyancy of newly calculated barge

여섯 번째로 Step 2의 C.O.B값과 C.O.B_new 값을 비교하여 tol 값을 만족할 때까지 반복 계산한다. 반복계산을 통하여 계산된 좌초선의 자세와 힘, 작용점은 Table 10과 같다. 검증을 위해 Table 10의 결과를 힘과 모멘트 평형 방정식에 대입하면 정확하게 평형을 이루고 있음을 확인할 수 있다.

Table 10

The forces and acting points of the barge calculated by Step 2

마지막으로 좌초선의 이초에 필요한 이초력은 Table 11과 같다. 좌초 지점의 저질을 바위로 가정하고 마찰계수는 1.5를 사용하였다 (Bartholomew, 1992).

Table 11

The calculation result of freeing force acting on barge

3.2 사다리꼴 형상 선박

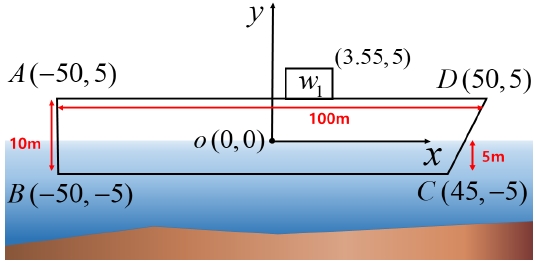
두 번째로 Fig. 13과 같은 사다리꼴 형상 선박에 대한 이초 해석을 수행하였다. Step 1 과정의 사다리꼴 단순 선박 형상의 입력 정보는 Table 12와 같다.

Fig. 13

Trapezoidal ship before stranded

Table 12

Input data of the trapezoidal ship

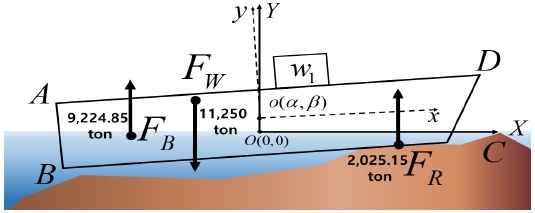
Step 1 과정을 통해 계산된 초기 지면반력의 크기와 좌초선에 작용하는 힘은 Table 13과 같다. Table 13의 결과를 힘과 모멘트 평형식에 대입하여 정확하게 힘과 모멘트 평형을 이룬 것을 검증하였다. 그때의 선박은 Fig. 14와 같다.

Table 13

Calculation result of Step 1 of the stranded ship using program

Fig. 14

Forces and acting points on the stranded ship(Step 1)

Step 2 과정에서 좌초선의 화물 W₁을 local 좌표계 기준으로 (-50, 0) 만큼 이동하였다. 화물 조정에 의해 변화된 힘과 각 힘의 작용점, 선박의 자세는 Table 14와 같다.

Table 14

The force and acting points of the trapezoidal ship calculated by Step 2

검증을 위해 Table 14의 결과를 힘과 모멘트 평형 방정식에 대입하면 정확하게 평형을 이루고 있음을 확인할 수 있다. 마지막으로 좌초선 이초에 필요한 이초력은 Table 15와 같다.

Table 15

The calculation result of freeing force acting on the trapezoidal ship

3.3 6,300 TEU container ship

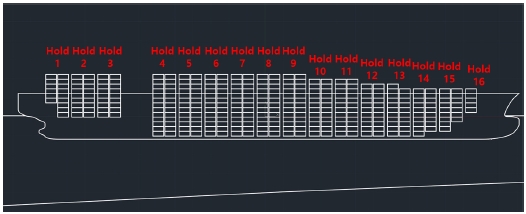
좌초선 내 화물의 다양한 변화와 실제 선박에 적용 가능성을 확인하기 위해서 6,300 TEU container ship 형상(Lee et al., 2016)에 이초 해석 방법을 적용하였다. 6,300 TEU container ship (14mt/TEU, 4,682TEU) 상태에서의 입력 정보는 Table 16과 같다. Table 17은 container ship cargo의 입력 정보이다.

Table 16

Input data of 6,300 TEU container ship

Table 17

Cargo data on 6,300 TEU container ship

Fig. 15에는 해석에 사용된 6,300 TEU container ship 형상과 각 cargo hold의 위치를 나타내었다.

Fig. 15

6,300 TEU container ship

6,300 TEU container ship의 입력 정보를 바탕으로 Step 1의 과정을 수행하였다. 좌초된 6,300 TEU container ship의 초기 지면반력, 좌초선에 작용하는 힘, 각 힘의 작용점은 Table 18과 같다. 좌초선의 부력은 hydrostatic table을 이용하는 부력계산 방법 2를 사용하여 trim과 draft에 따라서 보간하여 구하였다.

Table 18

Calculation result of Step 1 of stranded ship

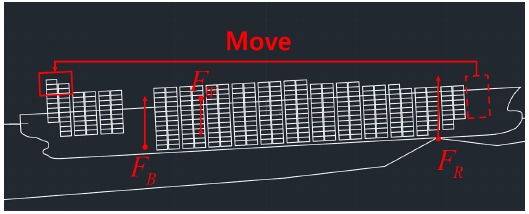
본 연구에서는 6,300 TEU container ship의 Step 2의 중량 조정 단계 화물의 이동, 제거 및 추가 세 방법에 대해서 모두 계산하였다. 첫 번째로 cargo hold 1의 화물을 cargo hold 16의 (-116.125, 23.35) 위치로 이동시켰다. 화물의 이동에 의한 좌초선의 Step 2 과정의 계산 결과는 Table 19와 같다. 그때의 좌초된 container ship의 자세는 Fig. 16과 같다.

Table 19

The result of calculating Step 2 of the container ship by cargo movement

Fig. 16

New attitude of the stranded ship by cargo movement

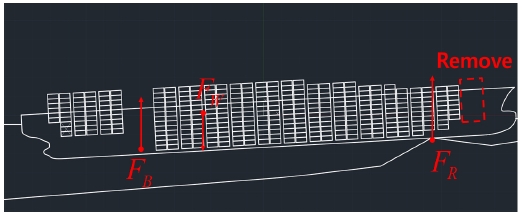
두 번째로 선수부 위치의 cargo Hold 1의 화물을 제거하였다. 화물 제거에 따른 Step 2 과정의 계산 결과와 자세를 Table 20과 같다. 그때의 좌초된 container ship의 자세는 Fig. 17과 같다.

Table 20

The result of calculating Step 2 of the container ship by cargo removal

Fig. 17

New attitude of the stranded ship by cargo removal

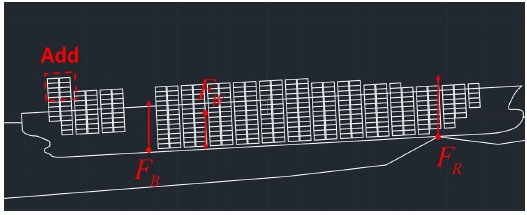
마지막으로 cargo hold 16에 새로운 화물(weight : 1,176 ton, C.O.G : (-115.466, 25.85))을 추가 시 Step 2 과정의 결과는 Table 21과 같다. 이 때 좌초된 container ship의 자세는 Fig. 18과 같다.

Table 21

The result of calculating Step 2 of the container ship by cargo addition

Fig. 18

New attitude of the stranded ship by cargo addition

4. 결 론

본 연구를 통하여 좌초된 선박의 정적 평형을 고려한 이초 계획 수립을 하고, 정적 평형을 고려한 좌초선 이초 해석을 시행하였다. 이초 해석을 초기 지면반력을 계산하는 step 1과 화물의 이동, 제거, 추가에 따른 반력의 변화와 선박 제세 변화 계산을 수행하는 step 2의 두 과정으로 분리하여 세부 계산과정을 제안하였다. 본 연구에서 제안한 이초 해석 방법을 바지선과 사다리꼴의 간단한 형상을 통하여 이초 해석 방법을 검증하였으며, 검증 내용을 바탕으로 6,300 TEU container ship에 적용하여 이초를 위한 지면반력과 화물 이동에 따른 선박의 자세 변화와 이초력을 계산하였다. 6,300 TEU container ship의 Step 2 과정에서 중량 조정 단계로 Hold 16 화물의 이동, 제거와 Hold 1에 화물을 추가하는 세 가지 방법을 사용하였으며, 각 방법에 따른 이초력과 트림 각도로 화물 이동 시 13,588 ton, 0.206°, 제거 시 14,204 ton, 0.129°, 추가 시 12,883 ton, 0.296°를 얻었다.

향후 연구로 선박의 자세 변화에 따른 액체 화물의 자유 표면 효과(free surface effect)를 고려할 계획이며, 현재 2차원으로 가정하여 폭 방향의 중심은 0으로 고정하였는데, 이를 3차원으로 확장할 예정이다. 또한 현재는 좌초 지점을 접촉점으로 가정하였는데, 추후에는 접촉면 또는 여러 점에 접촉한 것으로 확장할 계획이다.

Acknowledgments

본 연구는 (a) 정부(과학기술정보통신부)의 재원으로 한국연구재단 (No. 2019R1G1A1100187), (b) 2022년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원 (P0017006, 2022년 산업혁신인재성장지원사업), (c) 2021년도 교육부의 재원으로 한국연구재단의 지원을 받아 수행된 지자체-대학 협력기반 지역혁신 사업 (2021RIS-003)의 지원을 받아 수행된 연구임을 밝히며 이에 감사드립니다.

References

Bartholomew, C.A., 1992. US Navy Salvage Engineer’s Handbook. Naval Sea Systems Command, Washington D.C.
Beer, F.P., Johnston, Jr. E.R. & Mazurek, D.F., 2016. Vector mechanics for engineers: static, 11th Ed in SI Units. Translated from English by Han, B.K et al. McGraw-Hill Education Korea, Ltd, Inc.
Byun, S.H. Choi & Chum, T.B., 2001. Calculation of lifting force for a sunken ship considering the bottom soil property. Journal of the Korea Society for marine Environment and Energy, 4(2), pp.135-139.
Choi, K., Lee, S.G., Sohn, K.H. & Shin, M.K., 2000. Calculation of 4 crane lifting force for a sunken ship. Journal of the Korea Society for marine Environment and Energy, 14(1), pp.17-22.
Ham, S.H. et al,, 2015. Physics-based salvage simulation for wrecked ship considering environmental loads. Journal of the Society of Naval Architects of Korea. 52(5). pp.387-394. [https://doi.org/10.3744/SNAK.2015.52.5.387]
HECSALV, URL: https://www.herbert-abs.com/hecsalv, [Accessed 10 April 2021].
Lee, C.S., 2014. A study on the evaluation of lifting force and salvage method of submerged ship. Ph.D. Thesis. Interdisciplinary Program of Ocean Industrial Engineering, Graduate School, Pukyong National University.
Lee, K.Y. et al., 2016. Naval architectural calculation. Textbooks, Inc.
Wilkins, J.R., 2021. U.S. Navy salvor’s handbook, Naval Sea Systems Command.
Varsami, A.E., Chircor, M., Popescu, C. & Hanzu-Pazara, R., 2012. Refloating a ship using her own means. Proceedings of the 23rd International Daaam Symposium, pp.0263-0266. [https://doi.org/10.2507/23rd.daaam.proceedings.061]

이 우 용

함 승 호

구 남 국

Item	Abbreviation	Unit
Hullform	-	-
Lightweight(LWT)	w_LWT	ton
Longitudinal center of gravity of LWT	LCT_LWT	m
Vertical center of gravity of LWT	VCG_LWT	m
ith cargo weight	W_i	ton
ith cargo position	(X_wi, Y_wi)	m
Draft	T	m
Local origin	(α, β)	m
Trim angle	(θ)	degree

Item		Value	Unit
Hullform	A	(-50,5)	(m,m)
	B	(-50,-5)	(m,m)
	C	(50,-5)	(m,m)
	D	(50,5)	(m,m)
Lightweight		10750	ton
Longitudinal center of gravity of LWT		3.55	m
Vertical center of gravity of LWT		1	m
Cargo weight(w₁)		500	ton
Cargo position(w₁)		(3.55,5)	m
Draft		5	m
Local origin		(0,0.5)	m
Trim angle		1	degree

Hullform	Local	Global
A	(-50, 5)	(-50.08, 4.63)
B	(-50, -5)	(-49.90, -5.37)
C	(50, -5)	(50.08, -3.6266)
D	(50, 5)	(49.90, 6.37)

Item	Value	Item	Value
F_{W_new}	11,250 ton	C.O.G	(1.12, 1.25)
F_B′	9,686.14 ton	C.O.B	(-4.20, -2.41)
F_R′	1563.85 ton	(l_x, l_y)	(34.14, -3.90)
θ′	1.3775°	-	-

Item		Value	Unit
Hullform	A	(-50,5)	(m,m)
	B	(-50,-5)	(m,m)
	C	(45,-5)	(m,m)
	D	(50,5)	(m,m)
Lightweight		10,750	ton
Longitudinal center of gravity of LWT		3.16	m
Vertical center of gravity of LWT		1	m
Cargo weight		500	ton
Cargo position		(3.16,5)	m
Draft		5	m
Local origin		(0,0.1)	m
Trim angle		0.3	degree

Item	Value	Unit
F_W	11,250	ton
C.O.G	(3.53, 1.73)	m
F_B	9,224.8	ton
C.O.B	(-3.18,-2.28)	m

Item	Value	Item	Value
F_W	11,250 ton	C.O.G	(3.15, 1.07)
F_B	10299.89 ton	C.O.B	(0.42, -2.47)
F_R	950.1016 ton	(l_x, l_y)	(32.76, -4.73)

Item		Value	Unit
Hullform	LBP	264.050	m
	Breadth	40	m
	Depth	24.2	m
Lightweight		43746.3	ton
Longitudinal center of gravity of LWT		-5.208	m
Vertical center of gravity of LWT		2.973	m
Draft		14.5	m
Local origin		(100, 2.3)	m
Trim angle		0.2	deg

Cargo hold	Weight [ton]	TEU	C.O.G
1	980	70	(114.279, 8.35)
2	3,136	224	(102.702, 4.44)
3	3,696	264	(88.504, 2.78)
4	3,948	282	(74.124, 2.39)
5	4,256	304	(59.734, 3.35)
6	4,648	332	(45.274, 4.6)
7	4,648	332	(30.814, 4.6)
8	5,040	360	(16.354, 5.85)
9	5,040	360	(1.894, 5.85)
10	5,040	360	(-12.566, 5.85)
11	5,040	360	(-27.026, 5.85)
12	5,040	360	(-41.486, 5.85)
13	5,040	360	(-55.946, 5.85)
14	3,528	360	(-86.546, 10.85)
15	3,528	252	(-101.006, 10.85)
16	2,940	210	(-114.807, 12.3508)
Total	64,448	4,682	-

Item	Value	Item	Point
F_W	109,294.3 ton	C.O.G	(5.585,13.652)
F_B	101,194.65 ton	C.O.B	(-1.743,-4.867)
F_R	8,099.65 ton	(l_x, l_y)	(97.148,-11.86)

Item	Value	Item	Value
F_{W_new}	108,314.3 ton	C.O.G	(6.701,13.790)
F_{B_new}	99,859.506 ton	C.O.B	(-0.956,-4.808)
F_{R_new}	8,454.793 ton	(l_x, l_y)	(97.148,-11.86)
F_free	14,204.05 ton	θ′	0.129°

Item	Value	Item	Value
F_{W_new}	110,470.3 ton	C.O.G	(4.258,13.666)
F_{B_new}	102,801.8 ton	C.O.B	(-2.670,-4.938)
F_{R_new}	7,668.498 ton	(l_x, l_y)	(97.148,-11.86)
F_free	12,883.07 ton	θ′	0.296