해양 구조물의 흘수 변화에 따른 판형 구조물이 풍하중 추정에 미치는 영향
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this paper, wind load on a semi-submersible rig was investigated using Computational Fluid Dynamics (CFD). A maritime atmospheric boundary layer model for wind profile was implemented such that the wind profile shapes were retained throughout the computational domain. Wind load on the semi-submersible rig was calculated under the maritime atmospheric boundary layer and matched well with the results from wind tunnel test within a ±20% error. Overturning moments with variation of draft were investigated by decomposing into drag and lift components. It was observed that the contribution from lift to the overturning moments increased as the draft got higher. The majority of the lift components originated from deckbox which served as a lifting body due to the accelerated streamlines between waterline and the bottom of the deckbox.
Keywords:
Maritime atmospheric boundary layer, OpenFOAM, Wind load, Overturning moment, Lift키워드:
해양 대기경계층, 오픈폼, 풍하중, 전복 모멘트, 양력1. 서 론
풍하중은 해양구조물 설계의 주요 환경하중의 하나로써 정확한 풍하중 추정은 최적설계 관점에서 중요하다고 할 수 있다. 풍하중 추정에 활용되는 풍속분포(wind profile)는 주로 NPD(Norwegian Petroleum Directorate) 풍속분포(NPD profile) 또는 이를 근사화한 API 풍속분포(API profile) (API, 2000)이 활용되고 있다. 풍하중은 전통적으로 풍동을 이용한 모형시험을 통해 추정하지만, 모형시험을 수행하기 힘든 초기 설계 단계에서는 모형을 원기둥 또는 사각기둥과 같이 항력 계수를 알고 있는 도형들의 조합으로 단순화하여 풍하중을 추정하는 building block method를 활용하여 초기 설계에 사용하는 것이 일반적이다 (ABS, 2005; DNV, 2013; Walree, 2015). 하지만, 이들 기법은 엔지니어의 경험이나 주관이 강하게 들어가 결과의 일관성이 떨어지고 3차원적인 유동현상을 단순화하여 항력 계수만을 반영해 계산함으로 인해 풍하중을 과대 추정하는 경향이 있는 것으로 알려져 있다.
컴퓨터 하드웨어와 계산 기법의 발달로 전통적인 모형시험 대신 CFD(Computational Fluid Dynamics)를 활용하여 주어진풍속분포의 형상을 재현하여 풍하중을 추정하려는 시도가 있었다. Richards and Hoxey (1993)은 로그 풍속분포(log wind profile)가 Navier-Stokes 방정식의 해가 될 수 있음을 보이고 상용 코드를 사용해 수치적으로 정상상태(steady state)의 대기경계층을 처음으로 구현하는데 성공하였다. 이들이 구현한 대기경계층은 바람의 진행방향에 대해서 동일한 풍속분포를 유지하기 때문에(Horizontally Homogeneous Turbulent Boundary Layer, HHTBL)수치적으로 fetch length가 필요 없이 계산영역을 작게 사용할 수 있어 계산 비용 면에서 유리한 특징을 갖고 있다. SNAME OC-8 Comparative Wind Load Study (Kim et al., 2018) 는 Richards and Hoxey (1993)에서 시도된 방법을 NPD profile에 적용하여 해양 대기경계층 모델(Maritime Atmoshperic Boundary Layer, MABL)을 유도하고, 정보 가림 평가 기법으로 참여자들 간에 재현된 풍속분포가 NPD profile과 오차범위 1% 이내에서 일치하는 것을 확인하였다 (Kim et al., 2018; Kim et al., 2019).
본 연구에는 SNAME OC-8 Comparaive Wind Load Study에서 유도한 해양 대기경계층 모델을 공개 소스 코드 기반 CFD 개발 프레임워크인 OpenFOAM (Weller, 1998)을 통해 구현하여, 해양 구조물의 초기추정 방식에서 주로 판형(plate)으로 단순화되는 deckbox를 대상으로 building block method 가정의 타당성을 흘수 변화에 따른 전복 모멘트(overturning moment)에 기여하는 양력성분을 통해 평가해보고자 한다.
2. 이론적 배경
2.1 Wind profile modeling
해양구조물의 설계에 자주 활용되는 풍속분포는 로그 풍속분포(log wind profile)이며 식 (1)과 같은 형태로 표현된다 (DNV, 2010).
| (1) |
여기서, κ는 von Karman 상수로 0.4-0.42의 값을 가진다. u*는 마찰속도(friction velocity), z는 높이, z0는 조도 길이(roughness length)에 해당한다.
NPD 풍속분포(NPD profile)는 식 (2)의 형태로 표현할 수 있다.
| (2) |
여기서, Uref는 기준 풍속으로 보통 설계 풍속이나 풍동 시험조건에 해당하는 풍속에 해당한다. zref는 기준 높이로 실선 스케일에서 일반적으로 10m로 잡는다. C는 0.0573 √(1 + 0.15 Uref) 로 정의되는 상수이다.
식 (1)과 식 (2)를 이용하면, 일반적으로 실험을 통해 결정되어야 하는 조도 길이와 마찰속도를 식 (3), (4)와 같은 관계식을 통해 결정할 수 있다 (Kim et al., 2019; Kim et al., 2020).
| (3) |
| (4) |
2.2 난류 모델
NPD 풍속분포에 대해서 난류 에너지는 식 (5)와 같은 형태를 가지는 것이 알려져 있다 (Blocken et al., 2007; Richards and Hoxey, 1993; Richards and Norris, 2011; Sumner and Masson, 2010)
| (5) |
RANS 기법에서 와점성계수는 식 (6)과 같은 관계를 가지고 있다.
| (6) |
따라서 이를 이용하면 k-ω 난류 모델에 필요한 값들에 대한 관계식을 유도할 수 있다.
| (7) |
3. 해석 결과
3.1 Wind profile test
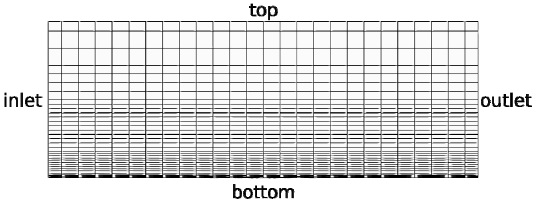
해양 대기경계층이 계산영역 전체에서 유지되는지를 검증하기 위해 Fig. 1과 같은 3차원 형상의 fetch length가 없는 계산영역(empty fetch domain)을 대상으로 테스트를 수행하였다. 계산영역의 크기는 7.04 m x 7.04 m x 3 m로서, x=-3.52 m 지점에 inlet x=+3.52 m 지점에 outlet, y=±3.52 m 지점을 side로 두고, z=0.0 m를 bottom, z=3.0m를 top 경계로 설정하였다. 격자의 크기는 x와 y방향으로는 등간격으로 26셀, z 방향으로 37셀을 배치하고 풍속분포를 표현하기 용이하도록 첫 번째 셀의 크기가 0.004m가 되어 상방으로 갈수록 단계적으로 격자의 크기가 커지는 형태를 가지도록 하였다. 계산에 사용할 풍속은 SNAME OC-8 Comparative Wind Load Study (Kim et al., 2018)에서 모형시험에 사용된 풍속 51.444 m/s를 적용하였다.
경계조건은 Yeon et al. (2020)에서 설명된 것처럼 식 (2)와 (7)을 inlet, side, top 경계에 적용하고 outlet 경계에는 압력출구(pressure outlet) 조건을 적용하였다. bottom 경계에는 조도 길이를 고려할 수 있도록 점착(no-slip) 경계조건을 적용하였다. 난류 모델은 식 (7)을 적용할 수 있는 k-ω SST 모델을 사용하였다. 지배방정식은 2차 정확도를 가진 linearUpwind, linear 기법을 각각 대류항과 확산항에 적용하여 이산화시켰고 속도-압력의 연성은 SIMPLE(Semi-Implicit Method for Pressure Linked Equations) 알고리즘을 이용하여 정상상태 해석을 수행하였다.
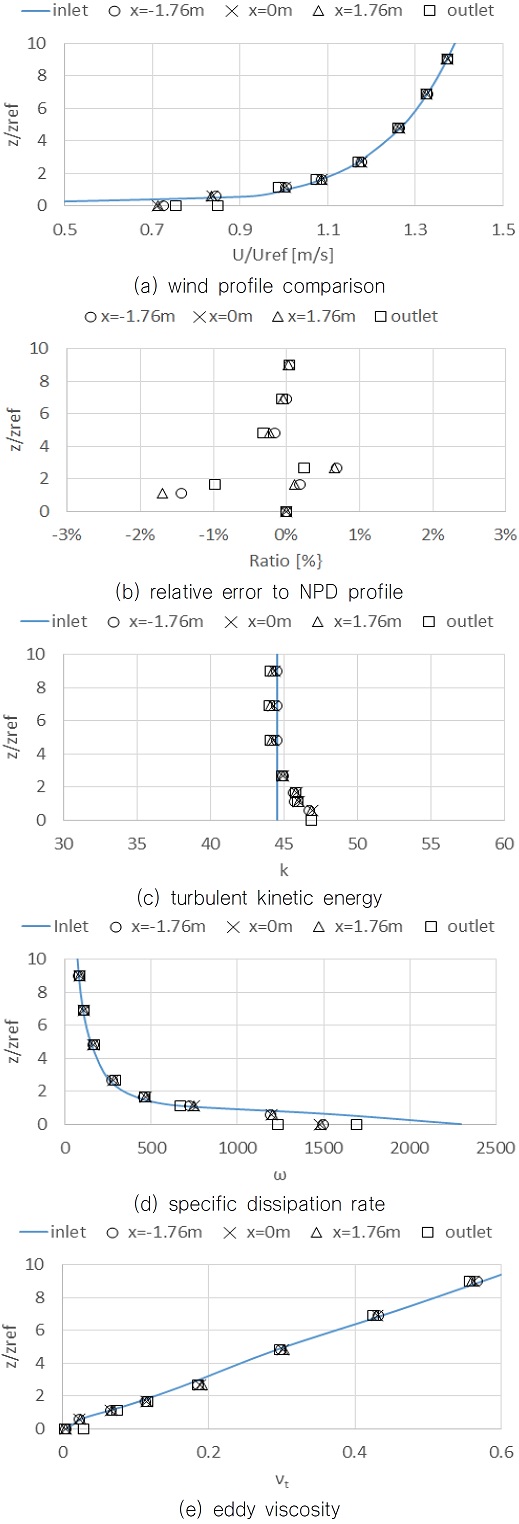
계산영역 내에서 식 (2)로 주어진 풍속분포가 유지되는지 평가하기 위해 inlet, x=-1.76m, x=0m, x=1.76m, oulet에 총 5개의 line probe를 설치하여 풍속분포를 계측하였다. Fig. 2(a)는 각 probe 위치에서 계측된 풍속분포를 inlet 경계에 주어진 NPD 풍속분포와 비교한 그림이다. 상대 높이 z/zref가 2보다 작은 구간(실선 스케일에서 20 m 이하 구간)에서는 약간의 차이가 나타나기는 하지만 그 이상인 구간에서는 거의 동일한 풍속분포를 유지하는 것을 알 수 있다. Fig. 2(b)는 각 probe 설치 위치에서 계측된 풍속분포와 NPD 풍속분포 간의 상대 오차를 나타낸 그림으로 상대 높이 z/zref가 2보다 작은 구간에서도 2% 이내의 오차를 보이고 있어 NPD 풍속분포와의 차이가 크지 않음을 알 수 있다.
Fig. 2(c), (d), (e)는 각각 난류 운동에너지(turbulent kinetic energy, k), 특정 소실율(specific dissipation ration, ω), 와점성계수(eddy viscosity, νt) 등의 난류 특성 값들을 비교한 그림들이다. 난류 운동에너지 분포와 특정 소실율의 경우 bottom 경계 근처에서 약간의 오차가 보이고 있으나 풍하중에 주로 영향을 미치는 z/zref가 2보다 큰 구간에서는 주어진 난류 운동에너지가 잘 유지되고 있는 것을 볼 수 있다. 특히, 난류 운동에너지 분포의 경우 bottom 경계 근처에서 오버슈트 현상이 나타나는데 이는 해양 대기경계층 모델 구현에서 익히 알려진 현상이며(Sumner and Masson, 2010; Richards and Norris, 2011) 하부에 나타난 오버슈트 현상은 풍속 분포의 재현에 큰 영향을 미치지 않아 무시할 만한 정도의 현상이다. 와점성 계수 또한 선형적인 형태로 모든 구간에서 거의 동일한 값들이 유지되는 것을 확인할 수 있다.
3.2 격자 민감도 분석
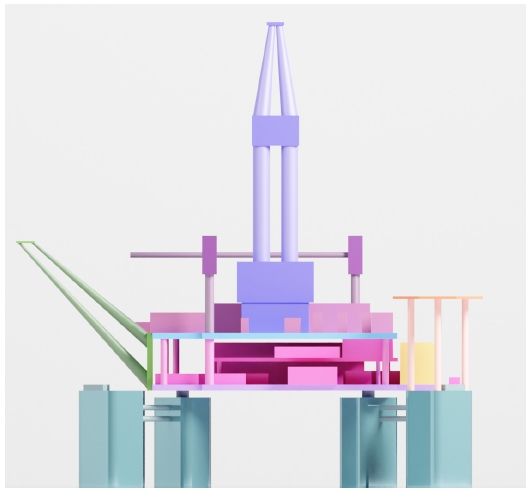
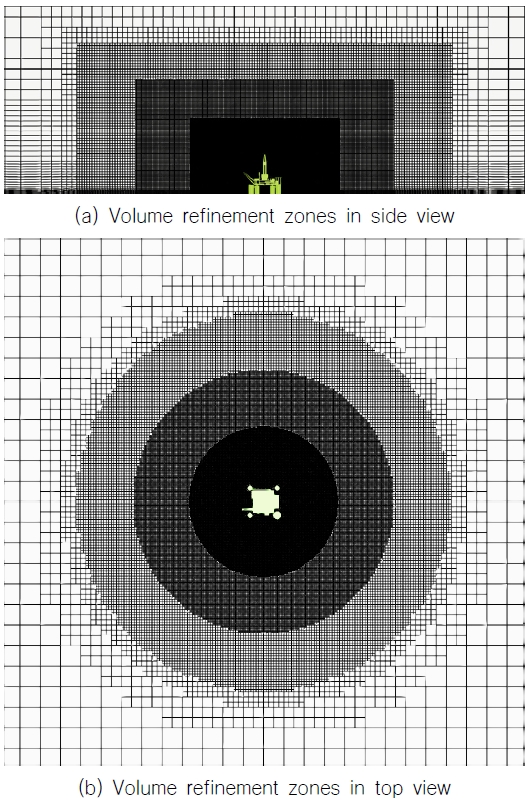
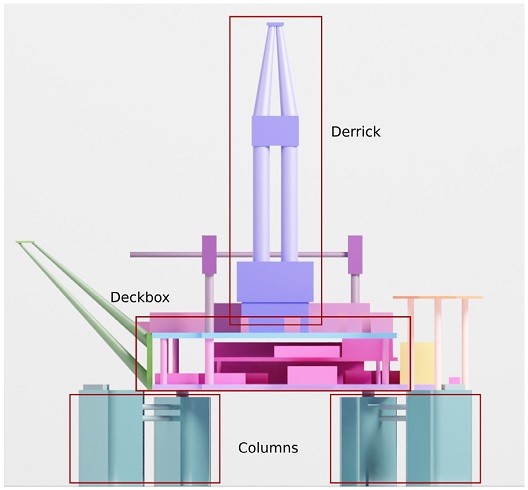
Fig. 1에 보인 계산 영역에 Fig. 3과 같은 반잠수식 시추선 모형을 적용하여 Fig. 4와 같은 격자를 구성하였다. 물체 주변의 반류장을 잘 모사하기 위해 Yeon et al. (2019)에서 사용된 격자구성방법을 따라 물체를 중심으로 3개의 동심원 형태의 영역을 추가하였다. 격자는 육면체 기반의 비정렬 격자의 trimmed mesh 형태로 구성하였다. 대상선의 주요치수는 Table 1과 같으며 풍하중 계산은 모형선 스케일에서 수행하였다. 이 때 모형선과 계산영역 사이의 폐색율(blockage ratio)는 약 1%이다. 계산에 사용된 풍향각은 0도부터 360도까지 30도 간격으로 총 12개의 풍향을 고려하였으며 풍향각은 OCIMF (OCIMF, 1994) 방식을 따라 선미에서 불어오는 방향을 0도, 선수에서 불어오는 방향을 180도로 하는 반시계방향으로 정의하였다. 계산에 사용된 기법은 앞 절 wind profile test에 적용한 것과 동일한 설정을 적용하였다.
모형시험 결과와의 비교에 앞서 격자 민감도 테스트를 진행하였다. 사용한 격자는 총 세 가지로 Table. 2에 나타내었으며, 각 격자의 평균 격자 크기 비율이 약 1.41배 정도 되도록 하였다. 계산은 총 10,000번의 반복계산을 거쳐 마지막 1/3만을 사용하여, 풍향각 0, 30도에 대한 평균 풍하중을 구해 풍하중 계수를 계산하였다, 풍향각 0도에 대한 횡방향 하중은 유의미하지 않아 평가에서 제외하였다. 동일한 스케일 내에서의 비교이므로 무차원 계수는 아니지만 풍하중 계수는 식 (8), (9)와 같이 설계 풍속 정보만을 사용하고 풍하중 면적에 대한 정보가 필요 없는 SNAME T&R Bulletin 5-4 (2020)에서 제안된 형태로 계산하였다.
| (8) |
| (9) |
여기서 Fi, Mi는 각각 i방향에 대한 힘과 모멘트, qref=0.5ρUref2는 기준높이(reference height)에서의 기준 풍속(Uref)에 대해 계산한 동압력 (reference dynamic pressure)을 의미한다.
격자 수렴 정도를 정량적으로 파악하기 위하여 식 (10)와 (11)과 같이 Celik et al. (2008)에 의해 제안된 방법을 적용하였다.
| (10) |
| (11) |
여기서 하첨자 1은 fine 격자, 2는 medium 격자 및 3은 coarse 격자를 뜻한다. r21은 fine, medium 격자 크기 사이의 비를 뜻하며, s= 1·sgn(ϵ32/ϵ21), ϵij = Qi – Qj, Qi는 i 격자에서 얻어진 물리량을 뜻한다. GCI는 격자 수렴 인덱스(grid convergence index)를 의미하고 fine 격자의 물리량이 갖는 격자에 대한 불확실성을 나타낸다. Fine 격자에 대한 불확실성은 풍향각 0도에 대한 종방향 계수는 1.6 %정도의 불확실성을 가지고, 풍향각 30도에 대한 종방향, 횡방향 계수는 각각 3.0 %, 1.2 %의 불확실성을 가진다.
수렴율(Convergence ratio) R=ϵ21/ϵ32을 사용하여 격자의 수렴 특성을 평가하였다(Xing and Stern, 2010). 수렴율은 0과 1사이의 값을 가질 경우 단조 수렴(monotonic convergence)에 해당하며 테스트에 사용된 값들은 모두 단조 수렴하는 경향을 보이는 것을알 수 있다. 본 계산에서는 medium 격자와 fine 격자사이의 상대 오차가 최대 3 % 이내인 것과 계산비용을 고려하여 medium 격자를 사용하였다.
3.3 풍하중 해석
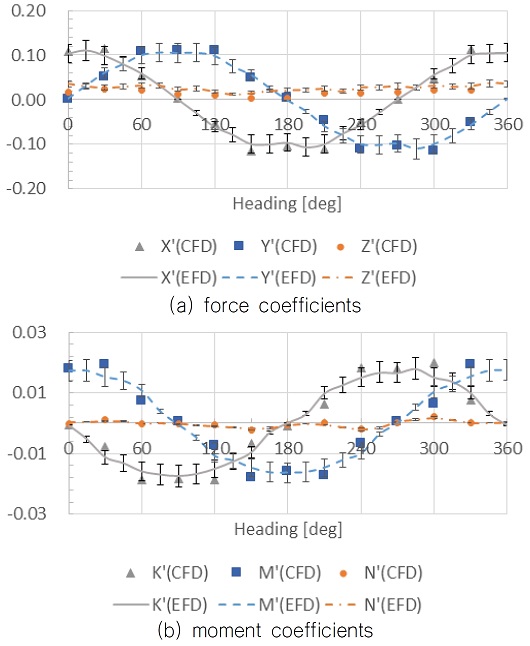
Table 1에 주어진 흘수 조건에 대해서 계산한 결과를 풍동 시험 결과와 함께 Fig. 5에 비교하였다. 풍동시험 결과는 ±20 %의 오차 막대와 같이 표현하였으며 계산된 풍하중 계수들은 대부분 오차범위 내에서 풍동시험 결과를 잘 따르고 있는 것을 확인할 수 있다.
모멘트 계산은 식 (12)과 같이 나타낼 수 있으며, 이 때 횡, 종동요 모멘트는 각각 항력(drag)과 양력(lift)의 성분으로 분해되고, 선수동요 모멘트는 항력 성분만으로 표현됨을 알 수 있다.
| (12) |
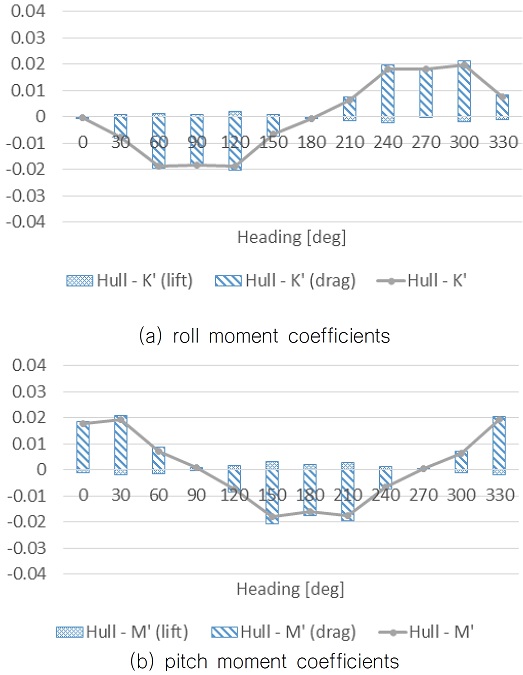
반잠수식 시추선과 같은 부유체의 경우, 초기 풍하중 추정단계에서 전복모멘트(overturning moment)가 중요한 설계 인자 중 하나이기 때문에 횡동요와 종동요 모멘트만을 고려하여 항력과 양력에 의한 기여분을 분리하여 도시하면 Fig. 6와 같이 나타낼 수 있다. 전체 모멘트 분포 중에서 항력에 의한 부분이 거의 대부분을 차지하지만 양력에 의한 영향이 상대적으로 크게 나타나는 풍향각이 나타나고 있다. 이들 양력에 의한 성분은 항상 항력에 의한 성분과 부호가 반대가 되어 최종 풍하중 계수의 추정값을 낮추는 역할을 하고 있음을 알 수 있다.
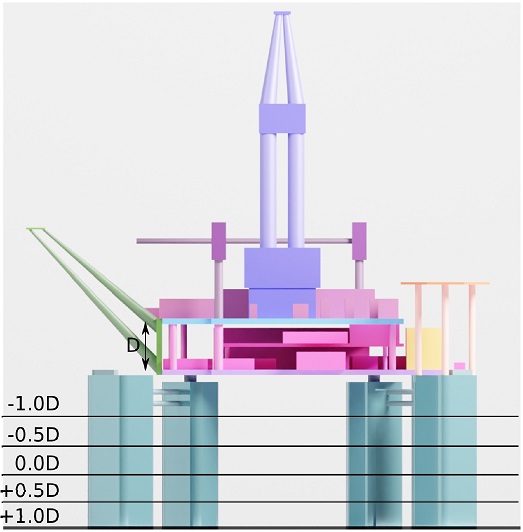
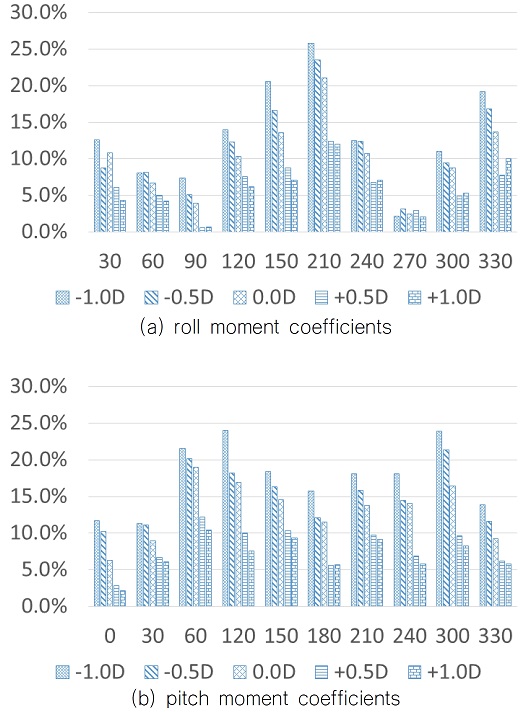
횡, 종동요 모멘트에 대한 양력 성분이 흘수 변화에 의해 변화를 보이는지 확인하기 위해 deckbox간 거리(Distance between deckboxes)를 D로 하여 Fig. 7와 같이 4개의 흘수 변화를 추가하여 항력 성분에 대한 양력 성분의 비를 Fig. 8에 도시하였다. 각 그림에서 횡동요 모멘트와 크게 연관이 없는 풍향각 0, 180도와 종동요 모멘트와 크게 연관이 없는 풍향각 90, 270도는 제외하였다. 정도의 차이는 있지만 전체적으로 흘수가 높아 deckbox가 수면에 가까울수록 양력성분의 크기가 커지는 것을 알 수 있고 최대 25 %에 이르는 것을 알 수 있다. 반면 흘수가 낮아질수록 양력에 의한 영향은 약 5 %이하로 낮아져 거의 항력 성분만으로 나타남을 알 수 있다.
일반적으로 building block method에서 전복모멘트를 추정하는 방식은 항력 성분만을 이용하기 때문에 흘수 조건에 따라 25 %정도의 과대추정이 발생할 수 있다고 예상할 수 있다.
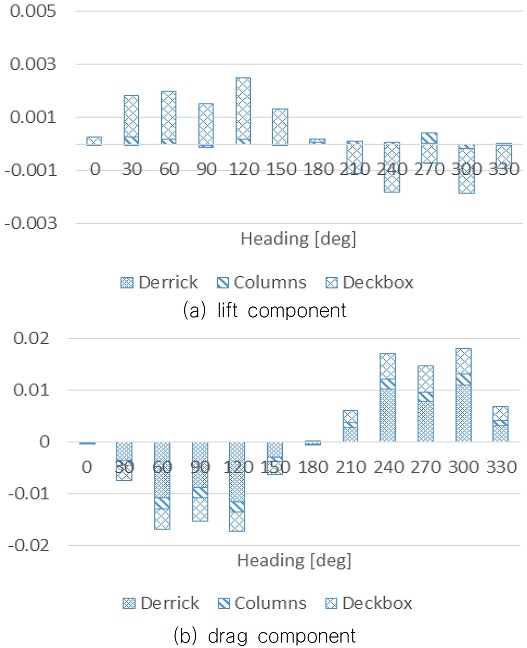
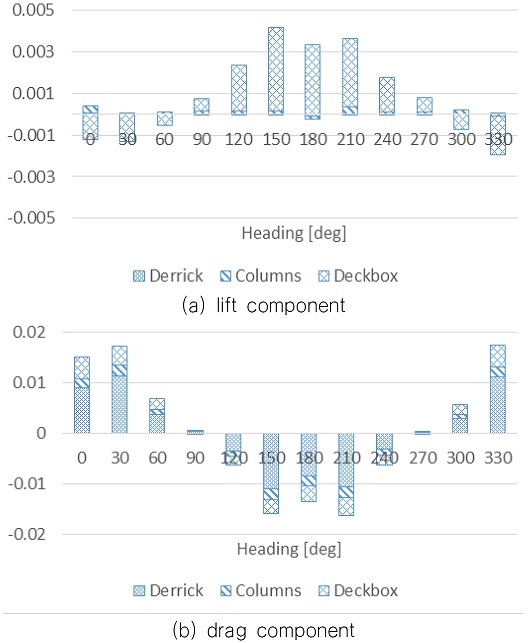
양력 성분에 영향을 미치는 구조물을 파악하기 위해 Fig. 9와 같이 derrick, deckbox, columns로 3개의 주요구조물에 대한 풍하중을 분리하여, 대표적으로 흘수 변화가 없는 조건(0.0D)에 대해서 Fig. 10과 11에 비교하였다. 횡동요 모멘트와 종동요 모멘트 모두 비슷한 경향으로 가장 풍하중 면적이 많은 derrick에 의한 항력 성분이 지배적인 것으로 나타났다. 반면 양력 성분은 deckbox에 의한 영향이 지배적이고 나머지 구조물들의 영향은 미미한 것으로 나타났다. 따라서 양력 성분에 가장 많은 영향을 미치는 것은 deckbox인 것을 알 수 있다.
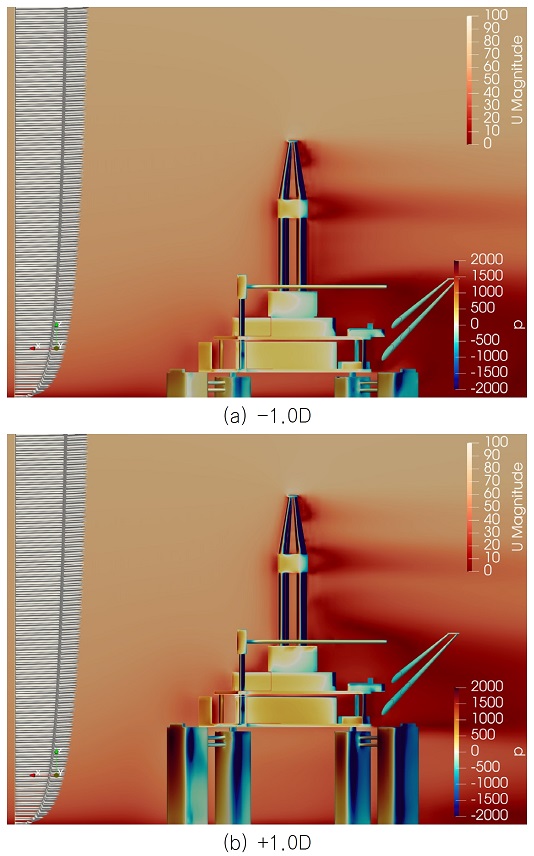
Fig. 12는 흘수 변화로 인한 유체장의 특성을 살펴보기 위해 흘수 조건의 양 극단에 있는 –1.0D와 +1.0D 조건에 대한 속도장과 구조물 상의 압력분포를 나타낸 그림이다. 비교를 용이하게 하기 위해 상류에서 유입되는 풍속분포를 왼편에 같이 나타내었다. Fig. 12(a)의 경우 deckbox가 풍속분포의 하단부에 위치하여 낮은 속도 하지만 속도의 구배가 큰 영역에 위치하고 있다. Fig. 12(b)의 경우 deckbox가 풍속분포의 상부에 위치하여 높은 속도 하지만 속도의 구배는 크지 않은 영역에 위치하고 있다. column을 제외한 deckbox 상부 구조물에서 보이는 압력분포는 유사한 것으로 보이며 이는 상부 구조물이 놓인 위치에서의 유입 풍속이 유사하기 때문인 것으로 보인다. 하지만 columns는 직접적으로 노출되는 풍하중 면적에 대한 풍속 분포의 차이가 커 column 주변의 압력 분포는 서로 차이가 크게 나타나고 있다.
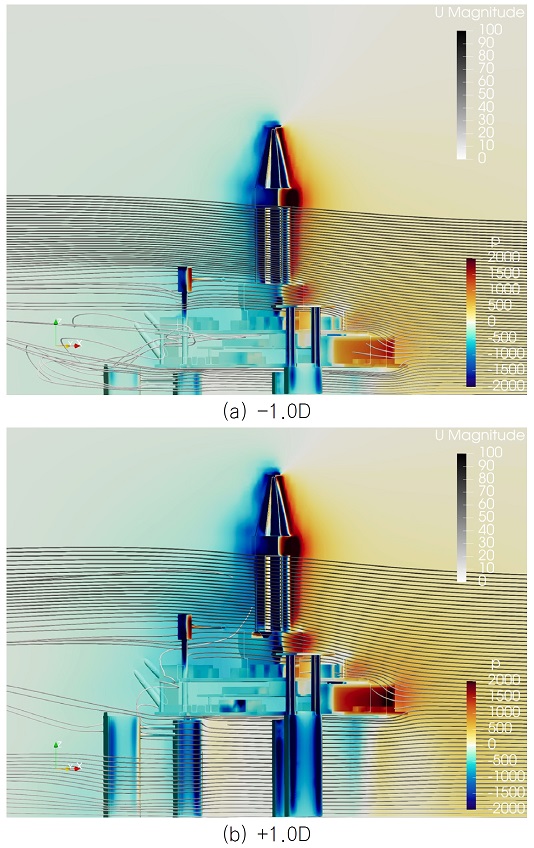
Fig. 13는 deckbox 하부 공간의 유선과 압력장의 분포를 나타낸 그림이다. deckbox 상부에서의 압력장 분포는 풍속분포의 유사함으로 인해 흘수 변화에 관계없이 두 조건 모두에서 비슷한 경향을 보이는 것을 볼 수 있다. 반면 deckbox 하부에서는 높은 흘수 조건(-1.0D)에서, 보다 낮은 압력이 형성되는 것을 확인할 수 있다. 유선분포를 보면 낮은 흘수 조건(+1.0D)에서 형성되는 유선간 간격보다 높은 흘수 조건에서 형성되는 유선간 간격이 더 좁아져 유속의 가속이 쉽게 발생하는 것을 알 수 있다. 좁아진 유선간 간격은 베르누이 효과로 인해 deckbox 하부에 보다 낮은 압력분포를 유발하여 높은 흘수 조건에서 높은 양력을 발생시킨다고 볼 수 있다.
4. 결 론
본 연구에서는 해양 대기경계층 모델을 이용하여 초기 설계에사용되는 building block method에 기반한 풍하중 추정 방법이 흘수 변화에 따라 불확실성이 나타날 수 있음을 CFD 기법을 활용하여 파악하고자 하였다.
해양 대기경계층을 OpenFOAM으로 구현하여 주어진 기준 풍속에 대한 풍속분포가 계산영역 전체에서 거의 동일한 형태를 유지하는 것을 보이고 반잠수식 시추선에 적용하여 풍동시험 결과를 20% 오차범위에서 잘 모사할 수 있음을 보였다.
대상선에 작용하는 풍하중 모멘트를 항력과 양력 성분으로 분리하고 deckbox의 위치를 변화시켜 양력 성분에 미치는 영향을 살펴보았다. 전복 모멘트의 대부분은 항력에서 기인하고 있으나 흘수가 높아 수면에 가까울수록 양력에 의한 기여도가 커져 흘수 조건에 따라 최대 약 25% 정도의 기여도가 나타나고 있음을 확인하였다. 따라서 초기 설계에 사용하는 방식으로 항력 성분만을 사용하여 전복 모멘트를 추정하면 최대 25% 정도의 과대 추정이 발생할 것을 예상할 수 있었다.
상부구조물을 주요 구조물로 구분하여 각 구조물이 모멘트 형성에 기여하는 정도를 비교하였다. 대부분의 상부 구조물은 항력에 의한 기여도가 높았지만 deckbox의 경우 풍향각별로 차이가있기는 하지만 양력 성분의 대부분을 차지하고 있는 것을 확인하였다. 유동 가시화를 사용하여 deckbox 주변의 유선분포를 확인한 결과, deckbox 주변의 유선 분포는 deckbox 하부와 수선면 사이 좁은 공간을 빠른 속도로 지나는 유선이 형성되어 하부에 낮은 압력이 발생하게 되어 상대적으로 강한 양력이 발생할 수 있음을 확인하였다. 따라서, building block method는 대상선의 흘수에 따라 추정 정도에 영향이 있을 수 있음을 예상할 수 있다.
추후 연구에서는 해양 구조물의 상부구조물의 lift의 영향을 고려하여 초기 추정 결과의 정확도를 보완할 수 있는 기법에 대한 연구가 필요하다고 생각된다.
Acknowledgments
본 연구는 선박해양플랜트연구소 주요사업 “첨단 운송체의 항내 운항성능향상을 위한 축척효과를 고려한 운항제어원천기술 개발”로 수행된 연구결과입니다 (PES3860). 본 연구에 사용된 반잠수식 시추선은 Houston Offshore Engineering’s Paired-Column Semisubmersible(PC-Semi)에서 파생된 모형임을 밝힙니다.
References
- ABS, 2005. Commentary on the ABS rules for building and classing mobile offshore drilling units, 2001 Part 3 – Hull Construction & Equipment. ABS.
- API, 2000. Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design. American Petroleum Institute.
-
Blocken, B., Stathopoulos, T. & Carmeliet, J., 2007. CFD Simulation of the atmospheric boundary layer: wall function problems. Atmospheric Environment, pp.238-252.
[https://doi.org/10.1016/j.atmosenv.2006.08.019]

-
Celik, I.B., Ghia, U. Roache, P. & Freitas, C., 2008. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. Journal of Fluids Engineering, 130(7), pp.078001–078004.
[https://doi.org/10.1115/1.2960953]

- DNV, 2010. DNV-RP-C205: Environmental Conditions and Environmental Loads October 2010 – Recommended Practice. DNV.
- DNV, 2013. Rules for the Certification and Construction, IV Industrial Services. DNV.
- Kim, J. et al., 2018. Numerical modeling of neutrally-stable and sustainable atmospheric boundary layer for the CFD simulation of wind load on offshore floating facilities. 37th International Conference on Ocean. Offshore and Arctic Engineering, Madrid, Spain.
-
Kim, J., Jang, H., Shen, Z. & Yeon, S.M., 2019. Developing industry guidelines for the CFD-based evaluation of wind load on offshore floating facilities. Offshore Technology Conference, Houston, USA.
[https://doi.org/10.4043/29270-MS]

-
Kim, J., Jang, H., Yeon, S., & Kim, H., 2020. Numerical modeling of sustainable atmospheric boundary layers for offshore floaters. 39th International Conference on Ocean. Offshore & Arctic Engineering, FL, USA.
[https://doi.org/10.1115/OMAE2021-63807]

- OCIMF, 1994. Prediction of wind and current loads on VLCCs, Oil Companies International Marine Forum London.
-
Richards, P. & Hoxey, R., 1993. Appropriate boundary conditions for computational wind engineering models using the k-e turbulence model. Journal of Wind Engineering and Industrial Aerodynamics. 46, pp.145-153.
[https://doi.org/10.1016/0167-6105(93)90124-7]

-
Richards, P. & Norris, S., 2011. Appropriate boundary conditions for computational wind engineering models revisited. Journal of Wind Engineering and Industrial Aerodynamics, pp.257-266.
[https://doi.org/10.1016/j.jweia.2010.12.008]

-
Sumner, J. & Masson, C., 2010. kE simulations of the neutral ABL: achieving horizontal homogeneity on practical grids. 48th AAIA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition.
[https://doi.org/10.2514/6.2010-1373]

- Walree, F. van, 2015. WINDOS (Version 9.0.3) [Computer program], MARIN:Wageningen, The Netherlands.
-
Weller, H.G., Tabor, G., Jasak, H. & Fureby, C., 1998. A tensorial approach to computational continuum mechanics using object-oriented techniques. Computers in Physics. 12(6), pp.620-631.
[https://doi.org/10.1063/1.168744]

-
Xing, T. & Stern, F., 2010. Factors of safety for richardson extrapolation. Journal of Fluids Engineering, 132.
[https://doi.org/10.1115/1.4001771]

-
Yeon, S.M. et al., 2019. Numerical modeling practice and verification of the wind load estimation for FPSO and semi-submersible. In: 38th International Conference on Ocean. Offshore & Arctic Engineering, Glasgow, Scottland.
[https://doi.org/10.1115/OMAE2019-96429]

-
Yeon, S.M., Kim, J.-S., & Kim, H.J. 2020. Numerical wind load estimation of offshore floating structures through sustainable maritime atmospheric boundary layer. International Journal of Naval Architecture and Ocean Engineering, pp.819-831.
[https://doi.org/10.1016/j.ijnaoe.2020.07.003]