가상 자유 항주를 이용한 KCS 선형의 정수 중 선회 및 변침 성능 해석

2.1 좌표계 및 지배방정식

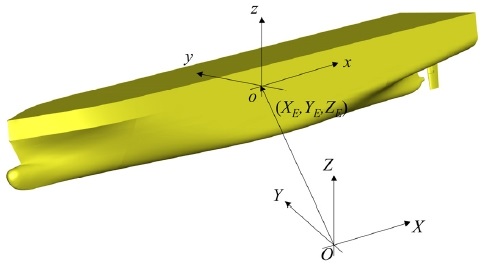
정수 중 선회하는 선박 문제 해석을 위해 Fig. 1과 같이 물체 고정 좌표계 o-xyz와 지구 고정 좌표계 O-XYZ를 도입하였다. 초기 각 좌표계의 원점은 선박의 길이 및 폭 방향 중심 그리고 정수면 높이에 위치한다. +x과 +X축은 선수에서 선미방향, +y 및 +Y 축은 우현방향이고, +z와 +Z축은 오른손 법칙에 따라 결정되어 정수면 위쪽을 향한다. 물체 고정 좌표계의 원점 o의 지구 고정 좌표계 O에 대한 상대속도 벡터를 물체 고정 좌표계에서 나타낸 것을 (u,v,w)라 하고, 물체의 각속도 벡터를 물체 고정 좌표계에서 나타낸 것을(p,q,r)이라 하면, 유체에 의한 외력 및 모멘트와 속도 및 각속도 벡터와의 관계는 다음과 같다 (Faltinsen, 2005).

Fig. 1

Two coordinate systems for simulation of ship maneuvering

여기서 m과 I_ij는 선박의 질량 및 관성 모멘트를 뜻하며, [X,Y,Z]와 [K,M,N]은 각각 물체 고정좌표계에서 표현된 각 축 방향 힘과 모멘트를 나타낸다. 선박의 무게중심 좌표는 (x_g,y_g,z_g)이며 좌우대칭인 선박의 y_g는 0이다.

선박의 6자유도 운동을 해석하기 위하여 오일러 각(Euler angle)을 도입하였으며, Yaw(Ψ)-pitch(Θ)-roll(Φ) 순서로 회전을 정의하였다. 이상의 연립 미분 방정식은 2차의 외재적(explicit) 룬게-쿠타(Runge-Kutta)법을 통해 풀이할 수 있으며, 각 시간 단계에서 선박의 위치와 자세를 계산할 수 있다.

초기 선속 U₀와 선체 길이 L_BP 및 물의 밀도를 이용하여 무차원화 한 비압축성 난류 유동의 지배방정식은 다음과 같이 표현된다.

여기서 u_i와 V_i는 각각 i방향 유체 속도와 검사 체적의 움직이는 속도를 의미한다. p는 압력을 나타내며, Re와 Fr은 레이놀즈 수(Reynolds number)와 프루드 수(Froude number)를 의미하고, δ_ij는 크로네커 델타(Kronecker delta)이다. μ_T와 k는 각각 난류 와 점성 계수(turbulent eddy viscosity)와 난류 운동에너지(turbulent kinetic energy)를 의미한다.

2.2 수치 해법

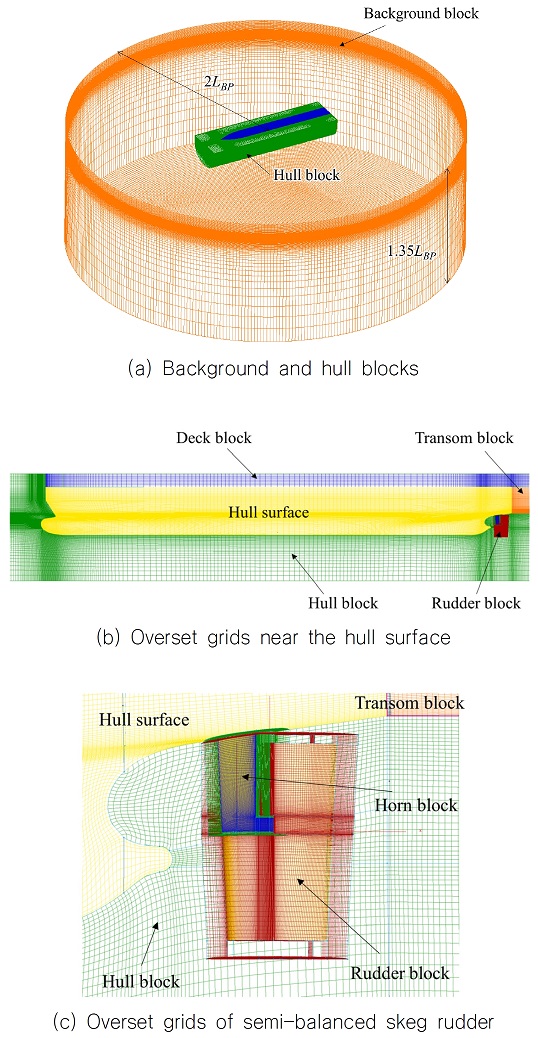
유체영역 지배방정식을 해석하기 위하여 유한체적법(finite volume method)을 적용하였다. 선박의 조종 문제는 선체와 타 같은 복잡한 형상 처리와 선체를 따라 움직이면서 타축을 중심으로 회전하는 타를 처리할 수 있는 격자 구성이 요구된다. 이를 위해 본 연구에서는 블록 정렬 격자(block structured mesh)를 이용하여 배경 격자와 선체 주변 및 타(rudder) 격자를 별도로 생성하였으며, 각 격자 블록을 중첩하여 해석하는 중첩격자계(overset grid system)를 적용하였다. 선체 주변 유체영역을 나타내는 선체 블록을 부모 물체(parent body)로 정의하고 선체와 함께 움직이는 타 격자는 자식 물체(child body)로 정의하였다. 부모 물체 운동방정식의 외력과 외력 모멘트는 자식 물체에 작용하는 외력 성분도 포함하며 이를 통해 얻은 새로운 위치로 부모 물체와 자식 물체는 이동한다. 자식 물체의 움직임은 사전에 정의된 자식 물체의 회전축을 부모 물체의 움직임에 따라 변환하여 구현하였다.

본 연구에서 사용한 격자 시스템의 예를 Fig. 2에 정리하였으며, 선박의 정수 중 조종 문제 해석을 위해 총 8개의 블록으로 구성하였다. 타 블록과 선체 주변 블록 사이에는 완충 블록을 추가하여 블록 경계에서 이웃 셀을 찾지 못한 고아 셀(orphan cell)이 발생하지 않도록 하였다. 본 연구에서 사용된 격자의 y+ 최소값은 대략 75 정도이며 총 격자 개수는 약 1,200만이다.

Fig. 2

Dynamic overset meshes for maneuvering simulations of KCS hull

앞서 정리한 운동 방정식의 결과로 선박의 위치와 자세가 결정되면 이에 따라 물체 주변 격자를 이동시키고 중첩 격자 기법 라이브러리 중 하나인 Suggar++ 라이브러리 (Noack, 2005)를 이용하여 배경 격자와의 관계를 새로 계산한다. 이때 배경 격자는 선박의 수평면 운동인 X_E, Y_E 및 Ψ에 따라 움직이게 된다. 본 연구에서 활용한 WAVIS 프로그램과 중첩 격자 기법의 연성 내용은 Kim et al. (2019)에서 찾을 수 있다.

중첩 격자 사이의 연결 관계를 파악한 이후 유체 영역의 수치해석은 기존에 개발된 WAVIS 프로그램을 활용하였다 (Park et al., 2013). 본 연구에서 아래와 같이 확산항은 2차의 중앙차분법(central difference method)을, 대류항은 3차 정도의 MUSCL(Monotonic Upstream centered Scheme for Convection Laws)기법을 이용하였다.

여기서 Γ^j 는 격자 경계면의 j방향 면적 요소, 아래 첨자 e와 w는 격자 중심 P를 기준으로 경계면의 방향(동쪽, 서쪽 등)을 나타내는 약자이다. m의 시간 미분은 질량 유량(mass flux)을 나타내며 아래 첨자 L은 1차의 풍상차분법으로 구한 물리량을 뜻하고 H는 MUSCL 방법으로 내삽하여 구한 물리량을 뜻한다. 위첨자 n과 n+1은 현재 시간 단계와 다음 시간 단계를 뜻한다.

시간에 대한 수치 적분은 1차의 역 오일러 방법(implicit Euler method)을 적용하였고, 속도-압력 연성은 SIMPLEC 방법을 적용하였다. 난류 유동 해석을 위해 EARSM(Explicit Algebraic Reynolds Stress Model, Kim et al., 2014)과 벽함수(wall function)를 이용하였다. 자유표면 문제를 해석하기 위하여 레벨셋 방법을 이용하였다.

2.3 추력 모델

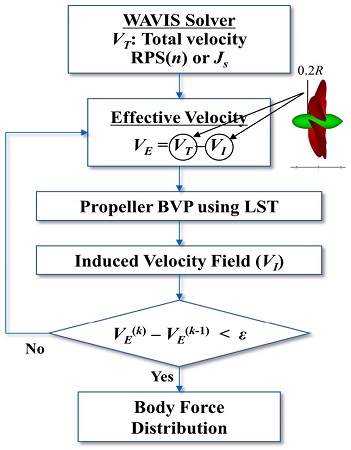
프로펠러 단독 성능 해석 시에는 실제 프로펠러를 모델링하여 회전하는 프로펠러 주위의 유동을 계산하지만, 선체 및 타와의 상호작용을 동시에 해석하기에는 계산 시간 관점에서 매우 비효율적이다. 이는 프로펠러 주변 유동을 해석하는 데 요구되는 시간 간격과 선체의 조종 운동을 해석하는 데 요구되는 시간 간격의 차이로 발생하며, 본 연구에서는 프로펠러에 의한 추력을 고려하기 위해 양력면 이론을 이용한 패널법 코드와 연성을 통해 계산 효율성을 높였다 (Kim et al., 2016). 전체적인 해석 과정의 절차는 우선 난류 유동을 계산하여 추진기 면에 유입되는 통합 속도(total velocity) 분포를 도출하고, 패널법 코드로부터 추진기 유기 속도(propeller induced velocity)를 계산한다. 이 둘의 차이를 통해 추진기로 유입되는 유효 속도(effective velocity)를 계산하고, 유효 속도 분포의 평균값을 이용하여 반류계수 (w)와 전진비를 얻을 수 있다.

이 과정을 유효 속도의 변화가 일정 수준 이하로 작아질 때까지 반복하여 최종 추력 계수 및 토크 계수를 계산할 수 있으며, 이러한 과정은 Fig. 3에 도식화 하였다. 결과적으로 얻어진 추력을 추진기 면에 분포되는 등가의 체적력으로 변환하고 이를 공간상에 대응되는 격자에 외력항으로 추가하였다. 이를 통해 추진기로 인한 선미 유동장의 가속 효과가 고려된다.

Fig. 3

Flow chart for calculating distribution of body force due to rotating propeller

선박이 자유 항주하며 직진하는 구간에서 일정한 방위각을 유지하기 위해 타각의 제어가 필요하다. 본 연구에서는 간단한 PD-제어기 모듈을 이용하여 초기 직진하는 상황에서 방위각을 유지하였다.

여기서 δ_target은 목표 타각으로 타의 최대 회전 각속도로 타각을 변경하였다. Ψ_target은 목표 방위각을 뜻하며 직진하는 선박은 0이다. 본 연구에서 이득(gain) 값은 모형시험을 통해 얻은 K_P = 1.0, K_D = 0.993을 사용하였다.

3.1 대상 조건

본 연구에서는 KCS 선형의 자항 성능, 선회 성능 및 지그재그 해석을 수행하였다. 이 때, 비교를 위한 모형시험은 MARIN에서 수행되었으며 (SIMMAN, 2020) 프로펠러는 KP505가 아닌 MARIN 5533 모델이다. 선박의 기본제원은 Table 1에 정리하였고, 여기서 선박의 회전반경(radius of gyration)은 공기 중에서 값이다. 본 연구에서는 Table 2에 정리한 바와 같이 선박의 자항 해석으로 프로펠러 회전수를 결정하였고, 35° 좌현 선회와 20°/20°, 10°/10° 좌현 및 20°/20° 우현 지그재그 시험을 통해 개발된 프로그램의 선박 조종성능 해석 정확도를 검증하였다.

Table 1

Principal dimensions of KCS

Table 2

Test cases

자항 관련 변수들은 구해진 추력을 설계 프로펠러의 단독 성능 시험결과에 대응시킨 후 해당되는 전진 비, 효율과 토오크를 찾은 후 계산된다. 점성 유동과 포텐셜 유동 해석 간의 반복 계산은 위 조건이 완벽히 만족할 때까지 수행되어야 하지만, 무차원화된 값이 10^-6이하면 충분히 수렴된 자항점을 얻은 것으로 판정할 수 있다. 모형시험에서 결정된 프로펠러 회전수는 11.7 rps이고 계산 결과는 12.5 rps로 약 6.84% 오차를 보인다.

3.2 선회 성능 해석

선박의 선회 테스트를 수행하기 위하여 본 연구에서는 개발된 WAVIS 프로그램을 활용하였으며, 직진하는 선박에 최대 타각(δ = 35°)을 발령하여 좌현(port side)으로 선회하도록 하였다.

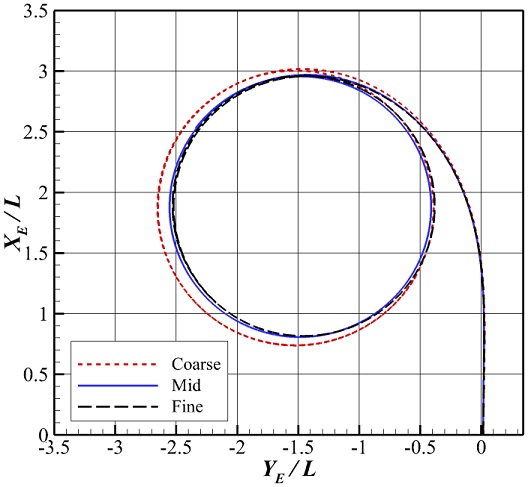
모형시험과의 비교에 앞서 격자에 따른 수렴도를 확인하였다. 사용한 격자는 총 세 가지로 Fig. 4에 나타내었으며, 각 격자의 평균 격자 크기 비율이 약 1.4배 정도 되도록 하였다. 격자 수렴 정도를 정량적으로 파악하기 위하여 Celik et al. (2008)에 의해 제안된 다음 방법을 적용하였다.

Fig. 4

Three different grid resolutions: coarse (top), mid (middle), and fine (bottom)

여기서 아래 첨자 1은 가장 조밀한 격자, 2는 중간 격자 및 3은 가장 성긴 격자를 뜻한다. r은 평균 격자 크기 사이의 비를 뜻하고, s = 1·sgn(ϵ₃₂/ϵ₂₁), ϵ_ij = Q_i – Q_j, Q_i는 i 격자에서 얻어진 물리량을 뜻한다. GCI는 격자 수렴 인덱스(grid convergence index)의 약자로 가장 조밀한 격자의 물리량이 갖는 격자에 대한 불확실성을 나타낸다.

각 격자에 따른 선박의 선회 궤적을 Fig. 5에 비교하였고, 방위각(Ψ) = 90° 기준 전진거리(advance, AD) 및 횡 방향 이동 거리(transfer, TR), 전술직경(tactical diameter, TD)에 대한 GCI 값을 Table 3에 정리하였다. 조밀한 격자를 사용함에 따라 선회 궤적이 수렴하며 정량적으로 1% 이내의 불확실성을 갖는다.

Fig. 5

Grid convergence test for 35° turning to port side

Table 3

Characteristics of 35° turning test to port side

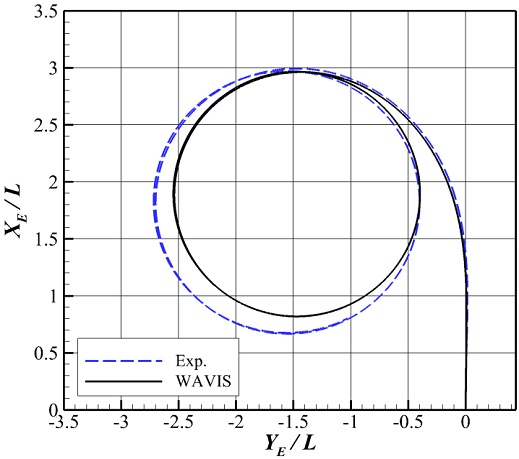
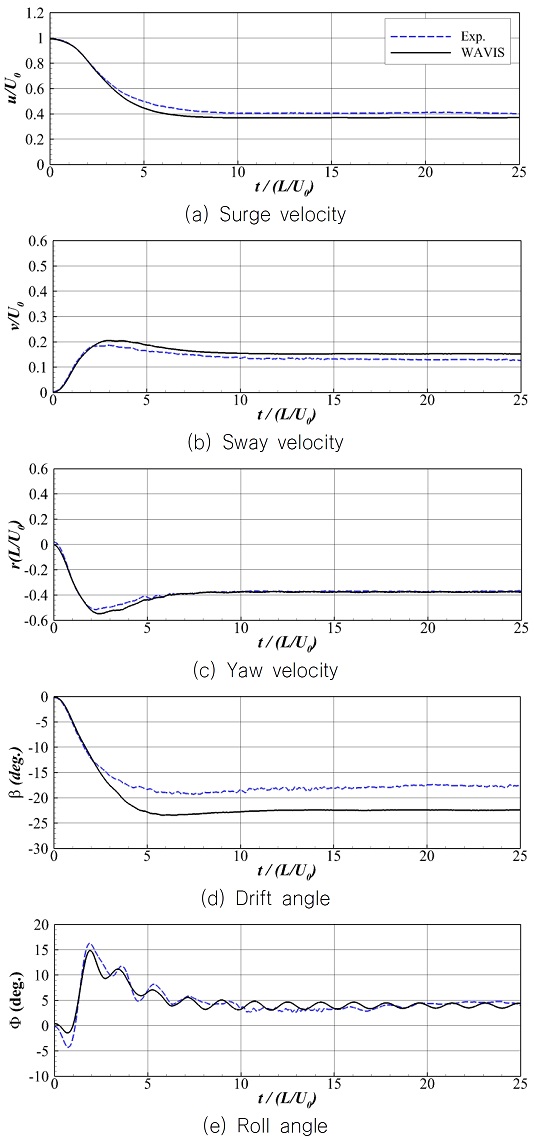
가장 조밀한 격자의 해석 결과를 실험 결과 (SIMMAN, 2020)와 비교하여 Fig. 6과 Fig. 7에 나타내었다. Fig. 6은 선체 중심 좌표의 궤적을 나타내고, Fig. 7은 시간에 따른 선체 고정 좌표계 기준 물체의 전후동요 속도(u) 및 좌우동요 속도(v), 선수동요 각속도(r), 표류각(drift angle, β) 값과 선박의 횡동요각(Φ)을 정리한 자료이다. 선체의 궤적과 여러 물리량의 시계열은 전체적으로 유사한 경향을 보이지만 정상상태 구간에서 u와 v 값이 차이를 보이며 이는 표류각의 차이로 귀결되고 이로 인해 선박의 궤적이 실험에 비해 작은 것으로 판단된다. 정량적인 비교를 위해 앞서 언급했던 전진거리 및 횡 방향 이동거리, 전술직경과 정상상태에서 횡동요 각(Φ_c) 값을 실험과 비교하여 Table 4에 정리하였다. 여기서 실험(E)과 수치해석(S)의 차이는 다음 식으로 계산하였다.

Fig. 6

Comparison of trajectory for 35° turning to port side

Fig. 7

Time histories during 35° turning to port side

Table 4

Characteristics of 35° turning test to port side

전진거리는 약 2%, 횡 방향 이동거리는 11% 정도 차이가 난다. 전술직경은 약 8% 정도 차이를 보이며 이러한 차이는 앞서 궤적을 통해 살펴본 정성적인 결과와 일치한다. 횡동요 각의 정상상태 값은 약 8% 정도 차이를 보이지만 실제 값으로 보면 0.4° 정도로 실질적인 차이는 크지 않은 것으로 판단된다.

선박이 선회하는 경우 일정한 표류각이 존재하며, 이 경우 선미뿐만 아니라 선수와 선저에서 유동의 박리가 발생하고 프로펠러 유입류도 영향을 받게 된다. 또한, 타에 유입되는 유동은 프로펠러 후류로 인해 매우 복잡한 양상을 보이고 이를 정확하게 해석하기 위한 난류 모델 관련 추가 연구가 필요하다(Mofidi & Carrica, 2014). 또한, 프로펠러 추력 모델에 따른 선회 궤적 결과가 크게는 10% 이상 차이를 보인 선행 연구(Broglia et al., 2012)로 미루어 실제 회전하는 프로펠러가 아닌 체적력을 이용한 영향도 존재할 것으로 판단된다. 본 논문에서는 현재 개발된 프로그램의 조종성능 해석의 정확도를 분석하고자 하였으며, 실제 회전하는 프로펠러와 타의 상호작용 및 난류 모델에 따른 국부 유동 분석 등은 추후 체계적인 연구가 필요하다.

3.3 지그재그 해석

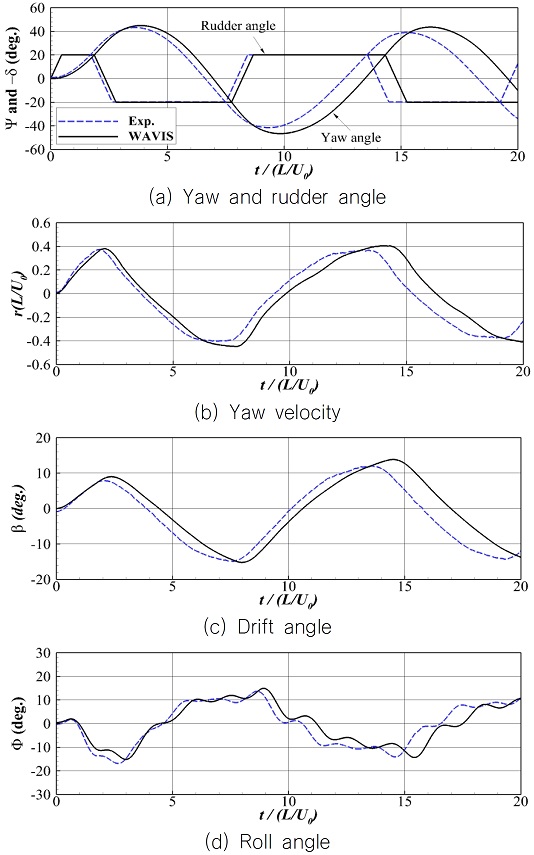
통상 선박의 변침성을 평가하기 위해 지그재그(zig-zag) 시험을 수행하며, 본 연구에서는 좌현 10°-10°, 좌, 우현 20°-20° 총 세 가지 경우의 지그재그 시험을 수행하고, 이를 기존의 실험 결과와 비교하였다.

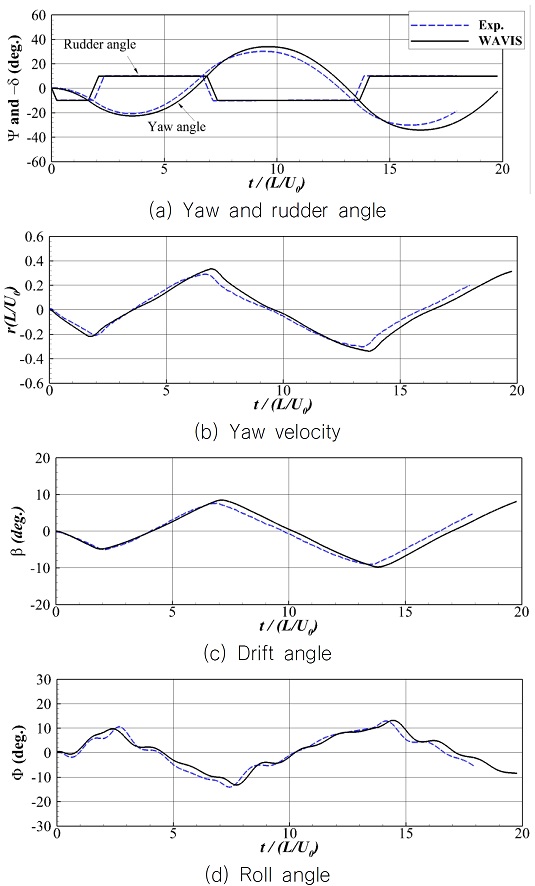
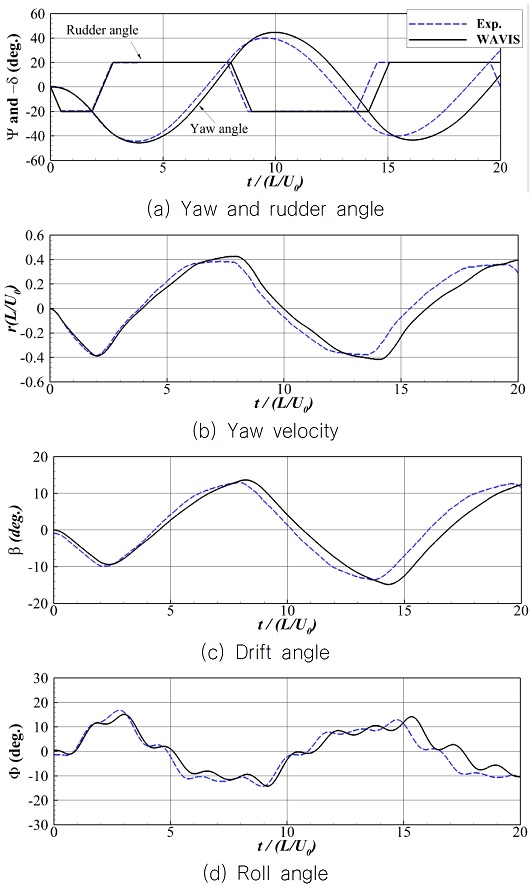
각 지그재그 테스트에 따른 방위각(Ψ)과 타각(δ) 및 선수동요 각속도(r), 표류각(β), 횡동요 각(Φ)을 Fig. 8-10에 나타내었고, 정량적인 비교를 위해 반대로 타를 작동시킨 이후 오버슈트 각의 최대가 나타나는 시점(time to check yaw) 및 오버슈트 각, 최대 선수동요 각속도, 최대 횡동요 각을 Table 5-7에 정리하였다. 점선은 실험 결과이고 실선은 계산 결과이다. 앞선 선회 성능과 유사하게 각 시계열은 실험과 유사한 경향을 보이며, 특히 횡동요 시계열이 유사한 것은 본 연구에서 추가 구현한 6자유도 운동 해석 모듈의 정확도를 보여준다. 다만, 두 번째 오버슈트 각(2nd overshoot angle) 부근에서 그 크기와 발생 시점이 차이를 보인다. 특히 계산 결과가 타각의 변화에 더 큰 방위각 변화가 발생하는 것으로 나타났으며, 이는 앞선 선회 성능 결과와 일치하는 결과이다. 정량적인 비교 결과 첫 번째와 두 번째 오버슈트 각 부근에서 각각 5-15%, 10-24% 정도의 차이를 보인다.

Fig. 8

Time histories for 10°/10° zig-zag test to port side

Fig. 9

Time histories for 20°/20° zig-zag test to port side

Fig. 10

Time histories for 20°/20° zig-zag test to starboard

Table 5

Characteristics of 10°/10° zig-zag test to port side

Table 6

Characteristics of 20°/20° zig-zag test to port side

Table 7

Characteristics of 20°/20° zig-zag test to starboard

기존의 유사한 연구인 Mofidi & Carrica (2014) 결과를 보면 CFD 해석 결과가 모형시험 대비 약 6% 정도의 차이를 보인다. 본 연구에서 사용한 난류 모델보다 박리 유동을 잘 모사할 수 있는 DES(detached eddy simulation) 모델을 사용하였고, 실제 회전하는 프로펠러를 구현한 점을 미루어 난류 모델과 직접 회전하는 프로펠러 모델에 따른 선체 주변 유동 박리 및 프로펠러, 타 유입류의 차이가 주요한 오차의 원인으로 판단된다.