유빙 하중을 받는 내빙 선박의 피로손상도 추정Part I - 직접 해석법
Abstract
In this study, a fatigue damage estimation for an ice-going vessel navigating through broken ice fields was carried out. A numerical model to simulate the interaction between ice and structure developed using the finite element method was introduced. Time series of stresses calculated by the proposed model and the corresponding fatigue analysis results are presented. The numerical model enables the long time analysis through an efficient interaction model, the application of the periodic media analysis and the convolution integral, and it allows the stress time history to be extracted directly using the finite element method. To describe the probability distribution of stress amplitudes, the 2-parameter Weibull model was applied to the calculated stress time history, and the fatigue damage was calculated using the Palmgren-Miner rule. Finally, the fatigue damage considering the ice conditions of the Baltic Sea was calculated using the proposed method and LR method, and the results were compared to each other.
Keywords:
Fatigue damage estimation, Ice-going vessel, Broken ice fields, Ice-structure interaction, Periodic media analysis, Weilbull model키워드:
피로 손상도 평가, 내빙선, 유빙 지역, 빙-구조 연성, 주기적 매체 해석, 와이블 모델1. 서론
최근 북극해 항해를 준비하고 있는 선주들의 큰 관심 분야 중 하나는 내빙 선박의 빙유기 피로 문제이다. 북극 지역은 오염에 매우 민감하기 때문에 일체의 기름 유출이 허용되지 않을 뿐만 아니라, 빙유기 피로균열 또한 일반 상선의 파도에 의한 균열만큼이나 자주 보고되기 때문이다 (Zhang et al., 2011). 따라서, 내빙 선박의 빙유기 피로는 설계 단계에서 반드시 평가되어야 한다. 특히, 보통의 내빙 선박은 쇄빙선으로 인해 부서진 유빙들 사이를 지나가기 때문에 유빙조건에서의 피로 강도를 추정하는 것이 필요하다.
그럼에도 불구하고, 관련된 연구의 수는 부족한 실정이다. 로이드 선급을 제외하면, 설계자들이 참고할 수 있는 지침도 없다.
Lloyd's Register (2014)는 빙하중으로 인한 선체 구조물의 피로 손상을 평가하기 위한 피로 평가 절차인 ShipRight FDA ICE를 발표하였다. 비교적 간단한 피로 해석을 가능하게 하기 위해 경험적 지식과 현장 계측 결과를 바탕으로 결정론적 (deterministic) 피로해석 절차를 개발하였다. 하지만 이 방법은 설계자가 절차를 따라 쉽게 설계할 수 있도록 만들어졌기 때문에 와이블 형상계수를 빙두께의 함수로 표현하는 등 수식들에 많은 가정이 포함되어 있다. 따라서, 정확한 피로 수명을 예측하기에는 적절하지 못하다. Suyuthi et al. (2013)은 KV Svalvard의 계측 결과를 바탕으로 내빙 선박의 피로 손상 평가 절차를 제안하였다. 얼음의 상태, 선박 속도 및 운항 모드의 변화를 반영하며 응력 진폭의 통계 모델을 도출하였으며, 최종적으로 3-parameter exponential model이 국부 빙하중을 표현하기에 최적의 모델이라고 결론 내렸다.
빙하중 기인 피로 해석에 필요한 응력 진폭(stress amplitude) 및 사이클 수와 같은 주요 모수(parameter)들은 주로 실선 계측, 모형 시험, 수치해석의 세 가지 방법을 통해 얻을 수 있다. 지금까지 대부분의 빙유기 피로에 관한 연구는 실선 계측 결과를 기반으로 수행되었다 (Bridges et al., 2006, Zhang et al., 2011, Suyuti et al., 2013, Chai et al., 2018). 하지만, 실선 계측은 다양한 경우에 대한 데이터를 얻기가 힘들고, 그 결과가 게이지의 위치나 선박 모양에 따라 달라지기 때문에 적용에 어려움이 따른다. 모형 시험 또한 높은 비용으로 인해 현실적인 대안이 되기 어렵다. 반면, 수치 해석은 앞에서 언급한 다른 방법의 단점들을 비교적 쉽게 극복할 수 있기 때문에 빙하중 기인 피로 해석에 적절한 방법으로 여겨진다.
본 연구에서는, 수치해석을 이용하여 유빙 하중을 받는 내빙 선박에 대한 피로 손상도 평가를 수행하였다. 유한요소법을 이용하여 개발된 유빙과 구조물 사이의 상호작용을 구현하는 수치 모델을 도입하고 (Kim and Kim, 2018), 수치모델에 의해 계산된 일련의 응력 시계열 및 피로 해석 결과를 제시하였다. 또한, 효율적인 빙-구조 상호작용 모델, 주기적 매체 해석(periodic media analysis) 기법의 적용 및 컬볼루션 적분(convolution integral)을 통해 장시간의 비선형 시간영역 해석을 가능케 하였다. 계산된 응력 시계열에 2-parameter 와이블(Weibull) 모델 을 적용하여 응력 진폭의 확률 분포를 도출하였으며, Palmgren-Miner rule을 적용하여 최종 피로 손상도를 평가하였다. 마지막으로, 발트해(Baltic Sea)의 실제 얼음 조건을 고려한 피로 해석을 통해 제안된 방법과 LR 방법의 결과를 비교하였다.
2. 해석 방법
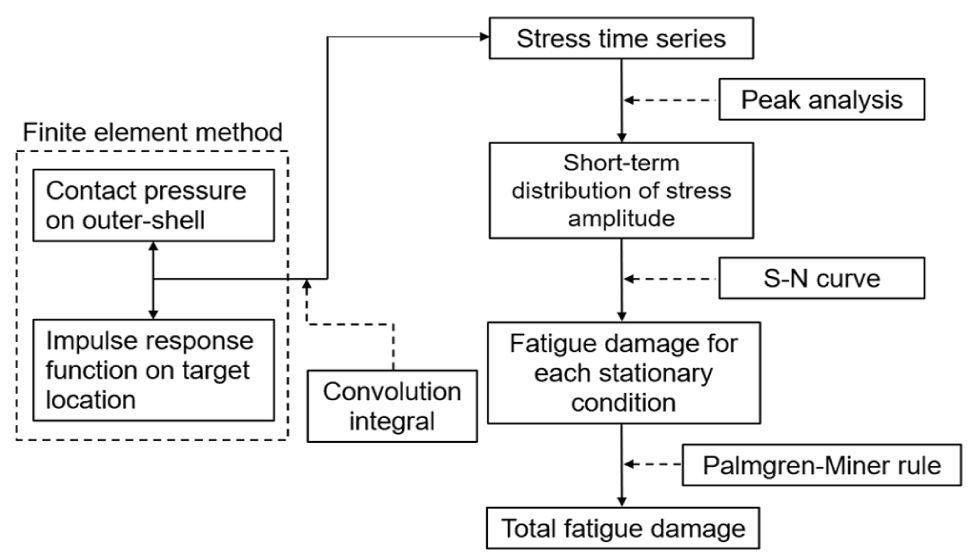
전체 계산과정은 Fig. 1에 간략히 나타내었다. 계산에 필요한 구조물 모델은 변형체(deformable body)로 이루어진 선박의 전체 모델과 강체(rigid body)로 이루어진 선체 외판(outer-shell) 모델이다. 먼저, 시뮬레이션을 통해 선체 외판에 걸리는 접촉 압력(contact pressure)을 얻는다. 그 다음, 접촉이 되는 요소(element)들을 분류한 다음 변형체 모델의 해당 요소들에 단위 임펄스(unit impulse)를 가하여 대상 위치의 응답 즉, 충격응답함수를 (IRF, impulse response function) 구한다. 계산된 접촉 압력과 충격응답함수를 이용하여 컨볼루션 적분(convolution integral) 하면 대상 위치의 응력 시계열을 바로 얻을 수 있다. 일단 응력 시계열이 계산되면 피크 분석(peak analysis)과 확률모델을 적용하여 응력 진폭의 단기 분포를 도출할 수 있다. 이를 통해 계산된 피로 손상도는 하나의 조건에 대한 손상도 이므로 Palmgren-Miner rule을 통해 모두 더하면 최종 피로 손상도를 계산할 수 있다.
2.1 접촉 압력 시계열의 계산
이 단계에서 요구되는 유한요소 모델은 임의의 형태를 가진 유빙과 접촉 압력을 계산하기 위한 선체 외판 모델이다. 사용된 프로그램은 상용 유한요소해석 프로그램인 ABAQUS/Explicit이다. 선체 외판 모델은 구조 모델로부터 추출하여 사용할 수 있고, 압력의 계측이 목적이므로 효율적인 계산을 위한 강체로 구성한다. 임의의 크기, 두께, 모양 및 분포를 가진 유빙은 자동 모델링 기법을 통해 모델링하며, 유빙의 거동은 User subroutine을 통해 모사하였다. 유빙의 충돌로 인한 얼음의 국부적 손상(local failure)은 압력-침투량(pressure-penetration) 관계를 통해 구현하였다.
2.1.1 해수-얼음의 상호관계 모델링
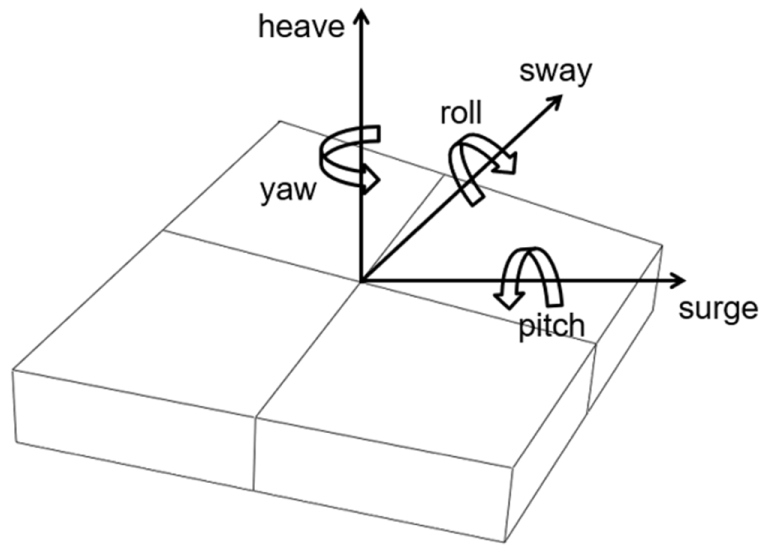
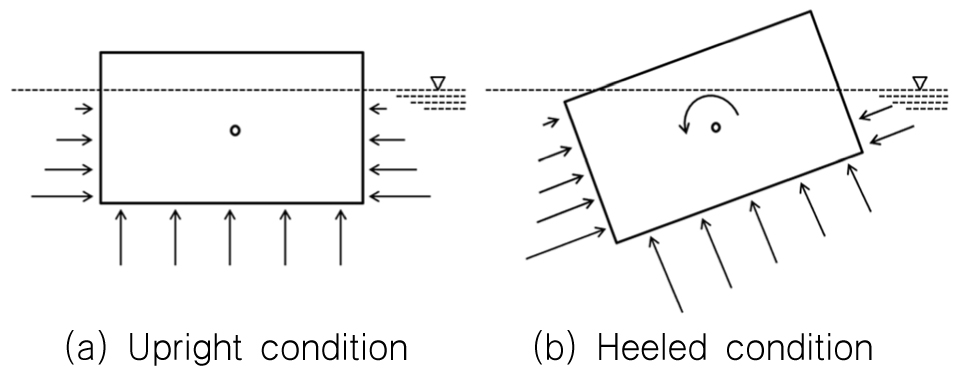
해수와 얼음의 상호작용으로 인해 발생하는 유체동역학적 하중은 Fig. 2와 3 그리고 식(1), (2), (3)에서 나타낸 바와 같이 6자유도를 고려한 식으로 표현하였다. 먼저, Surge, sway, yaw와 같은 평면 운동(planar motion)의 경우에는 항력(drag force, )과 항력 모멘트(drag moment, )를 적용하였다 (Hopkins and Shen, 2001). 반면, Heave, roll, pitch의 경우에는 식(3)과 같이 얼음의 표면에 부력의 형태로 적용하였다. 또한, Roll과 Pitch와 같이 기울어진 상황을 고려하기 위해 해당 면에 국부좌표계 와 를 따라 압력을 계산하여 적용하였다. 부가질량을 고려하기 위해 기존 질량에 을 곱한 값을 질량으로 사용하였으며, 여기서 은 Newman (1977)에 따라 0.41을 적용하였다.
| (1) |
| (2) |
| (3) |
여기서, 여기서 는 항력 계수를 나타내며, 는 해수의 밀도, 는 투영면적을 의미한다.
2.1.2 얼음-구조의 상호관계 모델링
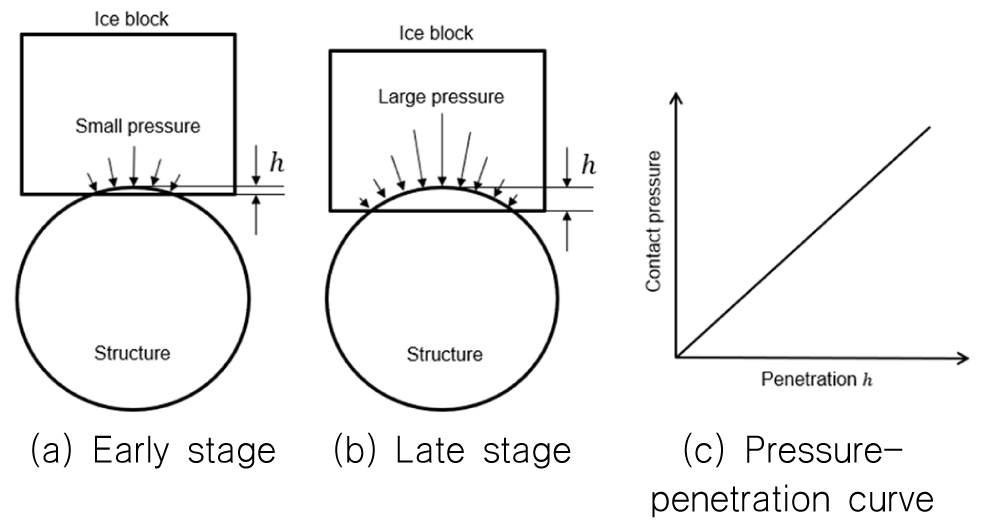
본 연구에서는 유빙과 구조물 간의 충돌 시에 발생하는 얼음의 국부적 손상을 요소들 간의 침투(penetration)를 통해 구현하였다. Fig. 4에서는 본 연구에서 적용한 압력-침투(pressure-penetration) 관계를 나타내고 있다. 즉, 충돌 시 발생하는 압력의 크기에 따라 침투량을 다르게 하여 국부적 손상에 의한 얼음의 거동과 하중의 변화를 구현하였다. 압력-침투 관계는 다양한 충돌 시나리오를 고려한 상세해석을 통해 도출하였다. 1년생 빙(first-year ice)의 두께와 크기, 그리고 충돌방향에 따라 시나리오를 정하여 탄소성 해석을 수행하였으며, 최종적으로 도출된 각 Time step별 압력과 침투량의 관계를 x-y 평면에 나타내었다. 얼음의 재료 특성과 다양한 시나리오의 결합으로 인해 도출된 압력-침투량 관계에서 비교적 큰 산포도를 볼 수 있었지만, 해석의 효율성을 위해 선형회귀(linear regression)하여 직선의 기울기를 얻었다. 상세한 사항은 Kim and Kim (2018)에서 확인할 수 있다.
2.1.3 주기적 매체 해석(Periodic media analysis)
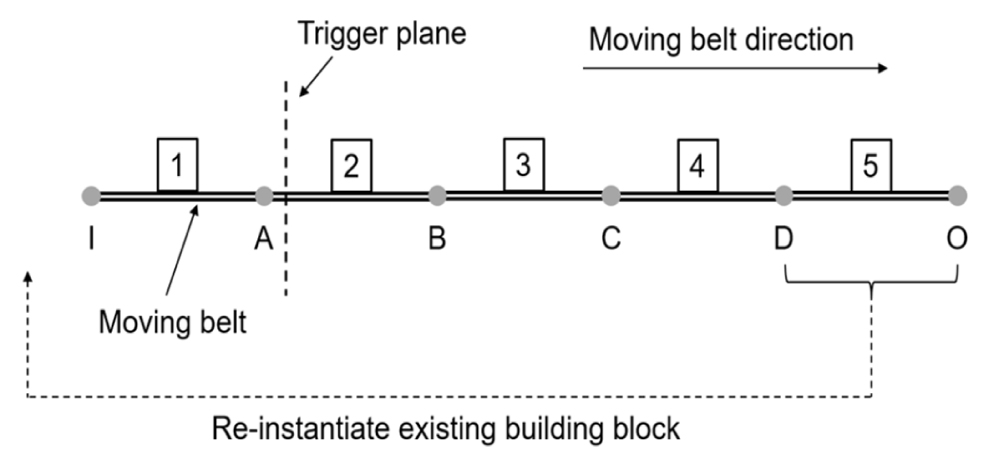
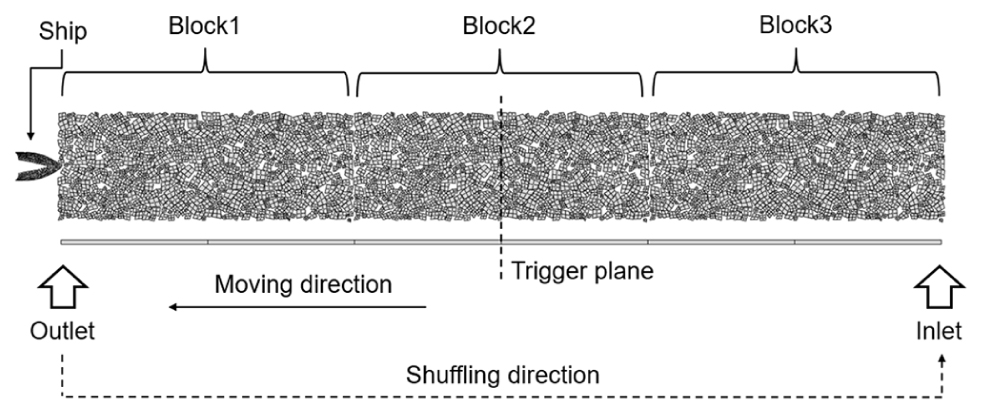
빙하중의 시계열을 피로 해석에 적용하기 위해서는 통계적인 특성을 얻을 수 있을 정도의 충분한 해석시간이 필요하다. 주파수가 높은 충격 하중의 특성을 고려하면, 최소 5~10분 이상의 시간 영역 해석을 수행해야 단기 분포를 얻을 수 있을 것으로 예상된다. 따라서 이러한 해석을 위해서는 해석 시간과 선박의 속도를 고려하여 충분한 수의 유빙이 준비되어야 한다. 예를 들어, 4노트의 선박 속도로 10분 동안 해석하려면 최소 1200m의 길이로 유빙이 모델링 되어야 한다. 이런 경우 모델링, 계산 및 후처리에서 엄청난 시간이 소요되므로 사실상 거의 불가능한 해석이라고 볼 수 있다. 본 연구에서는 이러한 문제를 해결하기 위해 주기적 매체 해석(periodic media analysis) 기법을 적용하였다. Fig. 5에서는 주기적 매체 해석 방법의 개략적 설명을 위해 컨베이어 벨트에 올려진 박스의 이동을 예로 나타내고 있다. 전체 모델은 동일한 여러 블록(block)으로 구성된다. 각 블록은 하나의 박스(box)와 벨트(belt)로 이루어 지고, 각 벨트는 서로 연결되어 있다. 각 블록의 연결점은 I, A, B, C, D 및 O로 나타내었다. 여기서 I 및 O는 각각 입구(inlet) 와 출구(outlet)를 나타낸다. 전체 모델이 벨트의 이동 방향으로 이동하다가 입구의 연결점(I)이 트리거 평면(trigger plane)을 만나면 출구에 연결된 블록이 사라지고 다시 입구로 연결된다. 이 과정을 셔플링(shuffling)이라고 하며, 트리거 평면이 셔플링이 발생하는 시점을 제어하는 역할을 한다. 따라서, 제한된 수의 요소(element)를 이용하여 무한 반복이 가능하게 된다.
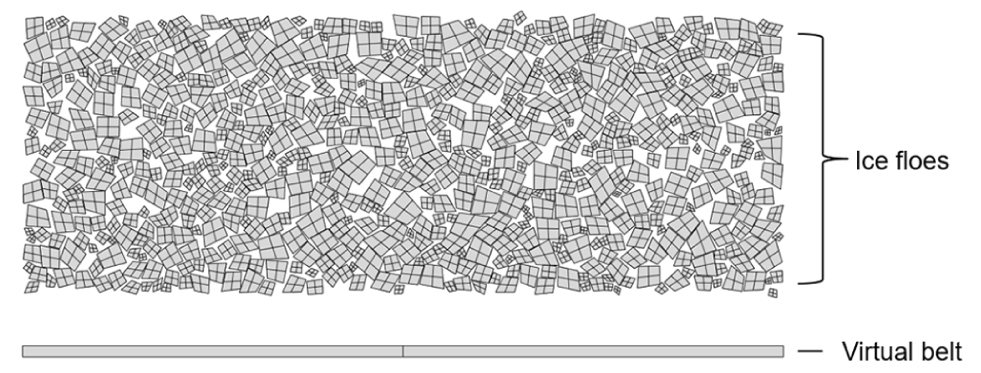
이 방법을 얼음-구조의 상호작용 해석의 시뮬레이션에 적용하기 위해, 각 박스는 유빙들로 구성된 하나의 그룹(group)으로 대체되었다. Fig. 5에서 설명된 벨트는 본 해석에서 실제로 적용되지 않기 때문에 가상의 벨트(virtual belt)를 모델링하여 유빙들의 셔플링을 제어하였다. 자세한 내용은 3장에서 설명하였다.
2.2 응력 시계열의 계산
2.1장에 설명된 방법을 적용하여 선체 외판 모델의 의 각 요소에 대해 접촉 압력의 시계열을 계산하였다. 접촉 압력이 대상 위치(target location)에 미치는 영향을 알아보기 위해 대상 위치에서의 충격응답함수(impulse Response Function)를 계산하였다. 결국, 응력의 시계열은 계산된 접촉 압력과 IRF에 컨볼루션 적분(convolution integral)을 적용하여 얻을 수 있다.
시스템이 선형이고 시간 불변일 때, 시스템의 응답은 컨볼루션 식(convolution equation)을 통해 표현될 수 있다. 연속 선형 시스템의 응답은 식(4)와 같이 컨볼루션 적분을 사용하여 시간 영역에서 표현할 수 있다.
| (4) |
여기서, 는 시간 에서 요소 의 접촉 압력에 의한 대상 위치 의 응력을 나타낸다. 는 요소 에서 계산된 접촉 압력이며, 는 요소 에 단위 임펄스를 가했을 때 발생하는 대상 위치 의 응력을 의미한다. 식(4)에서 계산된 응력은 선체 외판의 하나의 요소에 대한 값이기 때문에 대상 위치 의 응력 시계열 는 식(5)와 같이 계산될 수 있다.
| (5) |
여기서, 여기서 은 시간 에서 접촉된 요소의 총 개수를 의미한다.
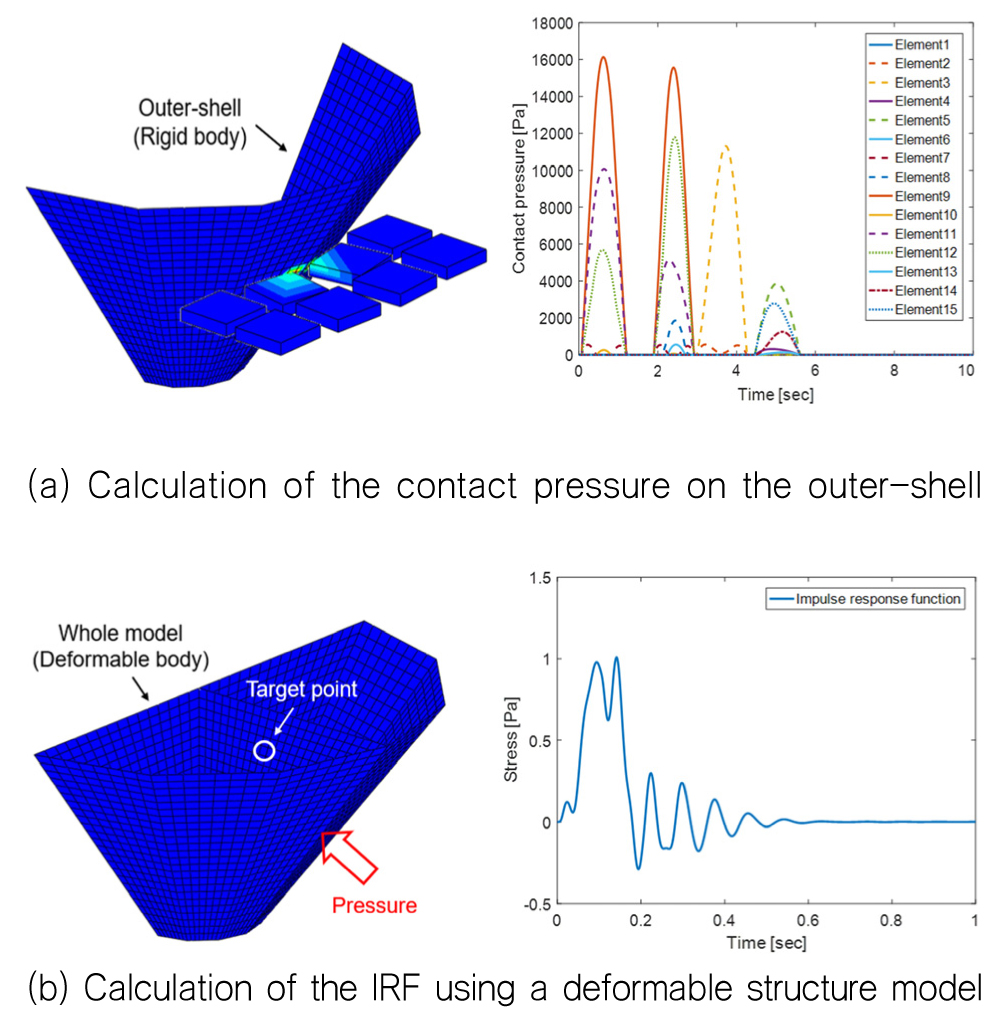
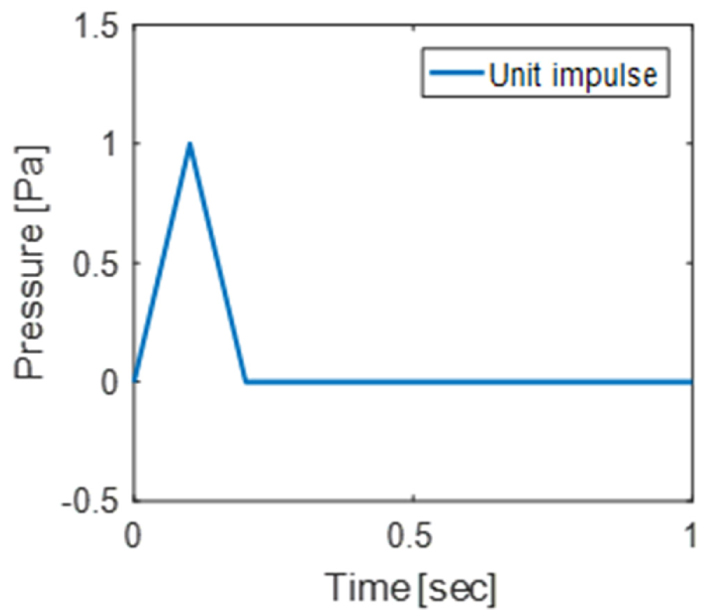
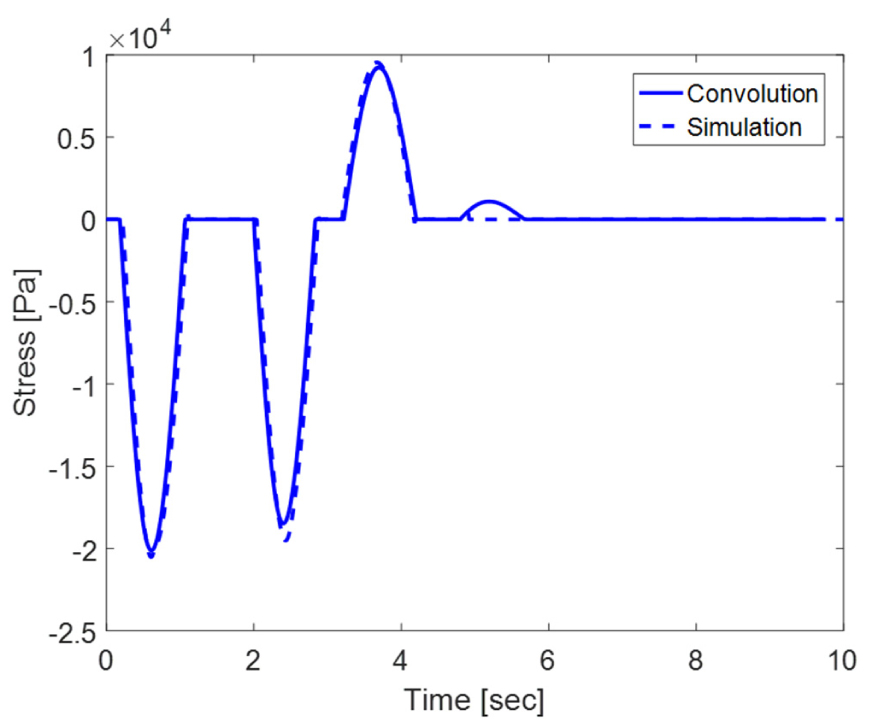
응력 시계열 계산에 적용된 컨볼루션 적분을 이용한 방법의 검증을 위해 간단한 모델을 이용한 해석을 수행하였다. 선박의 형상을 단순화한 모델을 만든 후, 8개의 직육면체 얼음 모델과 충돌시켰다. 먼저, 첫 번째 경우에서는 비교대상이 되는 결과를 도출하기 위해 변형체로 구성된 전체 선박 모델을 이용하였다. 선박 모델에서 직접 응력을 계산할 수 있기 때문에 한 번의 해석만으로 결과 도출이 가능하지만, 실제 계산에서는 막대한 해석 시간으로 적용이 불가능하다. 두 번째 경우에서는, 본 연구에서 제안한 컨볼루션 적분을 이용한 방법을 적용하였다. 선박 외판 모델에서 계산된 접촉 압력과 전체 선박 모델로부터 도출한 충격응답함수를 이용하여 응력의 시계열을 계산하였다. Fig. 6에서는 컨볼루션 적분을 적용한 방법을 접촉 압력 계산을 위한 단계 (a)와 충격응답함수 계산을 위한 단계 (b)로 구분하였다. Fig. 6 (a)에서 선박과 유빙의 충돌에 의해 발생하는 접촉 압력의 시계열은 선체 외판의 각 요소에 따라 계산된다. Fig. 6 (b)는 선체 외판의 각 요소에 압력의 형태로 가한 단위 임펄스에 대한 결과를 나타내며, 적용된 임펄스는 Fig. 7과 같다. 여기서 구조 모델은 변형체로 모델링되었으며, 적용된 감쇠비(damping ratio)는 0.5%이다 (Kim et al., 2009). Fig. 8은 검증 시험의 결과를 나타낸다. 결과적으로, 첫 번째 경우에서 수행된 변형체 전선 구조모델을 적용한 해석 결과('Simulation')와 컨볼루션 적용을 적용한 결과('Convolution')가 거의 일치한다는 것을 볼 수 있다.
2.3 응력 진폭의 단기 분포
응력 범위를 사용하는 일반적인 피로문제와는 달리 빙하중으로 인한 피로에서는 임펄스의 형태를 띄는 하중의 특징으로 인해 주로 응력 진폭을 사용한다. 따라서, 빙하중에 의한 응력은 0에서부터 점차 증가하여 피크(peak)에 도달한 후 다시 감소하여 0으로 돌아가는 삼각형의 패턴을 가지게 된다 (Suyuthi, et. al, 2013, Lee, et. al, 2016). 만약, 한 번에 하나의 유빙이 대상 위치에 영향을 준다면 응력의 시계열은 하나의 피크를 가지는 삼각형의 모습을 가지게 될 것이다. 하지만, 실제로는 여러 개의 유빙들이 대상 위치에 동시에 영향을 끼칠 수 있기 때문에 보통 Fig. 9과 같이 하나의 충격에 대해 여러 개의 피크를 가지는 시계열 패턴을 가질 수 있다 (Kotilainen et al., 2017). 하지만, 본 연구에서는 계산의 효율성을 위해 하나의 삼각 패턴에 대해 가장 큰 피크만을 추출하여 피로해석에 적용하였다. 즉, 0에서 시작하여 피크에 도달한 후 다시 0으로 돌아오는 하나의 패턴에 대해 가장 큰 피크 하나를 추출하고 그 보다 작은 작은 피크들은 무시하였다.
빙하중 피크의 확률 분포를 예측하는 데 사용되는 확률적 모델은 와이블 분포(Suominen and Kujala, 2010, Suyuti et al., 2013), 지수 분포(Kujala and Vuorio, 1986) 등이 있다. Kujala et al.(2009)은 실선 계측 결과에 대해 지수 분포, 감마 분포 및 와이블 분포를 적용하였고, 형상 모수(shape parameter) 0.75인 와이블 분포가 가장 적합한 모델이라는 것을 발견하였다. Su et al. (2011)은 수치해석을 통해 도출한 빙하중이 역시 형상 모수 0.75인 와이블 분포와 잘 일치한다고 확인하였다.
와이블 모델은 위치 모수(location parameter)의 존재에 따라 2-parameter 와이블 모델과 3-parameter 와이블 모델로 나눌 수 있다. 각 모델의 확률밀도 함수는 식(6)과 (7)과 같다 (Suyuthi et al., 2013).
| (6) |
| (7) |
여기서 는 응력 진폭 의 확률 밀도 함수이다. 는 와이블 형상 모수이며, 와 는 각각 와이블 척도 모수(scale parameter)와 위치 모수를 의미한다. 각 모수는 Maximum likelihood estimator (MLE)를 이용하여 도출하였다 (McCool, 2012).
2.4 피로 손상도 계산
2.3장에서 도출된 와이블 분포와 Palmgren-Miner rule을 이용하면 식(8)과 (9)와 같이 해당 조건에서의 피로 손상도를 계산할 수 있다. 식(8)은 2-parameter 와이블 모델을 이용하는 경우이며, 식(9)는 3-parameter 와이블 모델을 이용하는 경우의 피로손상도 계산식을 나타낸다 (Suyuthi et al., 2013).
| (8) |
| (9) |
여기서, 와 은 S-N 선도 상의 모수(parameter)를 나타낸다. 는 응력 싸이클의 총 횟수를 의미하며, 빙 충돌로 표현하면 식(10)과 같이 충돌 빈도()와 특정시간 동안 선박의 이동 거리()의 곱으로 나타낼 수 있다. 충돌 빈도는 식(11)과 같이 실선 계측을 통해 도출한 Zhang et al. (2011)의 식을 적용하였다.
| (10) |
| (11) |
여기서, 는 등가 빙두께를 의미한다 (Kujala, 1994).
이 정수라고 가정하면, 이항정리와 감마함수를 이용하여 식(12)와 (13)과 같이 정리할 수 있다 (Suyuthi et al., 2013). 여기서, 는 감마함수를 의미한다.
| (12) |
| (13) |
3. 빙하중 기인 응력의 단기 분포
본 장에서는 실제 발트해의 빙 조건을 고려한 피로해석의 시작 단계로서, 대상 선박이 발트해를 운항할 때에 겪을 수 있는 대표적인 빙 조건들을 선정하여 일련의 계산을 수행하였다. 또한, 계산된 결과를 바탕으로 응력의 확률 분포를 도출하고 와이블 모수들의 경향을 분석하였다. 계산된 단기 분포 결과는 4장에서 실제 빙조건에 적용하여 대상 선박의 피로 손상도 계산에 적용된다.
3.1 해석 조건
극지를 항해하는 배의 피로 문제에 있어서 가장 중요한 요인은 빙조건과 선속이다. 빙조건은 빙두께, 밀집도(concentration), Ridge 두께 및 Ridge 출현률(rate of ridge occurrence)로 특징지을 수 있다(Suyuthi et al., 2013). 실제로 빙조건은 정의하기가 매우 어려워 다양한 요인에 기초하여 도출한 등가 빙두께()가 주로 해석에 적용된다. 간단히 설명하면, 이는 특정 지역의 모든 얼음의 평균 두께를 의미한다. (Riska, 2010)
Suyuthi et al. (2013)은 피로 해석에 빙두께와 선속을 변수로 사용하였으며, Lloyd's Resister (2014)는 빙두께 만을 변수로 사용하였다. 본 연구에서는 대상 빙조건이 유빙 조건임을 고려하여 빙두께, 선속에 밀집도를 변수로 추가하였다.
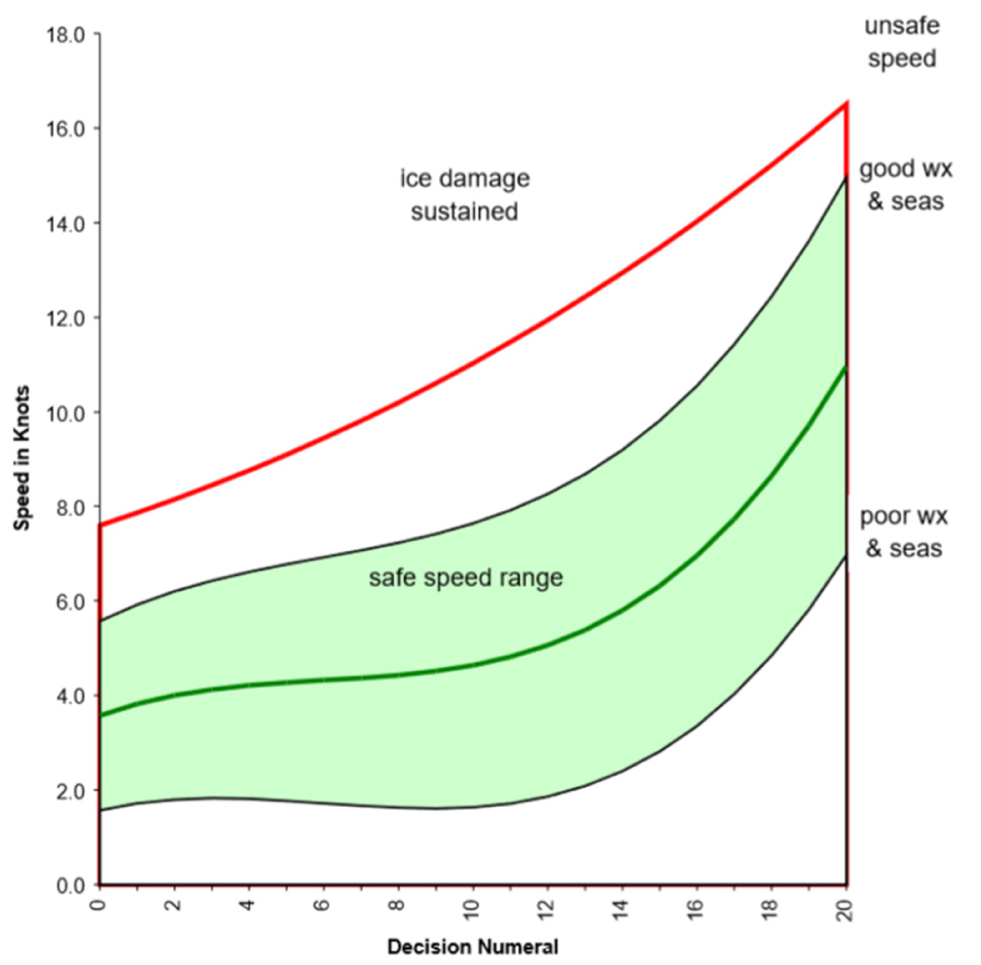
본 연구에서는 대상 빙조건을 1년생빙으로 가정하여 피로 해석에 사용된 빙두께를 0.3, 0.6, 0.9m로 정하였다 (Kim and Kim, 2018). 유빙의 경우, 밀집도가 중요한 변수가 될 수 있기 때문에 40%, 60%, 80%의 밀집도 조건을 추가하였다. 선속의 경우는 빙조건에 따라 달라지기 때문에 Fig. 10에 명시된 선박의 안전 속도를 고려하여 4knots, 6knots, 8knots를 해석조건에 적용하였다. 여기서, x축의 Decision numeral은 선박이 특정 빙해역에 진입할 수 있을지 여부를 결정하는 지표를 나타낸다 (Transport Canada, 1996). Table 1은 피로해석을 위해 수행한 해석 Case를 나타낸다.
3.2 유한요소 모델링
3.2.1 대상 선박
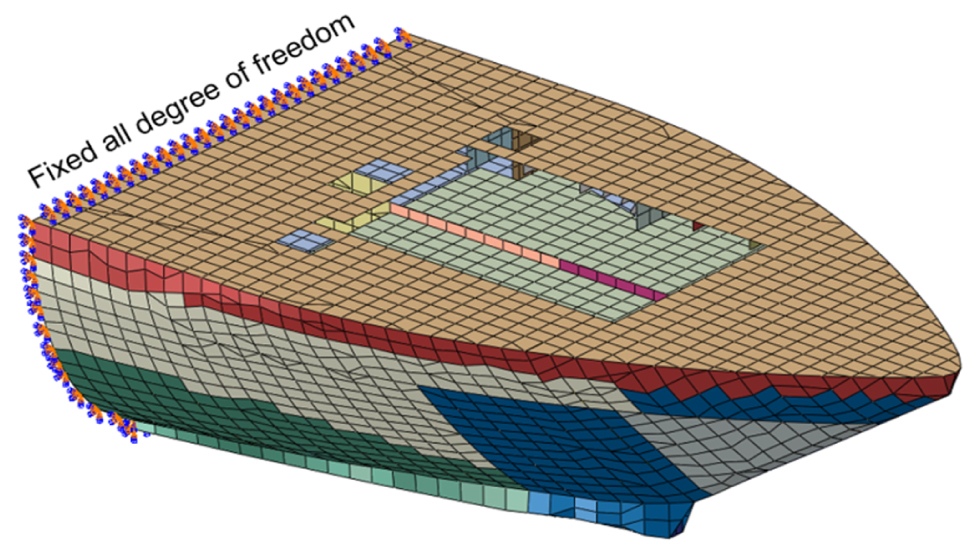
Fig. 11은 본 연구에서 사용된 한국 쇄빙연구선 아라온호(Araon)의 유한요소 모델을 나타낸다. 본 연구의 대상 선박은 내빙 선박이지만, 관련 도면과 가용할 수 있는 유한요소 모델이 없어 부득이 아라온호의 모델을 해석에 적용하였다. 대부분의 빙하중이 선수부(bow region)에 작용한다고 가정하여 선수부 모델만을 사용하였다. 경계조건 효과를 최소화하기 위해 모델의 범위는 충분히 크게 하였으며, 절단면에 6자유도를 고정하였다. Table 2는 대상 선박의 주요 요목을 나타낸다.
3.2.2 주기적 매체 해석 모델링
해석 시간을 줄이기 위해 유한요소 모델에 주기적 매체 해석 기법을 적용하였다. 한편, 하나로 연결된 모델이 아닌 수많은 유빙들의 그룹에 이 기법을 적용하기 위해서는 적절한 수정이 필요하다. 먼저, Fig. 12와 같이 모든 유빙의 제어를 위한 가상의 벨트를 만들었다. 그리고 가상의 벨트와 유빙들을 하나의 블록으로 포함시켰다. 즉, 가상의 벨트는 컨베이어 벨트와 같이 한 방향으로 계속해서 이동하고, 그와 연결된 유빙들은 벨트에 따라 셔플링을 반복하게 된다.
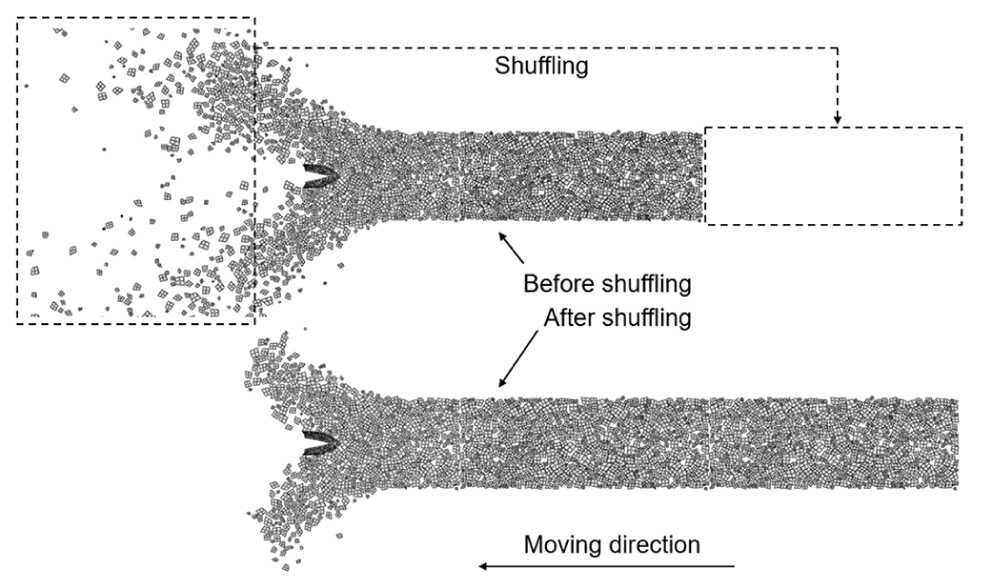
Fig. 13에서는 주기적 매체 해석 기법이 적용된 전체 유한요소 해석 모델을 나타낸다. 유빙 채널(channel)의 전체 폭은 80m이고, 채널의 양쪽에는 별도의 경계조건을 가하지 않아 얼음이 자유롭게 퍼지도록 하였다. 전체 모델은 3개의 블록으로 구성된다. 각 블록이 사라지고 새롭게 나타나기를 반복하기 때문에 해석의 연속성을 보장하기 위해 트리거 플랜의 위치를 결정하였으며, 각 블록의 길이는 200m로 충분히 길게 구성하였다. 또한, 해석의 효율성을 위해 선박이 움직이는 대신 유빙이 선박의 속도대로 이동하도록 하였다. Fig. 14에서는 셔플링 순간을 나타내고 있다. 셔플링으로 인해 이미 충돌하고 난 후 더 이상 사용되지 않을 유빙들이 사라지고 원래의 블록으로 정렬되어 충돌할 다음 차례를 기다리는 것을 볼 수 있다. 블록을 충분히 길게 구성하여 셔플링이 진행되어도 선박의 바로 앞에서 충돌되고 있는 유빙에는 아무런 영향을 끼치지 않는 것을 확인할 수 있다.
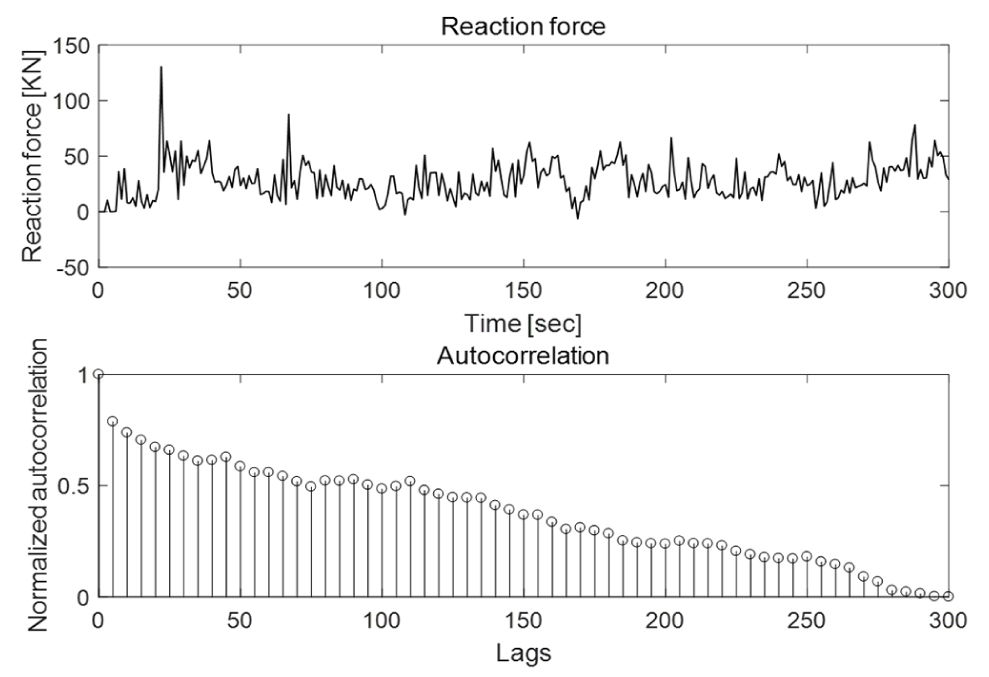
한편, 동일한 블록들이 계속해서 반복되기 때문에 선박의 응답 또한 반복되는 것이 아닌가하는 의문이 있을 수 있다. 하지만, Fig. 14에서 보는 바와 같이 선박 앞에는 충돌하고 있는 유빙으로 인해 진입하는 유빙들이 흩어지기 때문에 선박은 계속해서 새로운 하중을 받는다고 할 수 있다. 이를 수치적으로 확인하기 위해 Fig. 15에서는 셔플링이 반복되는 동안 선박에서 시간영역으로 계측되는 반력에 대해 자기 상관관계(autocorrelation)를 도출하였다. 두께 0.9m, 밀집도 80%, 속도 4knots 조건으로 해석을 수행하였으며 결과적으로, 자기 상관 결과에서 아무런 주기성을 보이지 않아 선박은 주어진 시간동안 계속해서 새로운 하중을 받는다는 것을 알 수 있다.
3.2.3 대상 위치 선정
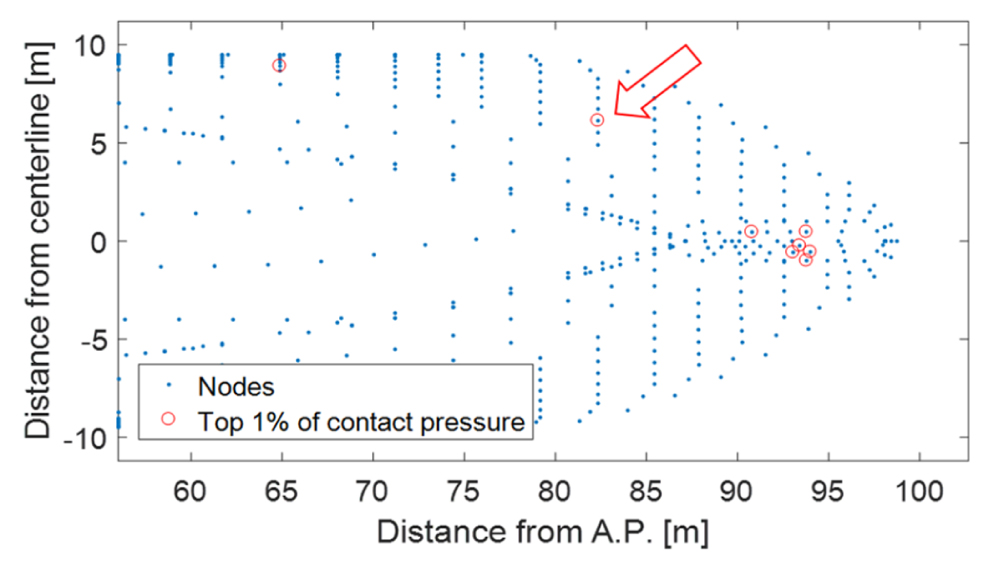
피로 손상도 계산을 수행할 대상 위치를 선정하기 위해 임의의 조건에 대해 스크리닝(screening) 해석을 수행하였다. 선정된 조건은 두께 0.9m, 밀집도 60%, 속도 4knots 조건이며, 제안된 방법을 통해 300초 동안 해석을 수행한 후 선체 외판에서 계측되는 접촉 압력을 크기 별로 분류하였다. 충돌 횟수는 별도로 고려하지 않고, 상위 1%의 접촉 압력이 계측된 위치를 선별하였다. 즉, 각 절점(node)에서 겪게 되는 최대 접촉 압력을 나열한 후 상위 1%만 추출하였다. 결과적으로 Fig. 16에서 나타낸 바와 같이 중심선(centerline) 근처의 몇몇 절점에서 상위 1%의 접촉 응력이 발견되었지만, 이 부분은 구조적으로 강하여 피로 손상이 발생할 위험이 거의 없다고 판단하여 화살표로 표시한 지점을 대상 위치로 결정하였다.
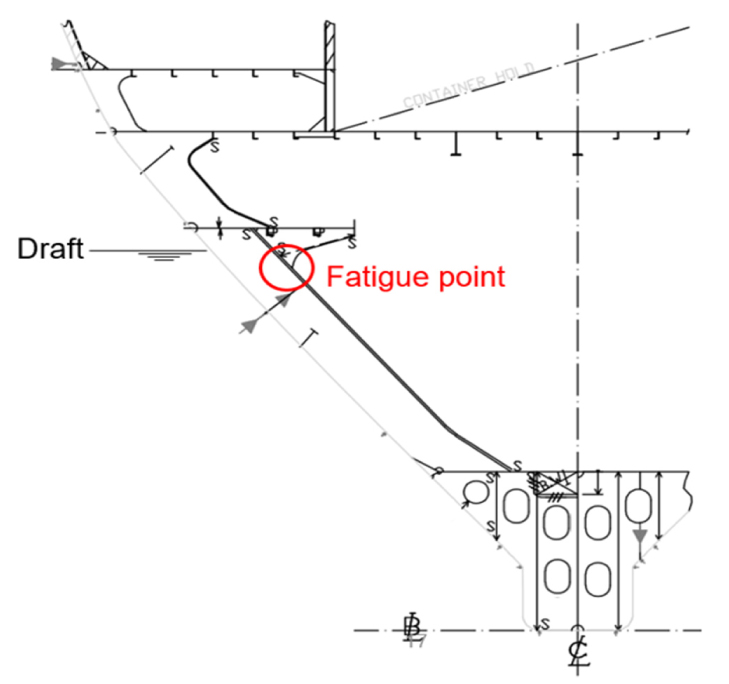
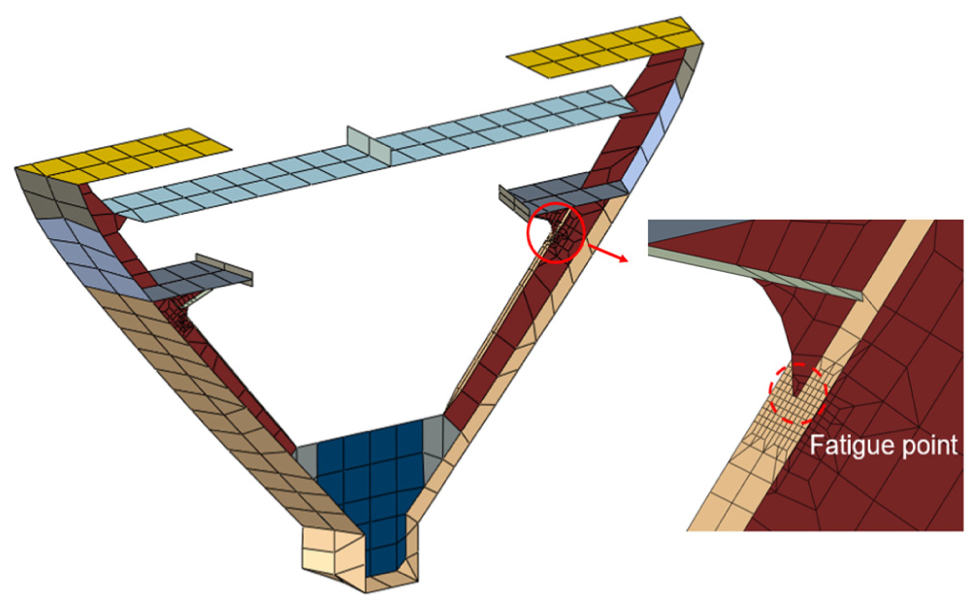
Fig. 17에서는 스크리닝 해석을 통해 선정된 대상 위치를 나타내고 있다. 빙하중을 주로 받게 되는 흘수선에서 가장 가까운 용접부를 해석대상으로 선정하였다. Fig. 18에서는 해당 용접부에 대해 상세 메쉬(fine mesh)를 수행한 모습을 나타낸다. 핫스팟 응력(hot spot stress)의 계산을 위해 판두께 크기의 요소로 모델링하였다 (Det Norske Veritas, 2012).
3.2.4 응력 진폭의 단기 분포 계산
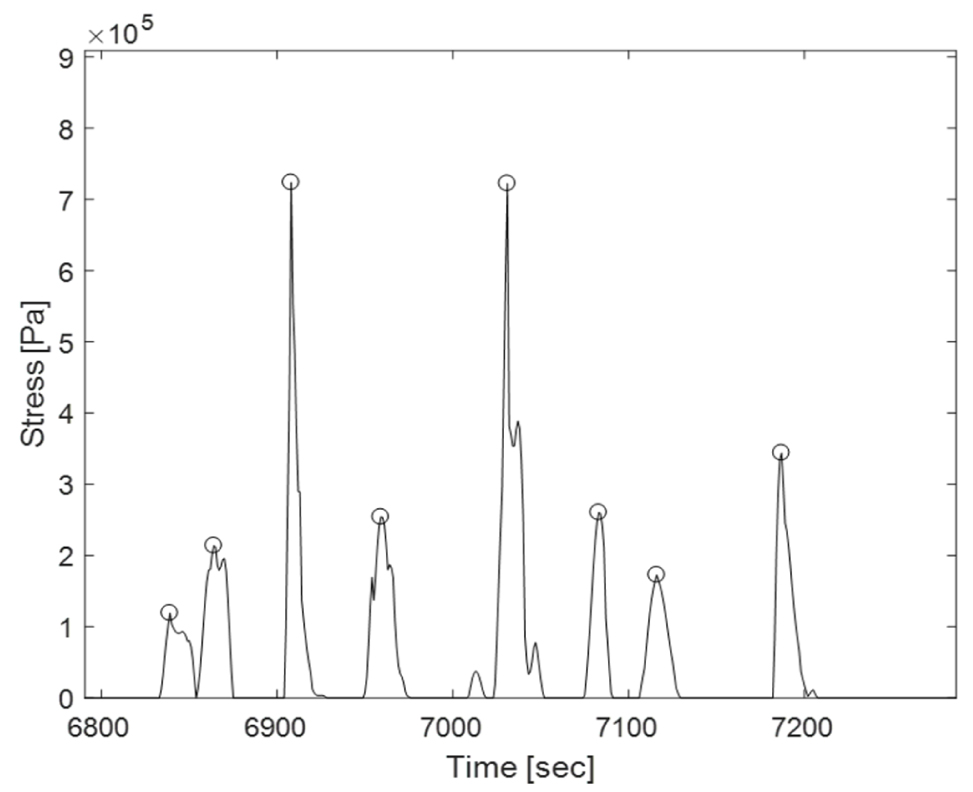
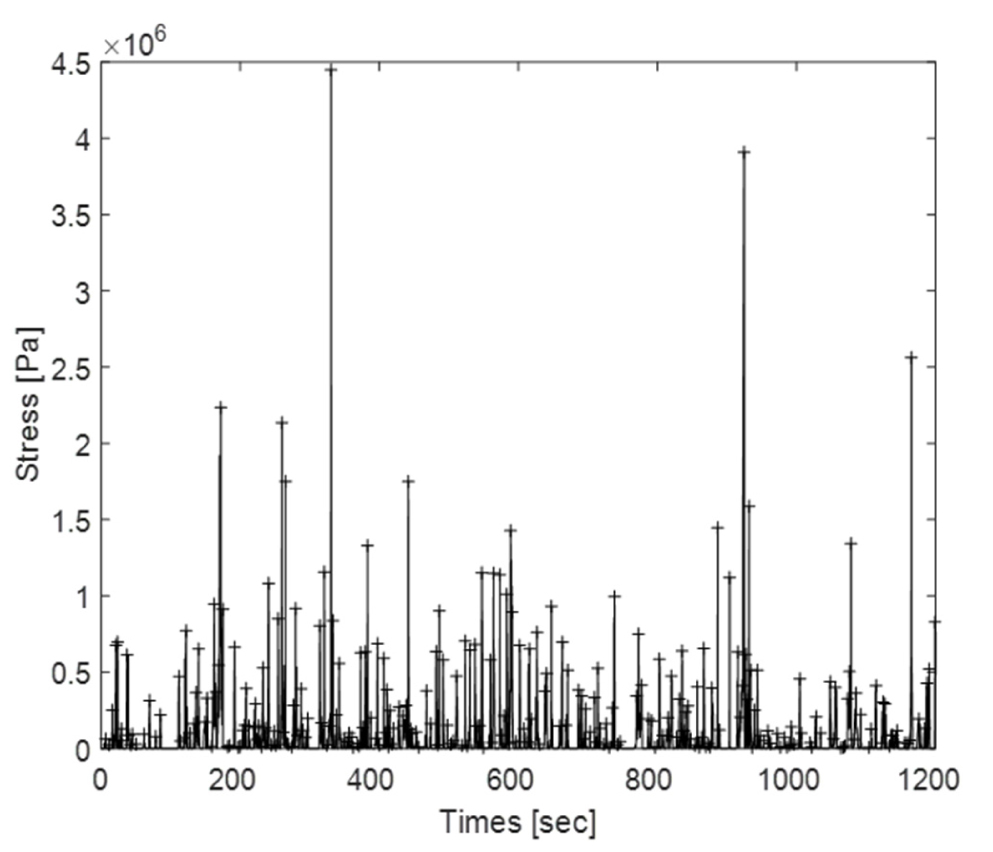
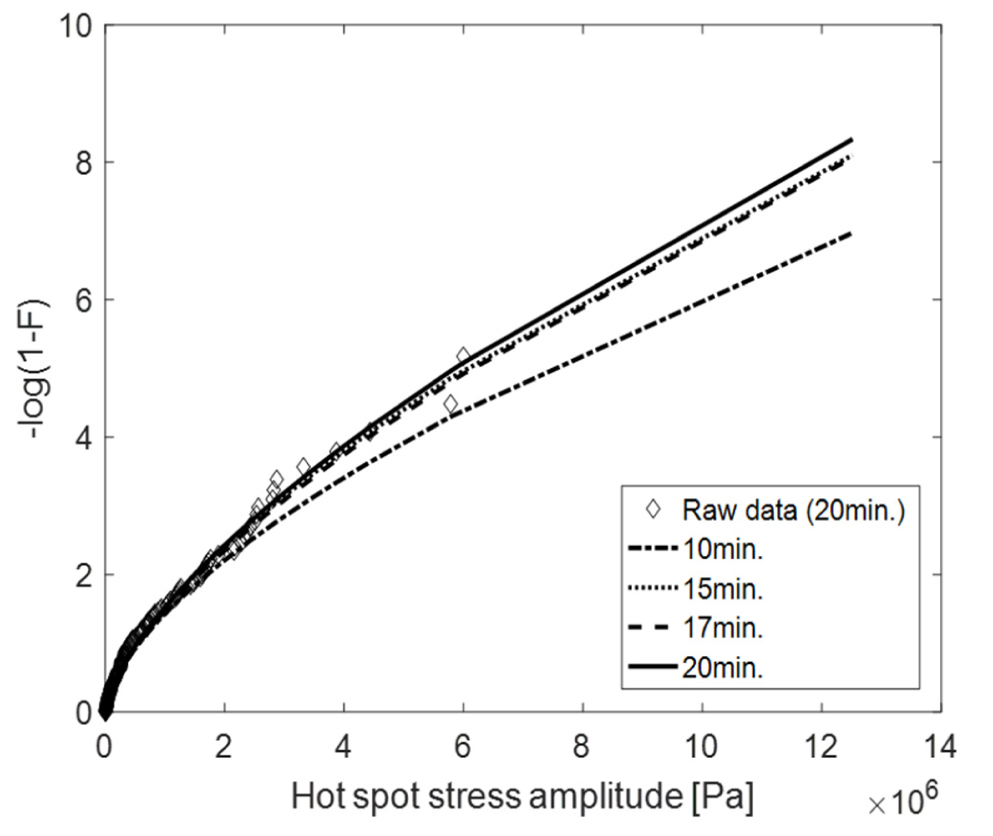
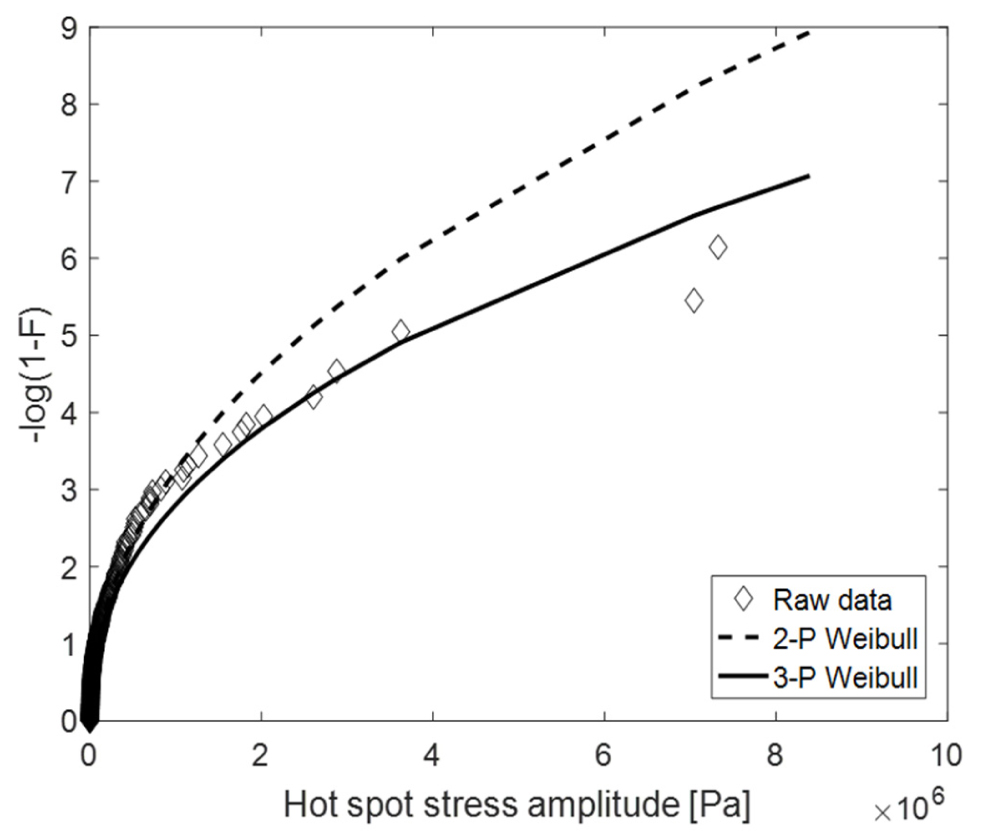
Table 1에서 나타낸 서로 다른 빙두께, 밀집도, 선속에 대한 모든 경우를 조합하여 총 27개의 해석 조건에 대해 해석을 수행하였다. Fig. 19에서는 하나의 조건에 대해 계산된 응력의 시계열을 나타낸다. 확률적 특성을 얻을 만큼의 충분한 시계열 데이터에 필요한 시간을 알아보기 위해 Fig. 20과 같이 해석시간에 따른 와이블 Fitting의 수렴성을 알아보았다. 2-parameter 와이블 모델을 적용하였으며, 충돌 횟수가 가장 적을 것으로 예상되는 빙두께 0.9m, 밀집도 40%, 선속 4knots 조건으로 평가하였다. 결과적으로 15분 이후부터 와이블 곡선이 수렴하는 모습을 보여 해석시간을 20분으로 결정하였다. 추가로, 와이블 모델의 결정을 위해 Fig. 21과 같이 2-parameter와 3-parameter 와이블 모델을 이용하여 빙두께 0.9m, 밀집도 80%, 선속 4knots 조건에 대한 계산결과를 Fitting 하였다. 그 결과, 2-parameter 모델의 경우 대부분의 데이터가 밀집되어 있는 중앙부를 잘 Fitting하는 반면, 3-parameter 모델의 경우는 Tail 부분을 잘 Fitting하는 것을 볼 수 있다. 이러한 특성으로 인해 2-parameter 모델이 극한값(extreme value)을 과소평가하는 경향이 있다. 하지만, 피로의 경우 극한값 보다는 반복횟수가 많은 중간 지점의 응력이 더 중요하기 때문에 2-parameter 모델이 더 적합하다고 할 수 있다. 따라서, 본 연구에서는 2-parameter 모델을 피로해석에 적용하였다.
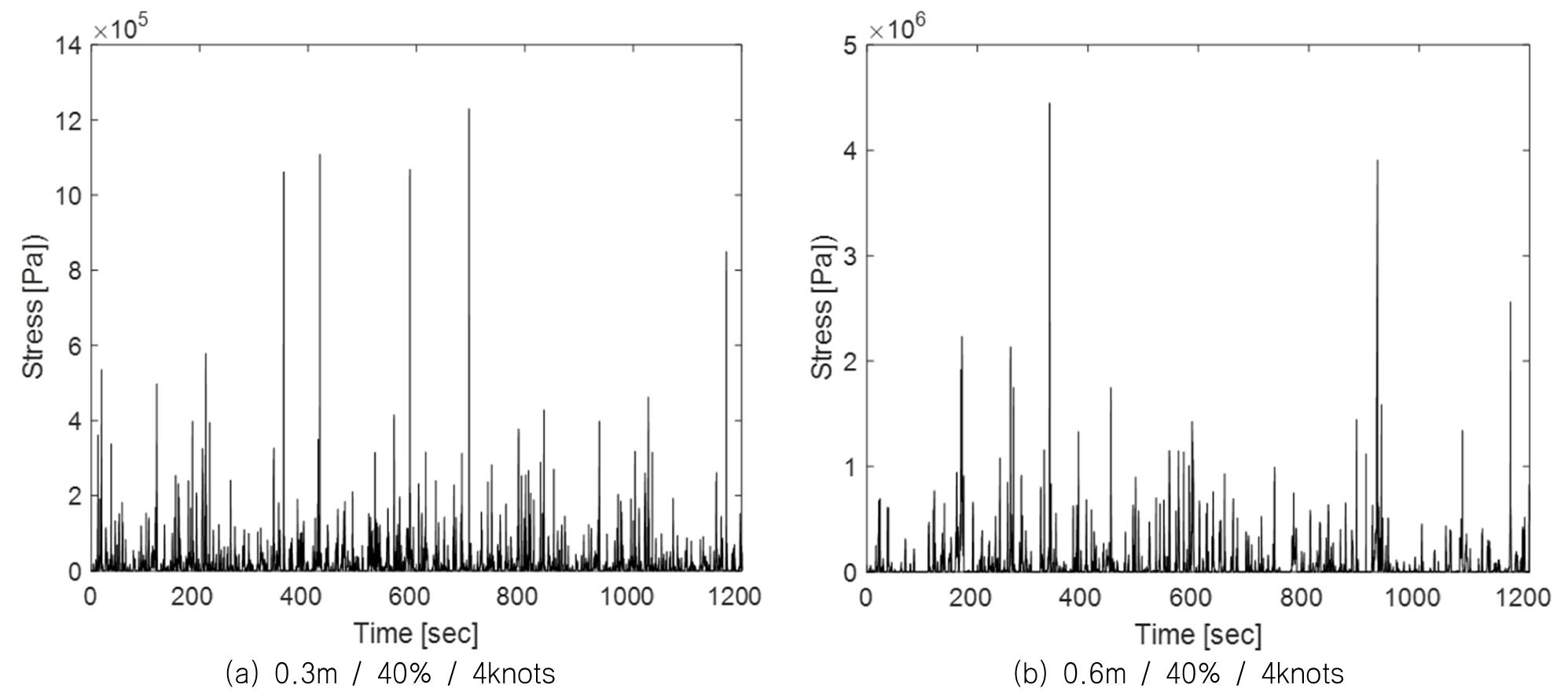
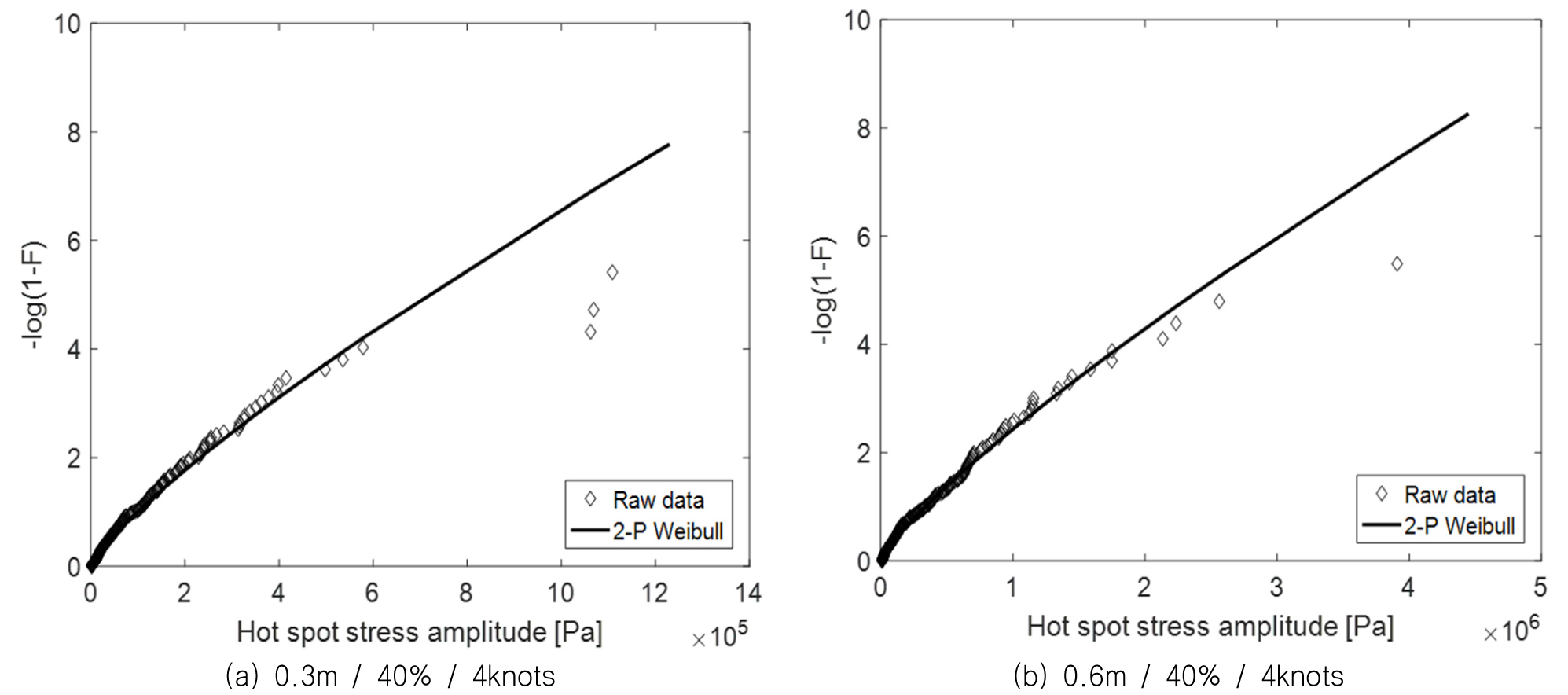
Fig. 22에서는 제안된 방법을 통해 계산된 응력의 시계열 예시를 나타내고 있다. 같은 밀집도와 선속하에서 두꺼운 얼음에 의해 발생하는 응력의 값이 상대적으로 높게 나타나고 있음을 확인할 수 있다. Fig. 23에서는 각 시계열 데이터에 대한 2-parameter 와이블 Fitting의 모습을 보여준다. Tail 부분에서 다소 오차가 있지만, 대부분의 데이터를 잘 근사하고 있으므로 그 영향은 제한적인 것으로 판단된다.
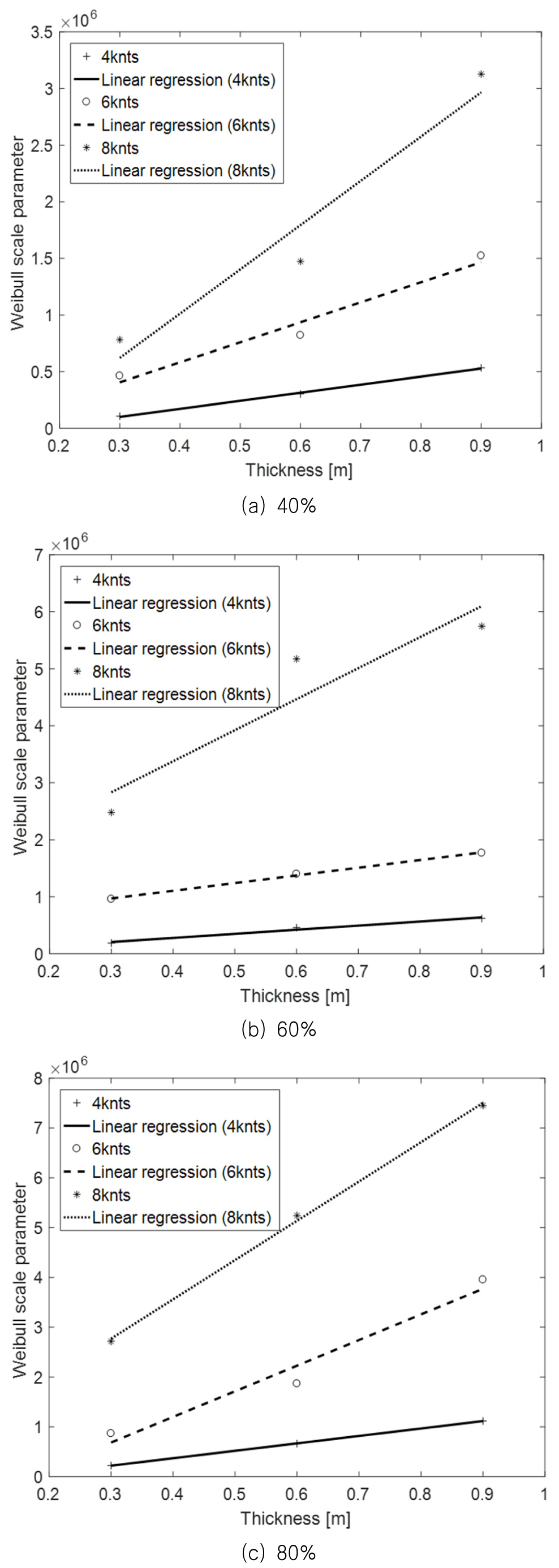
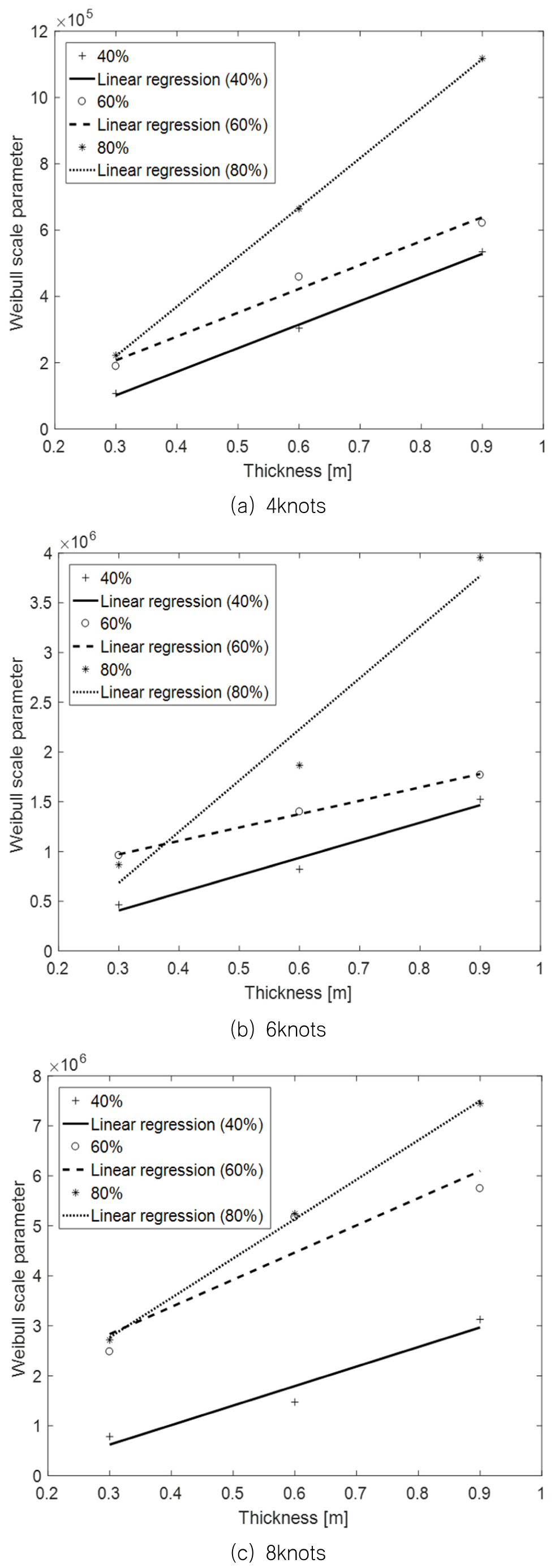
Fig. 24와 25에서는 계산된 모든 조건에 대한 와이블 척도 모수 도출 결과를 정리하여 나타내었다. 먼저, x-축은 가장 중요한 변수로 여겨지는 빙두께로 고정하였다. Fig. 24에서는 밀집도의 각 조건을 하나씩 고정하여 속도와 두께에 대한 결과를 나타내었으며, Fig. 25에서는 선속의 각 조건을 하나씩 고정하여 밀집도와 두께에 대한 결과로 나타내었다. 결과적으로 모든 조건에서 빙두께가 증가할수록 와이블 척도 모수가 증가한다는 것을 알 수 있다. 또한, Fig. 24로부터 선속이 증가할수록 와이블 척도 모수가 증가한다는 것을 볼 수 있다. 밀집도의 경우는 전체적으로 와이블 척도 모수와 선형관계에 있다고 할 수 있으나, 6knot 조건에서 그렇지 않은 결과를 도출하기도 하였다.
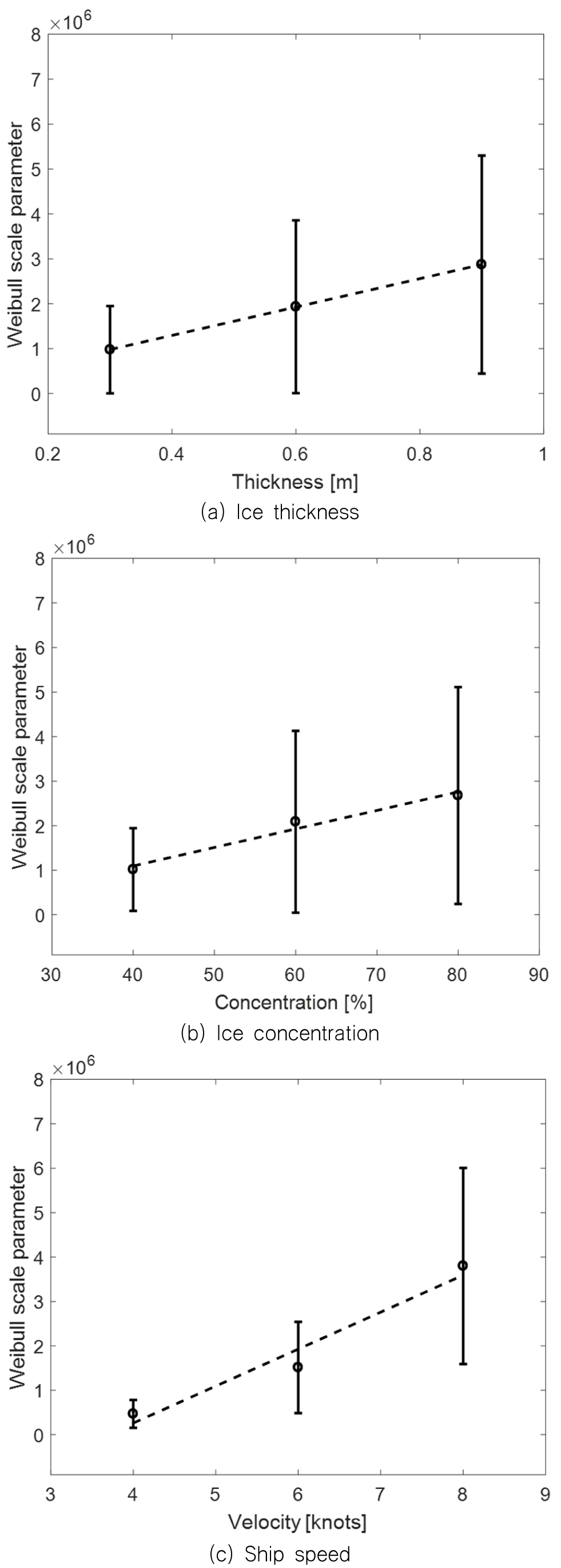
Fig. 26에서는 평균과 표준편차를 이용하여 각 조건에 따른 와이블 척도 모수의 경향성을 알아보았다. 결과적으로, 평균값 측면에서 빙두께와 밀집도 그리고 선속은 와이블 척도 모수와 선형관계에 있다는 것을 볼 수 있다. 표준편차 또한 각 조건이 증가할수록 증가한다는 것을 발견할 수 있다.
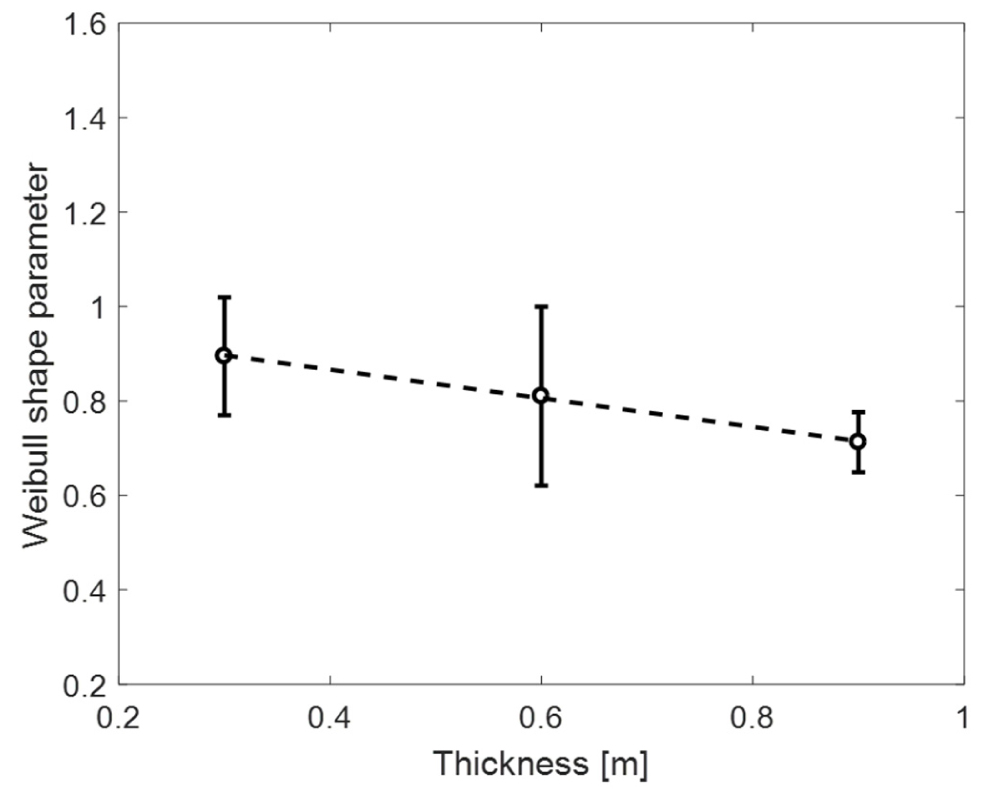
Fig. 27에서는 각 조건에 따른 와이블 형상 모수의 경향성을 알아보았다. 빙두께를 제외한 다른 조건들에 대해서는 산포도가 매우 커서 경향성을 발견할 수 없었다. 다만, 빙두께에 대해서는 와이블 형상 모수와 반비례 관계가 있는 것을 알 수 있다.
4. 실제 조건에 대한 피로 손상도 분석
4.1 해석 조건
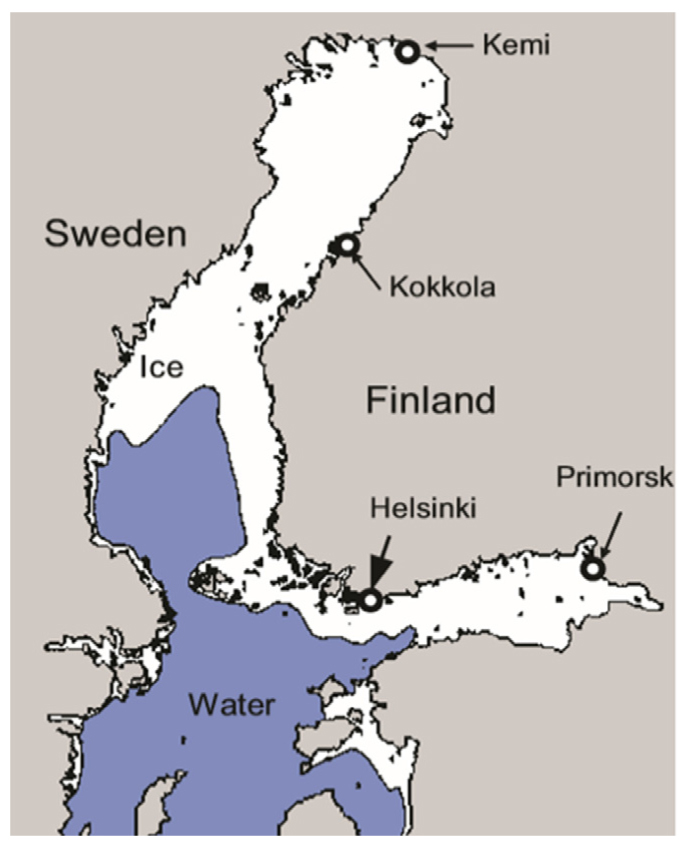
제안된 방법을 적용하여 실제 환경조건에 대한 대상 선박의 피로 손상도를 평가하였다. 대상 루트(route)는 Fig. 28에 나타낸 발트해의 케미 루트(Kemi route)로 정하였다. Lloyd's Register (2014)에 따라 연간 헬싱키와 케미를 3.5회 왕복하는 것으로 가정하였고, 상세한 환경조건은 Table 3에 나타내었다. 선속은 발트해에서 계측된 선박들의 속도를 참고하여 8knots로 가정하였다 (Löptien and Axell, 2014). 밀집도는 해당 루트가 겨울 동안 대부분 얼어있는 상태이기 때문에 100%의 유빙조건으로 가정하였다. 최종 피로 손상도의 허용 기준(acceptance criteria)은 파랑하중에 의한 피로 손상도를 고려하여 0.5로 정하였다.
4.2 제안된 방법과 LR 방법을 이용한 피로 손상도 비교
제안된 방법과 LR 방법을 이용하여 케미 루트의 피로 손상도를 비교하였다. 먼저, 제안된 방법을 적용할 때는 3.2장의 Figs. 22, 23, 24, 25에서 요약된 와이블 척도 모수와 형상 모수를 이용하여 계산하였다. 특정 빙두께의 와이블 모수는 각 빙두께에 대해 도출된 선형 회귀 방정식을 이용하여 추정할 수 있다. 100% 밀집도에 대한 값은 Fig. 26 (b)의 결과를 외삽하여 얻을 수 있다. 충돌 빈도의 경우는 Zhang et al. (2011)의 식을 적용하였다. 마지막으로 각 조건에서의 피로 손상도는 식(12)를 이용하여 계산할 수 있다.
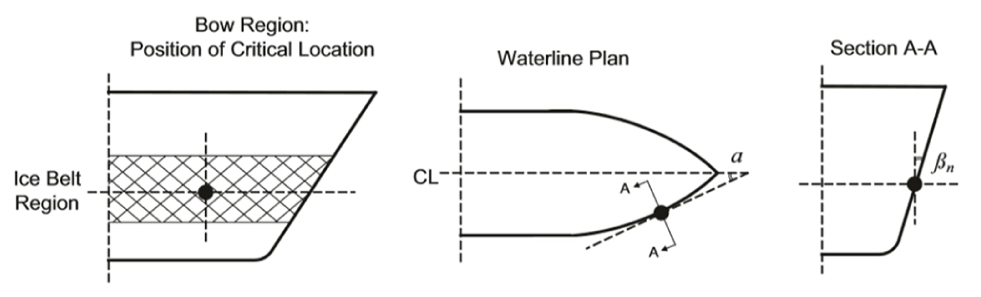
다음으로, LR 방법을 이용하여 피로 손상도를 평가하였다. Table 4는 계산에 필요한 대상 위치의 기하학적 정보를 보여준다. 선체 각도 와 에 대한 정의는 Fig. 29에 나타내었다. LR 방법에서는 환경 조건과 Table 4의 기하학적 정보만 있으면 대상 위치의 피로 손상도를 간단한 식을 통해 계산할 수 있다.
피로 계산에서, 제안된 방법의 경우는 Det Norske Veritas (2012)에서 제안하는 Hot spot stress를 위한 선도인 D-curve를 적용하였고, LR 방법의 경우는 공칭응력을 사용하므로 용접부의 형상에 따라 F2-curve를 적용하였다. Table 5에서는 각 조건에 대한 피로 손상도 결과를 나타내며, Table 6에서는 각 방법으로 계산된 최종 피로 손상도율을 비교하였다. 여기서, DPR과 DLR은 각각 제안된 방법과 LR 방법을 통한 피로 손상도율을 나타낸다. 그 결과, LR 방법으로 계산한 결과가 제안된 방법으로 계산된 결과에 비해 2배이상 큰 피로 손상도를 도출한 것을 알 수 있다. 이는 LR 방법의 경우 설계자들이 간편하게 사용하는 대신 안전을 보장하기 위해 보수적으로 만들어졌기 때문이라고 이해할 수 있다. 제안된 방법의 경우 허용 기준인 0.5 보다 적은 0.18이 계산되었지만, 피로 손상도의 경우 와이블 척도 모수, 즉 응력 진폭에 매우 민감하기 때문에 결과 안전한 수준이라고 할 수 없다. 즉, 평소보다 더 두꺼운 유빙을 만난다든지 용접부에 결함이 있다면 피로 균열의 가능성이 충분히 있다고 할 수 있다.
5. 결 론
본 연구에서는 유빙 조건을 항해하는 내빙 선박의 피로 손상도 평가에 있어서 수치해석을 이용한 새로운 방법을 제안하였다. 상기의 연구 결과를 토대로 다음과 같은 결론을 도출할 수 있었다.
유빙과 구조물간의 상호작용을 모사할 수 있는 수치 모델이 개발되었다. 효율적인 계산을 위해 얼음과 유체, 얼음과 구조물 사이의 상호작용은 간략한 방법을 통해 구현되었으며, 이 과정에서 필요한 항력 계수나 접촉 모델과 같은 주요 모수들은 별도의 상세 해석을 통해 도출하였다.
긴 시간의 비선형 시간영역 해석을 효율적으로 수행하기 위해 주기적 매체 해석 기법을 적용하였다. 결과적으로, 제한된 수의 요소를 통해 20분의 시간영역 해석이 가능하게 되었고, 전체 해석시간동안 선박은 계속해서 새로운 하중을 받는다는 것을 확인하였다.
선체 외판에서 계산된 접촉 압력의 시간 이력은 컨볼루션 적분을 통해 대상 위치에서의 응력의 시계열로 변환되었다. 이 방법은 간단한 모델을 통해 검증되었으며, 따라서 적은 시간으로 정확한 응력의 시계열을 도출할 수 있게 되었다.
빙두께, 밀집도, 선속을 고려한 다양한 조건에 대하여 해석을 수행하였고, 각 조건에 대한 와이블 모수들을 도출하였다. 본 연구에서는 2-parameter 와이블 모델을 적용하였으며, 이를 통해 각 조건과 와이블 모수들 간의 관계를 도출하였다. 결과적으로, 와이블 척도 모수는 모든 경우에 대해 빙두께와 선속과 비례관계에 있다는 것을 알 수 있었다. 하지만, 밀집도의 경우는 몇몇 경우에서 비례관계가 아닌 부분이 발견되었다. 와이블 형상 모수의 경우는 빙두께를 제외하고는 어떠한 경향성을 발견하기 어려웠다. 와이블 형상 모수는 빙두께와 반비례 관계에 있다는 것을 알 수 있었다.
제안된 방법을 통해 발트해의 실제 조건에 대한 피로 손상도 평가를 수행하고, LR의 Simplified 방법의 결과와 비교하였다. 결과적으로, LR의 방법이 제안된 방법에 비해 두배 이상의 보수적인 결과를 도출하였다. 이는 LR 방법은 간편하지만 안전한 설계를 위해 보수적인 결과를 도출하도록 만들어졌기 때문으로 판단된다.
Acknowledgments
본 연구는 산업통상자원부의 산업핵심기술개발사업(10063417, ARC7 극지 환경용 해양플랜트 내빙구조 설계기술 개발)의 재정지원을 받아 수행된 연구 결과의 일부임을 밝힙니다.
References
- Bridges, R., Riska, K. & Zhang, S., 2006. Fatigue assessment for ship hull structures navigating in ice regions. Proceedings of the Icetech 2006, Banff, Canada.
-
Chai, W., Leira, B. & Naess, A., 2018. Short-term extreme ice loads prediction and fatigue damage evaluation for an icebreaker. Ships and Offshore Structures, 13.
[https://doi.org/10.1080/17445302.2018.1427316]

- Dassault Systèmes Simulia Corp., 2014. Abaqus 6.14 Theory Manual.
- Det Norske Veritas, 2012 DNV Recommended Practice, Fatigue design of offshore steel structures, DNV-RP-C203.
-
Hopkins, M. & Shen, H., 2001. Simulation of pancake-ice dynamics in a wave field. Annals of Glaciology, 33, pp.355-360.
[https://doi.org/10.3189/172756401781818527]

-
Kim, J. & Kim, Y., 2018. Numerical simulation on the response of moored semi-submersible under ice load. Journal of Ocean Engineering and Technology, 32(3), pp.177-183.
[https://doi.org/10.26748/KSOE.2018.6.32.3.177]

- Kim, Y., Kim, K. & Kim, Y., 2009. Analysis of hydroelasticity of floating shiplike structure in time domain using a fulling coupled hybrid BEM-FEM. Journal of Ship Research, 53(1), pp.31-47.
-
Kotilainen, M., Vanhatalo, J., Suominen, M. & Kujala, P., 2017. Predicting ice-induced load amplitudes on ship bow conditional on ice thickness and ship speed in the Baltic Sea. Cold Regions Science and Technology, 135, pp.116-126.
[https://doi.org/10.1016/j.coldregions.2016.12.006]

- Kujala, P. & Vuorio, J., 1986. Results and statistical analysis of ice load measurements on board icebreaker Sisu in winters 1979-1985. Helsinki: Winter Navigation Research Board.
- Kujala, P., Suominen, M. & Riska, K., 2009. Statistics of ice loads measured on MT Uikku in the Baltic. Proceedings of POAC 2009.
- Kujala, P., 1994. On the statistics of ice loads on ship hull in the Baltic. Ph.D. Acta Polytechina Scandinavica, Mechanical Engineering Series No. 116. Helsinki, Finland.
-
Lee, J., Kwon, Y., Rim, C. & Lee, T., 2016. Characteristic analysis of local ice oad signals in ice-covered waters. International Journal of Naval Architecture and Ocean Engineering, 8(1), pp.66-72.
[https://doi.org/10.1016/j.ijnaoe.2016.01.001]

- Lloyd's Register, 2014. ShipRight Design and Construction, Fatigue Design Assessment - Application and Notations.
-
Löptien, U. & Axell, L., 2014. Ice and AIS: ship speed data and sea ice forecasts in the Baltic Sea. The Cryosphere, 8, pp.2409-2418.
[https://doi.org/10.5194/tc-8-2409-2014]

-
Newman, J., 1977. Marine Hydrodynamics. MIT Press.
[https://doi.org/10.7551/mitpress/4443.001.0001]

- Riska, K., 2010. Ship-ice interaction in ship design: theory and practice, Encyclopedia of Life Support Systems (EOLSS), Developed under the Auspices of the UNESCO, Eolss Publishers, Oxford, UK.
-
Su, B., Riska, K. & Moan, T., 2011. Numerical simulation of local ice loads in uniform and randomly varying ice conditions. Cold Regions Science and Technology, 65, pp.145-159.
[https://doi.org/10.1016/j.coldregions.2010.10.004]

- Suominen, M. & Kujala, P., 2010. Analysis of short-term ice load measurements on board MS Kemira during the winters 1987 and 1988. Espoo: Aalto University, School of Science and Technology.
-
Suyuthi, A., Leira, B. J. & Riska, K., 2013. Fatigue damage of ship hulls due to local ice-induced stresses. Applied Ocean Research, 42, pp.87-104.
[https://doi.org/10.1016/j.apor.2013.05.003]

- Transport Canada, 1996. Safe speed in ice: an analysis of transit speed and ice decision numerals. Ship Safety Northern (AMNS).
- Zhang, S., Bridges, R. & Tong, J., 2011. Fatigue design assessment of ship structures induced by ice loading - an introduction to the ShipRight FDA ICE procedure. Proceeding of the Twenty-First International Offshore and Polar Engineering Conference, Maui, Hawaii, pp.1082-1086.