파이프 지지구조와 하부 보강의 설계와 강도 평가에 관한 연구
Abstract
In the case of gas carriers and oil tankers, pipes are installed on the upper deck as a moving passage to load LPG, LNG, crude oil, etc. Pipes used for loading or unloading liquid cargo in cargo holds are connected to the hull through support structures. However, many cases of hull damage have been reported where the various equipment and support structures are installed on the upper deck. It is assumed that not only the structural discontinuity where the hull and the pipe support structure meet, but also action due to the pipe loads and the hull girder bending moment are simultaneously affected. This paper deals with the design and strength evaluation of the support structure of pipes and cables installed on the upper deck of commercial ships and offshore structures. For these supporting structures, design conditions and working loads were defined. The design procedure was established through the structure analysis on the method of determining the member dimensions. A series of finite element analysis was performed on the factors to be considered in the design and the effects were discussed. The accuracy and design periods of the strength evaluation was improved and reduced by application of the automation program in the finite element analysis. It is also expected that the design reliability of the shipyard is improved.
Keywords:
Pipe support structure, Hull reinforcement, Strength evaluation, Structural design and analysis, Automatic FE model generation키워드:
파이프 지지구조, 선체 보강, 강도 평가, 구조 설계 및 해석, 자동 유한요소 모델 생성1. 서 론
본 논문은 상선과 해양구조물의 상갑판 상에 설치되는 파이프 지지구조와 그 하부의 선체보강을 위한 설계와 강도 평가에 관한 것이다. 지지구조의 설계 개념과 작용 하중들을 정의하였으며 부재치수를 결정하는 방법을 정립하기 위하여 유한요소 모델링 자동화 프로그램을 개발하여 시리즈 구조 해석을 수행하고 덧판(double plate), 카링(carling) 등 설계인자들의 영향을 이론적 계산 결과와 비교/검토 하였다.
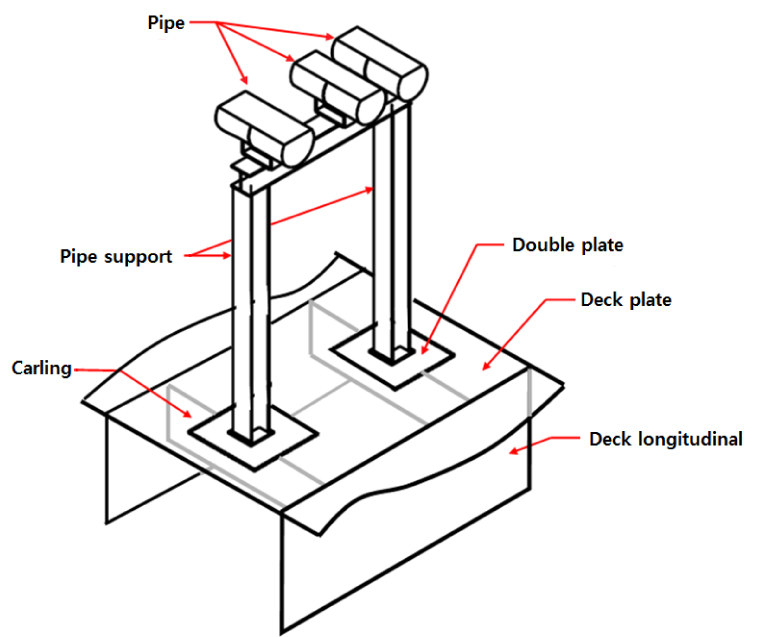
Fig. 1은 선박의 상갑판상에 설치된 파이프 지지구조와 그 하부 선체 보강을 나타낸 것이다. 가스선과 유조선에 설치된 파이프는 LPG, LNG, 원유 등을 선체내부의 화물창에 적재하거나 외부로 하역 위하여 이동 통로로 사용하며 지지구조를 통하여 선체에 연결되고 지지구조 하부는 통상 카링, 덧판 그리고 브랏켓 등으로 보강한다.
TSCF IP 001(2011)에 따르면 선체 상갑판상에 설치되는 각종 의장품들 주변에서 선체 파손사례가 다수 보고되고 있다. 선체와 파이프 지지구조가 만나는 곳은 구조적 불연속부일 뿐 아니라 파이프로부터의 하중과 선체의 굽힘 모멘트에 의한 영향을 동시에 받기에 손상사례가 다수 보고 되는 것으로 나타났다.
선체의 기본설계도에는 중소형 의장품의 하부와 인접한 부재에 대한 국부적 보강 등을 나타내는 상세 설계가 포함하고 있지 않아 선급도면 승인 단계에서 그 영향을 검토하지 못하고 있으며 의장품 하부의 선체 보강은 파이프로부터 전달되는 정적 하중뿐만 아니라 선체의 동적 거동에 의한 영향도 고려하여야 한다.
파이프로부터 전달되는 하중은 지지구조를 통하여 선체에 전달됨으로 지지구조 하부는 국부적 응력집중 현상이 발생한다. 이에 대한 보강방법으로, 지지구조의 하부와 상갑판 사이에 덧판의 설치, 상갑판 하부에 카링의 설치, 상갑판 두께의 증가, 지지구조하부에 브라켓의 설치 등이 널리 사용되고 있다.
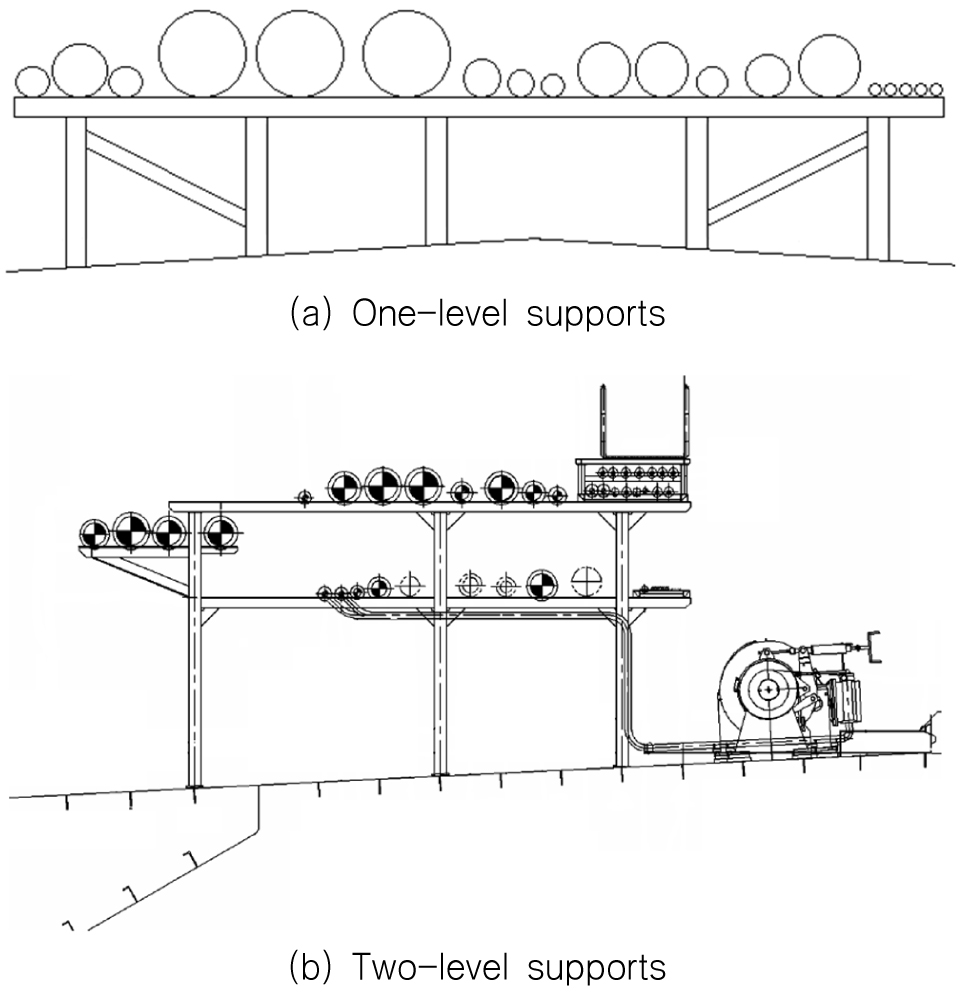
Fig. 2는 선박의 횡단면상에서 본 상갑판상의 파이프와 그 지지구조를 나타낸 것이다. 1개 또는 여러 개의 지지구조에 위에 크기가 다른 각종 파이프들이 놓여 있다. 지지구조는 1층 또는 다층의 구조로 구성된다.
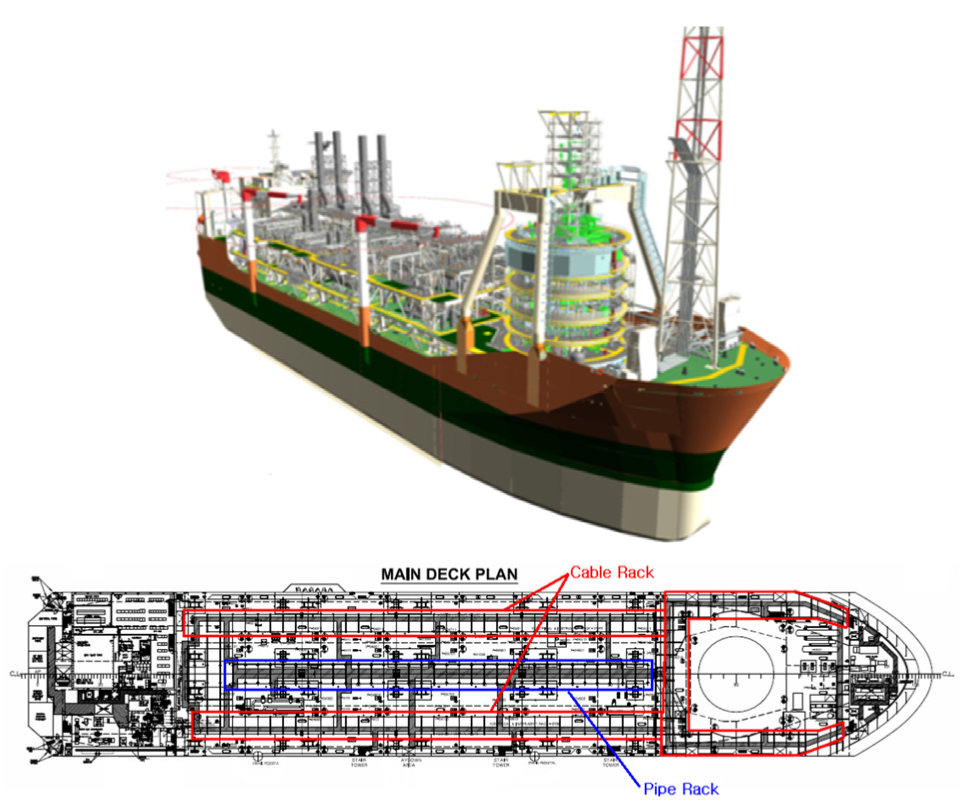
Fig. 3은 2011년 영국 BP사로부터 현대중공업이 수주한 Q204 FPSO의 상갑판상에 설치된 파이프와 케이블 지지구조의 배치를 나타낸 것이다. 파이프 지지구조는 FPSO의 중앙부에, 케이블지지구조는 양쪽 선측에 선수부터 선미에 걸쳐 배치되어 있다.
Fig. 4는 가스운반선과 탱크선의 상갑판상에 설치된 각종 용도의 파이프들, 이들의 지지구조 그리고 통행로(catwalk)의 사진을 나타낸 것이다.
이와 같이 최근에 건조하고 있는 다양한 선박과 해양구조물의 갑판상에는 수많은 파이프가 배치되고 이를 지지하는 구조부재가 설치된다.
TCIF IP 001(2011)은 의장품들 설치영역에서의 수많은 파손사례를 소개하며 작용하중이 클 때와 작을 때로 나누어 개념적 보강안을 제시하고 있으나 단순히 손상사례를 조사하여 보고하는 형태로 되어 있어 파손사고의 예방적 차원에서의 문제해결책은 제시하지 못하였다.
IACS(2015)은 크레인(crane pedestal)하부와 상갑판 사이에 두꺼운 덧판을 설치하여 선체가 국부적으로 손상되는 것을 막도록 규정하고 있다. 또한 빌지킬(bilge keel)은 선체에 직접 부착하지 않고 덧판을 부착하여 선체의 반복하중에 의한 피로파손이나 충돌로 인하여 빌지킬 근방에서 파손이 발생하여도 선체가 손상되지 않도록 규정하고 있다.
조선소의 설계자가 참고자료로 활용하고 있는 선급/산업 규정들에서는 파이프 지지구조에 대한 구조부재 배치와 보강방법들에 대한 가이드를 일반론적으로 언급하고 있어 상세설계에 어려움을 겪고 있으며 이에 대한 대응으로 각 조선소 별로 독자적으로 정립하여 사용하고 있다. 선박 설계와 제작단계에서 다양한 종류의 지지구조에 대하여 안전성을 점검할 때 선급/선주사에서는 강도해석 보고서를 요구하고 있어 설계표준의 미비로 공정 지연 사례가 종종 발생하고 있다. 따라서 구조부재의 손상을 예방하고 구조적으로 취약한 부분을 제거하기 위하여 선체와 지지구조의 보강 방법에 대한 연구가 필요하다.
파이프 지지구조는 해양구조물의 상부모듈(topside module) 을 지지하는 대규모 지지구조도 있지만 본 연구에서는 소규모의 파이프/케이블 지지구조에 대한 설계와 강도 평가를 다룬다.
2. 현재의 문제점과 해결 방안
2.1 현재 방법의 문제점
최근 가스선과 유조선의 수요가 증가함에 따라 상갑판상에 화물창에 액체화물을 선적하고 하역하기 위한 파이프들이 많이 설치되고 이들을 지지하는 구조의 개수도 증가하고 있다. 특히 기존 선박에 대비하여 구조배치가 변경되었을 때 경험이 부족한 설계자는 많은 어려움을 겪고 있다.
파이프 지지구조 부재의 단면형상은 O, H, +, L 등 다양하다. 이들 중 O 단면형상은 하중작용 방향에 관계없이 동일한 강성을 갖도록 설계할 수 있으며 상대적으로 고강도/저중량 설계가 가능하고 바람과 물(green water)에 대하여 구조물이 저항을 덜 받기 때문에 선주사에서 선호하는 경향이 있다. 그러나 코드(chord)와 브레이스(brace) 연결시 용접작업에 어려움이 있다.
다양한 지지구조들과 선체 보강을 단순 재료역학 개념으로 계산시 복잡한 하중과 경계, 기하학적 형상 등을 고려한 정확한 해를 찾는데 어려움 있기 때문에 선주는 강도 증명을 위하여 유한요소법을 이용한 구조해석 수행을 요구하고 있다. FPSO와 같이 상부구조물이 많은 경우, 지지구조의 수도 증가하여 유한요소 구조해석으로 모든 구조부재의 치수를 선정하는데 많은 어려움이 있다. 또한 초기 설계시 개별적(case by case)으로 수행하면 많은 시간과 노력이 요구된다. 또한 지지구조 설계와 선체하부 보강방법에 대하여 발주처의 시방서와 선급규정에 명시적으로 기술하고 있지 않아 각 조선소는 한정적으로 설계 표준을 정립하여 사용하고 있다. 지지구조에 의한 상갑판의 손상을 방지하기 위하여 덧판을 설치하는 경우에도 명확한 기준 설정에 어려움을 겪고 있다.
2.2 해결 방안
본 논문에서는 2.1절에서 열거한 어려움들을 극복하기 위한 하나의 방법을 제시한다. 즉, 설계자가 손쉽게 사용할 수 있는 유한요소 모델링 자동화 프로그램을 개발하여 선주의 요구사항에 적극 대응하며 설계에 많은 영향을 미치는 구조부재들의 특성을 분석하여 초기 설계 단계에서 적용 가능한 가이드를 제공하고자 한다.
이로써 지지구조의 수가 많아서 발생하는 유한요소 모델 생성 시간을 절감하며 덧판 설치로 나타나는 인장과 굽힘하중에서의 접촉(gap)부의 거동, 지지부재 하부보강을 위한 카링 개수와 치수 결정, 하중 작용점에서의 힘의 전달, 선체 종굽힘모멘트에 의하여 유발된 응력 등을 정확히 묘사하는 것이 가능하다. 또한 구조해석 모델을 자동으로 구성하고 재료의 물성치, 경계와 하중조건 등 일련의 작업들을 자동화하여 신속하고 정확하게 구조부재 치수를 결정하는 것이 가능하다.
3. 하중과 모델링 자동화 프로그램 개발
3.1 설계하중
파이프 지지구조의 경우, 그 치수를 결정하기 위하여 작용하는 하중의 종류로는 파이프와 지지구조의 자중에 의한 고정하중, 파이프 속의 유체 무게에 의한 활하중, 그리고 풍력과 파이프 상부에 쌓이는 눈 그리고 그린워터(green water) 등에 의한 계절하중, 파이프 속의 유체의 온도변화에 따른 파이프의 수축과 팽창에 의한 열하중, 파이프 지지구조가 선체와 연결되어 있기 때문에 선체 거어더의 굽힘에 기인한 상호 작용력(interaction force), 선체의 운동에 의한 가속도 등이 있다.
파이프에 작용하는 하중 조합조건으로는 항구 내에서 액체화물을 적재하거나 하역하는 운용, 선박의 항해, 해상에서의 침수/충돌/폭발 사고, 건조 중 운송과 권상, 건조 후 탱크시험 조건 등을 고려할 수 있다.
ⅰ) 항구 또는 선박 접안시설에서 통상적인 액체화물을 적재하거나 하역(loading-offloading)하는 조건(operation condition)
ⅱ) 대양 항해 조건으로, 파이프에 어떤 액체화물도 없이 최대 설계속도로 대양을 항해하는 조건(transit condition)
ⅲ) 화물을 만재상태에서 선박의 사고로 30도로 경사(heeling) 하는 사고 조건 (accidental flooding condition)
ⅳ) 선수방향 가속도를 고려하는 선박 충돌사고 조건(ship collision condition)
ⅴ) 가스 또는 기름의 누출로 폭발 사고가 발생한 조건(blast condition)
ⅵ) 건조작업에서 발생하는 운송과 권상 조건(transport & lifting condition)
ⅶ) 탱크 시험 조건으로, 선박 건조 후 안벽에서 LNG 또는 물을 파이프를 통하여 시험하는 조건(test condition)
파이프로부터 지지구조에 전달되는 하중을 구하기 위하여 사용하는 프로그램으로는 CAESAR II(2018) 또는 MSC/NASTRAN (2015)과 같은 상용 유한요소 해석 등이 있다. 파이프로부터의 하중과 선체굽힘에 의한 하중을 설계하중으로 선정하고 지지구조와 선체 하부보강재의 치수를 결정한다.
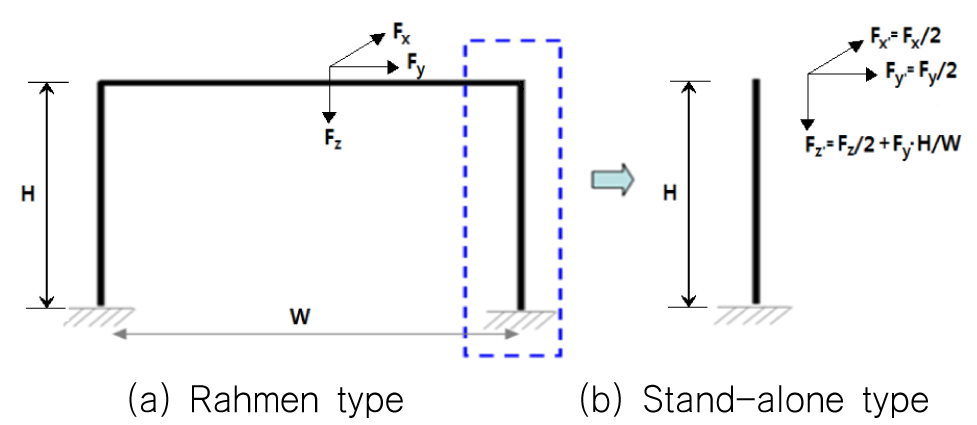
Fig. 5는 2열로 배치된 파이프 지지구조에 작용하는 반력을 외팔보의 1개 구조에 작용하는 하중으로 치환하는 방법의 예이다.
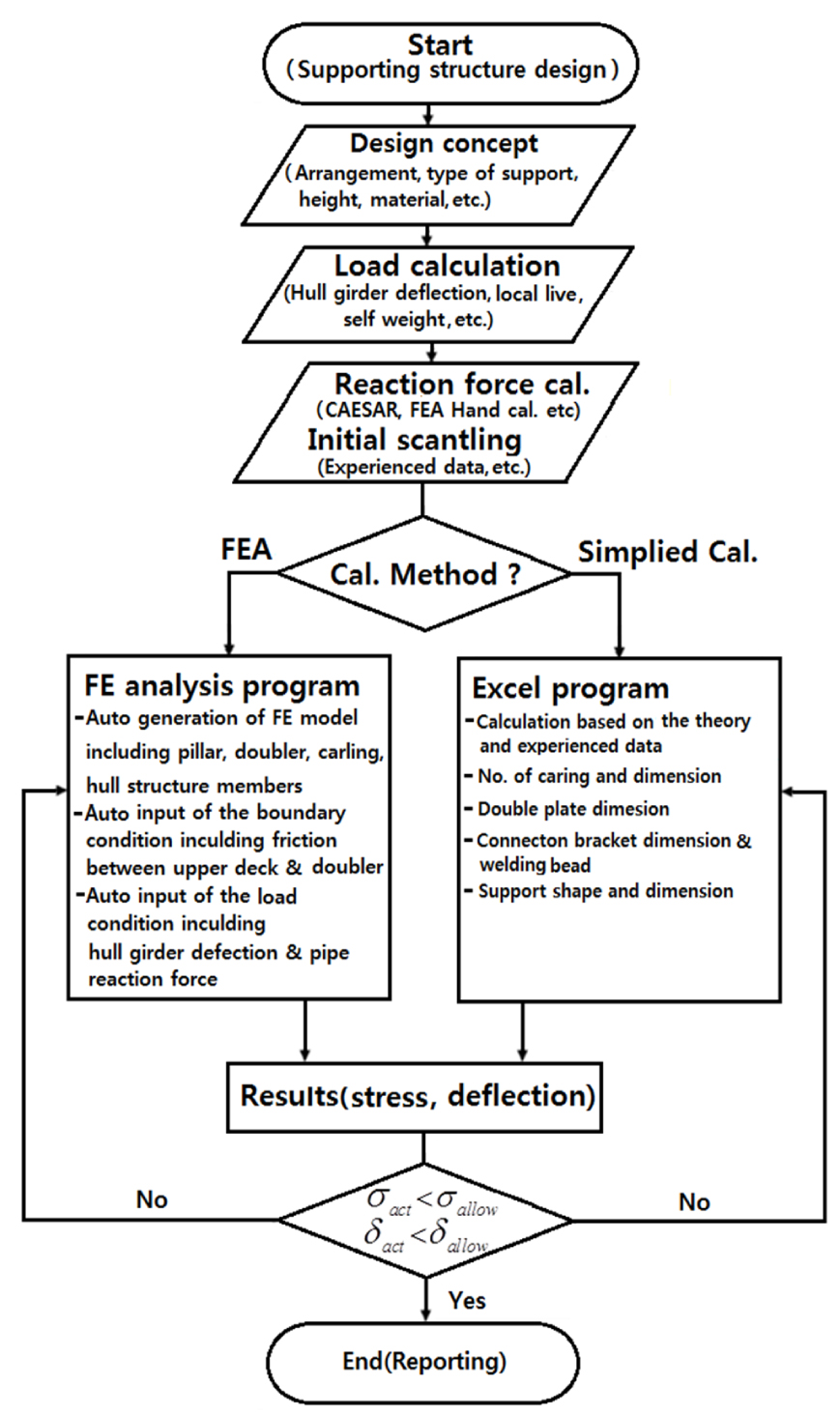
Fig. 6은 본 연구의 지지구조의 설계와 강도평가를 위한 일련의 순서를 나타낸 것이다. 지지구조의 형태와 재질 등 설계개념이 확립되면 각종 작용하중들을 계산하고 과거 경험적 자료로 초기 치수를 선정한다. 이후 유한요소해석 또는 이론적 설계식으로 계산과 해석 그리고 강도평가를 수행한다.
3.2 구조해석 모델링 자동화 프로그램 개발
3.1절에서 구한 설계하중으로 지지구조와 선체 하부보강재를 충분히 안전하도록 설계하기 위하여 구조강도 계산을 수행하여야 한다. 그러나 지지구조가 복잡하고 수행해야 할 경우의 수가 많기 때문에 유한요소법에 의한 선형/비선형 해석을 수행하는데 많은 시간이 소요된다. 이를 해결하기 위하여 본 연구에서는 유한요소 구조해석 모델 구성과 하중 생성을 쉽게 할 수 있는 유한요소 모델링 자동화 프로그램을 개발하였다.
파이프에 작용하는 다양한 하중조건으로 파이프의 치수와 지지구조의 치수를 결정한다. 우선 파이프 지지구조의 치수와 형상이 결정되면 덧판의 설치유무와 치수를 결정한다. 다음으로 하부 카링의 치수와 개수를 결정하고 필요 시 보강재의 치수를 조절하며 설계를 수행한다. 이들 과정을 이론적 계산으로 강도 평가를 수행하는 것에 어려움이 있다. 즉, 덧판의 설치 유무, 덧판의 접촉 문제, 카링의 강성과 강도 결정 등의 어려움이 있기에 유한요소 구조해석을 도입할 필요가 있다.
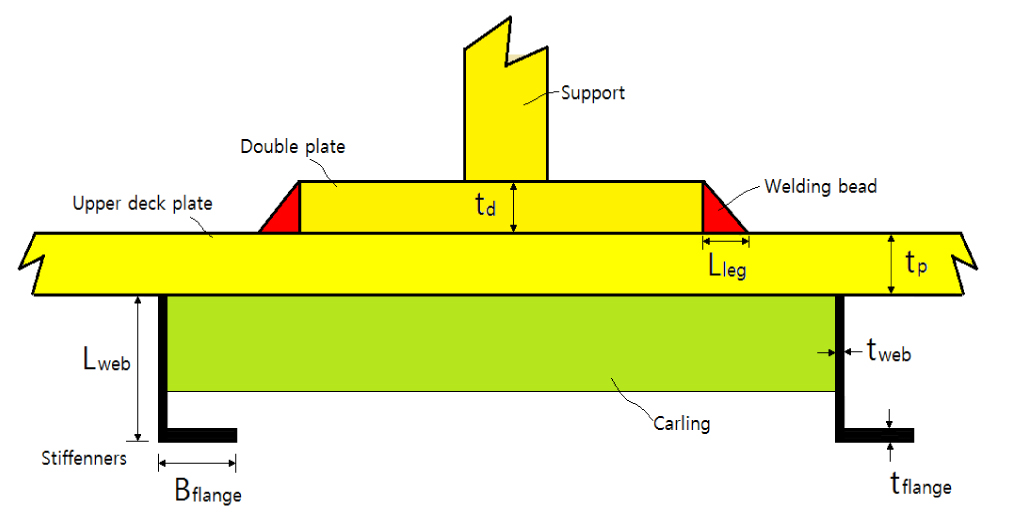
Fig. 7은 설계하고자 하는 지지구조, 덧판, 상갑판, 카링, 보강재 등 설계 인자들을 나타낸 것이다.
유한요소 모델링 자동화 프로그램 개발은 MSC/PATRAN (2015) 환경에 구동하도록 구축하였다. 즉, PATRAN화면의 Command창에 Option으로 부착하여 필요 시 사용하도록 구축하였으며 부재치수와 크기, 하중 등을 입력하면 자동으로 비선형 해석을 위한 준비가 되도록 구성하였다. 용접비드와 덧판은 3차원 입체요소를 사용하였으며 일반 다른 부재들은 판부재로 모델링 하도록 하였다. 하중 작용점과 지지구조 사이의 연결은 MPC요소를 사용하여 연결하도록 하였으며 덧판과 상갑판 사이는 갭요소를 사용하여 인장 또는 굽힘하중이 작용할 때 보다 현실적 거동을 잘 반영하도록 하였다.
다음의 기능들을 자동으로 수행하여 업무를 편리성을 도모하였다.
ⅰ) 유한요소 해석 모델 자동 생성과 요소 크기 임의 조절 기능 단, 용접비드와 덧판은 3차원 입체요소로 모델링하고 다른 것은 모두 판요소로 생성
ⅱ) 재료 물성치, 파이프로부터 전달된 하중, 선체 종굽힘모멘트와 데크상의 횡압력 작용, 그리고 대칭조건을 고려한 경계조건 입력
ⅲ) 덧판과 상갑판 사이의 갭을 고려한 비선형 구조해석 입력 자료 생성
ⅳ) 보강재, 카링의 치수/개수/설치 위치, 지지구조의 형상을 구현
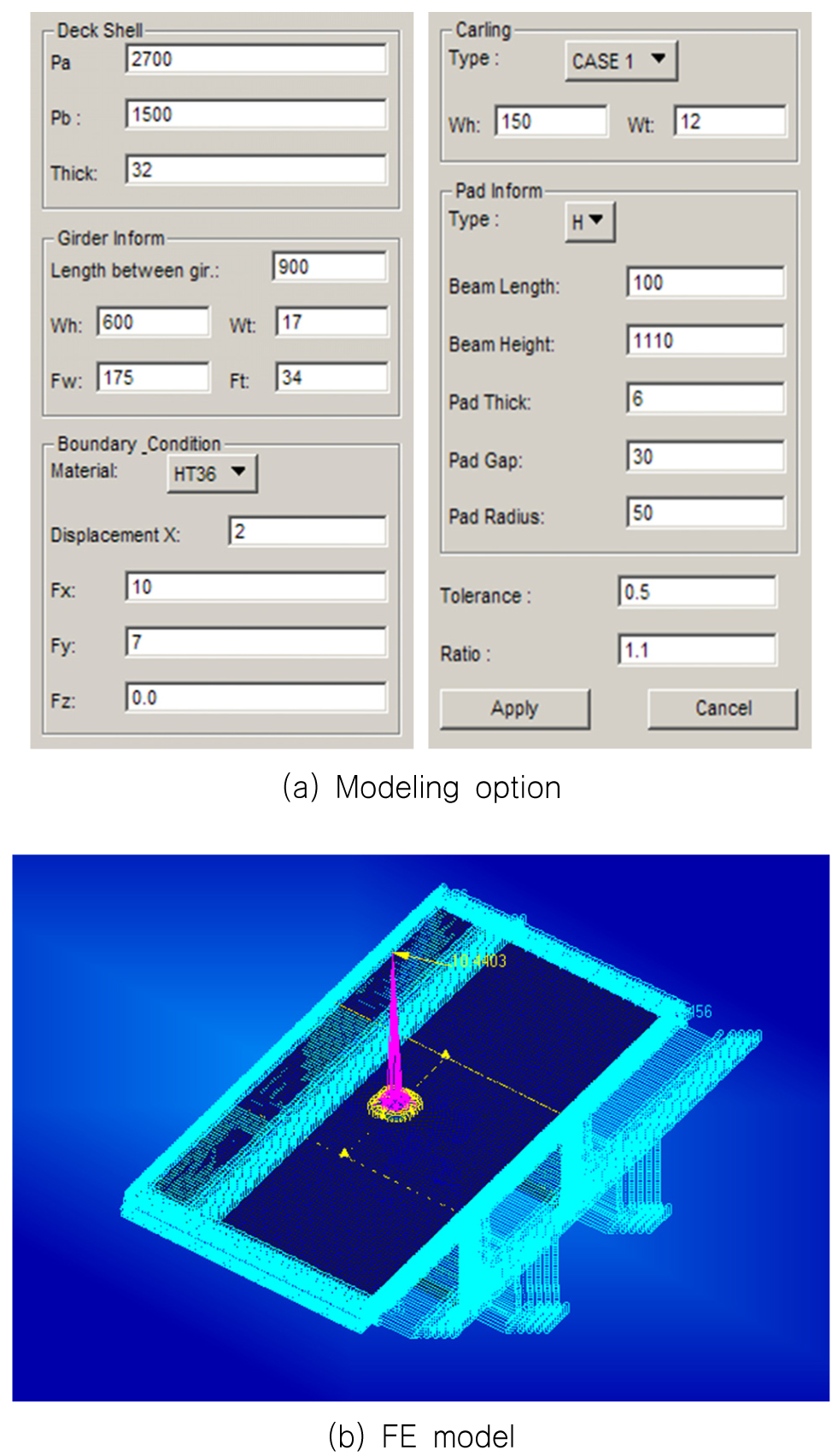
Fig. 8은 개발한 프로그램의 부재치수, 하중/경계조건 등을 입력하는 옵션(option), (a)를 사용하여 자동으로 구조해석 모델을 생성한 예, (b)를 나타낸 것이다.
Fig. 9는 개발한 프로그램으로 선체와 연결되는 다양한 형상의 지지구조 하부 형상(H, L, +, O)과 덧판을 생성한 예이다.
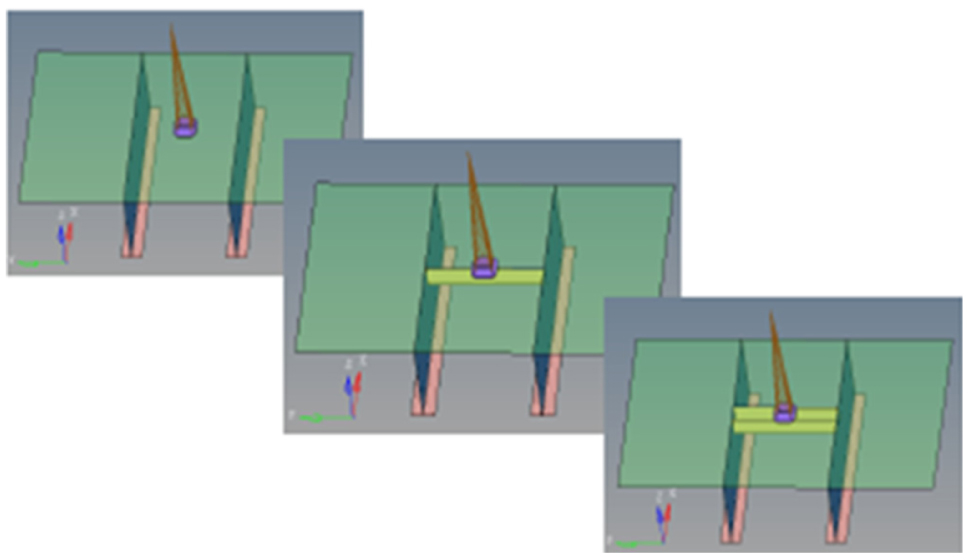
Fig. 10은 지지구조 하부의 선체구조를 보강하기 위한 카링을 보강재 사이에 0개, 1개, 2개 배치한 예이다.
4. 개발 프로그램의 적용
4.1 선체굽힘에 의한 지지구조 하부의 영향 검토
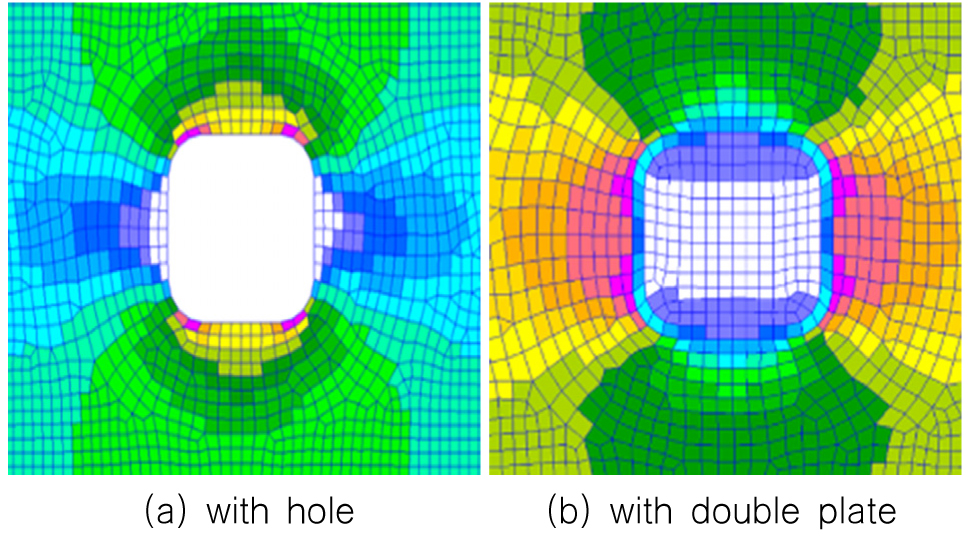
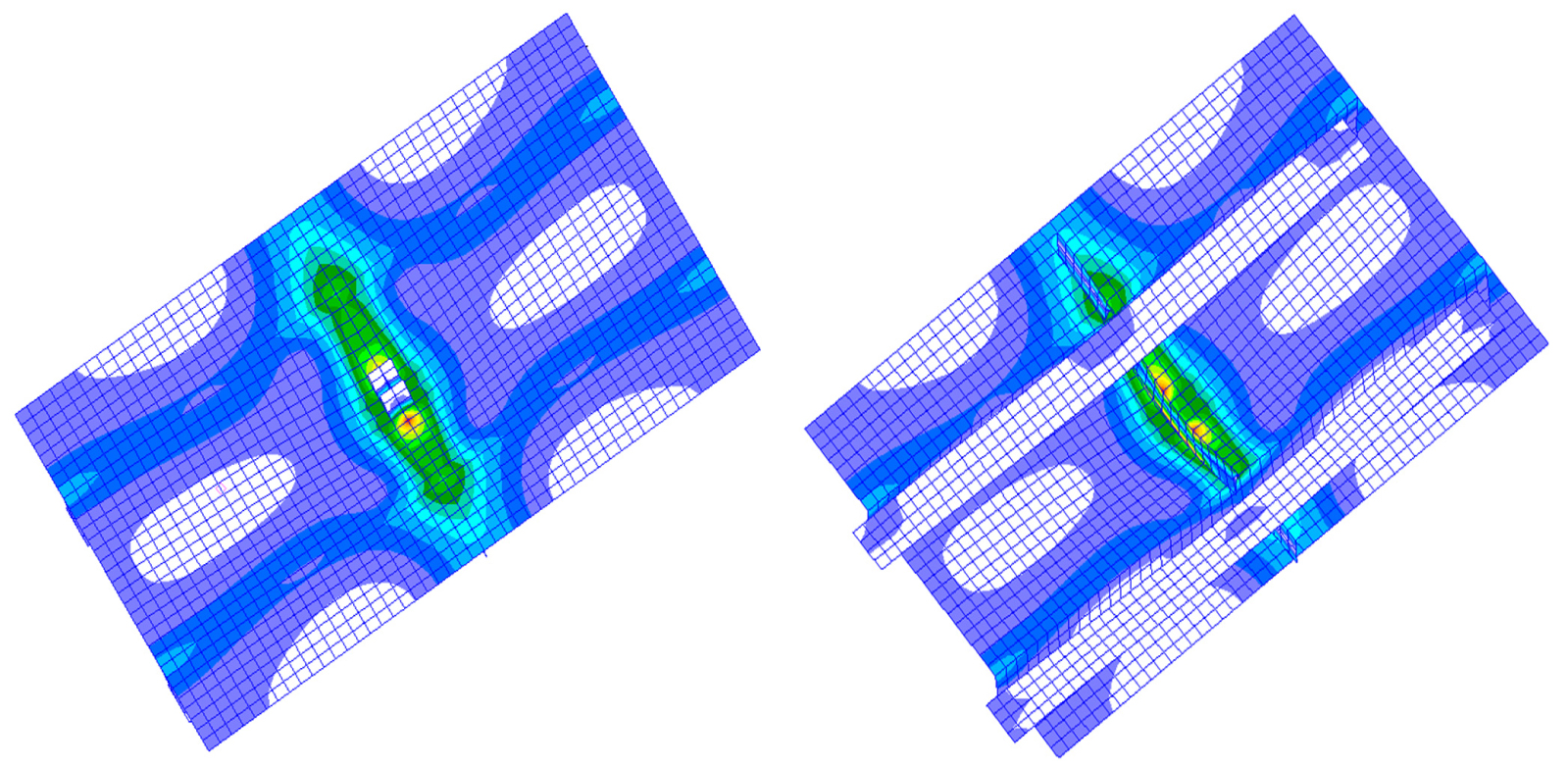
Fig. 11은 판부재에 홀(opening)과 덧판을 각각 설치하고 면내 인장력을 작용하여 나타난 등가응력 분포를 나타낸 것이다. 최대응력이 나타나는 위치가 홀이 있을 때와 덧판을 설치한 경우에 서로 바뀌어 나타나는 것을 알 수 있다. 이는 선체에 파랑하중에 의하여 종굽힘모멘트가 작용하였을 때 상갑판에서도 동일 현상이 나타난다. 선체 상갑판에 지지구조를 설치하거나 덧판을 설치하는 경우, 선각거어더의 종굽힘만 작용하여도 발생하는 상갑판부의 응력이 균일하지 않고 국부적으로 증가한다는 것을 의미한다.
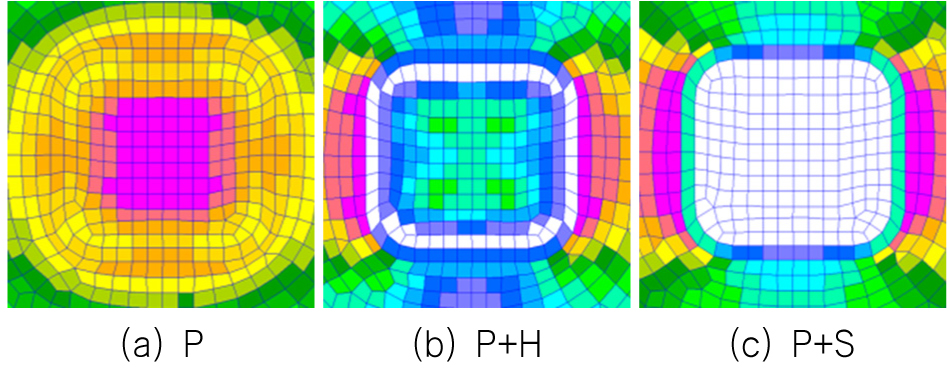
Fig. 12는 상갑판부에 지지구조를 덧판 없이 설치하고 파이프로부터 전달된 수직하중과 선체 종굽힘모멘트를 작용하였을 때 나타난 von-Mises 등가응력 분포를 나타낸 것이다. (a) 경우는 파이프로부터 전달된 수직하중(P)만 작용하였을 때로 지지구조 하부의 중앙부에서 최대 인장응력이 발생하는 것으로 나타났다.
(b) 경우는 파이프로부터 전달된 수직하중(P)과 선체의 호깅(hogging, H) 굽힘모멘트를 동시에 작용하는 경우로, 최대 인장응력이 굽힘모멘트의 영향으로 지지구조 좌우에서 나타나지만 최소 응력은 지지구조 직하방 테두리에서 나타났다. (c) 경우는 파이프로부터 전달된 수직하중(P)과 선체의 새깅(sagging, S) 굽힘모멘트를 동시에 작용하는 경우로, 최대 압축응력은 굽힘모멘트의 영향으로 지지구조 좌우에서 나타나지만 최소 응력은 지지구조 하부에서 나타났다.
일반적으로 파이프 지지구조 설계는 파이프 하부를 고정하고 파이프로부터 전달된 하중으로 설계를 수행하고 있으며 선각거어더 종굽힘모멘트에 의한 지지구조와 선체사이의 상호 작용력은 고려하지 않고 있다. 이 경우, 기본설계 단계에서 선체의 종굽힘모멘트로 상갑판의 허용응력 근처까지 맞추어 설계한 구조부재에 상세설계 단계에서 파이프로부터 전달되는 큰 수직하중이 추가되면 국부적 구조부재의 손상이 일어날 수 있다는 것을 의미한다.
4.2 덧판의 영향 검토
덧판은 판의 상부 또는 하부면에 추가의 강도 또는 강성을 얻기 위하여 설치하는 판부재로, 두께와 크기 그리고 용접 각장 크기가 중요 설계요소이다. 덧판은 면외방향의 압축력을 받을 때는 유효하지만 지지구조에 횡하중과 인장, 굽힘모멘트를 받을 때는는 접촉부에서 들림현상이 발생하여 용접부에서의 파손 가능성이 높아진다.
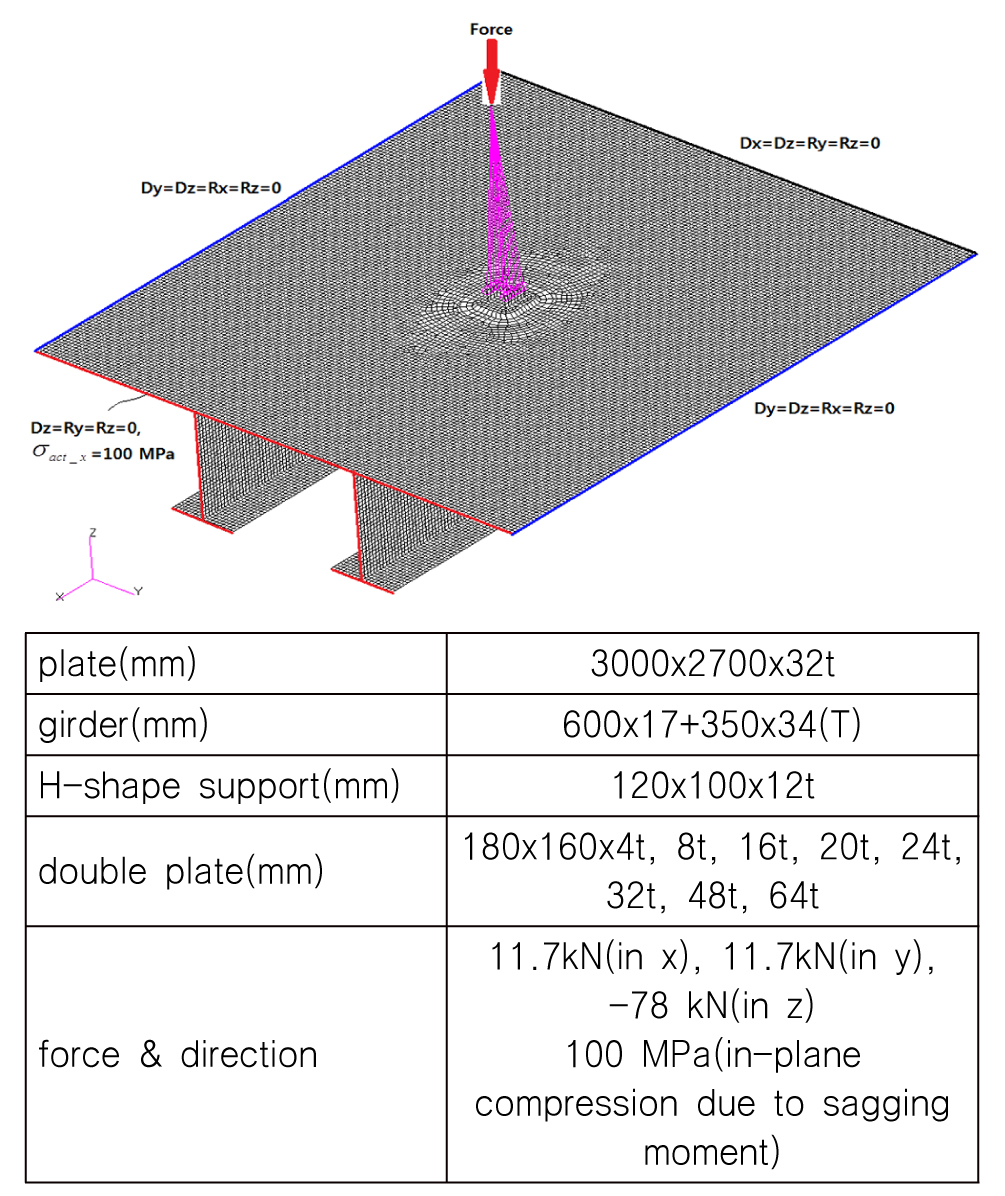
Fig. 13은 개발한 유한요소 모델링 자동화 프로그램으로 생성한 모델로, 경계조건과 하중 그리고 각 부재의 치수를 나타낸 것으로 파이프와 관내 유체의 자중 그리고 선체운동에 기인한 가속도 효과를 고려한 하중들의 조합을 지지구조 하부에 작용하고 추가로 선체 종굽힘에 기인한 면내 압축력을 작용하였다.
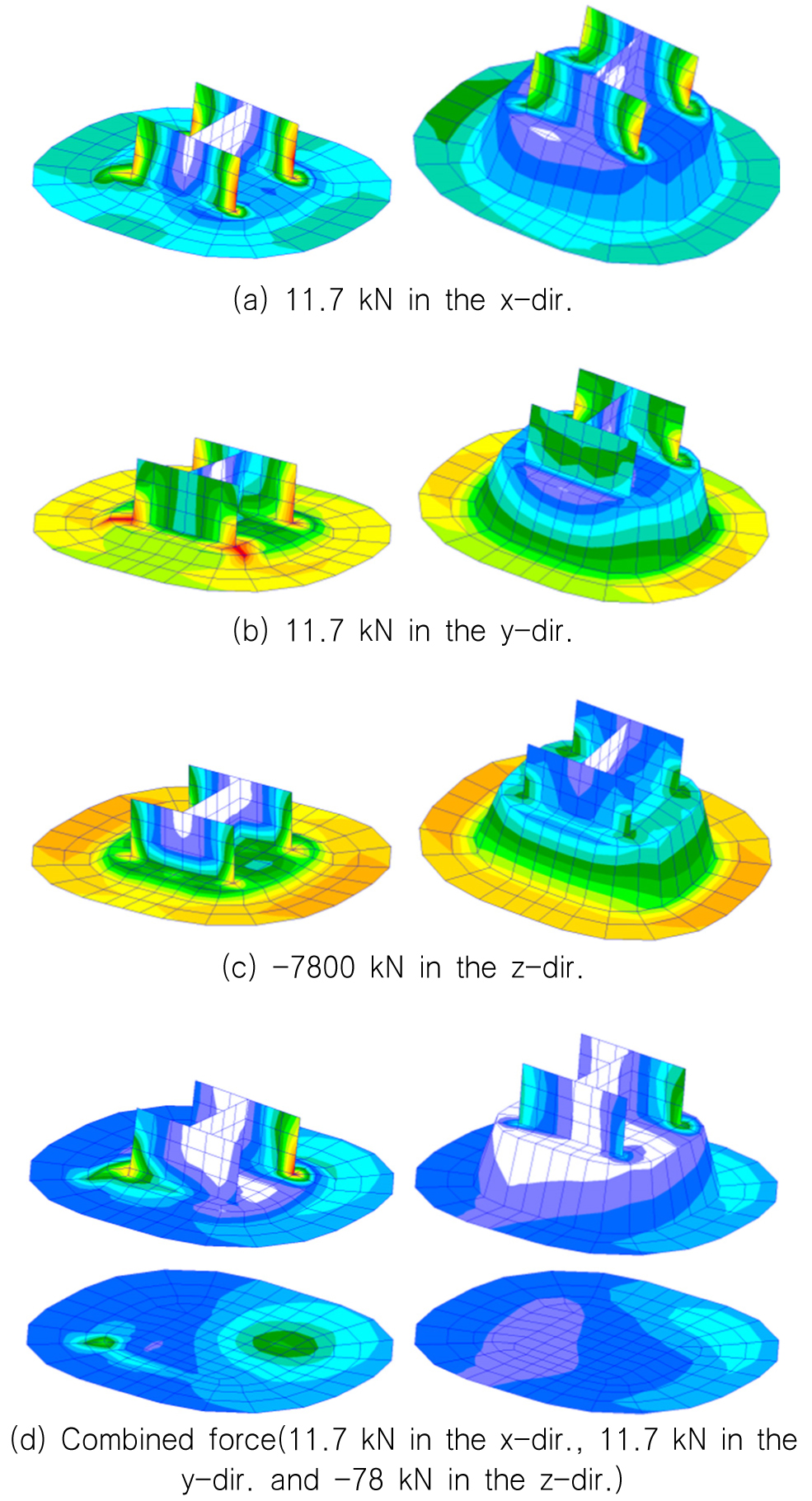
덧판의 두께 영향을 검토하기 위하여 Fig. 13의 덧판 두께가 얇은 8mm 인 것과 두꺼운 인 것에 대하여 구조해석을 수행하고 등가 응력을 Fig. 14에 나타내었다.
Fig. 14에서 나타낸 바와 같이 덧판의 두께가 8mm로 얇은 경우, H형의 지지구조 하부와 덧판이 만나는 곳에서 각 하중에 유발된 수직응력, 굽힘응력과 전단응력의 조합인 등가응력은 크게 나타난다. 이 경우, 덧판의 두께가 얇아서 발생한 응력이 상갑판쪽으로 직접 영향을 미친다. 이에 반하여 덧판의 두께가 64mm로 두꺼운 경우, H형지지구조로부터 덧판으로 전달된 하중이 상갑판부재로 직접 전달되는 것을 완화시키는 역할을 수행한다. Fig. 14 (d)의 아래부문에 나타난 상갑판에서의 응력을 보면 덧판의 두께가 얇은 경우에 H형 지지구조의 모서리부분에 전달된 하중으로 응력 집중 현상이 나타나는 것을 알 수 있다.
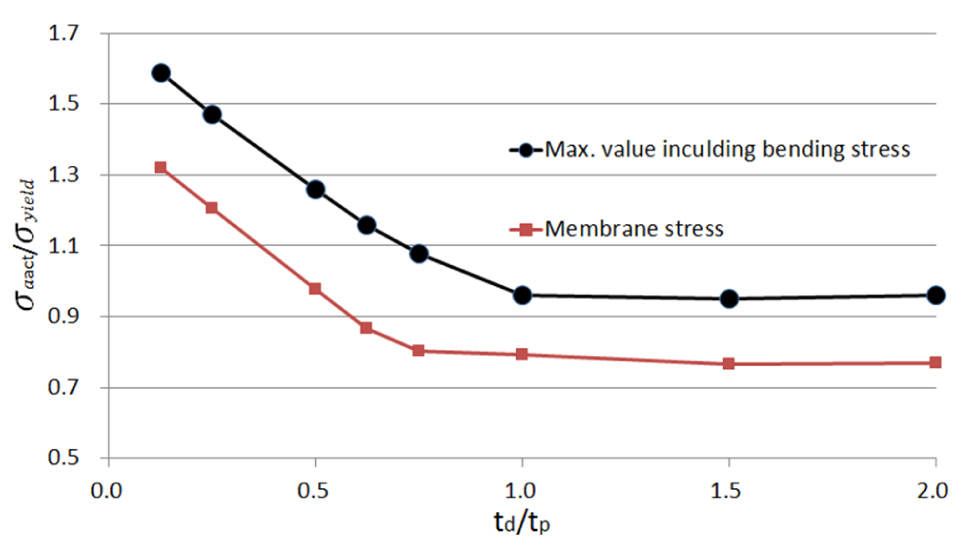
Fig. 15는 Fig. 14 (d)의 경우에 대하여 상갑판에서의 최대 등가응력을 나타낸 것으로 덧판의 두께를 상갑판의 두께로 나누어 무차원화한 가로축과 작용응력을 항복응력으로 나누어 무차원화한 세로축으로 나타낸 것이다. 덧판의 두께가 얇은 경우에는 두께가 증가함에 따라 작용응력이 현격하게 줄어들지만 상갑판 두께의 75% 이상의 경우 응력 변화는 거의 없다. 따라서 덧판의 두께를 과도하게 보강할 필요는 없을 것으로 사료된다.
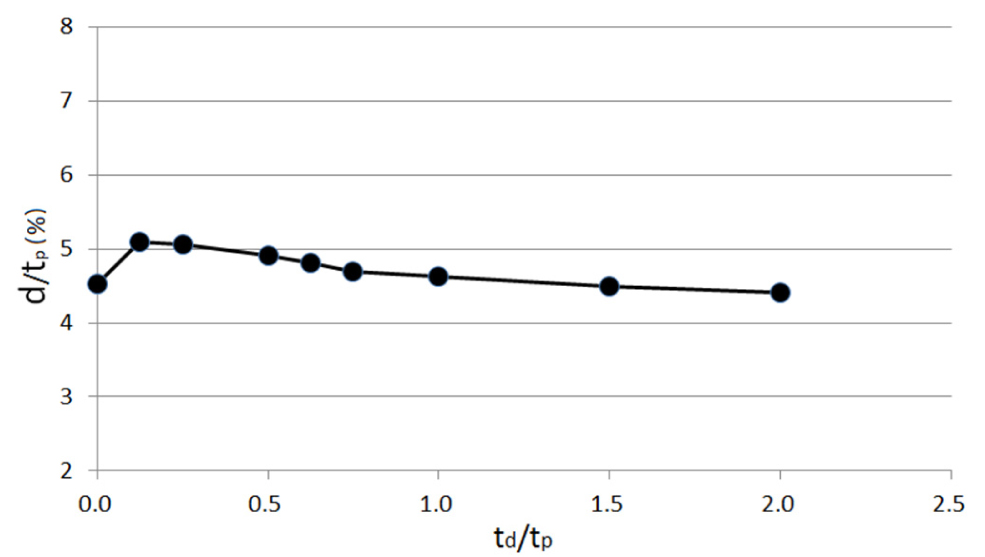
Fig. 16은 Fig. 14 (d)의 경우에 대하여 상갑판에서의 최대 최대 처짐을 나타낸 것으로 덧판의 두께를 상갑판의 두께로 나누어 무차원화한 가로축과 상갑판의 처짐량을 상갑판두께로 나누어 무차원화한 세로축으로 나타낸 것이다. 덧판의 두께 변화에 따른 처짐량의 변화는 거의 나타나지 않는 것으로 나타났다. 이는 지지구조 하부의 국부적 처짐량이 카링을 포함한 전체 처짐량에 비하여 적게 나타나기 때문이다.
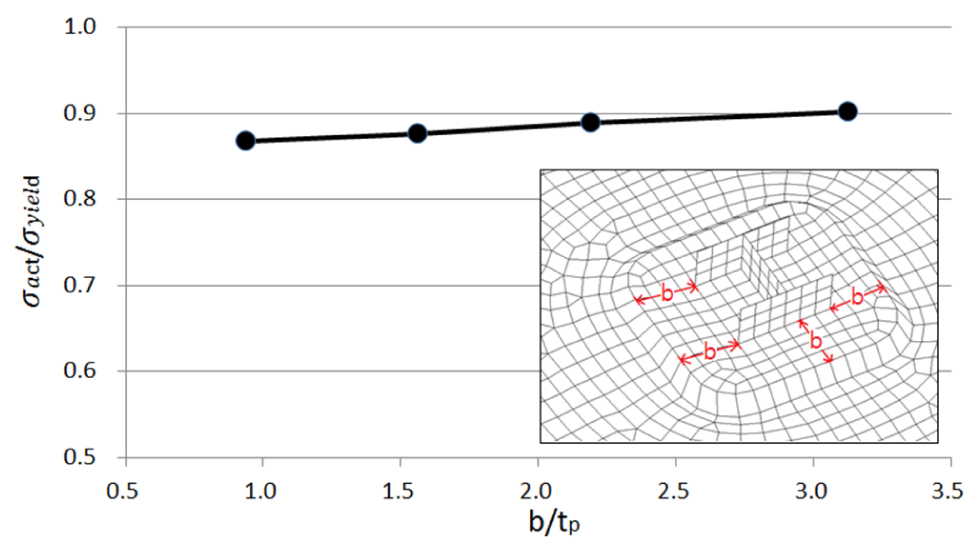
Fig. 17은 덧판의 폭을 상갑판의 두께로 나누어 무차원화한 가로축과 상갑판에서의 최대 등가응력을 항복응력으로 나누어 무차원화한 세로축으로 나타낸 것이다. 덧판의 폭(b)이 증가함에 따라 작용응력이 조금씩 증가하는 것으로 나타났다. 따라서 적정크기 이상으로 덧판의 폭을 증가시키는 것은 상갑판의 강도에 도움이 되지 않는 것으로 나타났다.
4.3 선체 보강용 카링 설치
선체 종굽힘모멘트와 파이프로부터의 반력에 견디게 설계하기 위하여 지지구조의 하부 선체에 카링을 설치한다.
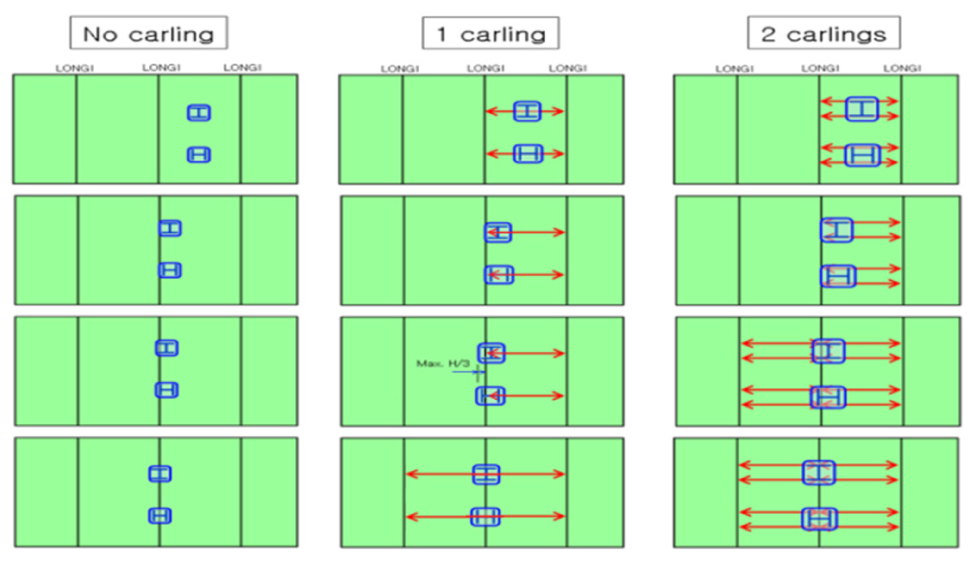
Fig. 18은 파이프 지지구조가 설치된 곳의 선체 하부를 보강하기 위하여 설치하는 카링의 배치와 개수의 예이다. 일반적으로 지지구조에 작용하는 파이프의 반력이 작은 경우, 카링을 설치하지 않지만 그 크기가 증가함에 따라 카링 치수와 개수를 증가시키며 보강한다. 지지구조는 선체 보강재 또는 웨브가 설치된 위치의 상부에 설치하는 것이 일반적이며 카링 또는 브라켓으로 추가의 하부보강을 수행할 수도 있다.
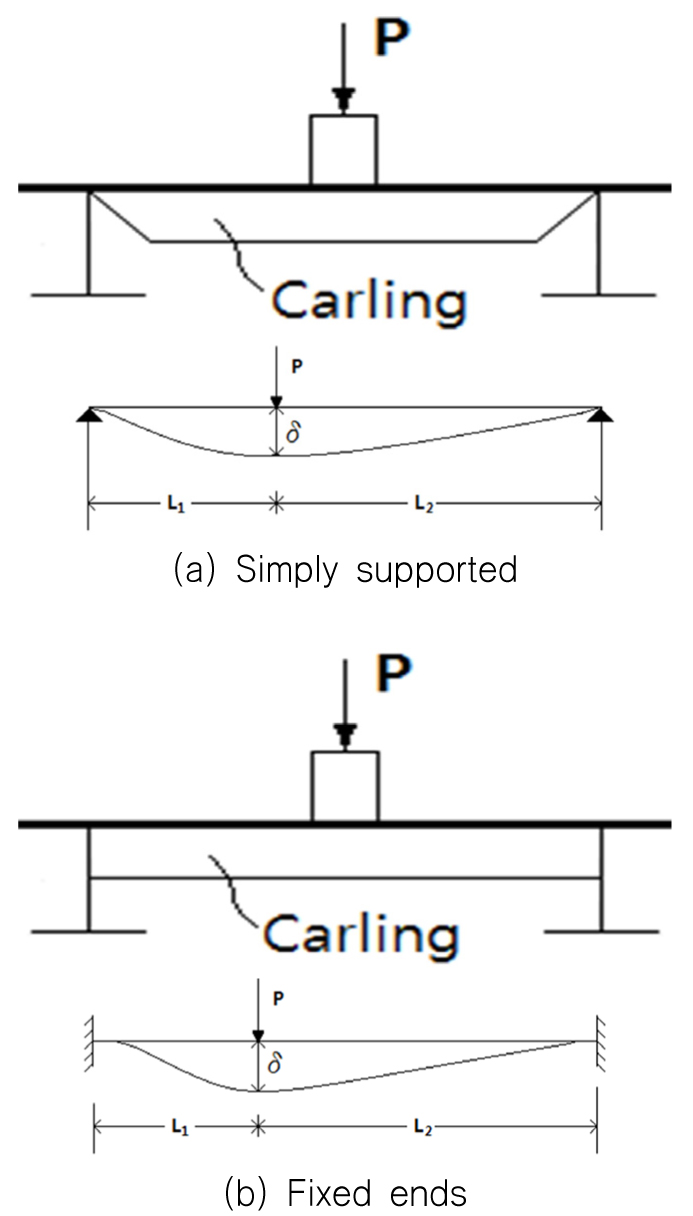
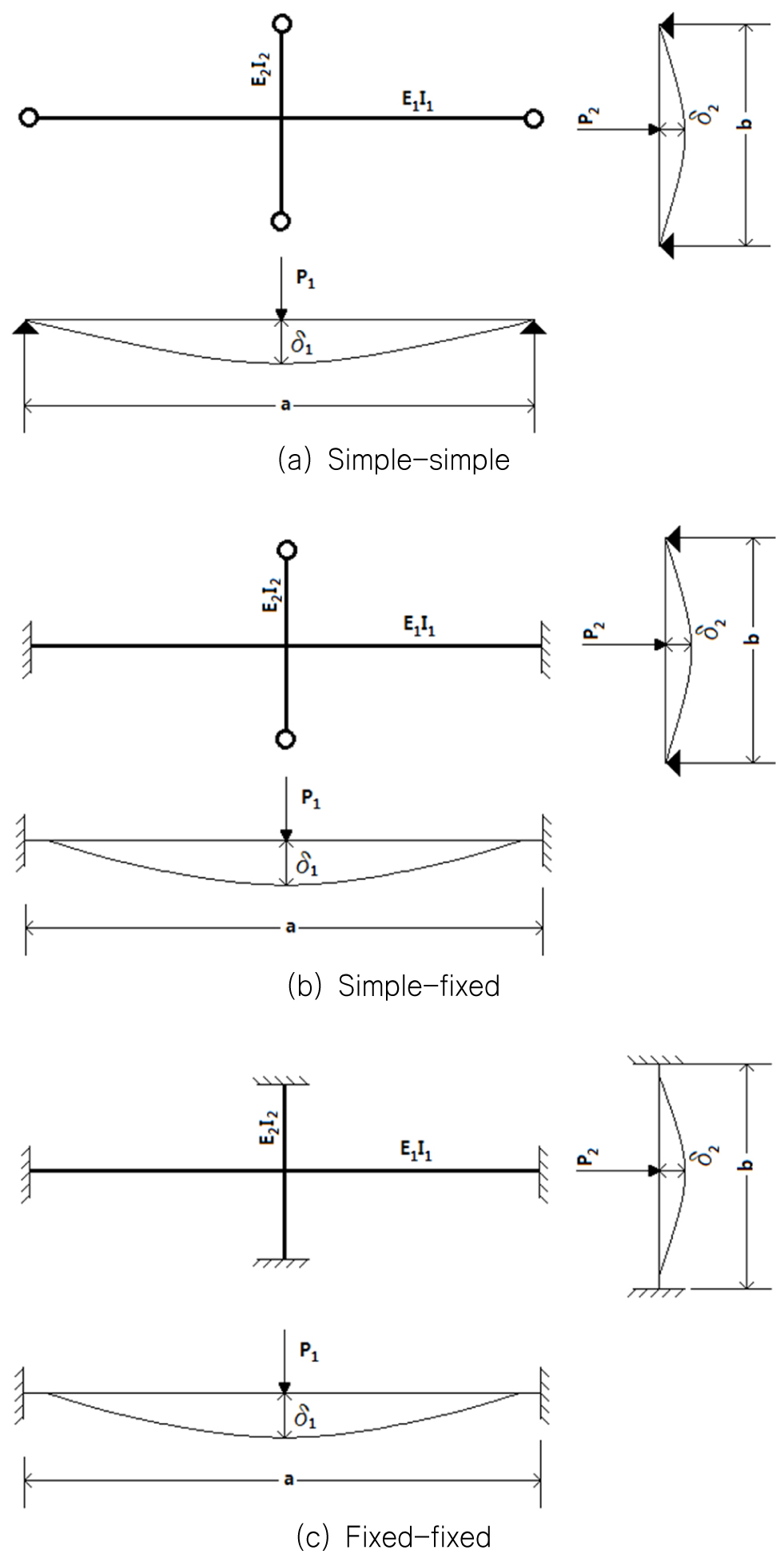
Fig. 19는 Fig. 18의 두개의 종보강재(longitudinal stiffener) 사이에 1개의 카링으로 보강된 상단에 지지구조로부터의 하중이 작용하는 경우에 대하여 카링 치수 결정과 카링과 연결되는 인접 보강재와의 연결상태를 이상화 하기 위하여 카링 양단을 단순지지하는 조건과 양단을 고정하는 조건으로 나타낸 것이다.
이 경우, 이론적 처짐 계산은 양단의 경계조건에 따라 식 (1)로 수행한다.
For simply supported
| (1-1) |
For fixed ends
| (1-2) |
where,
: Young’s modulus
: 2nd moment of area
또한 굽힘응력 계산은 식 (2)로 수행한다.
For simply supported
| (2-1) |
where,
: section modulus
: moment
For fixed ends
| (2-2) |
또한 전단응력 계산은 식 (3)으로 수행한다.
| (3) |
where,
: sectional area
또한 카링의 국부좌굴을 방지하기 위한 트리핑(tripping) 검사는 식 (4)로 수행한다.
| (4) |
where,
: depth of web
: thickness of web
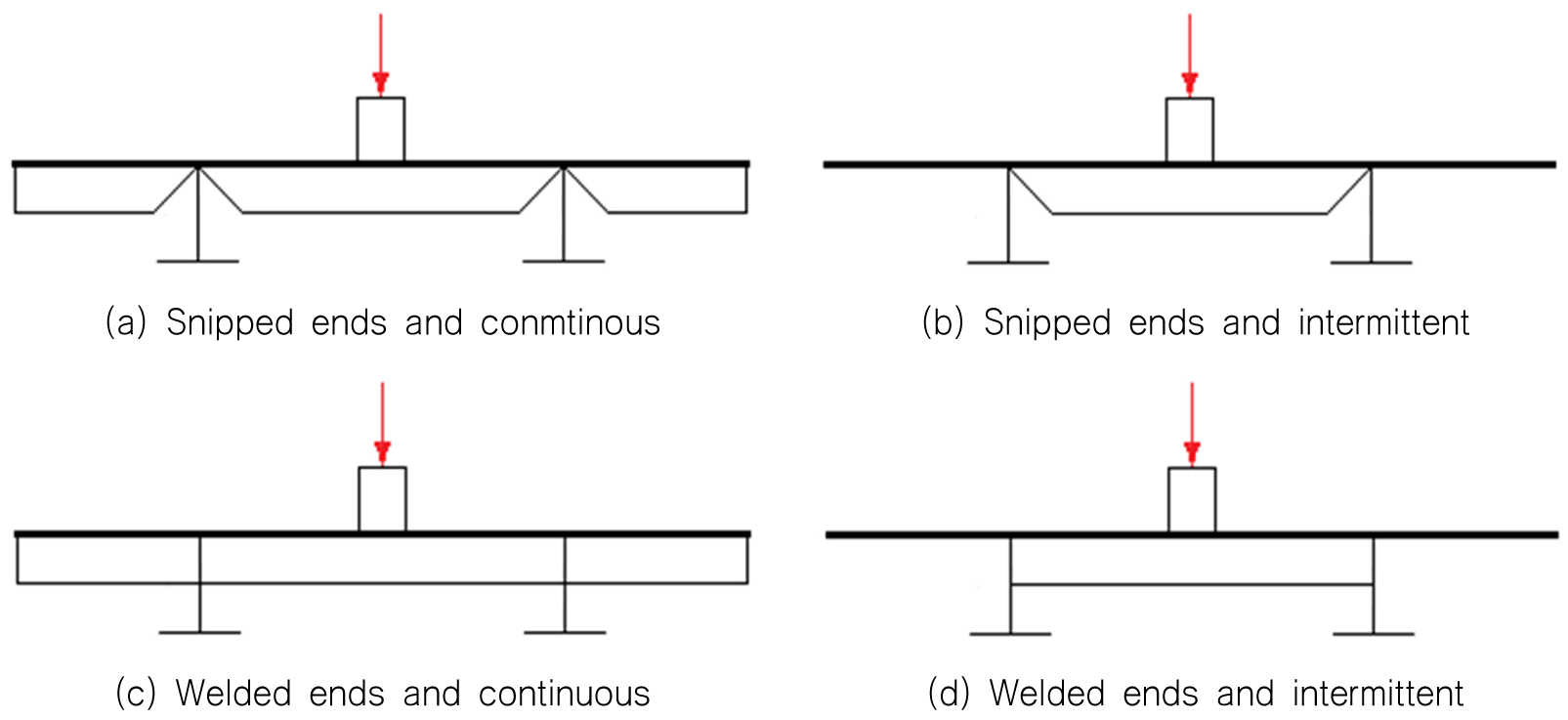
Fig. 20은 카링과 종보강재의 연결상태를 나타낸 것이다. 지지구조에서 작용하는 하중이 작은 경우, 카링의 양끝단을 스닙(snipped)하여 종보강재와 연결하고 그 다음 종보강재까지 연장하지 않는 단속(intermittent) 배치를 한다. 그러나 상대적으로 큰 하중이 작용하는 경우, 종보강재와 용접(welded)하여 연결하고 그 다음의 종보강재까지 연장하여 하중을 전달하는 연속(continuous) 배치를 수행한다.
Fig. 21은 지지구조 하부에 카링을 종보강재에 스닙하여 연속하여 배치한 구조물에 대한 유한요소 구조해석 결과이다. 지지구조로 부터의 하중이 선체의 상판과 카링에 의하여 지지되며 최대 von-Mises 등가응력은 지지구조 하부의 카링에서 나타난다.
von-Mises equivalent stress and deformed shape of structures supported by carling with snipped ends and continuous arrangement
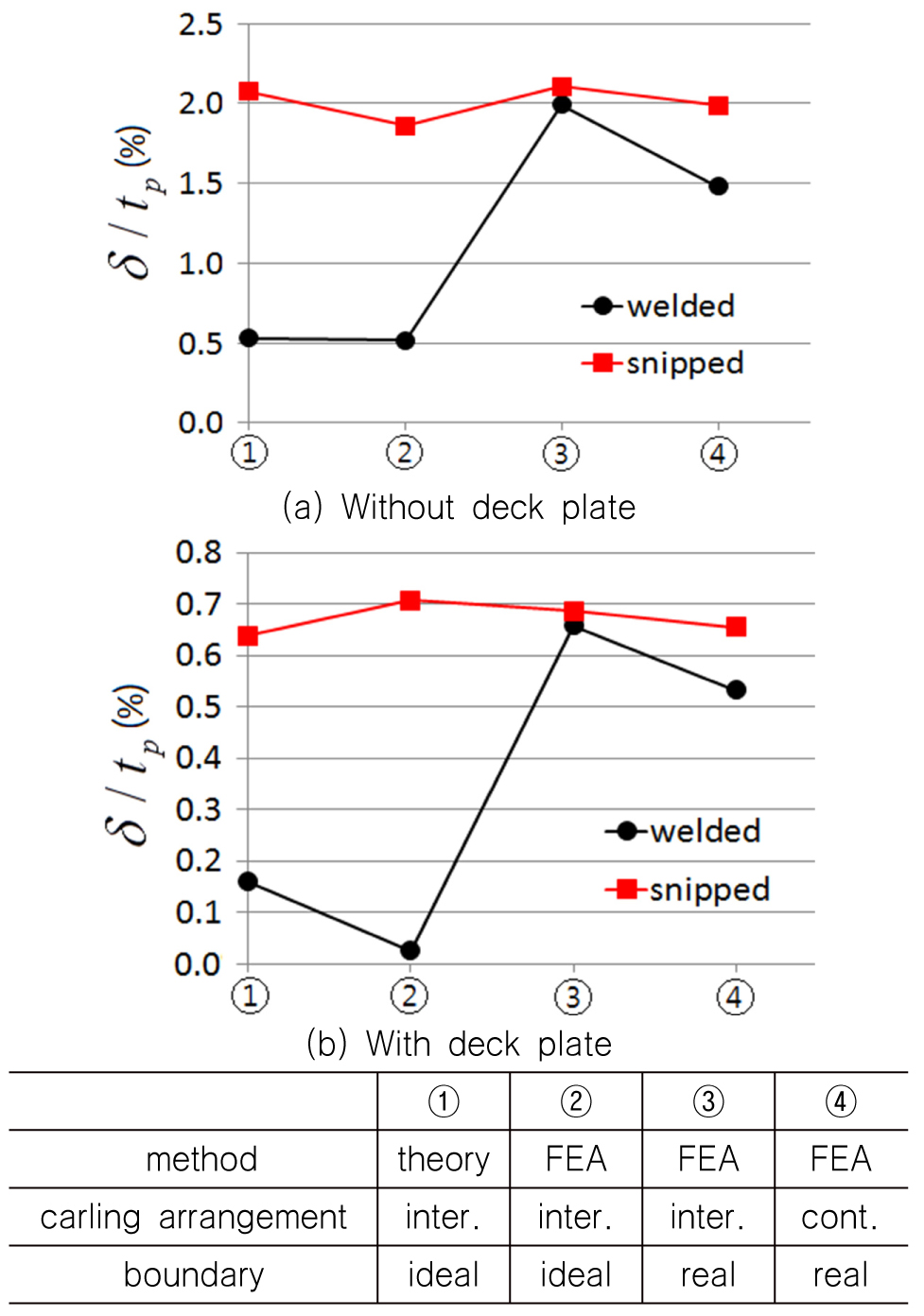
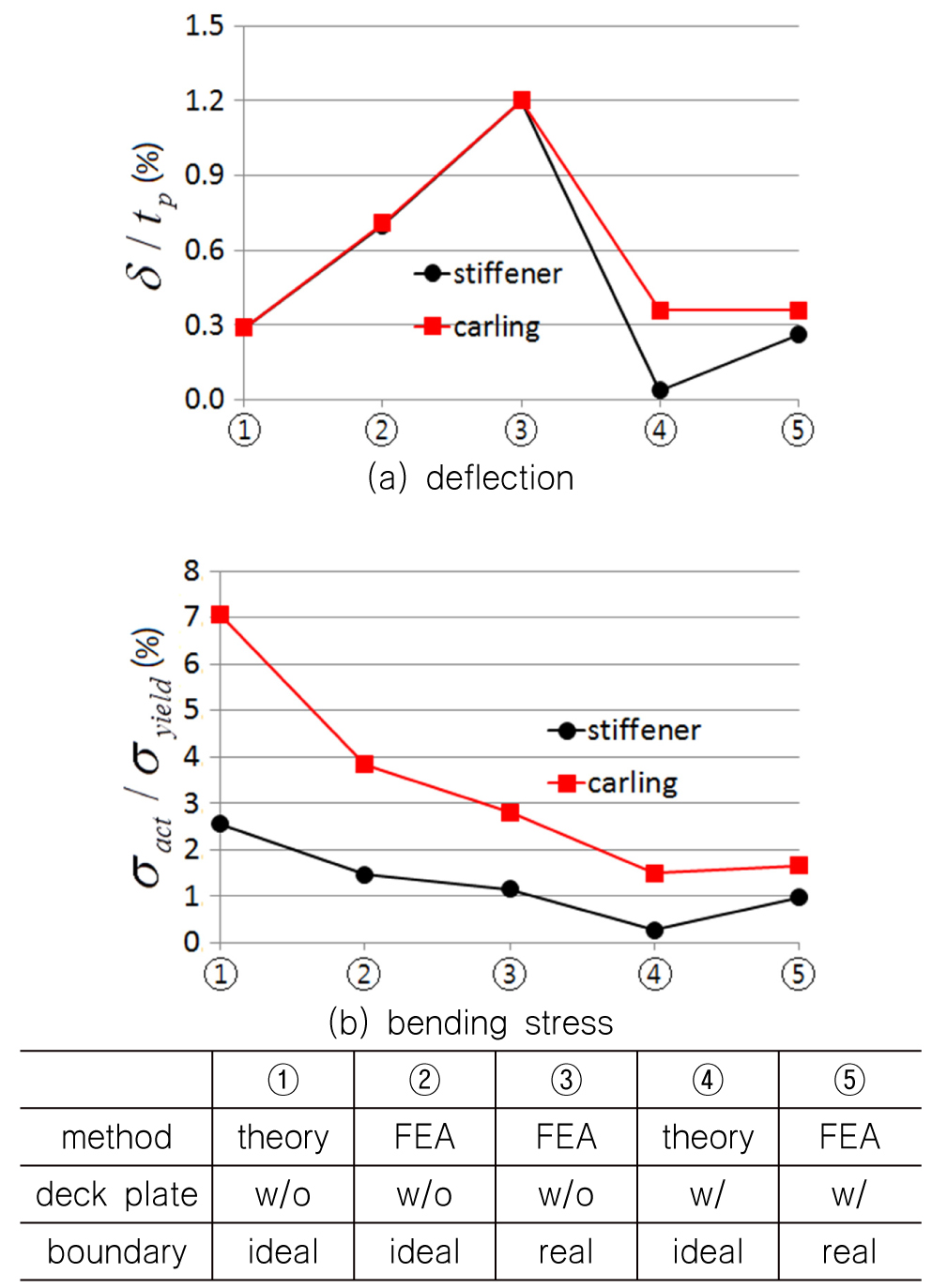
Fig. 22는 조선소에 많이 사용되고 있는 구조부재 치수에 대하여 유한요소법과 이론식 또는 유한요소법으로 구한 처짐 값(δ)을 상갑판의 두께()로 나누어 무차원하여 비교한 것이다. ①은 이론적 계산(theory)으로 카링이 단속적으로 배치되었으며 경계조건은 단순지지이다. ②, ③ 그리고 ④은 유한요소 해석(FEA) 결과로 카링을 연속적 배치한 경우와 단속적으로 배치한 경우에 대하여 이론적 계산(①)과 동일하게 국부구조에 구속한(②의 ideal)와 전체구조 모두를 모델링한 실제조건(④의 real)으로 수행한 것을 나타낸 것이다. 여기서 경계조건이 ideal의 경우, 용접은 양단 완전고정이고 스닙은 양단 단순지지 조건을 의미한다. 또한 Real의 경우, 유한요소 해석모델에서 카링과 보강재 연결을 실제와 동일하게 구현하고 전체 구조해석 모델로 해석을 수행한 것을 의미한다.
상갑판을 고려하지 않고 순수하게 카링만으로 고려한 Fig. 20 (a)에서 양끝단을 단순지지로 계산한 이론적 계산 값은 단순지지 또는 스닙한 형상으로 모델링한 유한요소해석 결과와 비교적 잘 일치한다. 그러나 양끝단을 완전 고정으로 계산한 이론적 값은 경계조건을 완전 고정으로 수행한 유한요소 결과(ideal 조건)와 잘 일치하나 카링과 보강재를 용접으로 연결한 조건(real)보다는 처짐량이 적게 나타난다. 상갑판을 고려하지 않은 (a) 결과와 비교하여 상갑판을 고려한 (b) 결과는 그 경향은 유사하나 처짐량이 1/3 이상 감소하는 것으로 나타났다.
Fig. 23은 Fig. 21과 동일한 계산 결과에 대하여 굽힘응력()을 재료의 항복응력()으로 나누어 무차원한 것을 나타내었다. 상갑판 없이 순수하게 카링만으로 계산한 결과에 의하면 이론적 계산 값이 유한요소 해석 결과보다 큰 응력 값을 나타내고 있다. 데크판의 유효폭 개념을 도입하여 계산하면 카링만으로 계산한 응력보다 약 절반 정도로 된다. 그러나 초기치수 선정 단계에서는 안전을 생각하여 데크판의 영향을 고려하지 않고 하부 지지구조로만 계산하는 것을 추천한다.
Fig. 24는 Fig. 18의 1개의 종보강재의 중앙 상단에 지지구조를 위치시키고 종보강재에 수직하게 카링으로 보강한 경우에 대하여 종보강재와 카링이 인접 종/횡보강재와의 연결 상태를 고려하기 위한 이론적 경계조건을 나타낸 것이다.
Fig. 24에서 하중 P가 작용하는 지점에서는 카링과 종보강재가교차함으로 처짐 값이 동일하며 분배되는 각각의 하중 합은 P가 되는 식 (5)가 성립한다.
| (5) |
따라서, 하중 과 가 각 부재에 작용할 때 재료역학의 단순 보이론에 의한 처짐은 식 (6)으로 된다.
| (6) |
where,
: Young’s modulus for each structure member
: 2nd moment of area for each structure member
: length for each structure member
또한, 하중 P가 작용하는 위치에서는 식 (5)의 조건으로부터 각각의 부재에 작용하는 하중의 분배는 식 (7)로 구할 수 있다.
| (7) |
또한 각각의 부재에 대한 전단응력은 식 (8)로 구한다.
| (8) |
Fig. 25는 지지구조를 카링과 종보강재가 교차하는 곳에 설치하고 카링의 끝단과 종보강재는 용접으로 연결하고 카링을 연속 배치한 구조물에 대한 유한요소 구조해석 결과이다. 나타난 von-Mises 등가응력 분포를 보면 카링보다 강성이 큰 종보강재로 주 하중이 분배됨을 알 수 있다.
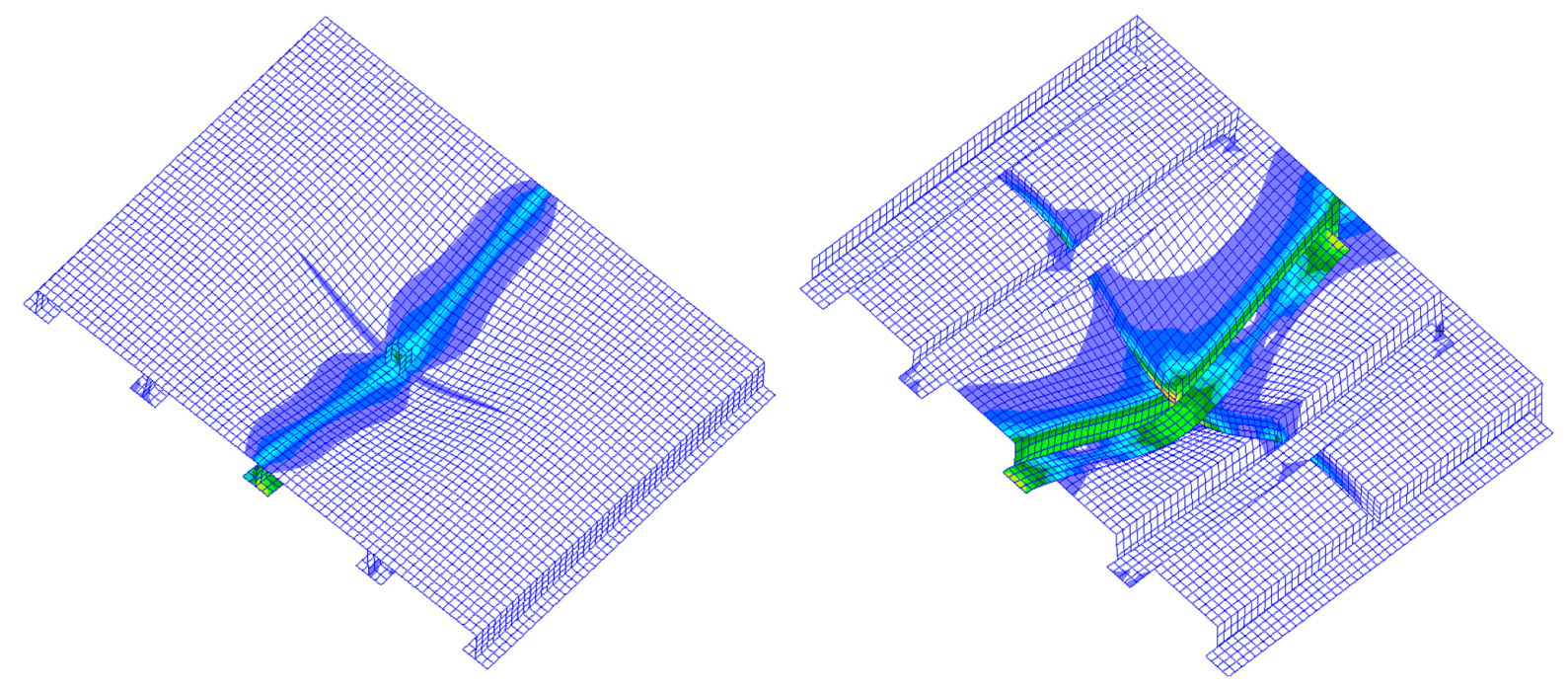
von-Mises equivalent stress and deformed shape of structures supported by the stiffener and carling with welded ends and continuous arrangement
Fig. 26는 지지구조 하부에 카링과 종보강재로 보강한 경우, 처짐과 응력발생에 대하여 상갑판 부재의 고려 유무, 이론적 계산과 유한요소 해석(FEA) 결과 비교, 카링 끝단의 경계조건에 변화에 따른 결과로 처짐을 상갑판두께로 나누어 무차원화한 (a)와 작용응력을 항복응력으로 나누어 무차원화한 (b)로 나타내었다.
①은 상갑판 없이 카링과 보강재로 구성된 국부구조에 대하여 이론적 계산을 수행한 경우이고, ④는 ①과 동일한 경우에서 상갑판을 추가로 고려한 경우(with)이다. ②, ③ 그리고 ⑤는 유한요소 해석 결과로 ②와 ③은 상갑판을 유한요소 모델에 고려하지 않은 것(without)이고 ⑤는 고려한 경우이다. 또한 ②는 이론적 계산과 동일하게 Fig. 25의 단위 판부재, 카링과 보강재로 구성된 국부구조의 끝단에 경계조건을 구현한 경우(ideal)이고 ③과 ⑤는 Fig. 25의 전체구조의 네끝단에 대칭조건을 구현하여 실제조건(real)으로 수행한 것을 나타낸 것이다.
처짐의 경우, 상갑판 없이 순수하게 종보강재와 카링만으로 된 구조에서는 이론적 계산 값은 실제 경계조건을 고려한 유한요소 해석보다 대체로 안전측에서 나타났다. 여기서 ideal은 카링과 보강재에 대한 계산시 양끝단을 완전히 고정한 것이고 real은 유한요소 구조해석에서 인접부재와의 연결상에 실제 경계조건을 부여한 것이다.
응력의 경우, 상갑판이 없이 순수하게 카링만으로 된 경우, 이론적 계산값이 유한요소 해석 결과보다 큰 응력 값을 나타내고 있다. 데크판의 유효폭 개념을 도입하여 계산하면 응력의 경우 약 절반 정도 낮추어 진다.
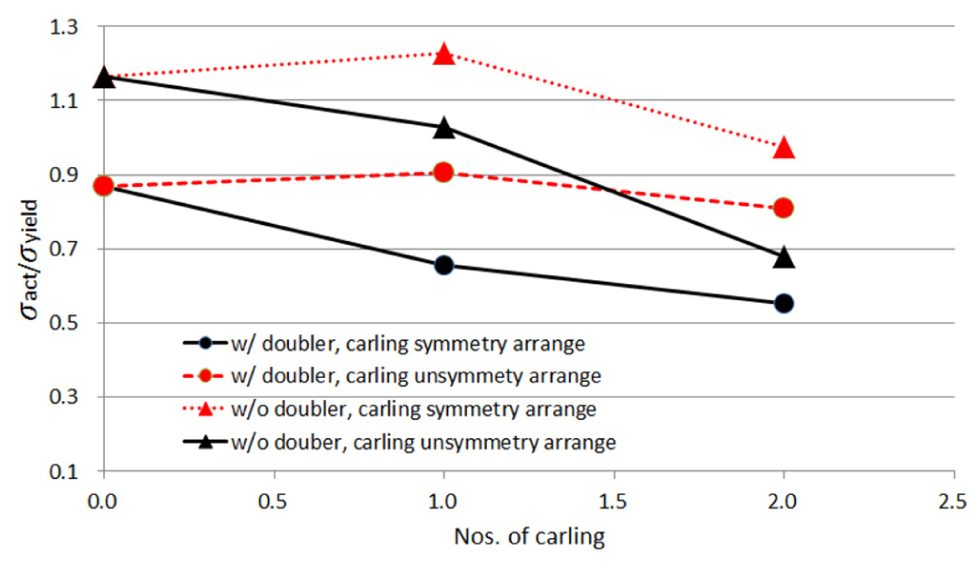
Fig. 27은 카링의 개수 변화와 덧판의 설치 유무에 따른 응력변화를 나타낸 것이다. 카링 개수가 증가함에 따라 나타나는 응력은 감소하는 것으로 나타났으며 덧판이 없는 경우가 있는 경우보다 크게 나타났다.
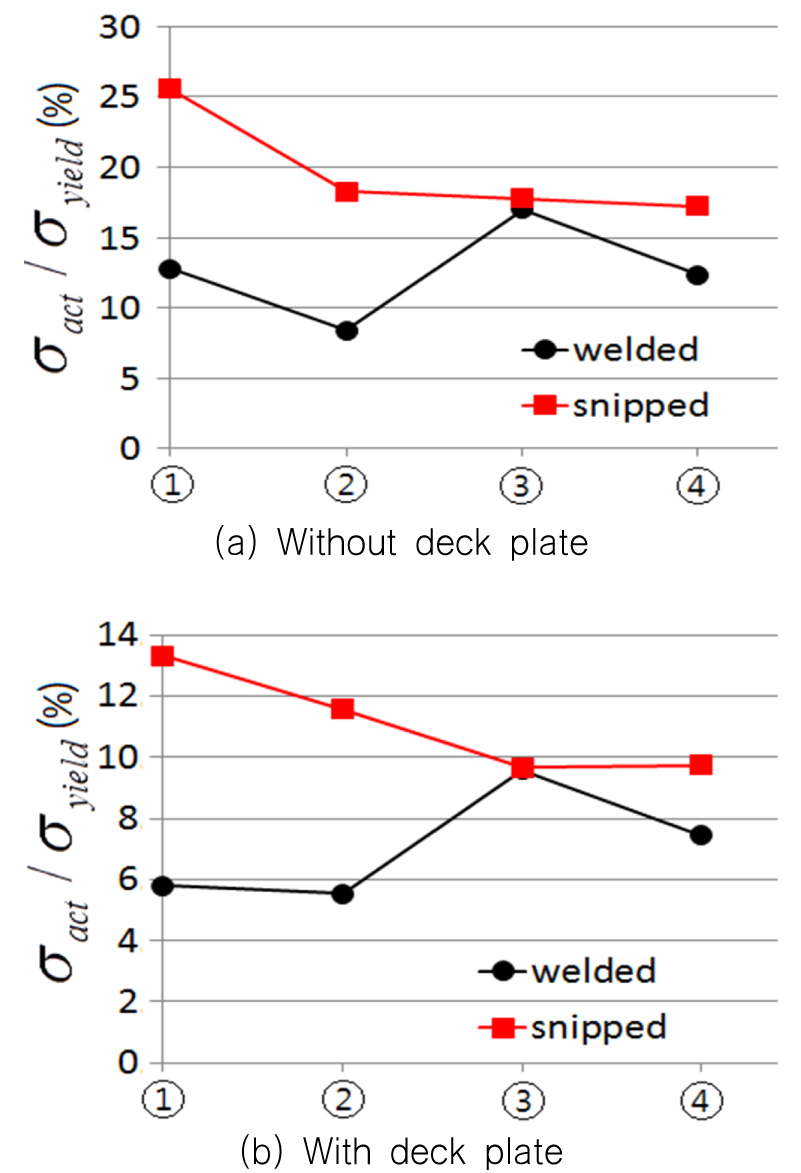
4.4 허용응력과 강도평가 기준
선박, 시추선, FPSO 등은 입급하는 선급과 선주의 시방서 사항에 따라 선정된 규정으로 수행하며 이에 따른 하중과 허용응력이 정해진다. 파이프 지지구조는 선체에 부착되는 선체 부가물(appurtenance)로 분류 할 수 있다.
통상 구조물 설계는 최종 한계상태(ultimate limit state, ULS), 피로 한계상태(fatigue limit state), 사고 한계상태(accidental limit state), 서비스 한계상태(serviceability limit state)로 수행한다. 이중, 최종 한계상태로 설계시 구조부재의 작용응력을 평가하기 위하여 허용응력을 선정하여야 하는데 Table 1은 유한요소의 크기에 따라 DNVGL AS(2015b)와 IACS(2015)를 기준으로 허용응력을 결정한 예이다.
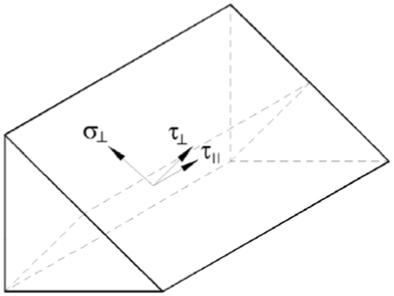
Fig. 7에 나타낸 바와 같이 덧판은 용접으로 선체 상갑판과 연결되며 이때 필렛 용접부에 대한 강도평가를 수행해야 한다. 최종 한계상태로 설계할 때 유한요소 해석으로부터 추출한 용접각장에서의 응력으로 DNVGL AS(2015a)에서 주어진 식 (9)로 평가할 수 있다.
| (9) |
where,
: normal design stress perpendicular to the throat
: shear design stress(in plane of the throat) perpendicular to the axis of the weld
: shear design stress(in plane of the throat) parallel to the axis of the weld
: nominal lowest ultimate tensile strength of the weaker part joined
: appropriate correlation factor
: material factor for welds
5. 결 론
본 논문은 파이프 지지구조와 선체하부 구조물의 설계와 강도 평가 대하여 현재 나타나는 문제점들을 열거하였으며 그 해결방법으로 보다 신속하고 정확하게 강도평가를 수행하기 위하여 유한요소 모델링 자동화 프로그램을 개발하였다. 이를 이용한 시리즈 구조 해석을 수행하고 이론적 계산 결과와 비교하여 중요 설계 인자들의 영향을 검토하였다.
ⅰ) 선체 상갑판에 지지구조 또는 덧판을 설치한 경우, 선각거어더의 종굽힘만 작용하여도 발생하는 상갑판부의 응력이 균일하지 않고 국부적으로 증가한다. 또한 지지구조에 작용하는 하중만 고려하여 설계하는 현재의 방법 보다 선각거어더의 굽힘과 지지구조에서 작용하는 하중을 상호 조합하여 설계를 하는 것이 바람직하다.
ⅱ) 덧판의 두께와 폭은 작용하중의 크기와 방향에 따라 달라지므로 적절히 선정하여 사용할 것을 권장한다.
ⅲ) 지지구조 하부에 카링을 설치하는 경우에 대하여 유한요소법으로 설계영향 인자들을 변화시키면서 강도 변화를 검토하였으며 이론적 계산 결과는 설계 목적으로 사용할 수 있음을 확인하였다.
ⅳ) 지지구조 하부에 카링과 종보강재를 동시에 설치하는 경우에 대하여 이론적 계산식을 제시하였으며 유한요소 해석 결과와 비교하여 설계에 적용 가능하다는 것을 확인하였다.
ⅴ) 유한요소 모델링 자동화 프로그램을 개발하여 구조해석을 정확하고 신속히 수행할 수 있도록 하였으며 설계업무의 능률향상이 기대된다.
ⅵ) 본 연구의 수행으로 파이프 지지구조와 하부구조 보강에 대한 강도 평가에 소요되는 공기의 단축과 계산 정확도의 향상이 기대된다.
References
- CAESAR II, 2018. Industry Standard for Pipe Stress Analysis, HEXAGON PPM.
- DNVGL AS, 2015a. Design of offshore steel structures, general -LRFD. DNVGL-OS-C101, [Online] (Update July 2015) Available at : http://www.dnvgl.com/ [Accessed March 2018].
- DNVGL AS, 2015b. Structural design of offshore ships. DNVGL-OS-C102, [Online] (Update July 2015) Available at : http://www.dnvgl.com/ [Accessed March 2018].
- International Association of Classification Societies (IACS), 2015. Common structural rules for bulk carriers and oil tankers. [Online] (Update January 2015) Available at : http://www.iacs.org.uk/ [Accessed May 2016].
- MSC/NASTRAN, 2015. Quick reference guide. Tokyo, Japan: MSC software Simulating Reality.
- MSC/PATRAN, 2015. User's guides, Santa Ana, CA, USA: Macneal-Schwendler Corporation(MSC).
- TSCF IP 001, 2004. Outfitting Related Structural Defects, Tanker Structure Co-operative Forum.