몬테카를로 시뮬레이션을 이용한 시운전 선속-동력 성능에 대한 불확실성 해석
Abstract
The speed and power performance of a ship is not only a guarantee issue between the ship owner and the ship-yard, but also is related with the Energy Efficiency Design Index (EEDI) regulation. Recently, International Organization for Standardization (ISO) published the procedure of the measurement and assessment for ship speed and power at sea trial. The results of speed and power performance measured in actual sea condition must inevitably include various uncertainty factors. In this study, the influence for systematic error of shaft power measurement system was examined using the Monte Carlo simulation. It is found that the expanded uncertainty of speed and power performance is approximately ±1.2% at the 95% confidence level(k=2) and most of the uncertainty factor is attributed to shaft torque measurement system.
Keywords:
Uncertainty analysis, Monte Carlo simulation, ISO 15016:2015, Sea trial, Speed-power performance키워드:
불확실성 해석, 몬테카를로 시뮬레이션, 시운전, 선속-동력 성능1. 서론
최근 국제해사기구(International Maritime Organization, IMO)에서는 해상오염 방지를 위한 규제 중 하나로, 설계단계의 평가지수인 선박에너지 효율 설계지수(Energy Efficiency Design Index, EEDI)와 운항단계의 평가지수인 에너지효율 운항지표(Energy Efficiency Operational Indicator, EEOI), 선박 에너지 효율관리계획(Ship Energy Efficiency Management Plan, SEEMP)등을 강제화 하였다. 이에 따라 선박의 선속-동력 시운전은 선주, 조선소, 선급 등 모든 기관에게 중요한 관심사항이 되었으며, 국제표준화기구(ISO)에서는 선속-동력 시운전의 해석법을 표준화하여 제정한 바 있다(ISO 15016, 2015).
시운전 시 실제해상에서 계측된 선속-동력을 정수 중에서의 선속 성능으로 치환하여 평가하기 위해서는 실제 해상조건의 외력항을 보정해주는 과정이 필요하다. 이러한 일련의 과정이 바로 ISO 15016에서 제시한 시운전 해석법이다. 따라서 실제 해상 상태에서 계측된 자료의 신뢰도에 따라 정수중 환경조건으로 보정된 선속-동력성능의 불확도가 큰 차이를 보일 수 있다(Insel, 2008).
실선의 선속-동력 시운전 시험에서 계측해야 할 물리량은 상당히 많으며, 계측 값들 각각의 신뢰도 수준에 따라 선속-동력 성능의 불확도가 결정된다. 선속-동력 결과의 불확도를 낮추기 위해서는 계측기의 오차를 줄이고, 이상적인 시험환경(정수 중)에서 계측하는 것이 추천되나 실제 해상에서 이뤄지는 시운전의 경우 이상적인 시험환경조건에서 수행하기가 쉽지 않다. 따라서 모든 시운전 계측결과에는 계측 장비가 가지는 불확도와 시운전 환경조건에 기인하는 불확도가 모두 포함되어 있다고 할 수 있다.
실험실 단위에서 이루어지는 시험에 대해서 국제수조협회(ITTC)에서는 저항시험, 프로펠러 단독 성능시험 등 다양한 유체역학 실험의 불확실성 해석 지침을 제안하고 있다(ITTC 2002, 2005). 이를 바탕으로 Park et al.(2003, 2015), Han et al.(2017)은 저항 및 자항 모형실험에 대한 불확실성 해석을 수행한바 있으며, Park et al.(2012), Seo et al.(2016)은 운동 및 저항 해석에 사용된 수치계산 기법에 대한 불확실성 해석을 수행한 바 있다.
그러나 아직까지 실제 해상에서 수행되는 시운전 시험의 경우 표준화된 불확실성 해석 절차(안)는 없는 실정이다. 다만 ISO 15016에서는 불확실성 해석을 위해서 시간에 따른 각 계측 값을 기록하고 제공하도록 되어 있다. 이러한 이유는 선박의 시운전이 외란의 영향이 다소 큰 해상조건에서 이뤄질 경우, 속도성능 관점에서 조선소-선주간의 분쟁이 발생될 소지가 있으며, 이러한 분쟁의 해결책이 바로 불확실성 해석이기 때문이다. 현재까지 대부분의 조선소에서는 각각의 계측자료에 대한 평균값만을 고려하여 판단하고 있으나, 향후 시간에 따른 각 계측 값을 바탕으로 시운전 선속-동력에 대한 불확실성 해석 연구가 필요한 실정이다.
본 연구에서는 축동력 계측시스템에 대한 불확실성 요소를 조사하고, ISO 15016에 제시된 방법을 바탕으로 전달동력에 대한 불확실성 해석을 수행하였다.
2. 불확실성 해석법
불확실성 해석 방법은 크게 세 가지로 나눌 수 있다(ISO 19030, 2016). 첫 번째는 ISO JCGM 100(2008a)에서 제시한 불확도 전파법칙을 이용하는 방법이다. 여기서 모델식은 테일러급수를 이용하여 감도계수, 불확도 기여량, 자유도를 계산하게 된다. 다만, ISO GUM방법의 경우, 수계산이 가능하다는 장점이 있지만, 모델식이 선형이여야 하고, 입력 자료의 분포가 반드시 가우시안(Gaussian)분포를 따를 때에만 사용이 가능하다는 단점을 가지고 있다. 본 절차를 자세히 살펴보면, 각 입력변수에 대해서 Table 1과 같이 A형 표준불확도와 B형 표준불확도를 각각 산정한다. 여기서 A형 표준불확도는 실험과정에서 무작위성으로부터 기인되는 불확도 성분을 의미하고, 반복측정을 통해서 평가할 수 있다. 반면 B형 불확도는 A형 불확도를 제외한 모든 성분의 불확도로 정의되며, 과거 측정값 및 경험, 일반적인 지식, 장비 설명서 등을 통해 산정가능하다. 이렇게 산정된 A형, B형 표준불확도를 식(1)을 이용하여 각 입력변수에 대해 표준불확도를 계산한다.
| (1) |
또한 모델식이 여러 가지 변수들의 함수로 표현되는 경우, 식(2)를 통해 합성표준불확도를 계산한다.
| (2) |
여기서 첫 번째 항은 감도계수와 표준불확도 곱의 형태이며, 각 입력변수에 대한 불확도 기여량이 된다. 두 번째 항은 각 입력 변수들 간의 상관관계를 나타내는 항으로 대부분의 문제에서 입력 변수들 간의 상관관계는 없는 것 간주하기 때문에 0이 된다.
또한, 확장불확도(U)는 식(3)과 같이 포함인자(k)와 합성표준불확도의 곱의 형태이며, 정규분포로 가정할 경우 95%신뢰구간에서 k는 약 2가 된다.
| (3) |
두 번째 방법은 몬테카를로 시뮬레이션을 이용하여 불확도를 추정하는 것이다(ISO JCGM 101, 2008b). 본 방법은 불확도 전파법칙을 이용하는 방법과는 달리 모델식에 대한 제한이 없으며, 중심극한정리에 따라 입력변수들이 가우시안 분포를 따르지 않더라도 반복횟수를 증가시켜 그 평균값을 정규분포로 수렴시킬 수 있는 장점을 가진다. 몬테카를로 시뮬레이션의 가장 큰 핵심은 표본의 개수를 증가시킴에 따라 보다 정확한 추정결과를 얻을 수 있다는 개념을 바탕으로 가상의 반복적 시행을 통해 결과를 예측하는 것이다(Kim, 2011). 컴퓨터의 계산능력의 발전과 더불어 몬테카를로 시뮬레이션 방법이 체계화되었으며, 실제 상황을 재연하는 모델링 방법의 기초로 사용되고 있다. 특히 몬테카를로 시뮬레이션 방법은 입력 자료의 확률분포 및 모델식에 대한 제한이 없어 다양한 방면에서 사용되고 있으며, 조선해양 분야에서는 선박의 손상에 대한 신뢰도 평가(Brown & Chen, 2002; Sun et al., 2017), 실선의 추진 성능해석(Kamal et al., 2013; Coraddu et al., 2014; Insel 2008)분야에서 사용되어 오고 있다.
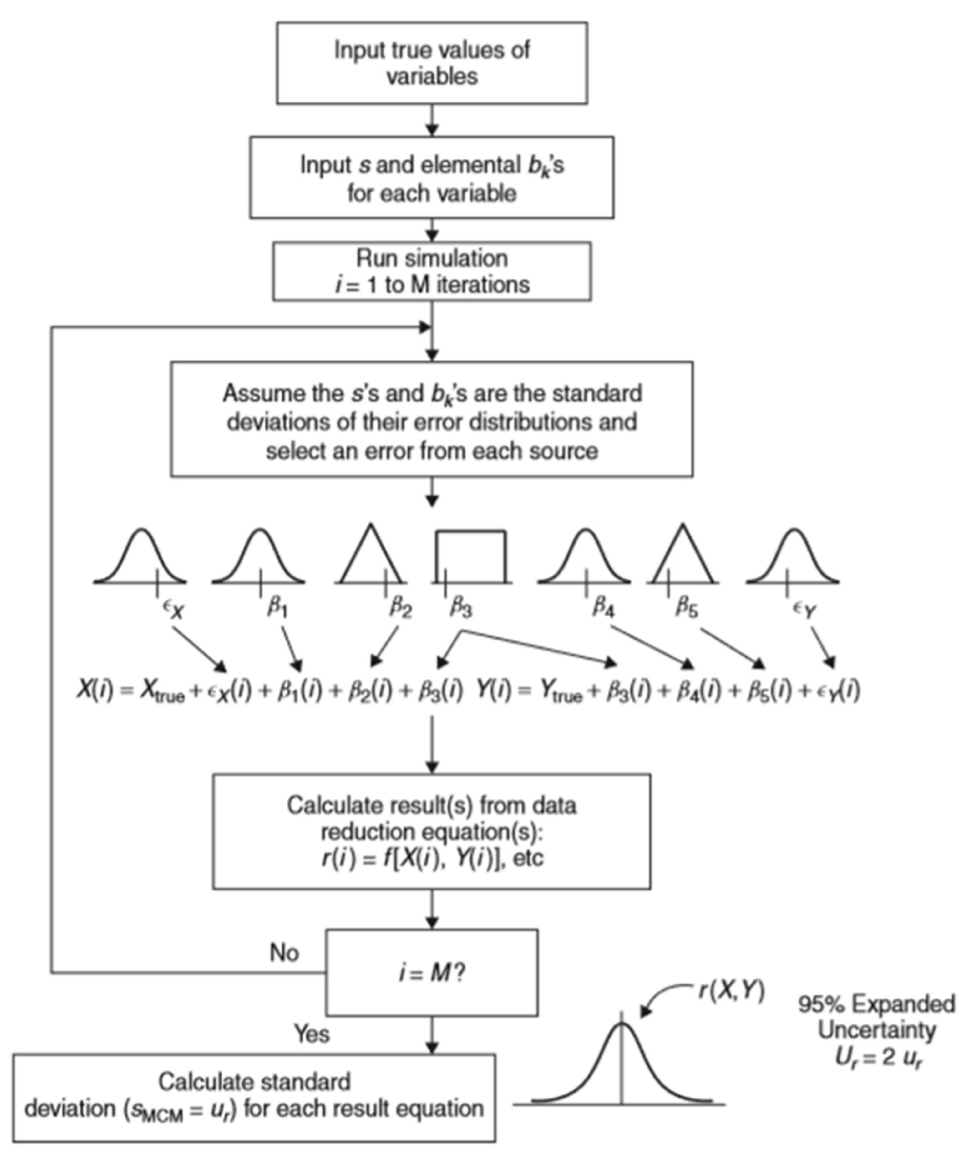
몬테카를로 시뮬레이션의 구현과정을 Fig. 1에 도시하였고, 이는 크게 아래의 4단계로 구분 할 수 있다.
(1) 수학적 모델식 정의
(2) 각 입력변수에 확률분포함수 부여
(3) 입력변수를 모델식에 입력하여 반복계산 수행
(4) 결과 분석
3. 시운전 자료 및 불확도 요소
3.1 시운전 자료
대상선박은 170K LNG 선이며(Kim et al., 2017), 총 3가지 조건에서 왕복시험이 수행되었다. 이때 계측된 풍향, 풍속, 파고, 파장, 파향은 Table 2와 같다.
모든 조건에서 계측된 상대풍속은 1.9~16.7m/s 이며, 유의파고는 1.2~1.4m로 시운전 해상조건은 온화한 것으로 나타났다. 계측된 자료는 MCR의 50%, 75%, 90%의 시운전 결과이며, 제공된 자료는 각 왕복 시험(1st run, 2nd run)에 대한 선속, 선박의 방향, 축 토크, 프로펠러 회전속도, 상대풍속, 풍향, 파도, 기온, 수온 등의 평균값이다. 측정 장비들의 불확도는 장비사양 및 관련 문헌을 바탕으로 적절하게 가정하였다.
3.2 선속-동력성능 추정에 포함된 불확도 요소
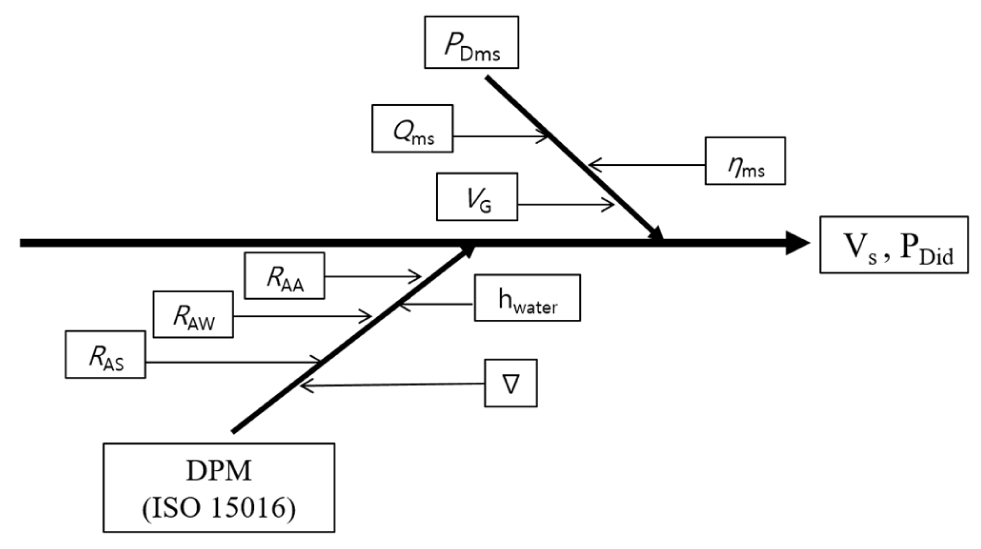
ISO 15016에서 제시된 방법을 통해 축동력을 산정할 때 발생 가능한 불확도 요소는 Fig. 2와 같이 축 동력계측시스템(PDms)과 외란의 의한 보정요소로 크게 두 가지로 나눌 수 있다. 축동력 계측시스템에서는 축 토크(Qms), 축 속도(ηms)에 포함된 불확도가 존재하며, 각각에 대한 세부 불확도 입력요소는 4장에서 상세히 설명한다. 또한 외란에 의한 보정요소로는 바람에 의한 부가저항 보정(RAA), 파도에 의한 부가저항 보정(RAW), 수온 및 밀도에 의한 보정(RAS), 천수 영향에 따른 저항 보정(hwater)항 등으로 구성되며, 각각에 대한 세부 불확도 요소는 5장에서 상세히 설명한다.
축 동력을 도출하기 위하여 우선 프로펠러축에 설치된 스트레인게이지를 통해 축 토크를 측정하고, 광학 센서 등을 이용하여 축의 회전속도를 측정한 후 이를 축 동력으로 계산한다. 또한 계측된 축동력은 외란에 의한 영향을 제거하기 위해 ISO 15016 시운전 해석법에 따라 각종 부가저항을 계산하여 보정하게 된다. 따라서 각 요소별 불확도가 최종적인 선속-동력 성능에 영향을 미치게 된다.
PDms : Delivered power in the trial condition
PDid : Delivered power in the ideal condition
Qms : Measured torque at the propeller shaft
VG : Measured ship’s speed over ground
RAA : Resistance increase due to wind
RAW : Resistance increase due to wave
RAS : Resistance increase due to deviation of water temperature and density
hwater : Water depth
∇ : Displacement volume
4. 축 동력 계측 시스템의 불확실성 해석
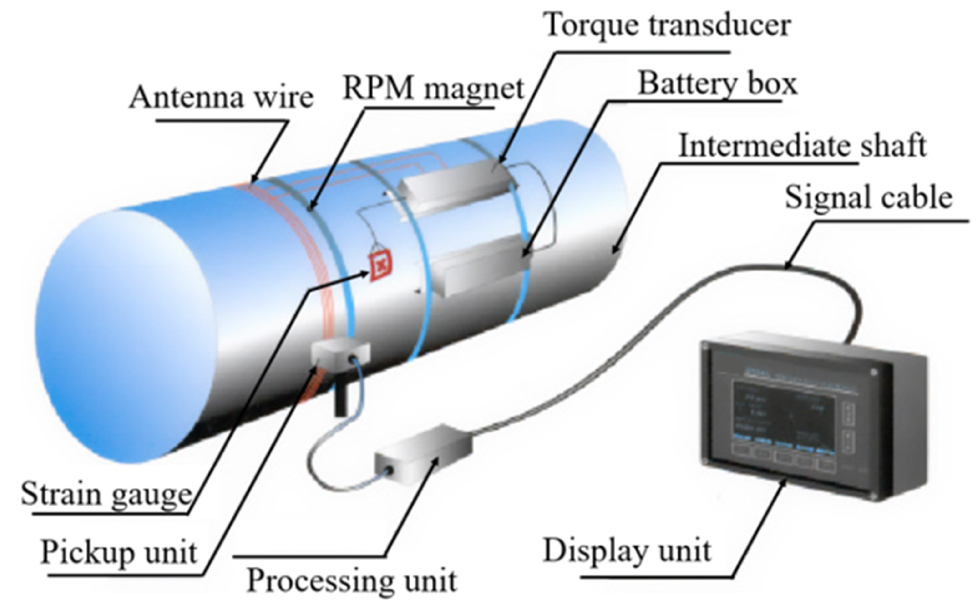
선박의 축 동력을 측정하는 방법으로는 스트레인 게이지나 광학식 측정장치를 축에 직접 부착하여 축의 응력을 연속적으로 계측하는 직접적인 방법과 실린더 내부의 연소압력을 측정하여 동력으로 환산하는 간접적인 방법이 있다. 실린더 내부의 연소압력을 측정하는 간접적인 방법은 엔진의 주기적인 폭발로 인해 변동이 커 부정확한 것으로 알려져 있으며, 대부분의 시운전 속도성능 시험 시 스트레인 게이지를 축에 직접 설치하여 계측하는 방법이 주로 이용되고 있다(Han, 1994).
스트레인 게이지를 이용하는 경우, Fig. 3과 같이 축의 비틀림 변형에 의한 전위차를 휘트스톤 브리지의 스트레인 게이지를 통해 검력한 후 전압을 증폭하고, 이를 주파수 변조를 통해 반송전파에 싣고, 축에 감긴 송신용 코일(antenna wire)을 통해 내보낸다. 출력된 신호는 축으로부터 일정거리에 고정된 수신기(pickup unit)를 통해 취득되며, 신호 분석기(processing unit)를 통해 반송파를 분리한 진동신호를 동력으로 환산하여 나타내어 준다(Song, 2008).
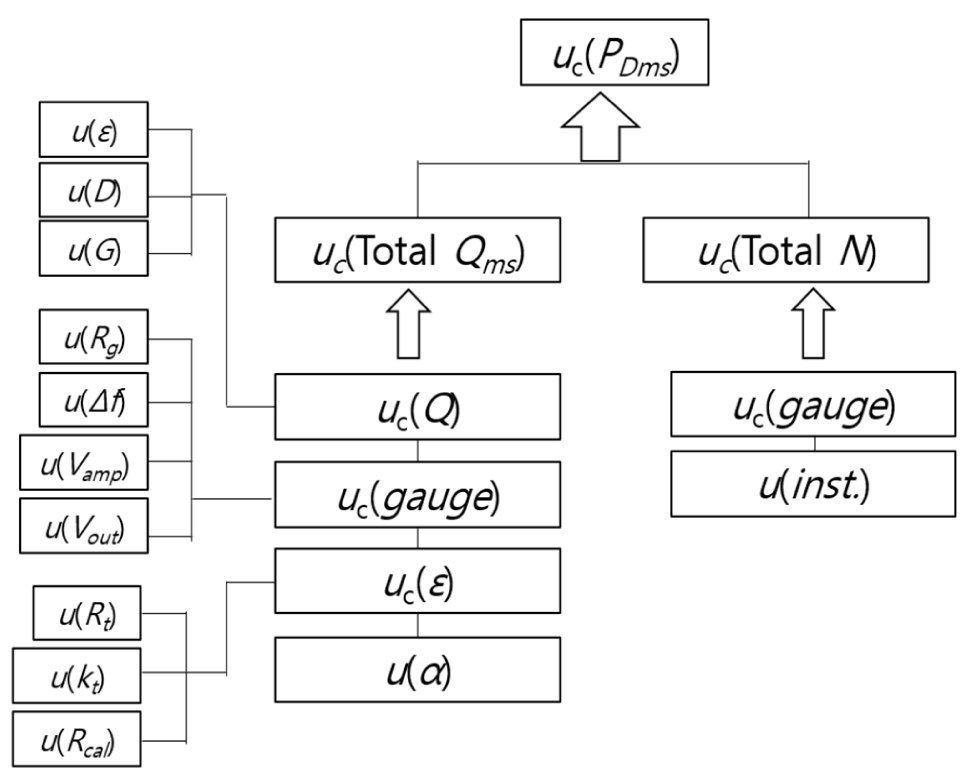
다만, 이러한 축 동력 계측시스템의 경우 스트레인 게이지 설치 시 발생할 수 있는 오차뿐만 아니라 신호 전송 과정, 동력으로의 환산 과정에서 다양한 불확도 요소가 존재하게 된다. 축 동력 계측 시스템의 불확도 uc(PDms) 요소는 Fig. 4와 같이 크게 토크 계측 시스템 uc(Total Qms)의 불확도와 축 속도 계측 시스템 불확도 uc(Total N) 성분으로 구분된다.
토크 계측시스템의 불확도는 스트레인게이지의 상대변위를 토크로 산정하기 위한 토크 재산정 불확도 uc(Q)와 게이지에 따른 불확도 uc(gauge), 스트레인 게이지 교정 시 발생 가능한 교정 불확도 uc(ε), 스트레인 부착과정에서 발생할 수 있는 설치 불확도u(α)로 구성된다.
여기서 토크 재산정은 식(3)과 같이 스트레인 게이지의 상대변위(ε)와 축 계수(αQ)의 곱으로 표현되며, 스트레인 게이지의 상대변위 불확도 u(ε), 축 직경 측정에 대한 불확도 u(D), 축의 전단계수에 대한 불확도 u(G) 등이 존재하게 된다.
| (3) |
ε : Relative strain of the strain gauge
G : Shear modulus
D : Shaft diameter
J : Moment of inertia for solid shaft
스트레인 게이지에 따른 불확도 uc(gauge)에는 스트레인 게이지 브리지 불확도 u(Rg), 송수신기 불확도 u(Δf), 증폭기에서 발생되는 불확도 u(Vamp), A/D 컨버터 불확도 u(Vout)로 구성된다. 또한 게이지를 교정할 때 발생되는 불확도 uc(ε)는 스트레인 게이지의 유효저항 불확도 u(Rt), 게이지 상수가 가지는 불확도 u(kt), 스트레인 게이지 교정 시 사용되는 표준 저항기가 가지는 불확도 u(Rcal)로 구성되며, 마지막으로 스트레인 게이지를 축에 부착할 때 발생되는 불확도 u(α)가 있다.
축 속도 측정시스템 불확도 성분은 축의 회전속도를 측정하는 게이지의 불확도 uc(gauge)와 게이지 설치 시 발생할 수 있는 불확도 uc(inst.)로 구성된다.
Fig. 4에서 각각의 기호가 가지는 의미는 다음과 같다.
uc(PDms) : Uncertainty of the power measurement system
uc(Total Qms) : Combined uncertainty of the total torque
uc(Total N) : Combined uncertainty of the total shaft speed
uc(Q) : Uncertainty due to recalculation of the torque
uc(gauge) : Uncertainty due to the gauge of shaft speed
u(inst.) : Uncertainty due to installation on a shaft
uc(ε) : Uncertainty due to calibration
u(α) : Uncertainty due to strain gauge installation
u(ε) : Standard uncertainty of the relative strain of the gauge
u(D) : Standard uncertainty of the diameter
u(G) : Standard uncertainty of the shear module
u(Rg) : Standard uncertainty of the strain gauge bridge
u(Δf) : Standard uncertainty of the transmitter and receiver
u(Vamp) : Standard uncertainty of the Amplifier plug-in module
u(Vout) : Standard uncertainty of the digital voltage meter
u(Rt) : Standard uncertainty of the strain gauge effective resistance
u(kt) : Standard uncertainty of the gauge factor at 75˚
u(Rcal) : Standard uncertainty of the resistance of standard resistor
축 토크 계측시스템의 총 합성표준불확도 uc( Total Qms)는 식(4)를 통해 얻어진다.
| (4) |
다양한 방법을 통해 축동력을 계측할 수 있겠지만, 일반적으로 스트레인 게이지를 통해 축 토크를 계측한 후 축 속도와의 관계를 통해 동력으로 환산한다. 축 토크 계측장비의 경우 대부분 350Ω의 스트레인 게이지를 사용하는 것으로 조사되었으며, ITTC (2002)를 참고하여 Table 3과 같이 게이지에 따른 불확도 uc(gauge)는 0.462, 토크 재산정 불확도 uc(Q)는 1.211, 스트레인 게이지 교정 시 발생 가능한 교정 불확도 uc(ε)는 0.370, 스트레인 게이지 설치 불확도uc(α)는 0.316으로 가정하였다. 여기서 토크 재산정 불확도가 다른 불확도에 비해 상대적으로 크며, 이는 축의 전단 탄성계수의 불확도 u(G)를 1.15%로 가정한 것으로 기인된다.
또한, 축 회전속도 계측시스템의 총 불확도 uc(Total N)는 ±0.1% 총 합성 불확도는 약 0.06%로 무시할만한 값으로 간주할 수 있다. 따라서 축동력 계측시스템의 총 합성불확도 uc(Pms)는 식(5)를 통해, 약 1.385%로 산정된다.
| (5) |
5. 외란 보정량에 대한 불확실성 해석
5.1 바람에 의한 부가저항 보정량 불확실성 해석
ISO 15016에서는 바람에 의한 부가저항을 산정하기 위해 풍하중 계수를 풍동시험, 선종별 풍하중계수데이터, 회귀식의 3가지 방법에 대해 언급하고 있으며, 본 연구에서는 선종별 풍하중계수데이터를 바탕으로 식(6)을 통해 산정하였다.
| (6) |
선박의 풍향·풍속계로는 풍배식, 풍차식, 초음파식이 사용될 수 있으며, 현재까지 대부분 풍차식이 사용되고 있다. 선박에 사용되는 대부분의 풍향·풍속계를 조사한 결과, 풍차식 계측장비의 정확도는 Table 4와 같은 정도로 조사되었다. 각 MCR조건에서 바람에 의한 부가저항의 불확도를 계산하기 위한 입력 자료의 확률분포는 풍속에 대해서는 정규분포로 가정하였으며, 풍향은 균일 분포로 가정하여 몬테카를로 시뮬레이션을 수행하였다.
Table 5는 바람에 의한 부가저항의 불확도 해석결과를 나타내고 있다. MCR의 50%-1st run, 50%-2nd run 해석결과에 대해 포함인자인 k가 2에 해당하는 95%신뢰구간에서 각각 ±4.4%, ±14.0%인 것으로 나타났으며, 75% MCR 조건과 90% MCR에서는 최대 12%, 18.1% 로 나타났다.
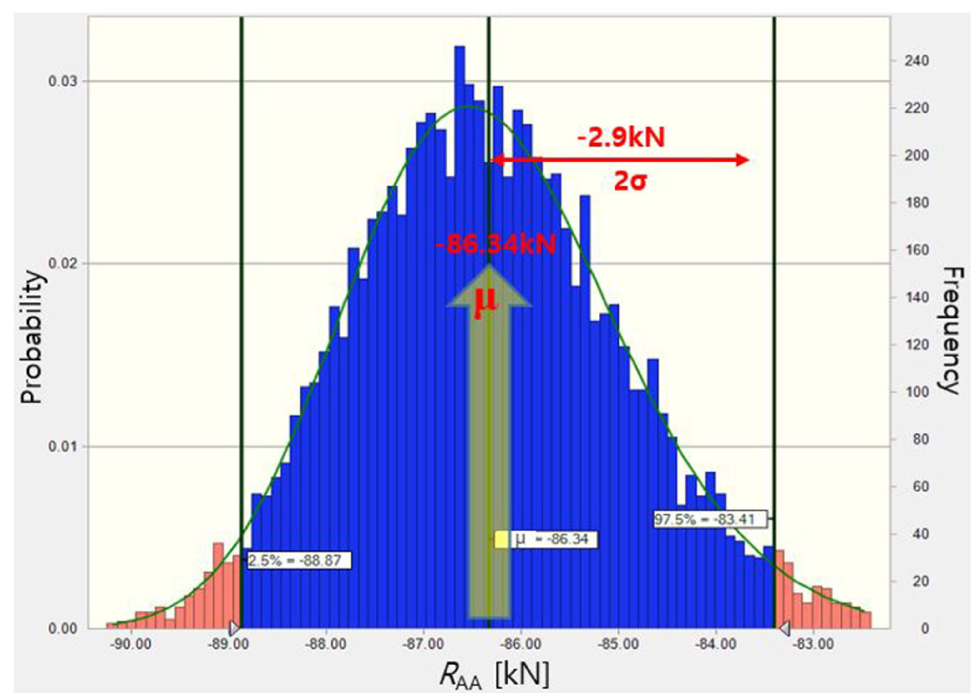
Fig. 5는 MCR 75% 1st 경우에 대한 바람에 대한 부가저항으로, 몬테카를로 시뮬레이션 해석결과인 도수분포를 나타내고 있다. 바람에 의한 부가저항의 평균이 –86.3kN이며, 95%신뢰구간에서 바람에 의한 부가저항의 확장불확도는 ±2.9kN로 평균값을 기준으로 약 ±3.3%로 나타났다. 해당 조건에서 상대풍속이 2.5m/s로 작기 때문에 불확도는 크지 않은 것으로 나타났다.
5.2 파도에 의한 부가저항 보정량 불확실성 해석
ISO 15016에서는 파도에 의한 부가저항 보정방법을 STAWAVE-1, STAWAVE-2, Theoretical method 방법 등 총 3가지 방법을 제시하고 있다. Insel(2008)의 경우 STAWAVE –1과 같은 단순한 보정 식을 사용하여 파도에 의한 부가저항을 계산하였다. 그러나 이러한 경우 선박의 운동에 기인하는 부가저항이 무시됨에 따라 장파조건에서만 사용이 가능하다는 단점이 있다. 이에 따라 본 연구에서는 선박의 운동에 의한 부가저항과 반사파에 의한 부가저항을 적절히 고려한 STAWAVE-2방법 식(7)을 적용하였다.
| (7) |
여기서, RAW는 파도에 의한 부가저항의 총량을 의미하고, 이는 선박의 운동에 기인하는 저항증가량(RAWML)과 반사파에 의한 저항증가량(RAWRL)의 합을 통해 구해질 수 있고, E(ω,α)는 단위면적당 방향 스펙트럼을 의미한다.
파도에 의한 부가저항을 구하기 위해서는 파고, 파향, 파주기가 필수적이며, 시운전 해역조건에서 너울(swell)이 존재할 경우, 추가적으로 너울의 파고, 파향, 파주기가 필요하다. 또한 STAWAVE-2를 적용한 경우 ±45°이내의 파에 대해서만 고려하므로, ±45°를 넘는 파에 대해서는 파도에 의한 부가저항은 0으로 간주하였다.
일반적인 시운전 조건에서, 파도에 의한 보정의 불확도를 낮추기 위해 가능하면 잔잔한 해역에서 시운전을 수행하는 것이 요구된다. 그러나 상황에 따라 잔잔한 해역에서 시운전을 못 할 경우, 파도의 특성정보가 정확히 계측 되어야 한다. 파도의 특성정보는 목측, 부이, 레이더, 라이더, 인공위성을 이용한 방법이 사용될 수 있다.
Insel(2008)의 경우, 파도에 대한 특성을 직접 계측하는 대신 풍속으로부터 얻어진 beaufort scale를 바탕으로 파고를 계산하여 적용하였으나, 이러한 경우 각 beaufort number에 해당되는 파고의 편차가 커져 대부분의 불확도가 beaufort scale 추정 항으로 기인되는 문제점을 가지고 있다. 따라서 본 연구에서는 레이더 장비를 사용하여 파고를 직접 계측하는 것으로 가정하고, 파고 계측에 사용되는 레이더의 장비 정확도를 Table 6과 같이 가정하였다.
파도 계측장비의 확률분포 입력 시, 파고에 대해서는 정규분포로 가정하고, 주기 및 파향에 대해서는 균일분포로 가정하여 몬테카를로 시뮬레이션을 수행하였다.
Table 7은 파도 계측장비의 정확도에 대한 입력변수 이용하여 파도에 의한 부가저항의 불확도 해석결과를 나타내고 있다. 모든 MCR 조건에서 파도에 의한 부가저항 불확도 해석결과 포함인자 k =2에 해당되는 95%신뢰구간에서 약 ±16%로 크게 나타났다. 이는 파고 계측장비의 표준불확도가 ±10%로 크기 때문이다. 그러나 시운전이 수행된 해상조건이 상당히 온화하여 파도에 의한 부가저항 증가량은 크지 않으며, 이로 인해 파도에 의한 부가저항의 전체 불확도 성분은 크지 않을 것으로 예상할 수 있다.
5.3 수온 및 밀도에 대한 보정량 불확실성 해석
ISO15016에서는 수온에 따른 밀도변화, 즉 점성에 대한 영향을 고려하기 위해, 식(8)을 통해 15°C, 1,026kg/m3을 기준으로 시운전의 점성항을 보정하고 있다.
| (8) |
일반적으로 시운전 수행 시, 수온은 실시간으로 계측하는 것이 아니라, 시운전 시작 전에 해수의 온도를 계측하고 이 값을 사용하게 된다. 이때 사용되는 온도계의 정확도를 Table 8과 같이 ±0.1℃로 가정하였다.
몬테카를로 시뮬레이션 방법을 적용하여 불확도를 계산할 때 모형선의 전 저항(RT) 불확도를 입력하도록 되어 있으나, 모형시험 시 전 저항에 대한 불확도는 크지 않을 것으로 간주하고 본 연 구에서는 무시하였다.
Table 9는 수온 및 밀도에 의한 부가저항 보정량에 대한 불확실성 해석결과를 보여주고 있다. 모든 MCR 조건에서 95% 신뢰구간(k=2)에서 약 3.3%의 확장불확도를 갖는 것으로 나타났다.
6. 전달동력(PDid)에 대한 불확실성 해석
ISO 15016의 해석법에서는 PDid의 계산은 식(9)를 통해 산정하게된다.
| (9) |
여기서, △R은 바람에 의한 부가저항, 파도에 의한 부가저항 등 시운전 해상조건을 정수 중으로 보정하기 위한 부가저항의 합이다.
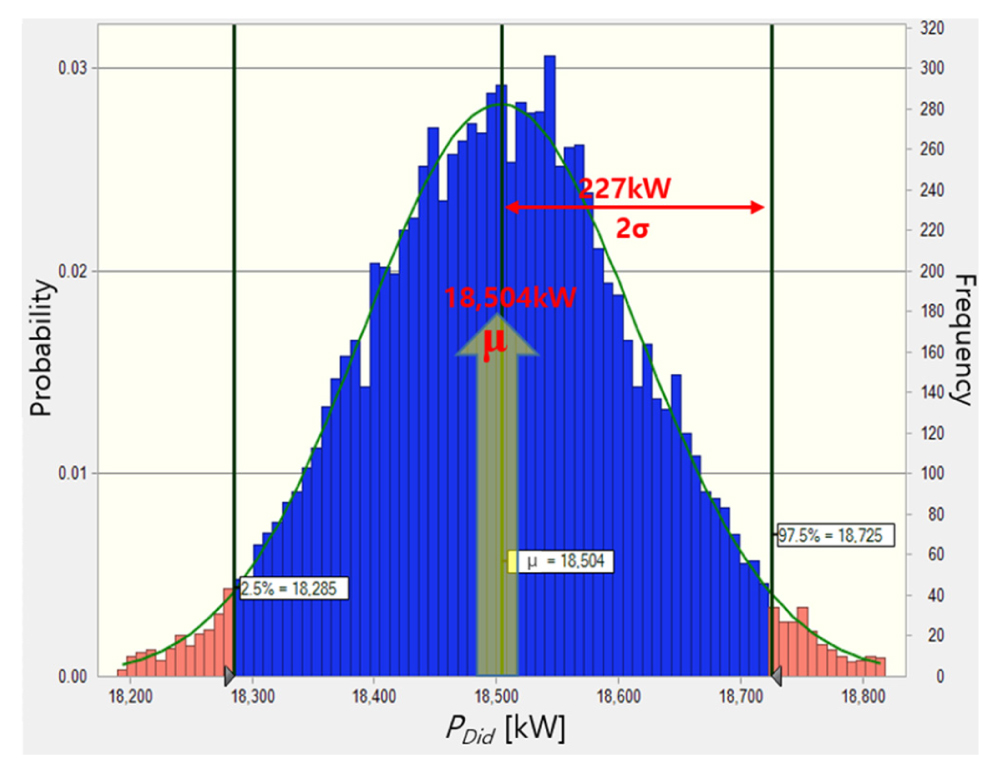
앞서 4장 앞장에서 계산된 축 동력불확도와 5장의 부가저항의 불확도를 바탕으로, 이상적인 환경조건으로 환산한 전달동력(PDid)에 대한 불확실성 해석을 수행하였다. 불확실성 해석 결과 Table 10과 같이 각각의 MCR조건에서 포함인자 k=2인 95%신뢰구간에서 약 ±1.2%의 확장불확도를 갖는 것으로 나타났다. 특히, MCR 75%에서 시운전 데이터를 바탕으로 ISO 15016의 시운전 해석법을 이용하여 축 동력(PDid)을 계산할 경우 Fig. 6과 같이 18,504 kW로 계산되며, 불확실성 해석을 수행한 결과 95%신뢰구간에서 ±227kW(약 ±1.2%)의 범위를 갖는 것으로 나타났다. 이를 선속관점에서 보면, 포함인자 k=2에 해당하든 95%신뢰구간에서 ±0.1 knot의 선속 편차를 보이는 것으로 해석할 수 있다.
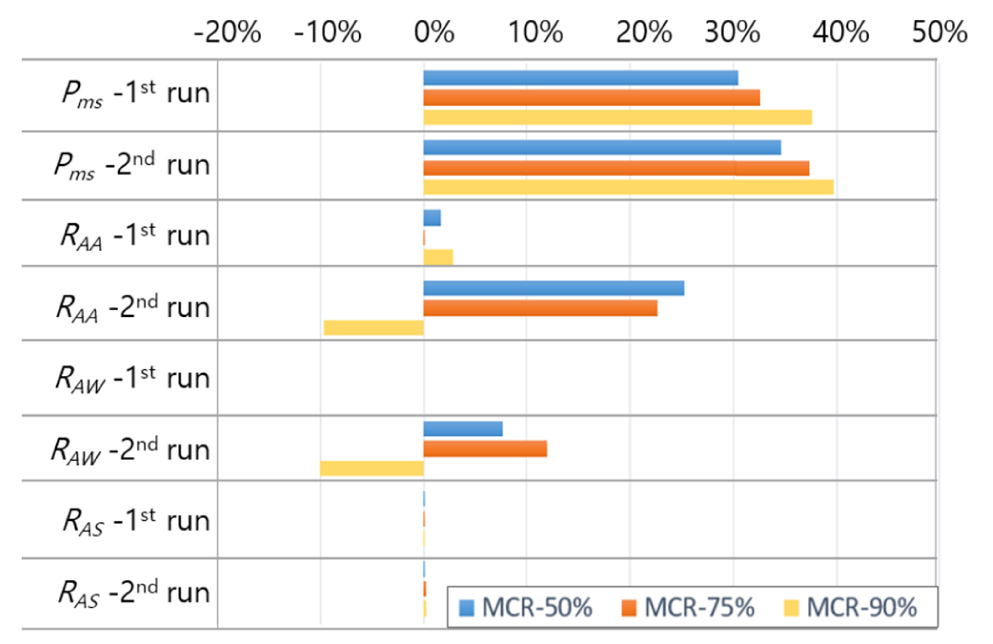
Fig. 7은 각 MCR 조건에서 왕복 시운전 결과를 바탕으로 추정된 전달동력(PDid)의 분산기여도를 나타낸 것이다. 모든 MCR조건에서 불확도에 기여도가 가장 큰 성분은 왕복시험 시 계측된 축동력 계측시스템(Pms-1st run+Pms-2nd run)으로 약 60% 이상으로 나타났으며, 나머지 40%는 바람, 파도, 수온밀도의 영향이 합산된 외란의 보정량 (RAA+RAW+RAS)에서 발생된 것으로 나타났다.
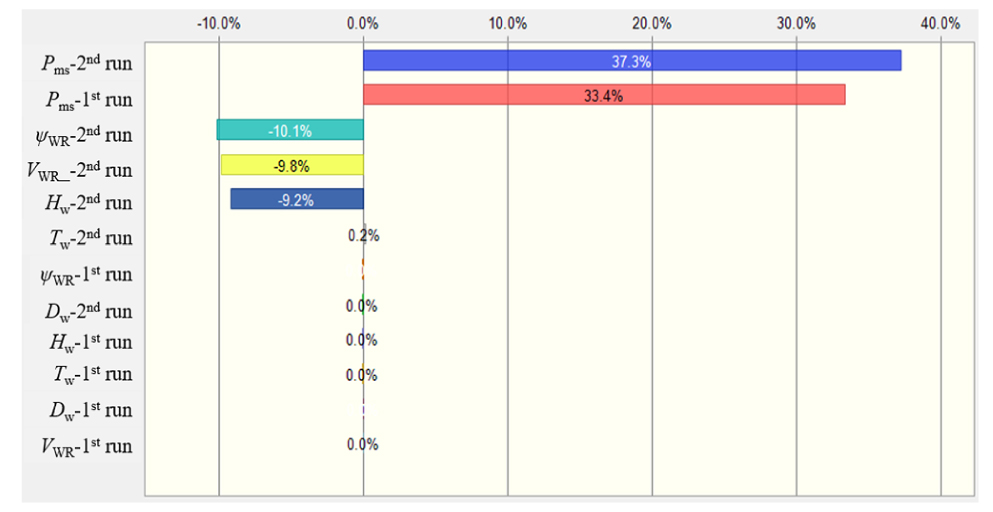
Fig. 8은 MCR 75%에서 왕복 시운전 결과를 바탕으로 추정된 동력(PDid)의 분산기여도를 나타낸 것이다. 75% MCR조건에서 해석결과 불확도에 가장 큰 영향을 주는 인자는 왕복 시운전시 축 동력계측시스템(Pms-1st run, Pms-2nd run)로 각 각 34%, 38%의 기여도를 갖는 것을 알 수 있다. 두 번째로는 풍향(ψWR-2nd run)과 풍속(VWR-2nd run)이 각각 10%정도를 차지하는 것으로 나타났으며, 세 번째로는 파고(Hw-2nd run)가 9.2%인 것으로 나타났다.
7. 결 론
본 연구는 축동력 계측시스템에 대한 불확실성 요소를 조사하고, ISO 15016에 제시된 방법을 바탕으로 전달동력에 대한 불확실성 해석을 몬테카를로 시뮬레이션을 통해 수행하였으며, 그 결과는 다음과 같다.
1) MCR 75%조건에서 수행한 왕복시운전에 대해 선속-동력 불확실성 해석결과 95%신뢰구간 (k=2)에서 바람에 의한 부가저항(RAA)의 확장불확도는 ±3.3%, ±12%이며, 파도에 의한 부가저항(RAW)의 확장불확도는 ±16%, 수온 및 밀도에 의한 부가저항(RAS)의 확장불확도는 ±3.3%로 나타났다.
2) 이상적인 조건으로 환산한 전달동력(PDid)의 확장불확도는 약 ±1.2%이며, 이를 선속으로 환산 시 약 ±0.1knot에 해당한다.
3) 전달동력에 대한 불확실성 요소 중 가장 큰 비율을 차지하는 요소는 축동력 계측 시스템이며, 전체 불확도 중 약 60%의 비중을 차지하는 것으로 나타났으며, 이는 축의 전단탄성계수 불확도를 ITTC(2002)의 자료에 근거하여 1.15%로 가정한 것에 기인된 것으로 보인다. 따라서 불확도를 줄이기 위해서는 축의 재료 물성치에 관한 실험적 연구 등이 필요할 것으로 보인다.
4) 본 논문에서 고려한 시운전의 경우 비교적 온화한 해양환경에서 수행되었고, 이로 인해 선박 전체 저항에서 외란에 의한 부가저항이 차지하는 비율이 크지 않았다. 결과적으로 시운전 시 선속-동력성능의 불확도에 있어 부가저항이 미치는 영향은 미미하였고, 축 동력계측 시스템이 지배적인 영향을 끼치는 것으로 분석되었다.
향후 외란의 영향이 큰 해상조건에서 수행된 시운전 자료를 바탕으로 불확실성 해석을 수행하여, 해상상태별로 전달마력에 대한 불확실성 해석이 필요할 것으로 보인다.
Acknowledgments
본 연구는 산업통상자원부 주관 "선박의 연료소비량 5%이상 절감을 위한 공기윤활시스템 개발 및 실해역 성능 검증[10073164]" 과제의 일부로 수행되었음을 밝힙니다.
References
- Brown, A. & Chen. 2002. Probabilistic method for predicting ship collision damage. Ocean Engineering International Journal, 6(1), pp.55-65.
-
Coleman, H.W., & Steele, W.G., 2009. Experimentation, validation, and uncertainty analysis for engineers, 3rd Ed., John Wiley & Sons, Inc.
[https://doi.org/10.1002/9780470485682]

-
Coraddu, A., Figari, M. & Savio S., 2014. Numerical investigation on ship energy efficiency by Monte Carlo simulation. Journal of Engineering for the Maritime Environment, 228(3), pp.220-234.
[https://doi.org/10.1177/1475090214524184]

- Han, M.C., 1994. On the development of speed trial data measurement and processing system. Journal of the Society of Naval Architects of Korea, 31(2), pp.22-28.
-
Han, B.W., Seo, J.H., Lee, S.,J., Seol, D.M. & Rhee, S.H., 2017. Uncertainty assessment for a towed underwater stereo PIV system by uniform flow measurement. International Journal of Naval Architecture and Ocean Engineering, 10(5), pp.596-608.
[https://doi.org/10.1016/j.ijnaoe.2017.11.005]

- Kamal, I.M., Binns, J., Bose, N. & Thomas, G. 2013. Reliability assessment of ship powering performance extrapolations using Monte Carlo methods. Third International Symposium on Marine Propulsor, Tasmaia, Australia, May, 2013.
- Kim, H.J., 2011. Uncertainty analysis for a calibration process of fringe projection profilometry by using Monte Carlo method, Master's Thesis, Division of Mechanical Engineering, KAIST.
- Kim, J.H., Kim, J.J., Kim, S.M., Kim, J.K., Choi. S.H., Lee, D.H. & Kim, B.K., 2017, A study on full scale application of Samsungs air lubrication system(SAVER Air) for an LNG carrier. The Korean Association of Ocean Science and Technology Societies, Busan, Republic of Korea, 19-20 April 2017.
- ISO JCGM 100, 2008a. Evaluation of measurement data - Guide to the expression of uncertainty in measurement.
- ISO JCGM 101, 2008b. Evaluation of measurement data - Guide to the expression of uncertainty in measurement - Propagation of distributions using Monte Carlo method.
- ISO 15016, 2015. Ships and marine technology - Guidelines for the assessment of speed and power performance by analysis of speed trial data.
- ISO 19030, 2016. Ships and marine technology - Measurement of changes in hull and propeller performance.
-
Insel, M., 2008. Uncertainty in the analysis of speed and powering trials. Ocean Engineering, 35, pp.1183-1193.
[https://doi.org/10.1016/j.oceaneng.2008.04.009]

- International Towing Tank Conference (ITTC), 2002. Final report and recommendations to the 23rd ITTC - The Speicialist Committee on Speed and Powering Trials.
- International Towing Tank Conference (ITTC), 2005. Recommended procedures and guidelines - Testing and extrapolation methods loads and responses, seakeeping experiments (7.5-02-07-02.1).
-
Park, D.W., Kim, M.G. & Kang, S.H., 2003. Uncertainty analysis for the resistance and self-propulsion test of ship model. Journal of the Society of Naval Architects of Korea, 40(5), pp.1-9.
[https://doi.org/10.3744/SNAK.2003.40.5.001]

-
Park, D.M., Kim, T.Y. & Kim, Y., 2012. Study on numerical sensitivity and uncertainty in the analysis of parametric roll. Journal of the Society of Naval Architects of Korea, 49(1), pp.60-67.
[https://doi.org/10.3744/SNAK.2012.49.1.60]

-
Park, D.M., Lee, J.H., & Kim, Y., 2015. Uncertainty analysis for added resistance experiment of KVLCC2 Ship, Ocean Engineering, 94, pp.143-156.
[https://doi.org/10.1016/j.oceaneng.2014.12.007]

-
Seo, S., Song, S. & Park, S., 2016. A study on CFD uncertainty analysis and its application to ship resistance performance using open source libraries. Journal of the Society of Naval Architects of Korea, 53(4), pp.329-335.
[https://doi.org/10.3744/SNAK.2016.53.4.329]

- Song, M.H., 2008. A Study on the Shaft Power Measurement of Diesel Engine Using Strain Gauge in Marine Vessel, Maters' Thesis, Division of Marine Engineering System Graduate School, Mokpo National Maritime University
-
Sun, L., Zhang, Q., Ma, G. & Zhang, T. 2017. Analysis of ship collision damage by combining Monte Carlo simulation and the artificial neural network approach. Journal Ships and Offshore Structures, 12, pp.S21-S30.
[https://doi.org/10.1080/17445302.2016.1258759]