유빙 하중을 받는 내빙 선박의 피로손상도 추정 Part II - 간이 해석법
Abstract
In this study, a simplified analysis method was developed to evaluate the fatigue damage of an ice-going ship under broken ice condition. The global ice load, which is essentially calculated at the design stage of the Arctic vessel, and the hull form information were used to estimate the local ice load acting on the outer-shell of the ship. The local ice load was applied to the finite element analysis model, and the Weibull parameters for the target fatigue point were derived. Finally, fatigue damage was evaluated by applying the S-N curve and the Palmgren-Miner rule. For the verification of the proposed method, numerical analyses using direct approach were performed for the same conditions. A numerical model that implements the interaction between ice and structure was introduced to verify the local ice load and the stress calculated from the proposed method. Finally, the fatigue analyses of the Baltic Sea for actual ice conditions were performed, and the results of the proposed method, the method using numerical analysis, and the LR method were compared.
Keywords:
Fatigue damage estimation, Ice-going vessel, Broken ice fields, Simplified analysis method, Ice-structure interaction키워드:
피로 손상도 평가, 내빙선, 유빙 지역, 간이 해석법, 빙-구조 연성1. 서론
선박이 점차 대형화되면서 파랑하중으로 인한 선박의 피로 문제는 여전히 선주들의 큰 관심을 끌고 있다. 이론과 해석 방법 등에 관한 수많은 연구가 활발히 진행되고 있으며, 관련된 평가절차 또한 잘 만들어져 있어 설계자들이 설계에 적용하는데 큰 어려움이 없다. 반면, 빙하중으로 인한 피로 문제는 아직도 연구가 미비한 실정이다. 이에 대한 가장 큰 이유는 빙하중으로 인한 피로 손상은 드물게 발생하며, 선박에 치명적이지 않다는 인식 때문이다 (Bridges et al., 2006). 하지만, 실제로 빙유기 피로 손상은 파도에 의한 피로 못지않게 자주 보고 되고 있으며 (Zhang et al., 2011) 또한, 북극 지역은 환경 오염에 매우 민감하여 어떠한 형태의 기름 유출도 허용되지 않기 때문에 각별한 주의가 필요하다.
지금까지 빙하중 기인 피로에 대한 연구는 주로 실선 계측 결과를 기반으로 수행되었다 (Bridges et al., 2006, Zhang et al., 2011, Suyuthi et al., 2013, Chai et al., 2018). 하지만, 비용 등의 문제로 다양한 경우에 대한 데이터를 얻을 수가 없고, 그 결과 또한 선박에 따라 달라지기 때문에 적용에 어려움이 있다. 또한, 로이드 선급을 제외하면 내빙 선박의 설계 시에 적용할 수 있는 지침이 없다. Lloyd's Register (2014)는 ShipRight FDA ICE에서 선체 구조물의 빙유기 피로 손상도를 평가하기 위한 결정론적 (deterministic) 피로 평가 절차를 제시하고 있다. 실선 계측 결과와 경험적 지식을 통해 비교적 간단하게 피로 손상도를 평가할 수 있도록 하였지만, 피로해석에 필요한 주요 변수들을 계산하는데 있어서 많은 가정을 포함하고 있어 적용에 한계가 있다. 따라서 내빙 선박의 피로 설계에 폭넓게 적용할 수 있는 절차 또는 지침의 개발이 필요하다.
본 연구에서는, 유빙 하중을 받는 내빙 선박에 대한 피로 손상도 평가를 위해 간이 해석을 이용한 방법을 개발하였다. 내빙 선박의 설계 단계에서 필수적으로 계산되는 전체 빙하중(global ice load)과 선형(hull form) 정보를 이용하여 선체 외판에 작용하는 국부 빙하중을 추정하였으며, 이를 유한요소해석 모델에 적용하여 대상 위치(target fatigue point)의 와이블 모수(Weibull parameter)를 도출하였다. 최종적으로 S-N 선도와 Palmgren-Miner rule을 적용하여 피로 손상도를 평가하였다. 제안된 방법의 검증을 위해 동일한 조건에 대한 수치해석을 수행하였다. 유빙과 구조물 사이의 상호작용을 구현하는 수치 모델 (Kim and Kim, 2018)을 도입하여 국부 빙하중과 이를 통한 기준 응력을 비교하였다. 마지막으로, 발트해(Baltic Sea)의 실제 얼음 조건에 대한 피로 해석을 수행하여 제안된 방법과 수치해석을 이용한 방법, 그리고 LR 방법의 결과를 비교하였다.
2. 해석 방법
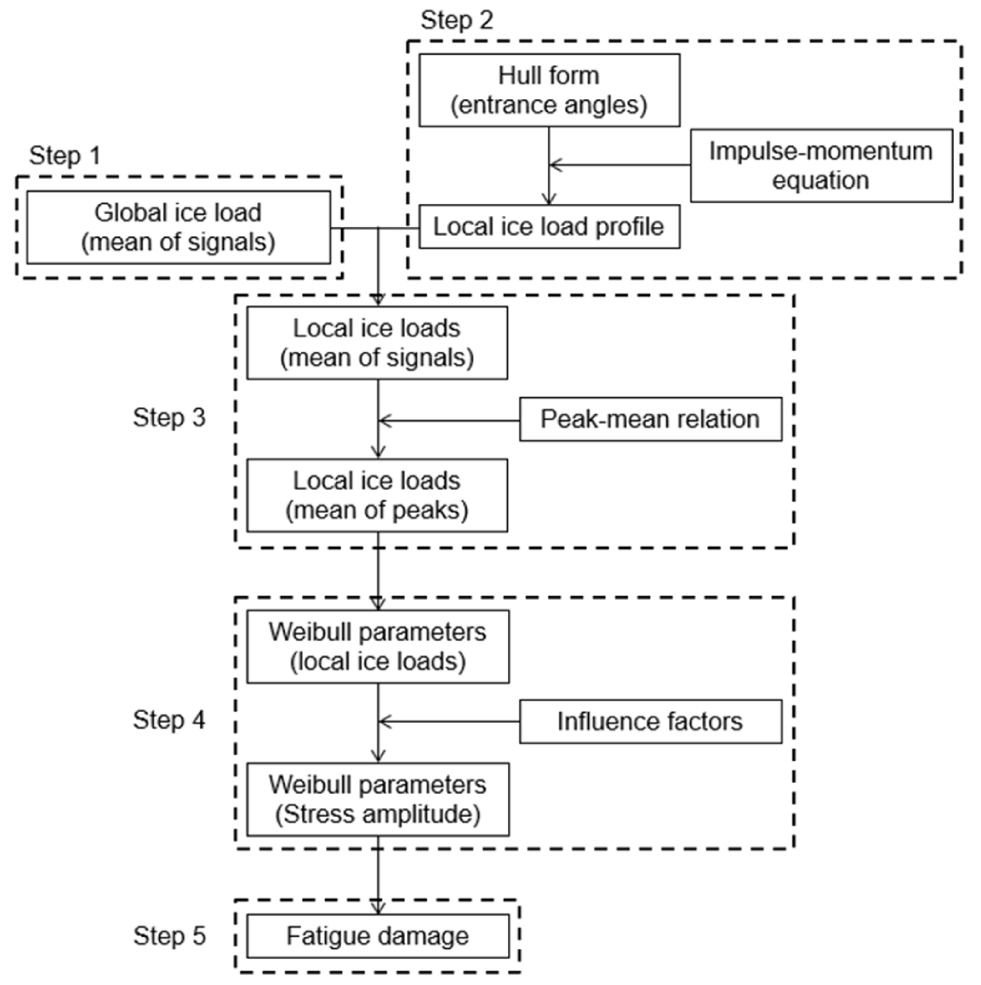
본 연구에서 개발된 간이 해석을 이용한 빙하중 기인 피로 평가법은 Fig. 1와 같이 모두 5개의 단계로 구성되어 있다. 전체 빙하중과 흘수선의 선형 정보, 환경 조건과 유한요소해석 모델이 있으면 해당 조건의 피로 손상도를 간단히 계산할 수 있다. 각 단계를 요약하면 아래와 같다.
- 1단계: 전체 빙하중의 계산
- 2단계: 국부 빙하중(local ice load) Profile 도출
- 3단계: 국부 빙하중 피크(peak)의 도출
- 4단계: 와이블 모수 도출
- 5단계: 피로 손상도 계산
2.1 전체 빙하중의 계산
전체 빙하중은 선박이 어떠한 형태의 얼음과 충돌했을 때 발생하는 전체 접촉력(total contact force)을 의미한다. 얼음으로 인해 선박이 받는 특정 시점의 접촉력을 모두 더한 값과 같기 때문에 선박의 선체 거더(hull girder)와 같은 대형 구조 요소(structural element)의 강도를 결정하는 중요한 요소가 되고 내빙 선박의 빙성능(performance in ice)을 결정하게 된다. 선박의 빙성능은 선박이 마주칠 수 있는 가장 가혹한 빙조건에 대한 것이 아니라 평균적인 조건에서의 성능에 대해 산정된다. 따라서, 등가 빙두께 (equivalent ice thickness) 개념이 도입되며, 전체 빙하중의 종방향(longitudinal) 성분으로 내빙 선박의 빙성능을 결정한다. 선박의 빙성능과 유사한 개념으로 사용되는 빙저항(ice resistance)은 전체 빙하중의 종방향 성분의 시간 평균(time average)을 의미한다 (Riska, 2010).
본 연구에서 개발된 계산법은 전체 빙하중의 계산으로부터 시작된다. 내빙 선박의 설계에서 필수적으로 고려되는 요소인 빙저항 계산 결과, 즉 전체 빙하중 종방향 성분의 시간 평균값을 통해 선체 각 위치에서의 국부 빙하중의 시간 평균을 도출하게 된다. 또한, 빙저항은 내빙 선박이 겪게 되는 평균적인 조건을 바탕으로 산출되기 때문에 이를 통해 계산된 국부 빙하중은 피로해석에 사용되기에 아무런 문제가 없다.
유빙 조건(pack ice condition)에 대한 빙저항 계산법은 여러 논문에서 소개된 바 있다 (Poznyak and Ionov, 1981, Enkvist, 1972). 특히, 최근 Kim et al. (2018)은 다양한 유빙 조건에 대한 빙저항을 경험식을 통해 도출해내는 In-house code(I-RES)를 개발하였다. 본 방법에서 사용되는 전체 빙하중은 사용자가 결정한 방법으로 계산한 빙저항 값을 의미한다.
2.2 국부 빙하중 분포 도출
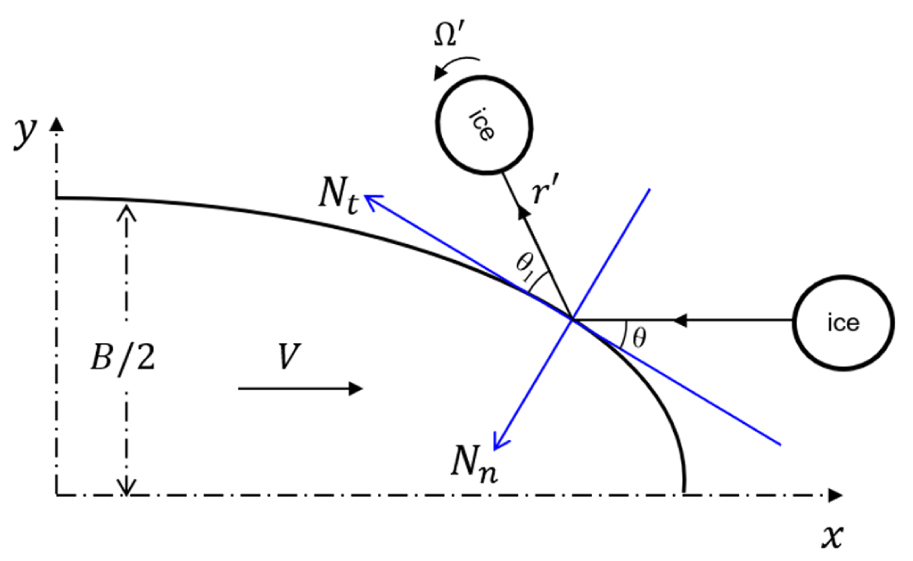
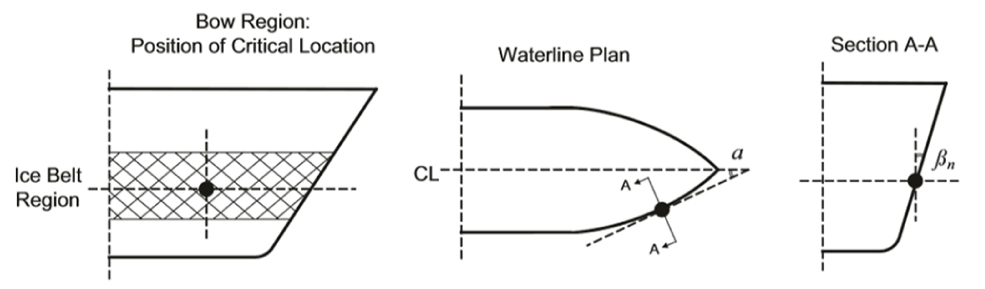
본 연구에서 고려된 선박과 유빙 간의 충돌 현상은 진행하는 선박이 유빙을 쳐서 밀어내는 과정이므로 충격량-운동량 식(impulse-momentum equation)으로 표현이 가능하다. 또한, Fig. 2와 같이 충돌 시에 선박의 선형에 따라 흘수선에서의 충돌 지점과 유빙 간에 입사각 (incident angle, )이 발생하므로, 하나의 유빙과 선박이 충돌한다고 가정하면 유빙에 대한 충격량-운동량 관계는 식(1), (2), (3)과 같이 정리할 수 있다.
| (1) |
| (2) |
| (3) |
여기서, 선박의 질량과 속도는 과 이며, 유빙의 질량과 속도는 과 이다. 과 는 각각 선박과 유빙의 충돌 이후 속도를 의미한다. 는 임펄스 의 접선방향 성분이며, 는 법선방향 성분이다. 와 은 각각 입사각과 반사각을 나타내며, 는 얼음의 관성 모멘트를 의미한다.
한편, 물체의 충돌 전후 속도의 비율을 나타내는 반발 계수(coefficient of restitution, )는 식(4)와 같이 정의될 수 있다. 유빙과 선박의 반발 계수는 얼음의 재료 특성과 선박의 강직도(rigidity)에 따라 결정된다. 본 연구에서는 Aboulazm (1989)의 논문에 따라 0.1을 적용하였다. 또한, 마찰 계수 는 식(5)와 같이 와 로 나타낼 수 있다.
| (4) |
| (5) |
식(1), (2), (3), (4), (5)를 이용하면 유빙과의 충돌에 의한 빙저항을 식(6)과 같이 표현할 수 있다. 자세한 식의 전개과정은 Aboulazm (1989)을 참고할 수 있다. 이 식은 유빙 조건을 항해하는 선박의 빙저항을 계산하기 위한 식으로 USCGS Katmai Bay의 빙저항을 계산하는데 사용되었고 실선 계측 결과와도 비교된 바 있다.
| (6) |
여기서, 는 밀집도를 나타낸다. 는 형상 계수인데, 원형으로 가정하면 와 동일한 값을 가진다. 는 유빙의 반지름이다.
한편, 식(6)으로부터 위치에 따른 국부 빙하중의 분포를 유추할 수 있다. 즉, 이 식에서 마찰이 없다고 가정하면 식(7)과 같이 고칠 수 있고, 이는 의 함수이므로 이 식을 통해 각 위치에 따른 무차원화된(dimensionless) 국부 빙하중 분포를 알 수 있다.
| (7) |
결국, 식(8)과 같이 국부 빙하중의 총합은 전체 빙하중과 같으므로 이 관계를 이용하면 흘수선상 임의 위치에서의 국부 빙하중의 산정이 가능하다.
| (8) |
여기서, 는 종방향 전체 빙하중의 평균을 의미한다. 따라서, 식(7)의 빙저항()을 그대로 사용할 수 있다. 은 국부 빙하중이 계산되는 패널(Panel)의 개수를 의미한다. 국부 빙하중은 흘수선의 선형을 따라 임의로 나누어진 패널에 대해 계산된다. 는 번째 패널에서 계산되는 국부 빙하중 평균의 종방향 성분을 의미한다.
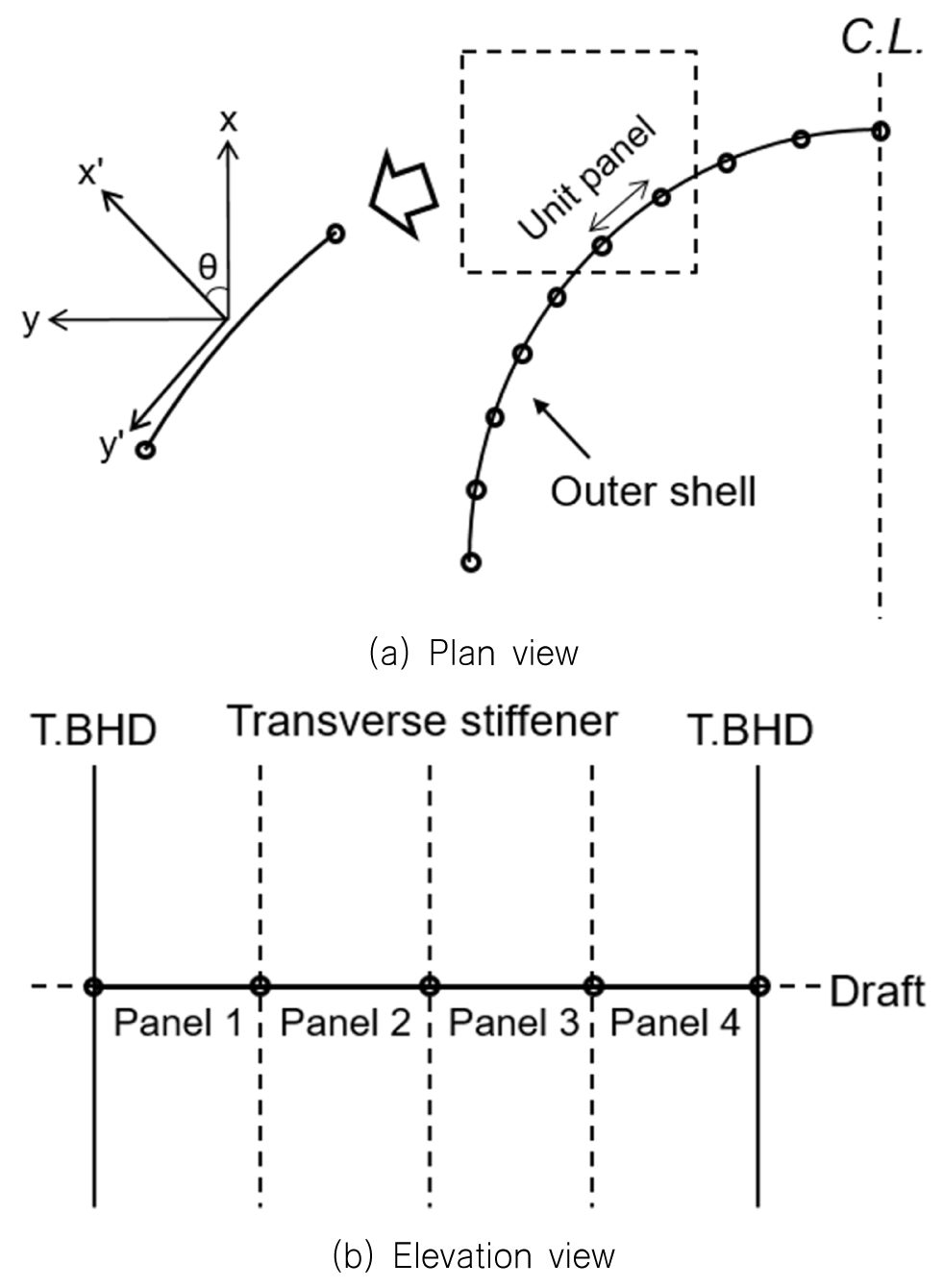
Fig. 3은 국부 빙하중의 계산을 위해 만들어지는 패널의 예를 보여준다. 패널은 빙하중을 받게 되는 선체 외판을 따라 만들어지며, 패널의 크기는 주로 내빙 선박의 횡 보강재(transverse stiffener) 간격에 따라 정해질 수 있다. 피로 손상도 계산 위치가 포함되는 양 수밀격벽(water-tight bulkhead)을 벗어난 지점은 대상 위치에 영향을 거의 미치지 않기 때문에 해당 수밀격벽 사이의 패널들을 더 촘촘하게 배치할 수 있다. 식(7)과 (8)을 통해 계산된 위치에 따른 국부 빙하중은 패널별로 평균하여 각 패널에 해당하는 하나의 값을 가지게 된다. 이때, 유빙의 두께의 영향은 무시한다. 또한, 여기서 계산된 국부 빙하중은 종방향 값이기 때문에 패널의 중심점에 대하여 수직인 방향()의 값으로 변환하게 된다.
2.3 국부 빙하중 피크의 도출
충격 하중의 형태를 보이는 빙하중의 특성으로 인해 빙하중으로 인한 응력의 피크값은 피로해석에서 응력 진폭으로 바로 사용될 수 있다. 2.2장에서 계산된 국부 빙하중은 신호(signal)의 평균값이기 때문에 이는 피크의 평균값으로 변환되어야 한다.
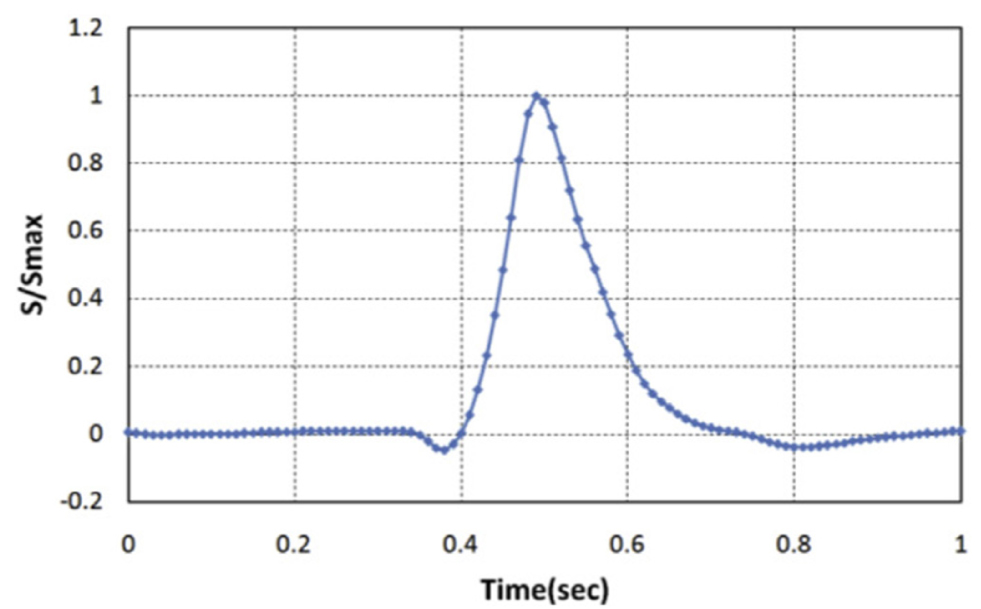
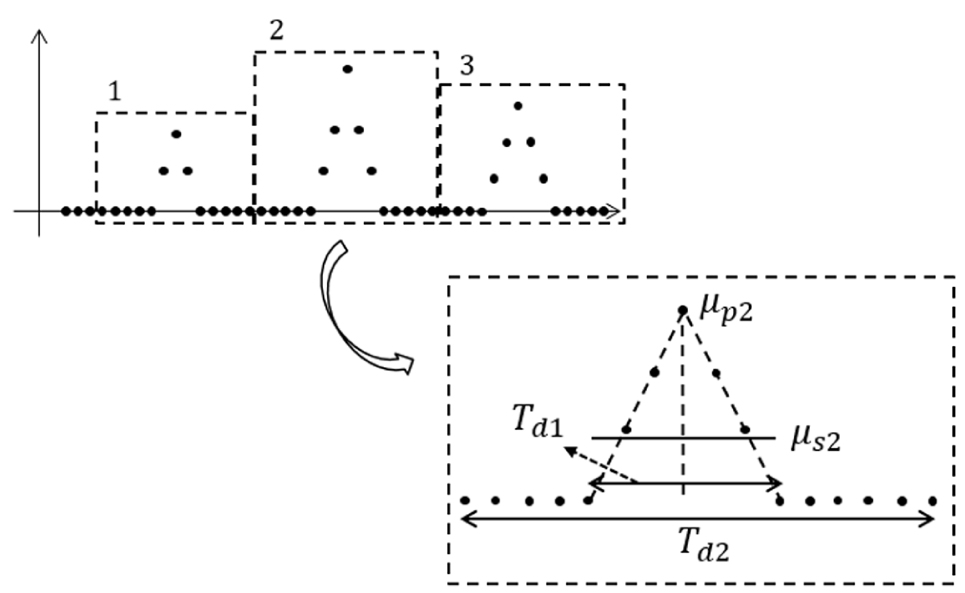
국부 빙하중이 Fig. 4와 같이 삼각 시계열의 패턴을 보인다고 가정하면, Fig. 5와 같이 하나의 충격에 대해 신호의 평균()과 피크의 평균() 간의 상관관계를 근사적으로 도출해 낼 수 있다. 먼저, 신호의 평균은 식(9)와 같이 각 충격에 해당하는 신호들을 평균하면 구할 수 있다. 여기서, 은 충격의 횟수이며, 은 번째 충격에 대한 신호의 평균을 의미한다. Fig. 5에서는 두 번째 충격에 대한 데이터를 예로 들어 그 관계를 설명하였다. 와 는 두 번째 충격에 대한 피크와 그로 인한 신호의 평균을 의미한다. 과 는 각각 피크의 폭(width)과 충격 지속시간 (impact duration)을 의미한다. 피크의 폭은 주로 얼음의 재료 물성치나 크기에 따라 결정되는 값이며, 충격 지속시간은 얼음의 두께나 밀집도, 선속 등에 따라 결정되는 값이다. Lee et al. (2016)은 아라온호의 정상 운항(normal operation)을 통해 계측된 신호의 피크의 폭을 정리하였다. 그 결과 대부분이 0.1초에서 0.4초 사이에 분포하며 최대값은 1초를 나타내었다. 또한, 피크의 폭을 응력과 선속과의 관계로 나타내었으므로, 사용자는 이를 바탕으로 상황에 맞는 값을 선택할 수 있다. Suyuthi et al. (2013)과 Bridges et al. (2006)은 충격 주파수(impact frequency)를 얼음의 두께와 선속의 함수로 나타내었다. 본 연구에서는 Bridges et al. (2006)의 식을 이용하여 충격 기간을 도출하였다. 과 가 결정되면, 삼각형 형태로 인해 와 와 관계도 식(10)과 같이 유도할 수 있다. 결론적으로 이 둘의 관계를 라고 하면, 피크의 평균()은 식(11)과 같이 구할 수 있으며, 이를 통해 신호의 평균을 피크의 평균으로 변환할 수 있다.
| (9) |
| (10) |
| (11) |
2.4 와이블 모수 도출
Olkin et al. (1980)에 따르면, 2-parameter 와이블 분포의 평균값()는 식(12)와 같이 척도 모수(scale parameter, )와 형상 모수(shape parameter, )표현할 수 있다.
| (12) |
빙하중에 대한 형상 모수의 경우, 여러 연구 (Zhang et al., 2011, Suyuthi et al., 2013)에서 두께의 함수로 간단히 계산할 수 있는 식을 제시하였다. 본 연구에서는 계산의 효율성을 위해 Zhang et al. (2011)이 제안한 식(13)을 이용하여 각 조건에 대한 형상 모수를 도출하였다. 각 조건에서의 와이블 형상 모수와 각 패널의 빙하중 피크의 평균값()을 안다면, 식(12)를 이용하여 각 패널에 해당하는 빙하중 피크의 척도 모수를 계산할 수 있다.
| (13) |
여기서, 는 등가 빙두께(equivalent ice thickness)를 의미한다 (Kujala, 1994).
피로 해석에서 사용되는 기준 값은 빙하중이 아니라 이로 인한 대상 위치에서의 응력 진폭이기 때문에 각 패널에서 계산된 빙하중의 와이블 척도 모수는 응력에 해당하는 값으로 변환되어야 한다. 충격하중을 받는 선박의 경우, 시스템이 선형이고 시간 불변(time invariant)이면 대상 위치의 응력은 식(14)와 같이 컨볼루션 적분(convolution integral)을 통해 시간 영역에서 표현할 수 있다.
| (14) |
여기서, 는 시간 에서 패널 의 국부 빙하중에 의한 대상 위치 의 응력을 나타낸다. 는 패널 에서 도출된 국부 빙하중이며, 는 패널 에 단위 하중을 가했을 때 발생하는 대상 위치 의 응력을 의미한다. 식(14)에서 계산된 응력은 선체 외판의 하나의 패널에 해당하는 값이기 때문에 대상 위치 의 응력 시계열 는 식(15)와 같이 계산될 수 있다.
| (15) |
여기서, 은 대상 위치에 영향을 미치는 패널의 총 개수를 나타낸다.
하지만, 외력의 주파수가 구조물의 고유 주파수와 멀어 준정적(quasi-static) 상태로 간주할 수 있을 때는 단순히 정적 해석을 통한 영향 계수(influence factor) 만으로도 변환이 가능하다. 내빙 선박의 경우 철강 소재로 만들어지며, 선수부에 많은 보강재를 설치하여 고유 주파수가 높기 때문에 일반적으로 0.1초 이상인 빙하중의 주파수와는 많은 차이가 날 것으로 판단된다. 따라서, 동적 효과(dynamic effect)가 거의 없을 것으로 판단하여 본 연구에서는 식(16)과 같이 정적 해석을 통한 영향 계수()를 이용하여 빙하중에 대한 척도 모수()를 응력의 척도 모수()로 변환하였다.
| (16) |
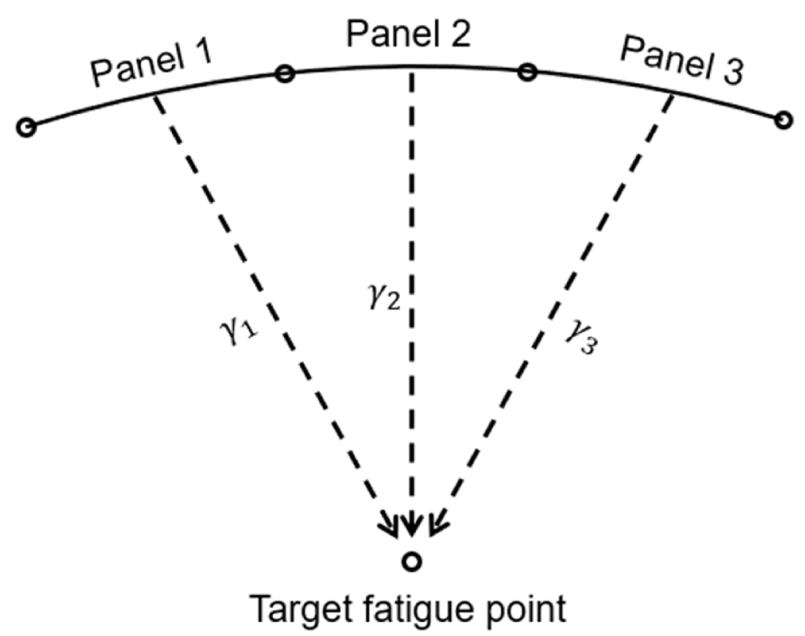
Fig. 6에서는 영향 계수를 이용하는 모습을 나타내었다. 각 패널이 서로 독립이라고 가정하면, 각 패널 에서 계산된 빙하중의 와이블 척도 모수는 식(17)과 같이 영향 계수에 의해 각 패널에 의한 대상 위치의 응력의 척도 모수로 그대로 변환이 가능하다. 여기서, 는 패널의 번호를 의미한다.
| (17) |
2.5 피로 손상도 계산
2-parameter 와이블 모델을 이용하는 경우, 응력 진폭 ()의 확률 밀도 함수는 식(18)과 같이 표현할 수 있으며, 이를 통한 피로 손상도()는 식(19)와 같다 (Suyuthi et al., 2013).
| (18) |
| (19) |
여기서, 와 은 S-N 선도 상의 모수(parameter)를 의미한다. 는 응력 싸이클의 총 횟수이며, 빙 충돌로 표현하면 식(20)과 같이 충돌 빈도()와 특정시간 동안 선박의 이동 거리()의 곱으로 나타낼 수 있다. 충돌 빈도는 실선 계측을 통해 도출한 Zhang et al. (2011)의 식을 적용하면 식(21)과 같이 계산할 수 있다.
| (20) |
| (21) |
을 정수로 가정하면, 식(19)는 이항정리와 감마함수를 이용하여 식(22)와 같이 정리할 수 있다 여기서, 는 감마함수를 의미한다 (Suyuthi et al., 2013).
| (22) |
2.4장에서 언급한 바와 같이 각 패널이 독립적이라고 가정하면, 식(23)과 같이 각 패널로부터 계산된 피로 손상도를 모두 더하면 대상 위치의 최종 피로 손상도를 계산할 수 있다.
| (23) |
여기서, 은 패널의 총 개수를 나타내며, 는 번째 패널에 대해 계산된 피로 손상도를 의미한다.
3. 수치해석 모델
2장에서 소개한 간이 해석을 이용한 방법의 검증은 동일한 대상에 대한 직접해석 모델을 이용하여 수행되었다. 본 장에서는 검증에 사용된 수치해석 모델에 대해 소개하고자 한다.
3.1 수치해석 기법
상용 유한요소해석 프로그램인 ABAQUS/Explicit를 이용하여 선박와 유빙의 상호작용(interaction)을 구현하였다. 자동 모델링 기법을 통해 임의의 크기, 두께, 모양 및 분포를 가지는 유빙을 모델링하였으며, 유빙의 충돌과 거동은 Kim and Kim (2018)에서 소개한 방법을 통하여 구현하였다.
3.2 유한요소 모델링
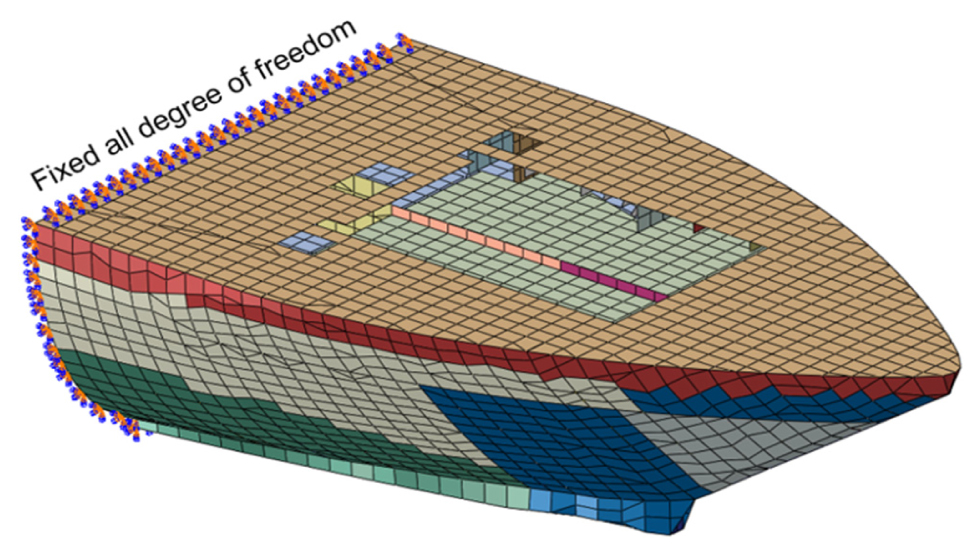
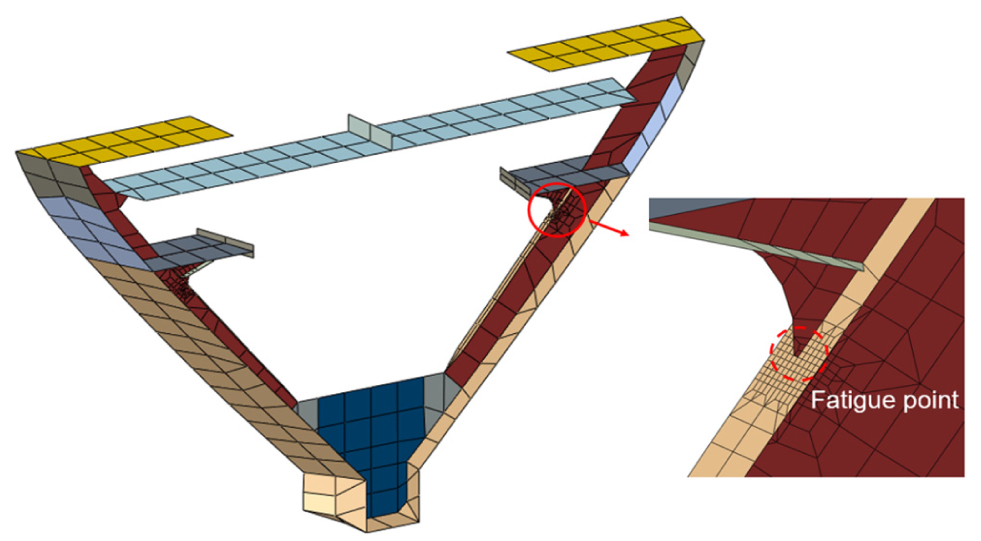
Fig. 7에서는 대상 선박인 한국 쇄빙연구선 아라온호(Araon)의 선수부 유한요소 모델을 나타낸다. 모델의 범위를 충분히 길게 하여 경계조건 효과를 최소로 하였으며, 선수부 절단면의 6자유도를 고정하였다. Table 1에서는 아라온호의 주요 요목을 나타낸다.
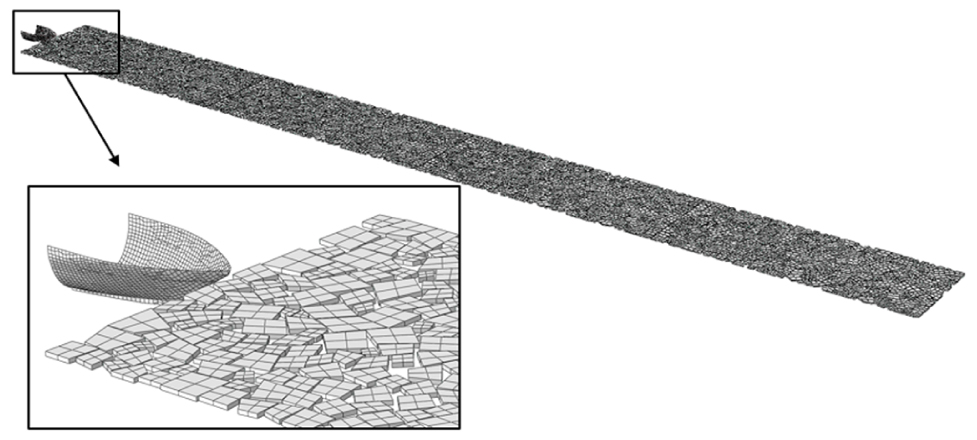
Fig. 8에서는 유빙과 선박 외판 모델을 나타내고 있다. 피로 해석 대상 위치에서 응력의 시계열은 선체 외판에서 계산된 압력의 시계열에 영향 계수를 곱하여 도출하였다. 영향 계수는 선체 외판의 각 요소에 단위 압력을 가했을 때 대상 위치(target fatigue point)에서 계산된 응력을 의미한다.
Fig. 9에서는 피로 해석을 위해 선정된 대상 위치의 유한요소 모델을 나타낸다. 스크리닝 해석을 통해 선수부에서 가장 큰 빙하중을 받는 위치를 선정하였으며, 핫스팟 응력(hot spot stress)의 계산을 위해 판두께 크기 요소로 상세 메쉬(fine mesh)를 수행하였다 (Det Norske Veritas, 2012).
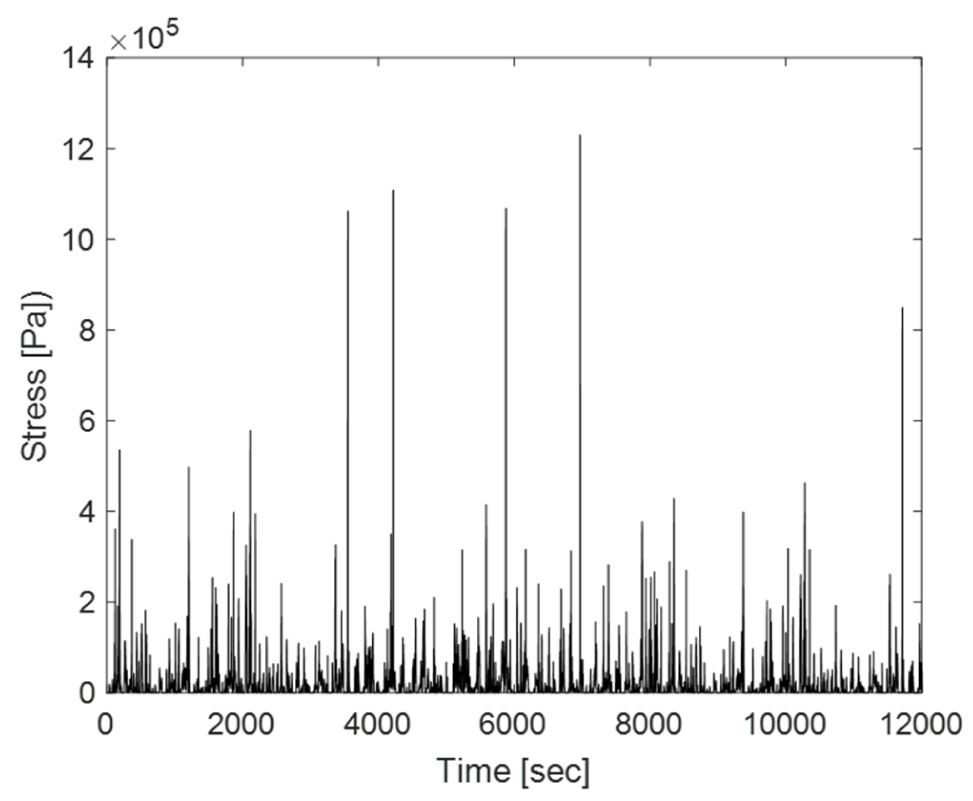
Fig. 10에서는 수치해석을 통해 계산된 대상 위치에서의 응력 시계열을 나타낸다. 임펄스 형태의 하중으로 인해 응력의 시계열 또한 매우 짧은 지속시간을 가지는 형태를 나타내고 있다.
4. 간이 해석을 이용한 방법의 검증
본 연구에서는 두 가지 방법을 이용하여 간이 해석을 이용한 방법을 검증하였다. 첫 번째 검증에서는 국부 빙하중에 대한 비교를 수행하였다. 수치모델을 이용해 계산된 국부 빙하중과 간이 해석 방법을 통해 추정된 국부 빙하중을 각 패널 별로 비교하였다. 두 번째 검증에서는 각 방법을 통해 계산된 기준 응력을 비교하였다. 국부 빙하중과 그에 따른 와이블 척도 모수가 각 패널 별로 계산되어 하나의 기준 응력을 도출하기 까다롭기 때문에 먼저 이를 이용한 피로 수명을 도출 한 후 그 결과에 대한 세제곱근을 비교에 적용하였다. 하나의 기울기()를 가진 S-N 선도를 이용하여 피로 손상도를 계산할 경우 피로 손상도는 기준 응력의 승에 비례하기 때문이다. 본 연구에서는 Det Norske Veritas (2012)를 참고하여 기울기 3을 적용하였다. 비교에 사용된 계산 조건은 Table 2에 나타내었다.
4.1 국부 빙하중 비교
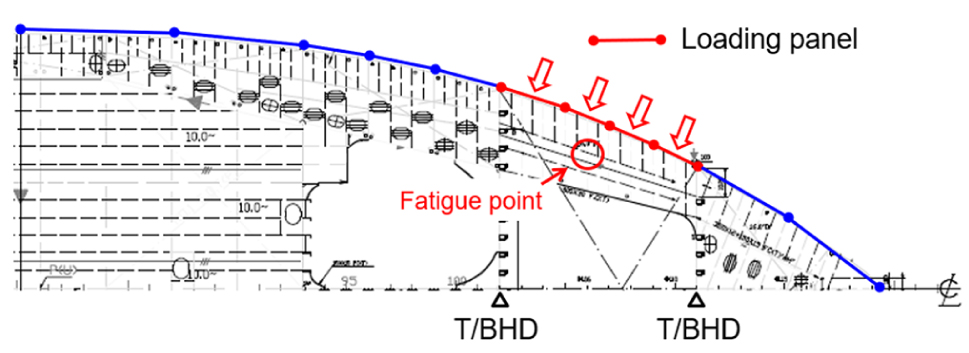
먼저 Fig. 11과 같이 흘수선 높이의 선체 외판을 따라 패널을 생성하였다. 대상 위치가 속해 있는 양쪽 T/BHD 사이를 4개의 패널로 나누고, 그 외 부분은 하중이 직접 적용되지 않기 때문에 선형을 고려하여 적당한 크기의 패널을 생성하였다.
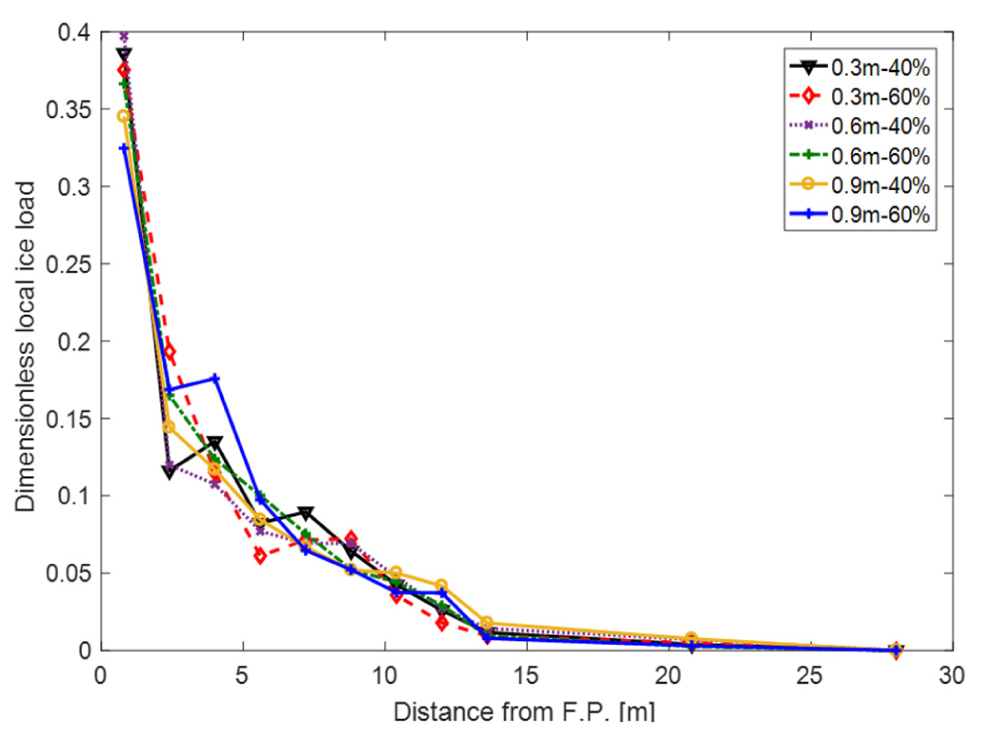
먼저, 각 조건에 대해 수치해석을 통해 도출된 요소별 하중을 패널 위치별로 구분하였다. 그리고 각 패널 에 해당하는 요소들의 하중을 평균한 후 전체 하중으로 나누어 Fig. 12와 같이 무차원화하여 나타내었다. Fig. 12의 각 점은 패널의 중심점을 나타낸다. 그 결과 국부 빙하중의 분포는 해석 조건에 상관없이 F.P.로 부터의 거리의 함수로 표현 될 수 있다는 것을 발견하였다. 선박의 선형에 의해 F.P.로 부터의 거리는 입사각으로 변환할 수 있기 때문에, 국부 빙하중이 입사각의 함수가 될 수 있다는 것을 알 수 있다. 따라서, 국부 빙하중의 분포는 선형에 의해 정해질 수 있다는 본 연구의 가정을 잘 뒷받침한다고 할 수 있다.
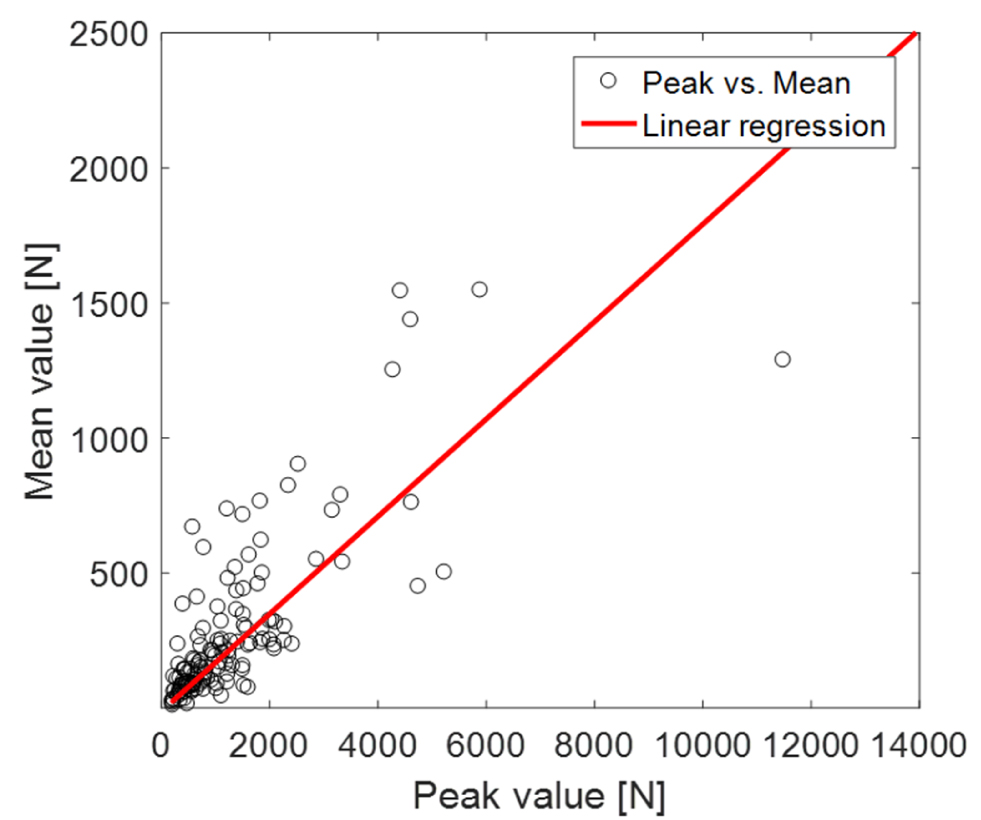
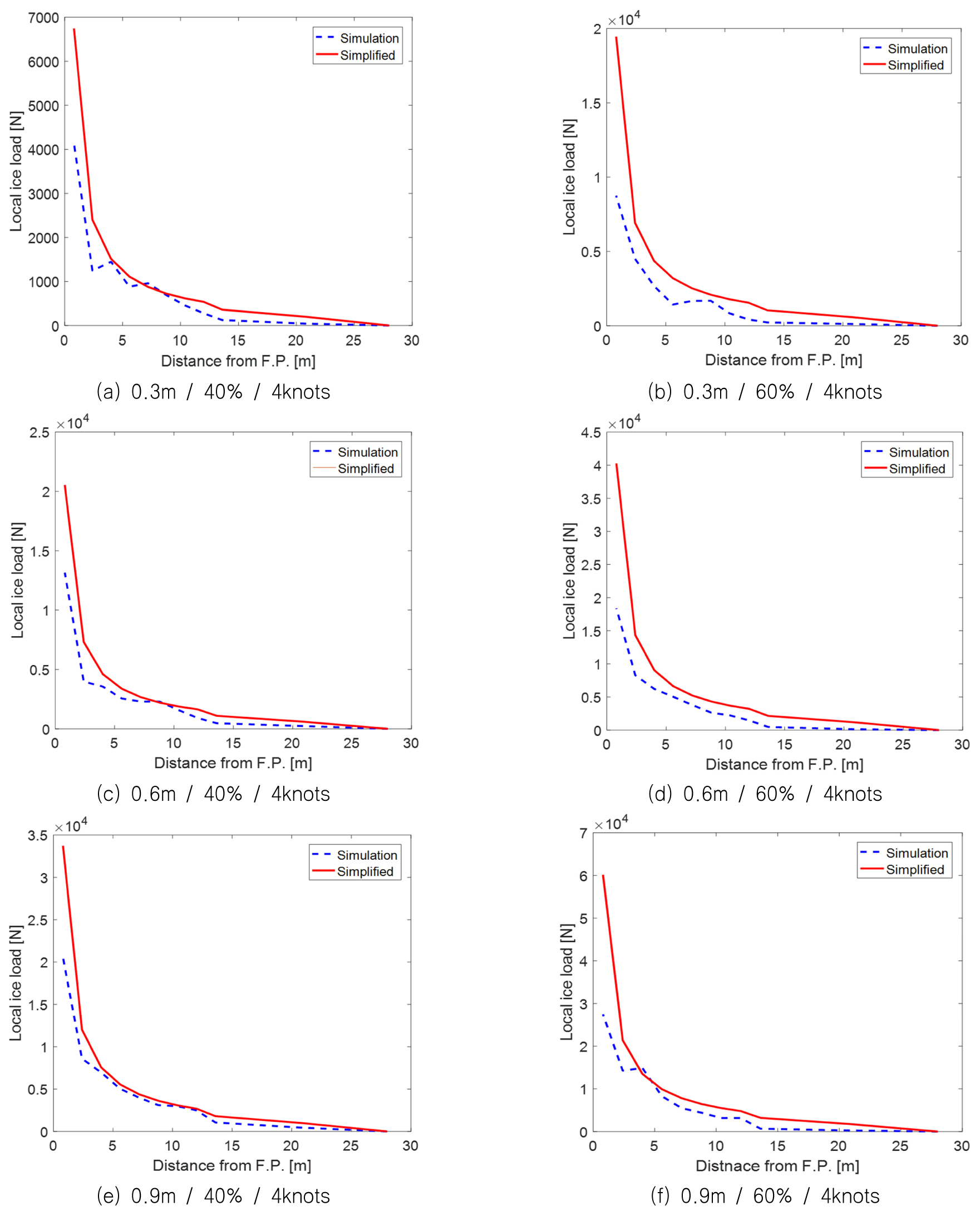
간이 해석 방법을 통해 국부 빙하중을 산정할 때는 식(7)을 이용해 국부 빙하중의 분포를 도출한 후 식(8)과 같이 국부 빙하중의 평균을 계산한다. 본 비교에 사용된 전체 빙하중은 3장에서 소개한 수치해석 결과로부터 얻은 값을 사용하였다. 신호의 평균을 피크의 평균으로 변환하기 위해 사용된 식(11)의 역시 수치해석을 통해 도출하였다. 를 얻기 위해 수치해석 결과를 통해 도출한 국부 빙하중의 시계열에 대해 Fig. 13과 같이 하나의 신호에 대한 피크와 평균값을 x-y 평면에 나타내어 그 관계를 알아보았다. 수치해석의 무작위성(randomness)로 인해 피크-평균 관계에서 다소 큰 산포도를 보이지만 전체적으로 5.5:1의 비율을 보이고 있다. 본 검증에서는 이 결과를 적용하여 국부 빙하중 신호의 평균을 피크의 평균으로 변환하였다. Fig. 14에서는 각 조건에 따른 국부 빙하중의 분포를 수치해석을 이용한 결과('Simulation')와 간이 해석 방법을 이용한 결과('Simplified')로 비교하여 나타내었다. 간이 해석을 이용한 결과가 전반적으로 큰 경향을 보이긴 하지만, 두 결과가 비교적 잘 일치하는 것을 확인할 수 있다.
4.2 기준 응력의 비교
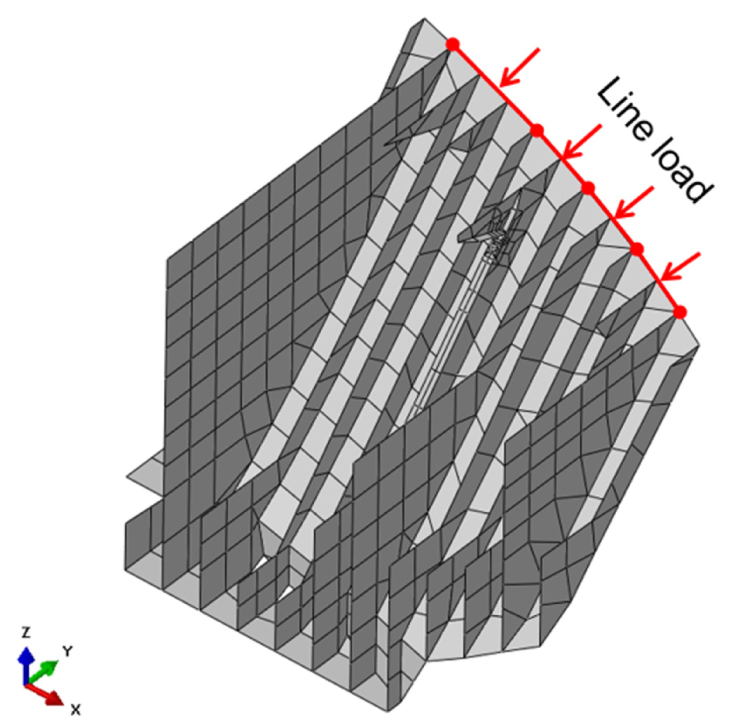
두 번째 검증에서는 각 방법으로 도출된 기준 응력을 비교하였다. 먼저, 4.1장에서 계산된 각 패널에 대한 국부 빙하중 피크의 평균을 Fig. 15와 같이 유한요소해석 모델에 적용하여 핫스팟 응력을 계산하였다. 이 때, Fig. 11의 패널에 해당하는 위치에 선하중(line load)의 형태로 하중을 적용하였다. 하중을 받는 패널을 벗어난 부분은 대상 위치에 미치는 영향이 미비할 것으로 판단하여 해석에 고려하지 않았다. 실제로 본 모델의 경우 T/BHD를 벗어난 곳과 대상 위치와 가까운 패널에 동일한 하중을 가하였을 때, 40배 이상의 응력차를 보였다.
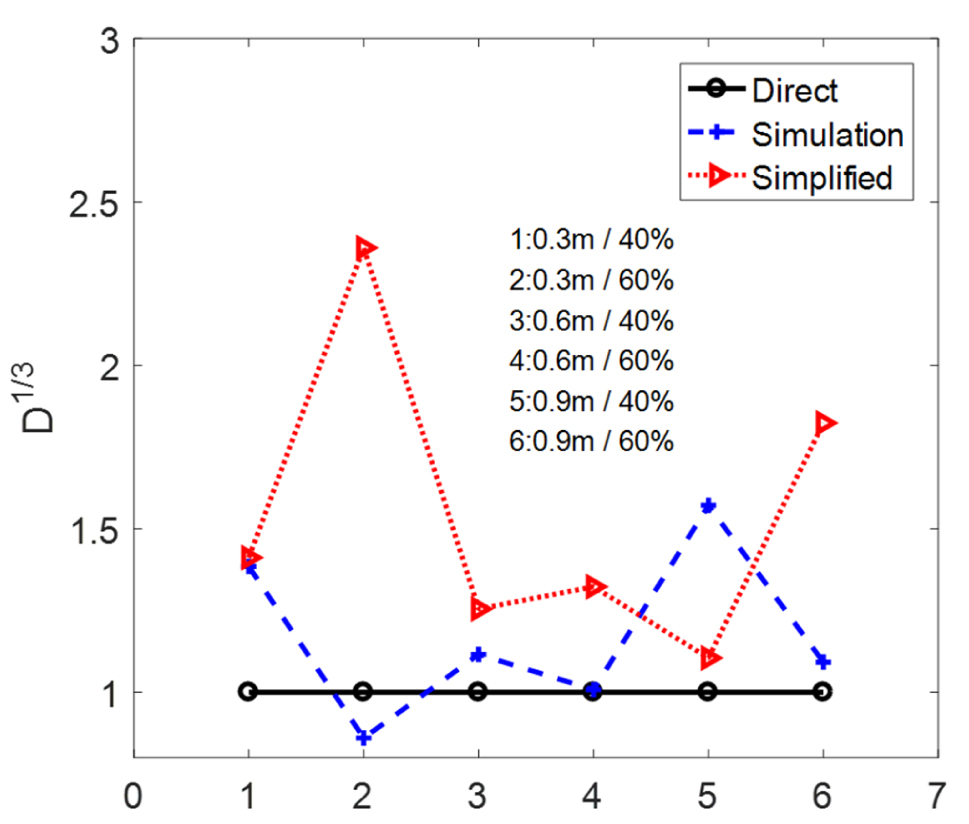
계산된 핫스팟 응력은 국부 빙하중의 평균으로부터 선형변환하여 도출하였기 때문에 식(12)에서 응력의 평균()에 해당한다고 할 수 있다. 따라서, 식(13)에서 계산된 와이블 형상 모수를 이용하면 와이블 척도 모수로 변환될 수 있으며, 이를 이용하면 식(22)와 (23)에 따라 대상 위치에서의 피로 손상도를 계산할 수 있다. 앞서 언급한 바와 같이 각 방법을 통한 기준 응력을 비교하기 위해 Fig. 16과 같이 계산된 피로 손상도의 세제곱근을 이용하여 비교에 적용하였다. Fig. 16에서는 세 가지 방법에 대한 결과를 비교하였다. 첫 번째 방법(‘Direct')에서는 계산에 필요한 2개의 와이블 모수와 유빙의 충돌 횟수를 수치해석을 통한 직접 계산으로 도출하였다. 두 번째 방법(’Simulation')에서는 와이블 척도 모수를 도출할 때 Fig. 14에서 나타낸 ‘Simulation' 값을 유한요소해석 모델에 적용하여 계산하였다. 다시 말하면, 수치해석을 통해 계산된 각 패널 별 국부 빙하중을 이용하여 와이블 척도 모수를 도출한 결과이다. 이 때 사용된 와이블 형상 모수와 충돌 횟수는 수치해석 결과가 아닌 이론식을 통하여 도출하였다. 세 번째 방법(’Simplified')에서는 본 연구에서 제안한 간이 해석 방법을 이용하였다. 두 번째 방법과 마찬가지로 와이블 형상 모수와 충돌 횟수는 이론식을 적용하였다.
각 방법을 통한 기준 응력을 ‘Direct' 결과를 기준으로 비교하기 위해 모든 결과를 ’Direct' 결과로 나눈 값으로 나타내었다. 결과적으로, 'Simplified'가 ‘Simulation’에 비해 전체적으로 더 큰 차이를 나타내는 것을 볼 수 있다. 각 방법에 대한 결과의 차이를 Table 3에 정리하여 나타내었다. Case2의 경우 'Simplified'에서 최대 136%의 차이를 나타내었는데, 이는 Fig. 14(b)에서도 볼 수 있듯이 대상 위치가 있는 5m 근처에서 큰 차이가 나기 때문으로 판단된다.
5. 실제 조건에 대한 피로 손상도 분석
5.1 해석 조건
본 논문에서 소개한 방법들을 이용하여 실제 환경조건에 대한 대상 선박의 피로 손상도를 계산하였다. 적용된 루트(route)는 발트해의 케미 루트(Kemi route)이며 Lloyd's Register (2014)에 따라 헬싱키와 케미를 연간 3.5회 왕복하는 것으로 가정하였다. 상세한 환경조건은 Table 4에 나타내었고, 피로 손상도의 허용 기준(acceptance criteria)은 파랑하중에 의한 피로 손상도를 고려하여 0.5로 가정하였다.
5.2 각 방법을 이용한 피로 손상도 비교
수치해석을 통한 방법과 간이 해석을 이용한 방법, 그리고 LR 방법을 이용하여 해당 루트의 피로 손상도를 비교하였다. 수치해석을 이용한 방법과 간이 해석 방법은 4장에서 언급한 ‘Direct' 방법과 ’Simplified' 방법과 동일하다. LR 방법에 사용되는 선박의 기하학적 정보는 Table 5와 Fig. 17에 나타내었다.
S-N선도의 적용 시, 수치해석을 통한 방법과 간이 해석 방법의 경우는 Det Norske Veritas (2012)에서 제안하는 핫스팟 응력을 위한 선도인 D-curve를 적용하였고, LR 방법의 경우는 공칭응력를 적용하므로 용접부의 형상에 따라 F2-curve를 적용하였다 (Lloyd's Resister, 2014).
Table 6에서는 각 조건에 대한 피로 손상도 결과를 정리하였다. 여기서, DDI는 수치해석을 통한 피로 손상도, DSI는 간이 해석 방법을 통한 피로 손상도를 의미하며, DLR은 LR 방법을 통한 결과를 의미한다. Table 7에서는 각 방법으로 계산된 최종 피로 손상도율을 비교하였다. 그 결과, 간이 해석 방법으로 계산한 결과가 수치해석을 이용한 방법으로 계산된 결과에 비해 3배가량 큰 피로 손상도를 도출한 것을 볼 수 있다. 이는 Table 3에서 도출된 기준 응력의 차이의 평균인 54.7%를 3승하여 피로 손상도에 해당하는 차이로 바꾼 값(3.7배)과 유사한 결과라고 할 수 있다. 또한, 비교적 보수적인 결과를 도출할 것으로 예상되는 LR 방법과 30% 이하의 차이를 보였으며, 간이 해석을 이용한 방법이 오히려 더 보수적인 결과를 도출한 다는 것을 알 수 있다.
6. 결 론
본 연구에서는 유빙 조건을 항해하는 내빙 선박의 피로 손상도 평가에 있어서 간이 해석을 이용한 방법을 제안하였다. 상기의 연구 결과를 토대로 다음과 같은 결론을 도출할 수 있었다.
∙내빙 선박의 설계 시에 필수적으로 계산되는 전체 빙하중과 선형 정보를 이용하여 선체 외판에 작용하는 국부 빙하중을 추정하였으며, 제안된 피크-평균 관계를 통해 빙하중 신호의 평균을 피크의 평균으로 변환하였다.
∙도출된 국부 빙하중 피크의 평균을 이용하여 와이블 모수를 도출 한 후 유한요소해석 모델에 적용하여 대상 위치의 응력에 대한 값으로 변환하였다. 최종적으로 S-N 선도와 Palmgren-Miner rule을 이용하여 피로 손상도를 평가하였다.
∙제안된 방법의 검증은 동일한 대상에 대한 수치모델을 이용하여 수행되었다. 수치모델에서는 유한요소해석을 이용하여 선박과 유빙의 상호작용을 구현하였으며 이를 통해 선체 외판에 작용하는 국부 빙하중과 대상 위치에서의 응력의 시계열을 도출할 수 있었다.
∙두 가지 방법으로 제안된 방법을 검증하였다. 먼저, 국부 빙하중에 대한 비교를 수행하였다. 수치모델을 통해 계산된 값과 제안된 방법을 통해 추정된 값을 각 패널별로 비교하였다. 그 결과, 제안된 방법을 통한 값이 다소 보수적이나 전체적으로 유사한 결과를 보였다. 다음으로, 기준 응력에 대한 비교를 수행하였다. 각 방법을 통해 계산된 국부 빙하중을 가하여 대상 위치에서의 피로 손상도를 계산한 후 세제곱근하여 비교에 적용하였다. 그 결과, 제안된 방법이 평균 54.7% 만큼 큰 값을 도출하였다.
∙마지막으로 제안된 방법을 통해 발트해의 실제 조건에 대한 피로 손상도 평가를 수행하고, 수치해석을 통한 결과와 LR 방법을 이용한 결과와 비교하였다. 결과적으로, 제안된 방법은 수치해석을 통한 방법에 비해 약 3배 가량 보수적인 결과를 도출하였다. 또한, LR 방법과 비교했을 때는 30%가량 큰 결과를 얻을 수 있었다. 간이 해석을 통해 간편하게 결과를 얻을 수 있는 대신 다소 보수적인 결과를 도출하는 것을 알 수 있다.
본 연구에서 제안한 간이 해석법을 이용한 방법의 경우 간단하고 신속하게 빙유기 피로손상도를 평가할 수 있는 장점이 있지만, 계산과정에 몇몇 가정이 포함되어 있어 적용에 주의를 요구한다. 평균을 피크로 변환하는 과정과 같이 결과에 중요한 영향을 미치는 부분은 추후 연구를 통해 추가 검증되어야 할 것으로 판단된다.
Acknowledgments
본 연구는 산업통상자원부의 산업핵심기술개발사업(10063417, ARC7 극지 환경용 해양플랜트 내빙구조 설계기술 개발)의 재정지원을 받아 수행된 연구 결과의 일부임을 밝힙니다.
References
- Aboulazm, A., 1989. Ship resistance in ice floe covered waters. Ph.D. Memorial University of Newfoundland, Newfoundland, Canada.
- Bridges, R., Riska, K. & Zhang, S., 2006. Fatigue assessment for ship hull structures navigating in ice regions. Proceedings of the Icetech 2006. Banff. Canada.
-
Chai, W., Leira, B. & Naess, A., 2018. Short-term extreme ice loads prediction and fatigue damage evaluation for an icebreaker. Ships and Offshore Structures, 13.
[https://doi.org/10.1080/17445302.2018.1427316]

- Det Norske Veritas, 2012 DNV Recommended Practice, Fatigue Design of Offshore Steel Structures, DNV-RP-C203.
- Enkvist, E., 1972. On the Ice Resistance Encountered by Ships Operating in the Continuous Mode of Ice Breaking, Report No.24. The Swedish Academy of Engineering Sciences in Finland, Helsinki.
-
Kim, H. S., Jeong, S., Woo, S. & Han, D., 2018. Study on the procedure to obtain an attainable speed in pack ice. International Journal of Naval Architecture and Ocean Engineering, 10(4), pp.491-498.
[https://doi.org/10.1016/j.ijnaoe.2017.09.004]

-
Kim, J. & Kim, Y., 2018. Numerical simulation on the response of moored semi-submersible under ice load. Journal of Ocean Engineering and Technology, 32(3), pp.177-183.
[https://doi.org/10.26748/KSOE.2018.6.32.3.177]

-
Lee, J., Kwon, Y., Rim, C. & Lee, T., 2016. Characteristic analysis of local ice load signals in ice-covered waters. International Journal of Naval Architecture and Ocean Engineering, 8(1), pp. 66-72.
[https://doi.org/10.1016/j.ijnaoe.2016.01.001]

- Lloyd's Register, 2014. ShipRight Design and Construction, Fatigue Design Assessment - Application and Notations.
- Olkin, I., Gleser, L. & Derman, C., 1980. Probability, models and applications. New York: Macmillan Publishing Co., Inc..
- Poznyak, I.I. & Ionov, B.P., 1981. The division of ice breaking resistance into components. In: Proceedings of the Sixth STAR Symposium. SNAME, New York, pp.249e252.
- Riska, K., 2010. Ship-ice interaction in ship design: theory and practice, Encyclopedia of Life Support Systems (EOLSS), Developed under the Auspices of the UNESCO, Eolss Publishers, Oxford, UK.
-
Suyuthi, A., Leira, B. J. & Riska, K., 2013. Fatigue damage of ship hulls due to local ice-induced stresses. Applied Ocean Research, 42, pp.87-104.
[https://doi.org/10.1016/j.apor.2013.05.003]

- Zhang, S., Bridges, R. & Tong, J., 2011. Fatigue design assessment of ship structures induced by ice loading - an introduction to the ShipRight FDA ICE procedure. Proceeding of the Twenty-First International Offshore and Polar Engineering Conference, Maui, Hawaii, pp.1082-1086.