잠수함시뮬레이터의 운동재현필터: 제1보. 기본이론 및 일반적용

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Most of vehicle simulators, such as airplanes, cars, and ships have motion bases that provide the motion feeling of vehicle motions to the trainee or user. However, the motion base has a limit on its movement due to its constrained mechanism, so the motion of it is somewhat different from the real motion. Low frequency components of the vehicle motion make large movements, but a person feels these movements small. Therefore, the 'washout filter' that wash the low frequency components of signal (so the signal tends to its origin slowly) was developed in the field of airplane simulator. The 'classical washout filter' uses the forces acting on trainee as its inputs, but it is hard to determine many parameters in it appropriately. This paper proposed a new motion filter of a simulator: uses the motion states as inputs, provides the method of determining parameters, homing action, and measurement method of motion fullness. Using this proposed motion filter, the forces acting on the trainee on both real vehicle and simulator are compared, and the results are assessed by the ratio of fullness of motion realization. This part 1 paper deals with the basic theory and general applications, and the part 2 will deal with applications to a BB2 submarine.
Keywords:
Submarine, Simulator, Washout filter, Motion base, Motion feeling키워드:
잠수함, 시뮬레이터, 워시아웃필터, 운동재현기, 운동체감1. 서 론
시뮬레이터는 대상체의 특성을 훈련자 또는 연구자에게 잘 묘사하여 보여주거나 느끼게 하는 장비이다. 용도에 따라 연구용과 훈련용으로 구분을 할 수 있지만, 실제의 적용에서는 훈련용 시뮬레이터가 가장 많이 활용되고 있다. 1970년대부터 비행훈련용 시뮬레이터(flight simulator)가 활용되어 현재 비행훈련용 시뮬레이터는 항공사의 규정에 포함되어 필수적으로 사용되고 있다. 훈련용 시뮬레이터는 실제 대상체를 가지고 훈련을 하기에는 위험하거나, 또는 긴급 상황에 대한 훈련이 필요한 경우에 효과적으로 사용된다.
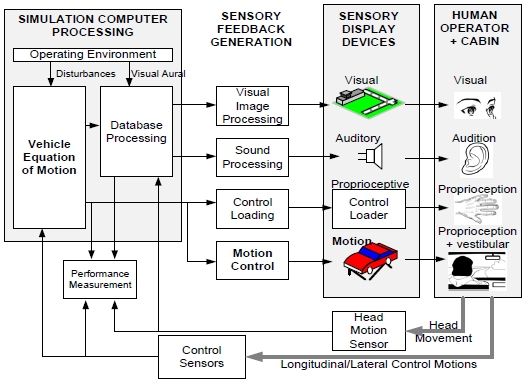
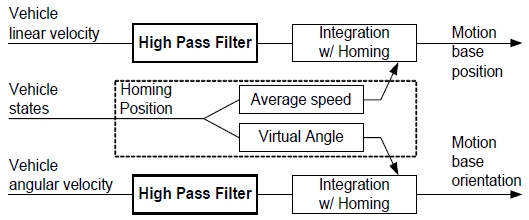
시뮬레이터에서 가장 많이 사용되는 기법은 가시화 시뮬레이터이다. 인간의 정보 습득은 대부분 시각을 통하여 이루어지므로 그 중요성은 상당히 크고, 효과도 또한 크다. 그러나 몰입감을 위해서는 운동도 함께 재현하는 것이 바람직하다. 대상체의 특성에 따라 운동의 재현이 필수적인 시뮬레이터도 있다. 비행훈련용 시뮬레이터도 이에 속한다. 어떤 기기를 동작하면 대상체가 어떻게 움직이고, 어떤 느낌인지를 탑승자에게 알려주면서 기기 작동 훈련을 할 필요가 있기 때문이다. 잠수함의 경우에는 외부환경이 보이지 않아, 장비의 작동상태를 계기만으로 보여주게 되는데, 이것만으로는 실제 잠수함에 타고 있는지를 느끼게 해줄 수 없으므로, 운동재현을 하여 잠수함을 동작시키는 훈련을 하는 것이 바람직하다. Fig. 1은 Allen (2011)이 설명한 현대적인 시뮬레이터의 전체 구조도이다.
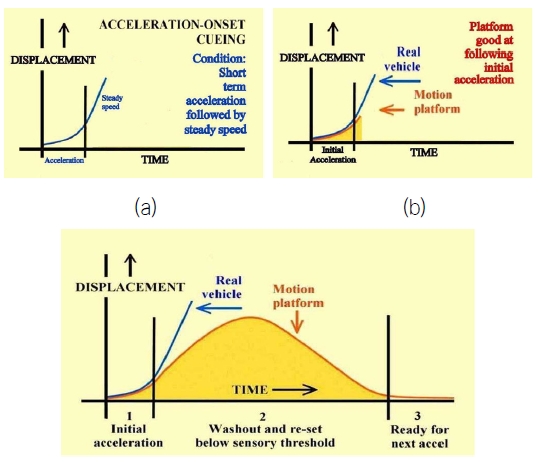
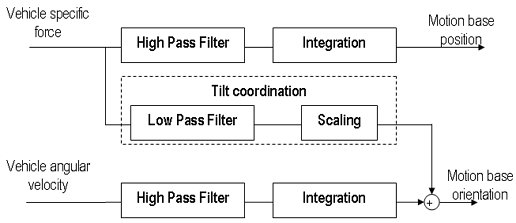
시뮬레이터는 그것이 가지는 운동한계 때문에 실제 대상체의 운동을 그대로 재현할 수가 없다. 따라서 1970년대부터 사용하여 온 기법은 탑승자가 받는 힘을 유사하도록 느끼게 하는 방향으로 시뮬레이터의 운동을 재현하는 방법이다. 인간은 주로 전정기관(vestibular system)을 통하여 운동을 느낀다고 가정하여, 이석기관(otolith)에서 느끼는 힘과, 세반고리관(semicircular canals)에서 느끼는 회전각속도를 유사하게 만들어 내는 것을 기본으로 한다. 선형가속도에 의한 힘은 시뮬레이터상의 운동한계 때문에 크게 부족할 수밖에 없으므로, 시뮬레이터를 기울여서 중력가속도에 의한 힘으로 부족한 부분을 보상하는 기법을 사용한다. 전정기관과 인간의 운동감지에 대한 연구들이 여러 연구자들에 의하여 이루어져 있다 (Reid and Nahon(1985)에 잘 정리되어 있다). 비행훈련용 시뮬레이터의 운동재현 신호에 대하여서는 Schmidt and Conrad (1970), Reid and Nahon (1985) 등에 의하여 소개되어 있다. 이 기법을 ‘classical algorithm’이라고 부른다. 고주파통과필터(High-pass Filter)를 사용하였으며, 이것을 저주파성분은 제거한다는 의미인 ‘Washout Filter’라고도 부른다. 이 개념은 Davison (2018)에 의하여 Fig. 2와 같이 그림으로 잘 설명되어있다. 이 기법을 좀 더 개량하기 위하여, ‘adaptive’, ‘optimal’, ‘predictive’ 기법들이 연구되어 왔다 (Colombet et al., 2008; Stroosma, 2013; Fang, 2014; Affan, 2019; Natal, 2019). Colombet (2008)은 Fig. 3와 같이 ‘Classical washout filter’를 설명하였다.
본 연구에서는 운동재현에 사용되는 고주파통과필터(high-pass filter)의 특성에 대하여 알아보고, 필터의 입력으로 변위, 속도, 가속도를 입력할 때의 차이에 대하여 계산하여 차이가 없음을 보이고, 이에 따라 속도를 입력으로 하는 운동재현필터(motion filter)를 제안한다. 제안하는 필터는 운동기반(motion-oriented)기법으로 파라미터 설정이나 실제 구현시 동역학 지식, 경험을 활용할 수 있다. 또한 시뮬레이터의 최대 운동한계와 대상체의 운동특성을 이용하여 필터에 사용되는 파라미터를 결정하는 방법을 제시한다. 예제를 통하여 대상체의 운동 시나리오에 따른 시뮬레이터의 운동재현이 어느 정도로 이루어지는 지를 탑승자가 느끼는 힘과 운동재현충실도를 계산하여 분석한다.
잠수함의 경우, 외부 환경이 보이지 않기 때문에 주로 계기에 의존한 시뮬레이터를 제작할 수밖에 없다. 그러나 이 경우 계기만으로 훈련을 하게 되면, 잠수함의 움직임을 전혀 느끼지 못하게 되고, 계기가 보여주는 운동과 탑승자가 느끼는 운동이 전혀 다르기 때문에 훈련효과가 떨어진다. 따라서 잠수함 시뮬레이터에서는 운동을 재현하는 것이 훈련의 효과를 높일 수 있는 방법이다. 본 논문에서는 잠수함 시뮬레이터의 운동재현 기법에 대하여 알아보고, 모형시험 및 동역학 시뮬레이션을 통하여 얻어진 잠수함 운동과 제안된 운동재현기법을 통하여 얻어진 운동과의 비교를 통하여 운동재현효과가 어느 정도인지를 알아보고자 한다. 또한 운동재현기의 운동자유도에 따른 효과를 분석하여 적합한 자유도를 선택하는데 도움을 주고자 한다. 본 논문은 두개로 분리하여 작성하였다. 첫 번째 논문은 washout filter의 일반특성과 본 연구에서 제안하는 운동재현필터(motion filter)의 상세한 사항과 일반적인 적용에 대하여 다루고, 두 번째 논문 (Lee et al., 2024)에서는 선박해양플랜트연구소에서 수행중인 잠수함 자유항주모형시험의 대상인 BB2 잠수함의 운동재현기법에 대한 결과들을 수록한다.
2. Washout 필터의 특성
시뮬레이터는 운동한계를 가지고 있기 때문에 저주파 운동을 재현하기가 힘들다. 저주파 운동은 그 변위가 크지만 인간이 운동을 느끼기도 힘들어 시뮬레이터에서는 저주파 운동을 제외하는 것이 필요하다. 따라서 고주파통과필터(high-pass filter)를 채택하는 것이 유리하다. 이것이 통상적으로 지칭하는 ‘washout filter’이다. Washout filter의 개념을 항공기 시뮬레이터에 적용시킨 것은 1960년대에 시작되었다고 알려져 있다. 이 Washout Filter에 대하여 잘 정리된 보고서는 Schmidt and Conrad(1970) 의 보고서이다. 이후 운동재현기법의 발전이 이루어졌고, 1985년에 Reid and Nahon(1985)이 당시까지의 운동재현기법을 일반화하면서 ‘Classical Washout Filter’로 칭하였다.
이 Classical Washout Filter의 개념은 아직도 유용하게 사용되고 있다. 현재는 이 개념을 기초로 적응(adaptive), 최적(optimal), 예측(predictive)의 개념이 접합되어 사용되고 있지만, 기초적인 알고리즘은 앞에 설명한 ‘Classical Washout Filter’를 기초로 하고 있다.
Washout filter인 고주파통과필터(high-pass filter)는 보통 1차필터나 2차필터로 구현한다. 각각의 특성을 다음에 정리하였다.
2.1 1차 고주파통과필터(High-pass Filter)
1차필터의 전달함수는 다음과 같다.
| (1) |
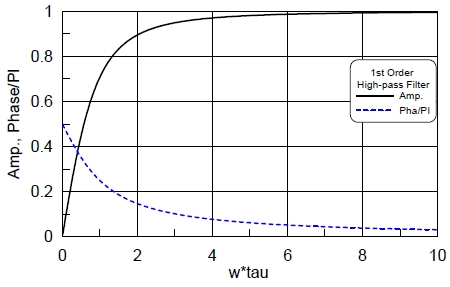
여기서 x는 입력이고, y는 출력, τ는 시간상수로 차단주파수(cut-off frequency)의 역수이다. 이 전달함수의 크기와 위상은 Fig. 4와 같다.
크기 비를 보면 ωτ=1일 때 약 0.7이 되고, 2일 때 약 0.9가 된다. 저주파 성분은 잘 통과시키지 않는다. 위상지연은 주파수 0인 운동은 1/2 π, 즉 90도 이고, ωτ=2일 때 약 0.15 π 즉 27도 정도 지연된다. 일정비율증가입력(Ramp input)에 대한 해를 구해보면 다음과 같다.
| (2) |
계속 증가하는 입력을 주면, 시간이 충분히 흐른 후 위와 같이 vτ만큼 출력이 나온다.
2.2 2차 고주파통과필터(High-pass Filter)
다음은 2차 고주파통과필터의 전달함수 이다.
| (3) |
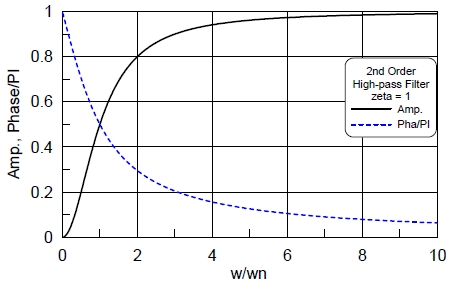
여기에서 ωn은 고유주파수이고, ζ는 감쇠비이다. 감쇠비가 1보다 작으면 오버슈트를 하거나 진동하는 해가 얻어진다. 이 전달함수의 특성은 Fig. 5와 같다.
ω/ωn=1일 때 크기 비는 약 0.5, 2일 때 크기 비는 0.8정도 된다. 위상지연은 각각 90도, 54도 정도이다. ζ가 작아지면 같은 ω/ωn에서 크기비가 커지며, 위상지연이 줄어든다. 이 필터의 일정비율증가입력(Ramp input)에 대한 해는 0으로 수렴한다.
2.3 필터 입력
운동을 재현하기 위해서는 최종적으로 운동재현기 변위를 알아야 하므로, 여러 가지 필터 입력에 대한 운동재현기의 변위는 다음과 같다.
- - 변위입력 고주파통과필터
필터 입력을 변위로 한다. 2차필터는 속도도 입력한다. - - 속도입력 고주파통과필터
필터 입력을 속도로 한다. 출력을 시간 적분하여 변위로 사용한다. - - 가속도입력 고주파통과필터
필터입력을 가속도로 한다. 출력을 두 번 적분하여 시뮬레이터의 변위로 사용한다.
1차필터는 미분방정식으로 다음과 같이 표현된다.
| (4) |
2차필터도 미분방정식으로 표현하면 다음과 같다.
| (5) |
각각의 필터는 다음과 같이 구현하였다.
여기서 x는 필터입력이고, ξ는 중간변수, y는 필터출력이다. 구현하는 식에서 (x)i는 변위입력이고, (v)i는 속도입력, (a)i는 가속도 입력값이다. 마찬가지로 ξ는 중간변수, y는 필터출력이며 yd는 필터출력을 이용하여 구한 변위이다. 위에서 가속도입력은 알고리즘상 가속도의 미분에 해당하는 변수는 계측되거나 물리적 의미가 있는 것이 아니므로 2차필터에서는 제외하였다.
대상체의 운동은 전진방향으로 10초 동안 0.1g의 가속도로 가속하고 그 이후에는 가속이 없는 일정속도 운동을 가정하였다. 또한 τ=2, b=0.5를 사용하였다. Fig. 6은 1차 필터를 사용하였을 때의 결과이다. 2차필터를 사용하면 결과가 Fig.7 과 같다.
이 결과들을 보면 필터입력을 변위로 하거나, 속도로 하거나, 가속도로 하거나 결과는 거의 비슷하다는 점, 전진속도처럼 속도가 일정 값을 유지하는 경우 시뮬레이터 변위를 0근처로 수렴시키려면 2차필터를 사용하여야 한다는 것을 알 수 있다.
3. 제안하는 운동재현필터
Classical Washout Filter의 개념으로는, 선형운동에서는 힘을 필터입력으로 하고, 회전운동에서는 회전각속도를 입력으로 한다. 이것은 탑승자가 느끼는 운동은 전정기관에서 느끼는 힘과 각속도를 통하여 경험적으로 인지하기 때문이다. 본 연구에서 제안하는 운동재현필터(motion filter)는 기본 운동변수인 속도를 입력으로 한다. 제안된 필터에 의한 결과가 classical 알고리즘과 같게 나오더라도, 운동재현에 중점을 두어 필터를 설계하고, 문제가 있을 경우 운동재현이 잘되는 방향으로 해결하기 쉬운 특성을 가진다. Fig. 8은 제안하는 새로운 운동재현필터의 블록다이어그램이다.
3.1 제안하는 운동재현필터(Motion Filter)
앞장에서 1차 필터와 2차 필터의 특성을 알아보았고, 또한 필터의 입력을 변위로 하거나, 속도로 하거나, 가속도로 하여도 결과는 거의 같다는 것을 알아보았다. 운동체의 경우 전진방향이란 항상 변하는 것이고, 또한 운동방정식을 보면 대부분의 경우, 물체고정좌표계에서의 기본 변수는 속도이다. 따라서 속도 입력을 사용하기로 한다. 제안하는 필터는 다음과 같다.
| (6) |
| (7) |
여기에서 x는 입력이고, ξ는 중간변수, y는 필터출력이다. 필터입력으로는 속도를 선택한다. 시뮬레이터 변위 z는 필터출력을 적분하여 얻는다. 또한 zH는 호밍위치이다. 즉, 적분을 하되, 적분값이 호밍위치로 천천히 다가가게 하는 방법이다. 이 방법을 말로 표현하면 1차 고주파통과필터(High-pass Filter)와 호밍위치를 가지는 적분을 결합한 방법이라고 할 수 있다.
이 필터의 전달함수를 구하면 다음과 같다.
| (8) |
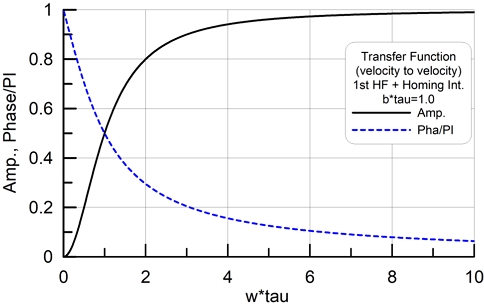
이것은 속도입력 변위출력에 대한 전달함수이므로 속도입력 속도출력에 대한 전달함수를 구하면 다음의 식과 같이 표현되며 그래프는 Fig. 9와 같다.
| (9) |
이 필터는 입력을 속도로 하고, 출력을 시뮬레이터 변위로 하였을 경우, 2차 필터의 특성을 가진다. 입력이 일정가속도일 때 즉 속도의 일정비율증가입력(ramp input)이 있을 때의 해는 다음과 같다. (zH=0 일 때)
| (10) |
이것은 단조 증가 함수이다. 유한한 시간에서 최댓값이 나오지 않고 무한시간에서 최댓값으로 수렴한다. 따라서 최댓값은 다음과 같다.
| (11) |
일정 가속도 운동을 하는 경우, 위 식으로 계산된 위치에 시뮬레이터가 움직인다는 의미이다.
일정 속도 입력(step input)에 대한 해석해는 다음과 같다.
| (12) |
이것의 최댓값은 다음과 같다.
| (13) |
bτ값을 0.5 - 1 사이의 값을 사용한다면, 최댓값을 다음과 같이 근사할 수 있다.
| (14) |
3.2 파라미터의 결정
파라미터들은 운동특성에 따라 결정되어야 하는데, 하나의 운동방향에 대하여 기본적으로 τ와 b를 결정하여야 한다. 그런데 이 값에 따라 시뮬레이터 운동이 작아질 수도 커질 수도 있으므로 시뮬레이터 운동제한 조건에 맞는 파라미터가 결정되어야 한다. 또한 운동체의 운동특성이 속도, 가속도가 큰 운동체라면 시뮬레이터의 운동범위가 커지므로 이것도 고려해 넣어야 한다. 물론 대상체의 특성을 반영하고 적합화를 거쳐서 세밀하게 결정이 되겠지만, 최초 값들을 결정하는 방법이 필요하다.
선형운동
파라미터 선정을 위한 무차원수를 검토하였다. 일정 가속운동의 입력이 주어졌을 때, 즉 속도 입력이 일정비율증가입력(ramp input)으로 주어졌을 때의 시뮬레이터 운동변위는 식(8)에 구해져 있고, 최대 운동변위는 aτ/b이다. 이 최대 운동변위를 시뮬레이터의 최대 운동변위로 나눈 무차원수를 선정한다. 이것을 ‘amplitude ratio coefficient’라고 하였을 때 다음과 같이 나타낼 수 있다.
| (15) |
여기서 aM은 운동체의 지속가능 최대 가속도, 는 시뮬레이터의 최대 운동변위이다. 이 값이 1보다 작으면 필터를 거친 시뮬레이터의 운동변위가 시뮬레이터 최대변위보다 작게 된다.
또 하나의 무차원수를 검토하였다. 필터를 거친 운동변위는 τ로 표시되는 1차필터에서 주어지는 값과 b에 관계되는 호밍행위에 따른 값으로 구성되어 있다. 이 값을 곱하여 무차원수 ‘restoring ratio coefficient’를 다음과 같이 선정한다.
| (16) |
이 값이 커지면 호밍위치에 더 잘 추종한다는 의미이다. 이 값이 1보다 크면 호밍위치에 빨리 추종하여 고주파통과필터(High-pass filter)에 의한 값이 나중까지 많이 남아 있다는 뜻이고, 1보다 작으면, 고주파통과필터(high-pass filter)에 의한 값이 빨리 줄어들어 나중에 남는 운동은 호밍위치를 가지는 적분에 의한 운동이라는 뜻이다. 둘의 영향을 비슷하게 하려면 이 값을 1로 하면 된다. 호밍위치로의 복귀를 약간 천천히 하고자 한다면 이 값을 0.5 정도로 하는 것이 도움이 될 것이다.
- b : 작으면 호밍위치에 천천히 수렴한다. 그러나 외부에서 호밍위치를 지정한 것이라면 빨리 추종할 필요가 있다.
- τ : 크면 입력에 빨리 추종한다. 1/τ가 차단주파수(cut-off frequency)이기 때문에, 크면 조금 더 낮은 주파수까지 통과시킨다. 입력에 보다 빨리 추종한다.
시뮬레이터의 운동범위를 전체적으로 이용하려면 ka를 1에 가깝게 사용하면 된다. 호밍위치에 부드럽게 가게 하려면 kr을 1/2정도로 사용하면 될 것이다. 이렇게 ka, kr을 정하면 이것으로 τ, b를 결정할 수 있다.
| (17) |
이 값을 적합화의 시작점으로 사용하는 것이 바람직하다. τ 또는 b를 결정하고 다른 것들을 결정할 수도 있겠지만, 그것보다는 시뮬레이터 운동특성과 변위, 원하는 복원성능의 비율을 먼저 정하고 위의 방법을 이용하는 것도 상당히 유용할 것이다.
회전운동
최대가속도는 알 수 없고, 최대속도를 아는 경우도 있을 것이다. 이 대표적인 경우는 선수동요(yaw)인데, 회전각속도의 최댓값은 어느 정도 추정이 가능하나, 최대각가속도의 추정이 힘든 경우이다. 이 경우 최대속도를 주었을 때 시뮬레이터는 최댓값에 도달하였다가 줄어드는 거동을 보인다. 이 최댓값은 앞서의 식 (14)와 같이 근사할 수 있다.
이 최댓값을 시뮬레이터 최댓값으로 나눈 ‘amplitude ratio coefficient’는 다음과 같이 정의하였다.
| (18) |
‘restoring ratio coefficient’는 앞의 경우와 같다. 위식으로 τ를 정하고, 복원계수 b를 정하여 사용한다.
| (19) |
선형운동은 순간 최대가속이 아닌 지속가능 최대 가속도를 주는 방법으로 파라미터를 구하고, 회전운동도 마찬가지로 지속가능 최대 속도를 주는 방법으로 파라미터를 구한다.
3.3 호밍위치(Homing Position)
식 (7)을 보면 입력의 변화가 없을 때 운동재현기는 호밍위치로 천천히 가게 된다. 이것으로 운동체 동작의 추가변화가 없으면 시뮬레이터의 변위를 0점에 가져다 놓는 것을 구현한다. 또한 전진방향 가속의 부족한 부분을 종동요(pitch)각과 중력가속도를 이용하여 보완 하는 데에 이것이 필요하다. 또한 전진방향의 속도가 있으면, 향후 속도가 줄어들 가능성이 더 높기 때문에 시뮬레이터를 앞으로 조금 가져다 놓는 게 유리한 면이 있다. 따라서 다음과 같이 호밍위치를 준다.
- - 전후동요(Surge) : 전진방향 최대속도일 때 시뮬레이터 전진방향 최대 변위의 1/2
- - 좌우동요(Sway) : 옆방향 속도에 따라 결정, 전후동요(Surge)의 배율과 같게 줌
- - 상하동요(Heave) : 0
- - 횡동요(Roll) : 가상횡경사각(Virtual Roll Angle)
- - 종동요(Pitch) : 가상종경사각(Virtual Pitch Angle)
- - 선수동요(Yaw) : 최대 회전각속도일 때 시뮬레이터 선수동요(Yaw) 최대각의 1/2
여기에서 전후동요, 좌우동요, 선수동요의 호밍위치 결정에 사용되는 속도는 현재평균(running average)를 사용한다.(현재평균은 시간상수 τ를 10초로 한 저주파통과필터(low pass filter)를 거친 값으로 한다.) 이렇게 호밍위치를 설정하면, 시뮬레이터 외부에서 보았을 때, 대상체의 속도 등 움직임을 알 수 있어서 편리하다. 가상각(virtual angle)은 다음 절에서 설명하였는데, 탑승자가 느끼는 각도이다.
호밍위치 중 다른 것들은 문제를 발생시키지 않을 것이나, 횡동요각과 종동요각의 경우 가상각이 급격하게 변화하는 경우가 발생할 수가 있다. 이 값들은 동역학시스템을 통하지 않고 계산에 의한 값이므로 급격한 변화를 가질 수 있다. 따라서 가상각은 필요시 적절한 저주파통과필터(Low-pass Filter)를 거쳐 사용한다.
3.4 가상각(Virtual Angles)
전후동요(surge)와 좌우동요(sway) 운동 가속은 시뮬레이터가 가지는 운동한계 때문에 똑같이 재현하지 못하므로, 종경사(pitch)와 횡경사(roll)각을 주어 중력가속도를 이용하여 보상을 해주어야 한다. 방법은 탑승자가 느끼는 가상종경사각(virtual pitch), 가상횡경사각(roll angle)을 구하여 이것으로 종동요와 횡동요 운동을 재현하는 것이다.
운동체의 단위질량당 관성력은 다음과 같이 표현된다. (선형운동의 경우, 물체고정좌표계에서 기술됨)
| (20) |
여기서 u, v, w는 선형속도이고, p, q, r는 각각 횡동요, 종동요, 선수동요 각속도이다. x, y, z는 대상운동체의 물체고정좌표계에서의 위치이다.
인간은 운동체의 가속방향의 반대방향의 힘을 받는다. 인간이 받은 힘은 이것 이외에 중력이 있다. 물체고정좌표계에서의 중력은 다음과 같이 Euler각을 이용하여 표현된다.
| (21) |
여기서 g는 중력가속도, ϕ는 횡동요각, θ는 종동요각이다. 탑승자가 받는 힘은 다음과 같이 표현된다.
| (22) |
이 힘들로 겉보기 각도, 가상종경사각과 가상횡경사각을 구하면 다음과 같다.
| (23) |
뱅크선회(bank turn)를 하는 경우, 실제로 횡동요각이 있지만 중력에 의한 옆방향 힘과 원심력에 의한 옆방향 힘이 상쇄되어, 가상횡경사각은 0으로 갈 수 있다. 물체의 가속도가 없으면, 실제 종동요, 횡동요각은 가상각들과 같아진다.
3.5 운동 한계
시뮬레이터를 운용하다보면, 시뮬레이터의 운동 한계를 넘어가는 경우가 발생할 수 있다. 이때는 운동한계 내에서 작동을 하도록 운동을 줄여줄 필요가 있다. 이 때 사용하는 함수가 속칭 시그모이드함수(sigmoid function)이다. 시그모이드로 많이 사용하는 함수는 로지스틱함수(logistic function)로 1800년대에 인구증가를 모델링하기 위하여 도입되었다. 그러나 이 함수는 운동한계 훨씬 전부터 값을 줄이는 특성이 있어서 운동한계 근처에서 값을 부드럽게 줄이는 다음과 같은 시그모이드 함수를 제안한다.
| (24) |
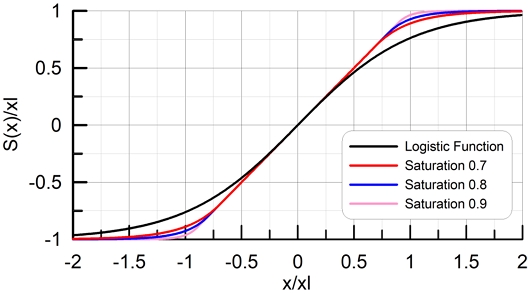
여기에서 xl은 운동한계이고, k는 선형범위를 나타낸다. 이렇게 하면 kxl보다 x가 작으면 선형함수가 되고, 크기가 kxl보다 커지면 기울기와 값이 이어지면서 포화(saturation)되는 시그모이드함수(sigmoid function)가 된다. 참고로 원점에서 기울기가 1이고 크기가 1인 로지스틱함수(logistic function)는 다음과 같다.
| (25) |
Fig. 10에 여러 가지 k값에 대한 시그모이드함수와 로지스틱함수를 나타내었다. k값으로 0.7 이상을 사용하면 원하는 운동제한의 결과를 얻을 수 있다.
3.6 운동재현 충실도
시뮬레이터의 운동이 실제의 운동을 얼마만큼 충실하게 재현하고 있는가를 알려주는 지표가 필요하다. 이것이 있으면 이를 이용하여 운동재현기법을 수정할 수도 있고, 운동재현기의 설계에도 반영할 수도 있기 때문이다. 본 연구에서는 이러한 지표로 충실도(ratio of fullness) 지표를 고려하였다. 선형운동에서는 탑승자가 받는 힘으로 운동재현충실도를 계산하고, 회전운동에서는 탑승자가 느끼는 회전각속도를 기준으로 한다.
실제 대상운동체의 탑승자가 느끼는 힘을 fV라고 하고, 시뮬레이터 탑승자가 느끼는 힘을 fS라고 하고, 두 값의 비슷한 정도를 나타내는 충실도(rate of fullness)를 다음과 같이 제안한다.
| (26) |
fS와 fV가 같을 때 1이 되고, 움직이지 않을 때 0이 되며, 음수도 나올 수 있다. 반대로 움직이는 경우 음수가 된다. 둘 다 값이 0일 때는 1로 정의한다. 윗식은 fV보다 fS가 커도 1보다 작은 값이 되도록 고안된 식이다. fV가 0일 경우 충실도가 0이 되는데, fS가 작은 값으로 대상운동체의 힘을 따라간다고 하여도 0으로 표시되므로 문제가 된다. 따라서 대상운동체의 fV가 설정된 최댓값의 1%이내로 값이 작아지면 다음처럼 계산한다.
| (27) |
이렇게 하면, fV가 0일 때 fS가 충분히 작으면 운동충실도를 1에 가까운 값으로 얻을 수 있다. 이 값을 적분하여 평균을 내면 전체 충실도가 나오고, 현재평균을 구하면 현재의 평균 충실도가 나온다. 선형운동의 경우 fV, fS는 탑승자가 받는 힘을 기준으로 하고, 회전운동의 경우에는 탑승자가 느끼는 회전각속도를 기준으로 한다.
4. 적용 예
제안한 운동재현필터의 적용을 위하여, 우선 대상운송체의 특성을 간략하게 알아보자. 좌표계는 전진방향을 X로 하고 윗방향을 Z로 하는 우수좌표계를 사용하였다,
◆ 가감속 성능
대형 여객항공기
대형항공기의 경우 이륙 가속 시 약 30초에서 약 300km/h의 속력이 나온다. 이 속력정도가 나와야 이륙을 할 수 있다. 이 속력까지 일정가속도 운동을 한다고 하면, 약 0.3g 의 가속도를 낸다.
자동차
자동차의 경우 100km/h 의 속도를 내는데 걸리는 시간에 대한 자료들을 광고하고 있다. 초고성능차의 경우 3초, 고성능차 5-6초, 일반차 9-10초 정도 걸리는 것을 나와 있다. 고성능차를 기준(5초)으로 한다면 0.5665 g의 가속성능이 있다. 일반차는 이것의 절반 정도 되고, 대형항공기와 비슷하다.
선박
선박의 경우, 이런 자료가 없다. 설계속도와 설계마력이 있다. 이것을 가지고 유추하여야 한다. 또는 Bollard Pull Test의 자료를 사용하여야 한다. 군함의 경우 그 크기가 약 1500톤 이상으로 하고 최고속력이 약 30노트를 기준으로 하면(Frigate 함 수준), 이것보다 작은 선박의 경우 가속능력이 더 크다. 폭을 길이의 1/6, 흘수를 폭의 1/4로 가정하고 배수량이 1500톤이 되는 조건을 부여하여 길이를 구하면, L=75.6m, B=12.6m, T=3.15m 정도 된다. (CB=0.5로 하였음) 이 선박의 마찰저항은 30노트에서 어림잡아 482,233 N이 되고, 전체저항은 마찰저항의 약 3배가 될 것이다. 즉 1,446,700N 정도 될 것이다. 이 힘을 추력으로 낼 수 있다고 가정하면, 가속도는 0.098 g 정도 된다, 약 0.1g 수준이다. 이것은 물론 군함의 경우이다. 보통 선박은 이것의 절반 정도로 판단하면 0.05g 수준으로 생각된다. 대형 선박은 이것보다 작을 것으로 판단한다. 잠수함의 경우 조파저항이 없고 이에 맞추어 추진기를 설계하고 또한 수중 속력을 고려할 때 가속도는 Frigate 함의 1/5정도 될 것이다. 즉 0.02g 정도 될 것이다.
◆ 선회 성능
여기에서는 완화곡선이 없는 정상 선회를 생각한다. 선회반경 R을 속도 V로 달리고 있을 때 선회각속도를 구하면 Vt가 원주길이가 될 것이다. 이때 변화하는 각도는 Vt/R이다. 이것을 시간미분하면 결국 각속도(rad/s)는 r' = V/R 이다. 원심력은 r'V로 표현되는데, 이것과 중력의 합이 운동체에 작용한다. 합력의 각도를 뱅크(Bank)각이라고 한다면 다음과 같이 표현된다.
| (28) |
항공기의 경우 위의 뱅크(Bank)각을 횡경사각으로 하여 선회를 한다. 이렇게 하면 원심력이 느껴지지 않고 모든 힘이 아랫방향으로 느껴진다.
자동차
자동차의 경우 평탄한 지면에서 선회를 한다고 가정한다. 원심력이 작용하게 되면 옆방향 힘이 발생하고 이것을 타이어가 받쳐주어야 하는데, 타이어의 옆방향 미끄럼 마찰력에는 한계가 있어 일반적으로 옆방향 기울기가 약 20도 정도 되면 미끄러지기 시작한다고 알려져 있다. 타이어가 미끄럼 마찰력 성능이 좋다고 하면 약 30도 정도가 될 것이다. 이것으로 옆방향 최대 원심력의 크기로 가정한다. 이것으로 선수동요(yaw) 각속도를 추정할 수 있다.
| (29) |
속도 80km/h의 경우, 각속도는 0.2548 rad/s 가 된다. 180도를 돌아나가는데 12.33s 소요된다.
항공기
항공기의 경우 최소 선회반경이 있을 것이다. 뱅크선회(Bank Turn)를 하는 경우 뱅크각을 45도로 하면 옆방향으로도 1g의 힘이 걸리고 아랫방향으로도 1g의 힘이 걸리므로 인간에게는 g의 힘이 걸리게 된다. 이것보다 약간 작게 뱅크각 30도를 기준으로 한다. 이것으로 각속도를 추정할 수 있다.
| (30) |
속도 600km/h의 경우, 각속도는 0.03397 rad/s 가 된다. 180도를 돌아나가는데 92s 소요된다. 이때의 선회반경은 R = V/r'으로 4907m가 된다.
선박
선박의 경우, 설계속도에서 타를 최대한 작동하였을 때의 최소선회반경이 보통 주어진다. 그런데 이때 속도가 약 1/2로 떨어지면서 최소선회반경이 나온다. 이것으로 각속도를 추정한다. 통상적인 선회경은 약 3.5 - 4L 이다. 길이 100m, 속도 20노트의 경우 , 10.288m/s , 반경 200m, 반경의 π배가 반원의 거리, 이것을 속도로 주행하는 경우 시간은 61.073s, 이 시간동안 180도를 돌아나가므로 0.05144 rad/s 가 된다.
위에서 설명한 것들을 종합하여 항공기, 자동차, 선박의 대표적인 운동특성을 다음과 같이 선정한다.
시뮬레이터 운동재현필터는 3장에서 제안한 것을 사용한다. 시뮬레이터의 안전 한계는, 선형운동은 ±1m, 회전운동은 ±30degree 로 한다.
시뮬레이터의 파라미터는 다른 언급이 없는 한, 무차원수 ka=1, kr=1로 한다. 횡동요와 종동요는 가상각(virtual angle)을 빨리 추종하기 위하여 kr=2로 한다. 이 값들은 기준으로 사용하는 것이고, 대상체의 특성에 따라 적절한 값을 구하여 사용한다. 옆방향과 윗방향에 대한 파라미터는 전진방향에 대한 파라미터와 같은 값을 사용하기로 한다. 그 이유는 같은 선형운동이므로 자연스러운 선택이다. 그러나 옆방향과 윗방향 운동을 다르게 설정하여도 된다.
본 절에서 다루는 대상운동체는 자동차로 한다. 따라서 전진방향 최대가속도는 0.3g, 최대속도 22.22m/s, 최대각속도는 90 deg/s로 선정하였다.
4.1 전진 가속
전진방향 가속시의 시뮬레이터 운동은 대상체의 분류와 상관없이 최대가속도를 가지고 파라미터들을 설정하고 운동을 재현한다. 3장에 제시된 방법으로 계산을 수행하였다. 최대가속도를 0.3g로 한다. 이렇게 설정하고 amplitude ratio coefficient ka, restoring ratio coefficient ka를 모두 1로 설정한다. 횡동요와 종동요에서만 kr을 2로 설정한다.(Table 2 참조)
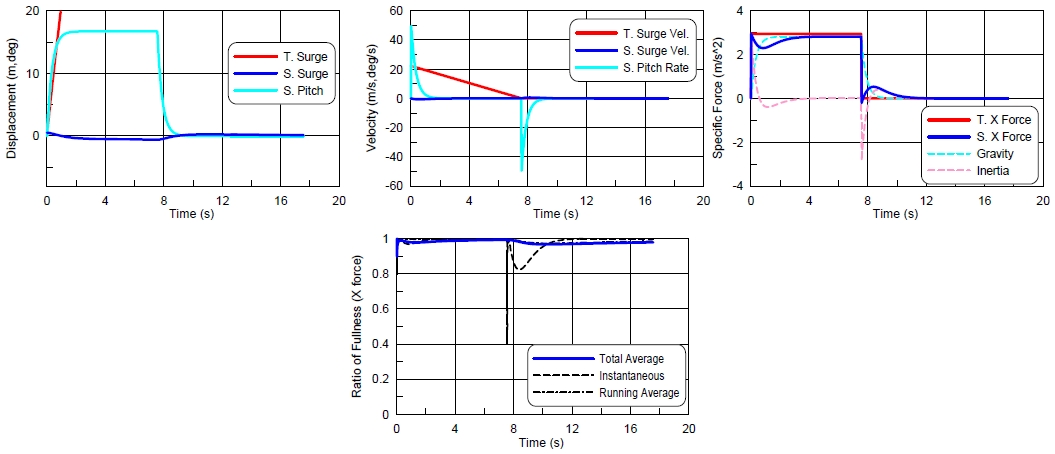
대상운동체의 운동은 정지상태에서 10초간 0.1g로 가속을 하고, 10초 후 가속을 0으로 하였다. 이에 대한 계산 결과는 Fig.11과 같다. 가상각은 필터를 거치지 않고 그대로 사용하였다. 이 결과를 보면 전진 방향 힘을 잘 재현하고 있다. 초기 가속시 전진방향 가속에 의하여 힘을 주고 이후에는 약 6도 가까이 종경사각을 주어서 중력으로 전진방향의 힘을 보충하고 있다. 그러나 대상운동체의 가속이 변하는 순간 시뮬레이터의 종동요 각속도가 15 deg/s 까지 갑자기 나온다. 이대로 시뮬레이터가 움직인다면 운동재현기 위에 올려져 있는 시스템 및 훈련자에게 충격을 줄 수 있다.
그런데 이것은 대상운동체의 가속도를 갑자기 주어서 그런 것일 수 있으므로, 가속도를 갑자기 0.1g로 변경하지 말고, 1초의 시간을 주어 0에서 0.1g로 선형적으로 올리고, 또한 가속도를 없앨 때도 1초의 시간을 주어 0.1g에서 0으로 선형적으로 내리는 경우에 대한 계산 결과를 Fig.12에 수록하였다. 여기에서는 가상각에 저주파통과필터(Low-pass filter)를 걸지 않았다. 이것을 보면, 종동요각은 약 6도 가까이 피크(peak)를 가지지만 큰 무리 없는 운동이고, 관성력의 피크가 많이 부드러워 졌다는 것을 알 수 있다. 또한 운동재현 충실도는 거의 1로 아주 좋은 것으로 판단된다. 따라서 굳이 가상각에 저주파통과필터(low pass filter)를 걸어주지 않아도 될 것이다.
4.2 수평선회(Level Turn)
수평선회(level turn)란 횡경사각을 0도로 유지하면서 선회를 하는 경우이다. 이때는 탑승자에게는 원심력이 작용한다. 이 원심력은 ru로 표현되어 속도가 클수록, 선회각속도가 클수록 커진다.
선회는 직선운동을 하다가 갑자기 선회반경 R로의 선회를 하는 것이 아니라, 정상선회반경에 들어가기 전 완화곡선을 거쳐서 정상선회에 들어간다. 이 개념은 철도에서부터 시작되었는데, (Wikipedia ‘Track transition curve’, Euler Spiral 참조) 철도나 도로에서는 선회를 하는 구간과 직선구간의 연결부위의 완화곡선을 준다. 개념은 곡률(curvature) 1/R이 0으로부터 시작하여 선형적으로 원하는 선회반경의 곡률이 되도록 선을 구하는 것이다. 이 선은 클로소이드(clothoid)라고 불리는 선인데, 수학적 용어로는 Fresnel 적분(또는 Euler 적분)을 이용한 선이다. 그 위를 달리는 입장에서 보면 궤적의 x,y 보다는 1/R이 중요하고, 이것에 의한 원심력이 중요하다.
주행은 일정속도로 전진한다고 가정한다. 처음 0도에서 45도까지는 완화곡선을 지나고, 45도부터 135도까지는 일정 선회반경에 의한 선회를 하고, 135도부터 180도까지는 완화곡선을 통하여 선회에서 직진운동으로 선형적으로 변화되도록 한다. 최종적으로 선회는 180도 돌아서 나오는 것으로 한다.
선회반경 R을 속도 V로 달리고 있을 때 선회각속도를 구하였다. Vt가 원주길이가 될 것이다. 이때 변화하는 각도는 Vt/R이다. 이것을 시간미분하면 결국 각속도는
가 될 것이다. 도입부 완화곡선을 지나는 시간 TC, 일정선회구간을 지나는 시간 TST, 도출부 완화곡선을 지나는 시간 TC 라고 하면 선회각속도는 다음과 같아진다.
| (31) |
이것을 적분하여 선수각(yaw)을 구하면 다음과 같다.
| (32) |
180도 돌아서 나오는 것으로 하면 이 값이 π가 되도록 한다. 즉,
| (33) |
가 되도록 한다.
속도는 설계속도로 하고, 선회반경에 대한 자료가 있으면 그것을 사용하고, 없다면 뱅크각도를 선정하여 R을 계산한다. 이것으로 TST를 알아낼 수 있다.
원심력은 r'V로 표현되는데, 위의 변수로 표시하면 V2/R로 표현된다. 이에 따른 뱅크(Bank)각은 다음과 같이 표현된다.
| (34) |
표현을 다르게 하여 다음과 같이 표현하여도 된다.
| (35) |
여기에서는 TC = 1/2 TST 로 하는 것을 기준으로 한다.
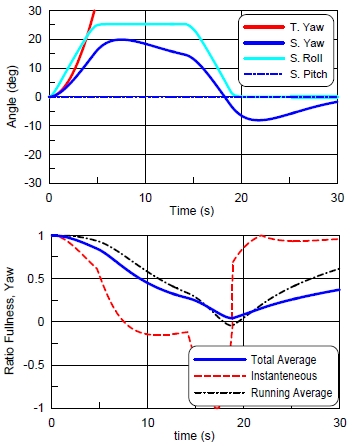
자동차 속도 80km/h(22.22m/s), 선회반경 100m, TST=9.42778s 를 기준으로 삼아서 계산을 하였다. 운동재현 파라미터를 결정하기 위한 자료는 앞 절과 같게 한다. 계산결과는 Fig. 13에 수록하였는데, 결과를 보면, 당연한 결과이겠지만, 선수동요(yaw) 방향으로 시뮬레이터가 계속 움직일 수 없으므로 선수동요 방향의 충실도가 아주 낮은 수준이다.
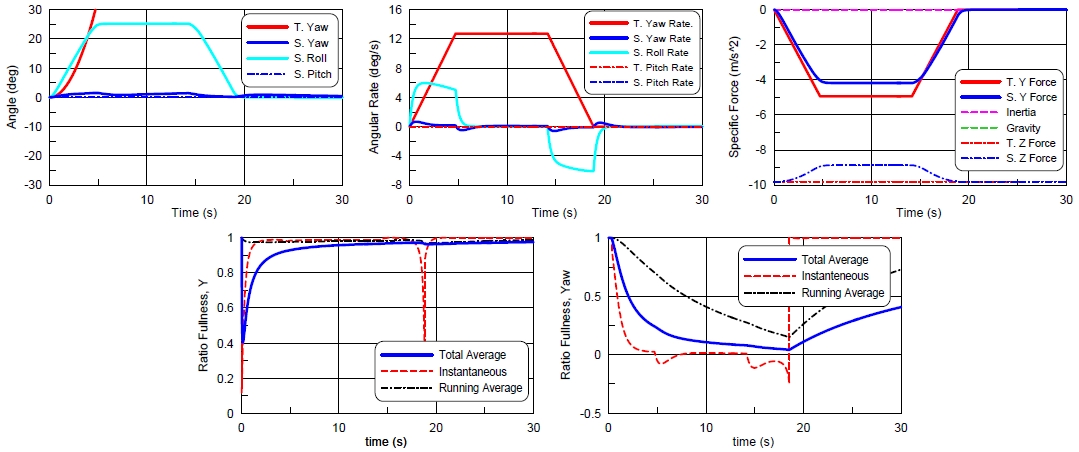
Simulator movements of the level turn simulation(turn radius 100m, max rate : roll 90, pitch 90, yaw 90 deg/s)
대상이 되는 이번 운동의 특성만을 가정하여 선수동요 각속도를 15도/초로 하였다. 이 결과는 Fig. 14에 나타내었다.
다른 것들은 거의 같기에 선수동요각과 운동재현충실도만을 Fig.14에 그렸다. 보다 많이 개선되었음을 알 수 있다. 이것으로 선수동요 운동에 대하여서는 대상이 되는 운동의 최대각속도 값을 그대로 사용하여도 될 것이라는 것을 알았다.
선수동요각은 초기에는 대상체의 선수동요각을 따라가다가, 20도 정도 되어서는 점차 줄어든다. 대상체의 횡동요각은 원래 없는데 옆방향 힘을 중력가속도를 이용하여 나타내어야 하므로 횡동요각이 발생한다. 단위힘(specific force)를 보면 옆방향 힘은 대상체에 걸리는 힘을 추종하고 있다. 다만 정확하게 따라가지는 못하고 있다. 또한 아랫방향 힘은 시뮬레이터에서는 중간에 줄어드는 현상을 보인다. 이것은 시뮬레이터에서 이용하는 힘이 결국에는 중력가속도임으로 어쩔 수 없는 현상이라고 할 수 있다.
4.3 뱅크선회(Bank Turn)
뱅크선회(Bank Turn)의 경우 위에 제시한 것과는 조금 다른 운동을 겪는다. 궤적은 앞의 선회와 같은데, 횡동요각을 주어 옆방향 힘을 중력에 의하여 상쇄시켜 합력으로는 옆방향 힘이 없어지게 한다. 또한 이때 선회는 선수를 위로 올리는 종동요 각속도도 발생하여야 높이를 유지하면서 선회를 할 수 있다.
뱅크는 횡동요각으로 표현한다. 위에서의 선회 각속도 r'은 선수동요 각속도와 종동요 각속도로 분해된다.
| (36) |
- Yaw Rate r = r'cosϕB
- Pitch Rate q = r'sinϕB
여기에서도 최대 선수동요 각속도를 15도로 하여 계산하여 Fig. 15에 수록하였다. 힘은 큰 문제가 없는 것으로 보이나, 회전운동은 운동재현 충실도가 높지 않다. 선수동요의 경우는 최대 각속도를 작게 택하여 시뮬레이터의 선수동요 각도를 크게 움직여 주어서 충실도가 조금 나아졌으나, 종동요와 횡동요의 경우에는 충실도가 아주 낮은 수준이다. 이것을 해결하고자 종동요와 횡동요의 최대각속도를 30deg/s로 줄여서 계산을 하여 Fig. 16에 수록하였다. 종동요와 횡동요의 운동재현 충실도는 개선이 되었으나, X,Y 방향 힘에 차이가 발생하여 이 방향의 운동충실도가 낮아졌다. 힘의 운동 충실도는 낮아졌다지만, 종동요의 운동충실도가 선회초기부분에서 개선이 되어, 선회가 시작되었다는 것을 보다 잘 느끼게 되었다.
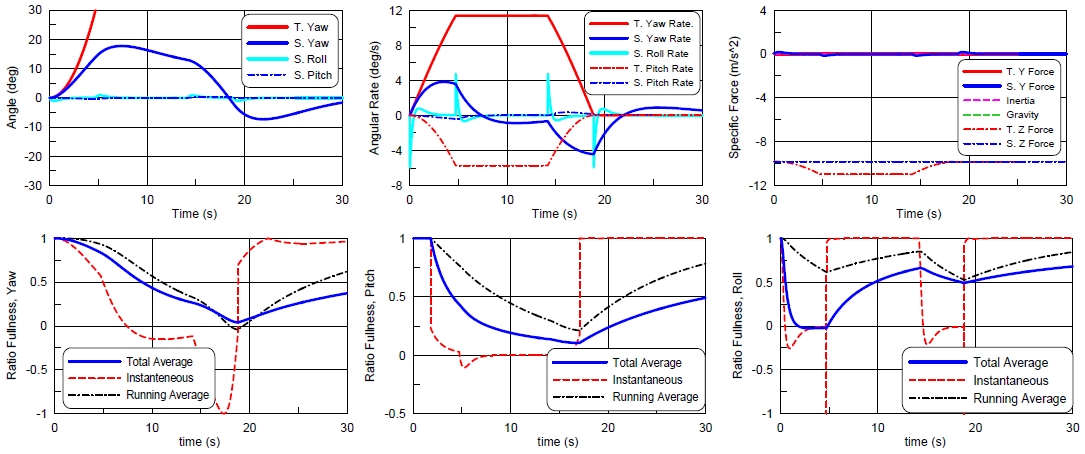
Simulator movements of the bank turn simulation(turn radius 100m, max rate : roll 90, pitch 90, yaw 15 deg/s)
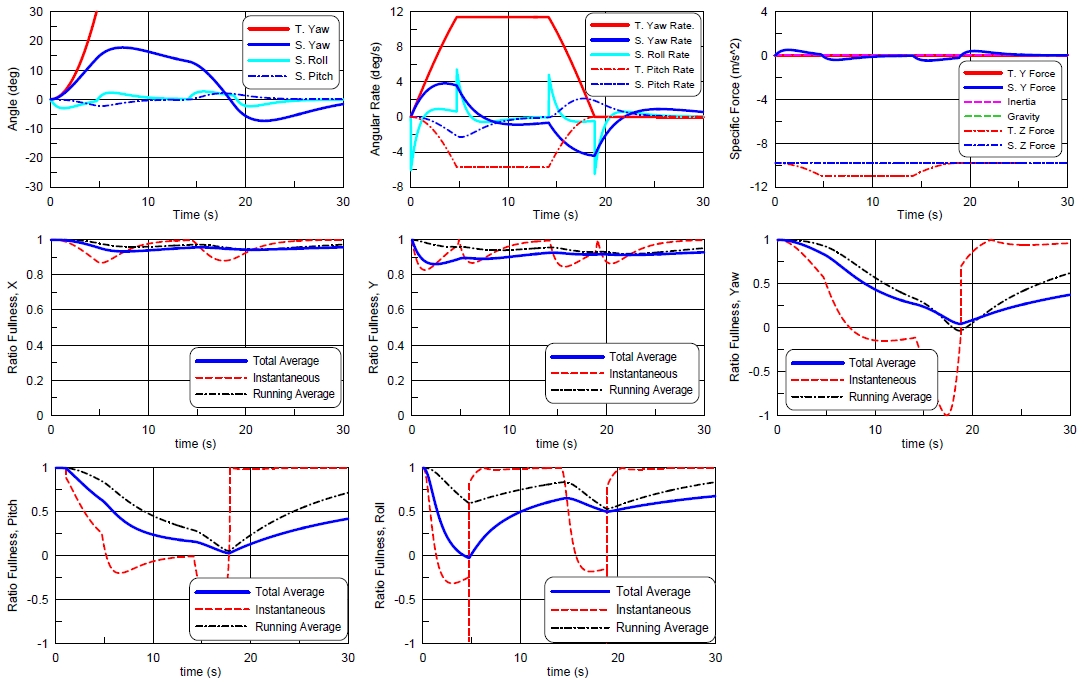
Simulator movements of the bank turn simulation(turn radius 100m, max rate : roll 30, pitch 30, yaw 15 deg/s)
여기에서 보면 횡동요각이 초기에는 뱅크각을 따라가다가 금세 0으로 줄어든다. 뱅크선회시 발생하는 종동요도 초기에는 구현된다. 이것도 시간이 지나면서 0으로 줄어드는 거동을 보인다. 힘의 경우 옆 방향으로 큰 힘이 발생하지 않는다. 이것은 뱅크선회의 특별한 거동이다. 다만 뱅크선회시 아랫방향으로 힘이 더 커지는데 이것은 시뮬레이터에서 재현하기 힘든 특성이다.
4.4 정지(Stopping)
정지상황은 자동차에서 일상적으로 나타나고, 항공기에서는 활주로에서 나타나고, 선박에서는 통상적인 경우 아주 천천히 정지하므로 크게 나타나지 않는다고 할 수 있다. 자동차의 정지는 가속보다 더 큰 크기로 감속되는 것이 보통이다.
일정속도로 달리다가 속도가 0이 될 때까지 0.3g 로 감속되는 경우를 검토하였다. 초기 속도가 80km/h 로 달리고 있다가 정지하면 시간은 7.55s, 0.5g로 감속하면 4.53s 소요된다.
최대각속도를 그 전의 값으로 하여 계산한 결과를 Fig. 17에 수록하였다. 이것을 보면 운동재현 충실도가 양호한 값을 주고 있는 것을 알 수 있다. 하지만 종동요 각속도가 초기에 큰 값을 가진다는 것이 문제로 남아있다. 만일 여기서 시뮬레이터의 x 방향 운동한계를 크게 하면 이 문제는 해결될 것이다. 하지만 이렇게 하면, 항상 한계를 크게 하면 좋아진다는 당연한 사실만을 알려주는 것이므로 이에 대한 계산은 수행하지 않기로 한다.
4.5 적용 예 종합분석
앞 절에서 일반자동차의 중요한 움직임, 즉, 전진가속, 선회, 정지의 움직임에 대하여 운동재현필터를 통하여 시뮬레이터 운동재현기의 움직임과, 이에 따른 탑승자가 느끼는 힘, 운동재현충실도를 계산하여 보였다.
그 결과 가상각으로 전후방향, 좌우방향으로 발생하는 힘을 충분히 표현하고 있다. 또한 이 가상각으로 빨리 회전하여야 하므로, 횡동요와 종동요 각속도 최댓값은 Table 1에 있는 것 정도를 사용하고 작게 선정하지 않는 것이 좋다. 나머지 파라미터를 선정하기 위한 운동최댓값들 즉, X,Y,Z 방향 최대가속도, 선수동요(yaw) 최대 각속도는 안전을 위하여 큰 값을 주는 것이 아니라, 시뮬레이터에서 재현하고자 하는 운동에서의 최댓값을 주는 것이 바람직하다. 작은 값을 주었을 때 운동이 커지는 것은 3.5절에서 설명한 시그모이드함수 식 (23)으로 충분히 해결된다. 시뮬레이터 운동재현기가 운동한계 범위 내에서 충분히 크게 움직이는 것이 탑승자에게 운동을 느끼게 하는 면에서 바람직하다.
Table 1과 Table 3를 사용하면 일반적인 자동차에 대한 운동재현필터를 사용하기에 적합하다고 할 수 있다.
5. 결 론
본 연구는 장차 사용하게 될 차세대 잠수함의 훈련을 위하여, 시뮬레이터 운동재현기에 사용될 운동재현기법을 다루었다. 힘이 아닌 운동변수를 기반으로 한 운동재현필터(motion filter)를 제안하였으며, 필터에 사용되는 파라미터를 간단하게 설정하는 방법을 제시하였다. 또한 호밍위치(homing position)를 주는 방법으로 가상 각도들을 주어 중력에 의하여 힘을 보상하는 방법을 제안하였으며, 현 운동상태에 적합한 호밍위치(homing position)를 주는 방법도 제시하였다.
제안하는 운동재현필터의 동작을 분석하기 위하여, 일반적인 운동체에 대하여 전진 가속, 선회(level turn, bank turn), 정지 감속에 대하여 적용을 하여 제안하는 운동재현필터의 유효성을 분석하였으며, 운동재현 충실도를 분석하여 효과 있는 파라미터를 선정하는 방법을 보였다. 그 결과 제안된 운동재현필터는 적용 예 모두에서 운동재현충실도 높게 효과적으로 작동하였다.
본 논문인 제1보에서는 운동재현필터의 이론적 배경과 일반사항에 대하여 다루었고, 본 논문의 후속편인 제2보에서는 BB2 잠수함 운동재현에의 적용을 다룬다.
Acknowledgments
본 연구는 한국해양과학기술원 부설 선박해양플랜트연구소의 주요연구사업 “수중운동체 운항성능 통합 추정 기술개발(5/5) [PES5070]”의 연구 결과 중 일부임을 밝힌다.
References
-
Affan, M., Ahmed, S.U., Manek, A.I. and Uddin, R., 2019. Design and implementation of the washout filter for the stewart-gough motion platform, 2019 International Conference on Computational Intelligence and Knowledge Economy (ICCIKE), December 2019, Dubai.
[https://doi.org/10.1109/ICCIKE47802.2019.9004317]

-
Allen, R. Wade, 2011. A short history of driving simulation, Handbook of Driving Simulation for Engineering, Medicine and Psychology (edited by Donald L. Fisher et al.) CRC Press, Taylor & Francis Group, New York, 2011.
[https://doi.org/10.1201/b10836-3]

- Colombet, F., Dagdelen, M., Reymond, G. Pere, C., Merienne, F. and Kemeny, A., 2008. Motion Cueing: what’s the impact on the driver’s behavior?, Driving Simulation Conference (DSC) 2008.
- Davison, Peter John, 2018. Motion in flight simulators - A story of evolution, Aviation Focus, Hong Kong
- Fang, Z. and Kemeny, A., 2014. Review and prospects of renault’s MPC based motion cueing algorithm for driving simulator, Driving Simulation Conference 2014, Paris, September 2014.
- Lee, G.J., Kim, D.J., Kwon, C.S., Yeo, D.J., Kim, Y.G. and Yun K., 2024. Motion filter of the submarine simulator: Part 2. Application to BB2 submarine, Journal of the Society of Naval Architects of Korea, 61(6), pp.460-469.
-
Natal, G.S., Arjoni, D.H., Oliveira, W.R., Rodamilans, G.B., da Silva, E.T., Silveira, L., Villani, E. and Trabasso, L., 2019. Implementation analysis of a washout filter on a robotic flight simulator - a case study, Journal of Aerosp. Technol. Manag. v11, 2019.
[https://doi.org/10.5028/jatm.v11.978]

- Reid, L.D. and Nahon, M.A. 1985. Flight simulation motion-base drive algorithms: part 1 - developing and testing the equations, 1985, UTIAS Report No. 296.
- Schmidt, S. F. and Conrad, B. 1970. Motion drive signals for piloted flight simulators, NASA CR-1601, 1970.
-
Stroosma, O., van Paassen, M.M. and Mulder, M., 2013. Appling the objective motion cueing test to a classical washout algorithm, AIAA 2013-4834, AIAA Modeling and Simulation Technologies(MST) Conference, August 2013 Boston.
[https://doi.org/10.2514/6.2013-4834]