주성분의 선형 결합을 통한 다변수 식별에 기반한 선박 조종 운동 모델 개발
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The present study suggests a data-driven multivariate identification method based on principal component analysis and shows an application to ship dynamics modeling in maneuver. A reduced order model of ship dynamics is built by linear combination of three principal components acquired from large angle zigzag maneuver test. For a given kinematic state with three variables, a proper span is found by least square method, therefore accompanying hydrodynamic force and moment is determined. Suggested dynamics model correctly estimates hydrodynamic force and moment, thus it showed good agreement in maneuver simulation with that of conventional ship dynamics model obtained by system identification of captive model tests.
Keywords:
Principal Component Analysis, Ship Maneuver, Dynamics Modeling키워드:
주성분 분석, 선박 조종, 동역학 모델링1. 서 론
2010년대 초반부터 데이터 기반 모델링 기법이 발전함에 따라 선박의 조종 운동 문제로의 응용이 시도되고 있다. 데이터 기반 모델링은 데이터 변수 간의 공간/시간적 상호상관성에 기반해 데이터를 분석하는 기법이다. 이는 기존의 구속모형시험을 통한 다항식 기반 모델의 시스템 식별(system identification)이나 전산유체역학(Computational Fluid Dynamics, CFD)과 같은 유체역학 문제의 지배방정식을 이용한 접근법에 비해 모델의 구성이 자유롭고, 실제 물리 현상의 결과를 이용하므로 현실성이 높다는 장점이 있다. 따라서 시스템 식별이나 수치해석에서 고려되지 못한 물리 현상이나 외란의 영향을 확인할 수 있다.
선박조종문제에 있어 데이터기반 접근법은 2010년대 초반 이후 서포트벡터머신 (Zhang and Zou, 2011; Jian et al., 2015; Luo and Li, 2017; Wang et al., 2019), 인공신경망 (Wakita et al., 2022; Lou et al., 2022; Wang et al., 2022) 그리고 유전알고리즘 (Sutulo and Soares, 2014; Bonci et al., 2015)이 주를 이루었다. 그리고 베이지안네트워크 (Xue et al., 2020) 방식이나 최소자승법(least square method, LSQ) (Chillcce and Moctar, 2023), 가우시안회귀방법 (Liu et al., 2023; Ouyang et al., 2023a; Ouyang et al., 2023b)의 적용 사례가 있다. 하지만 이런 연구에서 사용된 기법들은 변수 간의 관계를 사용자가 이해할 수 없는 블랙박스(black box)식 접근법이 다수를 이뤄, 모델 구성의 물리적 근거를 설명할 수 없다는 문제가 있다.
선박 조종과 같이 제어 실패 시 위험성이 큰 문제에 대해서 블랙박스 접근을 통한 데이터 기반 모델링을 할 때에는 다음의 사항을 고려해야 한다. 우선 모델링의 결과가 물리적으로 타당한지를 확인하는 별도의 절차가 필요하며, 학습 데이터를 넘어서는 영역에서도 모델링이 타당한 결과를 내는지를 검증해야 한다. 그리고 모델링을 위한 데이터를 대상 시스템의 실제 운용 과정 중에 얻는 경우가 대부분이므로 해석에 영향을 줄 수 있는 외란의 영향이나 계측 시 잡음에 대한 필터링이 요구된다. 필터링 과정에서 개발자가 자의적으로 변수 영향을 축소할 수 있으므로, 데이터 기반 모델링의 장점으로 든 다양한 변수 영향의 식별의 효용성은 기대되는 수준에 미치지 못할 수 있다. 마지막으로, 딥러닝과 같이 수학적 계산의 소요가 큰 모델링 방법을 택할 경우, 새 데이터를 추가하는데 따른 조종 모델의 즉각적인 수정이 불가능하다는 점이 있다.
이러한 문제를 해결하기 위해서는 수학적으로 간단하며 사용자가 내부를 이해할 수 있는 조종 운동 해석 기법이 필요하다. Kim et al. (2024)의 연구에서는 주성분 분석(principal component analysis, PCA)을 이용해 선박의 조종 운동 중 동역학적 변수, 즉 운동과 유체력의 주요한 패턴을 구하고, 주성분을 조종 시나리오에 투영하여 각각이 내포하는 물리적 특성을 설명한 바가 있다. 선박의 4자유도 운동에 대한 PCA를 통해 주성분은 선박의 선회 중 연성된 운동 성분이 지배적이며, 추가로 고유 횡동요, 천이영역의 동역학적 특성 순으로 중요도가 분포함을 주성분에 대응하는 고유값의 크기 비교를 통해 확인하였다.
앞에서 보인 사례와 같이 PCA는 여러 변수로 구성된 다차원의 공간에서 데이터의 분산이 최대가 되는 주성분을 구하는데 사용된다. 이는 데이터의 주요한 패턴으로 이해될 수 있다. PCA를 통해 데이터를 주요 패턴의 선형결합으로 저차원화하여 나타낼 수 있으며, 이러한 성질은 주요 패턴이나 변수간의 상관관계와 무관하게 나타는 잡음의 제거 문제에도 응용될 수 있다 (Bishop, 2006; Lever et al., 2017; Brunton and Kutz, 2019). 그리고 선형 결합을 통해 데이터를 표현하므로, 학습에 이용된 데이터의 범위를 벗어나는 상황에서도 안정적인 데이터 추정을 기대할 수 있다. 이런 장점을 선형성이 강한 물리 현상인 선박 조종 운동의 모델링에 적용한다면 한정된 수의 주성분으로 선박의 조종 운동을 저차원화하여 표현할 수 있고, 그 주성분들의 물리적 의미를 사용자가 이해할 수 있기 때문에 기존의 데이터 기반 블랙박스 모델링 기법에 비해 활용성이 클 것으로 생각된다.
본 연구에서는 선박의 운동에 대응하는 유체력의 추정을 위해 주성분의 선형 결합을 이용하는 방안을 제안하였다. 우선 학습용의 조종 운동 데이터에서 주성분을 구하여 조종 운동 모델의 기본 구성을 갖추었다. 그리고 매 순간에 대해 주어진 운동 변수를 재구성할 수 있는 주성분의 선형 결합을 LSQ를 이용해 구하는 방식으로 운동에 대응하는 유체력을 얻는 운동 모델을 개발하였다. 이 모델을 선박의 3자유도 운동에 적용하여 주요한 조종 시나리오의 해석이 가능함을 보였다.
본 논문은 다음과 같이 구성되었다. 2장에서는 주성분 기반의 다변수 식별 방법을 설명하였다. 3장은 연구 대상 선형과 조종 모델을 소개하였다. 4장에 주요 조종 시나리오에 대한 주성분 추출, 이를 이용한 조종 모델의 비교검증 결과를 다뤘다. 5장은 본 연구의 결론이다.
2. 다변수 식별 모델
2.1 주성분 해석
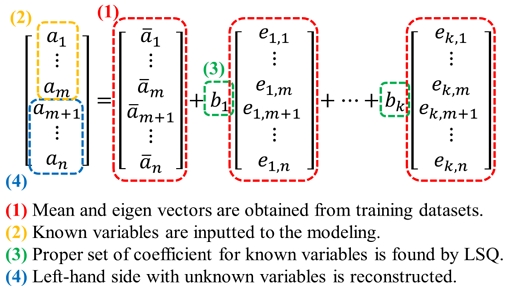
본 연구에서 제안되는 주성분의 선형 결합을 통한 다변수 식별법(multivariate identification by linear combination of principal components, MILP)을 선박 조종보다는 일반적인 관점에서 우선 설명하였다. 이를 선박의 조종 운동에 적용한 구체적인 내용은 이후 4장에서 다뤘다. n개의 변수로 구성된 데이터 벡터 를 다루는 시스템을 가정한다. a에 대한 여러 번의 계측으로 얻은 데이터 A에서 데이터의 공칭상태()를 빼서 요동 성분을 구한다. 그리고 각 변수들간의 Pearson coefficient로 구성된 n × n 크기의 상호상관행렬 AC를 구한다. PCA에서는 AC에서 얻을 수 있는 n개의 고유벡터()에 대해 대응하는 고유값(λi)의 크기를 각각 비교하여 유효한 k개의 를 추출한다. 그리고 식 (1)과 같이 의 선형 결합을 이용해 a를 근사하여 나타낸다.
| (1) |
선형 결합의 계수 벡터 b = [b1 ⋯ bk]는 식 (2)와 같이 직교 기저인 로 구성된 공간 상에 를 투영하여 얻는다.
| (2) |
2.2 변수 식별
식 (1)과 (2)를 이용한 저차원화 문제에서 b는 a를 이루는 변수를 모두 아는 때만 완성할 수 있다. 본 연구의 다변수 식별은 a에서 n보다 작은 m개의 일부 변수()만을 알고 있을 때, 나머지 (n - m)개의 변수()를 구하는 모델()을 구하는 과정이다. Fig. 1에 그 과정을 나타냈다.
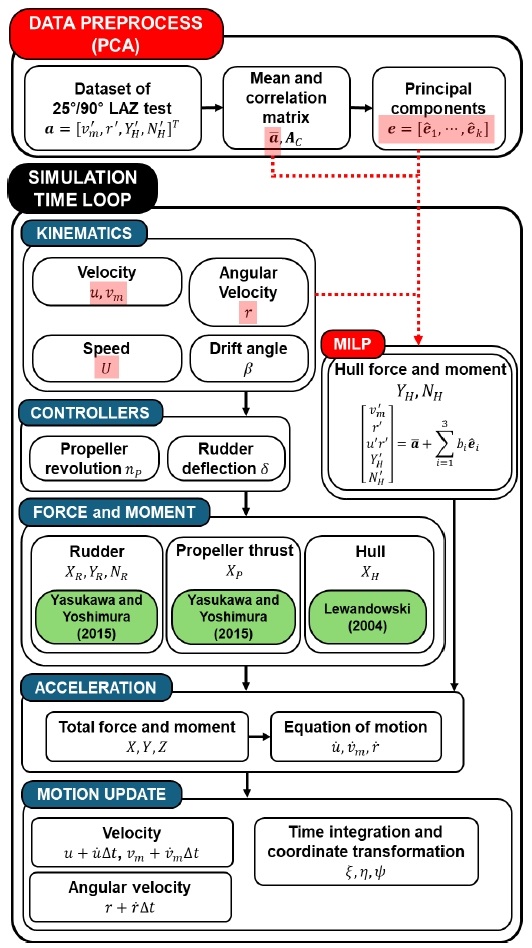
임의의 학습 데이터 A로부터 식 (1)을 구성하는데 필요한 , 를 얻는다. 학습에 사용되지 않은 데이터인 ain이 식의 좌변에 주어졌다면 우변에서 이를 근사할 수 있는 b를 구한다. k > m이라면 연립방정식의 수보다 구해야 하는 변수의 수가 더 많은 과소결정계(underdetermined system)가 되므로, k ≤ m일 때에만 b가 얻어진다. 본 연구에서는 b를 최소자승법을 통해 구하였다. 이제 식 (1)에서 우변이 완성되었으므로 좌변의 a도 유일하게 결정되어 그 일부인 aout를 구할 수 있다.
3. 해석 대상
3.1 선형
본 연구에서 조종 운동 모델의 개발을 위해 사용된 선형은 1/45.7 스케일의 KVLCC2 선형이다. 해당 선형은 Yasukawa and Yoshimura(2015)의 연구에서 조종 모델이 제안된 바 있다. Fig. 2와 Table 1은 각각 선형의 형상과 주요 요목이다.
3.2 좌표계
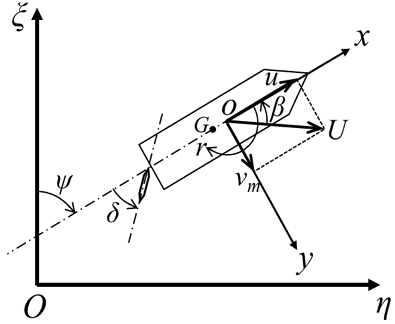
조종 중인 선박의 3자유도 운동은 전후동요(surge), 좌우동요(sway), 선수동요(yaw)만으로 구성된 수평면 상의 운동으로, 지구고정좌표계(O - ξη)와 물체고정좌표계(o - xy)를 이용해 동역학 해석을 수행했다. Fig. 3은 본 연구에 사용된 좌표계이다.
지구고정좌표계는 조종 운동 시작 시의 선체 중심의 수평면 투영 위치를 원점(O)으로 놓고, 같은 시점의 선수 방향을 ξ, 우현 방향을 η로 정의하였다. 이는 선체의 궤적을 표시하는데 사용된다. 물체고정좌표계는 이동하는 선체의 길이 중심을 원점(o)으로 하고, 선수 방향, 우현 방향을 각각 x, y로 정의하였다. 이 방향의 속도와 유체력은 각각 u, v, X, Y으로 정의하였다.
선수각(ψ)은 ξ와 x방향이 이루는 각도로, 오른손 직교좌표계의 정의를 따라 시계방향이 양의 방향으로 정의된다. 사항각(β)은 선체의 속도벡터()와 x방향이 이루는 각도로, 이는 선체가 운동하는 방향에서 선수가 얼마나 엇나갔는지를 의미한다. v와 β의 부호를 같게 하기 위해 ψ와 반대로 반시계방향을 양의 방향으로 정의하였다. 수평면상의 회전 운동에서 선체의 각속도와 모멘트는 각각 r, N으로 정의하였다. 방향타각(δ)은 선수가 시계방향으로 선회하도록 하는 방향을 양의 방향으로 정의하였는데, 이는 방향타의 반시계 방향의 회전에 대응된다.
3.3 조종 모델
조종 모델은 선체, 추진기, 방향타의 유체력과 모멘트를 조합해 전체 유체력과 모멘트를 구하는 컴포넌트 모델(component model)을 사용하였다. 식 (3)의 선체의 3자유도 운동방정식에서 H, P, R의 아래첨자는 각각 선체, 추진기, 방향타의 항을 의미한다.
| (3) |
여기서 M, Mx, My, Iz, Jz는 각각 선체 질량, x, y 방향의 부가질량, 선수동요에 대한 관성모멘트, 부가관성모멘트이다. , , 는 가속도와 각가속도이다. xG는 물체고정좌표계에서 무게중심의 x방향 위치이다. vm은 원점인 선체 중앙의 좌우동요 속도로, 무게중심의 속도 v와 식 (4)의 관계를 갖는다.
| (4) |
운동방정식의 운동 변수들은 물의 밀도(ρ), 선체의 수평면상 속력(), L, T를 이용해 무차원화하였다. 각 차원에 대한 무차원화 내용은 Table 2에 나타내었으며, 무차원화된 변수는 모두 '을 표시하였다.
무차원화된 선체의 유체력과 모멘트는 식 (5)와 같이 v'm, r'에 대한 다변수 테일러 급수(Taylor series)로 나타내는 경우가 일반적이다. 본 연구에서는 Yasukawa and Yoshimura (2015)의 연구에서 사용된 조종 계수 세트를 사용하였다. 이 계수를 사용한 동역학 모델은 뒤에서는 Original model이라고 부르도록 한다.
| (5) |
본 연구에서 개발된 데이터 기반 조종 운동 모델은 선체 유체력항 중 조종 운동에 큰 영향을 주는 YH와 NH를 2장에서 제안한 MILP 기반의 데이터 기반 모델링으로 대체하는 것을 목표로 한다. XH에 대해서는 경험식인 식 (6)으로 대체하였다 (Lewandowski, 2002). R0는 직진 중 저항이다.
| (6) |
MILP 기반 모델은 식 (5)의 운동과 유체력 및 모멘트의 입출력 관계를 식 (7)과 같이 주성분의 선형 결합으로 대체한다. 본 연구에서는 r'관련 성분의 비선형적 거동을 설명하기 위해 u'r'을 추가하였다. v'm, r', u'r'이 주어지면 이에 대응하는 b1, b2, b3를 최소자승법으로 식별하여 YH', NH'을 얻는다.
| (7) |
추진기의 추력(XP)과 방향타의 유체력, 모멘트(XR, YR, NR)는 Yasukawa and Yoshimura (2015)의 모델을 그대로 따랐으므로 본 연구에서 그 내용을 상세히 설명하지는 않았다. 추진기의 추력 모델은 추력감소비(tP)를 고려하여 전진비(JP)의 함수로 나타내었다.
| (8) |
여기서 nP는 추진기의 회전수이다.
방향타의 유체력과 모멘트는 식 (9)와 같이 타 직압력(FN)을 이용해 계산하였다. tR, aH, xH는 선체와 방향타의 상호작용에 대한 계수이고, xR은 방향타 위치의 x방향 좌표이다.
| (9) |
Fig. 4는 본 연구에서 제안된 MILP 모델 기반 조종 시뮬레이션의 전체적인 절차이다. 시뮬레이션 이전의 데이터 전처리(data preprocess)는 주어진 학습 데이터에 대해 2.1장의 내용을 통해 , e를 구하는 과정이다. MILP를 적용하는데 있어 데이터의 선형성을 최대한 확보하기 위해 서로 기함수의 구성을 갖는 v, r, YH, NH에 비선형성을 다루기 위한 ur을 추가해 a를 구성하였다. 따라서 n = 5, 입력 변수는 v, r, ur의 3개이므로 k = m = 3인 모델을 적용할 수 있다.
조종 시뮬레이션의 매 순간에서는 U, β의 계산과 nP, δ의 제어기가 순서대로 구동된다. 그리고 이 조건의 선체, 추진기, 방향타의 유체력과 모멘트를 계산한다. 식 (3)을 이용해 구한 , , 에 대한 수치적분을 통해 다음 time step의 u, vm, r을 구하는 과정을 반복한다.
3.4 조종 시나리오
모든 조종 시나리오는 모형스케일로 수행되었으며 직진 상태 프루드 수 (Froude number, ) 0.142에서의 자항점에서 시작하였다. 여기서 g는 중력가속도이다. 자항점에서의 프로펠러 회전수는 11.83rps이다.
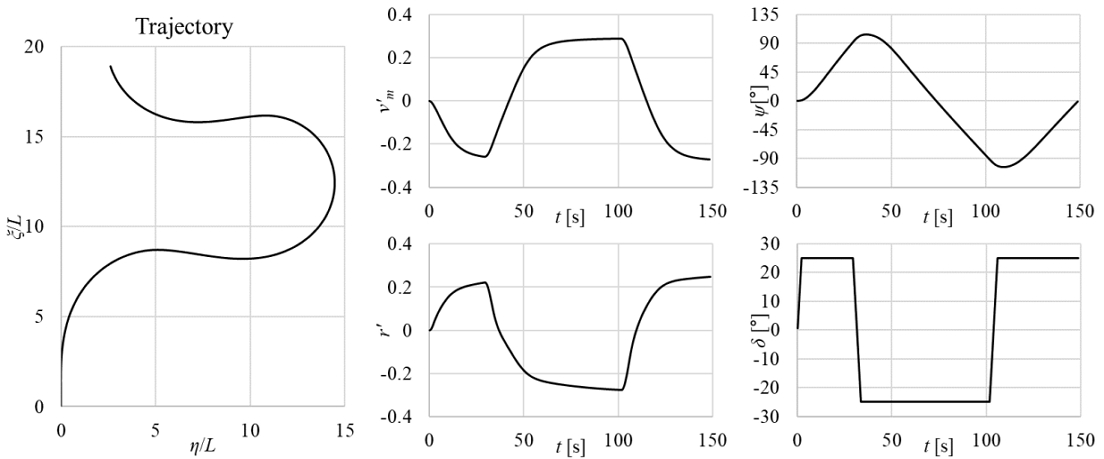
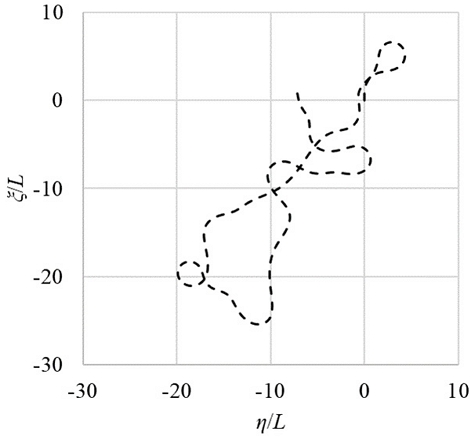
MILP 기반 조종 운동을 위한 학습 데이터는 Araki et al.(2012)에서 제안된 대각도 지그재그 시험(large angle zigzag test)을 통해 얻어졌다. 이는 통상적인 지그재그 시험에 비해 방향타각의 수정 시점을 δ보다 더 큰 Δψ에서 설정하는 방식으로, 선회 초기와 정속 선회 중의 동역학적 특성을 함께 다룰 수 있다. 조종 시나리오의 종료는 두 번의 선회 후 ψ = 0°이 되는 시점으로 하였다. 본 연구에서는 δ = 25°,ψ = 90°조건의 대각도 지그재그 시험을 수행한 결과만을 이용하여 주성분을 추출하여 MILP 모델을 구성하였다. Fig. 5는 25°/90° 대각도 지그재그 조종 시험의 궤적과 운동의 시계열이다.
MILP를 통해 개발한 조종 운동 모델의 검증은 무작위 조종 시나리오를 통해 수행하였다. 우선 δ 를 –35°에서 35°까지 5° 단위로 나누어 0°을 제외한 14개 조건 중 선택하게 하였다. 이를 편의상 Dice 1이라고 한다. 그리고 Dice 1으로 선택된 δ 에 대해 선수각 변화(Δψ)를 δ의 50%에서 300%까지 50% 단위로 나누어 6개 조건 중 선택하게 하였다. 이는 Dice 2라고 하였다. 예를 들어 δ = 20°, Δψ = 100%δ 가 선택되었다면 일반적인 20°/20° 지그재그 시험의 수행 조건과 같게 된다. 무작위 조종 시험은 이렇게 무작위로 선택된 Dice 1, 2로 구성된 단위 시나리오를 연속해서 수행하였다. 본 연구에서는 1000초 동안 조종 시나리오를 수행하였다. Fig. 6은 무작위 조종 시험의 궤적 예시이다.
4. 조종 모델 개발 결과
4.1 주성분 추출
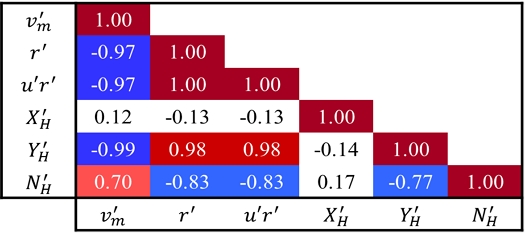
학습 데이터로 사용하기 위한 25°/90° 대각도 지그재그 조종 시험 시나리오를 Original model을 이용하여 좌, 우 선회에 대해 수행하고, 그 결과로부터 2.1장에서 제안된 방법을 통해 주성분을 추출하였다. Fig. 5의 시뮬레이션 결과로부터 각 변수 간의 상호상관도를 계산해 AC를 구해 Fig. 7에 나타내었다.
2.2장의 조종 모델 구성에서 설명한 바와 같이 XH'은 운동 성분에 대해 우함수의 구성을 가지므로 다른 변수와의 상호상관적인 관계가 드러나지 않았다. 따라서 AC는 XH'를 배제하고 v'H, r', u'r', YH', NH'의 5가지 변수에 대해서 구성하였다. u'r'에 대해서는 조종 운동 전반에서 u' ≫ um'의 이유로 그 값이 1에 가깝게 얻어진다. 따라서 u'r'과 r'은 거의 같은 상호상관도를 가지나, 둘의 작은 차이가 조종 운동에서의 비선형성을 설명하는데 도움이 될 것으로 판단하였다.
5개의 변수에 대해 구성된 AC는 5개의 를 갖는다. 그리고 의 중요도는 대응되는 고유값인 λi의 크기로 그 순서가 정해진다. 그리고 식 (10)의 유사도(si)를 이용해 문제를 저차원화하는데 필요한 의 수를 정할 수 있다.
| (10) |
Table 3은 AC에서 구한 와 sk이다. 이를 통해 s3 = 99.9%이므로 3개의 주성분으로 전체 운동을 표현하기에 충분할 것으로 보았다.
AC에 대한 주요한 3개의 고유벡터를 이용해 선체 유체력의 MILP 모델을 구성하였다. 학습 데이터로 사용하기 위한 조종 시나리오는 좌선회, 우선회 데이터를 포함하므로 데이터의 공칭상태()는 0으로 간주할 수 있다. 그 결과는 식 (11)과 같다.
| (11) |
4.2 주성분 계수 추정 결과 비교
MILP에서 최소자승법을 통해 구한 주성분 계수(b(t))가 실제 계수와 얼마나 일치하는지를 평가하였다. 식 (2)에서 매 순간의 b(t) 세트를 a(t)의 에 대한 투영을 통해 구할 수 있음을 보였다. 그리고 MILP에서는 b(t)를 LSQ를 통해 구하였으므로, 투영과 LSQ를 통해 각각 구한 b(t)를 비교함으로써 MILP가 b(t)를 올바르게 식별하는지를 알 수 있다.
Fig. 8은 Original model을 이용해 수행한 무작위 조종 시나리오의 시계열 운동(v'm, r', u'r')에서 매 순간에 대해 식 (2)의 투영과 최소자승법을 통해 구한 b(t)의 비교로, MILP 모델만을 이용해 수행한 조종 시뮬레이션이 아님에 유의한다. 조종 시나리오는 Fig. 6에서 보인 조건과 같다.
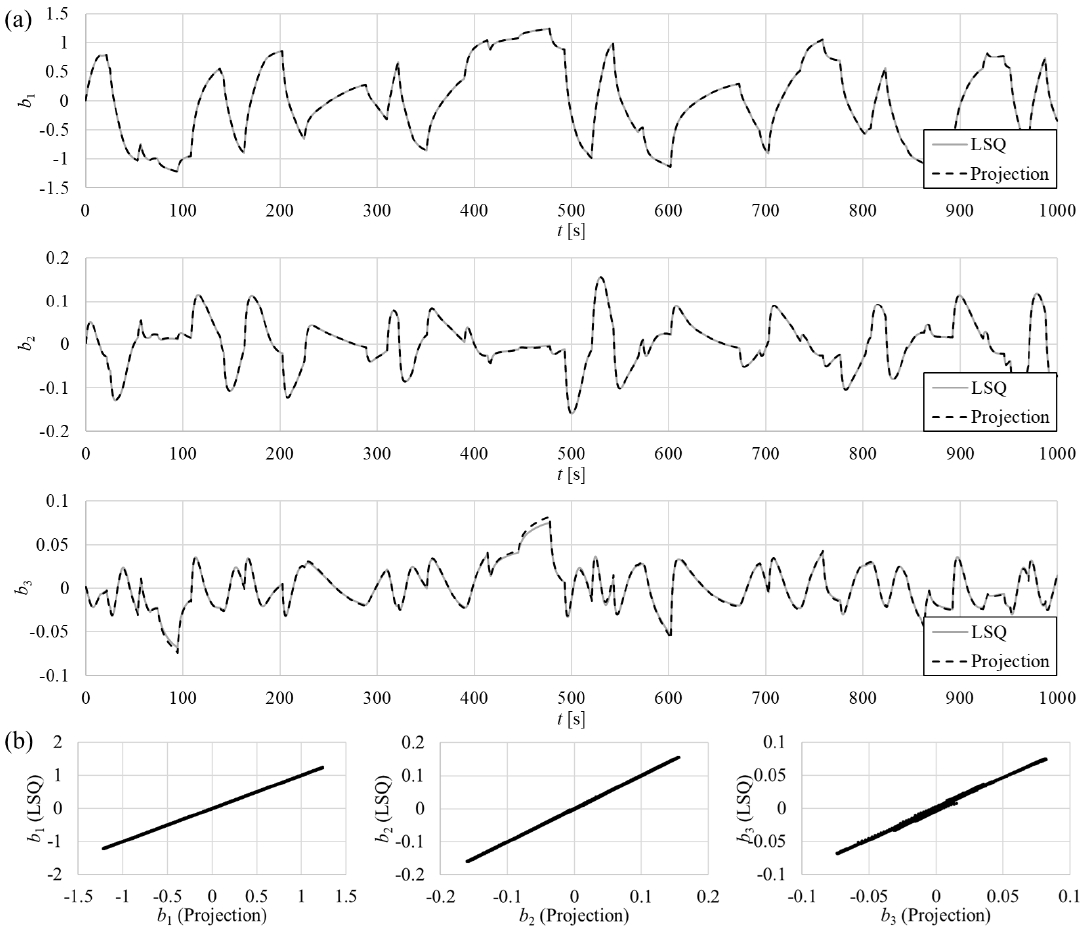
Comparison of b1, b2 and b3 in a random maneuver scenario, acquired by projection and least square method for principal components of 25°/90° large angle zigzag test: (a) time series and (b) correlation between projection and LSQ
b1과 b2에 대해서는 투영과 MILP간의 차이가 식별되지 않을 정도로 서로 같은 결과를 보였다. b3에 대해서는 일부 구간에서 값의 차이가 나타났지만, b1, b2, b3의 투영과 최소자승법 결과의 상호상관도는 각각 1.00, 1.00, 99.9로 최소자승법의 적용 신뢰도가 높은 것을 확인하였다. 따라서 본 연구에서 제안된 MILP 과정의 최소자승법으로도 3개의 주성분의 조합을 신뢰성있게 추정해내어 유체력과 모멘트를 얻을 수 있을 것으로 판단하였다.
4.3 유체력과 모멘트 비교
본 연구에서 개발한 MILP 기반의 선체 유체력 모델(MILP model)을 Original model과 비교하기 위해, 동일한 운동 조건에서 유체력과 모멘트의 추정값을 구하여 서로의 유사성을 검토하였다. 이를 위해, 식 (12)와 같이 주어진 운동 조건(u', v'm, r')에서 Original model과 MILP model로 얻은 유체력과 모멘트 변수(aOM, aMILP)의 차이를 전체 aOM에서의 동적 범위(dynamic range)로 나누어 ϵa(v'm, r',u'r')을 정의하였다.
| (12) |
Fig. 9는 전체 운동 범위에서의 비교 결과로, Yasukawa and Yoshimura(2015)의 구속모형시험 운동 범위와 본 연구의 25°/90° 대각도 지그재그 조종 시나리오의 v'm과 r'의 운동 범위를 각각 녹색 사각형 영역와 회색 점선으로 함께 표시하였다. 식 (4)와 β의 정의를 이용하면 v'm과 u'의 관계가 도출되므로 u'r'은 v'm과 r'이 주어지면 결정되는 값으로 보아 따로 표시하지는 않았다.
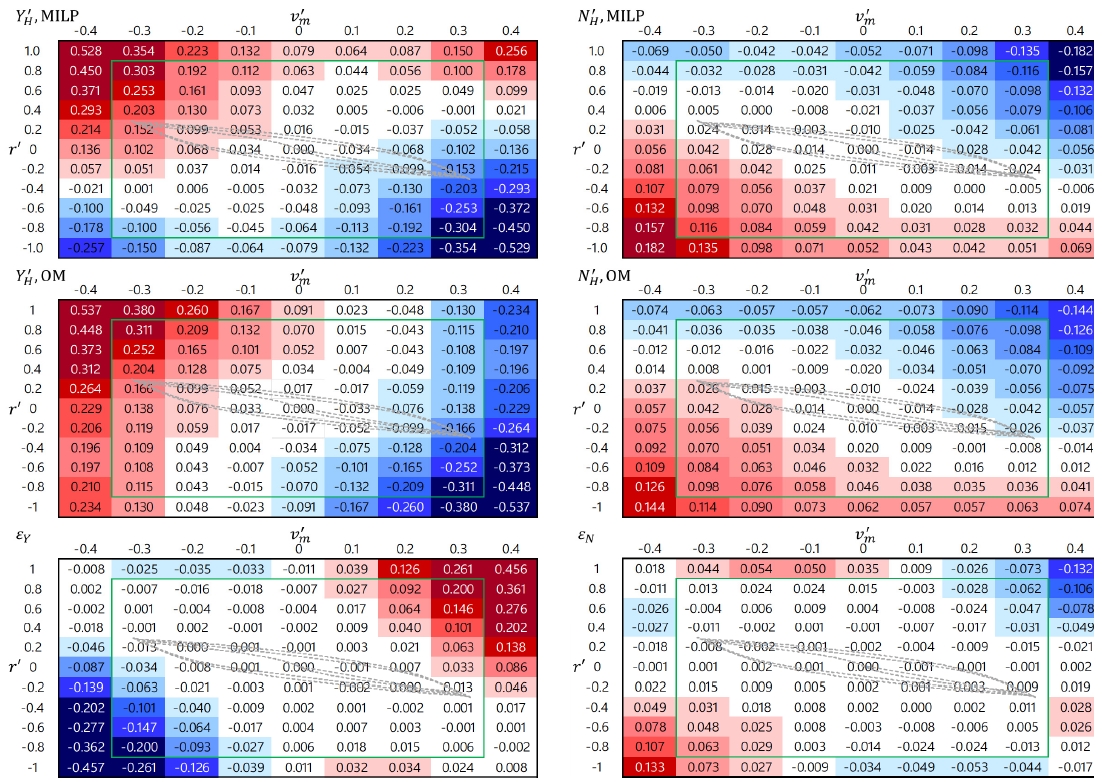
Comparison of YH' and NH' estimated by Original model and MILP model: green rectangular boundary is captive model test condition of Yasukawa and Yoshimura (2015), and broken grey curve is motion in 25°/90° large angle zigzag test.
전체 구속모형시험의 운동 범위에 비해 대각도 지그재그 조종 시험의 r'이 작은 범위로 나타났다. 대각도 지그재그 조종 시험의 운동 영역에서는 MILP model과 Original model 간에 YH', NH'의 차이가 작아서 ϵY, ϵN이 작게 나타날 것으로 기대하였다. 실제 비교 결과에서는 대각도 지그재그 조종에서 r'이 다양하지 않게 얻어졌지만, r'에 연관이 큰 NH'은 조종 운동 영역의 바깥에서도 Original model과 MILP model과의 차이가 작은 것을 확인하였다. 이는 MILP model이 한정된 데이터로도 원본 데이터를 효과적으로 재구성함을 시사한다. YH'에 대해서는 대각도 지그재그 조종 시험 영역에서는 차이가 줄어들었으며 v'm과 r'이 서로 다른 부호로 나타나는 운동 영역에서는 좋은 일치도를 보였다. Fig. 7에서 v'm과 r'는 서로 강한 음의 상관관계를 보이는 것을 확인했으므로, MILP를 이용한 YH'의 추정 또한 선박 조종에서 기대되는 2사분면, 4사분면의 운동 영역에서는 활용성이 확보된 것으로 보인다.
4.4 조종 시뮬레이션
Original model과 MILP model을 이용해 무작위 조종 시나리오와 정속 선회, 지그재그 조종 시험의 시뮬레이션을 수행하였다. MILP model의 유체력 추정에 대해서는 앞에서 그 신뢰성을 확인하였으나, 속도와 궤적을 구하기 위한 적분 과정에서는 오차의 누적으로 인해 결과에 차이가 발생할 수 있을 것으로 보았다. 그리고 XH'에 대해서는 MILP model에서는 경험식을 이용했으므로, 이에 대한 차이가 u'과 다른 운동 변수(v'm, r')로 어떻게 전파되는지를 확인하려 했다.
무작위 조종 시나리오의 수행으로 얻어진 운동과 유체력, 모멘트의 시계열을 Fig. 10에 나타내었다. XH'에 대해서는 MILP model에 비해 Original model에서의 변화가 더 크게 나타났다. 하지만 XH'에서 모델에 무관하게 일정한 R0'항의 비중이 가장 컸고, 방향타의 저항(XR') 또한 크게 발생하여 결과적으로 X'에서는 XH'의 모델 방법에 따른 영향은 제한적인 것으로 판단되었다. 이는 u가 두 모델에서 유사하게 나타난 것으로도 확인할 수 있다. 다른 운동 변수들은 서로 잘 일치하였으며, 조종 시나리오가 진행됨에 따라 예상한대로 운동의 위상이 조금 틀어지는 현상이 확인되었다.
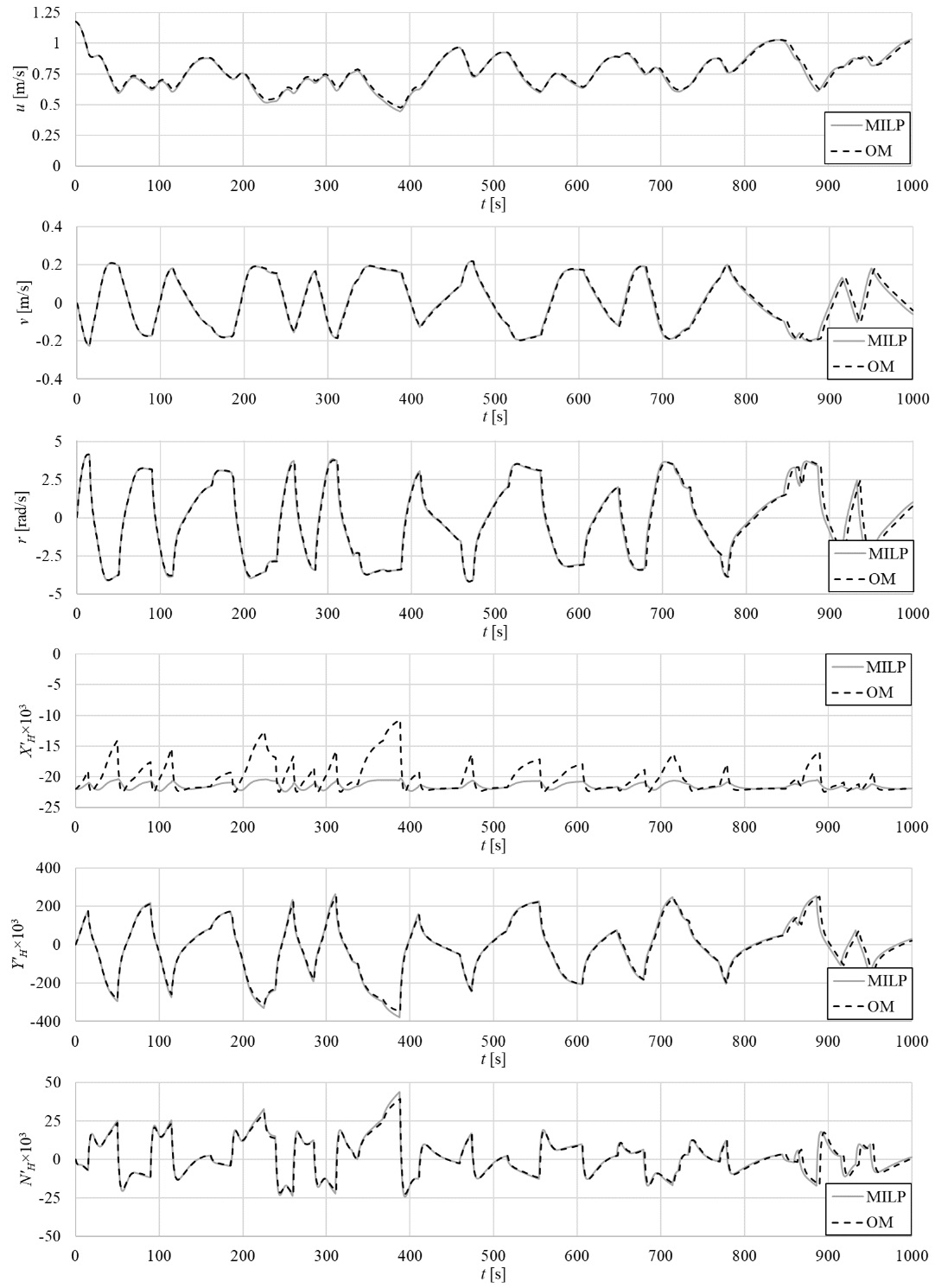
Time series of dynamics variables of random maneuver test simulation by Original model and MILP model
무작위 조종 시나리오와 정속 선회 시험에 대한 시뮬레이션 결과의 궤적을 Fig. 11에 나타내었다. 무작위 조종 시나리오에서는 Original model과 MILP model 모두 궤적이 잘 일치하여 Fig. 10에서 확인한 운동의 위상 차이가 궤적에 영향을 줄 수준은 아님을 알 수 있다. 정속 선회 시험 조건에서는 정상 상태에서 운동 변수의 차이가 누적되어 궤적의 차이가 나타났다.
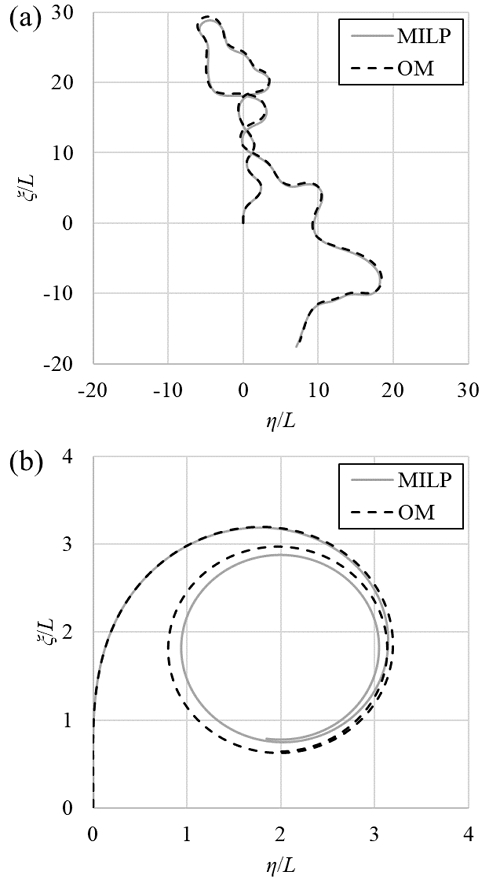
Comparison of trajectory by Original model and MILP model: (a) random maneuver and (b) 35° turning circle test
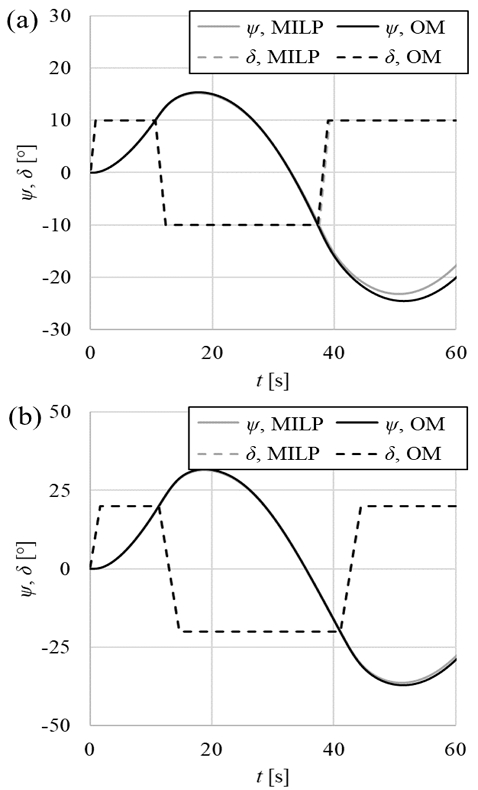
Fig. 12는 두 모델을 이용한 10°/10°, 20°/20° 지그재그 조종 시험의 선수각 시계열의 결과 비교이다. Fig. 11에서의 궤적과 같은 이유로 r'의 시간적분으로부터 얻어지는 ψ는 시간이 지남에 따라 Original model과 차이가 발생했다. 그 크기는 10°/10° 지그재그 조종 시험의 시뮬레이션에서 더 크게 나타났다. 이는 MILP model의 개발이 25°/90° 대각도 지그재그 조종 시험의 결과로부터 얻어졌기 때문에 타각이 유사한 20°/20° 지그재그 조종 시험이 상대적으로 동역학적 특성이 유사하기 때문으로 생각된다.
5. 결 론
주성분의 선형 결합을 통해 다변수를 식별하는 데이터 기반 모델링 기법을 제안하고 3자유도 선박 조종 운동에 적용하였다.
25°/90° 대각도 지그재그 조종 시나리오의 수행 결과로부터 주성분 분석을 통해 주요한 동역학적 패턴을 추출하였다. 동역학적 패턴의 선형 결합으로 저차원화된 동역학 모델을 구성하였다. 이에 대한 다음의 검증을 통해 선박의 3자유도 조종 운동 문제에서는 기존의 16개의 조종계수 대신 3개의 주성분으로도 조종 모델의 구성이 가능함을 확인하였다.
주어진 조종 운동에서 LSQ를 통해 주성분의 계수를 찾은 결과는 투영을 통해 구한 결과와 유의미한 차이는 발생하지 않았으므로, LSQ를 이용한 계수 식별이 유효함을 알 수 있었다. 선체의 운동 조건 별 유체력의 추정에 대해서는 시험에서 얻어진 운동 범위 밖에서도 좋은 예측 결과를 보였다. 그리고 저차원화된 동역학 모델의 시뮬레이션 결과는 원래의 조종 모델의 시뮬레이션 결과와 잘 일치하였다. 이를 통해 주성분 분석은 선박의 조종 운동을 효과적으로 저차원화하여 조종 운동 모델의 개발에 활용할 수 있음을 확인하였다.
제안된 MILP 기법은 인공신경망이나 다른 수학적 기법에 근거한 회귀분석 모델에 비해 모델링이 간단하여 새로운 데이터를 반영한 모델의 업데이트가 용이하다는 장점이 있다. 그리고 모델을 구성하는 주성분의 물리적 의미를 설명할 수 있기 때문에 자율운항선박의 다양한 분야에 적용될 경우 자동화된 시스템 운용의 신뢰성을 향상시킬 것으로 생각된다.
선박 조종 운동 분야에서의 MILP의 활용에 대해서는 향후 CFD나 모형시험을 통한 자유항주 데이터를 이용해 4자유도 조종 모델을 개발하는데 있어서의 적용 가능성을 평가하고자 한다. 그리고 자유항주 시험에서 얻어진 추진기와 방향타 유체력 정보 또한 현재의 수학적 모델 대신 데이터 기반 모델링에 MILP를 적용한다면 조종 모델이 설명 가능하면서도 간소하게 개선될 것으로 기대된다.
Acknowledgments
본 연구는 한국연구재단 지원의 ‘우수신진연구(NRF-2021R1C1C1014206)’사업으로 수행된 연구임.
References
-
Araki, M., Sadat-Hosseini, H., Sanada, Y., Tanimoto, K., Umeda, N. and Stern, F., 2012. Estimating maneuvering coefficients using system identification methods with experimental, system-based and CFD free-running trial data. Ocean Engineering, 51, pp.63-84.
[https://doi.org/10.1016/j.oceaneng.2012.05.001]

- Bishop, C.M., 2006. Pattern recognition and machine learning. Springer Nature.
-
Bonci, M., Viviani, M., Broglia, R. and Dubbioso, G., 2015. Method for estimating parameters of practical ship manoeuvring models based on the combination of RANSE computations and system identification. Applied Ocean Research, 52, pp.274-294.
[https://doi.org/10.1016/j.apor.2015.06.005]

-
Brunton, S.L. and Kutz, J.N., 2019. Data-driven science and engineering: machine learning, dynamical systems, and control. Cambridge University Press.
[https://doi.org/10.1017/9781108380690]

-
Chillcce, G. and el Moctar, O., 2023. Data-driven system identification of hydrodynamic maneuvering coefficients from free-running tests. Physics of Fluids, 35(5), Article No.057122
[https://doi.org/10.1063/5.0148219]

-
Jian, C., Jiayuan, Z., Feng, X., Jianchuan, Y., Zaojian, Z., Hao, Y., Tao, X. and Luchun, Y., 2015. Parametric estimation of ship maneuvering motion with integral sample structure for identification. Applied Ocean Research, 52, pp.212-221.
[https://doi.org/10.1016/j.apor.2015.06.007]

-
Kim, D., Kim, M., Lee, S. and J, Seo., 2024. A study on 4DOF ship dynamics in maneuver by principal component analysis. Journal of the Society of Naval Architects of Korea, 61(1), pp.29-44.
[https://doi.org/10.3744/SNAK.2024.61.1.29]

-
Lever, J., Krzywinski, M. and Altman, N., 2017. Points of significance: principal component analysis. Nature methods, 14(7), pp.641-643.
[https://doi.org/10.1038/nmeth.4346]

-
Lewandowski, E.M., 2004. The dynamics of marine craft: maneuvering and seakeeping. World scientific Publishing CO. Pte. Ltd.
[https://doi.org/10.1142/9789812562678]

-
Liu, S.Y., Ouyang, Z.L., Zhou, X. and Zou, Z.J., 2023. Black-box modeling of ship maneuvering motion based on Gaussian progress regression optimized by particle swarm optimization. International Journal of Offshore and Polar Engineering, 33(4), pp.337-345.
[https://doi.org/10.17736/ijope.2023.ak57]

-
Lou, J., Wang, H., Wang, J., Cai, Q. and Yi, H., 2022. Deep learning method for 3-DOF motion prediction of unmanned surface vehicles based on real sea maneuverability test. Ocean Engineering, 250, Article No.111015.
[https://doi.org/10.1016/j.oceaneng.2022.111015]

-
Luo, W. and Li, X., 2017. Measures to diminish the parameter drift in the modeling of ship manoeuvring using system identification. Applied Ocean Research, 67, pp.9-20.
[https://doi.org/10.1016/j.apor.2017.06.008]

-
Ouyang, Z.L., Zou, Z.J. and Zou, L., 2023a. Adaptive hybrid-kernel function based Gaussian process regression for nonparametric modeling of ship maneuvering motion. Ocean Engineering, 268, Article No.113373.
[https://doi.org/10.1016/j.oceaneng.2022.113373]

-
Ouyang, Z.L., Chen, G. and Zou, Z.J., 2023b. Identification modeling of ship maneuvering motion based on local Gaussian process regression. Ocean Engineering, 267, Article No.113251.
[https://doi.org/10.1016/j.oceaneng.2022.113251]

-
Sutulo, S. and Soares, C.G., 2014. An algorithm for offline identification of ship manoeuvring mathematical models from free-running tests. Ocean Engineering, 79, pp.10-25.
[https://doi.org/10.1016/j.oceaneng.2014.01.007]

-
Wakita, K., Maki, A., Umeda, N., Miyauchi, Y., Shimoji, T., RAchman, D.M. and Akimoto, Y., 2022. On neural network identification for low-speed ship maneuvering model. Journal of Marine Science and Technology, 22, pp.772-785.
[https://doi.org/10.1007/s00773-021-00867-1]

-
Wang, Z., Zou, Z. and Soares, C.G., 2019. Identification of ship manoeuvring motion based on nu-support vector machine. Ocean Engineering, 183, pp.270-281.
[https://doi.org/10.1016/j.oceaneng.2019.04.085]

-
Wang, T., Li, G., Hatledal, L.I., Skulstad, R., Æsøy, V. and Zhang, H., 2022. Incorporating approximate dynamics into data-driven calibrator: A representative model for ship maneuvering prediction. IEEE Transactions on Industrial Informatics, 18(3), pp.1781-1789.
[https://doi.org/10.1109/TII.2021.3088404]

-
Xue, Y., Liu, Y., Ji, C. and Xue, G., 2020. Hydrodynamic parameter identification for ship manoeuvring mathematical models using a Bayesian approach. Ocean Engineering, 195, Article No.106612.
[https://doi.org/10.1016/j.oceaneng.2019.106612]

-
Yasukawa, H. and Yoshimura, Y., 2015. Introduction of MMG standard method for ship maneuvering predictions. Journal of Marine Science and Technology, 22, pp.37-52.
[https://doi.org/10.1007/s00773-014-0293-y]

-
Zhang, X.G. and Zou, Z.J., 2011. Identification of Abkowitz model for ship manoeuvring motion using ε-support vector regression. Journal of hydrodynamics, 23(3), pp.353-360.
[https://doi.org/10.1016/S1001-6058(10)60123-0]