비선형 외란 관측기 기반 슬라이딩 모드 제어기를 활용한 자율 무인 잠수정 제어

1. 서 론

무인 잠수정(Autonomous Underwater Vehicle, AUV)은 해저에서의 다양한 작업과 국방 분야에서 무인화 작업으로 인명 손실 방지 및 장시간 운용이 가능한 장점 때문에 그 역할이 중대해지고 있으며, 자율임무를 수행하기 위해 무인 잠수정은 수중에서 위치와 방향을 유지하여 지정된 작업을 수행해야 한다. 그러나 무인 잠수정은 커플된 비선형 모델, 시변 동적 모델, 모델의 불확실성 및 조류와 파도와 같은 외부 외란의 영향을 받기 때문에 원하는 제어 성능에 도달하는 시스템을 설계하는 것은 어렵다.

따라서 무인 잠수정의 비선형적 특성과 불확실한 매개변수로 인해 비선형 강인 제어기를 무인 잠수정의 제어에 활용하는 연구가 활발히 진행되고 있다 (Jantapremjit and Wilson, 2008; Lea et al.,1999; Lekkas, 2014). 본 연구에서는 무인 잠수정의 동적 특성에 대한 성능을 향상하기 위한 강인 제어 방법 중에서 슬라이딩 모드 제어기(Sliding Mode Control, SMC) (Liu and Wang, 2011)를 사용하였다. 슬라이딩 모드 제어기는 시스템의 상태변수들을 미리 정의된 슬라이딩 평면(sliding surface)상에 계속 머무르게 하여 이 동안에는 시스템의 불확실성, 외란 등에 대해 안정성과 강건성을 보장하는 특징을 갖고 있다. 그러나 시스템의 불확실성을 보상하며 슬라이딩 평면상에서 시스템이 효율적으로 작동하기 위해서는 제어입력 값의 급격한 변화가 요구된다. 이러한 급격한 입력값의 변화는 슬라이딩 평면상에서 떨림 현상(chattering)이라고 불리는 구동기의 고주파 제어진동 현상을 발생시킨다. 떨림 현상은 이탈하려는 시스템 궤적을 슬라이딩 평면 위에 가둬두려는 제어 명령에 따라 생기며 이와 같은 떨림 현상은 시스템의 불확실성뿐만 아니라 실제 시스템에 적용 시 구동기의 기계적 성능에 나쁜 영향을 주게 된다. 그러므로 떨림 현상을 갖는 슬라이딩 모드 제어기의 실제적인 적용은 매우 어렵다.

본 연구에서는 이러한 떨림 현상을 완화하려는 방법의 하나인 불연속 슬라이딩 모드 제어기의 연속화 방법을 적용하였다. 연속화 방법은 슬라이딩 평면과 연계된 비선형 부호함수(signum function)를 제어 입력값으로 사용하는 것이 아니라 일정 범위 정도의 경계층(boundary layer)을 도입하는 하이퍼볼릭 탄젠트(hyperbolic tangent, tanh) 함수를 사용하여 경계층 영역 안에서는 제어 입력값을 연속적으로 근사화하여 사용하는 것이다 (Aghababa and Akbari, 2011).

또한, 외부 외란이 큰 경우 슬라이딩 모드 제어기를 사용하면 큰 제어 이득(control gain) 값을 요구하게 되므로 떨림 현상 또한 커지게 되어 성능 저하가 발생한다. 따라서 본 연구에서는 제어 시스템에서 비선형 외란과 모델 파라미터의 불확실성을 보상하기 위하여 비선형 외란 관측기(Nonlinear disturbance observer, NDOB) (Liu, 2017)를 사용하였다. 그에 따라 제어 이득을 작게 하면서 강인한 제어기를 구현할 수 있다. 외란 관측기는 실제 시스템의 모델과 공칭 모델 사이의 불확실성을 제어 과정에서 보상함으로써 실제 시스템의 거동이 공칭 모델과 근접하게 하는 역할을 한다. 따라서 외란 관측기의 도입은 제어기의 성능과 강인성을 향상한다.

본 연구에서 다루는 무인 잠수정 모델은 과작동(over- actuated) 특성이 있는 시스템이다. 그러므로 앞서 설계한 제어기를 통해 계산한 제어입력은 제어력 분배의 과정을 거쳐 무인 잠수정의 액추에이터로 전달되어야 한다. 이러한 과정을 통해 고 충실도(high-fidelity)를 갖춘 시뮬레이션을 수행하였으며 실제 시스템과 유사한 시스템을 구성하여 제어기를 검증하였다.

이러한 과정을 통하여 본 연구에서는 복잡한 비선형 특성이 있는 무인 잠수정 모델에 대하여 외부 외란과 조류의 영향을 받는 위험성이 높은 해양환경을 가정하여 무인 잠수정의 수평 운동을 제어하는 방법인 비선형 외란 관측기 기반 슬라이딩 모드 제어기를 제안한다.

본 연구에서는 MATLAB Simulink를 통해 비선형성과 불확실한 매개변수를 가진 무인 잠수정 모델이 조류와 외부 교란과 같은 외란을 받는 환경을 구현하였으며 슬라이딩 모드 제어기와 비선형 외란 관측기를 통해 외란과 불확실성을 보상하여 잠수정의 위치와 방위각에 대한 제어를 MATLAB 시뮬레이션을 통해 검증하였다.

이에 본문 2장에서 무인 잠수정 모델인 Delphin2 동역학 모델에 관한 내용을 다루고 3장에서 비선형 외란 관측기, 4장에서 슬라이딩 모드 제어기, 5장에서 제어력 분배, 6장에서 시뮬레이션 결과를 정리하고 7장에서 본 연구에서 얻은 결론을 정리한다.

2. Delphin2 동역학 모델

본 연구에서 사용한 무인 잠수정 모델은 6 자유도(six degree-of-freedom) 운동을 하는 Delphin2 모델을 사용하였다. Delphin2 모델은 관통형 수평 추진기와 수직 추진기를 각각 2개를 가지고 4개의 조종 면(러더(rudder), 스턴(stern))과 후방 프로펠러를 가지고 있다. Table 1에 모델의 제원을 나타내었다 (Tanakitkorn, 2017).

Table 1

Delphin2 particulars and key performances

2.1 Delphin2 동역학 모델

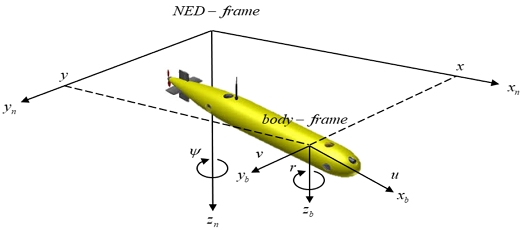
본 연구에서 사용한 무인 잠수정 동역학 모델은 6 자유도 운동을 하는 Delphin2 모델의 횡동요(roll) ϕ, 종동요(pitch) θ에 대한 운동을 무시하고 수평 운동인 전후동요(surge) u, 좌우동요(sway) v, 선수동요(yaw) ψ 운동에 집중하여 3 자유도 모델로 근사화하여 사용한다(Fig. 1 참조). 무인 잠수정 모델의 운동방정식은 Fossen (2011)에 의해 제시된 방정식을 사용하였다.

Fig. 1

AUV model in body-fixed frame and earth-fixed frame

무인 잠수정 모델은 지구 지표에 고정되어 있으며 x축이 진북, z축이 지구 중심을 가리키는 NED(north-east-down) 좌표계로 표현되며, 그 중심이 무인 잠수정의 부력의 중심인 선체 고정 좌표계(body-fixed frame)로 표현할 수 있다. 무인 잠수정 모델에 대한 3 자유도 동역학 식은 (1)과 같으며 동역학 계수는 Table 4와 같다 (Tanakitkorn, 2017).

$\[ M\dot{\nu }+C\left(\nu \right)\nu +D\left(\nu \right)\nu +G\left(\eta \right)=\tau \]$

(1)

$\[ \nu ={\left[u v r\right]}^T,\eta ={\left[x y \psi \right]}^T \]$

(2)

$\[ \tau ={\left[X Y N\right]}^T \]$

(3)

$\[ M\begin{array}{l}=M_{RB}+M_A\hfill \\ =\left[\begin{array}{ccc}m& 0& 0\\ 0& m& m{x}_g\\ 0& m{x}_g& I_{zz}\end{array}\right]+\left[\begin{array}{ccc}-X_{\dot{u}}& 0& 0\\ 0& -Y_{\dot{v}}& 0\\ 0& 0& -N_{\dot{r}}\end{array}\right]\hfill \\ =\left[\begin{array}{ccc}m-X_{\dot{u}}& 0& 0\\ 0& m-Y_{\dot{v}}& m{x}_g\\ 0& m{x}_g& I_{zz}-N_{\dot{r}}\end{array}\right]\hfill \end{array} \]$

(4)

$\[ C\left(\nu \right)=\left[\begin{array}{ccc}0& 0& -m\left(x_{q}r+v\right)+Y_{\dot{v}}v\\ 0& 0& -X_{\dot{u}}u+mu\\ m\left(x_{q}r+v\right)-Y_{\dot{v}}v& X_{\dot{u}}u-mu& 0\end{array}\right] \]$

(5)

$\[ D\left(\nu \right)=-\left[\begin{array}{ccc}{X}_u+X_{\left|u\right|u}\left|u\right|& 0& 0\\ 0& Y_v+Y_{\left|v\right|v}\left|v\right|& Y_r+Y_{\left|r\right|r}\left|r\right|\\ 0& N_v+N_{\left|v\right|v}\left|v\right|& N_r+N_{\left|r\right|r}\left|r\right|\end{array}\right] \]$

(6)

동역학 식 (1)에서 M은 관성 행렬, C(ν)은 코리올리(coriolis) 행렬, D(ν)은 감쇠 행렬, G(η)은 중력과 부력 행렬을 의미한다. 수평 운동에서 중력과 부력은 무시할 수 있으므로 G(η) = 0으로 가정한다 (Vu et al., 2020). Delphin2 모델에 대한 각 행렬은 위 식과 같다 (Tanakitkorn et al., 2017). τ는 제어입력을 의미하며 액추에이터로 인한 힘과 모멘트값이다.

$\[ \dot{\eta }=J\left(\eta \right)\nu \]$

(7)

$\[ J\left(\psi \right)=\left[\begin{array}{ccc}\mathrm{c}\mathrm{o}\mathrm{s}\psi & -\mathrm{s}\mathrm{i}\mathrm{n}\psi & 0\\ \mathrm{s}\mathrm{i}\mathrm{n}\psi & \mathrm{c}\mathrm{o}\mathrm{s}\psi & 0\\ 0& 0& 1\end{array}\right],J^{-1}\left(\psi \right)=J^T\left(\psi \right) \]$

(8)

식 (1)의 ν는 선체 고정좌표계에서 선속도와 각속도를 나타내고, η는 지구고정 좌표계에서 잠수정의 선형 위치, 오일러 각도를 의미한다. 회전행렬 J(η)는 선체 고정좌표계의 ν를 지구고정 좌표계의 $$ \dot{\eta }$$로 변환하는 행렬이다. 선수동요에 대한 행렬이므로 J(η) = J(ψ)으로 표현하며 식 (8)과 같이 정의된다 (Fossen, 2011).

3. 비선형 외란 관측기

비선형 외란 관측기는 시스템에 가해지는 외란을 예측하여 보상해준다. 본 논문에서는 비선형 외란 관측기를 사용하여 외부 교란, 조류의 영향과 동역학 모델 파라미터 오차를 예측하여 보상해주었다. 외란에 대한 식은 식 (18)을 통해 다음과 같이 정리된다.

보조 변수 z를 도입하여 외란의 추정값 $$ {\widehat{F}}_{dis}$$를 다음과 같이 정의한다. K는 비선형 외란 관측기의 게인(gain)으로 양의 상숫값이다.

외란 추정값의 시간에 대한 미분 값 $$ {\dot{\widehat{F}}}_{dis}$$은 $$ K\left(F_{dis}-{\widehat{F}}_{dis}\right)$$으로 정의한다. 또한, 위에서 정의한 F_dis 식을 대입하여 다음과 같이 정리한다.

외란과 외란 추정값의 차이를 $$ {\tilde{F}}_{dis}=F_{dis}-{\widehat{F}}_{dis}$$으로 정의하고 외란이 시간에 따라 매우 느리게 변화한다고 가정하여 $$ {\dot{F}}_{dis}$$ = 0이라고 가정한다 (Atsuo et al., 1994; Chen et al., 2000). 가정에 따라 외란과 외란 추정값의 차이의 시간에 대한 미분은 다음과 같이 정의된다.

보조 변수 z의 시간에 대하여 미분식은 식 (21), (22)에 의해 다음과 같이 정리된다.

$$ {\dot{\tilde{F}}}_{dis}$$ 식에 식 (24)을 대입하면 $$ {\tilde{F}}_{dis}$$에 대한 식으로 다음과 같이 정리되며 $$ {\tilde{F}}_{dis}$$는 시간에 따라 0으로 수렴하게 된다. 그러므로 외란 추정값 $$ {\widehat{F}}_{dis}$$은 외란 값 F_dis으로 수렴한다.

4. 슬라이딩 모드 제어기

비선형 강인 제어에 널리 사용되는 기법인 슬라이딩 모드 제어는 대표적인 강인 제어기로 외란과 모델의 변수에 불확실성이 있더라도 제어 성능과 안정성을 보장하는 효과적인 기법이다. 원하는 슬라이딩 평면을 정의하고, 이 슬라이딩 평면에 대한 리야푸노프 후보 함수(Lyapunov Candidate Function, LCF)를 설정하며, LCF가 0이 되도록 도달 법칙을 만든다. 이에 따른 제어입력을 만들어주는 방식으로 동작한다.

4.3 제어입력

제어입력은 식 (32) 같이 τ_eq와 τ_sw의 합으로 정의하며 LCF의 시간에 대한 미분 값을 0보다 작게 만드는 값으로 정의한다. τ_sw는 불확실성과 외란의 영향을 보상하는 항으로 비선형 부호함수가 게인 행렬 β와 곱해진 항으로 정의된다.

위에서 정의한 조건을 만족하는 제어입력을 시스템의 추정값을 이용하여 정의한다. 아래 식에서 $$ \widehat{•}$$는 각 시스템행렬에 대한 추정값을 나타내며, $$ {\widehat{F}}_{dis}$$는 외란의 추정값을 나타낸다.

$\[ {\tau }_E={\tau }_{eq}+{\tau }_{sw} \]$

(32)

$\[ {\tau }_{eq}={\widehat{M}}_E\left[\ddot{\eta }+\dot{s}\right]+\left({\widehat{C}}_E+{\widehat{D}}_E\right)\left[\dot{\eta }+s\right]+{\widehat{G}}_E-{\widehat{F}}_{dis} \]$

(33)

$\[ {\tau }_{sw}=\beta sign\left(s\right) \]$

(34)

(35)

제어입력에 포함된 시스템행렬들이 포함하고 있는 모델 불확실성은 위 식과 같이 시스템 오차가 크기에 대한 제한 조건을 만족한다고 가정한다. 제어입력을 위에서 정리한 LCF의 미분 식에 대입하고 크기에 대한 제한 조건을 통해 LCF의 시간에 대한 미분 값의 크기가 특정 한곗값보다 작다는 것을 알 수 있다.

$\[ \dot{V}=\begin{array}{l}-s^T{D}_{E}s+s^T\left[\left(M_E-{\widehat{M}}_E\right)\left[\ddot{\eta }+\dot{s}\right]\right.\hfill \\ +\left(C_E-{\widehat{C}}_E+D_E-{\widehat{D}}_E\right)\left[\dot{\eta }+s\right]\hfill \\ \left.+\left(G_E-{\widehat{G}}_E\right)-\left(F_{dis }-{\widehat{F}}_{dis }\right)-\beta sgn\left(s\right)\right]\hfill \end{array} \]$

(36)

$\[ \begin{array}{c}\dot{V}\le \begin{array}{l}-s^T{D}_{E}s+\left[\delta M_E‖\ddot{\eta }+\dot{s}‖\right.\hfill \\ +\left(\delta C_E+\delta D_E\right)‖\dot{\eta }+s‖\hfill \\ \left.+\delta G_E+{\stackrel{-}{F}}_{dis}\right]‖s‖-s^T\beta sgn\left(s\right)\hfill \end{array}\hfill \end{array} \]$

(37)

$\[ 0\le {\lambda }_{\text{min}}\left(\beta \right)‖s‖\le s^T\beta sgn\left(s\right) \]$

(38)

λ_min(β) 은 행렬 β의 최소 고윳값을 의미하고 위의 부등식을 만족한다고 가정한다. 이러한 조건을 이용하면 LCF의 미분 식이 아래와 같이 단순화된다.

$\[ \begin{array}{c}\dot{V}\le \begin{array}{l}-s^T{D}_{E}s+\left[\delta M_E‖\ddot{\eta }+\dot{s}‖\right.\hfill \\ +\left(\delta C_E+\delta D_E\right)‖\dot{\eta }+\dot{s}‖\hfill \\ \left.+\delta G_E+{\stackrel{-}{F}}_{dis}-{\lambda }_{\text{min}}\left(\beta \right)\right]‖s‖\hfill \end{array}\hfill \end{array} \]$

(39)

$\[ \begin{array}{c}{\lambda }_{\text{min}}\left(\beta \right)\begin{array}{l}\ge \delta M_E‖\ddot{\eta }+\dot{s}‖\hfill \\ +\left(\delta C_E+\delta D_E\right)‖\dot{\eta }+s‖+\delta G_E+{\stackrel{-}{F}}_{dis}\hfill \end{array}\hfill \end{array} \]$

(40)

LCF의 미분 식이 음의 정부호 특성을 갖기 위해서는 게인 행렬 β을 식 (40) 조건을 만족하도록 선택해야 한다. 리야푸노프 안정도(lyapunov stability) 이론에 의해 t → ∞일 때 s는 0으로 수렴한다. 따라서 $$ \dot{e}$$,e는 0으로 수렴한다. 시스템에 입력되는 비선형 부호함수는 빠르게 변하는 불연속적인 신호를 갖기 때문에 떨림 현상인 채터링 현상이 발생한다. 따라서 채터링 현상을 감소시키기 위하여 다음과 같이 하이퍼볼릭 탄젠트 함수로 불연속적인 신호를 연속적으로 변경한다.

$\[ {\tau }_{\mathrm{s}\mathrm{w}}=\beta \mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}\left(\frac{\mathrm{S}}{\mathrm{\Phi }}\right) \]$

(41)

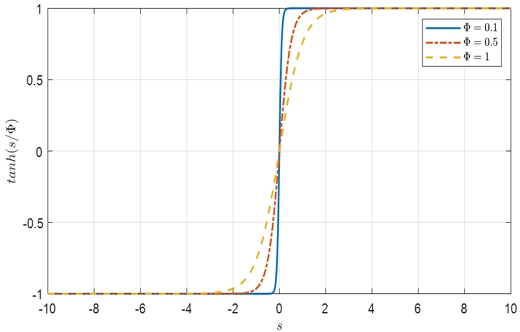
경계층 Φ는 슬라이딩 평면 근처 경계층을 의미한다. tanh(s/Φ)는 sgn(s)과 유사한 궤적을 보이며 경계층인 양수 Φ가 작을수록 tanh(s/Φ)가 sgn(s)에 더욱 근접한다(Fig. 2 참조). 하지만 Φ가 작을수록 실제 제어기 구현 시 채터링을 유발하기 쉽고 Φ가 클수록 수렴 안정도가 떨어지므로 그 점을 유의해서 Φ를 선택해야 한다.

Fig. 2

Tanh(*) function with various values of Φ

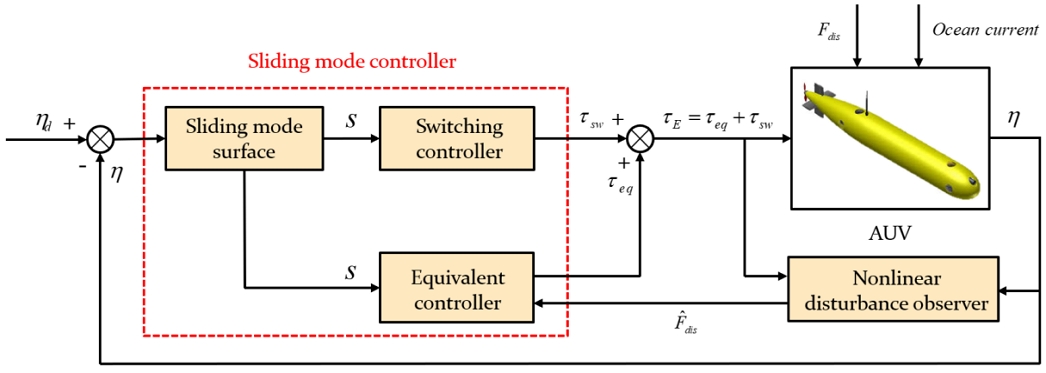
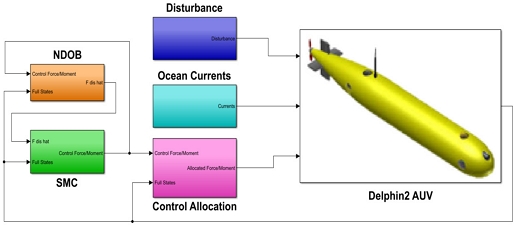
본 연구에서 제안하는 비선형 외란 관측기 기반 슬라이딩 모드 제어기는 Fig. 3의 다이어그램과 같이 구성된다. 제어기는 시스템의 상태변수 η의 오차 값과 비선형 외란 관측기에서 계산된 외란의 추정값을 입력받아 제어입력을 계산한다. 외부 외란과 조류의 영향을 받는 무인 잠수정은 제어기로 계산된 제어입력을 입력받아 목표 위치와 방위각으로 이동한다.

Fig. 3

Control architecture of the proposed controller

5. 제어력 분배

본 연구에서 다루는 무인 잠수정 모델은 과작동 특성을 가지고 있다. 그러므로 힘과 모멘트의 형태로 계산되는 제어입력은 실제 무인 잠수정의 거동을 위해서 무인 잠수정의 액추에이터에 분배되어야 한다. 본 연구에서는 제어분배 법칙(Tanakitkorn, 2017)에 따라 제어입력이 각 액추에이터로 분배되는 과정을 다룬다.

5.1 방위각 제어 제어력 분배

Delphin2 모델은 러더와 2개의 수평 추진기를 통해 방위각을 제어한다. 제어기를 통해 계산된 제어입력 중, 선수동요 모멘트는 제어분배 법칙(Tanakitkorn, 2017)에 따라 러더와 수평 추진기에 분배되며 제어력 분배는 후방 프로펠러의 요구값 u_prop에 따라 분배 방법이 결정된다. u_prop는 [10,-22] 사이의 값을 가지는 모터에 인가되는 무차원의 프로펠러의 요구값(propoller setpoint)이다.

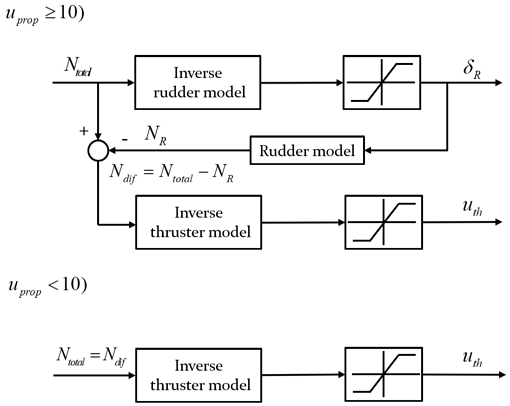
Fig. 4는 방위각 제어력 분배 법칙을 설명하기 위한 다이어그램이다. 프로펠러의 요구값이 10보다 크거나 같은 경우 제어기를 통해 계산된 제어입력은 역 러더 모델(inverse rudder model)에 입력되어 다음 식을 통해 러더 각도 δ_R(deg) ∈ [-30,30]가 계산된다.

$\[ {\delta }_R=\frac{N_{total }}{N_{\left|u\right|u{\delta }_R}\left|u\right|u} \]$

(42)

Fig. 4

A daisy-chaining heading control allocation diagram according to propeller demand

N_|u|uδR는 러더의 편향으로 인한 선수동요 감쇠 계수이다. 계산된 러더 각도는 러더 모델(rudder model) N_|u|uδR|u|uδ_R에 입력되어 러더로 인한 모멘트 N_R가 계산되고 러더로 인한 선수동요 모멘트를 제외한 나머지 모멘트 N_dif가 식 (43)과 같은 역 추진기 모델(inverse thruster model)을 거쳐 추진기에 추진기 요구량 u_th으로 입력된다.

$\[ u_{th}=sign\left(N_{dif}\right)\sqrt{\frac{\left|N_{dif}\right|}{L_h\rho D_{th}^4{ K}_{T,th}}} \]$

(43)

여기서 ρ는 물의 밀도, D_th는 추진기의 직경, K_T,th는 추진기의 추력 계수, L_h는 두 수평 추진기 사이의 거리를 의미한다(Table 4 참조). 추진기 요구량은 u_th (rpm) ∈ [-2500,-150] ∪ [150,2500]다음 범위 내에서 값을 가지며 rpm으로 측정되는 추진기 속도와 동일한 값을 가지고 (-150,150) 범위에서 불감대(deadband)를 갖는다.

프로펠러의 요구값이 10보다 작은 경우 무인 잠수정은 추진기만을 사용하여 방위각을 제어한다. 그러므로 제어기를 통해 계산한 선수동요 모멘트는 역 추진기 모델을 거쳐 추진기에 전달된다.

6. 시뮬레이션 결과

설계된 제어기의 성능을 검증하기 위하여 Table 2의 시뮬레이션 변수를 이용하여 시뮬레이션을 수행하였다. 이 시뮬레이션의 MATLAB Simulink 블록 다이어그램 프로그램은 Fig. 5과 같다. 식 (17)의 선체 고정좌표계에서 수평 운동 비선형 방정식을 이용하여 Delphin2의 MATLAB Simulink 모델을 개발하였으며 식 (18)의 지구고정 좌표계에서 수평 운동 비선형 방정식을 이용하여 Delphin2의 제어기와 비선형 외란 관측기를 개발하였다.

Table 2

Parameters of the simulation

Fig. 5

Simulation program using matlab-simulink

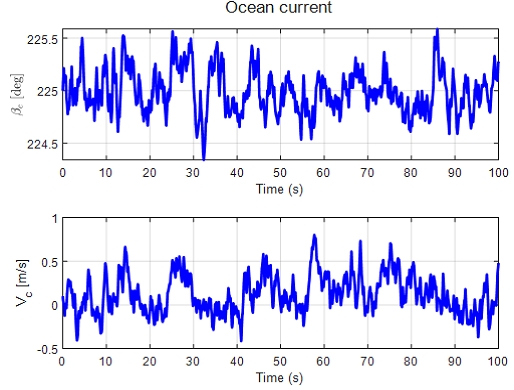
제어기에서 계산된 제어 입력값은 식 (8)의 좌표변환 행렬 이용하여 변환 후 Delphin2 운동 모델에 입력해주었다. 제어기의 강인성을 검증하기 위하여 시스템에 불확실성을 포함할 수 있는 시스템 변수 중 질량, 질량 관성모멘트 및 유체력 계수 값들에 대하여 +30%의 불확실성을 갖도록 설정하였으며 외부 외란이 지속해서 가해지는 상황을 설계하였다. 또한, 해양환경에서 발생할 수 있는 조류는 식 (14)의 가우스-마르코프 프로세스에 의해 발생하도록 하였으며 Fig. 6에 나타낸 바와 같이 225°의 방향각에서 기준 속도 0.1m/s의 크기로 무인 잠수정에 가해지고 있다. 이러한 환경에서 100s까지 η_d = [x_d, y_d, ψ_d]의 궤적을 추종하도록 하는 시뮬레이션을 수행하였다.

Fig. 6

Ocean currents parameters of βc and Vc

외란 F_dis은 X, Y, N에 대하여 식 (52)와 같이 다양한 주파수의 정현파 신호가 합해진 형태로 가해주었다.

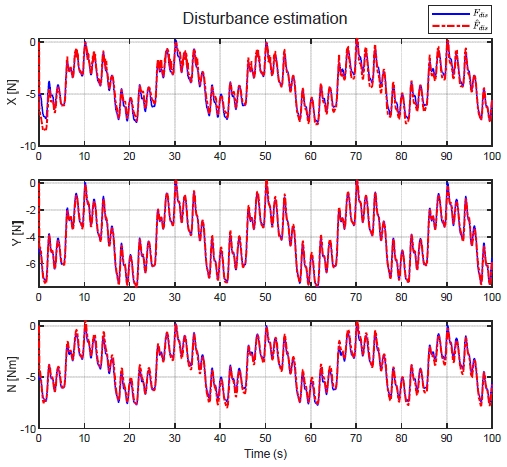
Fig. 7의 파란색 그래프는 가해지는 외란이며 빨간색 그래프는 비선형 외란 관측기를 적용한 슬라이딩 모드 제어기의 성능을 검증하기 위하여 시스템에 입력되는 외란 값을 추정한 결과인 $$ {\widehat{F}}_{dis}$$이다. 외란을 빠르게 추정하는 것을 확인할 수 있으며, 추정한 외란은 시스템에 입력되어 보상된다.

Fig. 7

True disturbance(blue line) and estimated value of disturbance(red line)

슬라이딩 모드 제어기와 비선형 외란 관측기를 적용한 슬라이딩 모드 제어기로 계산된 제어입력 τ은 Fig. 8과 같이 시스템에 입력된다. 경계층을 도입한 하이퍼볼릭 탄젠트 함수를 통해 채터링현상이 거의 없는 것을 확인할 수 있다.

Fig. 8

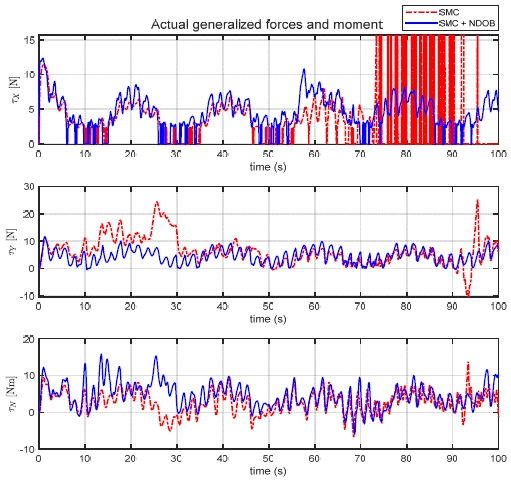
Comparison plot of actual generalized forces and moment(τX, τY, τN) of SMC+NDOB(blue line) and SMC(red line) controller

제어력 분배에 의해서 계산된 액추에이터 요구값은 Fig. 9와 같이 액추에이터에 입력된다. 그래프에서 볼 수 있듯이 u_prop의 크기에 따라 액추에이터의 사용이 결정되며 10보다 작은 경우, 러더의 사용이 없고 추진기만 사용하여 방위각을 제어하기 때문에 u_th,frt, u_th,aft만 발생하는 것을 확인하였다.

Fig. 9

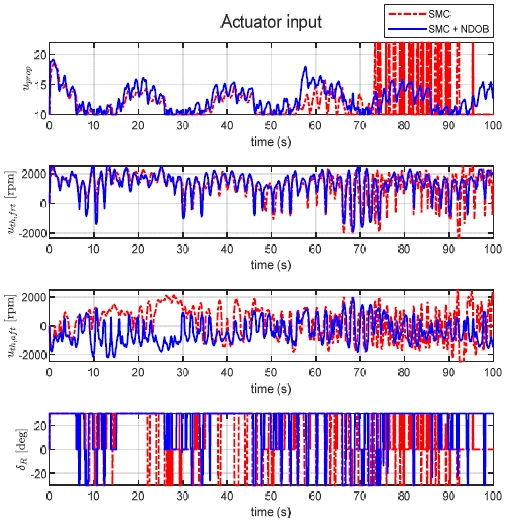
upropand uth,frt,uth,aft,δR actuator input comparison plot for SMC+NDOB(blue line) and SMC(red line) controllers

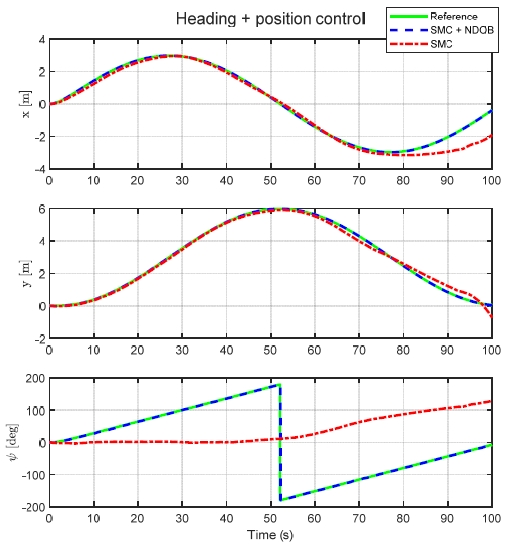
Fig. 10에서는 x, y를 그래프의 축으로 하여 무인 잠수정의 궤적과 도착점의 방위각을 표현하였다. Fig. 11에서는 시간에 따른 x, y, ψ 제어 결괏값을 표현하였다. 슬라이딩 모드 제어기만 사용하였을 경우 제어 목푯값을 추종하지 못하고 오차값이 크게 발생한다. 제어기의 성능을 수치를 통해 비교하기 위해 제어 오차 값의 제곱평균 제곱근(root mean square, RMS)을 구하여 비교하였다. 그 결과 Table 3에서 볼 수 있듯이 슬라이딩 모드 제어기에 비선형 외란 관측기를 적용한 결과 슬라이딩 모드 제어기만 사용하여 시뮬레이션한 결과보다 오차가 26배 이상 감소한 것을 확인할 수 있다.

Fig. 10

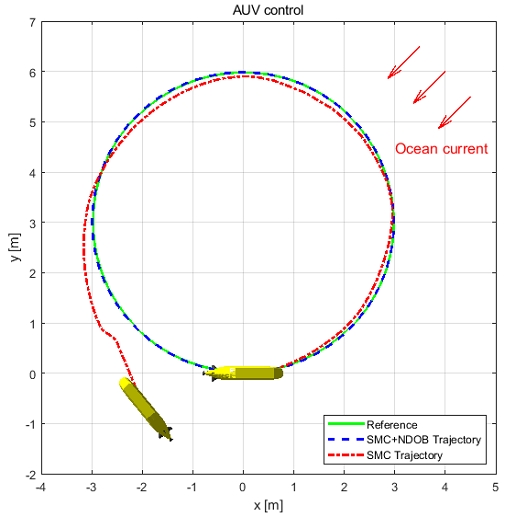
Comparison trajectory plot of heading and position control between SMC+NDOB (blue line) and SMC (red line)

Fig. 11

Comparison plot of x, y, ψ control between SMC+NDOB(blue line) and SMC(red line)

Table 3

Performance measures using RMS of errors for SMC+NDOB and SMC controllers

7. 결 론

무인 잠수정이 수중에서 원하는 작업을 성공적으로 수행하기 위해서는 모델의 불확실성이나 강한 조류와 같은 외란을 극복하고 원하는 위치와 자세로 이동 및 유지를 위한 강인한 제어 성능을 갖는 제어기가 필요하다. 본 연구에서는 외란에 강인한 성능을 갖는 슬라이딩 모드 제어기와 슬라이딩 모드 제어기의 한계를 보완해줄 비선형 외란 관측기를 설계하여 무인 잠수정이 외란을 보상하여 제어를 수행하도록 하였다. 이를 시뮬레이션을 통하여 알고리즘의 유효성을 검증하였다.

Table 4

3-DOF Delphin2 AUV model parameter

Acknowledgments

이 연구는 2023년 국방과학연구소 미래 도전 국방기술 연구개발사업 (No. 915071101)의 지원을 받았음.

References

• Aghababa, M.P. and Akbari, M.E., 2011. A chattering-free robust adaptive sliding mode controller for synchronization of two different chaotic systems with unknown uncertainties and external disturbances. Applied Mathematics and Computation, 218(9), pp.5757-5768. [https://doi.org/10.1016/j.amc.2011.11.080]
• Atsuo, K., Hirosh. I. and Kiyoshi, S., 1994. Chattering reduction of disturbance observer based sliding mode control. IEEE transactions on industry applications, 30(2), pp.456-461. [https://doi.org/10.1109/28.287509]
• Chen, W.H., Ballance, D.J., Gawthrop, P.J. and Reilly, J.O., 2000. A Nonlinear Disturbance Observer for Robotic Manipulators. IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, 47(4), pp.932-938. [https://doi.org/10.1109/41.857974]
• Fossen, T.I., 1994. Guidance and control of ocean vehicles. A John Wiley & Sons Ltd: USA.
• Fossen, T.I., 2011. Handbook of Marine Craft Hydrodynamics and Motion Control. A John Wiley & Sons Ltd: USA. [https://doi.org/10.1002/9781119994138]
• Lea, R.K., Allen, R.A. and Merry S.L., 1999. A comparative study of control techniques for an underwater flight vehicle. International Journal of Systems Science, 30(9), pp.947-964. [https://doi.org/10.1080/002077299291831]
• Lekkas A.M., 2014. Guidance and Path-Planning Systems for Autonomous Vehicles. Ph.D. Norway: Norwegian University of Science and Technology.
• Liu, J. and Wang X., 2011. Advanced sliding mode control for mechanical systems design, Analysis and Matlab Simulation. Tsinghua & Springer Press: Beijin. [https://doi.org/10.1007/978-3-642-20907-9_3]
• Liu, J., 2017. Sliding mode control using MATLAB. Academic Press: Beijing. [https://doi.org/10.1016/B978-0-12-802575-8.00005-9]
• Jantapremjit, P. and Wilson, P.A., 2008. Guidance-control based path following for homing and docking using an autonomous underwater vehicle. IEEE Kobe Techno-Ocean, (1), pp.1–6. [https://doi.org/10.1109/OCEANSKOBE.2008.4530935]
• Kim, D.H., 2016. Redundancy resolution and robust controller design for dynamic stability enhancement of underwater vehicle-manipulator systems. Ph.D. Korea Maritime and Ocean University.
• Tanakitkorn, K., 2017. Guidance, control and path planning for autonomous underwater vehicles. Ph.D. Southampton.
• Tanakitkorn, K., Wilson, P.A., Turnock, S.R. and Phillips, A.B., 2017. Sliding mode heading control of an overactuated, hover-capable autonomous underwater vehicle with experimental verification. Journal of Field Robotics, 35(3), pp.395-415. [https://doi.org/10.1002/rob.21766]
• Vu, M.T., Thanh, H.L.N.N., Huynh, T.T., Do, Q.T., Do, T.D., Hoang, Q.D. and Le, T.H., 2020. Station-keeping control of a hovering over-actuated autonomous underwater vehicle under ocean current effects and model uncertainties in horizontal plane. IEEE Access, 9, pp.6855-6867. [https://doi.org/10.1109/ACCESS.2020.3048706]