평판 경계층에 대한 스터드의 난류촉진 영향 연구

1. 서 론

UN 산하 국제해사기구(International Maritime Organization, IMO)에서는 선박의 온실가스 배출량 감소를 위해, 2013년부터 신조선에 대해 에너지효율설계지수(Energy Efficiency Design Index, EEDI) 규제를 시행하고 있다. EEDI는 단계적으로 강화되고 있으며, 온실가스 배출량 저감 목표달성을 위해 일부선종을 대상으로 EEDI phase 3의 조기시행이 예정되어 있다. MEPC(Marine Environment Protection Committee) 76차 회의에서는 신조선뿐만 아니라, 현존선에 대해서도 현존선에너지효율지수(Energy Efficiency Existing Ship Index, EEXI)를 도입하는 것이 결정되었다. 위와 같은 선박의 에너지효율규제를 만족하는 방법으로써, 주기관의 엔진출력을 감소시키는 방법이 주로 사용되고 있으며, 과거에 비해 선박의 운항속도는 감소되고 있다. 또한, IT기술의 발달로 인한 자율운항선박의 개발과 디지털 트윈 기술의 확대로, 저속운항 등 전 운항 속도 영역을 포함하는 선박의 물리 모형정립의 필요성이 증가하고 있다.

실제 선박의 속도 마력성능의 평가는 대부분 예인수조에서 모형시험을 통해 평가된다. 예인수조에서 실선의 속도마력 성능평가를 위한 모형시험은 실선과 기하학적으로 상사한 모형선으로, 프루드수(Froude number, Fr)가 동일하도록, 실선 속도에 상응하는 속도로 모형선을 예인하여 수행된다. 이 경우 모형선과 실선의 무차원화된 조파저항성분은 동일하다고 가정할 수 있으나, 레이놀즈수(Reynolds number, Re)의 괴리로 인해 무차원화된 점성저항성분은 불일치가 발생하게 된다. 국제수조회의(International Towing Tank Committee, ITTC)의 표준해석법에서는 등가평판의 마찰곡선을 활용하여 점성 또는 마찰저항 성분을 별도로 추정하여 이 문제를 해결한다. 이때 사용되는 등가평판의 마찰곡선은 완전히 발달된 난류상태에 대한 것으로, 모형시험 수행 시에도 선체의 침수된 영역이 난류가 되도록 하는 것이 중요하다.

선박의 성능평가를 수행하는 상업수조의 경우, 통상 선장이 6~9 m인 모형선을 사용하며, 선수부에 난류촉진장치를 설치하여 모형선 전체에 강제된 난류(forced turbulence)를 생성시킨다. 난류촉진장치는 높은 운동량을 갖는 유동을 경계층 하부 영역의 유동과 혼합시켜, 층류에서 난류로의 천이를 가속화시키는 역할을 한다. ITTC에서는 권장 절차(ITTC, 2017b)를 통해 난류촉진장치의 종류, 크기, 부착 위치 등에 대한 가이드라인을 제시하고 있으며, 정기적으로 이루어지는 저항분과 회의에서 난류촉진관련 분야에 대한 내용을 다루고 있다. 25차 저항분과 회의(ITTC, 2008)에서는 각국의 ITTC 회원들을 대상으로, 현재 사용하고 있는 난류촉진장치의 종류와 ITTC 권장 절차에 대한 인지 및 적용유무에 대해 조사하였다. 26차 저항분과 회의 (ITTC, 2011)에서는 과거 회의들에서 난류촉진관련 언급된 부분을 구분하여 정리하였으며, 난류촉진의 물리적 원리와 난류촉진장치 자체의 형상저항을 최소화하기 위한 적절한 난류촉진장치를 선택하는 방법을 제안하였다. 28차 저항분과 회의(ITTC, 2017a)에서는 권장 절차의 내용과 난류촉진장치의 장단점 설명하였으며, 다양한 Re의 정의를 사용한 난류촉진관련 연구 동향을 정리하였다.

난류촉진에 대한 연구들은 난류촉진장치의 형상, 실험대상 및 방법 등 다양한 연구들이 수행되었다. IIdstad (2018)는 트립 와이어(trip wire), Hama 스트립(Hama strip), 모래 스트립(sand strip)을 모형선에 적용하였으며, 실험적으로 얻은 저항성분을 이론해석의 결과와 비교하였다. Murphy (2010)는 Hama 스트립을 평판에 적용하였으며, 예인수조에서 동력계와 열필름유속계(hot-film anemometer)를 이용하여 제원변화에 따른 Hama 스트립 난류촉진영향을 확인하였다. 또한 이를 압력구배가 있는 Sub-off모델에 적용하였으며, 운동량 두께 레이놀즈수(momentum thickness Reynolds number, Re_θ)와 압력구배 변수인 K의 변화를 분석하였다. Lee (2014)는 γ-θ transition 모델을 사용한 전산유체역학(Computational Fluid Dynamics, CFD) 시뮬레이션을 이용하여 평판에 대한 해석을 수행하였다. 난류강도(turbulence intensity, Tu)와 표면 거칠기를 변수로 하여 Re_θ와의 상관관계를 분석하였으며, 이를 쌍동선에도 적용하여 분석하였다. Pearson (2015)은 모래 스트립이 적용된 쌍동선에 Lee (2014)의 방법과 동일하게 CFD 시뮬레이션을 수행하고, 열필름센서(hot-film sensor)를 이용한 모형시험 결과와 비교하였다. Lee (2018)는 스터드(stud)가 적용된 평판과 구상선수 형상에 대해 초저속 영역에서의 DNS (Direct Numerical Simulation)와 LES(Large Eddy Simulation)를 수행하였으며, 각 방법별 벽면마찰계수, 평균속도 및 난류강도의 분포를 구하여, 난류 특성을 비교하였다. Silvestri et al. (2018)은 여러 가지 형상의 트립 와이어와 거칠기가 다른 모래 스트립을 평판에 적용하였으며, 풍동(wind tunnel)에서 열선유속계를 이용하여 유속을 측정하고, 평균 속도분포 및 난류강도 분포, 형상인자(shape factor), 난류경계층의 고유구조(coherent structures)를 분석하여 난류촉진방법별로 비교하였다.

본 연구에서는 캐비테이션 터널(cavitation tunnel)에서 레이저 도플러 유속계(Laser Doppler Velocimetry, LDV)를 이용하여 평판 위 유동에 대한 스터드의 난류촉진영향을 분석하였다. 스터드의 형상과 폭방향 간격은 KRISO 예인수조 모형선에 적용하는 기준과 동일하게 설정하였다. 평판 유입류의 속도는 표준크기의 예인수조 모형선의 저속과 설계속도로 실험이 수행되었다. 스터드에 의한 난류촉진의 영향은 경계층 특성을 나타내는 평균속도분포, 난류강도분포, 경계층 두께, 형상인자를 이용하여 분석하였다.

2. 실험 구성

2.1 캐비테이션 터널

본 연구는 선박해양플랜트연구소(KRISO)의 중형 캐비테이션 터널(Medium-size Cavitation Tunnel, MCT)에서 수행되었다(Fig. 1). 중형 캐비테이션터널의 시험부 단면 크기는 폭 600 mm, 높이 600 mm이며, 자세한 터널의 제원은 Table 1과 같이 정리하였다. KRISO의 MCT에서는 과거 힘 계측과 LDV를 이용한 유속 계측을 통해 방오도료의 평판마찰저항과 난류 경계층에 대한 영향을 분석한 Paik et al. (2013)의 연구 사례가 있다.

Fig. 1

Photo of KRISO medium-size cavitation tunnel

Table 1

MCT specifications

2.2 Laser Doppler Velocimetry

평판 위 경계층 내 유속에 사용된 LDV의 제원은 Table 2와 같다. 실험에 사용된 LDV는 평판과 평행한 방향의 속도성분인 u를 측정하였다. LDV는 0.01 mm의 간격으로 이송 가능한 3차원 이송장치(traverse)에 설치되어, 평판과의 상대 위치를 변화시키며 계측을 수행하였다(Fig. 2).

Table 2

LDV specifications

Fig. 2

Photo of LDV & traverse system

2.3 실험 모형

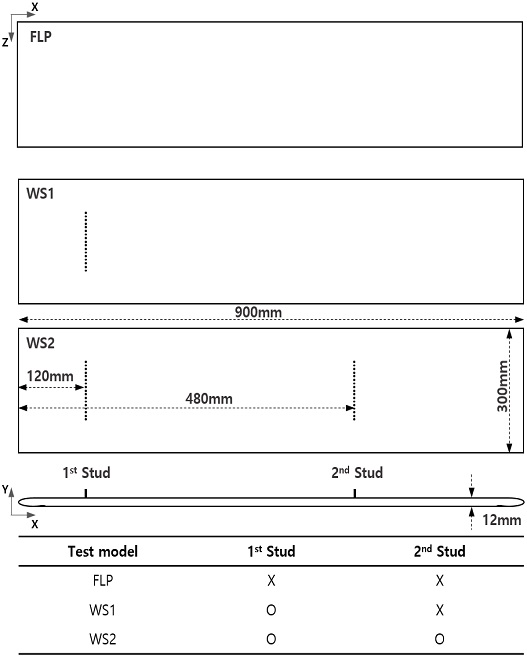
실험에 사용된 모형은 길이 900 mm, 폭 300 mm, 두께 12 mm의 평판이며, 유동박리의 최소화를 위해 앞단(leading edge)과 뒷단(trailing edge)을 타원형상으로 제작하였다. 평판은 중앙부에 설치된 스트럿을 통해 터널 상부와 고정되며, 유동계측은 평판 하부를 대상으로 이루어진다. 난류촉진장치로서, 직경 1.5 mm, 높이 2.0 mm의 원형실린더 형상의 스터드가 선정되었다. 스터드는 폭방향 10 mm 간격으로 하나의 열(row)당 17개가 설치되었다. 스터드의 배열은 앞단으로부터 120 mm와 480 mm에 설치되며, 이 위치는 KRISO 예인수조에서 사용되는 7 m 급 크기의 모형선에 설치되는 난류촉진장치 위치에 상응한다. 상업용 수조에서는 통상 6~9 m 길이의 모형선을 사용한다.

실험에는 스터드의 열 수에 따라 스터드가 없는 평판(FLP), 스터드 1열이 설치된 평판(WS1), 스터드 2열이 설치된 평판(WS2) 총 3가지가 사용되었다. 각 평판에 대한 제원 및 도식화된 형상은 Fig. 3에 나타내었다.

Fig. 3

Schematic figure of test models

3. 실험 조건

3.1 실험속도 및 계측위치

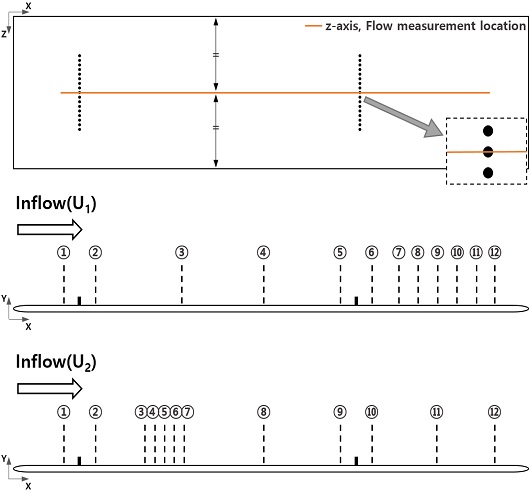
스터드의 난류촉진영향을 확인하기 위하여, 두 가지의 실험 속도에서 유속측정이 수행되었다. 실험속도는 선장이 7 m급 컨테이너 모형선을 기준으로 저속인 Fr= 0.09의 0.73 m/s(U₁)과 설계속도 부근인 Fr= 0.26의 2.20 m/s(U₂)로 선정하였다. 유속계측의 폭방향 위치는 평판의 중앙에 설치한 스터드의 위치를 대상으로 하였으며, 길이방향 위치는 스터드의 앞과 뒤를 포함하는 평판의 전체적인 위치에서 계측할 수 있도록 선정하였다(Fig. 4).예상되는 임계 레이놀즈수(critical Reynolds number, Re_x,crit)인 4.5~5.5x10⁵ 에서는 세부적인 유동양상 변화를 관측하기 위하여 측정 위치를 세밀하게 배치하였다. 일반적으로 평판에서 유동이 층류에서 난류로 천이하는 Re_x,crit는 5 x 10⁵ 부근으로 알려져 있다.

Fig. 4

Schematic of flow measurement location with LDV

각 실험속도에 따른 유속방향에 대한 측정 위치별 Re_x는 Table 3에 나타내었다. 높이방향으로는 경계층 외부까지 유속을 측정하였으며, 하나의 위치 당 2000개 신호가 샘플링 될 때까지 계측하였다.

Table 3

Rex(×105)at measurement locations

본 연구에서 수행한 실험 조건은 아래 Table 4에 정리하였다.

Table 4

Experimental conditions

3.2 MCT 유입류 속도 계측

본 실험수행에 앞서, MCT에서 생성되는 유입류 속도를 측정하였다. Fig. 5와 같이 평판이 달려있지 않은 상태에서, 계측부 중앙 위치의 유속을 측정하였다. MCT 구동 목표속도와 비교한 평균 계측값의 차이와 난류강도의 값을 Table 5에 정리하였다. 본 연구에서 난류강도는 u 속도성분만을 이용하여 분석하였으며, 식 (1)과 같이 유입류 속도로 무차원된 u_rms를 통하여 u 속도에 대한 난류강도를 구하였다.

$\[ Tu=u_{\text{r m s}}/\overline{U} \]$

(1)

Fig. 5

Photo of inflow speed measurement without test models

Table 5

measurement results with test models with LDV

실험 유입류 속도 범위에서 평균속도의 오차는 약 1 %였으며, 기저 난류강도(background turbulence intensity)는 1.2 %의 값으로 나타났다. 위와 같은 평균속도의 오차와 기저 난류강도의 값은 실험 유입류 속도범위에서 평판에 설치된 스터드의 난류촉진영향을 분석하기에 충분하다고 판단하였다.

4. 결과 및 고찰

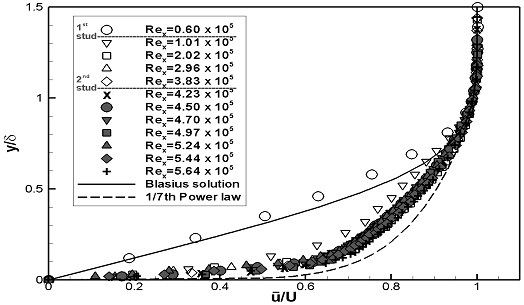
계측한 실험 결과는 층류 경계층과 난류 경계층의 이론해를 기준으로, 평균 속도분포의 형상과 경계층 특성을 나타내는 변수의 유사성을 비교하여, 경계층 내 유동발달 정도를 분석하였다. 이론해로 층류 경계층은 블라시우스 해(Blasius solution)를 난류 경계층은 1/7승 법칙(1/7th power law)을 통한 해를 이용하였다. 각 이론해는 식 (2)와 (3)과 같이 정의된다.

난류경계층은 벽면마찰속도 (wall-friction velocity, v^*)를 이용하여 무차원화 한 값으로 분석할 수 있다. 벽면마찰속도는 식 (4)와 같이 표면전단응력(wall shear stress, τ_w)을 통해 얻어지며, 식 (5)와 (6)으로 정의된 이론해를 이용하여 구하였다. 벽면마찰속도를 이용한 벽과 평행한 속도($$ \overline{u}$$)와 벽면으로부터 떨어진 거리(y)는 식 (7)과 같이 무차원화 된다.

난류 경계층은 점성전단응력(viscous shear stress)이 지배적인 내층(inner layer)과 난류전단응력(turbulent shear stress)이 지배적인 외층(outer layer)로 나뉜다. 내층은 y⁺ ≤ 5 인 경우, 점성의 영향이 지배적인 점성저층(viscous sublayer)으로 불리며, 평균 속도분포는 식 (8)과 같이 선형적으로 나타난다. 30 ≤ y⁺ ≤ 350인 영역에서는 평균 속도분포가 식 (9)과 같이 로그함수로 근사되며, 이 영역은 로그층(log layer)이라 불린다. 식 (9)의 κ와 B는 Coles (1968)가 제안한 0.41, 5.0의 값을 사용하였다. 5 ≤ y⁺ ≤ 30인 영역은 속도 분포가 선형과 로그함수의 중첩형태로 나타나며, 완충층(buffer layer)으로 불린다.

Spalding (1961)은 내층의 평균 속도분포를 하나의 식으로 나타낼 수 있는 식 (10)을 제안하였다.

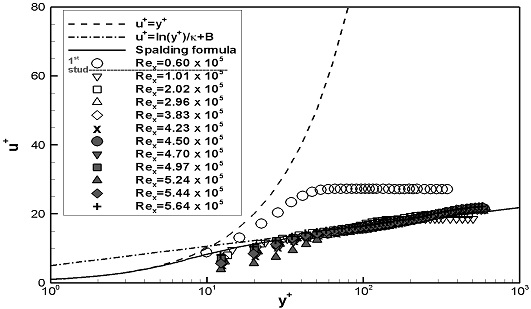
u⁺와 y⁺를 이용한 경계층 분석 시, 식 (10)의 형상과 유사정도를 확인하여 각 Re_x별로 표면전단응력에 대한 이론해의 적용을 식 (5)와 식 (6) 중 선택하여 사용하였다.

4.1 경계층 내 평균 속도분포 및 난류강도 비교

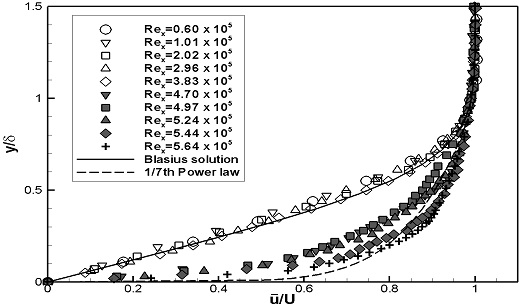
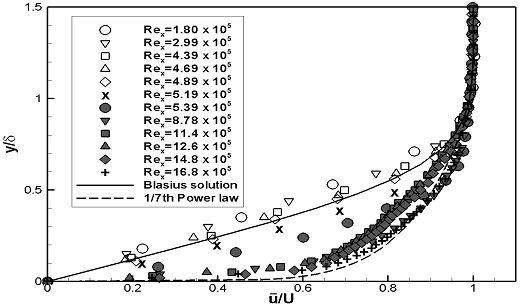
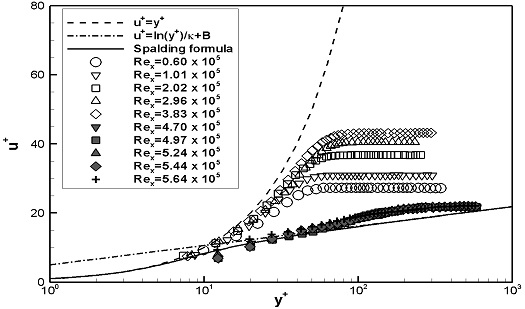
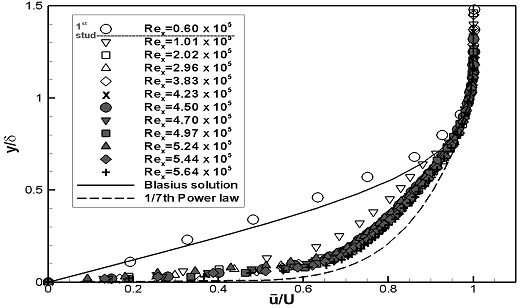
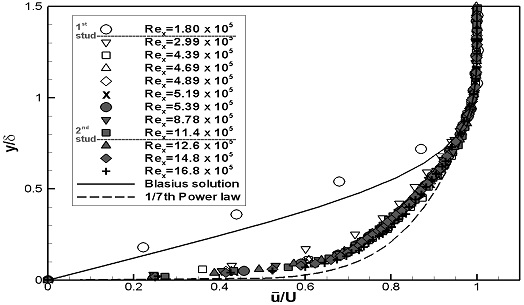
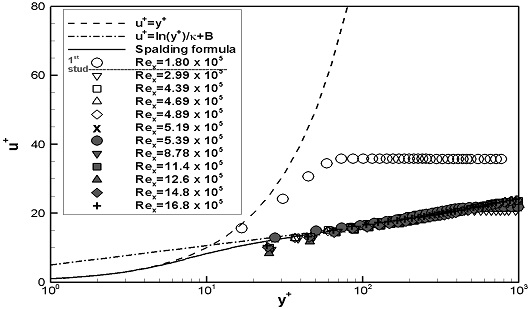
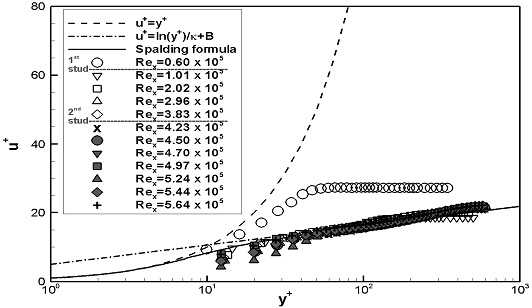
스터드가 설치되지 않은 평판(FLP)의 경계층 내 평균 속도분포를 이론해와 비교하였다. FLP의 실험 결과 중 이론적으로 설명하기 어려운 결과를 보이는 U₁의 Re_x= 4.23 x 10⁵와 4.50 x 10⁵의 데이터는 제외하였다. Fig. 6에서는 블라시우스 해와 1/7승 법칙과 비교하여 나타내었다. Fig. 7에서는 벽면마찰속도를 통해 무차원화된 u⁺와 y⁺로 내층을 나타내는 이론해와 비교하여 나타내었다. 두 가지 실험속도 모두, Re_x가 증가함에 따라 평균 속도분포의 형태는 층류에서 난류의 이론해 값과 유사하게 변화함을 보였으며, U₁에서는 3.83 ~ 4.70 x 10⁵ 부근에서 U₂에서는 4.89 ~ 5.19 x 10⁵ 부근에서 천이가 발생한 것으로 판단된다.

Fig. 6-a

Mean velocity(u¯/U) profiles of FLP(U1=0.73 m/s)

Fig. 6-b

Mean velocity(u¯/U) profiles of FLP(U2=2.2 m/s)

Fig. 7-a

Non-dimensional velocity(u+) profiles of FLP (U1=0.73 m/s)

Fig. 7-b

Non-dimensional velocity(u+) profiles of FLP (U2=2.2 m/s)

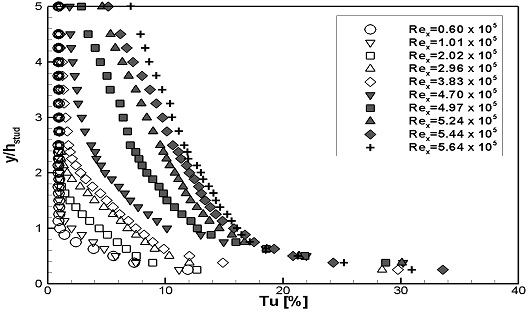
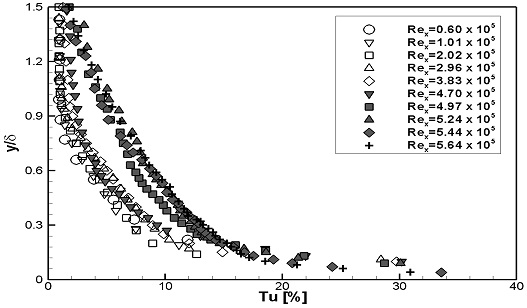
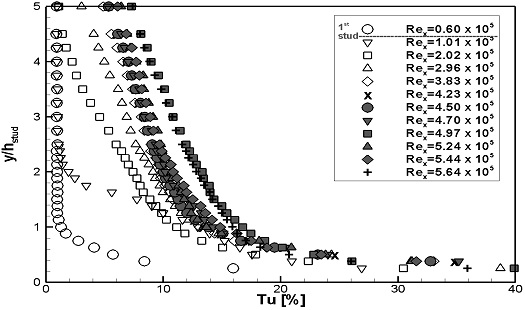
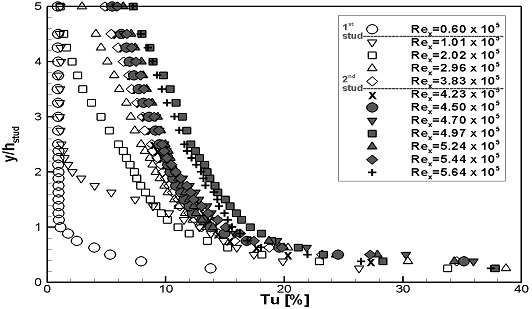
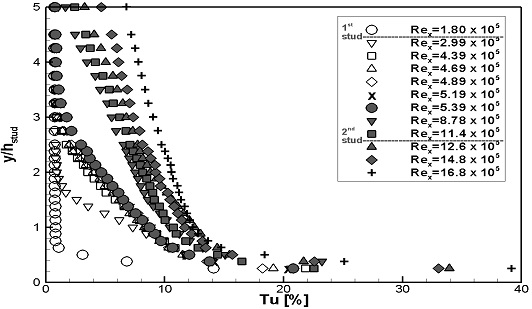
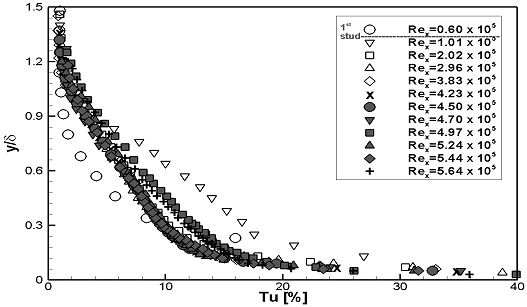
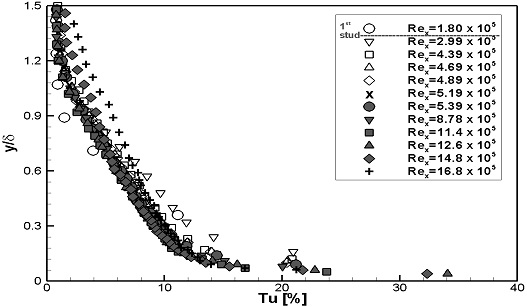
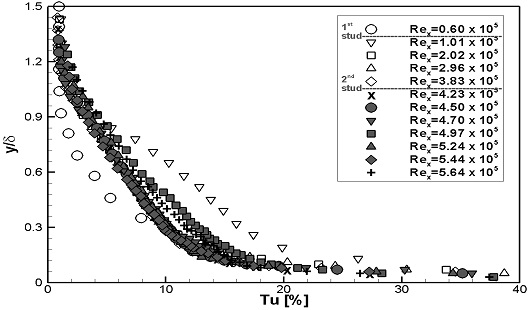
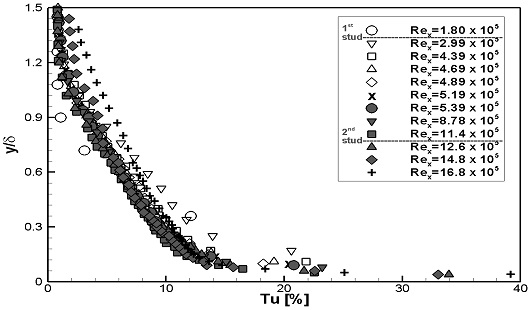
Fig. 8, 9에는 계측된 난류강도의 분포를 나타내었다. Fig. 8에는 스터드 부근에서의 변화를 확인하기 위해, 계측높이를 스터드의 높이로 무차원화하였다. 두 가지 실험속도 모두, Re_x가 증가하여 층류에서 난류로 변화됨에 따라, 난류강도가 점차적으로 증가하는 것으로 나타났다. Fig. 9에는 경계층 내에서의 난류강도 변화를 확인하기 위해, 계측높이를 경계층 두께로 무차원화하였다. 두 가지 실험속도 모두, Re_x가 증가하여 층류에서 난류로 변화됨에 따라, 경계층 내 난류강도가 증가하는 분포형상을 보이며, 일정 Re_x이상에서는 분포형상이 유사하게 형성되었다.

Fig. 8-a

Turbulence intensity profile(y/hstud) of FLP (U1=0.73 m/s)

Fig. 8-b

Turbulence intensity profile(y/hstud) of FLP (U2=2.2 m/s)

Fig. 9-a

Turbulence intensity profile(y/δ) of FLP (U1=0.73 m/s)

Fig. 9-b

Turbulence intensity profile(y/δ) of FLP (U2=2.2 m/s)

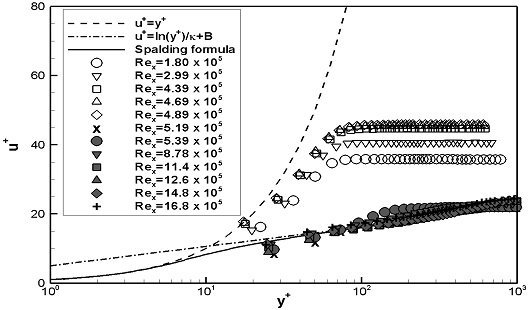
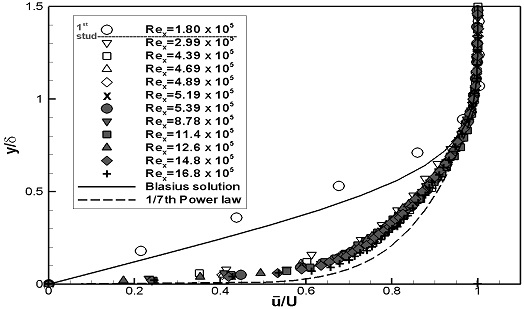
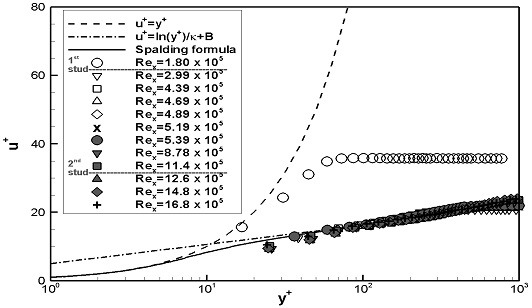
스터드가 설치된 WS1과 WS2의 경계층 내 평균 속도분포는 Fig. 10, 11에 나타내었으며, 벽면마찰속도를 통해 무차원화된 u⁺와 y⁺는 Fig. 12, 13에 나타내었다. 두 가지 실험속도 모두, Re_x가 증가함에 따라 두 평판의 평균 속도분포의 변화는 거의 동일하게 나타났다. 1열 스터드 통과 후 경계층 하부의 유속이 크게 증가하여, 층류에서 난류로 유동발달이 촉진됨을 보였다. FLP의 Fig. 6, 7과 비교하였을 때, 스터드의 유무에 따른 평균 속도분포의 차이가 확연하게 나타나며, 스터드로 인해 층류에서 난류로 유동발달이 가속되었음을 확인하였다. WS2의 결과로부터 2열 스터드에 의한 평균 속도분포의 변화는 거의 나타나지 않았다.

Fig. 10-a

Mean velocity(u¯/U) profiles of WS1 (U1=0.73 m/s)

Fig. 10-b

Mean velocity(u¯/U) profiles of WS1 (U2=2.2 m/s)

Fig. 11-a

Mean velocity(u¯/U) profiles of WS2 (U1=0.73 m/s)

Fig. 11-b

Mean velocity(u¯/U) profiles of WS2 (U2=2.2 m/s)

Fig. 12-a

Non-dimensional velocity(u+) profiles of WS1 (U1=0.73 m/s)

Fig. 12-b

Non-dimensional velocity(u+) profiles of WS1 (U2=2.2 m/s)

Fig. 13-a

Non-dimensional velocity(u+) profiles of WS2 (U1=0.73 m/s)

Fig. 13-b

Non-dimensional velocity(u+) profiles of WS2 (U2=2.2 m/s)

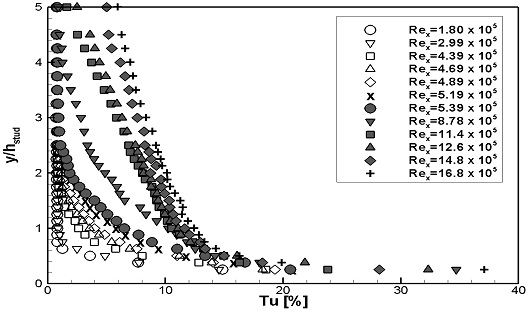
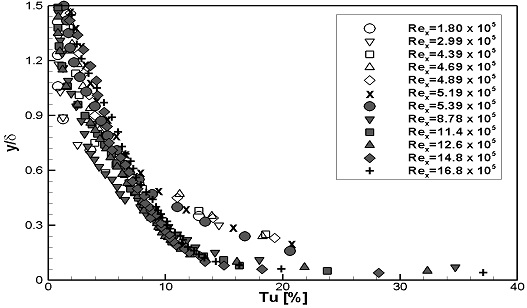
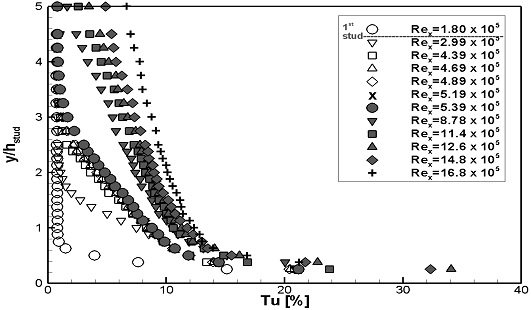
WS1과 WS2의 난류강도의 분포를 계측높이를 스터드 높이로 무차원화하여 Fig. 14, 15에 나타내었으며, 경계층 두께로 무차원화하여 Fig. 16, 17에 나타내었다. 두 가지 실험속도 모두, 1열 스터드 통과 후 난류강도가 크게 증가되었으며, 난류강도가 증가되는 양상은 두 실험속도에서 유사하게 나타났다. Fig. 14, 15에서는 1열 스터드 통과 후 스터드 부근에서 난류강도가 집중적으로 증가하였으며, 이후 유동이 진행하며 난류강도의 증가가 전체적으로 확산되었다. Fig. 16, 17에서는 1열 스터드 통과 후 급격한 난류강도의 증가를 보였으며, 이후 유동이 진행하며 경계층 내 난류강도 분포형상이 유사하게 형성되었다.

Fig. 14-a

Turbulence intensity profiles(y/hstud) of WS1 (U1=0.73 m/s)

Fig. 14-b

Turbulence intensity profiles(y/hstud) of WS1 (U2=2.2 m/s)

Fig. 15-a

Turbulence intensity profiles(y/hstud) of WS2 (U1=0.73 m/s)

Fig. 15-b

Turbulence intensity profiles(y/hstud) of WS2 (U2=2.2 m/s)

Fig. 16-a

Turbulence intensity profiles(y/δ) of WS1 (U1=0.73 m/s)

Fig. 16-b

Turbulence intensity profiles(y/δ) of WS1 (U2=2.2 m/s)

Fig. 17-a

Turbulence intensity profiles(y/δ) of WS2 (U1=0.73 m/s)

Fig. 17-b

Turbulence intensity profiles(y/δ) of WS2 (U2=2.2 m/s)

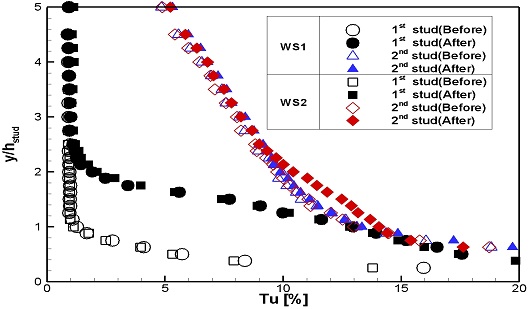
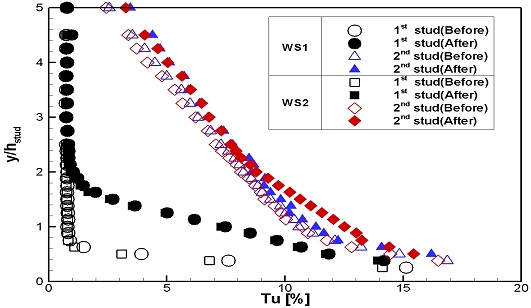
Fig. 18에는 스터드 전후의 동일한 위치에서 스터드 부근의 난류강도 변화를 확인하기 위해 스터드의 높이로 무차원화한 난류강도 분포를 나타내었다. WS1과 WS2 모두 동일하게 2열 스터드 통과 후 스터드 상단 부근에서 난류강도가 미소하게 증가됨을 보였다.

Fig. 18-a

Turbulence intensity profiles in vicinity of studs (U1=0.73 m/s)

Fig. 18-b

Turbulence intensity profiles in vicinity of studs (U2=2.2 m/s)

4.2 경계층 두께 및 형상인자 비교

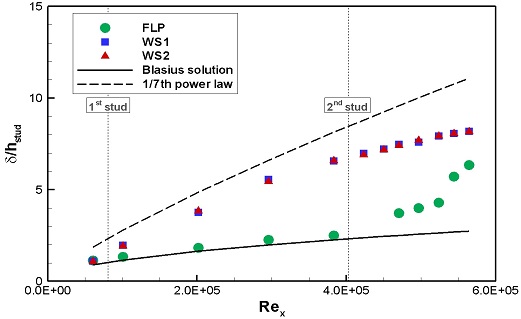
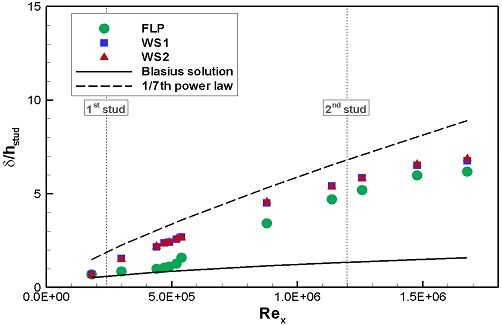
Fig. 19에는 FLP, WS1, WS2의 Re_x에 따른 경계층 두께를 나타내었다. FLP의 경우, 층류의 이론해와 유사한 경향을 보이다가, 특정 Re_x 부근에서 경계층 두께가 급격하게 증가하며 난류로의 천이가 시작되었다. 이후 Re_x가 증가하면서 난류의 이론해와 유사한 경향으로 경계층 두께가 발달되었다. U₁에서는 3.83 ~ 4.70 x 10⁵ 부근에서 U₂에서는 4.89 ~ 5.19 x 10⁵ 부근에서 천이가 발생한 것으로 판단된다. WS1과 WS2의 경우, 1열 스터드 통과 후 유동발달이 촉진되어 난류의 이론해와 유사한 경향을 보이며 경계층 두께가 발달되었다. FLP의 자연스럽게 발달된 난류경계층 두께에 비해, WS1, WS2의 강제된 난류의 경계층 두께는 더 큰 값을 보였다. Re_x가 증가할수록 자연적으로 발달된 난류와 강제된 난류의 경계층 두께의 차이는 감소하는 것으로 나타났다. 이것은 스터드에 의한 유동교란의 효과가 후류로 진행될수록 점차적으로 감소하기 때문으로 판단된다.

Fig. 19-a

Boundary layer thickness (U1=0.73 m/s)

Fig. 19-b

Boundary layer thickness (U2=2.2 m/s)

두 가지 실험속도 모두, 난류 경계층 두께의 결과값은 평판 뒷단으로 갈수록 난류 경계층 두께의 이론값과 기울기의 차이가 발생한다. 이것은 평판의 두께가 완전히 0이 아니기 때문에 발생하는 끝단 유동에 의한 것으로 추정된다.

형상인자(shape factor)는 유동발달 정도를 나타내는 변수로 식 (11)과 같이 정의된다. 형상인자는 층류는 2.6, 난류는 1.4의 값 부근에서 형성되는 것으로 알려져 있다 (Schlichting & Gersten, 2017).

$\[ H=\delta \text{*}/\theta \]$

(11)

여기서, δ^*는 배제두께(displacement thickness)이고, θ(momentum thickness)는 운동량 두께이며, 다음의 식 (12)와 (13)으로 정의된다.

$\[ \delta \text{*}={\int }_0^{\infty }\left(1-\frac{\overline{u}}{U}\right)dy \]$

(12)

$\[ \theta ={\int }_0^{\infty }\frac{\overline{u}}{U}\left(1-\frac{\overline{u}}{U}\right)dy \]$

(13)

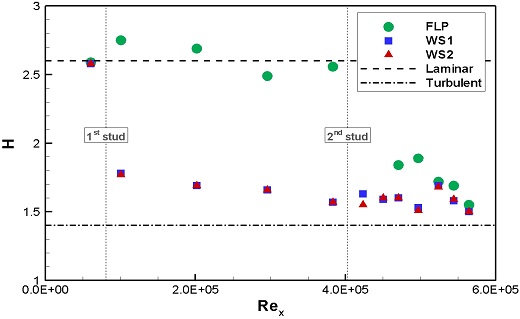
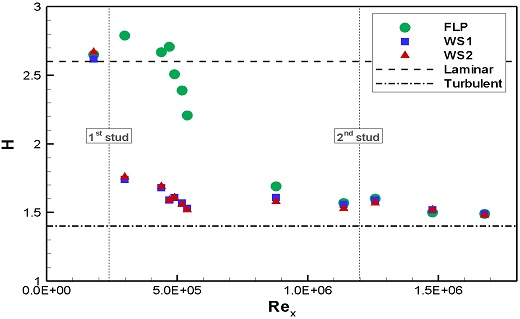
Fig. 20은 Re_x에 따른 형상인자 값을 나타내었다. FLP의 경우, 특정 Re_x 부근에서 형상인자 값의 급격한 감소를 보이며 천이가 시작되었다. U₁에서는 3.83 ~ 4.70 x 10⁵ 부근에서 U₂에서는 4.89 ~ 5.19 x 10⁵ 부근에서 천이가 발생한 것으로 판단된다. 이후 Re_x가 증가하면서 형상인자 값은 난류상태의 값으로 수렴한다. WS1과 WS2의 경우, 1열 스터드 통과 후 형상인자 값이 급격하게 감소하며 난류상태의 값으로 수렴한다. 2열 스터드 에 의한 형상인자 값의 변화는 관측되지 않았다.

Fig. 20-a

Shape factor (U1=0.73 m/s)

Fig. 20-b

Shape factor (U2=2.2 m/s)

스터드는 3차원적인 형상을 통해 유동을 교란시키므로, 형상의 제원에 따라 난류촉진의 효과가 달라진다. 본 연구에서 1열 스터드의 난류촉진 효과가 두 실험속도에서 모두 유효함을 확인하였다. Table 7에는 1열 스터드의 실험속도에 따른 형상특성을 정리하였다. 교란되지 않은 경계층 두께를 스터드의 높이로 나눈 δ/h_stud의 값을 통해 U₁에서는 경계층 내에 존재하지만, U₂에서는 스터드 상단이 경계층 외부로 노출되는 차이를 알 수 있다. 또한 1열 스터드 위치에서의 식 (14)와 같이 스터드 직경으로 정의되는 Re_stud를 통해 실험속도에 따른 차이를 보여준다. 이러한 차이에도 불구하고 1열 스터드 직후의 형상인자의 값은 U₁, U₂에서 각각 1.78, 1.75로 거의 유사하게 나타났다. 따라서 본 연구의 실험조건 내에서는 1열 스터드의 실험속도에 따른 형상특성에 대한 난류 촉진효과는 큰 차이가 없는 것으로 판단된다.

$\[ {Re}_{stud}={Ud}_{stud}/\nu \]$

(14)

Table 7

Characteristic value of 1st stud

4.3 토의

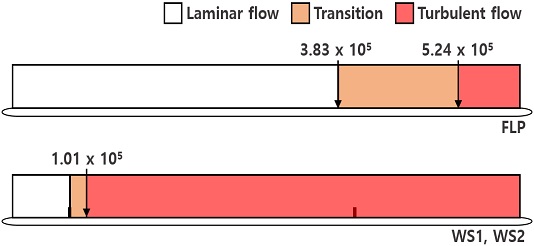
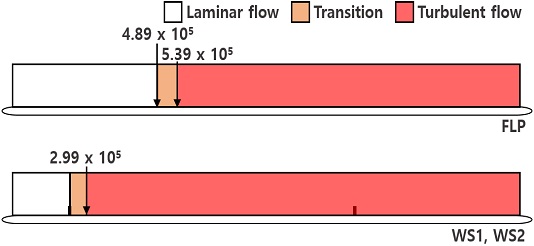
Fig. 18에는 앞서 분석한 결과를 종합하여, 층류, 천이, 난류로 경계층을 구분하여 나타내었다. 본 실험의 유입류 속도에서 평판 위 유동에 대한 스터드의 난류촉진 효과가 확인되었다. 이는 1열 스터드의 효과가 지배적이었으며, 이미 난류가 발달된 상태에서의 2열 스터드는 스터드 상단 부근의 난류강도를 미소하게 증가시키는 것을 제외하고, 경계층 특성에 큰 영향을 미치지 않았다.

Fig. 18-a

Classification of flow regime(U1=0.73 m/s)

Fig. 18-b

Classification of flow regime(U2=2.2 m/s)

본 실험에 사용된 제원의 스터드는 1열의 사용만으로도, 평판에서 난류촉진의 효과가 충분하게 나타났다. 그러나 역압력구배가 존재하고 횡단면적의 크기가 급격히 증가하는 모형선의 선수부에서는 스터드에 의한 난류촉진 효과가 다르게 나타날 수 있으므로, 추후 연구가 필요하다고 생각된다.

5. 결 론

본 연구에서는 KRISO 예인수조 모형선에 사용되는 난류촉진장치인 스터드의 난류촉진에 대한 유효성을 검증하기 위한 기초연구로, 동일한 제원의 스터드를 설치한 평판의 경계층 내 유속을 측정하여 난류촉진의 효과를 분석하였다. 유속측정은 중형캐비테이션 터널에서 LDV를 통하여 수행되었다. 스터드의 난류촉진에 대한 영향은 평균 속도분포, 경계층 두께, 난류강도, 형상인자를 통해 분석하였으며, 다음과 같은 결론을 얻었다.

• - 스터드가 없는 평판에서 층류에서 난류로의 천이는 Re_x=3.83 ~ 5.19 x 10⁵ 부근에서 나타났다. 스터드가 설치된 평판에서는 유동이 1열 스터드를 지난 직후부터 난류상태로 급격하게 유동이 발달되었다.
• - 유입류 속도에 따라, 1열 스터드의 교란되지 않은 경계층 대비 스터드의 상대높이, 스터드의 직경으로 정의된 레이놀즈수의 차이가 있다. 그러나 스터드 직후에서의 형상인자의 값은 거의 유사하게 나타났으며, 본 연구의 실험조건 내에서 1열 스터드의 형상특성에 따른 난류촉진효과는 유속별로 큰 차이가 없는 것으로 판단된다.
• - 이미 난류가 발달된 상태에서의 2열 스터드는 스터드 상단 부근의 난류강도를 미소하게 증가시켰으나, 평균 속도분포, 경계층 두께, 형상인자와 같은 경계층 특성에 큰 영향을 미치지 않았다.
• - 자연스럽게 발달된 난류경계층 두께에 비해, 1열 스터드에 의해 강제적으로 발달된 난류의 경계층 두께는 더 크게 나타났지만, Re_x가 증가할수록 두 경계층 두께의 차이는 점차적으로 감소되었다.

Acknowledgments

본 연구는 선박해양플랜트연구소의 주요사업인 “첨단운송체의 항내 운항성능향상을 위한 축척효과를 고려한 운항제어원천기술 개발(3/5)”에 의해 수행되었습니다 (PES3860).

References

• Coles, D.E., 1968. The young person’s guide to the data, In: Coles, D.E. & Hirst, E.A. Proceedings Computation of turbulent boundary layers-1968 AFOSR-IFP-Stanford Conference, Vol. 2, Stanford Univ., Stanford, Calif., pp.1-45.
• ITTC, 2008. Final report and recommendations to the 25th ITTC. 25th International Towing Tank Conference. Proceedings of 25th ITTC-Volume I, Fukuoka, Japan, 14-20 September, 2008.
• ITTC, 2011. Final report and recommendations to the 26th ITTC. 26th International Towing Tank Conference. Proceedings of 26th ITTC-Volume I, Rio de Janeiro, Brazil, 28 August-3 September, 2011.
• ITTC, 2017a. Final report and recommendations to the 28th ITTC. 28th International Towing Tank Conference. Proceedings of 28th ITTC-Volume I, Wuxi, China, 17-22 September, 2017.
• ITTC, 2017b, ITTC-recommended procedures and guidelines, ship models. International Towing Tank Conference, Revision 04, 7.5-01-01-01.
• IIdstad, J.B., 2018. Use of turbulence stimulation on ship models. Master Thesis, Norwegian University of Science and Technology.
• Lee, K.S., 2014. Tackling the laminar-turbulent transition at medium-speed catamarans using computational fluid dynamics. BEng Thesis, Australian Maritime College, University of Tasmania.
• Lee, S.B., 2018. Direct numerical and large eddy simulations of transitional flows around turbulence stimulators at very low speeds. Journal of the Society of Naval Architects of Korea, 55(3), pp.265-273. [https://doi.org/10.3744/SNAK.2018.55.3.265]
• Murphy, J.C., 2010. A novel approach to turbulence stimulation for ship⁃model testing. Tech Report U.S. Naval Academy no. 390.
• Paik, B.G. et al., 2013. Study on the drag performance of the flat plates treated by antifouling paints. Journal of the Society of Naval Architects of Korea, 50(6), pp.399-406. [https://doi.org/10.3744/SNAK.2013.50.6.399]
• Pearson, M., 2015. Modelling laminar-turbulent transition on wave⁃piercing catamarans for enhancing experimental techniques, BEng Thesis, Australian Maritime College, University of Tasmania.
• Schlichting, H. & Gersten K., 2017. Boundary-Layer Theory, 9th ed., McGraw Hill, New York, U.S.A., pp.419-424. [https://doi.org/10.1007/978-3-662-52919-5]
• Silvestri, A. et al., 2018. The application of different tripping techniques to determine the characteristics of the turbulent boundary layer over a flat plate. Journal of Fluids Engineering, 140(1):011204. [https://doi.org/10.1115/1.4037675]
• Spalding, D.B., 1961. A single formula for the law of the wall. Journal Applied Mechanics, 28, pp.455−457. [https://doi.org/10.1115/1.3641728]