하이브리드 방법을 사용한 고속 활주정의 내항성능평가 절차 개발

2.1 대상 선박 제원

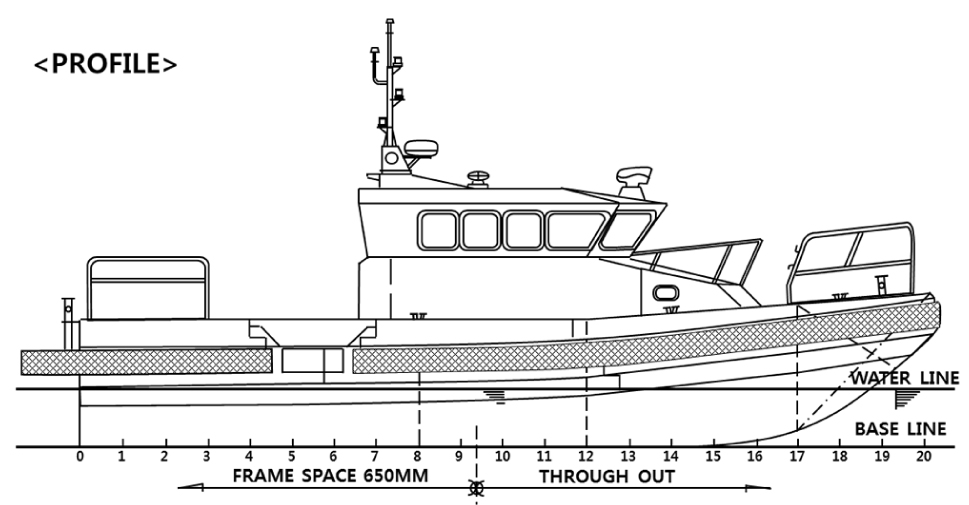
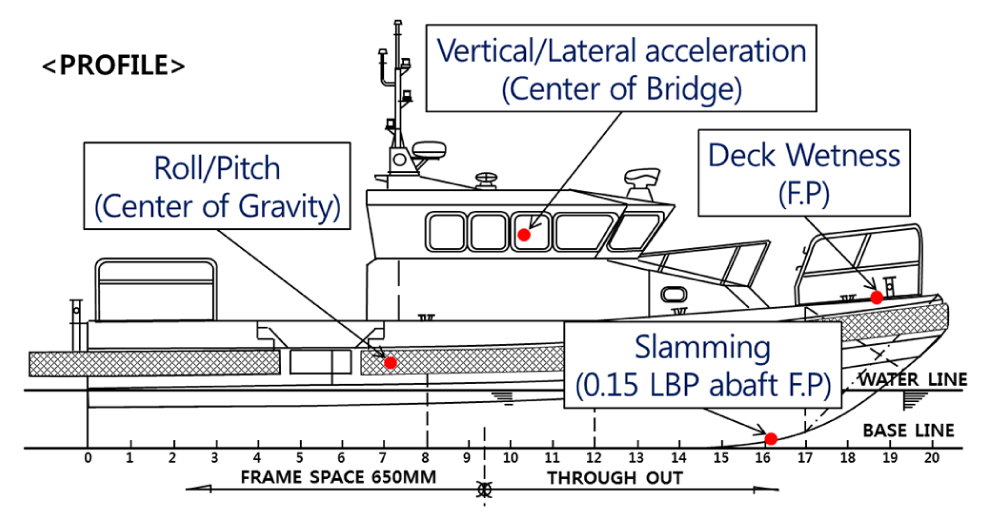
본 연구에 사용될 대상 선박의 제원은 Table 1과 같으며, Fig. 1은 대상선박의 측면 배치도를 나타낸다.

Table 1.

Principal particulars of the target ship

Fig. 1.

Profile of the target ship

2.2 수치 시뮬레이션 조건

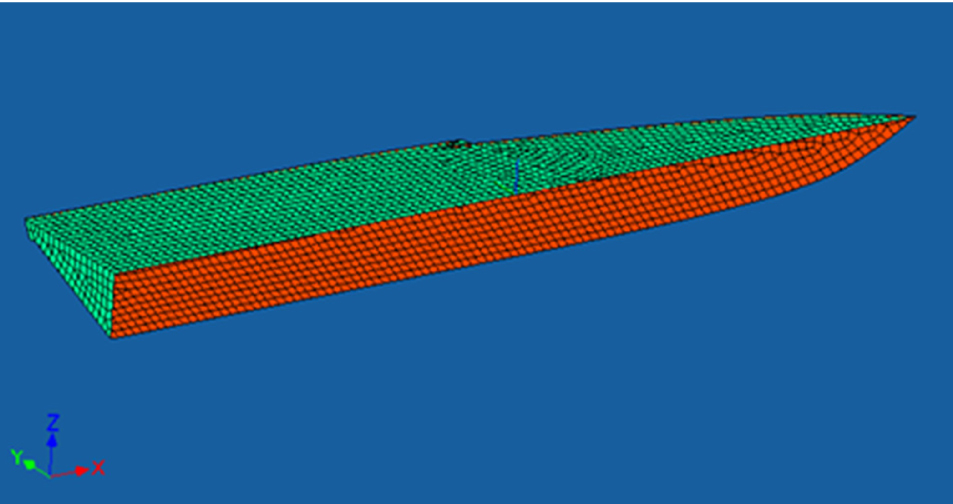
고속 운항하는 소형 선박의 동요운동으로 인한 감쇠계수는 횡동요 뿐만 아니라 다른 자유도에서도 반영되어야 하고 임의의 위치에서 선박의 속도와 가속도를 구해야하기 때문에, 선체 6자유도 운동에 대한 감쇠효과를 반영할 수 있고 원하는 위치에서의 속도 및 가속도를 구할 수 있는 로이드 선급의 ‘WAVELOAD-FD’를 사용하여 고속 활주정의 내항성능 해석에 사용하였다. 이는 3차원 Panel method를 사용하고 있다. 내항성능 계산을 위하여 대상선박의 자유수면 이하에 패널모델을 생성하였으며, Fig. 2는 해당 모델을 보여준 것이다.

Fig. 2.

Panel generation under free surface

Table 2는 운항 중 내항성능 계산을 위한 해석조건을 나타낸 것이며, 파 주파수 범위는 ABS 선급의 Guidance notes on ‘Dynamic Load Approach’ and Direct Analysis for High Speed Craft에 따라 2.5rad/s까지 고려하였다(ABS, 2003). 대상선박은 만재흘수 0.88m에서 선박의 설계속도인 15knot로 운항하는 조건에서 계산을 수행하였다.

Table 2.

Classification of simulation case

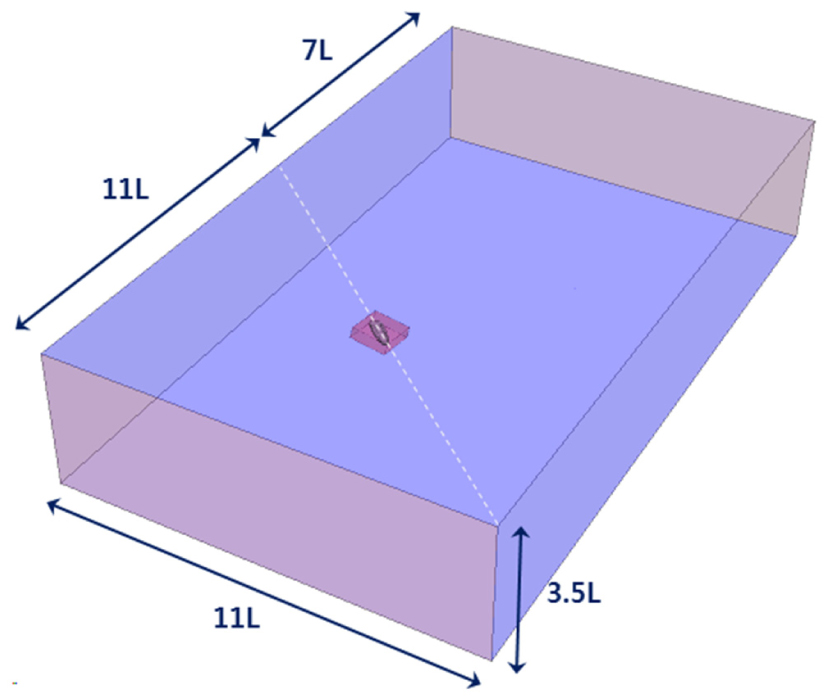
포텐셜 이론 기반의 프로그램을 보완하는 목적으로 사용하는 CFD 프로그램은 점성의 비압축성 유동장을 시뮬레이션하는 상용 CFD 프로그램인 ‘STAR-CCM+’을 이용하였다. 지배방정식은 연속방정식과 RANS(Reynolds-averaged Navier-Stokes) 방정식이며, 유한체적법에 의해 이산화하였다. 압력해법으로 SIMPLE(Semi-implicit Pressure Linked Equations) 알고리즘을 적용하였으며, 대류항은 3차 MUSCL 기법, 점성항은 2차 중심차분 기법을 적용하였다. 수치해석에 사용한 격자 시스템 및 물리모델은 Table 3과 Table 4에 각각 나타내었다. 또한 천수효과의 영향을 배제하기 위하여 Fig. 3과 같이 계산영역을 설정하였다.

Fig. 3.

Numerical towing tank with overset mesh

Table 3.

Condition of mesh system in CFD simulation

Table 4.

Condition of physics models in CFD simulation

2.3 파랑스펙트럼 조건

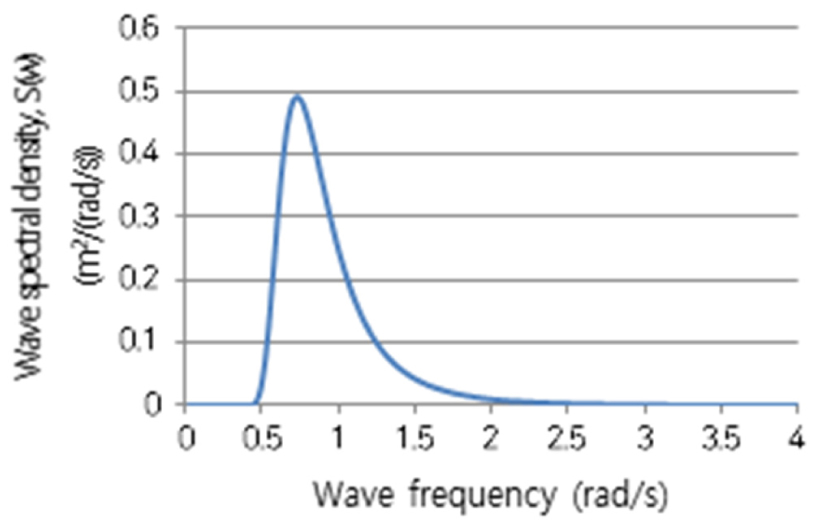
선박의 내항성능 해석을 위하여 본 연구에서는 대상선박이 실제로 운용될 해역의 해상조건인 해상상태 4등급(유의파고 2.00m, 피크주기 8.63sec)의 Pierson-Moskowitz 스펙트럼을 적용하였다(Seakeeping committee, 1981). 식 (1)은 해당 파랑스펙트럼이며, Fig. 4와 같이 나타낼 수 있다.

여기서, A=172.75*H_1/3²/T₁⁴, B=691/T₁⁴, $$ \omega $$는 파의 주파수, H_1/3는 유의파고, T₁는 파의 평균 주기를 나타낸다.

Fig. 4.

ITTC Spectrum of significant wave height 2.0m

3.1 고속선 내항성능 평가 절차 개발배경

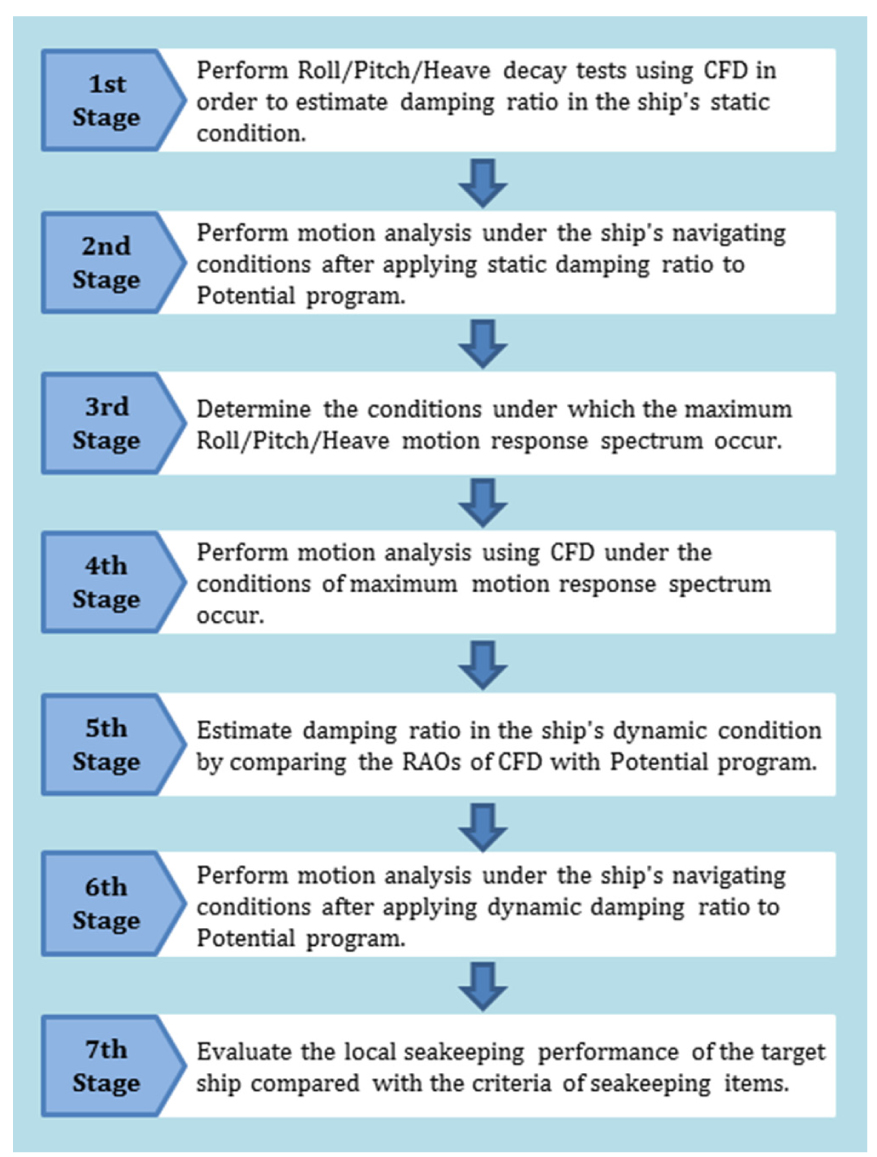
기존의 선박 내항성능 평가는 주로 모형시험, CFD 또는 포텐셜 이론 기반의 상용 프로그램들이 독립적으로 수행되어져 왔다. 하지만 본 연구에서는 Fig. 5와 같이 포텐셜 프로그램과 CFD 간의 장점을 상호 보완적으로 사용한 절차를 개발하였다. 다시 말해, 3차원 Panel method의 포텐셜 프로그램을 기본적으로 내항성능 해석에 사용하고, CFD 결과로 특정 조건에서 감쇠계수를 비교보정해주는 하이브리드 방법을 사용하였다.

Fig. 5.

Evaluation procedure of the hybrid-seakeeping performance

3.2 고속선 내항성능 평가 절차 설명

Fig. 5는 본 연구에서 제안하는 내항성능 평가 절차를 전반적으로 보여준 것이다. 1st Stage에서는 평가하고자 하는 대상 선박의 모형시험 또는 CFD 프로그램을 사용하여 정수 중 자유동요 감쇠 시험을 수행한다. 내항성능 평가를 수행하기 위해 포텐셜 프로그램에서는 감쇠계수가 필요하며, 이는 모형시험이나 CFD 프로그램을 사용하여 구할 수 있다. 즉, 선박의 동요 진폭변화를 측정하여 정수 중 초기 동요 감쇠를 추정한다. 2nd Stage에서는 추정한 초기 동요 감쇠계수를 포텐셜 프로그램에 적용하고, Table 2의 운항조건 하에서 운동해석을 수행하여 선박의 6자유도운동에 대한 운동응답함수(Response Amplitude Operator, RAO)를 구한다. 일반적으로 고속 활주정의 운항조건에서는 프루드 수가 높고 운동의 정도가 크기 때문에, 정수 중 초기 동요 감쇠로 포텐셜 프로그램의 RAO를 구하여 내항성능 평가에 사용하기에는 신뢰성이 부족하다. 따라서 Fig. 5의 2nd Stage의 운동 해석으로 얻은 RAO는 초기 결과로 봐야 한다. 3rd Stage에서는 정수 중 초기 동요 감쇠를 적용하여 운항 중 운동 해석으로 얻은 RAO로부터 선체응답스펙트럼을 식 (2)로부터 구하고 이 스펙트럼의 최대값을 갖는 선속, 조우각 및 주파수 조건을 찾는다.

여기서, $$ \omega $$는 파의 주파수이며, S_R($$ \omega $$), RAO($$ \omega $$) 및 S($$ \omega $$)는 식 (1)과 같은 파랑 스펙트럼, 선체운동의 응답진폭함수 및 응답스펙트럼을 나타낸다. 즉, 선체운동 응답스펙트럼은 식 (2)와 같이 운동 해석으로부터 얻은 RAO의 자승에 대상해역의 파랑스펙트럼을 곱하여 을 얻는다. 스펙트럼의 최대값을 얻는 이유는 Table 5의 고속선 내항성능 평가기준 단위가 식 (3)과 같은 유의단일진폭(Single Significant Amplitude, SSA)으로 평가하며, 이 식에 가장 영향을 많이 주는 위치가 응답스펙트럼의 최대값이 되기 때문이다. 이 식 (3)의 m₀는 식 (4)로부터 계산된다.

여기서, $$ \xi $$_1/3는 1/3 유의진폭을 의미하며, 유의단일진폭(SSA)이라 한다.

여기서, $$ \omega $$_e는 선박의 조우주파수, m_n은 응답스펙트럼의 n차 모멘트이다. 식 (4)의 적분에 가진 주파수인 조우 주파수($$ \omega $$_e) 대신에 파의 주파수($$ \omega $$)가 포함된 것은 파의 주파수 범위에 따른 에너지와 동등한 조우주파수 범위에 따른 에너지는 동일하여 $$ S_R\left(w_e\right)d{w}_e$$가 $$ S_R\left(w\right)dw$$가 되기 때문이다.

4th Stage에서는 최대 응답이 발생한 선속, 조우각 및 주파수에 대하여 다시 CFD 해석을 수행하고, 5th Stage에서는 해당 CFD 결과와 같은 RAO를 갖도록 운항 중 동요 감쇠계수를 다시 조정한다. 이는 두 해석 프로그램의 RAO가 일치하도록 운항 중 동요 감쇠계수를 추정하여 포텐셜 프로그램 결과의 신뢰성을 얻기 위한 것이다. 일반적으로 정수 중 조건에 비해 운항 중 선박은 동요가 커지고 동요감쇠도 정수 중에 비하여 증가하기 때문에, 운항 중 최대응답을 합리적으로 추정하기 위해서는 운항 중 CFD 결과와 비교하여 동요 감쇠계수를 다시 추정해야 한다. 6th Stage에서는 새로운 동요 감쇠계수를 적용하여 Table 2의 운항조건 하에서 해석을 재수행하고, 7th Stage에서는 계산된 결과를 Table 5의 고속선의 내항성능 평가기준과 비교하여 만족여부를 판단한다. 대상선박은 연안구조정으로 구조 활동을 위해서는 15knot이상으로 운항이 가능하나, 본 연구에서는 설계속도인 15knot에서 Table 5의 Operation조건의 평가기준을 적용하였다.

Table 5.

Seakeeping criteria of naval ship

내항성능 평가 요소 및 한계값에 대한 기준으로 사용되는 Table 5는 대한민국 해군의 내항성능 기준 설정 지침과 NORDFORSK 및 NATO에서 제안하고 있는 군함의 적용 기준을 참고하였다(Republic of Korea Navy, 2004; NORDFORSK, 1987; NATO, 2000). 참고문헌에 따라서 기준치의 표현에는 다소 차이가 있으나, 본 연구에서는 횡동요, 종동요, 수직 가속도 및 수평가속도에 대해서는 SSA를, 갑판침수 및 슬래밍은 시간 당 발생횟수를 사용하였다. 또한, 횡동요와 종동요의 각도는 무게중심에서, 수직가속도와 수평가속도는 요원의 임무수행의 기준이 되는 위치인 함교에서, Slamming 발생가능성 및 발생빈도는 선수수선(Fore Perpendicular, F.P)으로부터 0.15LBP 위치에서, 갑판침수(deck wetness) 발생가능성 및 발생빈도는 선수수선위치에서 평가하였다.

4.1 CFD를 이용한 정수 중 동요 감쇠 해석

횡동요 감쇠의 산출에는 횡동요로 소실된 에너지를 고려하는 상대감쇠법과 횡동요 운동의 진폭이 대수적으로 감소한다고 간주하는 대수감쇠법을 주로 사용한다. 본 연구에서는 유도과정이 상대적으로 단순하고, 횡동요 진폭의 비로 간단하게 감쇠를 계산할 수 있는 대수감쇠법을 사용하여 선박의 동요 감쇠를 산출하였다. 대수감쇠법은 선박의 정수 중 자유 횡동요 운동 방정식인 식 (5)로부터 유도된다(Van’t Veer, 2009).

여기서, I₄₄는 횡동요 질량 관성모멘트, A₄₄($$ \omega $$)는 횡동요 부가질량 관성모멘트, B₄₄($$ \omega $$)는 포텐셜 감쇠계수, B^*₄₄는 점성횡동요 감쇠계수, C₄₄는 배수량과 GM의 곱, $$ \varphi $$는 횡동요진폭이다.

식 (5)의 양변을 I₄₄+A₄₄($$ \omega $$)로 나누면 식 (6)과 같고, 좌변의 계수들을 식 (7)로 정의하면, 식 (5)를 식 (8)과 같이 나타낼 수 있다.

선박 동요 자유감쇠운동은 조화운동으로 선박의 동요 진폭 $$ \varphi $$의 일반해를 식 (9)와 같이 나타낼 수 있다. 또한 동요 대수 감쇠를 나타내면 식 (10)과 같으며, 이를 임계 횡동요 감쇠와 전체 횡동요 감쇠의 비로 무차원화하면 식 (11)과 같이 무차원 횡동요 감쇠비로 나타낼 수 있다.

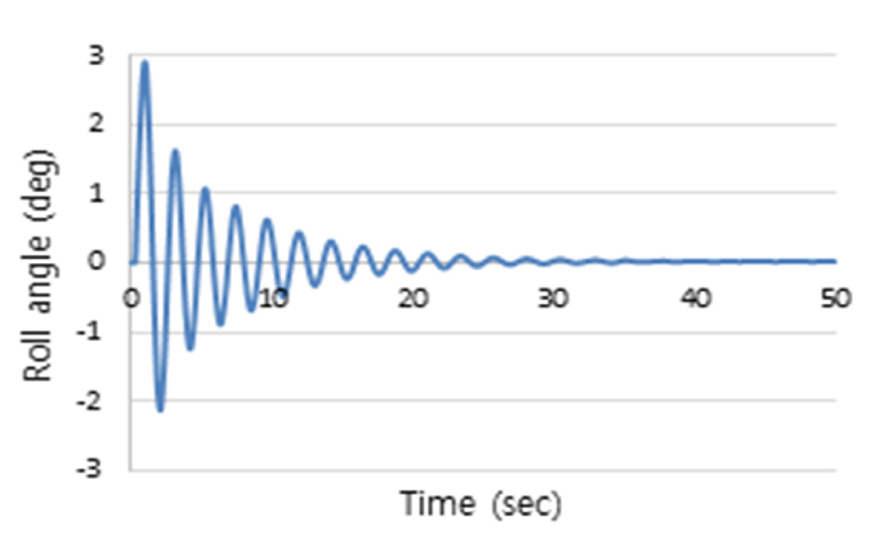
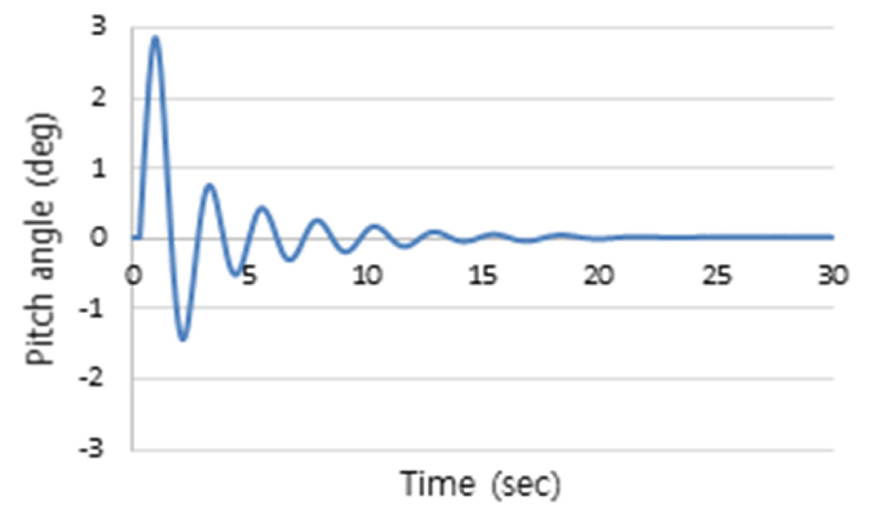
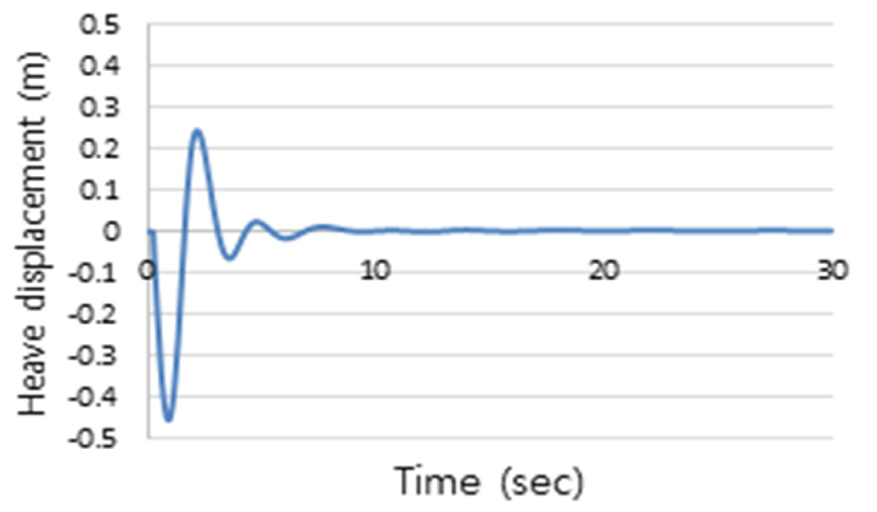
Fig. 6은 1st Stage를 수행한 결과로 CFD 프로그램을 이용하여 대상선박을 초기 경사각 0도에서 초기 각속도를 할당하여 자유 횡동요 감쇠 시험을 시행한 결과이다. 이 결과로부터 식 (11)을 활용하여 무차원 횡동요 감쇠비를 산출할 수가 있으며, 동일한 방법을 Fig. 7과 Fig. 8에 적용하면 종동요와 상하동요 감쇠비도 추정할 수 있다. Table 6은 CFD의 정수 중 자유 동요 감쇠시험을 통해 산출한 무차원 횡동요, 종동요 및 상하동요 운동 감쇠비를 나타낸 것이다.

Fig. 6.

The result of roll decay test at zero speed in CFD calculation

Fig. 7.

The result of pitch decay test at zero speed in CFD calculation

Fig. 8.

The result of heave decay test at zero speed in CFD calculation

Table 6.

Nondimensional damping ratio under decay tests

4.2 선체운동해석 결과 검토

초기결과의 적절성을 확인하기 위해 Table 6의 결과로부터 정수 중 동요 감쇠를 적용하여 선속이 없는 상태에서 파의 주파수에 따른 선박의 횡동요 RAO 및 종동요 RAO를 Fig. 9 및 Fig. 10과 같이 얻었으며, 이를 IACS에서 규정하고 있는 선박 동요주기식인 식 (12), (13), (14), (15)와 비교하였다(IACS, 2015).

여기서, T_θ는 횡동요주기, T_𝜙는 종동요 주기, k_r은 횡동요 회전반경, g는 중력가속도, GM은 메타센터의 높이, L은 선박의 길이, T_LC는 해당하는 적하조건에서의 흘수, T_SC는 최대만재 흘수이다. 본 연구에서는 Table 1에 있는 draft를 T_SC와 T_LC로 사용하였다.

Fig. 9에서 보는 바와 같이, 선박이 횡파를 받는 조건에서 최대 횡동요 RAO가 2.44rad/s에서 발생하였고, 선박의 횡동요 주기 식 (12)로부터 구한 주기는 2.41rad/s가 된다. 마찬가지로, Fig. 10으로부터 선수파에서 최대 종동요 RAO가 1.98rad/s에서 발생하였고, 식 (13), (14), (15)에 의하여 도출된 선박의 종동요 주기는 1.96rad/s가 되었다. 이를 비추어볼 때, 선체운동 계산 결과가 실제 선급 식의 결과와 잘 일치하며 신뢰성을 가지는 것을 알 수 있다.

Fig. 9.

Roll RAO at zero speed in potential calculation

Fig. 10.

Pitch RAO at zero speed in potential calculation

4.3 최대운동 응답스펙트럼 발생 선수각 및 주파수 도출

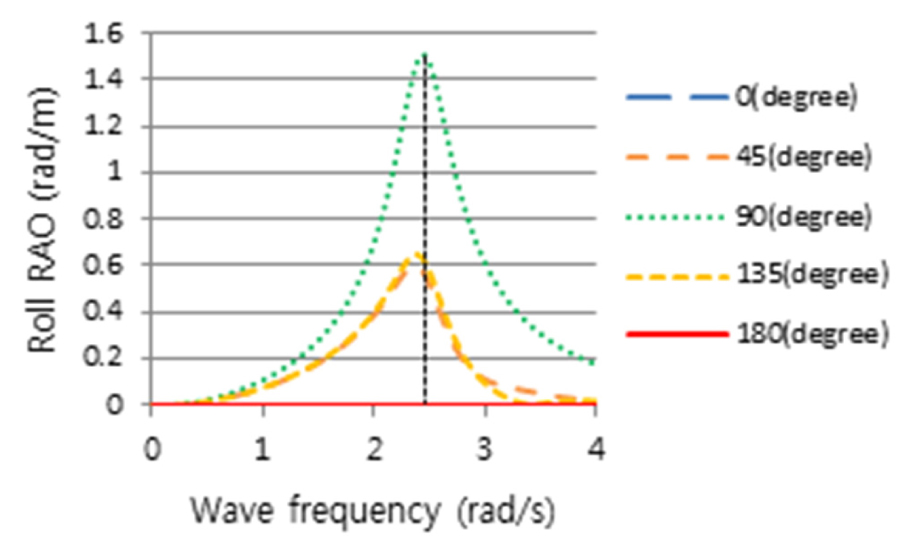
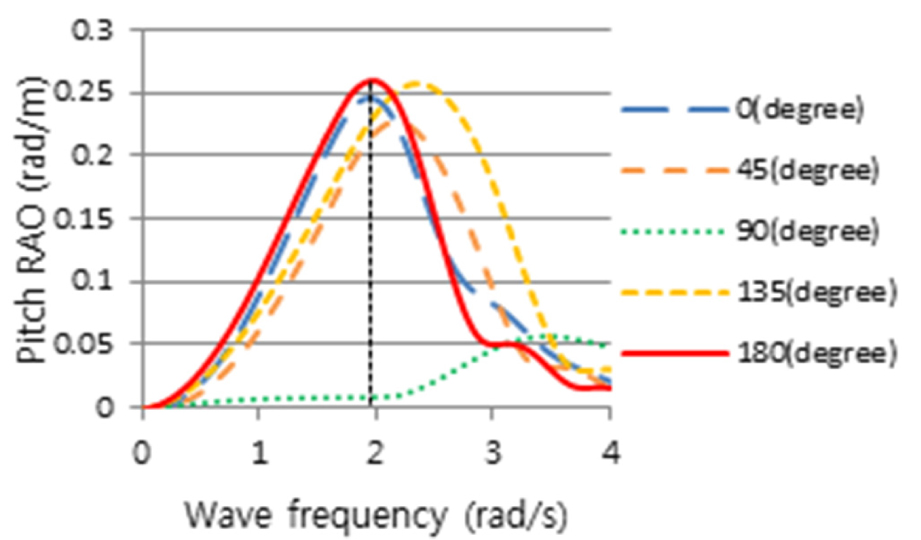
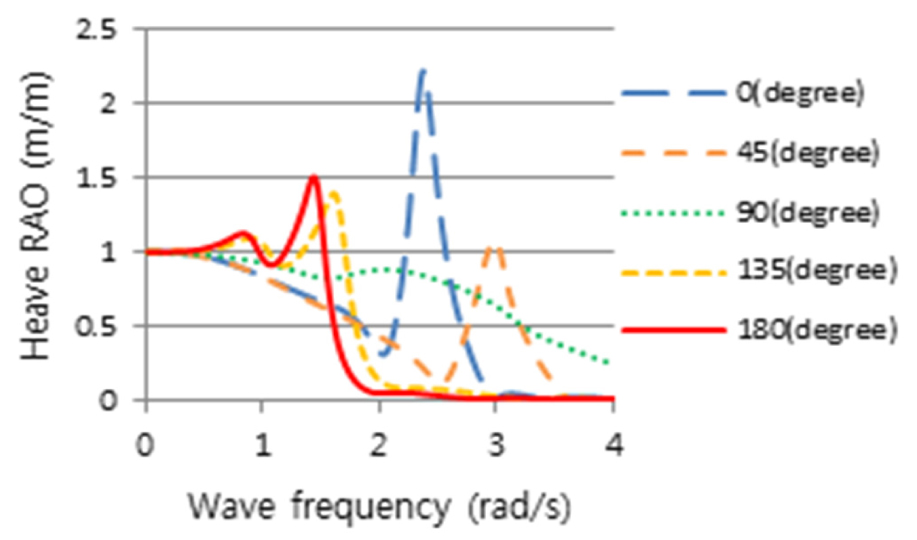
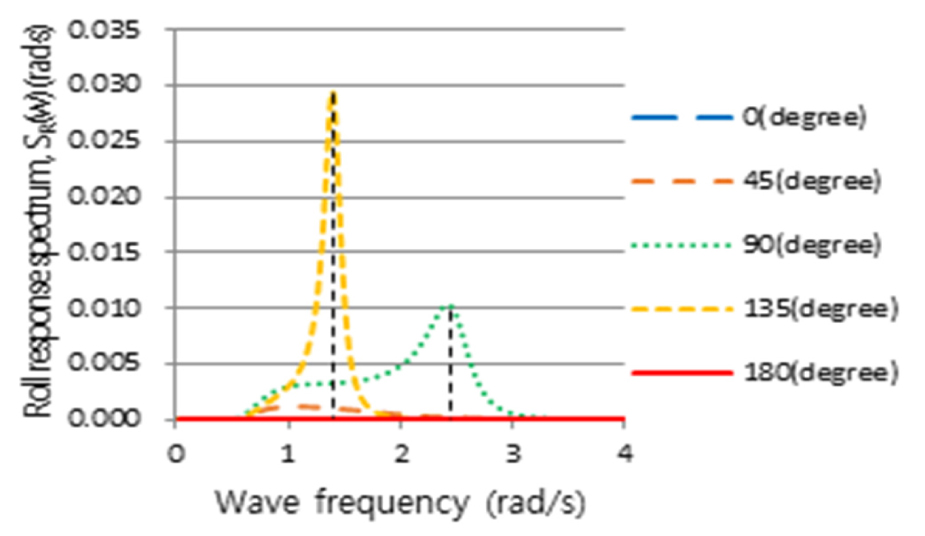
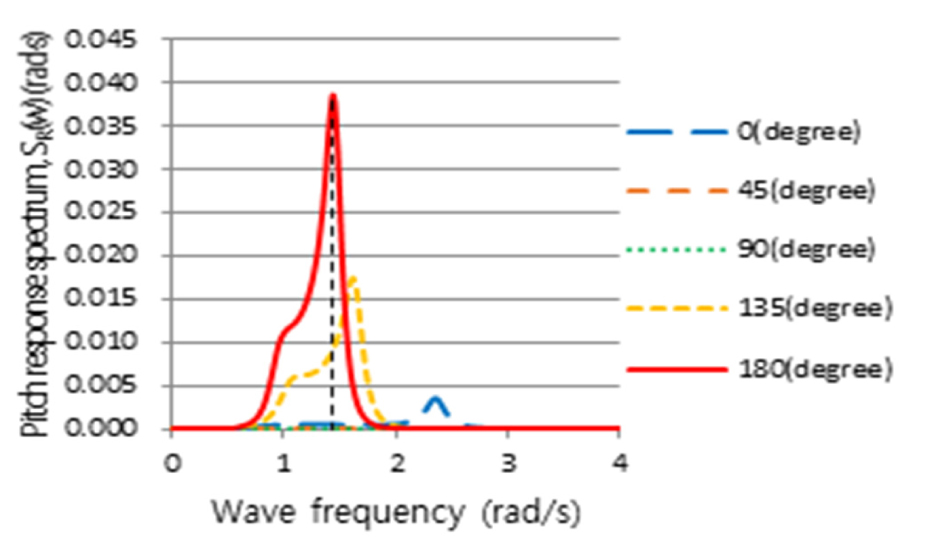
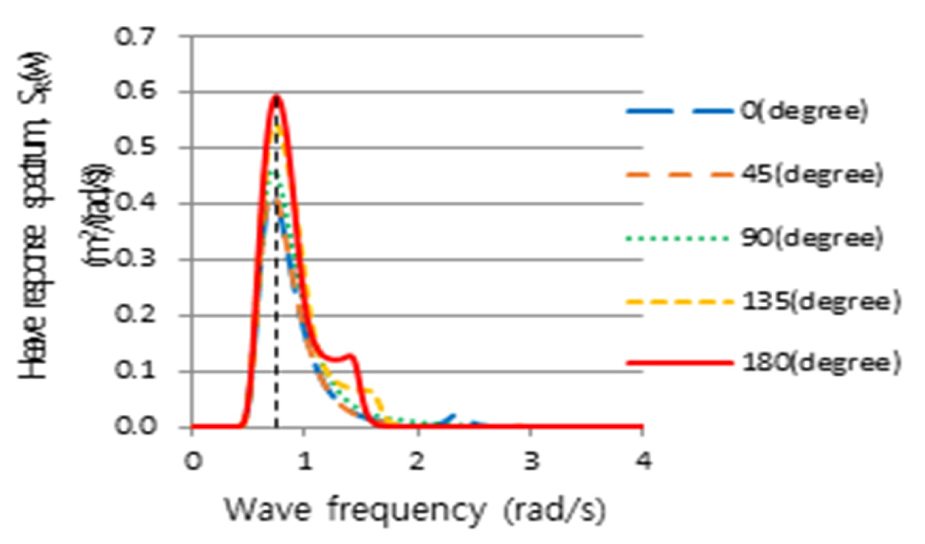
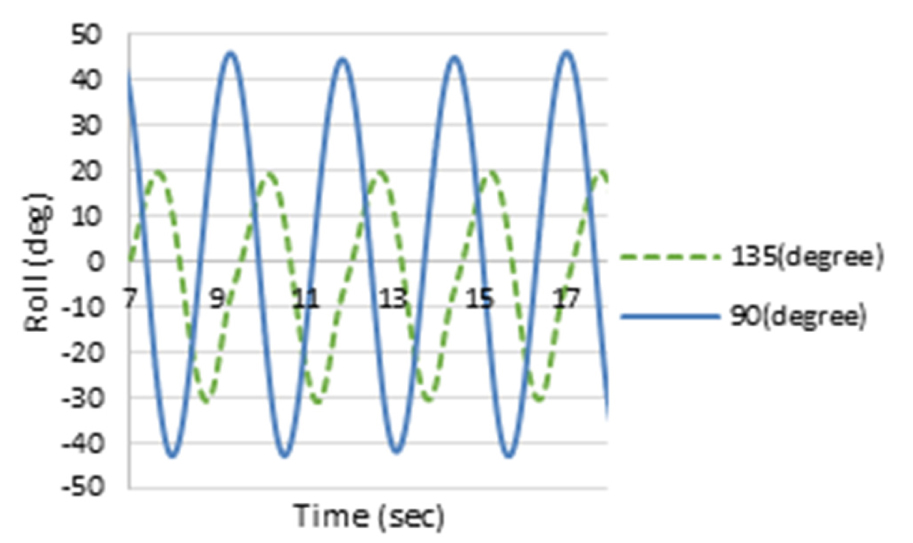
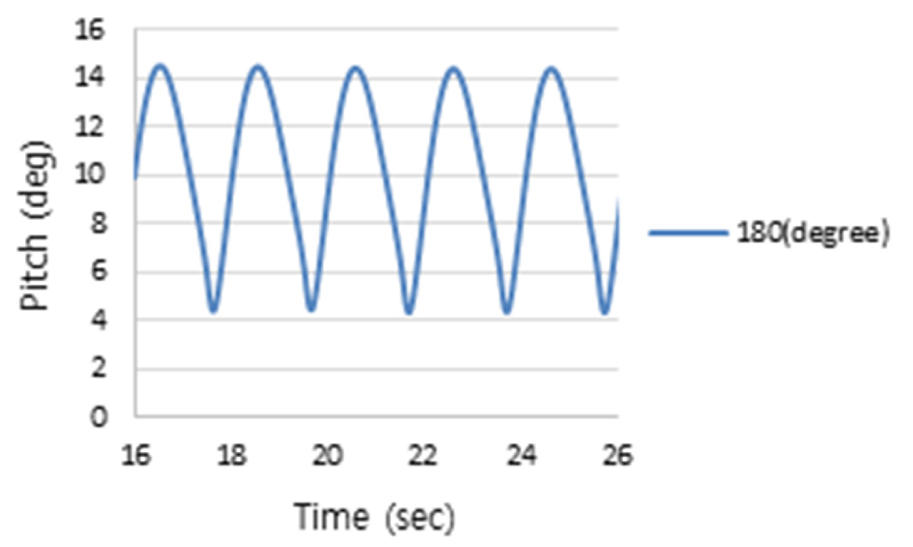
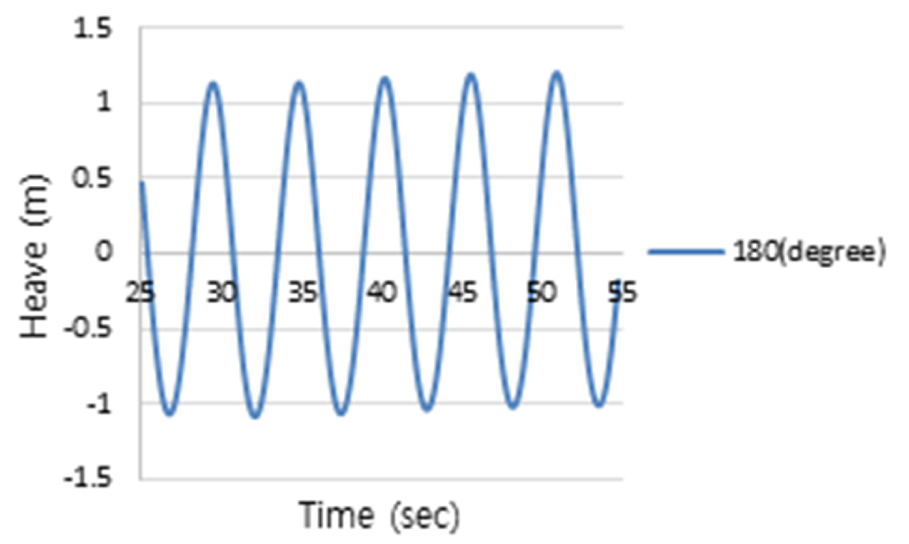
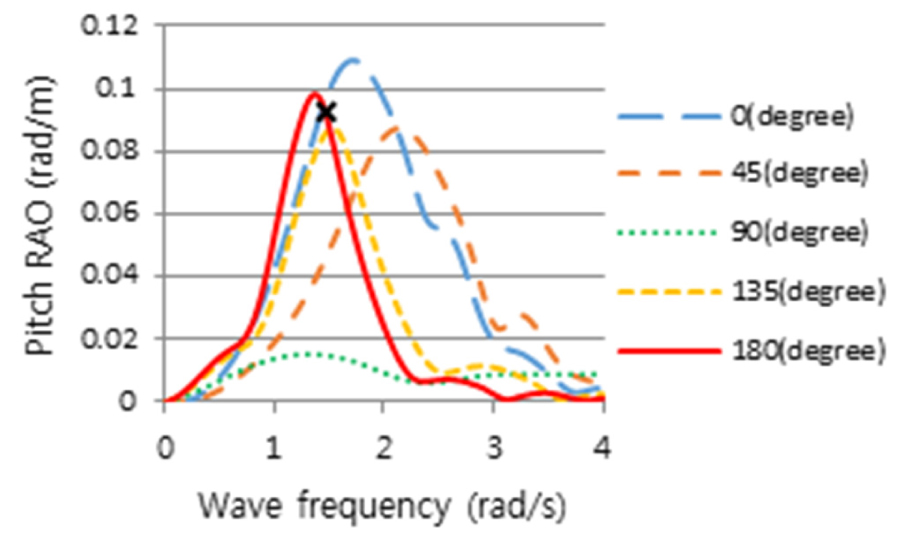
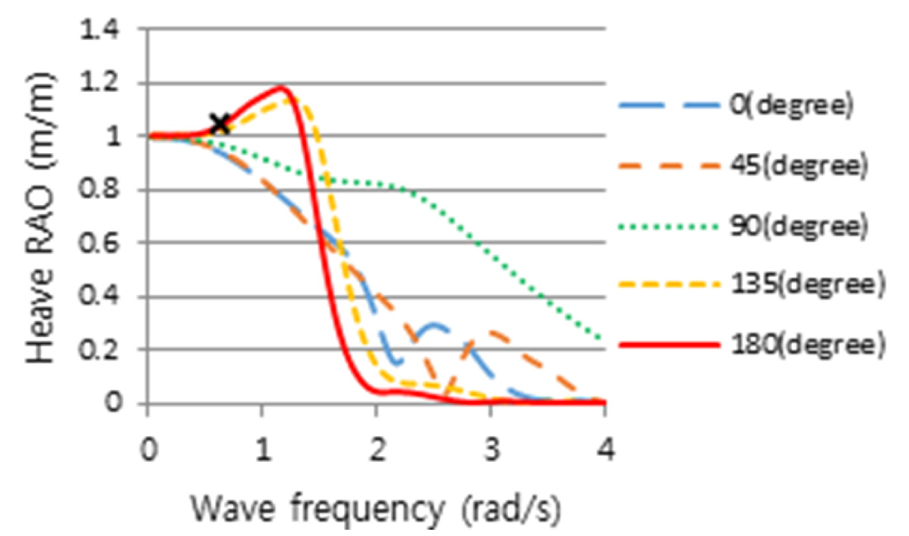
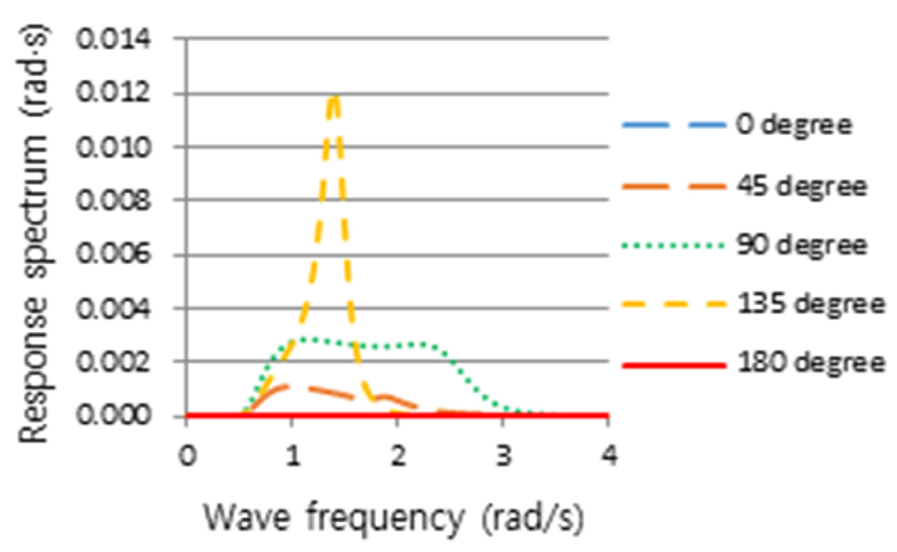
2nd Stage로 Table 6의 정수 중 동요 감쇠계수를 반영하여 Table 2의 운항 중 선체운동 해석으로 얻은 RAO(Figs. 11, 12, 13)와 파랑 스펙트럼 Fig. 4를 식 (2)에 적용하여, 선박의 횡동요, 종동요 및 상하동요운동에 대한 선체운동 응답스펙트럼을 얻었으며, 이 응답스펙트럼에 민감한 주파수를 Figs.14, 15, 16과 같이 얻었다.

횡동요에 대하여 얻은 선체운동 응답스펙트럼 Fig. 14를 보면, 주파수 1.38rad/s, 조우각 135도인 선수사파에서 가장 큰 선체운동 응답스펙트럼 모멘트(m₀)가 발생하였으며, 그에 비해 추사파(45도)는 상대적으로 작은 응답스펙트럼을 나타내었다. 횡파(90도)는 고주파인 2.4rad/s에서 피크가 발생하였으며 135도보다 작지만 응답스펙트럼 모멘트(m₀)가 무시할 수 없을 만큼 크고 피크 주파수를 전후로 크고 넓은 에너지 스펙트럼의 분포를 나타냄을 알 수 있다. 또한 횡파보다 선수사파에서 더 큰 선체 응답스펙트럼이 나타나는 이유는 선박의 전진속력에 대한 효과로 사료된다. 3rd Stage에 의하면, 최대 응답인 135도의 피크 주파수를 기준으로 동일한 동요 감쇠비를 고주파에서 피크를 갖는 횡파(90도)에 적용해야 하나 주파수 차이가 매우 커 이를 적용하기에는 다소 무리가 있다. 이는 Fig. 11에서 조우각 90도가 가장 큰 횡동요 RAO를 가지나, Fig. 14와 같이 선박의 최대 응답스펙트럼 모멘트가 135도에서 발생하는 것은 90도의 피크 주파수(2.4rad/s)보다 135도의 피크 주파수(1.38rad/s)에서 Fig. 4와 같이 파랑 스펙트럼, S($$ \omega $$)의 에너지가 보다 더 집중되어 있기 때문이다. 따라서 횡파에 대해서는 동요 감쇠비를 추가적으로 구하였다. 종동요 응답스펙트럼은 Fig. 15와 같이 선수파 주파수 1.44rad/s에서 큰 값을 가지는 것을 알 수 있다. Fig. 16은 상하동요에 대한 선체운동 응답스펙트럼이며, 선수파 주파수 0.74rad/s에서 가장 큰 선체운동 응답스펙트럼을 나타내는 것을 알 수 있다. Table 7은 3rd Stage의 결과로 선박의 횡동요, 종동요 및 상하동요 운동에 대한 응답스펙트럼의 최대값이 발생하는 조건을 나타내고 있다.

Fig. 11.

Roll RAO at operation condition after applying zero speed damping in potential calculation

Fig. 12.

Pitch RAO at operation condition after applying zero speed damping in potential calculation

Fig. 13.

Heave RAO at operation condition after applying zero speed damping in potential calculation

Fig. 14.

Roll response spectrum at operation condition in potential calculation

Fig. 15.

Pitch response spectrum at operation condition in potential calculation

Fig. 16.

Heave response spectrum at operation condition in potential calculation

Table 7.

Tuning conditions between CFD and potential based program

4.4 CFD를 이용한 운항 중 동요 감쇠 해석

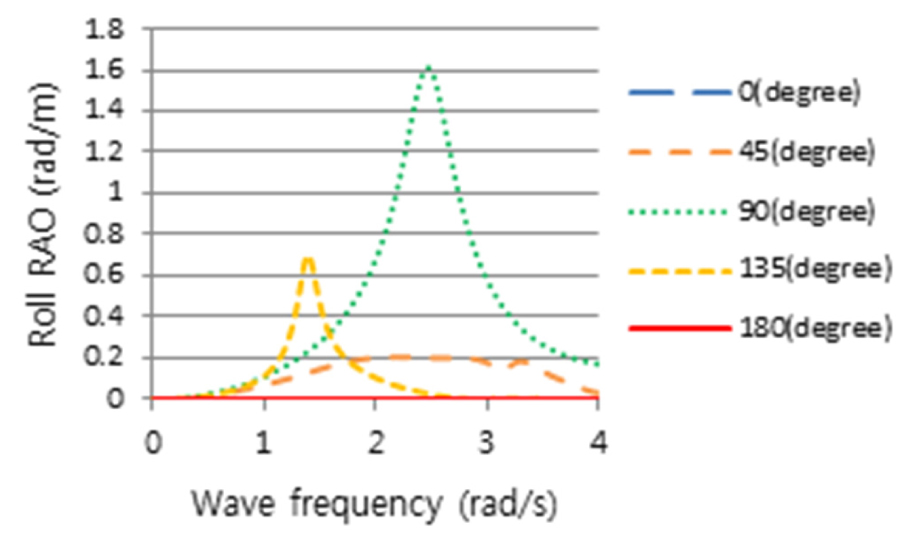
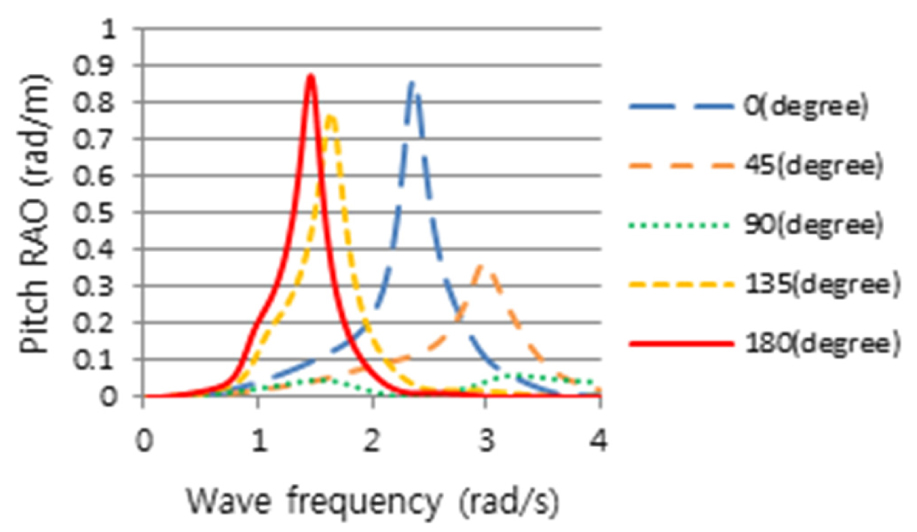
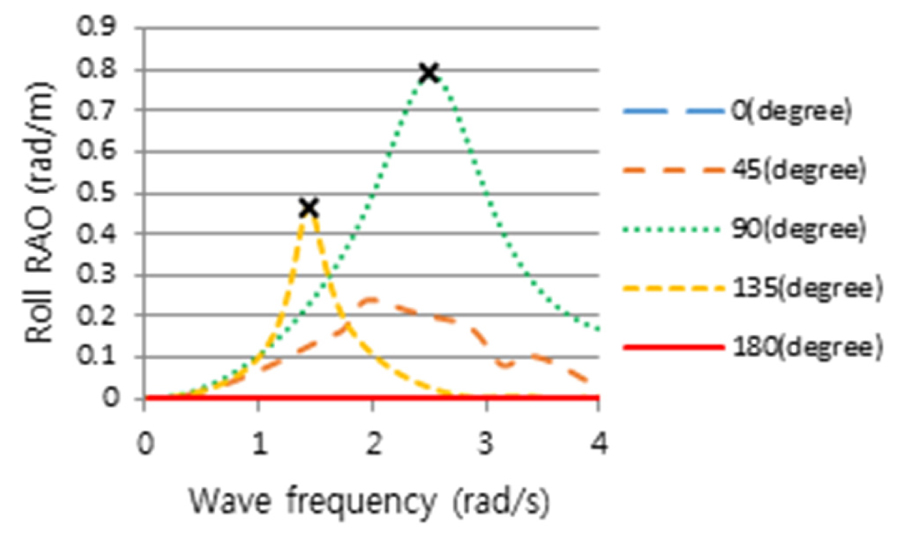
4th Stage로 Table 7의 조건하에서 CFD 계산을 수행하여 Figs. 17, 18, 19와 같이 횡동요, 종동요 및 상하동요 운동결과를 얻었으며, 5th Stage로 동일한 조건에서 CFD 결과와 일치하도록 포텐셜 프로그램의 감쇠계수값을 조정하였다. Figs. 20, 21, 22는 도출한 각 운동성분의 RAO 결과들이며, ‘X’표시는 해당 속도, 주파수 및 각도에서 최대운동 응답스펙트럼의 피크위치를 표시한 것이고 이 위치에서 CFD와 포텐셜프로그램의 결과를 보정하였다. Fig. 11에서 조우각 90도가 가장 큰 횡동요 RAO를 가지나, Fig. 14와 같이 선박의 최대 응답스펙트럼 모멘트가 135도에서 발생하는 것은 90도의 피크 주파수(2.4rad/s)에서는 Fig. 4와 같이 파랑 스펙트럼, S($$ \omega $$)의 에너지가 거의 없기 때문이다.

Fig. 17.

Roll RAO at tuning condition in CFD calculation

Fig. 18.

Pitch RAO at tuning condition in CFD calculation

Fig. 19.

Heave RAO at tuning condition in CFD calculation

Fig. 20.

Roll RAO at operation condition after applying dynamic damping in potential calculation

Fig. 21.

Pitch RAO at operation condition after applying dynamic damping in potential calculation

Fig. 22.

Heave RAO at operation condition after applying dynamic damping in potential calculation

선체운동 해석 결과와 CFD 결과가 동일하도록 조정하여 얻은 운항 중 동요 감쇠비는 Table 8과 같다. 나머지 내항성능 평가절차는 선박의 내항성능 해석 및 결과 분석으로 이는 5절에서 다루고자 한다.

Table 8.

Nondimensional damping ratio in dynamic condition

5.1 내항성능 평가요소의 발생확률 산출

6th Stage로 Fig. 23을 참고하여 Table 5에 있는 횡동요, 종동요, 수직 가속도 및 수평가속도는 SSA를, 갑판침수와 슬래밍은 시간 당 발생횟수로 국부 내항성능 평가를 수행하였다. 갑판침수는 파도와 선체의 상대수직변위가 선수부 위치에서 유효건현을 초과할 확률(P_DW)을 의미하고, 이는 Ochi and Motter (1974)에 의하여 식 (16)과 같다. 또한 시간당 갑판침수의 발생 횟수 N_W는 시간당 조우하는 파의 주기를 고려하여 식 (17)과 같이 구할 수 있다.

Fig. 23.

Local positions for measuring seakeeping performance of high speed planing boat

여기서, f는 파에 의한 상대선수운동을 고려한 유효건현, T는 파의 주기이며, m_0s 및 m_2s는 각각 평가위치에서 선박의 상대 수직변위운동과 상대 수직속도운동에 대한 응답스펙트럼의 면적을 나타내며, 식 (4)로 구할 수 있다.

슬래밍은 선박의 선저가 수면으로 노출될 때 파에 대한 선저의 상대수직속도가 한계속도를 초과할 확률(P_SLAM)로써, Ochi (1964)에 의하여 식 (18)과 같이 구할 수 있으며, 이때 시간당 슬래밍의 발생횟수 N_S는 식 (19)와 같다.

여기서, d는 계산위치에서 선박의 흘수, v₀는 상대속도의 한계치로 경험식 v₀=0.093*(g*L)^1/2을 사용하였다.

5.2 내항성능 해석 결과

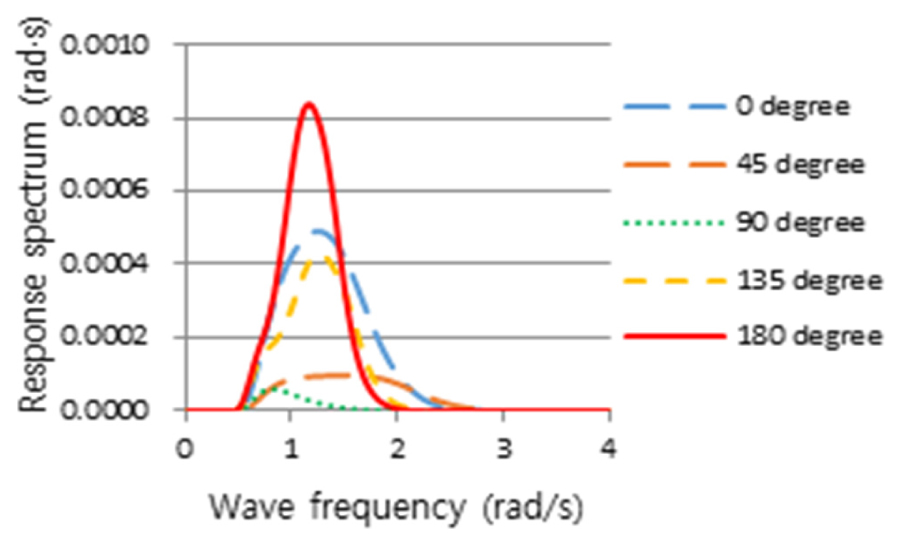
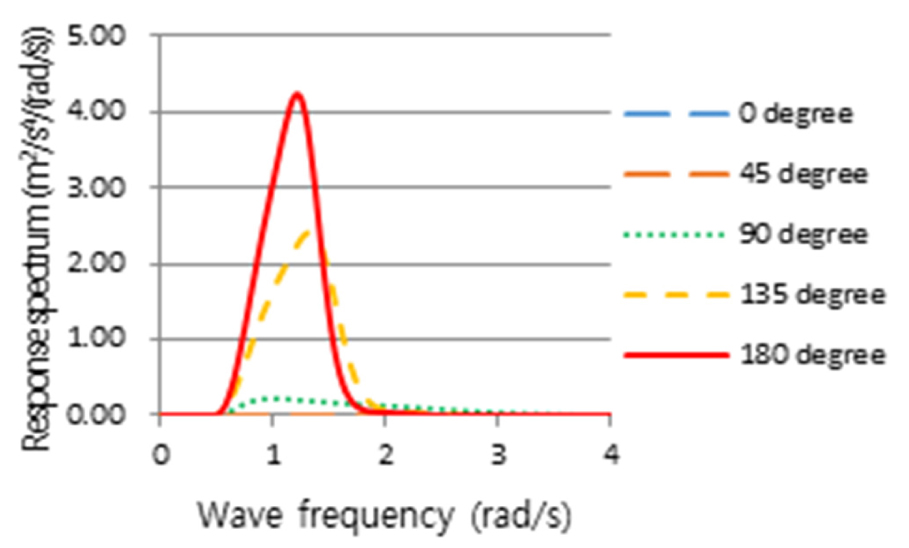
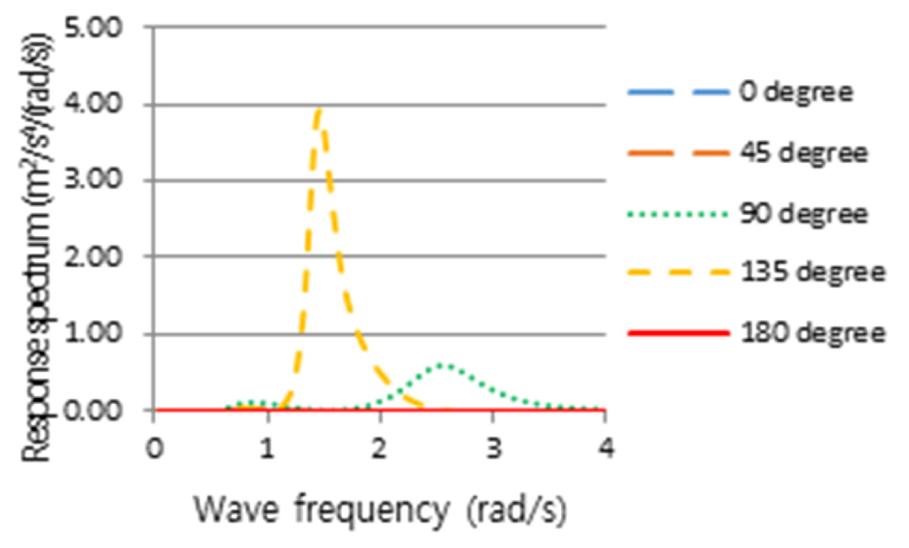
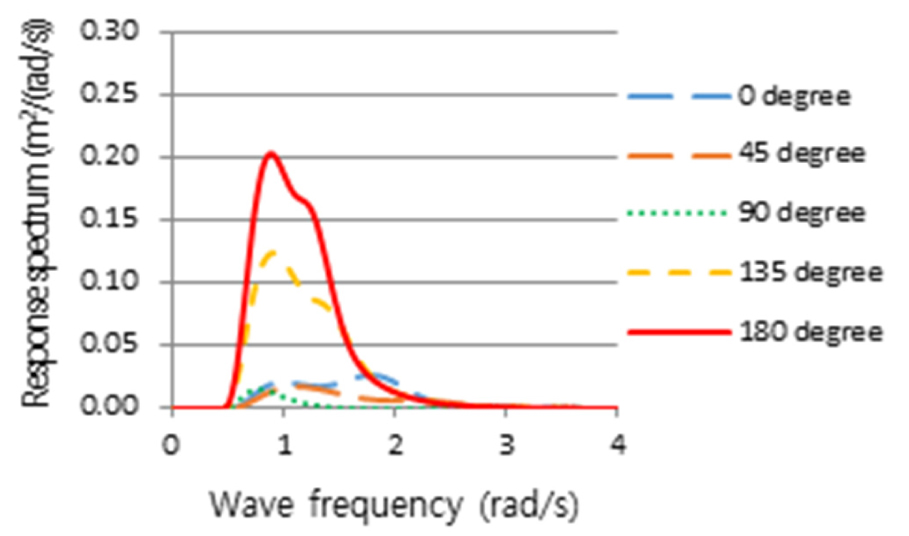
Figs. 24, 25, 26, 27, 28, 29, 30은 6th Stage의 결과로 Table 5의 국부내항성능의 항목별 평가기준 위치에서 계산한 선체운동 응답스펙트럼을 나타낸 것이다. 마지막 7th Stage로, 해당하는 선체운동 응답스펙트럼의 m₀ 및 m₂를 구하여 파랑 조우각에 따른 내항성능 항목별 발생정도를 산출하였으며, 그 결과를 Table 9과 같이 얻었다. 선박의 국부내항성능 계산에서 주파수 범위는 Table 2에서와 같이 2.5rad/s까지 고려하였으며, Figs. 24, 25, 26, 27, 28, 29, 30에서는 응답스펙트럼의 전반적인 경향을 보여주기 위하여 계산할 주파수 영역을 넘어서는 4.0rad/s까지 나타내었다.

Fig. 24.

Roll motion response spectrum calculated at assessment position in potential calculation

Fig. 25.

Pitch motion response spectrum calculated at assessment position in potential calculation

Fig. 26.

Vertical acceleration response spectrum calculated at assessment position in potential calculation

Fig. 27.

Lateral acceleration response spectrum calculated at assessment position in potential calculation

Fig. 28.

Relative vertical motion response spectrum calculated at slamming assessment position in potential calculation

Fig. 29.

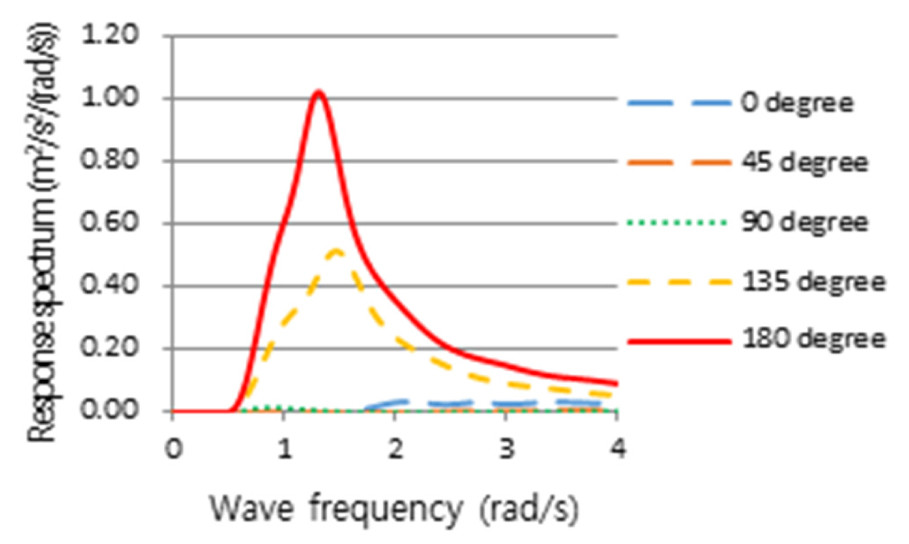
Relative vertical velocity response spectrum calculated at slamming assessment position in potential calculation

Fig. 30.

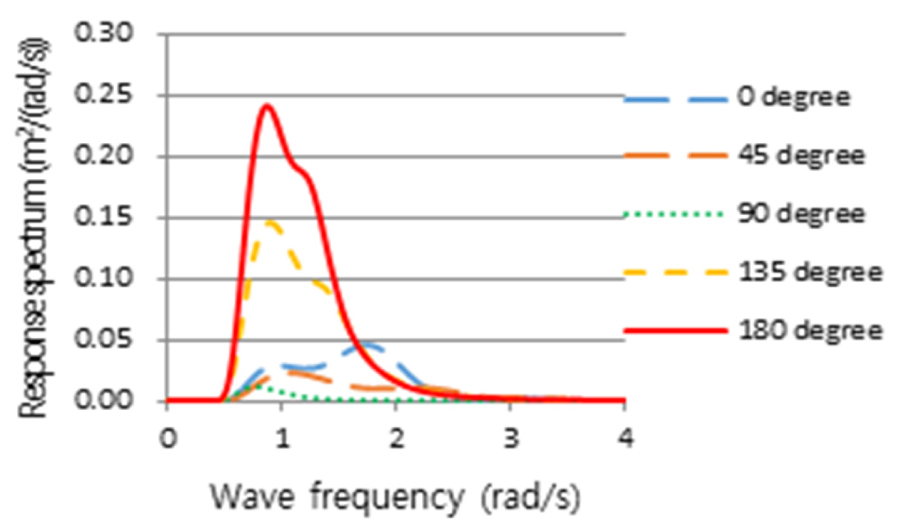
Relative vertical motion response spectrum calculated at deck wetness assessment position in potential calculation

Table 9의 수치해석 결과를 보면, 임무수행을 위한 내항성능 기준을 일부 값이 상회하는 것을 알 수 있다. 횡동요는 90도와 135도에서 최대허용 기준에 거의 만족시켰으며, 이 결과에서 경우에 따라 90도에서 최대응답이 나올 수 있기 때문에 횡동요의 경우 90도와 135도에 대한 응답을 모두 평가해야할 필요가 있다. 종동요, 수직가속도 그리고 수평가속도의 경우 모든 구간에서 한계치를 충분히 만족하고 있으며, 갑판 침수도 합리적인 수준의 내항성능을 보여주고 있다. 이는 선박의 운항조건에서 조우하는 파고에 대하여 선수 건현의 높이가 충분하여 갑판침수가 거의 일어나지 않는 것으로 사료된다.

Table 9.

Results of seakeeping for sea state 4

슬래밍 빈도의 한계값은 50회로 Head sea(180°) 조건에서 다소 과도하게 발생한 것을 알 수 있다. 하지만 해당 선박은 슬래밍 빈도를 줄이고자 계산에서 고려되지 않은 방현대를 비롯한 타 부가물들이 설치되어 있어 이에 대한 수정은 실무적인 차원에서 고려되어질 필요가 있다. 또한 슬래밍의 빈도 계산에 사용된 식 (18)에서도 상대수직변위와 상대수직속도가 협대역(narrow band) 거동을 보이는 것으로 가정하여 Rayleigh분포로부터 유도된 식이기 때문에, Fig. 28과 Fig. 29와 같이 응답스펙트럼이 넓은 주파수 영역에 걸쳐 퍼져있는 광대역 거동에서는 그 빈도수가 작아질 수 있다. 따라서 식 (18)을 개정하여 사용하거나 추가적인 CFD해석으로 Head sea(180°) 조건에서 파랑스펙트럼으로 생성된 무작위 파로 발생한 슬래밍 빈도를 검증해야 할 필요가 있다. Fig. 24를 보면 횡파의 응답스펙트럼도 광대역일 뿐만 아니라, 2.5rad/sec이상의 고주파 영역에서의 응답이 큰 것을 알 수 있다. 이러한 결과는 추가적인 CFD해석으로 검증해야 할 필요가 있다. 이러한 검증은 본 연구이외에 추가적인 연구로 수행될 예정이다.