횡경사상태 선박의 조종성능변화에 관한 실험적 연구

1. 서론

선박의 조종성능 추정 연구는 최근 해양사고분석과 관련하여 활발히 이루어지고 있는데, 특히 사고 선박의 이동궤적과 운항 상태를 보다 정확하게 시뮬레이션하기 위해 그 중요성이 대두되고 있다(Kim et al., 2017). 선박의 조종성능을 추정하는 전통적인 방법으로는 구속모형시험과 자유항주모형시험이 있는데(Kim et al., 2011), 이러한 방법은 선박의 일반적인 운항 상황을 가정하고, 그 운항범위 내에서 시험조건이 결정되고 시험이 수행된다. 이에 반하여 선박간의 충돌, 좌초, 침몰과 같은 예기치 않은 상황에서의 해양사고는 일반적으로 화물의 이동, 침수, 선박적재상태 변화 등에 기인하는 비정상적인 선박상태에 의하여 발생하는 경우가 많다. 따라서 이러한 비정상적인 선박상태에서의 선박조종성능을 추정하기 위해서는 일반적인 시험조건 범위를 벗어난 상태에서의 시험수행이 필요하다. Kim(2018)은 이러한 필요성에 의해 손상상태의 선박에 대하여 구속모형시험을 수행하여 비대칭 조종시뮬레이션 기법을 연구하였고, Yeo et al.(2016)도 구속모형시험을 통해 횡경사상태 모형선의 조종유체력 변화를 연구하였다. 또한 횡경사에 의한 저항성능 변화에 대해서도 실험을 통해 연구된 바 있다(Yang & Kim, 2005).

한편, 선박의 횡경사각, 종경사각은 설계 조건 혹은 운항 조건에 따라 결정되는 선박의 고정된 무게중심 위치와 선박의 경사각 변화에 따라 이동하는 부력중심 위치가 연직하방으로 같은 선상에 일치하는 곳에서 결정된다. 선박의 무게중심 변화는 횡방향, 종방향, 상하방향의 이동으로 구분할 수 있다(Fig. 1). 횡방향, 종방향 무게중심 변화는 각각 선박의 횡동요, 종동요 자세각을 변화시키고, 일반적으로 횡경사상태는 선박의 좌우 비대칭에 의한 불균형력을 유발하여 선박이 직선으로 항해하는 것을 방해하는 것으로 알려져 있다. 또한 종경사상태는 선박의 수선면적과 그 면적중심을 이동시켜 선박의 안정성을 변화시키는 것으로 알려져 있다. 반면 선박의 상하방향 무게중심 변화는 정적인 자세각을 변화시키지는 않으나 횡방향, 종방향 운동의 크기를 변경시켜 선박의 동적 운동특성 변화를 일으킨다. 일반적으로 높은 무게중심 위치는 선박이 선회 시 더 많은 횡경사각을 가지도록 하고, 선회직경을 줄어들게 하는 것으로 알려져 있으며, 이는 KVLCC1 선형에 대하여 실험으로 확인된 바 있다(Choe & Im, 2016).

Fig. 1.

Attitude of ships from relation of center of gravity and center of buoyancy

본 연구에서는 선박의 세 방향 무게중심 변화 중 횡방향 무게중심 변화에 의한 선박의 조종성능 변화를 연구하였다. 횡경사상태에 놓인 선박의 조종성능 변화를 실험적으로 규명하기 위하여 KCS 선형에 대하여 자유항주모형시험을 수행하였다. KCS 모형선의 무게중심을 좌현방향으로 이동시켜 0도, -10도, -20도의 세 가지 횡경사각에 대한 선회시험, 지그재그시험을 수행하여 횡경사에 의한 선박조종성능 변화를 확인하였고, 이를 다른 연구에서 비교검증용 데이터로 사용할 수 있도록 그 값을 정량적으로 제시하였다.

2. 자유항주모형시험

횡경사상태 선박의 변화된 조종성능을 확인하기 위하여 자유항주모형시험을 수행하였다. 1/65.83 크기의 KCS 모형선에 대하여 20노트의 대응속도로 좌우현 35도 선회시험, 20/20 지그재그시험을 수행하였다. 이를 위한 KCS 모형선과 사용된 시험장비, 상세 시험항목은 아래와 같다.

2.1 KCS 모형선 및 시험장비

KCS 선박은 Table 1에서와 같이 GM 값이 0.6 m로 다른 선형에 비하여 그 값이 상대적으로 작아 운항 중 횡동요 등이 더 크게 발생할 가능성이 높고, 무게중심 위치 변화 시 모형선이 더 큰 초기 횡경사상태에 놓일 수 있다. 모형선의 크기와 시험속도는 시험장소(선박해양플랜트연구소 내 해양공학수조)와 탑재 시험장비의 크기, 무게를 고려하여 각각 1/65.83 비와 실선기준 20노트의 대응속도인 1.268 m/s로 결정되었다. 표의 왼쪽 실선 값은 설계값이고, 오른쪽 모형선 값 중, GM, Kzz, Kxx는 시험 준비상태에서 계측된 값이다. 특히 모형선의 횡경사 구현 시 내부에 설치된 무게추를 동일한 높이에서, 모형선 중심기준 횡방향 대칭위치로 이동하여, GM, Kzz, Kxx 값이 변경되지 않게 하였다.

Table 1.

Principal dimensions of KCS

Fig. 2는 시험에 사용된 KCS 모형선의 사진이다. 모형선 상부에는 모형선의 위치를 계측하기 위한 위치계측판이 부착되어 있고, 내부에는 모형선의 상태를 계측하기 위한 3축 광자이로, 경사계 등의 센서장비가 설치되어 있다. 또한 시험항목대로 모형선을 움직이게 하는 컴퓨터 및 제어기, 전원공급을 위한 축전지가 설치되어 있다.

Fig. 2.

KCS model ship

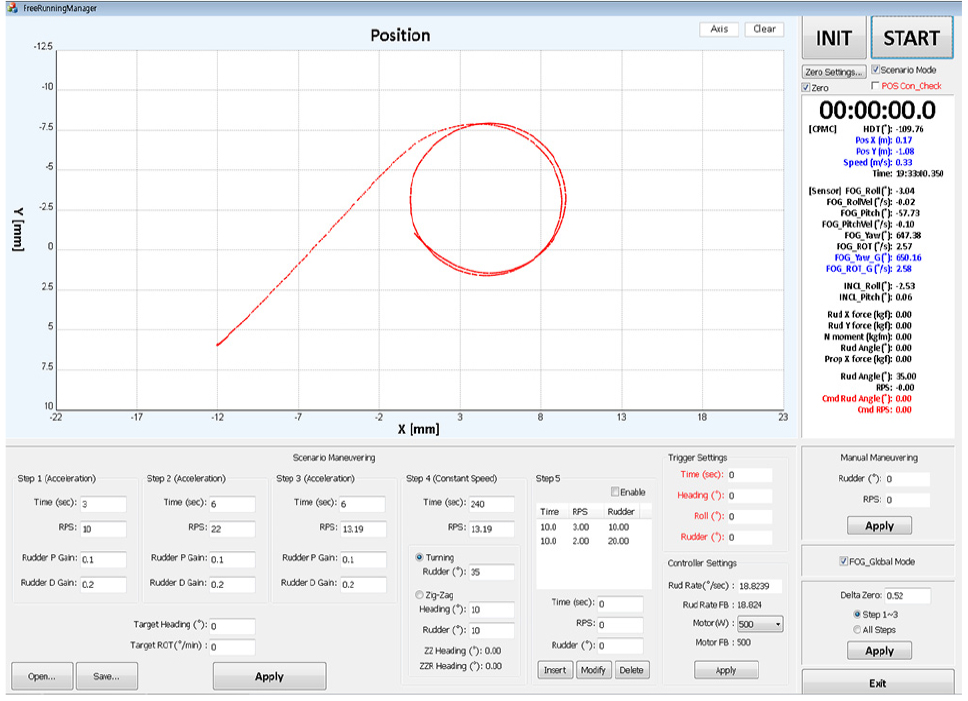
모형선에 탑재된 컴퓨터에는 Fig. 3과 같은 자유항주모형시험 운용프로그램이 설치되어 각종 센서장비의 데이터 취득, 타각 및 프로펠러 제어기로의 제어명령 및 그 결과값 송수신 등이 실시간으로 처리되고, 모형선의 위치, 속도, 선수동요각, 선수동요각속도, 횡동요각, 종동요각, 타각, 프로펠러 회전수 등이 동시에 기록된다(Yun et al., 2015).

Fig. 3.

Free running model test manager

2.2 시험항목

선박의 조종성능을 확인하기 위한 일반적인 표준시험항목(IMO, 2002) 중, Table 2와 같은 항목에 대하여 자유항주모형시험을 수행하였다.

Table 2.

Free running model test cases

속도시험에서는 횡경사 0도에 대하여 모형선 속도 1.268 m/s에 대응하는 프로펠러 회전속도와 모형선의 직선운항을 위한 중립타각 및 타각제어용 게인값을 찾는다. 여기서 결정된 프로펠러 회전속도는 이후 횡경사상태에서의 선회, 지그재그시험에서 동일한 값으로 적용되었고, 중립타각 및 타각제어용 게인값은 횡경사상태에 따라 그 값이 변경되었다.

속도시험에서는 각 항목의 상관관계가 명확하게 드러날 때까지 그 시험횟수가 반복되었고, 선회시험과 지그재그시험에서는 고정된 설정값에 따라 3회 이상의 반복시험을 수행하였다. 특히 시험 결과에 많은 영향을 줄 수 있는 초기 선수동요각속도와 초기 속도는 분석 시 그 범위를 한정하였다(Yun et al., 2018).

3. 시험 결과 및 고찰

세 가지 횡경사상태에 대하여 KCS 선형의 속도, 선회, 지그재그 자유항주모형시험을 수행하였고, 다음과 같은 운항궤적 및 운항데이터를 취득하여 분석하였다.

3.1 속도시험

횡경사상태에 놓인 선박은 수선면의 좌우비대칭과 그에 따른 유입류 변화로 인하여 선박의 저항이 변하게 되고, 직선으로 항해하는 것을 방해받게 된다. 이는 모형선의 초기속도 변화, 중립타각 변화, 0도 타각에서의 선수동요각속도를 확인하여 그 특성을 확인할 수 있다.

Table 3은 횡경사 0도에서 찾은 모형선의 속도 1.268 m/s에 대응하는 프로펠러 회전속도와, 고정된 동일 프로펠러 회전수에서 횡경사 –10도, -20도에서의 모형선 속도이다. 표에서와 같이 모형선의 횡경사각이 커질수록 그 속도가 작아지는 것을 확인할 수 있고, -20도 횡경사상태에서는 속도가 약 6.6% 감소하는 것을 확인할 수 있다. 이는 모형선의 경사에 의한 선체저항 증가, 중립타각 및 타 제어사용량 증가에 따른 타에 의한 저항 증가 등을 그 이유로 볼 수 있다. 특히 Yeo et al.(2016)의 구속모형시험에 의하면, 동일한 선형(1/42)에 대하여 -20도 횡경사상태에서 X방향 힘이 약 6% 증가하는 것을 확인할 수 있다. 이러한 저항증가 현상은 대형유조선 선형에 대해서도 연구된 바 있으며, 주로 형상저항의 변화에 기인함을 밝히고 있다(Yang et al., 2006).

Table 3

Relations of speed and propeller RPS

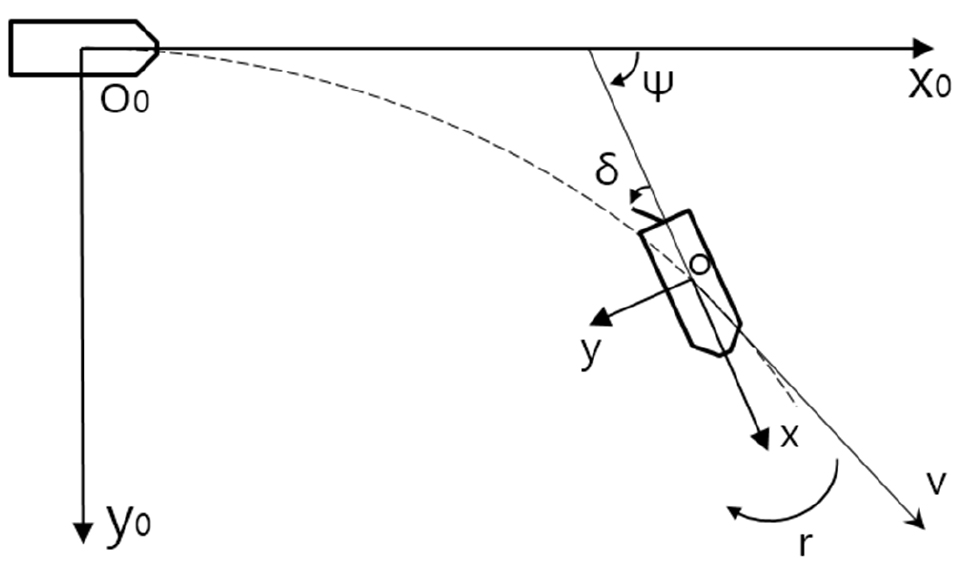
Fig. 4는 선체 및 타각의 좌표계를 나타낸 그림이고, 타각의 회전방향은 선체와 반대방향을 양의 부호로 설정하였다.

Fig. 4.

Coordinate system for FRMT

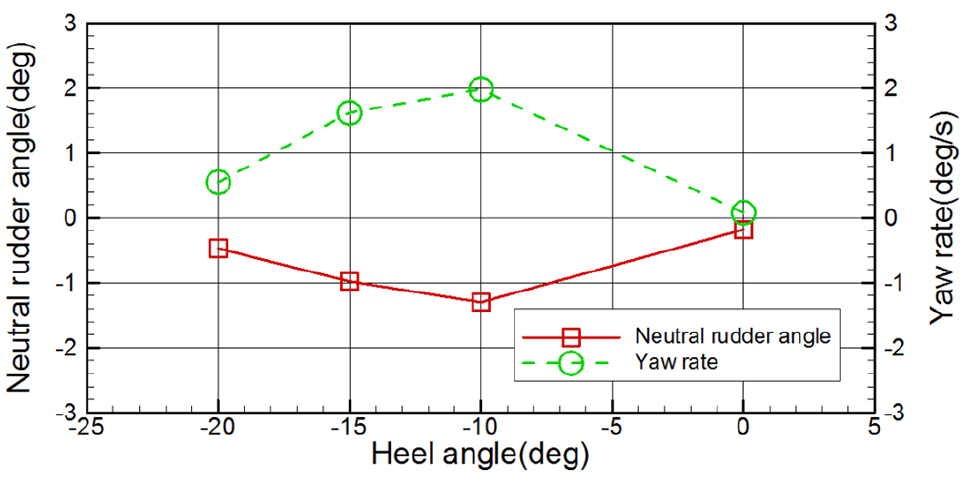
Fig. 5는 –15도의 횡경사각을 추가하여, 총 네 가지 횡경사각에서 모형선이 직선으로 운항하기 위한 중립타각과 타각 0도에서의 선수동요각속도를 나타낸 그림이다. 중립타각은 좌우현 미소 사용 타각과 그에 따른 선수동요각속도의 관계로부터 모형선의 선수동요각속도를 0으로 만드는 타각을 계산하여 구할 수 있다.

Fig. 5.

Neutral rudder angle and yaw rate at 0° rudder angle in four heeled conditions

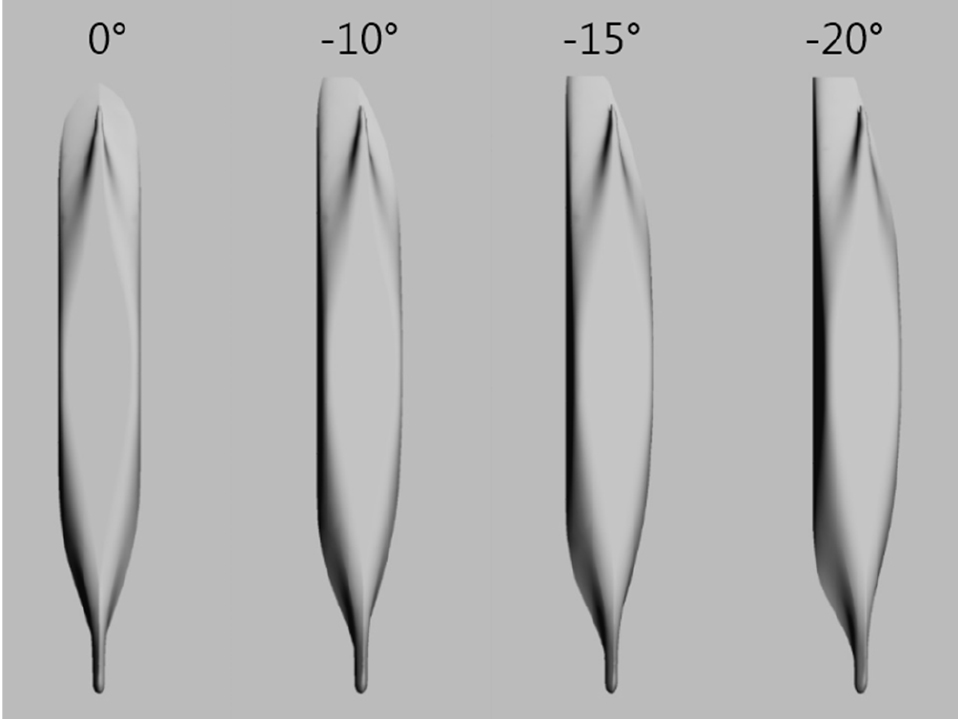
그림에서와 같이 좌현방향으로의 횡경사각이 발생하면, 모형선은 우현방향으로의 선수동요각속도가 발생하고, 그에 따라 중립타각 역시 좌현방향으로 결정되는 것을 확인할 수 있다. 중립타각을 결정함에 있어 시험에서 관측되는 특이한 사항은 KCS 모형선의 좌현 횡경사각에 따라 그 중립타각이 선형적으로 증가하지 않고 다시 감소하는 경향을 보였다는 것이다. Fig. 6에서와 같이 KCS 모형선의 횡경사별 수선면 하단 형상변화를 살펴보면, 좌우 비대칭성과 함께 –10도 이후 우현 선미 수선하단부가 물에 잠기지 않는 것을 확인할 수 있다. 또한 좌현 선수 수선하단부가 물에 잠기게 되면서 좌현선수부의 형상변화에 의한 저항이 커질 것임을 유추할 수 있다. 이에 대한 자세한 해석은 전산유체역학 해석 등을 통하여 횡경사별 모형선의 국부 압력변화를 추가적으로 살펴보아야 할 필요가 있을 것으로 판단된다.

Fig. 6.

Waterplanes of KCS in four heeled conditions

3.2 선회시험

세 가지 횡경사상태에 놓인 KCS 모형선의 35도 좌우현 선회시험 결과는 다음과 같다. 선회궤적은 모형선의 길이로 무차원화 되었고, 운항데이터는 모두 모형선에서 취득된 데이터 그대로 표현하였다.

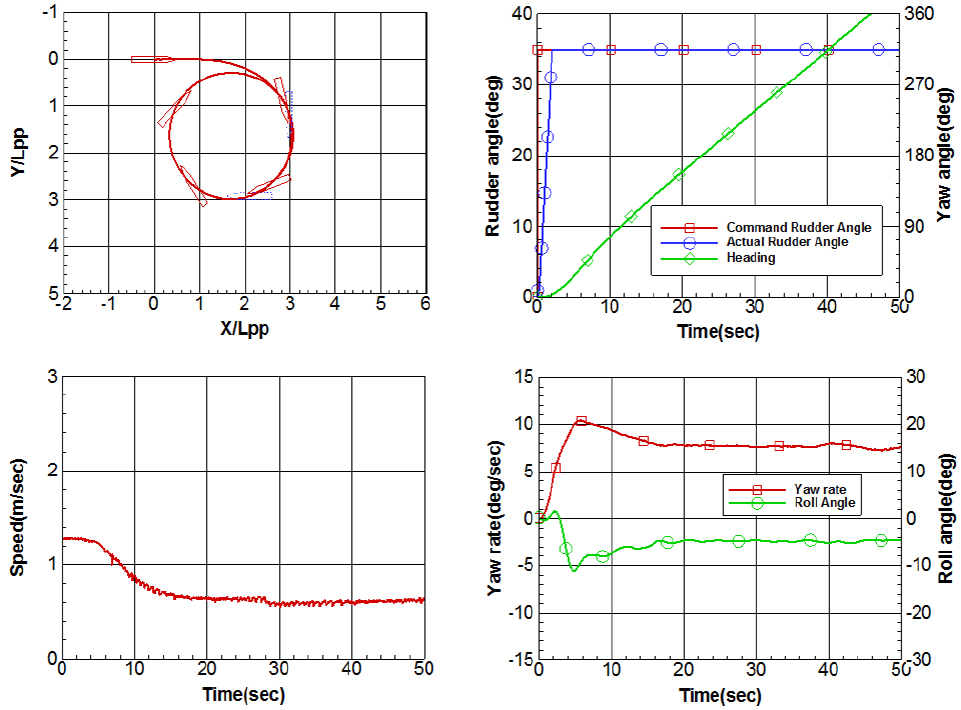
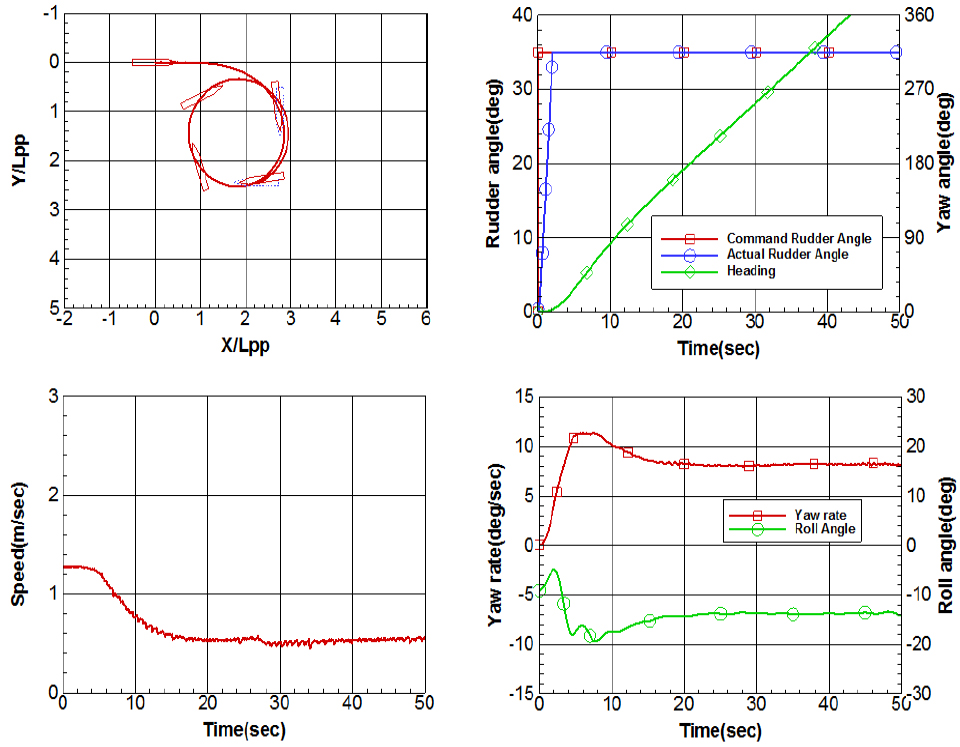
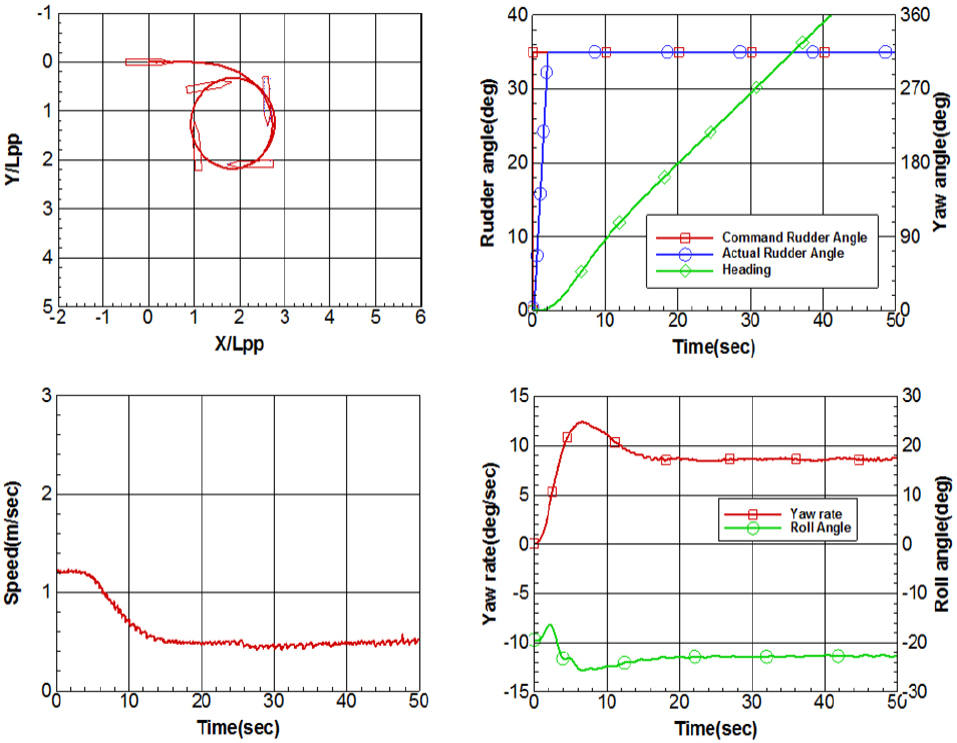
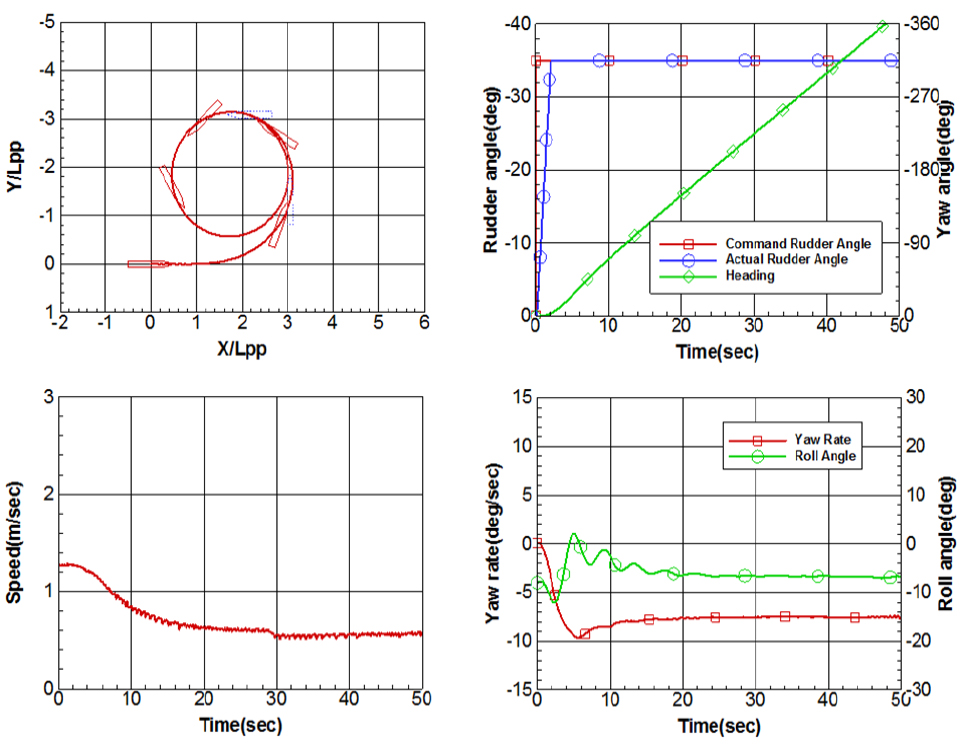
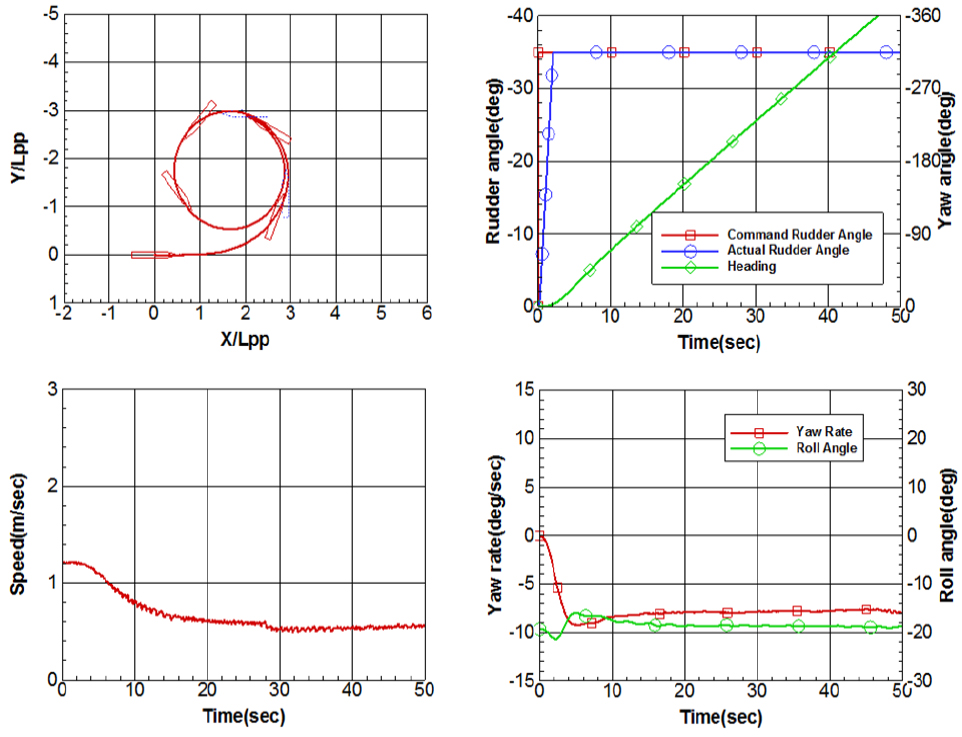
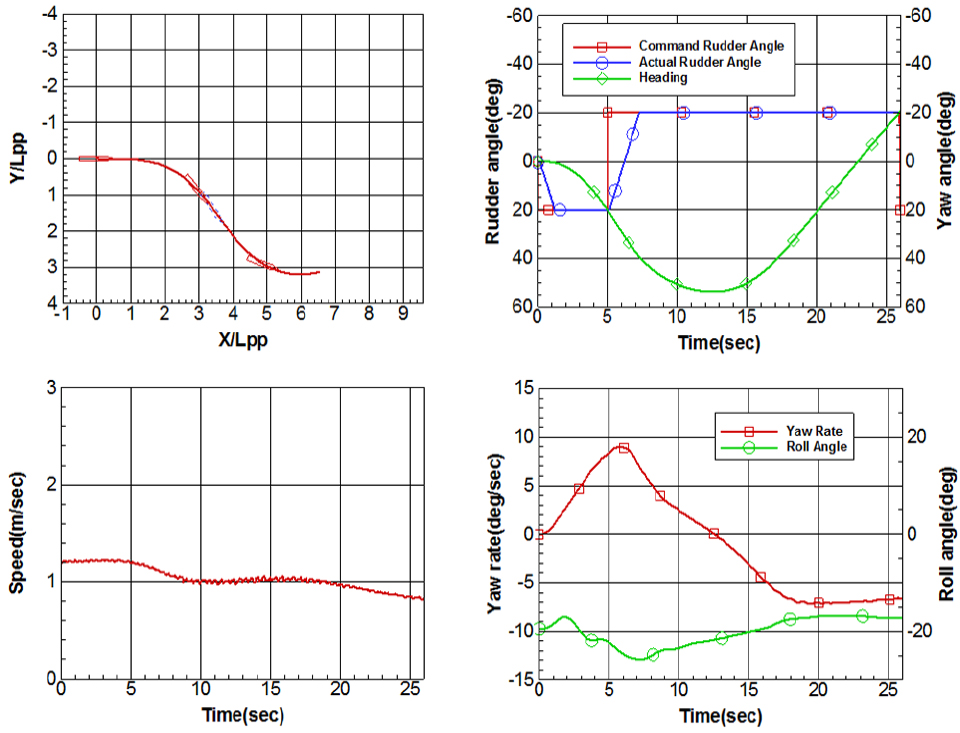
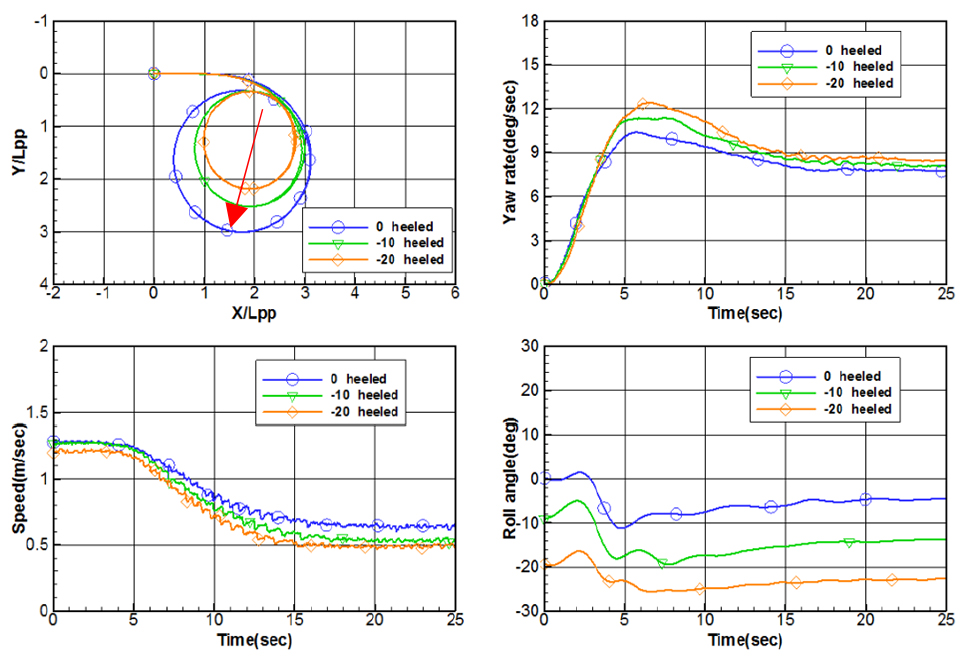
0도, -10도, -20도 횡경사각에서의 35도 우현선회궤적과 선회 중 타각, 선수동요각, 속도, 선수동요각속도, 횡동요각 데이터는 Figs. 7, 8, 9와 같다. 좌현 횡경사각이 커질수록 우현선회 시 그 선회직경이 작아지고 선회가 더 빨리 진행되는 것을 궤적과 시간에 따른 선수동요각속도 변화로부터 확인할 수 있다.

Fig. 7.

+35° STBD turning test in 0° heeled condition

Fig. 8.

+35° STBD turning test in -10° heeled condition

Fig. 9.

+35° STBD turning test in -20° heeled condition

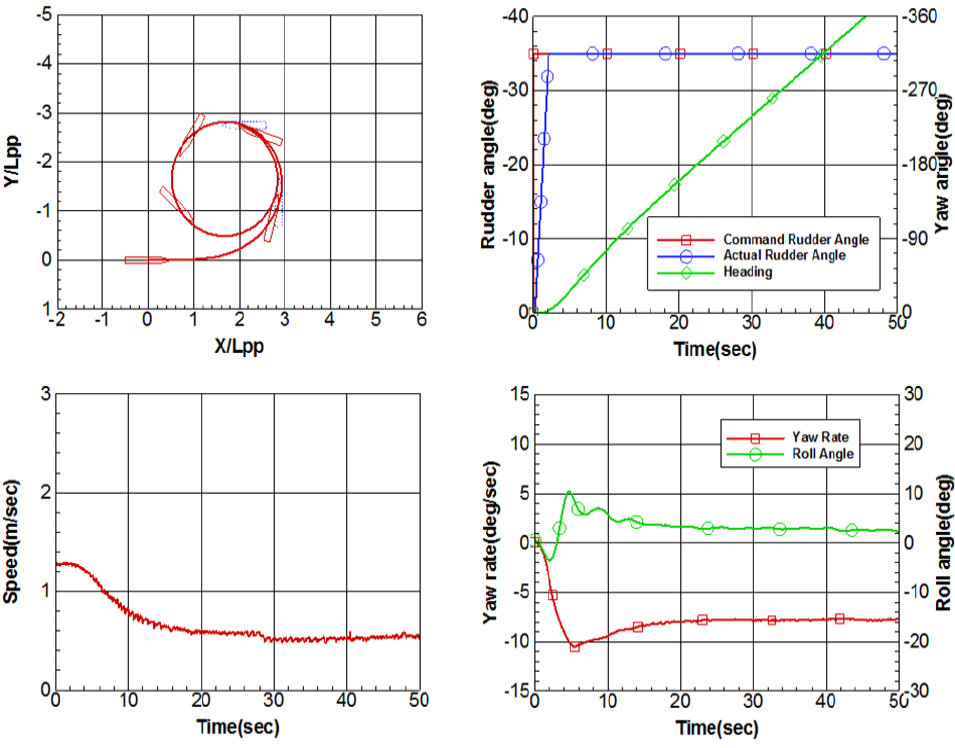
0도, -10도, -20도 횡경사각에서의 -35도 좌현선회궤적과 선회 중 타각, 선수동요각, 속도, 선수동요각속도, 횡동요각 데이터는 Figs. 10, 11, 12와 같다. 좌현 횡경사각 발생 시 좌현선회의 선회직경이 커지고, 선회가 늦게 진행되는 것을 궤적과 시간에 따른 선수동요각속도 변화로부터 확인할 수 있다.

Fig. 10.

-35° PORT turning test in 0° heeled condition

Fig. 11.

-35° PORT turning test in -10° heeled condition

Fig. 12.

-35° PORT turning test in -20° heeled condition

3.3 지그재그시험

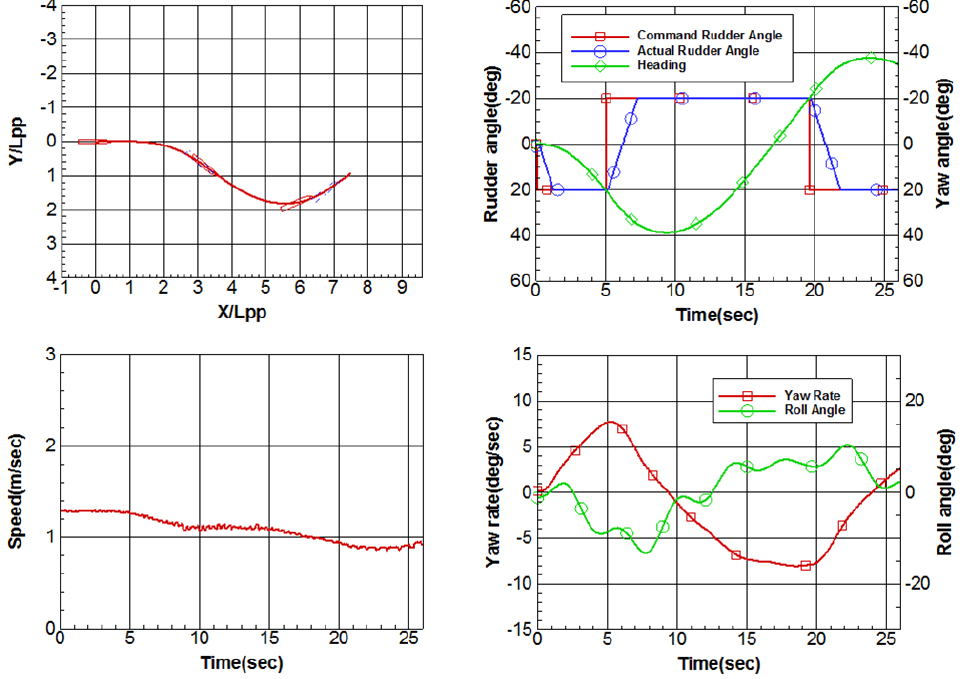
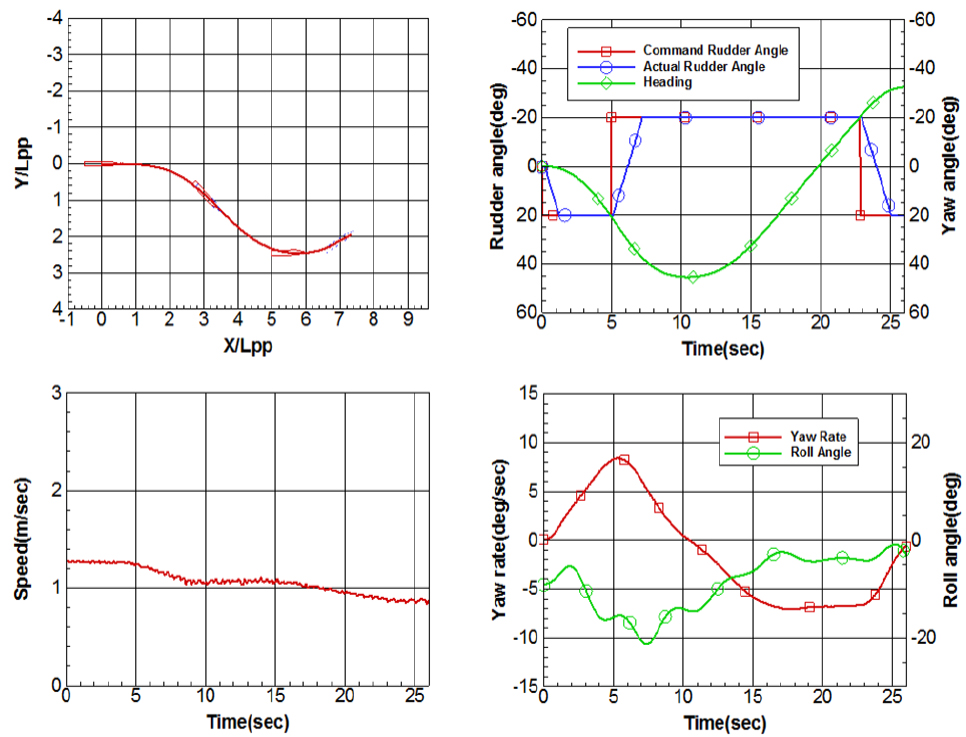
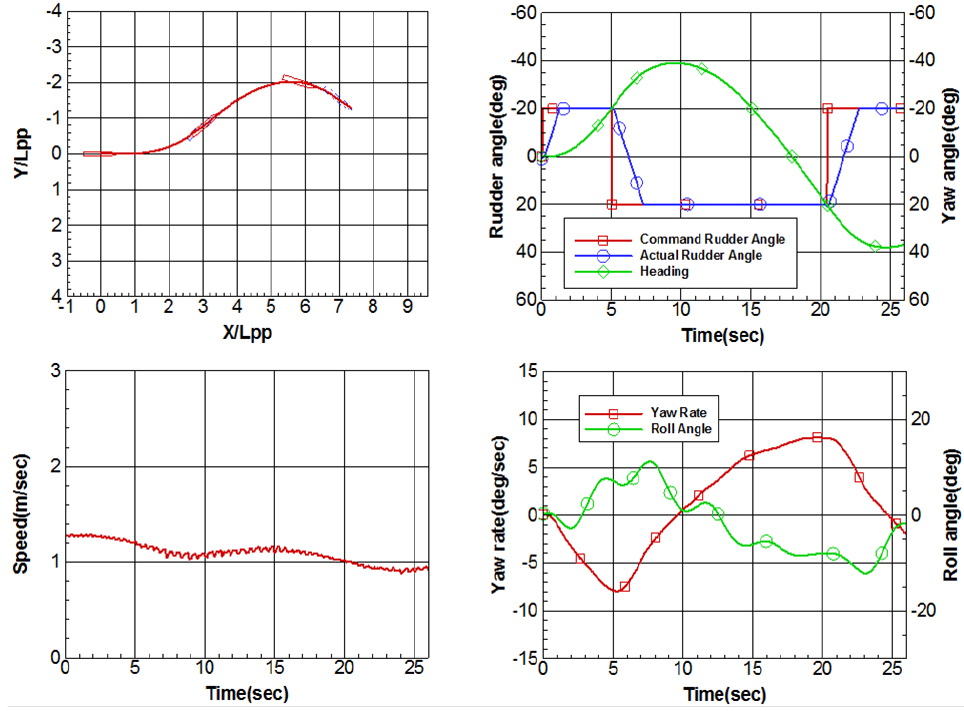
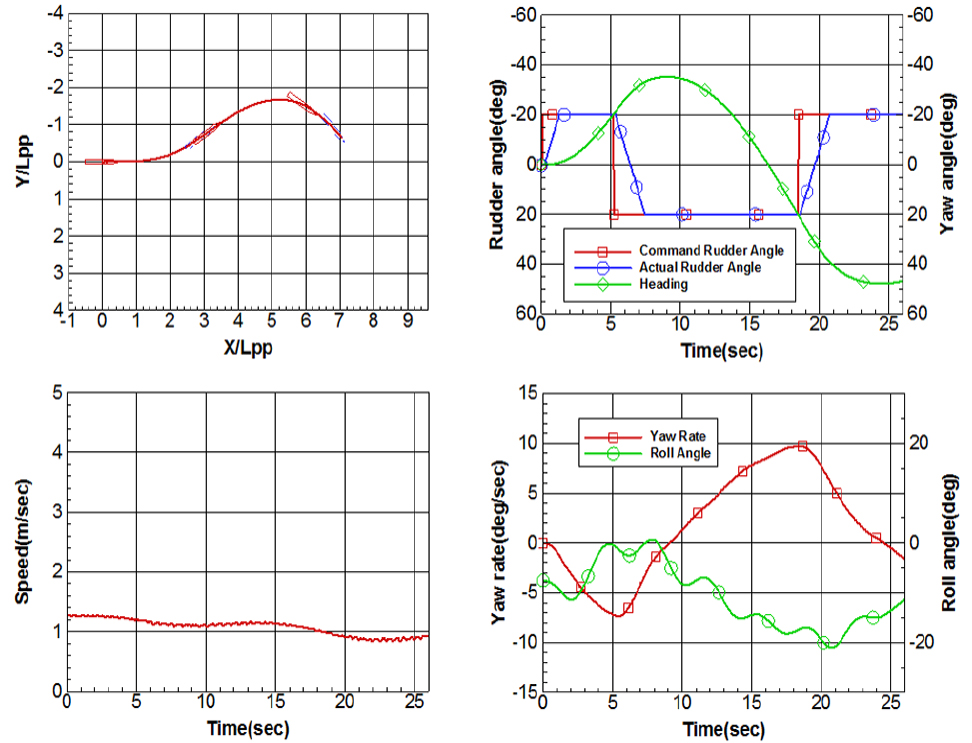
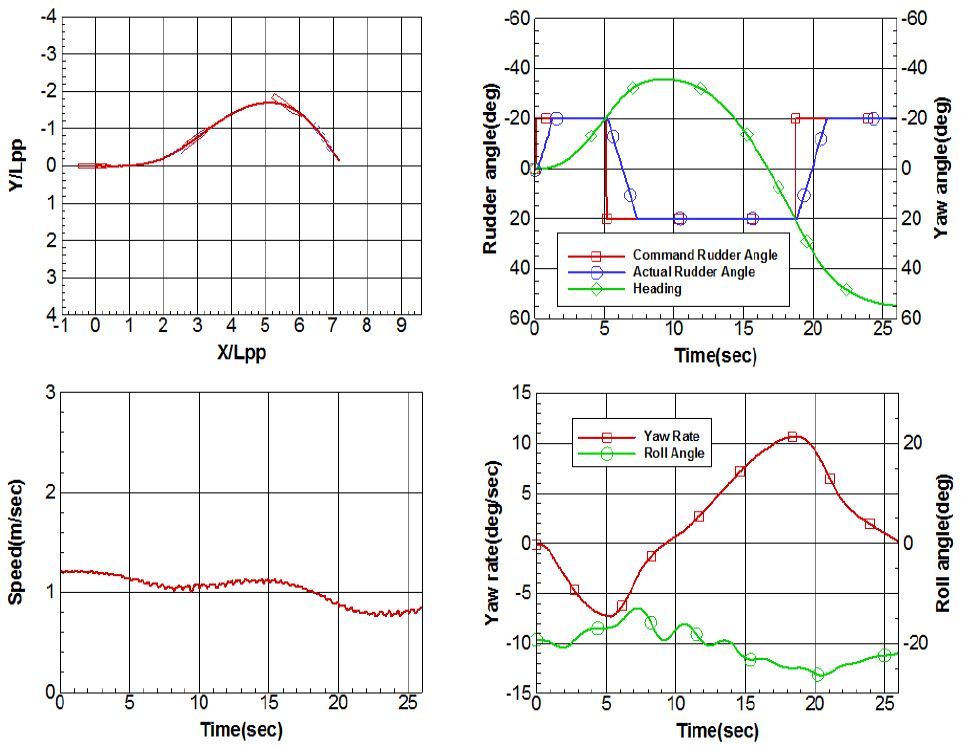
세 가지 횡경사상태에 놓인 KCS 모형선의 20/20 좌우현 지그재그시험 결과는 Figs. 13, 14, 15, 16, 17, 18과 같다. 선회시험과 동일하게 지그재그궤적은 모형선의 길이로 무차원화 되었고, 운항데이터는 모두 모형선에서 취득된 데이터 그대로 표현하였다.

Fig. 13.

+20/20 zigzag test in 0° heeled condition

Fig. 14.

+20/20 zigzag test in -10° heeled condition

Fig. 15.

+20/20 zigzag test in -20° heeled condition

Fig. 16.

-20/20 zigzag test in 0° heeled condition

Fig. 17.

-20/20 zigzag test in -10° heeled condition

Fig. 18.

-20/20 zigzag test in -20° heeled condition

선회시험 결과에서 언급된 바와 같이 횡경사에 따른 선회특성, 즉 좌현 횡경사 시 우현선회가 더 작게, 더 빨리 이루어지고, 좌현선회는 어려워지는 특성이 지그재그시험에서 좌우 반복적으로 나타나고 있으며, 이는 세번째 타각명령 시점 및 선수동요각 변화로부터 확인할 수 있다.

3.4 선회, 지그재그시험 결과 고찰

0도, -10도, -20도 횡경사각에서의 20노트 선회시험, 지그재그시험 결과를 수치화된 표로 정리하면 Tables 4, 5, 6, 7과 같다.

Table 4

+35° STBD turning indices

Table 5

-35° PORT turning indices

Table 6

+20/20° zigzag indices

Table 7

-20/20° zigzag indices

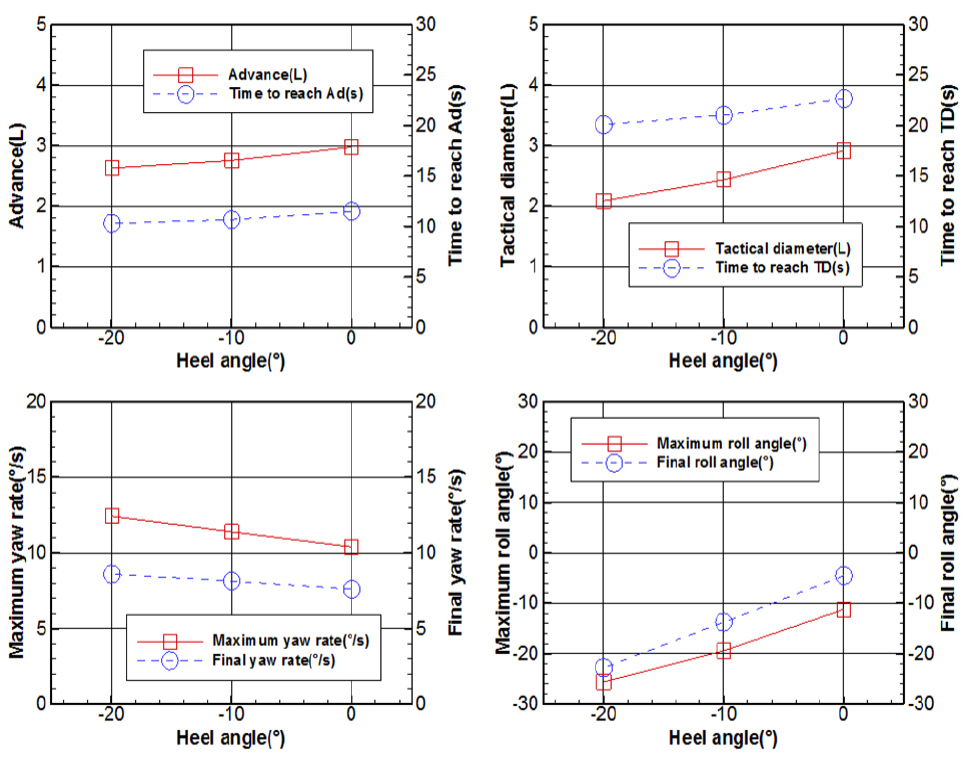
35도 좌우현 선회시험 결과 수치 중 몇 가지 중요한 인자를 그래프로 나타내면 Figs. 19, 20과 같다.

Fig. 19.

+35° STBD turning tests data

Fig. 20.

-35° PORT turning tests data

그래프에서와 같이 35도 우현선회 결과는 좌현 횡경사가 커질수록 선형적으로 전진거리와 선회직경이 작아지는 것을 확인할 수 있고, 선회 중 선수동요각속도 역시 선형적으로 증가하고 있는 것을 볼 수 있다. 또한 전진거리보다 선회직경의 변화 기울기가 더 큰 것을 볼 수 있는데, 이는 모형선의 선회가 어느 정도 진행된 시점, 즉 선수동요각속도 증가 및 전진속도 감소에 의한 영향이 누적되어 선회궤적으로 잘 드러나는 시점이 선수동요각 90도가 아닌 180도인 시점이기 때문이다. 특히 선회직경 값을 비교해보면, 횡경사 –20도에서 그 값이 약 71%로 감소하였다. 선회 중 횡동요각의 경우 그 초기값이 모두 다르고, 이에 따라 증가된 횡동요각에 따른 횡복원력 증가량이 서로 다르기 때문에 직접적인 비교에는 어려움이 있다. 다만, 최대 횡동요각과 최종 횡동요각의 차이가 횡경사각 0도에서 가장 크고, 초기 횡경사각을 기준으로 계산한 횡동요각 변화가 횡경사각 0도에서 가장 큰 것으로 볼 때, 횡경사각이 커질수록 그 복원력이 더 크게 작용하고 있음을 쉽게 추정할 수 있다.

또한 우현선회궤적을 겹쳐서 그려보면 Fig. 21과 같다. 궤적의 경우 동일한 방향으로 그 직경이 커지고 있음을 볼 수 있는데, 이는 앞서 언급한 선수동요각속도 및 속도감소가 반영되어 나타난 결과임을 재확인할 수 있다.

Fig. 21.

+35° STBD turning tests trajectories

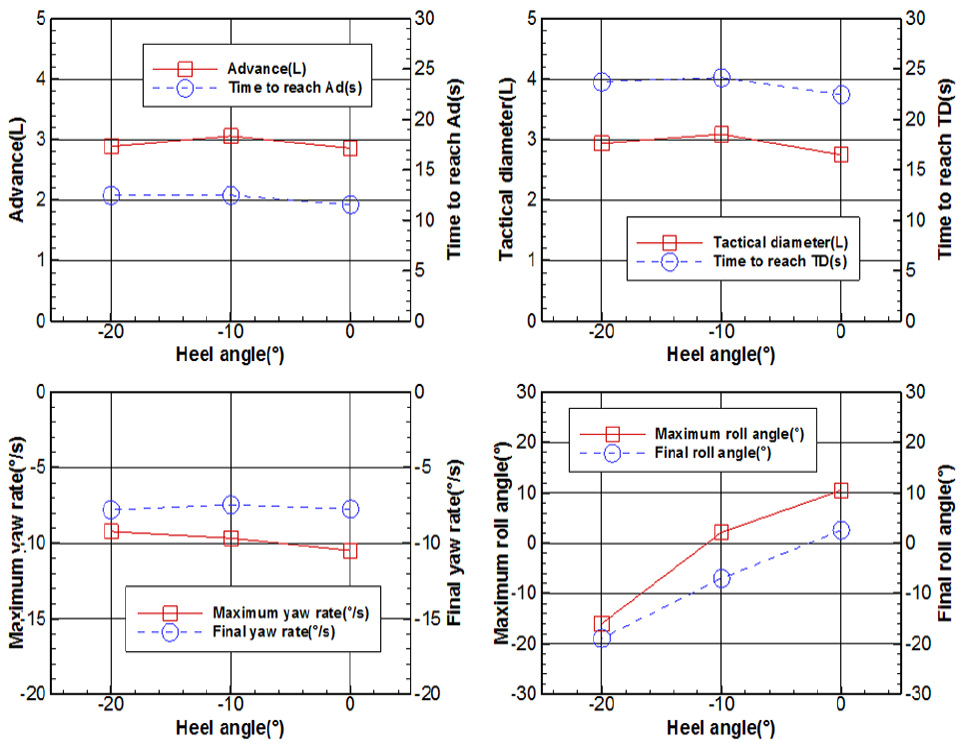
이와는 다르게 -35도 좌현선회 결과는 Fig. 20에서 보이는 것처럼 횡경사각 –10, –20도에서 다른 경향이 나타난다. 좌현 횡경사에 의하여 좌현선회직경이 더 크게 나타나기는 하나, 속도시험에서의 결과와 같이 횡경사상태 –20도에서의 전진거리 및 선회직경이 횡경사상태 –10도에서의 값보다 조금 더 작은 것을 볼 수 있다. 이와 관련하여 Yeo et al.(2015)의 구속모형시험 결과를 살펴보면, Y방향 힘이 횡경사 –15도까지 감소 후 –20도에서 다시 증가, Z방향 모멘트가 횡경사 –15도까지 증가 후 점차 수렴, X방향 모멘트가 –15도까지 증가 후 –20도에서 다시 감소하는 등, -20도 횡경사로 변화 시 선체에 작용하는 힘과 모멘트가 선형성을 보이지 않음을 확인할 수 있다.

따라서, 자유항주모형시험에서 얻은 이와 같은 결과는 본 선형의 좌현방향 횡경사에 따른 좌현방향 선회 특성으로 파악된다. 향후 구속모형시험과 관련하여, 계측된 힘과 모멘트의 관계에서부터 횡경사에 따른 직진안정성을 추가적인 시뮬레이션을 통하여 서로 비교해볼 필요가 있으며, 앞서 언급한 바와 같이 횡경사상태 및 유체의 흐름방향에 따른 압력장 및 선체에 작용하는 모멘트 변화를 전산유체역학 해석 등을 통하여 추가적으로 해석할 필요가 있다.

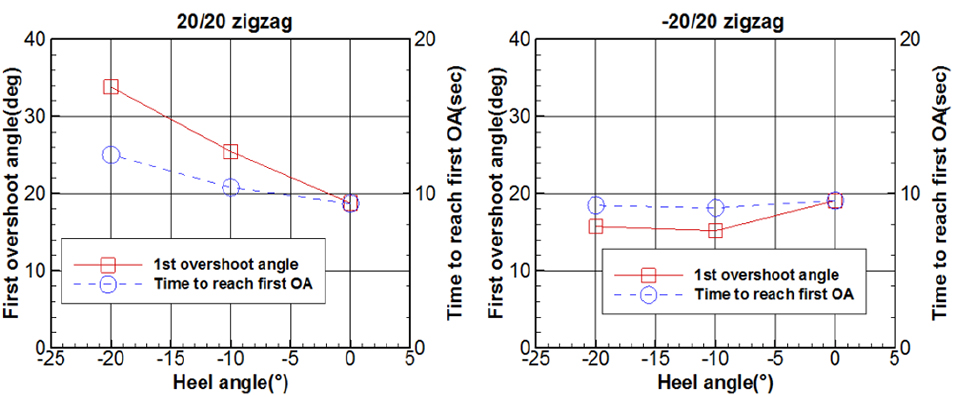
20/20 좌우현 지그재그시험 결과 수치를 그래프로 나타내면 Fig. 22와 같다.

Fig. 22.

20/20 and –20/20 zigzag tests data

20/20 지그재그시험의 경우, 좌현 횡경사에 의하여 우현방향으로의 침로변경이 쉽게 이루어지고, 그에 따라 반대방향으로 침로변경이 어려워 1차 오버슈트각과 그 도달시각이 횡경사각이 커질수록 점점 커지고 늦어지고 있으며, 그 선형성도 확인할 수 있다. 이는 우현선회 결과에서 나타난 경향과 동일하다고 볼 수 있다. -20/20 지그재그시험의 경우, 좌현 횡경사가 발생하면 좌현 지그재그시험의 1차 오버슈트각이 작아지는데, 앞서 언급한 좌현선회에서 나타난 경향이 동일하게 나타나고 있다. 즉 횡경사상태 –20도에서의 1차 오버슈트각이 –10도에서의 1차 오버슈트각보다 조금 더 큰 것을 볼 수 있다.

4. 결 론

본 논문에서는 KCS 모형선의 횡경사상태에서의 조종성능 변화를 확인하기 위하여 세 가지 상태(횡경사각 0도, -10도, -20도)에서 자유항주모형시험을 수행하고, 선회시험과 지그재그시험결과를 분석하였다.

그 결과, 선박이 좌현 횡경사상태에서 운항될 경우 우현 선회직경이 선형적으로 작아지고, 우현 지그재그 1차 오버슈트각이 선형적으로 커지는 결과를 확인하였다. 또한 좌현 선회직경이 커지고, 좌현 지그재그 1차 오버슈트각이 작아지는 것을 확인하였으나, 우현방향과 달리 그 선형성은 유지되지 않았다.

특히 본 연구에서는 KCS 선형에 대하여 20노트 대응속도에서의 자유항주모형시험을 통하여 정량적인 조종특성 수치를 획득하고 제시하였다. 이러한 정량적 수치는 손상선박 등 횡경사 상황에서 운항해야하는 선박의 조종특성을 이해하는데 도움이 될 것이며, 시뮬레이션 결과 검증 등에 중요한 기초자료로 사용될 수 있을 것으로 판단된다.

향후 연구사항으로, KCS 선형의 각 횡경사상태에 대한 전산유체역학 해석을 통하여, 특히 좌현 횡경사 시 좌현선회에서 나타난 결과에 대한 추가 분석 및 재해석이 필요하다. 또한 본 연구에서 다루고 있는 횡방향 무게중심 변화 뿐만 아니라, 종방향 및 상하방향 무게중심 변화에 따른 KCS 선형의 조종성능 변화를 관찰하여, 세 가지 방향의 무게중심 변화에 대한 조종특성 변화를 규명할 예정이다. 마지막으로 쌍축선형에 대하여 상하 및 횡방향 무게중심 변화를 가지는 자유항주모형시험을 수행하고, 프로펠러 비대칭력에 의해 발생 가능한 조종성능 변화에 대한 후속 연구를 수행할 예정이다.

Acknowledgments

본 논문은 선박해양플랜트연구소의 주요사업인 “해양사고 재현 및 분석 시뮬레이션 핵심기술 개발 – 2단계(3/3)”에 의해 수행되었습니다(PES3100).

References

• Choe, B.R. & Im, N.K., 2016. A Study on the Relationship between Ship Stability and Maneuverability Using Free Running Model Experiments. Journal of navigation and port research, 40(6), pp.353-360. [https://doi.org/10.5394/KINPR.2016.40.6.353]
• Kim, D.H., 2018. A study on the maneuvering characteristics for a damaged surface combatant ship, Ph.D Thesis. Seoul National University.
• Kim, Y.G., Yeo, D.J., Son, N.S., Kim, S.Y., Yun, K. & Oh, B.I., 2011. Prediction of Maneuverability of KCS with 4 Degrees of Freedom. Journal of the Society of Naval Architects of Korea, 48(3), pp.267-274. [https://doi.org/10.3744/SNAK.2011.48.3.267]
• Kim, Y., Seo, M.G. & Lee, J.H., 2017. Numerical simulation of Sewol ferry capsize. Proceedings of the Institution of Mechanical Engineers, Part M: Journal of Engineering for the Maritime Environment, 233(1), pp.186-208. [https://doi.org/10.1177/1475090217729045]
• Standards for ship manoeuvrability, IMO Resolution MSC.137(76)(adopted on 4 December 2002).
• Yang, J. & Kim, H., 2005. Prediction of Propulsive Performance of VLCC at Heeled and Trimmed Conditions. Journal of the Society of Naval Architects of Korea, 42(4), pp.307-314. [https://doi.org/10.3744/SNAK.2005.42.4.307]
• Yang, J., Rhee, S.H. & Kim, H., 2006. A Study on the Effect of the Heeled and Trimmed Conditions on Propulsive Performance of VLCC. Journal of the Society of Naval Architects of Korea, 43(3), pp.275-284. [https://doi.org/10.3744/SNAK.2006.43.3.275]
• Yeo, D.J., Kim, Y.G. & Yun, K., 2015. A Study on Captive Model Test of a Ship at Large Heel Condition. Proceedings of the International Conference on Ship Manoeuvrability and Maritime Simulation, Newcastle, UK, 8-11 September 2015.
• Yeo, D.J., Yun, K. & Kim, Y.G., 2016. Manoeuvring Captive Model Tests of KCS in Large Heel Conditions - Static Tests. Proceedings of 16^th Asian Conference on Maritime System and Safety Research, Busan, Korea, 18-19 August 2016.
• Yun, K., Yeo, D.J. & Kim, D.J., 2018. An Experimental Study on the Turning Characteristics of KCS with CG Variations. Proceedings of the International Conference on Ship Manoeuvrability and Maritime Simulation, Halifax, Canada, 12-16 August 2018.
• Yun, K., Yeo, D.J., Ryu, G. & Lee, Y.J., 2015. Experimental study on manoeuvrability of KVLCC2 in shallow water by free running model test. Proceedings of the International Conference on Ship Manoeuvrability and Maritime Simulation, Newcastle, UK, 8-11 September 2015. [https://doi.org/10.3744/SNAK.2015.52.6.494]