베이지언 추론에 기반한 확률론적 피로수명 평가

1. 서론

조선, 해양 공학 분야에서 피로 파괴에 대한 관심은 지속적으로 증가해 왔다. 구조물의 치수를 최적화 설계와 고장력강의 개발로 줄일 수 있는 반면, 피로 파괴에 취약한 구조를 가지게 되었기 때문이다. 일반적으로 피로 손상도는 결정론적 모델을 사용하여 최적의 파라미터를 추정하고 피로 해석을 수행하여 계산하였다. 하지만, 결정론적 모델은 여러 불확실성 요소를 내포하고 있는 피로 손상의 물리적 현상을 명확하게 설명하기 어렵다. Yang and Yoon(1991)은 피로 하중에 의한 균열 진전이 불확실성 요소를 내포하고 있으며, 확률론적 피로 손상 모델을 이용한 연구가 필요함을 주장하였다. 확률론적 모델의 필요성이 증가함에 따라 여러 불확실성 요소를 고려한 구조물의 피로 해석에 관련된 연구가 진행되었다(Yang et al., 1997; Lee et al., 1998).

부재의 피로 시험 결과를 토대로 확률론적 피로 손상 모델을 추정하는 연구도 진행되어 왔다. Guida and Penta(2009)는 베이지언-선형 회귀 모델을 이용하여 P-S-N 곡선의 파라미터를 추정하였으며, 빈도주의-추론 기법을 이용한 파라미터와 비교하였다. Liu et al.(2017)는 gibbs-sampling을 적용한 계층적 베이지언-모델을 통해 확률론적 S-N 곡선의 파라미터를 도출하고, 최대우도법(maximum likelihood method)의 결과와 비교하였다. Ruano(2014)는 복합재의 피로 수명에 대해 마르코프-체인 몬테카를로 시뮬레이션을 적용하여 수학적 피로 손상 모델의 파라미터와 물리적 피로 손상 모델의 파라미터를 도출하였고, 베이지언-추론을 모델 평가에 적용하여 해당 부재에 가장 적합한 모델을 찾는 것을 시도하였다.

본 연구에서는 OLS(ordinary least squares) 기법을 이용하여 1개의 결정론적 S-N곡선을 도출하고, 베이지언-선형 회귀 모델과 마르코프-체인 몬테카를로 시뮬레이션을 통해 2개의 P-S-N 곡선을 추정하였다. 3가지 방법론을 통해 얻은 S-N곡선의 파라미터와 Yang et al.(1997)에 의해 얻어진 장기 응력 분포를 이용하여 장기 피로 손상도와 피로 수명의 분포를 추정하고 비교하였다.

2. 이론적 배경

2.2 베이지언-선형 회귀 모델(BLM)

선형 회귀(linear regression)는 관측 자료 $$ D$$로부터 종속 변수 $$ y$$와 한 개 이상의 독립 변수 $$ x$$의 선형 상관 관계를 구하는 회귀분석 방법이다. 독립 변수 $$ x$$의 개수가 하나인 경우에는 단순 선형 회귀, 둘 이상의 독립 변수를 사용한 경우에는 다중 선형 회귀라고 부른다. 일반적으로 OLS(ordinary least squares) 기법을 이용한 결정론적 회귀 분석이 사용된다. OLS 기법은 오차의 제곱의 합(sum squared errors)을 최소화하는 기법이다. 오차 항 $$ e_i$$를 갖는 1차 회귀 모델은 아래 Fig. 1에 도식화하였고, 아래 식(2)로 정의할 수 있다. $$ \sum \left(e_i^2\right)$$이 최소가 되는 모델의 파라미터 $$ {\beta }_{ols}$$는 아래 식(3)과 같다.

Fig. 1.

Linear regression model(1st polynomial)

$\[ y_i={\beta }^T\left\{x_i\right\}+e_i (x_i, y_i\in D) \]$

(2)

$\[ {\beta }_{ols}={\left(X^{T}X\right)}^{-1}{X}^{T}y \]$

(3)

여기서 $$ \beta ={\left\{{\beta }_0, \cdots , {\beta }_p\right\}}^T$$, $$ p$$는 추정되는 모수의 개수이다. $$ y$$는 $$ y_i$$를 원소로 가지는 열벡터, $$ X$$는 $$ {\left\{x_i\right\}}^T$$를 I번째 행으로 갖는 $$ \left(n\times p\right)$$행렬이다. 여기서 $$ n$$은 관측 자료의 개수(number of observations)을 뜻한다.

반면, 모델의 불확실성을 고려하기 위한 통계학적 회귀 분석에는 최대 우도법(maximum likelihood method)이 주로 사용된다. 최대 우도법은 회귀 모델의 파라미터 $$ \beta $$를 확률 변수로 정의하고 우도 함수가 최대가 되는 $$ \beta $$를 구하는 방법이다. 회귀 모델의 오차 항이 정규 분포, $$ e~N\left(0,{\sigma }^2\right)$$를 따른다고 가정하면 확률 변수 $$ \beta $$도 정규 분포를 따르게 된다. 이 때 우도 함수는 아래 식(4)로 나타낸다.

$$\begin{gathered} \[ L\left(y|x,\beta ,{\sigma }^2\right)=\prod _{i=1}^{n}p\left(y_i|x_i,\beta ,{\sigma }^2\right) \\ ={\left(2\pi {\sigma }^2\right)}^{-\frac{n}{2}}\exp \left\{-\frac{1}{2{\sigma }^2}\sum _{i=1}^n{\left(y_i-{\beta }^T{x}_i\right)}^2\right\} \] \end{gathered}$$

(4)

우도 함수의 최대값을 구하기 위해서 식(4)의 양변에 자연 로그를 취하면 아래 식(5)로 표현할 수 있다.

$\[ \ln L=-\frac{n}{2}\ln 2\pi -n \ln \sigma -\frac{1}{2{\sigma }^2}\sum _{i=1}^n\left(e_i^2\right) \]$

(5)

로그 함수는 단조 증가 함수이기 때문에 식(5)가 최대값을 가질 때 식(4)도 최대값을 가진다. 식(5)에서 앞의 두 항은 상수이고, 세 번째 항은 오차의 제곱의 합을 뜻한다. 따라서 위의 경우에서는 우도 함수가 최대값을 갖는 파라미터 $$ {\beta }_{mle}$$와 $$ {\beta }_{ols}$$는 같다. 이 때 파라미터 $$ \beta $$는 $$ N\left({\beta }_{mle}, {\sigma }_{mle}^2{\left(X^{T}X\right)}^{-1}\right)$$를 따른다. 하지만 오차항의 분산 $$ {\sigma }^2$$은 관측 자료와 파라미터에 따라 다르게 측정되기 때문에 상수로 정의하기 어렵다. 이러한 문제를 해결하기 위해 베이지언 추론에 기반한 베이지언-선형 회귀법을 적용할 수 있다. 베이지언-선형 회귀법에서는 먼저 선형 회귀 모델의 파라미터와 오차 항의 분산을 확률 변수로 가정하고, 그 확률 변수들의 사전 분포를 가정 한 후, 관측 자료를 이용하여 우도 함수를 계산한다. 베이지언 정리에 따라 파라미터의 사후 분포를 앞서 구한 사전 분포와 우도 함수의 곱으로 계산한다. 하지만 임의의 사전 분포를 사용할 경우, 사후 분포를 해석적으로 구하기 어렵다. 이를 해결하기 위해, 켤레 사전 분포(conjugate prior distribution)를 이용한 방법이 널리 사용되고 있다. 켤레 사전 분포를 사용하면 그에 대응되는 사후 분포를 수학적으로 쉽게 계산할 수 있다. 대표적인 켤레 사전 분포로는 다변량 정규 분포, 정규-감마 분포, 정규-역 감마 분포, 정규-위샤트 분포, 정규-역 위샤트 분포 등이 있다. 본 연구에서는 정규-역 감마 분포를 사용하였고, 아래 식(6)~(7)로 나타낸다.

$$\begin{gathered} \[ p\left(\beta ,{\sigma }^2\right)=p\left(\beta |{\sigma }^2\right)p\left({\sigma }^2\right)=N\left({\mu }_{\beta },{\sigma }^2{V}_{\beta }\right)\times IG\left(a,b\right) \\ =NIG\left({\mu }_{\beta },V_{\beta },a,b\right) \] \end{gathered}$$

(6)

$\[ p\left({\sigma }^2\right)=\frac{b^{\alpha }}{\Gamma \left(a\right)}{\left(\frac{1}{{\sigma }^2}\right)}^{\alpha +1}\exp \left(\frac{-b}{{\sigma }^2}\right), {\mathrm{\sigma }}^2 > 0 \]$

(7)

여기서 $$ {\mu }_{\beta }$$와 $$ V$$는 $$ \beta $$의 사전 분포의 평균과 공분산 행렬을 뜻한다. $$ IG\left(a,b\right)$$는 역-감마 분포를 의미하며 $$ \Gamma \left(\right)$$는 감마 함수, $$ a$$와 $$ b$$는 각각 형상 매개변수와 크기 매개변수이다. 위 식에 대응되는 우도 함수는 식(4)와 같이 정규 분포의 형태로 정의 할 수 있으며, 자연 로그를 취한 형태는 식(5)와 같다. 베이지언 정리에 따라 위 식(4)와 식(6)의 선형 곱으로 사후 분포를 표현할 수 있으며, 아래 식(8)~(9)로 나타낸다.

$$\begin{gathered} \[ p\left(\beta ,{\sigma }^2|y\right) \infty {\left(\frac{1}{{\sigma }^2}\right)}^{a+(n+p)/2+1} \\ \times \exp \left\{\frac{-1}{{\sigma }^2}\left[b^{\mathit{*}}+\frac{1}{2}{\left(\beta -u^{\mathit{*}}\right)}^T{V}^{\mathit{*}-1}\left(\beta \mathit{-}{u}^{\mathit{*}}\right)\right]\right\} \] \end{gathered}$$

(8)

$\[ p\left({\sigma }^2|y\right)=\frac{b^{*a^{*}}}{\Gamma \left(a^{*}\right)}{\left(\frac{1}{{\sigma }^2}\right)}^{a^{*}+1}\exp \left(\frac{-b^{*}}{{\sigma }^2}\right) \]$

(9)

여기서

$$\begin{gathered} u^{*}={\left(V_{\beta }^{-1}+X^{T}X\right)}^{-1}\left(V_{\beta }^{-1}{\mu }_{\beta }+X^{T}y\right), \\ {V}^{*}={\left(V_{}^{-1}+X^{T}X\right)}^{-1}, \\ {a}^{*}=a+n/2, \\ {b}^{*}=b+\frac{1}{2}\left[{\mu }_{\beta }^T{V}_{\beta }^{-1}{\mu }_{\beta }+y^{T}y-{\mu }^{*T}{V}^{*-1}{\mu }^{*}\right]. \end{gathered}$$

식(8)을 $$ {\sigma }^2$$에 대해 적분하여 구한 $$ \beta $$의 사후 주변 분포는 다변량 t분포임이 알려져 있으며 아래 식(10)으로 나타낸다.

$$\begin{gathered} \[ p\left(\beta |y\right)={\int }_{}^{}p\left(\beta ,{\sigma }^2|y\right)d{\sigma }^2=MVS{t}_{v^{*}}\left({\mu }^{*},\sum _{}^{*}\right) \\ \left(v^{*}=2a^{*},\sum _{}^{*}=\left(b^{*}/a^{*}\right)V^{*}\right) \] \end{gathered}$$

(10)

여기서 $$ v^{*}$$은 t분포의 자유도, $$ {\mu }^{*}$$은 t분포 중심의 위치, $$ \sum _{}^{*}$$은 크기 매개변수를 의미한다(Marin and Robert, 2007).

2.3 마르코프-체인 몬테카를로 시뮬레이션(MCMC)

수치적으로 모델의 파라미터 $$ \beta $$의 사후 분포를 추정할 때, 특정 범위내의 모든 $$ \beta $$에 대해 직접 해석을 수행하는 몬테카를로 시뮬레이션을 이용할 수 있다. 하지만 직접 해석에 비용과 시간이 많이 드는 단점이 있으며, 이를 보완하기 위해 마르코프-체인을 이용하여 효율적으로 몬테카를로 시뮬레이션을 수행하는 방법이 MCMC이다. MCMC의 주요 특징은 아래와 같다.

∙ MCMC는 사후 분포를 따르는 샘플을 추출하는 알고리즘이다.

∙ 샘플이 ergodicity와 stationarity를 만족하면 마르코프-체인의 성질에 의해 사전 분포와 무관하게 추출한 샘플은 사후 분포를 따른다.

∙ 제안 분포는 샘플이 사후 분포를 따르기까지의 수렴 속도를 결정한다.

MCMC의 방법에는 Metropolis-Hastings algorithm(M-H algorithm), Gibbs Sampler algorithm 등이 있으며, 본 연구에서는 M-H algorithm을 이용하여 $$ \beta $$의 사후 분포를 추정하였다. M-H algorithm의 절차는 아래 Fig. 2와 같다(Ruano, 2014).

Fig. 2.

Metropolis-Hastings algorithm procedure

여기서 $$ r$$은 채택 확률이며 사전 분포와 제안 분포의 종류에 따라 이전 샘플 $$ {\beta }^{\left(k-1\right)}$$과 추출한 $$ \beta \text{'}$$의 우도 함숫값 혹은 사후 확률의 비를 뜻한다. $$ p(\beta \text{'})$$과 $$ p\left({\beta }^{k-1}\right)$$은 사전 분포로부터 해당 샘플이 추출될 확률이다. 사전 분포를 균일-분포로 가정하면 채택 확률에 영향을 주지 않는다. 본 연구에서는 사전 분포를 BLM과 동일한 정규-역 감마 분포, 식(6)~(7)로 가정하고 MCMC를 수행하였으며, 사전 분포의 파라미터 값은 아래와 같다.

$$\begin{gathered} {\mu }_{\beta }={\beta }_{ols}={\left(X^{T}X\right)}^{-1}{X}^{T}y=\left[-0.2758, 4.0522\right] \\ {V}_{\beta }={\sigma }_{ols}^2={\left(X^{T}X\right)}^{-1}=\left[\begin{array}{cc}0.8344& -4.8034\\ -4.8034& 28.0429\end{array}\right] \\ a=152.6197 \\ b=0.8070 \\ \end{gathered}$$

여기서 $$ {\mu }_{{\sigma }^2}=b/(a-1)$$, $$ {\mu }_{{\sigma }^2}=b^2/\left[{(a-1)}^2(a-2)\right]$$를 만족한다(Llera and Beckmann, 2016). $$ {\mu }_{{\sigma }^2}$$과 $$ v_{{\sigma }^2}$$는 각각 표본 오차항들의 평균과 분산을 의미하며, 아래 식(11)로 정의되는 모집단의 $$ k$$차 모멘트를 이용하여 계산할 수 있다. 본 연구에서는 $$ {\beta }_{ols}$$로 정의한 결정론적 S-N곡선을 이용하여 계산한 오차항들을 모집단으로 가정하였고, 아래 식(12)와 식(13)을 이용하여 $$ {\mu }_{{\sigma }^2}$$과 $$ v_{{\sigma }^2}$$을 계산하였다(Rose and Smith, 2002).

$\[ {\mu }_k=\frac{{\displaystyle \sum _{i=1}^n}{\left(e_{ols,i}-{\mu }_{e_{ols,i}}\right)}^k}{n} \]$

(11)

$\[ {\mu }_{{\sigma }^2}=\frac{\left(n-1\right)}{n}{\mu }_2 \]$

(12)

$\[ {\mu }_{{\sigma }^2}=\frac{{\left(n-1\right)}^2{\mu }_4-\left(n-1\right)\left(n-3\right){\mu }_2^2}{n^3} \]$

(13)

Fig. 2에서 $$ q$$는 제안 분포이며 매 step마다 제안 분포로부터 샘플을 추출하게 된다. 제안 분포를 균일-분포나 정규-분포와 같은 커널 분포를 사용하면 파라미터를 추출하는 영역만 정의하고 채택 확률에는 영향을 주지 않지만, 제안 분포의 분산 $$ {\sigma }_q^2$$에 따라 샘플이 사후 분포를 따르기까지의 수렴 속도가 결정된다. 작은 값을 사용하는 경우에는 추출한 파라미터의 채택 확률이 높게 계산되지만, 탐색 범위가 좁아져서 수렴 속도가 느려지게 된다. 반대로 큰 값을 사용하는 경우에는 넓은 범위를 탐색할 수 있으므로 수렴 속도가 빨라지게 되지만, 추출한 파라미터의 채택 확률이 낮게 계산될 우려가 있다. 따라서 파라미터의 추출이 완료되면, 채택률(acceptance ratio, $$ r$$)을 사용하여 제안 분포의 적절성을 판단한다. 채택률은 M-H algorithm에서 추출한 전체 파라미터 개수($$ N_S$$)와 사후 분포를 추정하기 위해 채택된 파라미터 개수($$ N_A$$)의 비율을 의미한다. 일반적으로 자유도가 10개 이하인 저차원 문제에서는 채택률이 20%~40%이내일 때, M-H algorithm의 효율성과 추출한 샘플 분포의 수렴성이 가장 높다(Roberts and Rosenthal, 2001).

Fig. 2의 과정을 거쳐서 M-H algorithm은 우도 함숫값 혹은 사후 확률이 상대적으로 큰 샘플 $$ {\beta }^k$$를 추출한다. 추출한 샘플들로부터 $$ \beta $$의 사후 분포를 추정할 수 있다. 본 연구에서는 MCMC를 이용하여 50,000개의 파라미터 샘플을 추출하여 사후 분포를 추정한 뒤, 채택률을 이용하여 제안 분포의 적절성을 검토하였다.

3. 장기 피로 수명 평가에의 적용

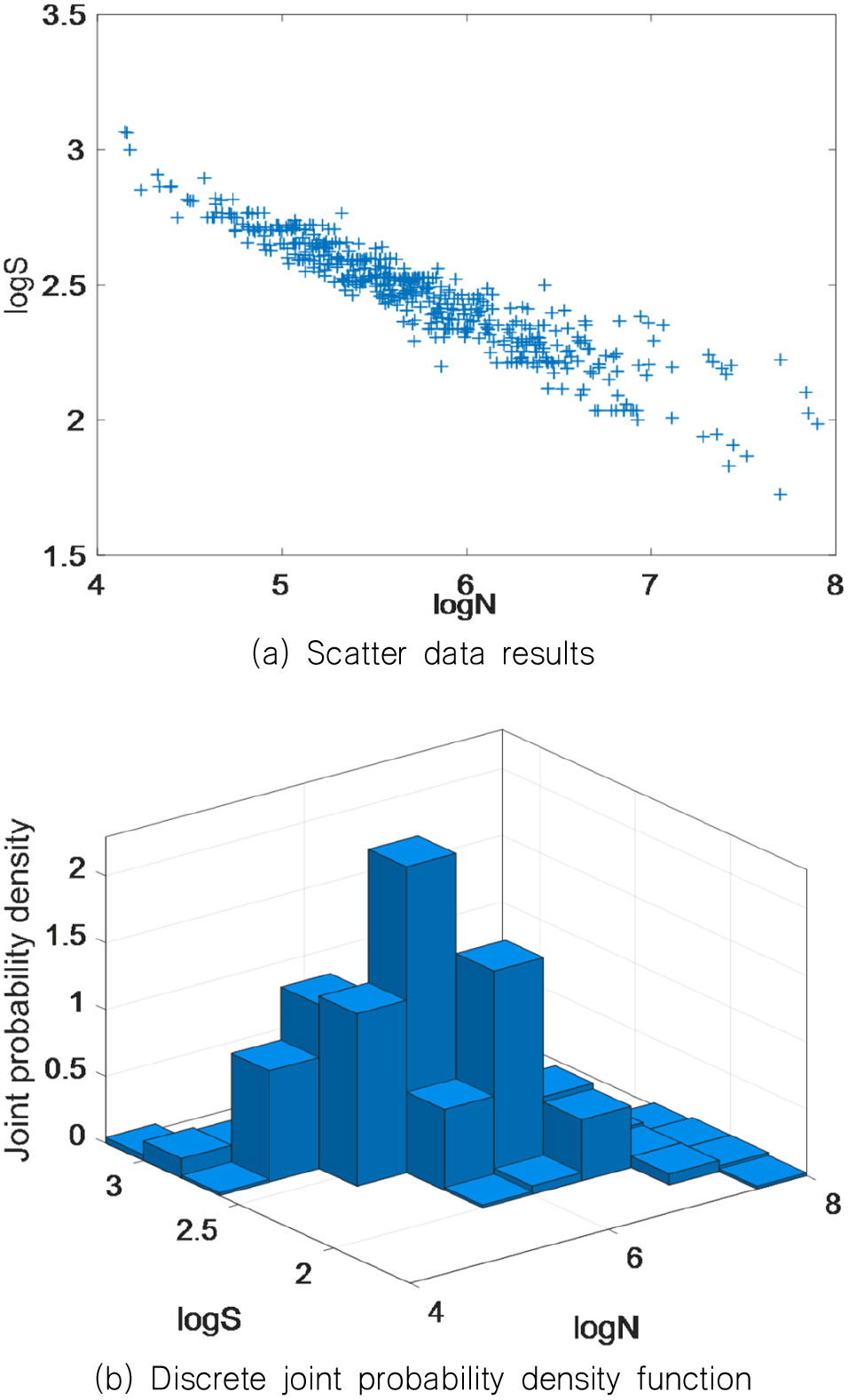
본 연구에서는 확률론적 선형 회귀법에 MCMC의 적용 가능성을 검증하기 위해, 피로 시험과 균열 진전에 대한 연구(Kang et al., 2004)에서 주로 사용되는 ‘Battelle Structural Stress JIP Final Report(Dong, 2003)’의 피로 시험 자료를 사용하였다. Fig. 3에 도식화한 피로 실험 결과에 BLM, MCMC와 OLS기법을 적용하여 아래 식(14)로 표현되는 S-N곡선의 파라미터($$ {\beta }_1, {\beta }_0$$)를 도출하였다. 식(14)의 파라미터와 Yang et al.(1997)에 의해 얻어진 설계 수명($$ L_D$$) 20년에 해당하는 장기 응력 분포를 이용하여 장기 피로 손상도를 계산하였다. 장기 응력 분포가 weibull 분포를 따를 때 장기 피로 손상도는 아래 식(15)로 나타낸다.

Fig. 3.

Results of fatigue test

여기서 $$ N_T$$는 설계 수명 동안 발생하는 응력 사이클 수, $$ \beta $$는 응력 범위의 편중계수, $$ S_0$$는 설계 응력 범위로서 장기 응력 분포에서 구한다. $$ h$$는 장기 응력 분포의 형상 매개변수이다. 본 연구에서 사용한 장기 피로 손상도 파라미터의 값은 Table 1과 같다.

Table 1.

Summary of parameters for long-term fatigue damage

식(14)에 OLS 기법을 적용하여 추정한 파라미터 $$ m$$과 $$ \log a$$를 식(15)에 대입하여 장기 피로 손상도와 피로 수명$$ (L_D/D)$$을 계산하였다. Table 2는 OLS 기법을 적용하여 구한 $$ m$$, $$ \log a$$, $$ \log D$$와 $$ \log (L_D/D)$$를 보여준다.

Table 2.

Results gained from OLS

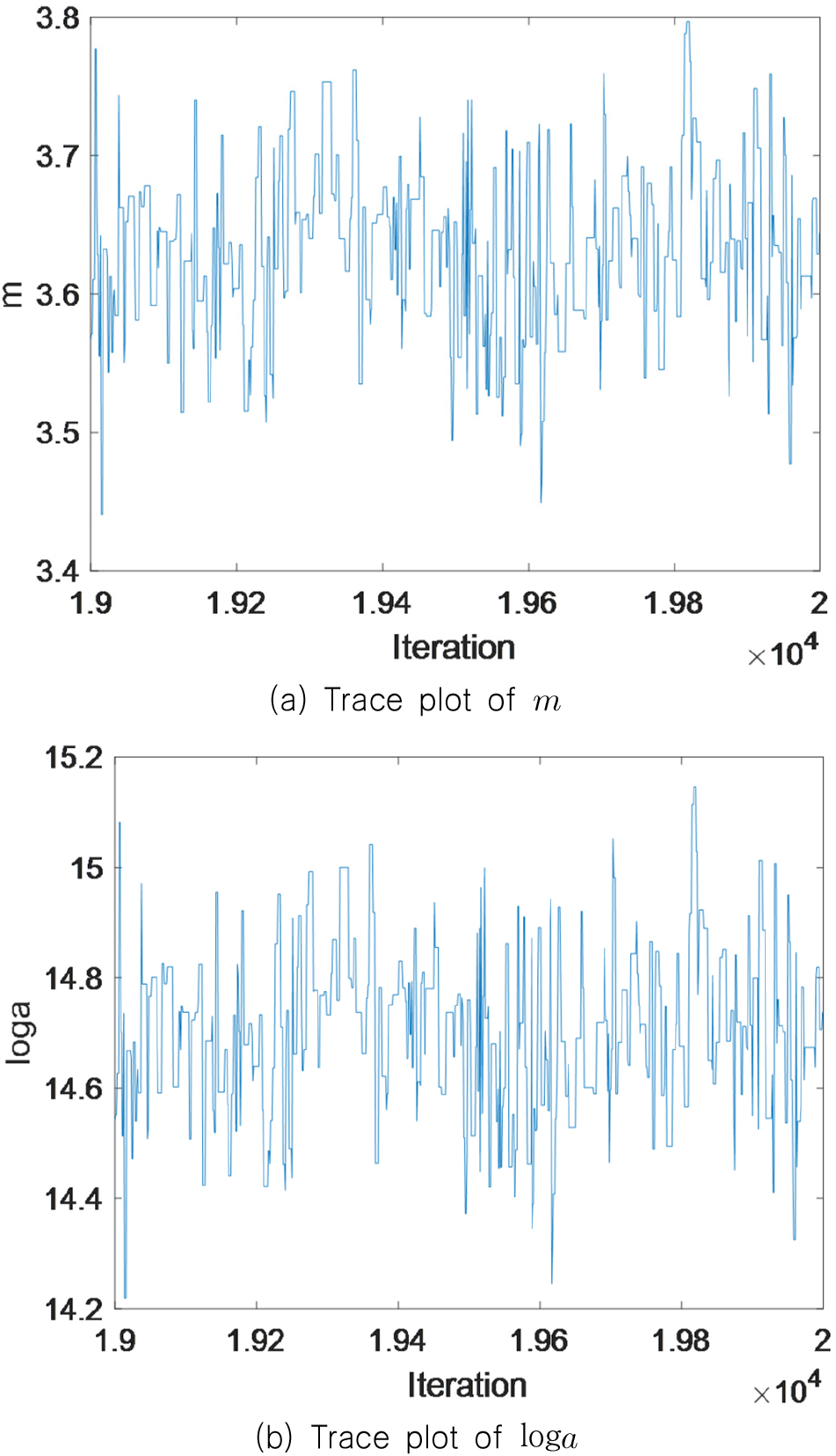
결정론적 피로 손상 모델의 결과와 비교하기 위해 MCMC를 먼저 수행하였다. MCMC를 수행하여 50,000개의 파라미터를 추출하였다. 19,000~20,000번째로 추출된 파라미터에서 채택된 파라미터들을 추적하여 Fig. 4에 도식화하였다.

Fig. 4.

Accepted parameters in MCMC

채택된 파라미터들의 분포가 OLS기법을 이용하여 구한 파라미터의 값을 크게 벗어나지 않음을 알 수 있다. 또한 파라미터의 값이 변하지 않는 구간을 확인할 수 있으며, 이는 추출한 파라미터가 채택되지 않았음을 의미한다. M-H algorithm에서는 추출한 파라미터의 우도 함숫값 혹은 사후 확률이 기존의 파라미터에 비해 크면 반드시 채택되며, 채택되지 않은 파라미터들은 상대적으로 낮은 우도 함숫값이나 사후 확률을 가진다.

마지막으로 파라미터 제안 분포의 적절성을 검토하기 위해 채택률을 계산하여 Table 3에 정리하였다.

Table 3.

Summary of acceptance ratio in MCMC

본 연구에서 사용한 MCMC의 파라미터 채택률은 약 30%이며, 이를 통해 적절한 제안 분포임을 확인하였다.

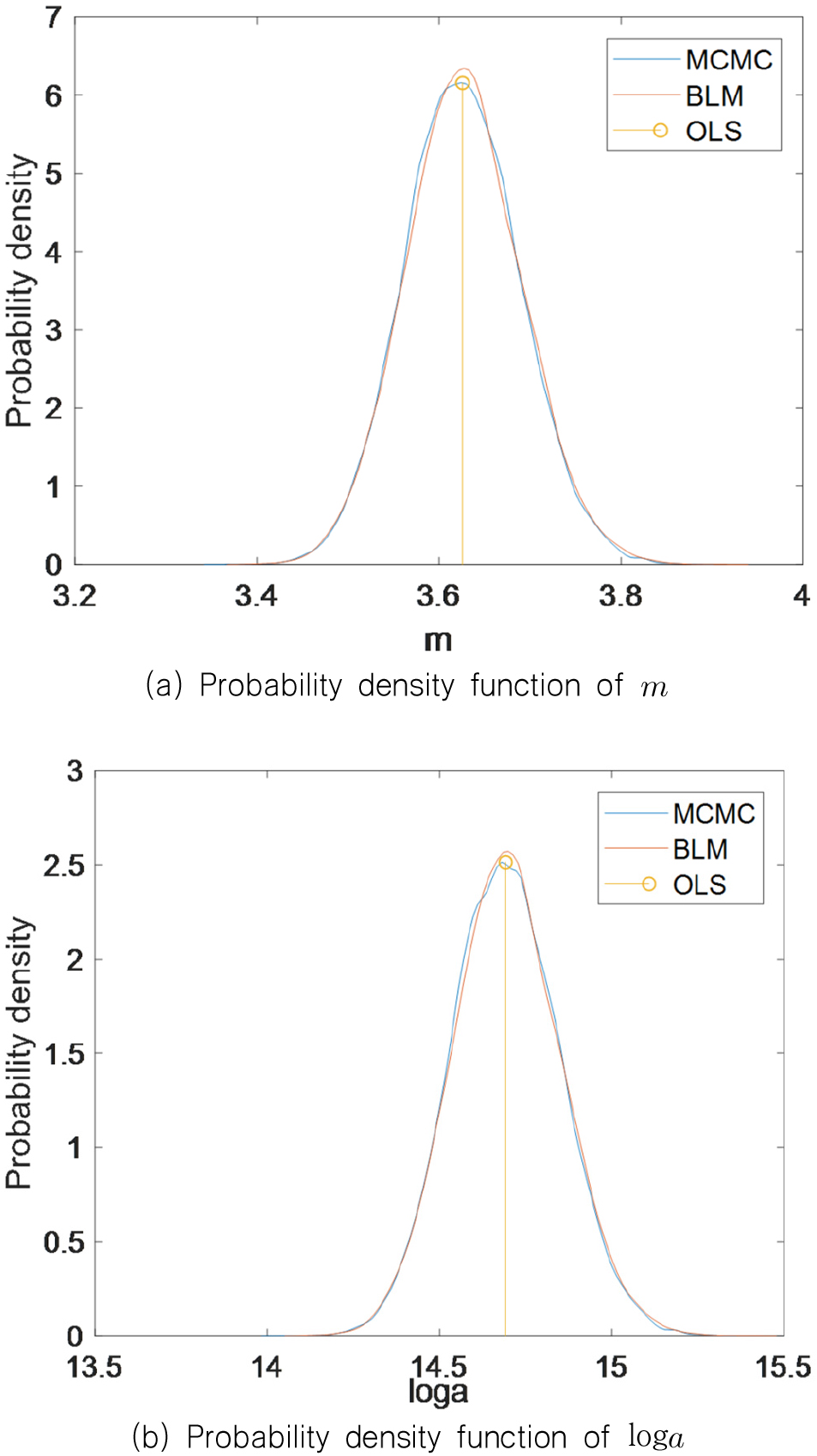
Fig. 5는 베이지언-선형 회귀 모델(BLM)과 마르코프-체인 몬테카를로 시뮬레이션(MCMC)을 통해 얻은 P-S-N곡선의 파라미터의 분포와 OLS 기법을 이용하여 얻은 파라미터를 보여준다. BLM과 MCMC를 통해 얻은 분포에서 최대 확률 밀도를 가지는 파라미터와 OLS 기법을 이용하여 얻은 파라미터가 유사한 것을 알 수 있다.

Fig. 5.

Comparison of parameters obtained from each methodologies

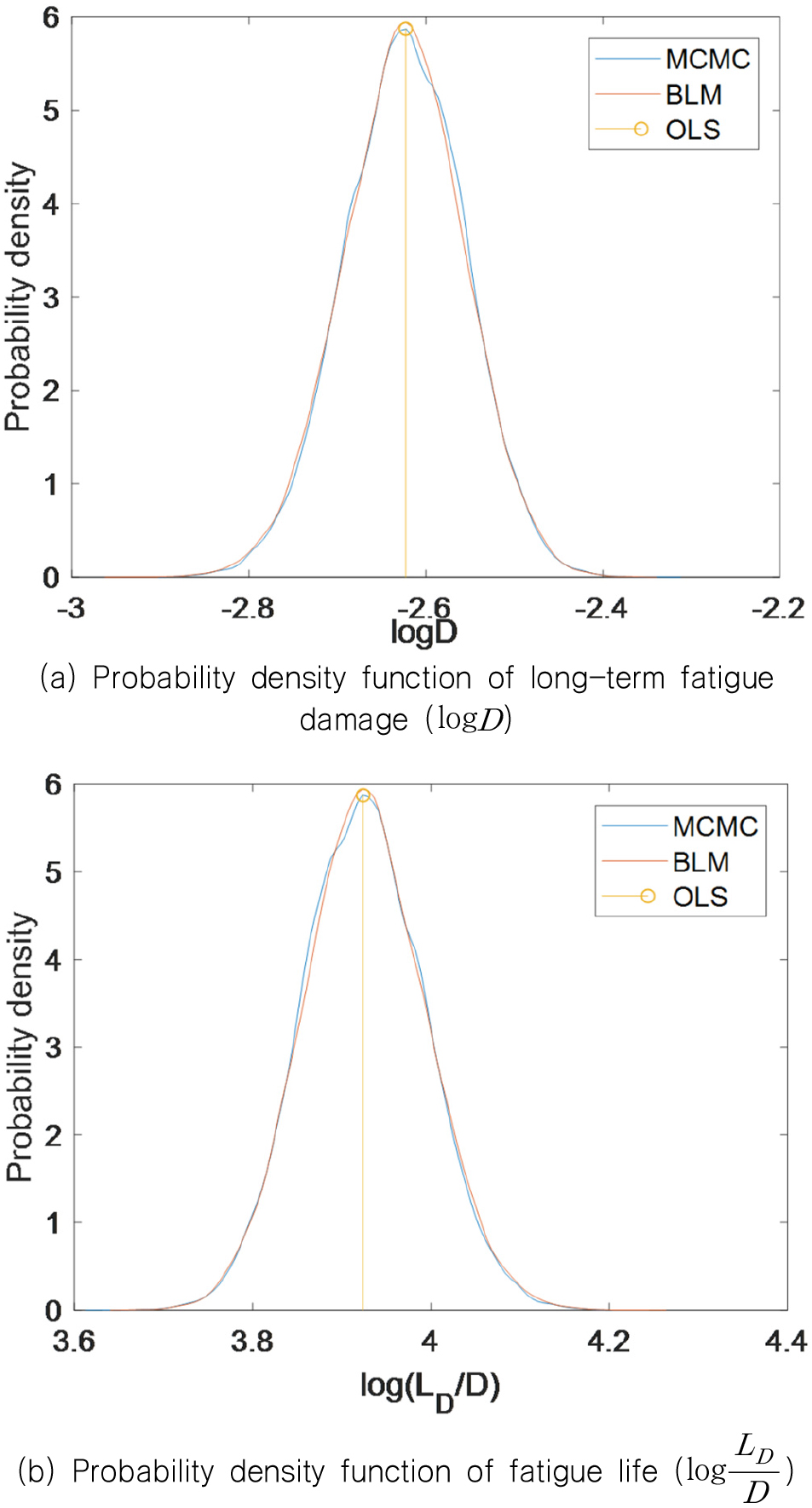
P-S-N 곡선의 파라미터와 식(15)를 이용하여 장기 피로 손상도를 구하고, 피로 수명($$ (L_D/D)$$)의 분포를 추정하였다. Fig. 6은 장기 피로 손상도와 피로 수명의 추정 분포를 보여준다. BLM과 MCMC를 통해 얻은 분포에서 최대 확률 밀도를 가지는 장기 피로 손상도와 OLS 기법을 이용하여 얻은 장기 피로 손상도가 유사한 것을 알 수 있다.

Fig. 6.

Predicted fatigue damage and fatigue life

확률론적 피로 손상 모델은 OLS기법으로 구한 장기 피로 손상도를 기준으로 좌우 영역이 비슷한 불편향성(unbiasedness)을 보이며, 그 형상은 정규 분포 혹은 t분포의 형상과 매우 유사한 것을 알 수 있다.

상기의 결과들을 통해, BLM을 이용하여 해석적으로 계산한 파라미터의 확률 분포와 MCMC를 수행하여 수치적으로 추정한 확률 분포의 유사성을 확인하였다. 이를 토대로 선형 회귀와 같은 저차원계 문제를 다룰 때에는 BLM과 MCMC가 모두 효과적인 것을 알 수 있다. 하지만 신뢰성 해석과 같이 해석적인 방법으로 해결하기 어려운 다차원계 문제에 대해서는 MCMC를 이용한 수치적인 해결 방법이 적합하다(Hamada et al., 2008). 따라서 P-S-N 곡선의 파라미터를 포함하여 여러 불확실성 요소를 고려한 장기 피로 손상도의 사후 분포 추정에 MCMC를 적용하기 위한 연구가 추가적으로 필요하다고 판단된다.

4. 결론

본 연구에서는 OLS기법을 이용하여 결정론적 피로 손상 모델과 베이지언-선형 회귀 모델, 마르코프-체인 몬테카를로 시뮬레이션을 이용한 두 가지 확률론적 피로 손상 모델에 대해 분석하고 이를 토대로 장기 피로 손상도와 피로 수명의 분포를 도출하였다. 상기의 연구 내용을 바탕으로 다음과 같은 결론을 도출할 수 있었다.

일반적으로 사용되는 OLS기법을 통해 얻은 결정론적 모델의 최적 파라미터와 $$ e~N(0,{\sigma }^2)$$인 확률론적 모델에 최대 우도법을 적용한 최적 파라미터는 같다.

켤레 사전 분포를 가정한 베이지언-선형 회귀 모델(BLM)을 사용하여 피로 시험 결과로부터 다변량 t분포를 따르는 P-S-N 곡선의 파라미터의 사후 분포를 추정할 수 있다.

확률론적 선형 회귀법에 MCMC의 적용 가능성을 검증하기 위해, 피로 시험 결과를 토대로 P-S-N곡선의 파라미터의 사후 분포를 추정하고 BLM과 OLS의 결과와 비교하였다.

MCMC의 파라미터 채택률은 약 30%이며, 이를 통해 적절한 제안 분포임을 확인하였다.

BLM과 MCMC를 통해 얻은 분포에서 최대 확률 밀도를 가지는 파라미터와 OLS 기법을 이용하여 얻은 파라미터가 유사한 것을 확인하였다.

BLM과 MCMC를 통해 얻은 장기 피로 손상도 분포에서 최대 확률 밀도를 가지는 장기 피로 손상도가 OLS기법으로 구한 장기 피로 손상도와 유사한 것을 확인하였다.

확률론적 피로 손상 모델은 OLS 기법으로 구한 장기 피로 손상도를 기준으로 좌우의 영역이 비슷한 불편향성(unbiasedness)을 보이며, 그 형상은 정규 분포 혹은 t분포의 형상과 매우 유사한 것을 확인하였다.

P-S-N 곡선의 파라미터를 포함하여 여러 불확실성 요소를 고려한 장기 피로 손상도의 사후 분포 추정에 MCMC를 적용하기 위한 연구가 추가적으로 필요하다고 판단된다.

References

• Dong, P., 2003. Battelle Structural Stress JIP Final Report. N004431-01.
• Guida, M. & Penta F., 2009. A Bayesian analysis of fatigue data. Structural Safety, 32(1), pp.64-76. [https://doi.org/10.1016/j.strusafe.2009.08.001]
• Hamada, M.S., Wilson, A., Reese, C.S. & Martz, H.F., 2008. Bayesian reliability. 1st Ed. Springer: New York. [https://doi.org/10.1007/978-0-387-77950-8]
• Lee, J.O., Lee, H.Y., Suh, Y.S. & Yoon, J.H., 1998. Reliability of fatigue life predictions for fixed offshore structures. Journal of the Society of Naval Architects of Korea, 35(2), pp.74-82.
• Liu, X.W., Lu, D.G & Hoogenboom P.C.J., 2017. Hierarchical Bayesian fatigue data analysis. International Journal of Fatigue, 100(1), pp.418-428. [https://doi.org/10.1016/j.ijfatigue.2017.03.043]
• Llera, A. & Beckmann, C.F., 2016. Estimating an inverse gamma distribution. Donders Institute Technical Report arXiv:1605. 01019v2.
• Marin, J.M. & Robert, C.P., 2007. Bayesian core:a practical approach to computational Bayesian statistics. 1st Ed. Springer: New York.
• Roberts, G.O. & Rosenthal, J.S., 2001. Optimal scaling for various metropolis-hastings algorithms. Statistical Science, 16(4), pp.351-367. [https://doi.org/10.1214/ss/1015346320]
• Rose, C. & Smith, M.D., 2002. Mathematical statistics with mathematica. 1st Ed. Springer: New York. [https://doi.org/10.1007/978-1-4612-2072-5_1]
• Ruano, J.C., 2014. A Bayesian approach to fatigue damage assessment in composite materials. Ph.D. University of Granada.
• Kang, S.W. et al., 2004. Testing and analysis of fatigue behavior in edge details. Proceedings of OMAE Specialty Conference on Integrity of Floating Production, Storage & Offloading (FPSO) Systems, Houston, Texas, USA, 30 August - 2 September, 2004, NO. 04-0025.
• Yang, P.D.C., Lee, J.S., Yoon, J.H. & Seo, Y.S., 1997. Fatigue strength analysis and reliability analysis of D/H VLCC. Journal of the Society of Naval Architects of Korea, 34(2), pp.64-74.
• Yang, Y.S. & Yoon, J.H. 1991. A study on the fatigue reliability of structures by Markov Chain model. Transactions of the Society of Naval Architects of Korea, 28(2), pp.228-240.