삼각형 패널 상에 선형적으로 분포된 다이폴 강도를 갖는 패널법의 정식화
Abstract
A high-order potential-based panel method based on Green's theorem, with piecewise-linear dipole strength on triangular panels, is formulated for the analysis of potential flow around a three-dimensional wing. Previous low-order panel methods adopt square panels with piecewise-constant dipole strength, which results in inherent errors. Square panels can not represent a high curvature lifting body, such as propellers, since the four vertices of the square panel do not locate at the same flat plane. Moreover the piecewise-constant dipole strength induces inevitable errors due to the steps in dipole strength between adjacent panels. In this paper a high-order panel method is formulated to improve accuracy by adopting a piecewise linear dipole strength on triangular panels. Firstly, the square panels are replaced by triangular panels in order to increase the geometric accuracy in representing the shape of the object with large curvature. Next, the step difference of the dipole strength between adjacent panels is removed by adopting piecewise-linear dipole strength on the triangular panels. The calculated results by the present method is compared with analytical ones for simple non-lifting geometries, such as ellipsoid. The results for an elliptic wing with zero thickness at finite angle of attack are compared with Jordan's results. The comparison shows reasonable agrements for the both lifting and non-lifting bodies.
Keywords:
High-order panel method, Triangular panels, Linearly distribution strength1. 서론
Lee(1987))에 의해 포텐셜 기저 패널법이 유체 중에서 운동하고 있는 프로펠러의 정상상태 문제에 적용된 이후로 포텐셜 기저 패널법은 프로펠러 문제뿐만 아니라 다양한 문제에 대해서 적용되어 왔다. Lee(1987))에 의해 최초로 적용된 포텐셜 기저 패널법은 저차패널법으로 해석법의 가정과 계산방법에 따라 발생하는 오차를 가진다. 먼저 사각형 패널의 사용으로 인해 프로펠러와 같이 곡이 심한 물체를 표현함에 있어서 어려움이 있다. 더욱이 사각형 패널의 각 꼭짓점은 한 평면상에 존재하지 않아 영향계수 계산 시 평균 평면으로 투영하여 계산을 하게 되는데, 이는 원 평면상에서 계산하는 것과의 오차를 발생시키는 원인이 된다. 이어서 저차 패널법은 패널상에 다이폴의 강도가 일정하다고 가정한다. 패널상에 다이폴의 강도가 일정하면 패널간 강도의 단차가 발생하여 계산의 정도를 낮추는 원인으로 작용한다.
본 연구에서는 저차 패널법의 상기 단점을 제거하여 정도 높은 결과를 얻기 위한 정식화를 진행하였다. 우선 기존 저차 패널법에서 사용하는 사각형 패널을 삼각형 패널로 변경하여 곡이 심한 3차원 물체의 표현 정도를 높이고, 평균 평면으로 투영함으로 인해 발생하는 오차를 제거하고자 하였다. 이어서 패널 중심에 정의된 다이폴 강도를 패널의 꼭짓점에서 정의하고, 강도가 선형적으로 분포된다고 가정하여 패널간 다이폴 강도가 연속적으로 분포할 수 있게 하였다.
정식화의 검증은 입사각이 없는 구와 타원체에 대해 해석해와 비교하였고, 입사각이 존재할 때 원형날개에 대해 Jordan(1973)의 두께가 없는 원형 날개의 해석해와 비교하였다.
기존 저차 패널법과의 정밀도 비교를 통해 저차 패널법의 단점이 개선되었는지 확인 하였다. 확인 방법은 두께가 코드길이의 1%인 타원체에 대해 포텐셜값의 해석해에 대한 표준 편차를 확인 하는 방식으로 진행 하였다.
2. 패널법의 기본이론과 경계조건
2.1 지배방정식과 경계조건
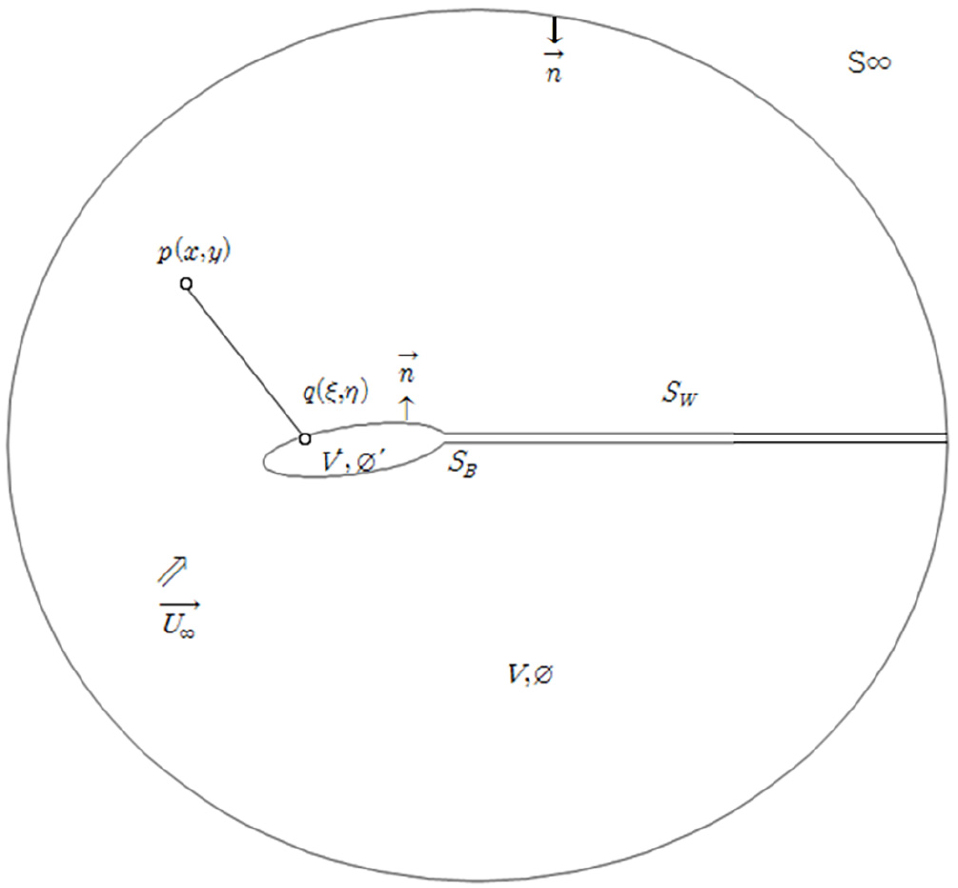
패널법에서의 대상유체의 유동장을 V, 경계면을 S, 경계면에서 유동장 방향의 법선 벡터를 으로 정의한다. 경계면 S는 물체 표면 , 후류 면 , 그리고 물체와 후류 표면 주변의 외부면(outer control surface) 로 구성되어 있고, 유입속도 를 Fig. 1과 같이 정의한다.
유동장은 비압축(incompressible), 비점성(inviscid)의 이상유체이고, 비회전성(irrotational)을 갖는 포텐셜유동으로 가정하였으며, 유동장 내에는 라플라스 방정식을 만족하는 섭동 속도 포텐셜, 가 존재한다.
| (1) |
경계조건은 다음과 같다.
⦁ 에서 운동학적 경계조건을 만족해야 한다.
| (2) |
⦁ 은 두께가 없다고 가정한다. 을 가로지르는 법선속도차이 와 압력 점프는 영이고, 포텐셜 점프는 허용 하며, 포텐셜 점프는 물체 주변의 순환(Circulation)의 크기와 같다.
| (3) |
| (4) |
| (5) |
⦁ 날개 뒷날에서 속도가 유한하다는 Kutta 조건을 만족한다.
| (6) |
⦁물체에서 무한한 거리에 있는 외부면, 에서는 물체로 인한 섭동 속도는 사라질 것이다.
| (7) |
2.2 적분방정식
제어점 p가 유체 중에 있을 때,
| (8) |
여기서, 는 섭동속도 포텐셜, 는 날개 뒷날에서의 포텐셜 점프, 는 Green 함수이고 다음과 같다
| (9) |
여기서, R은 임의점(q)에서 제어점(p)까지의 거리이다.
식 (8)에서 제어점 가 물체표면에 위치할 경우,
| (10) |
여기서, 는 입체각에 의해 구해진 자기유도 영향계수이고, 은 쏘오스의 강도이고 물체 표면의 운동학적 경계조건에 의해서 정의되므로, 식 (10)은 다이폴의 강도 를 미지수로 갖는 적분방정식이 된다. 여기서 구해진 는 물체표면에서의 포텐셜 값이다. 후류면을 가로지르는 포텐셜 점프는 날개 뒷날의 윗면과 아랫면의 포텐셜 차이이다.
3. 경계치 문제의 정식화
3.1. 삼각형 패널의 배치
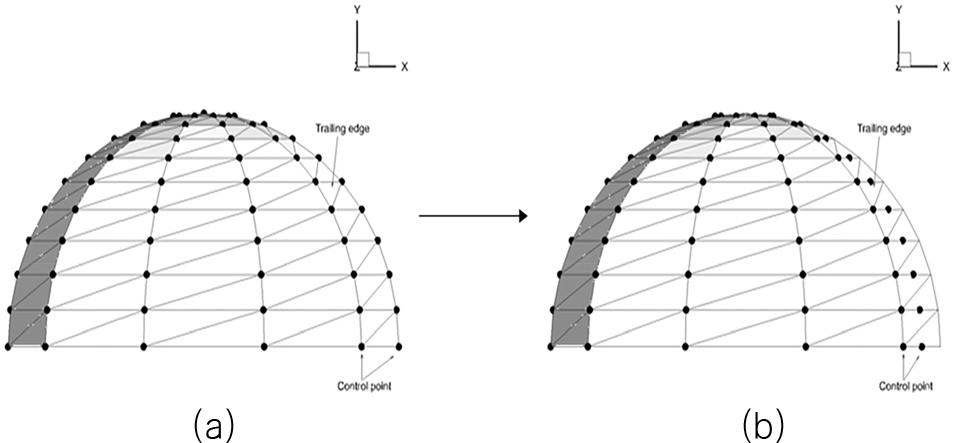
기존의 저차 패널법에서는 사각형 패널을 사용하여 물체를 표현한다. 그러나 사각형 패널은 프로펠러처럼 곡이 심한 물체를 표현함에 있어서 한계가 있고, 각 꼭짓점이 한평면에 있지 않아 평균평면에 투영하여 영향함수를 계산하게 된다. 본 연구에서는 이러한 문제를 삼각형 패널을 사용하여 해결하고자 하였다.
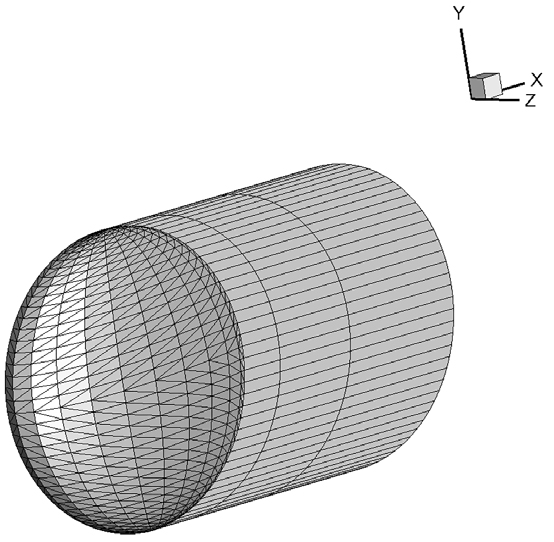
삼각형 패널의 배치는 정렬 삼각패널로 구성되고, 코오드 방향 패널의 개수는 로 표현되고, 동일 반경 상 아래와 위에 패널을 배치시키며 아래와 위 패널 개수의 합으로써 표현된다. 패널을 날개의 앞날과 뒷날에 집중 분포시킴으로써 포텐셜의 급격한 변화를 고려하였다. 반경방향 패널의 개수는 로 표현하고, 동일 반경상에 있는 아래와 위의 패널은 하나로 취급된다. 패널은 날개의 끝으로 갈수록 집중되어 배치된다. 삼각형 패널은 물체를 표현할때만 사용되고 후류는 사각형 패널을 사용하여 표현하였다.
3.2. 특이점 분포의 이산화
기존의 저차 패널법에서 이산화식을 만족하는 제어점은 패널의 중앙에 위치하고, 패널에 걸쳐 다이폴의 강도가 일정하게 분포되어 있다고 가정하였다. 본 연구에서는 인접한 패널들간에 다이폴 강도의 단차를 제거하고자 패널에 걸쳐 다이폴의 강도가 선형적으로 분포한다고 가정하고, 제어점과 특이점은 각 패널의 꼭짓점에 위치한다. 이러한 방법은 2차원 단면에 대해 연구가 진행되어 검증된 바 있다 (Park et al., 2015).
경계치 문제의 해는 적분방정식 식 (10)을 만족하는 특이점의 강도를 결정하는 것으로 구성된다. 쏘오스의 강도는 운동학적 경계조건에 의해 결정되고 오직 다이폴의 강도를 구하는 문제로 귀결된다 (Kim, 2003).
적분방정식 식 (10)을 이산화 시키면 다음과 같이 표현된다.
| (11) |
여기서, 은 총 절점의 개수이고 로 표현된다. 은 운동학적 경계조건에 의한 쏘오스의 강도이고, 은 번째 반경의 날개 뒷날에서의 포텐셜 점프이다. 는 날개에 분포하는 다이폴에 의한 영향계수이고, 는 날개에 분포하는 쏘오스에 의한 영향계수이다. 은 후류면에 존재하는 다이폴에 의한 영향계수이다.
이산화 식 (11)을 선형강도를 갖는 다이폴을 적용하여 선형대수 방정식으로 표현 하면 다음과 같다.
| (12) |
여기서,
여기서, 는 다이폴에 의한 영향계수이고, 는 날개에 분포하는 다이폴이 선형적으로 분포할 때 다이폴에 의한 영향계수이다. 입체각(solidangle)은 날개상에 분포하는 다이폴에 의한 자기유도 영향계수로 꼭짓점을 공유하는 패널들이 이루는 3차원 각으로 표현되고, 3.3절에 자세히 나타내었다. 는 후류면 상에 존재하는 다이폴에 의한 영향계수이다. 는 쏘오스에 의한 영향계수이다.
선형 강도의 분포는 Fig. 3에 보는 것처럼 패널의 각 꼭짓점에 단위강도의 다이폴이 존재하고, 그 외의 꼭짓점에서의 강도는 영이 된다고 가정하여 영향계수를 계산하였다.
Fig. 3에서 보인 선형 강도의 분포는 다음의 식으로 나타낼 수 있다.
| (13) |
여기서, 는 번째 꼭짓점에서의 다이폴 강도이고, 그리고 는 다이폴의 강도로부터 결정되는 계수이다. 패널 각 변의 방향벡터를 로, 꼭지점의 위치를 ()로 각각 정의한다. 선형강도 분포에 상응하는 패널의 기하학으로부터 를 계산할 수 있다.
| (14) |
여기서, 는 패널 각 변의 길이이고, 패널의 꼭짓점과 각 변은 반시계 방향으로 정의 된다. 식 (14)를 Cramer’s rule을 이용하여 계수 를 계산한다.
| (15) |
계산된 계수 를 이용하여 를 구한다.
| (16) |
다이폴에 의한 영향계수를 계산하는 경우, 제어점의 위치와 특이점의 위치가 같으면 자기 자신에 의해 유도되는 영향계수로 정의된다. 기존의 저차 패널법에서는 제어점의 위치가 패널의 가운데에 존재하여 그 값이 로 일정하다. 그러나 당 논문과 같이 삼각형 패널을 채택하는 경우 제어점의 위치가 패널의 꼭짓점에 위치하게 되며, 자기유도 영향계수는 꼭짓점을 공유하는 패널들사이의 각으로 표현되며 이는 각 꼭짓점을 잇는 내각으로 구성되는 입체각(solid angle)으로 표현된다 (Lee & Shu, 1995).
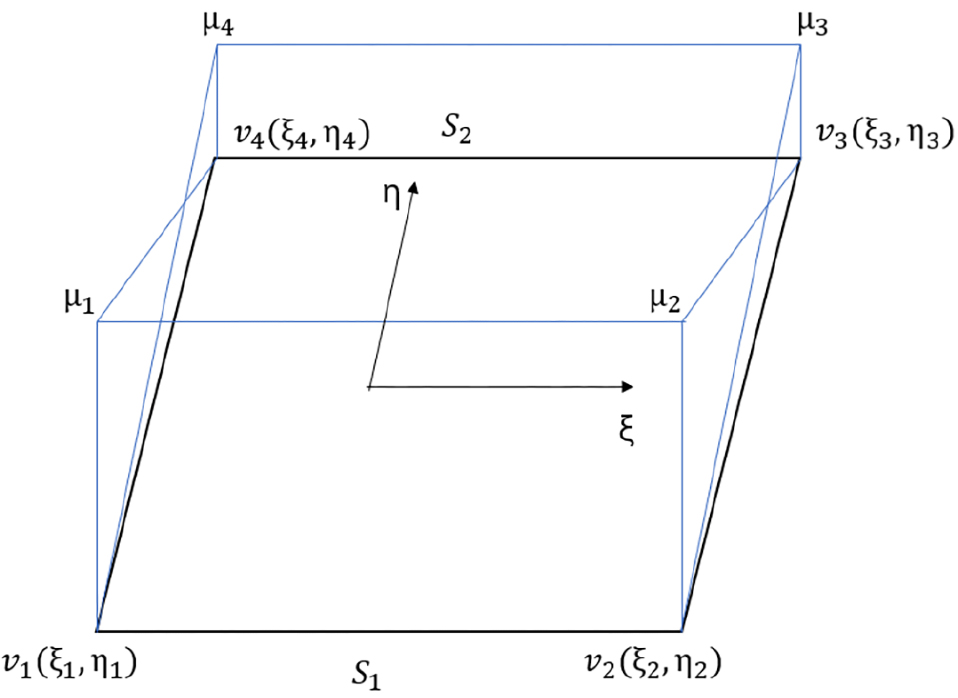
후류면에서의 다이폴은 사각 패널상에 쌍선형(bilinear)적으로 분포하고 있다고 가정하고, 그에 의한 영향계수는 Suh 등(1992)이 제안한 방법에 의해 계산한다 (Fig. 4).
패널은 의 평면에 있고, 축의 방향이 패널법의 법선 벡터의 방향과 같도록 - 국소 직교 좌표계(local coordinate system)를 정의한다. 축과 축 방향의 단위 벡터는 각각 와 로 나타낸다.
후류 패널상 다이폴의 쌍선형 강도 분포는 다음과 같이 나타낼 수 있다.
| (16) |
여기서, 는 다이폴의 강도이고, 그리고 는 꼭짓점에서의 다이폴 강도에 의해 구해진 상수이다. 후류면에서의 다이폴 강도는 후류면의 양변()에서 정의된다.
본 논문에서는 제어점이 꼭짓점에 있다고 가정하였다. 하지만 날개 뒷날에서 제어점의 위치가 패널의 꼭짓점에 존재하게 되면 kutta 조건을 적용함에 있어서 어려움이 존재하게 된다. 이를 회피하기 위해 Fig. 5와 같이 날개 뒷날에서의 제어점을 날개 앞날 방향으로 이동시켜 계산을 진행 하였다.
제어점의 적절한 위치를 파악하기 위해 입사각이 5.73°일 때 단면 NACA0005를 갖는 원형날개에 대해, 제어점의 위치를 날개 뒷날 패널 길이의 10~50% 까지 10% 단위로 앞날 방향으로 이동시켜 압력 Kutta 조건을 만족시키기 위해 수행된 반복계산 결과를 비교 하였다. 결과의 비교는 반복계산의 횟수와 날개 뒷날에서의 반경방향 최대 압력계수차를 기준으로 하였으며, 결과를 Table 1에 보였다. Table 1에서 보면 반복계산 횟수는 끝점에서 멀어질수록 줄어들고 있음을 확인 할 수 있다. 압력계수차의 경우 멀어질수록 커지는 현상을 보이지만 그 차이는 크지 않고 50%일 경우에도 충분히 수렴했다고 판단된다. 따라서, 본 연구에서는 제어점을 날개 앞날의 방향으로 50% 이동시켜 계산을 진행 하였다.
3.3. 입체각
본 연구에서는 제어점과 특이점의 위치가 동일한 경우의 다이폴에 의한 영향계수 를 계산하기 위하여 꼭짓점을 공유하는 패널들이 이루는 각을 3차원 각도인 입체각을 이용하여 계산하였다.
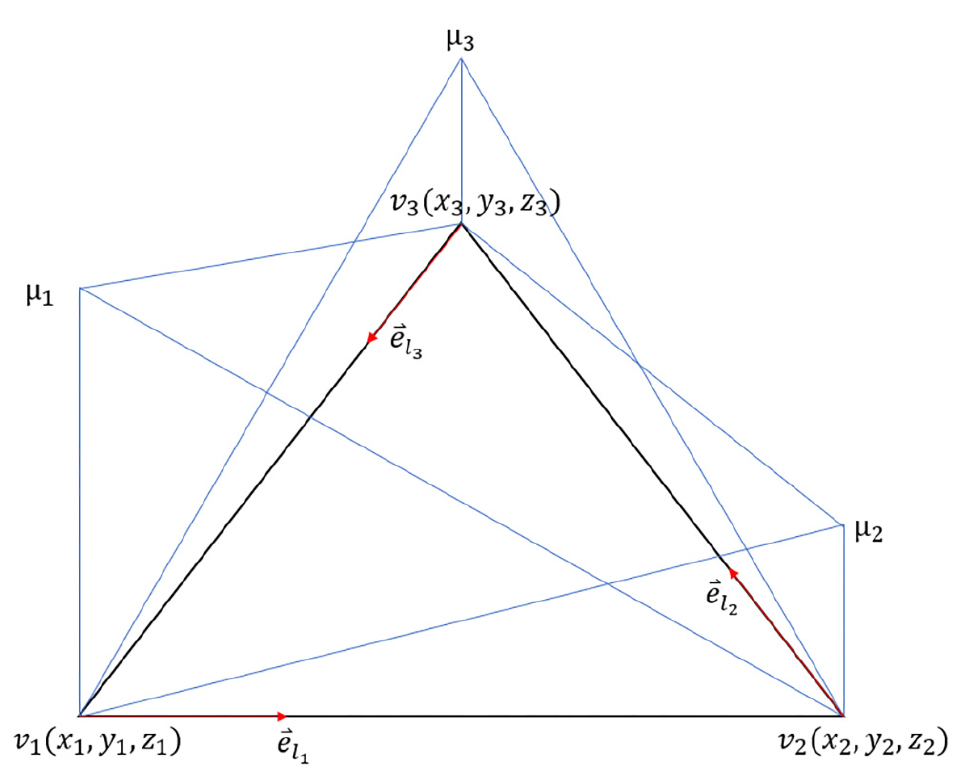
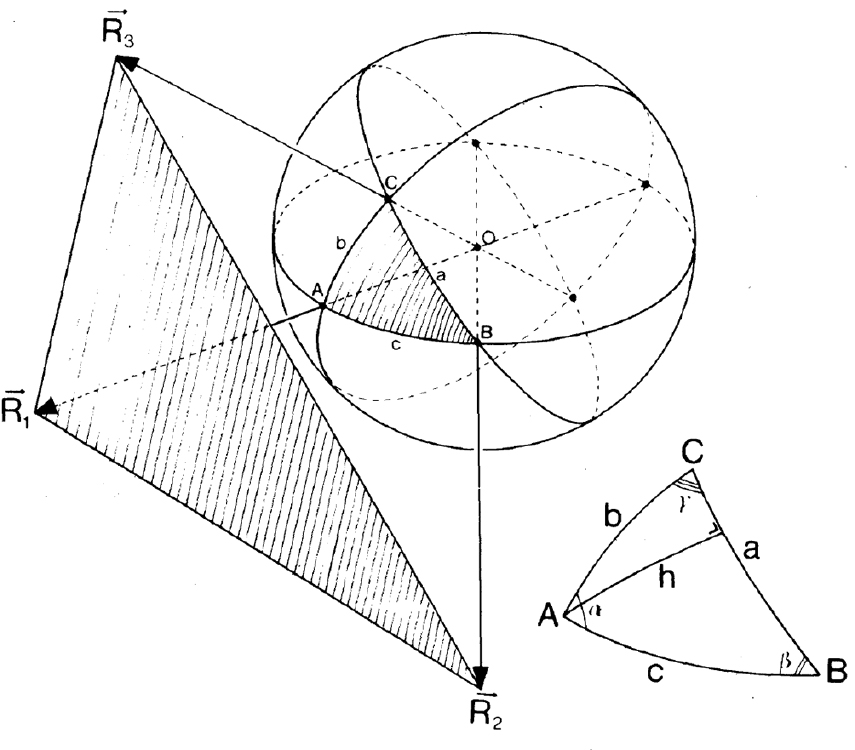
입체각은 각을 3차원으로 확장한 것이며, 2차원 각이 평면에서의 퍼짐 정도를 나타낸다면, 입체각은 공간에서의 퍼짐 정도를 나타내는 척도가 된다. 입체각의 기호는 일반적으로 로 나타내며, 라디안과 같이 무차원량이다. 입체각은 다음과 같이 표현 할 수 있다. 삼각형 패널의 꼭짓점을 Fig. 6처럼 벡터 그리고 으로 정의하고, 삼각형 패널에 의한 점에서의 입체각, 는 로 나타낼 수 있다. 여기서, 는 반지름이 인 구위의 삼각형 의 면적이고, 은 임을 의미 한다.
삼각형 패널에 의한 입체각을 구하는 방법은 van Oosterom, A. and Strackee, J.(1983)에 의해 다음과 같이 정리 되었다.
| (17) |
여기서,
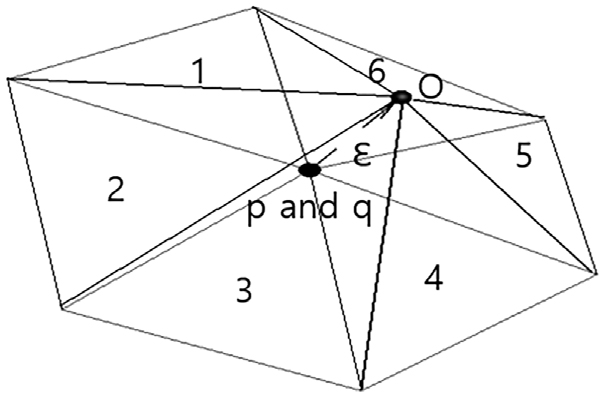
자기유도 영향계수를 입체각으로 표현하기 위해 제어점과 특이점이 위치하는 꼭짓점을 포함하는 패널들이 이루는 입체각을 계산하게 된다. 제어점과 특이점을 포함하고 있는 꼭짓점에서 만큼 떨어진 점을 원점 점으로 하여 각 패널별로 입체각을 구하고, 각 입체각을 더하여 해당 점에서의 자기유도 영향계수를 구한다.
| (18) |
여기서, i는 제어점과 특이점을 포함하고 있는 패널의 개수이다.
3.4. 압력 Kutta 조건
물체 주변의 순환(circulation)을 특정하기 위해 날개 뒷날 상, 하면에서의 압력이 같아지도록 압력 kutta 조건을 적용하였다. 비선형 압력 Kutta 조건은 Lee(1987)가 제안한 방법을 적용하였고 다음과 같다.
| (19) |
여기서, 와 는 날개 뒷날 상, 하면의 포텐셜 값이고, 는 유입속도, 는 날개 뒷날의 두 제어점 사이의 벡터, 는 후류의 포텐셜 점프에 영향을 주는 계수이다.
후류의 포텐셜 점프에 영향을 주는 계수, 는 날개 뒷날에서의 압력계수의 차이에 의해 결정되는 비선형항으로 반복계산을 통해 구할 수 있고, 본 연구에서는 secant 방법을 이용하여 구하였다.
| (20) |
여기서, 첨자 는 반복계산 횟수이고, 는 날개 뒷날에서의 압력계수 차이다.
| (21) |
이산화 식 (11)에 kutta 조건 식 (21)을 적용하면 다음과 같다.
| (22) |
3.5. 속도와 압력의 계산
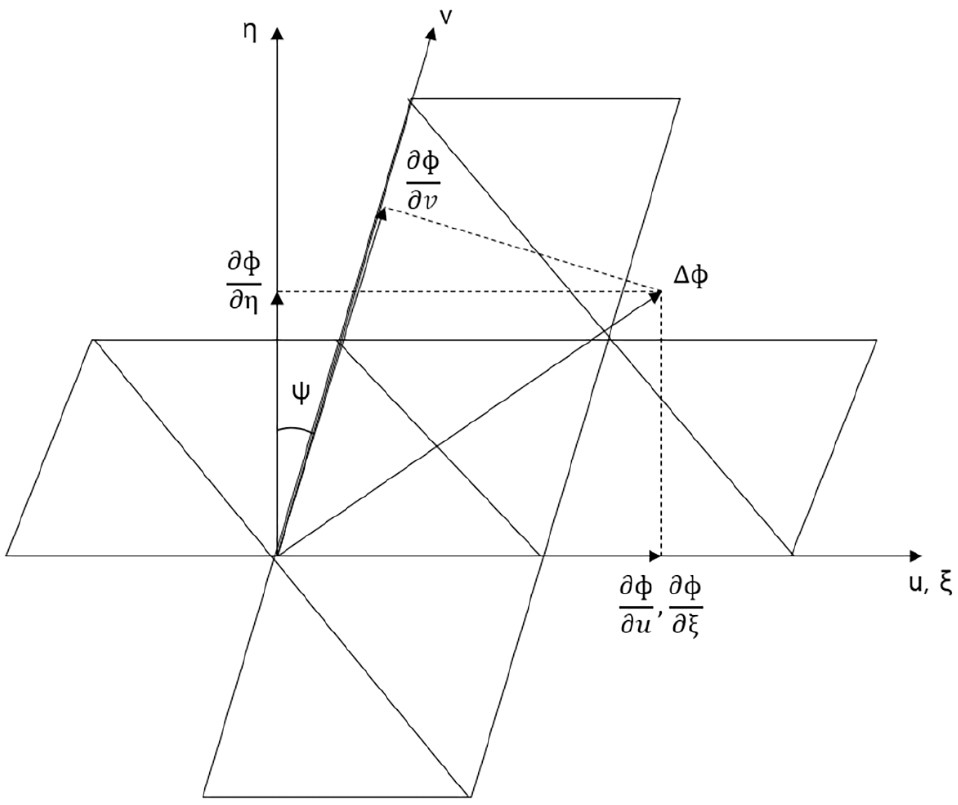
와 방향의 속도는 접선 방향의 속도를 와 의 방향으로 투영시킨 속도이고, 각 방향의 인접한 세점의 포텐셜 값의 미분으로 구할 수 있다. 접선방향의 섭동 속도는 와 방향의 속도를 와 방향의 속도로 변환하여 벡터의 합으로 구할 수 있다.
국소 좌표계(- coordinate system)은 와 는 서로 직교하고, 는 방향과 일치하도록 정의 한다. 국소 좌표계의 정의에 의해 방향의 속도는 방향의 속도와 같고, 방향의 속도는 다음과 같이 구할 수 있다.
| (23) |
여기서, 는 방향과 방향 사이의 각이다.
압력계수의 계산은 베르누이 방정식을 이용하여 구할 수 있다.
| (24) |
4. 계산 결과
4.1 양력이 없는 원형 날개
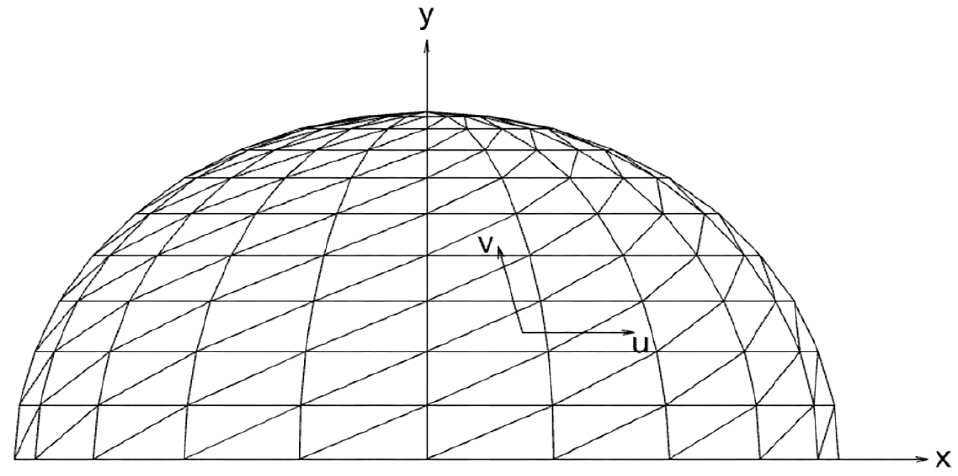
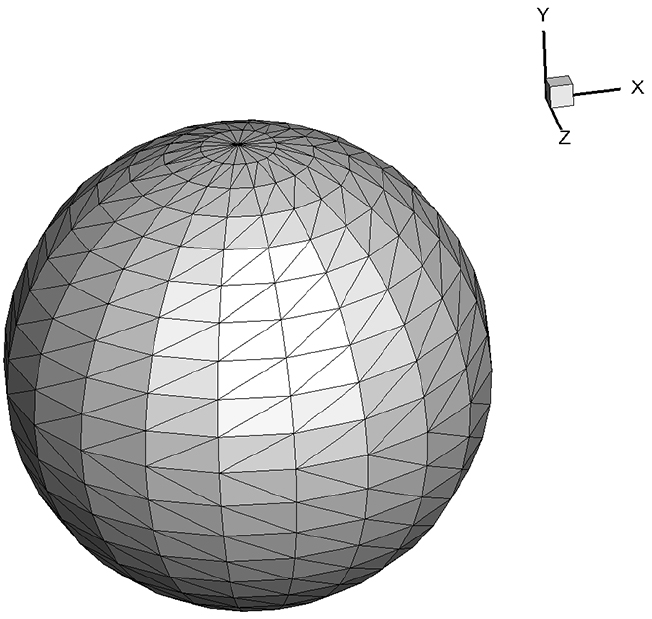
입사각이 영도일 경우 간단한 형상에 대해 해석해와 비교하였고, 와 의 방향에 대한 정의는 Fig. 9과 같다.
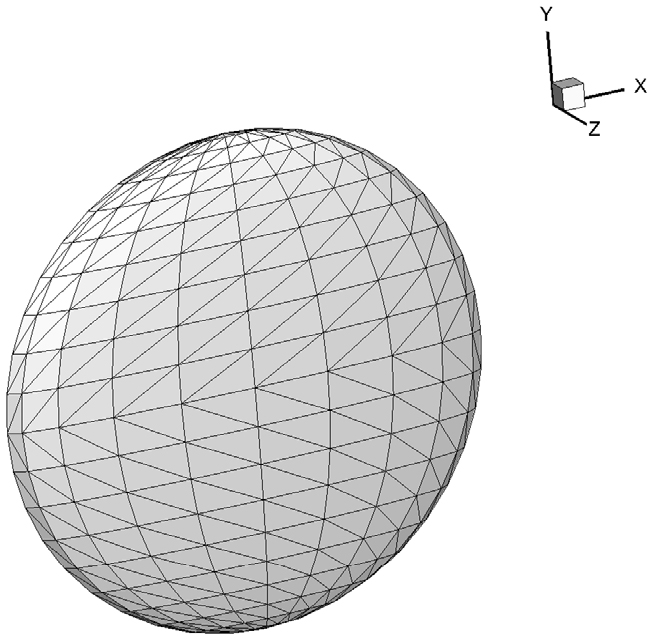
구의 형상은 타원체에 대한 식 (25)에서 각 축의 반경을 1()로 하고, Fig. 9에 나타내었다.
| (25) |
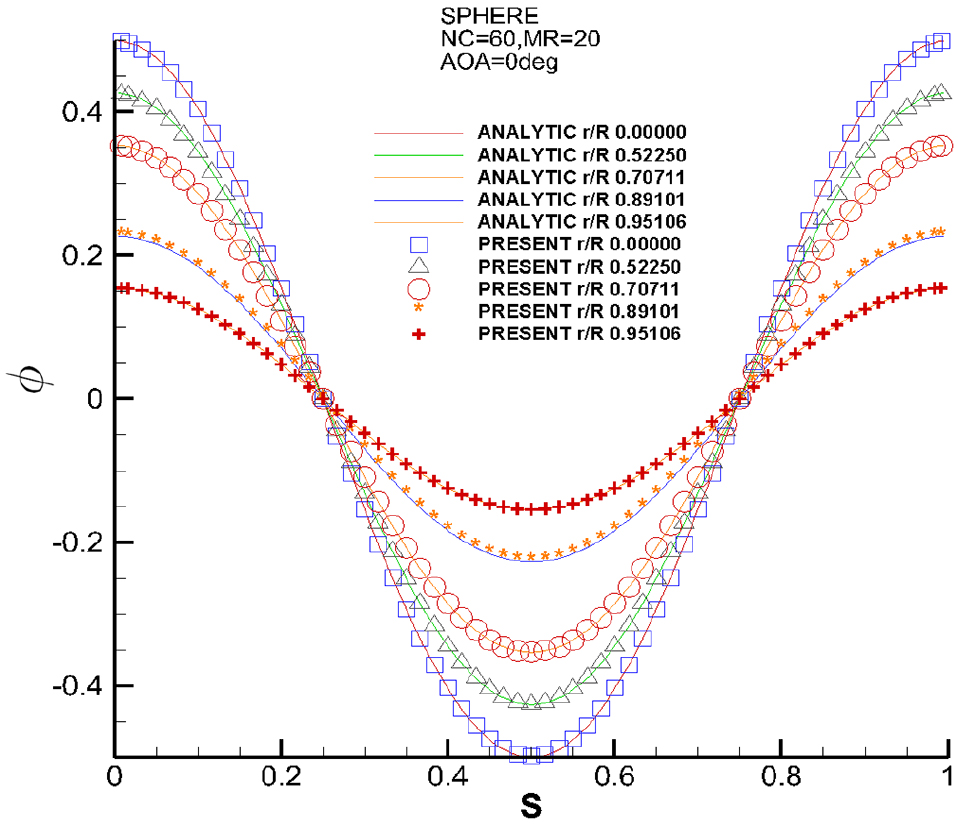
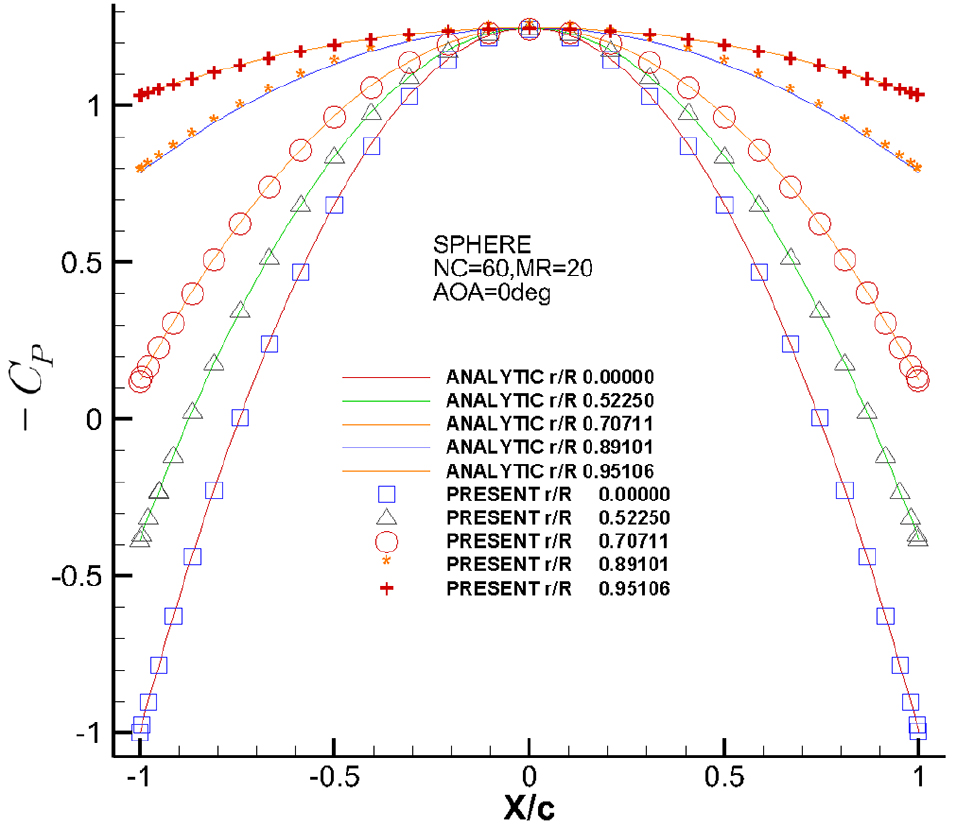
해석해와의 비교는 포텐셜과 의 코오드 방향 분포를 각각 비교하였다. 결과의 비교는 Fig. 11과 Fig. 12에 나타내었다. Fig. 11에 보인 그래프의 축은 물체의 코오드 방향의 둘레이고, 영과 1은 날개의 뒷날, 0.5는 날개의 앞날을 의미한다. Fig. 12에 보인 그래프의 축은 코오드 방향의 값을 코오드 길이로 무차원화 한 값이고, -1과 1은 날개의 뒷날, 영은 날개의 앞날을 의미한다.
Fig. 11에 보인 포텐셜 값의 비교를 보면 본 연구에서 시도한 방법과 해석해가 잘 일치함을 보이고 있다. Fig. 12의 값 또한 해석해와 잘 일치함을 보인다. 이것으로 보아 정식화가 정상적으로 이루어 졌다고 판단된다.
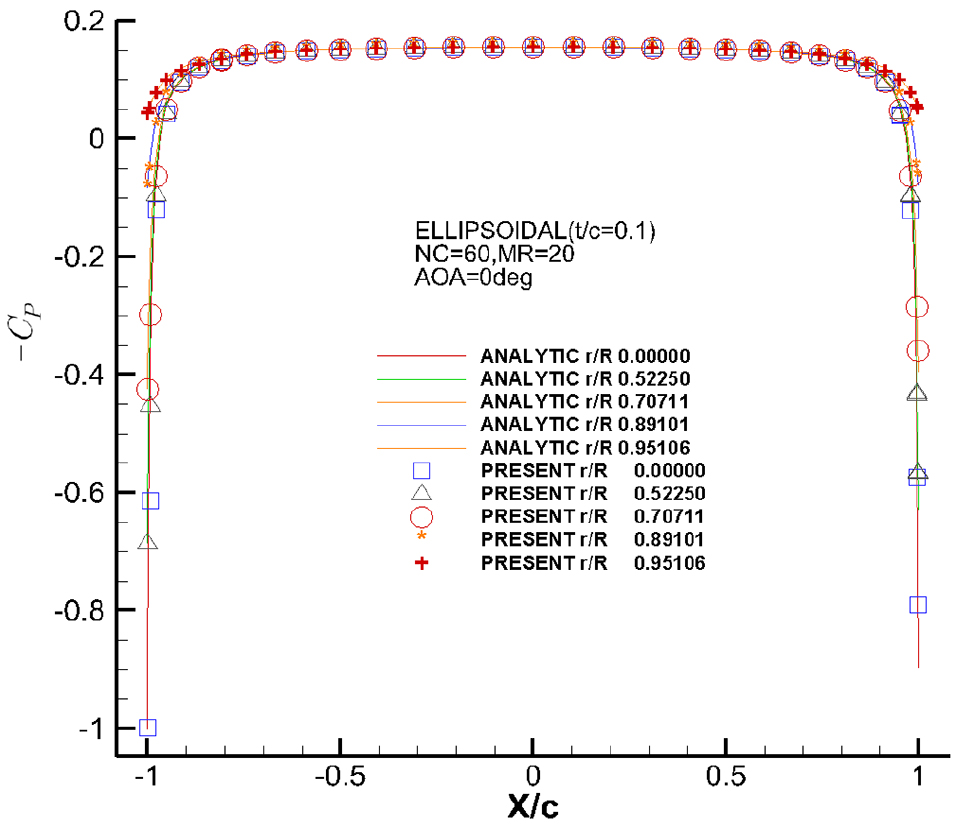
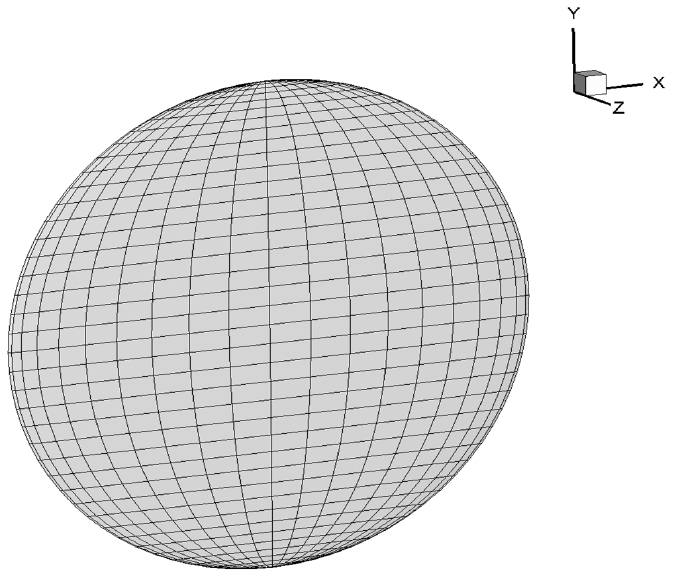
타원체의 형상은 각 축방향으로 , 을 반경으로 한다. 은 타원체의 두께가 코오드 방향 길이의 10%임을 의미하고 Fig. 13에 나타 내었다.
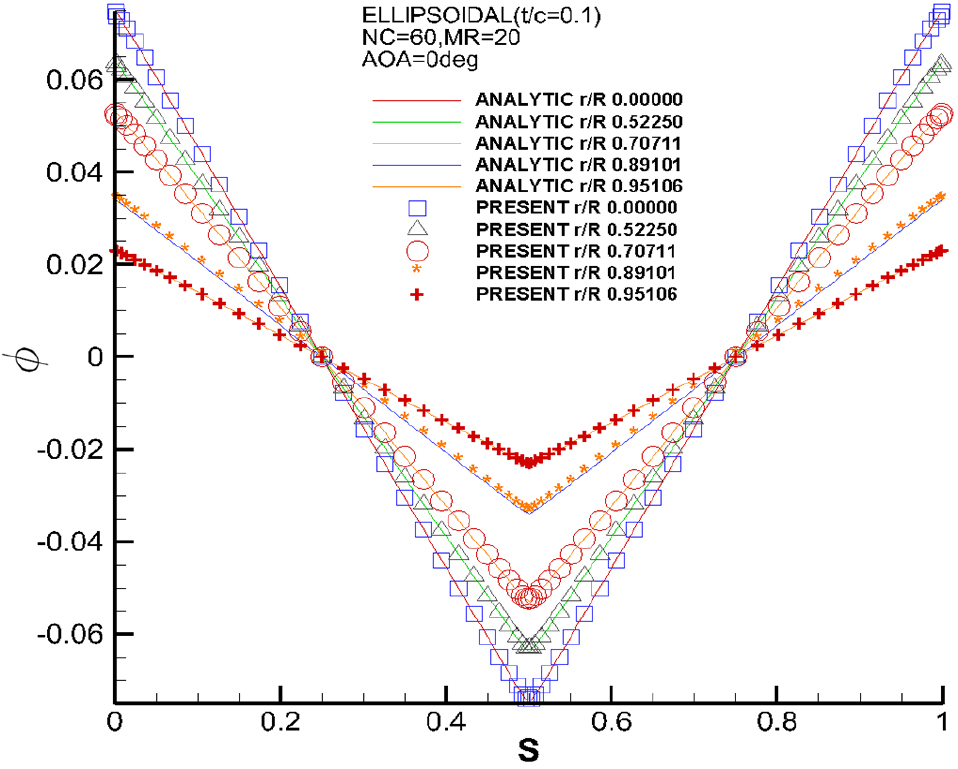
해석해와의 비교는 포텐셜과 의 코오드 방향 분포를 각각 비교하였다. 결과의 비교는 Fig. 14과 Fig. 17에 나타내었고, Fig. 14에 보인 그래프의 축은 물체의 코오드 방향의 둘레이고, 영과 1은 날개의 뒷날, 0.5는 날개의 앞날을 의미한다. Fig. 17에 보인 그래프의 축은 코오드 방향의 값을 코오드 길이로 무차원화 한 값이고, -1과 1은 날개의 뒷날, 영은 날개의 앞날을 의미한다.
Fig. 14에 보인 포텐셜 결과의 해석해와의 비교는 정식화 결과가 해석해와 대체적으로 잘 일치함을 알 수 있다. 다만 날개의 앞날과 뒷날에서 조금의 오차를 보인다.
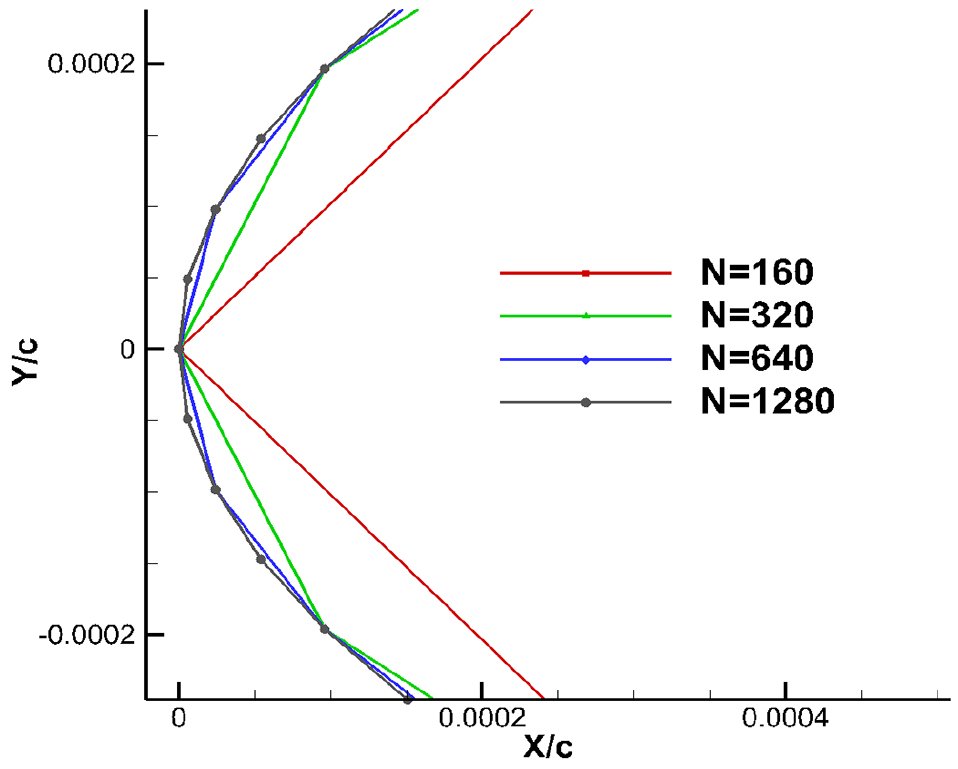
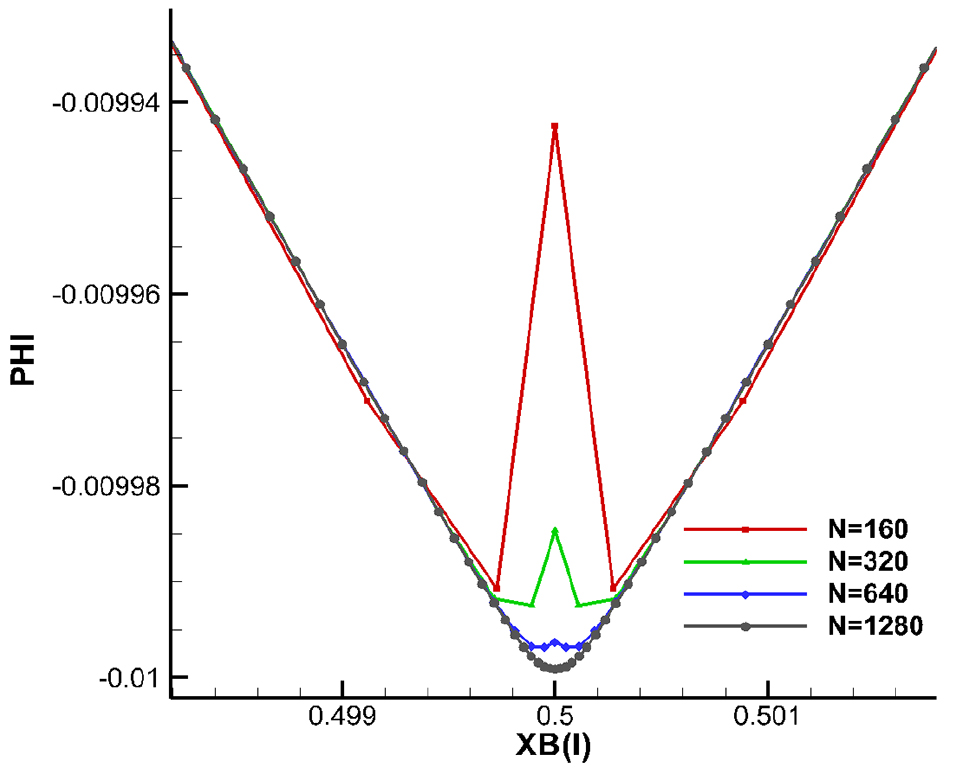
이는 기존 패널법의 경우 제어점의 위치가 패널의 중앙에 위치하여 자기유도 계수가 로 일정한 반면 본 연구에서는 패널의 절점에 제어점이 위치하고 있어 패널의 개수에 따라 자기유도 계수의 수렴성이 달라지기 때문이라 판단된다. 이 같은 현상은 2차원 단면에서 패널의 개수 변화를 통해 다음과 같이 확인 할 수 있다.
Fig. 17의 결과 비교를 보면 정식화 결과가 해석해와 잘 일치함을 알 수 있다. 이것으로 보아 날개의 앞날과 뒷날에서 발생한 오차는 무시할 만큼 작다고 보여 지고, 계산에 사용된 패널의 개수는 충분하다고 판단되어 진다.
4.2 양력이 있는 원형 날개
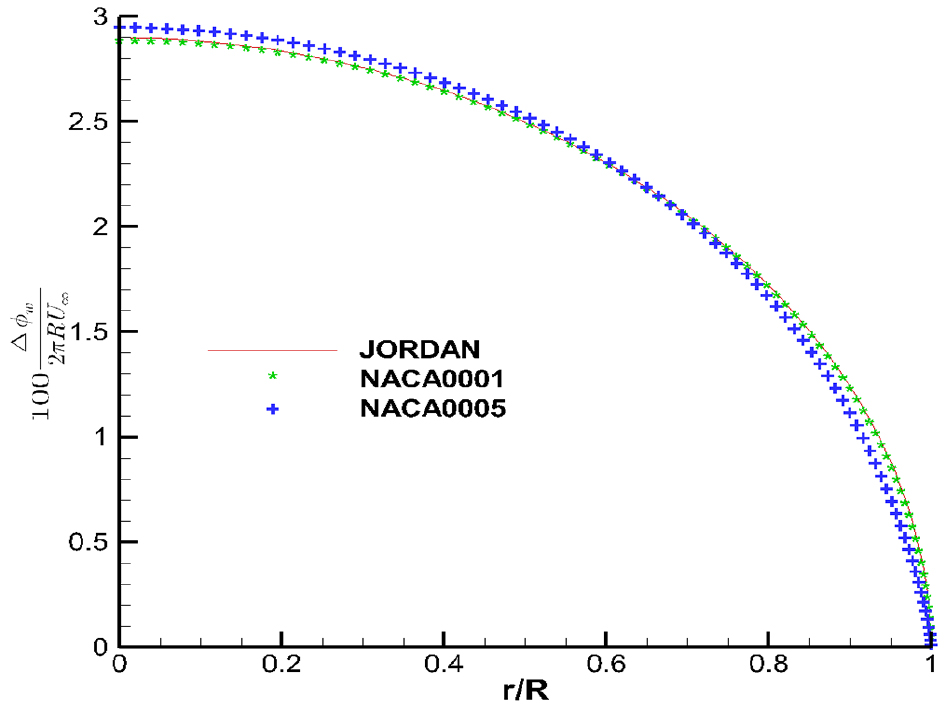
양력이 존재하는 원형 날개의 단면은 NACA 단면을 사용하였다. 단면은 두께와 코오드 길이의 비가 0.01과 0.05인 NACA 0001과 NACA 0005, 두 단면을 사용하였고, 코오드의 길이는 1, 반경 방향의 길이는 0.5이다. 계산결과는 Jordan(1973)의 두께가 영인 양력이 존재하는 원형 날개의 해석해와 비교하여 코오드 방향과 반경방향으로의 수렴성을 확인 하고, 반경방향 순환(circulation)의 크기에 대한 두께의 영향을 확인 하였다. 그리고 압력 kutta 조건이 정상적으로 적용이 되었는지 확인 하였다. 수렴성의 확인은 NACA 0001 단면에 대해 진행 하였다.
원형 날개에 유입되는 유동의 입사각은 5.73°이고, 코오드 방향 수렴성의 경우 은 40개, 반경 방향 수렴성의 경우 를 41개로 고정하였다.
Fig. 18과 Fig. 19에는 코오드 방향과 반경방향의 수렴성을 보였다. 양 방향 모두 패널의 개수가 증가함에 따라 Jordan(1973)의 값에 수렴하고 있음을 확인 할 수 있다. 수렴의 속도는 코오드 방향이 반경 방향보다 수렴이 천천히 되고 있음을 확인 할 수 있다. 이는 패널 개수에 대한 민감도가 반경 방향보다 코오드 방향으로 더 민감하기 때문인 것으로 판단된다.
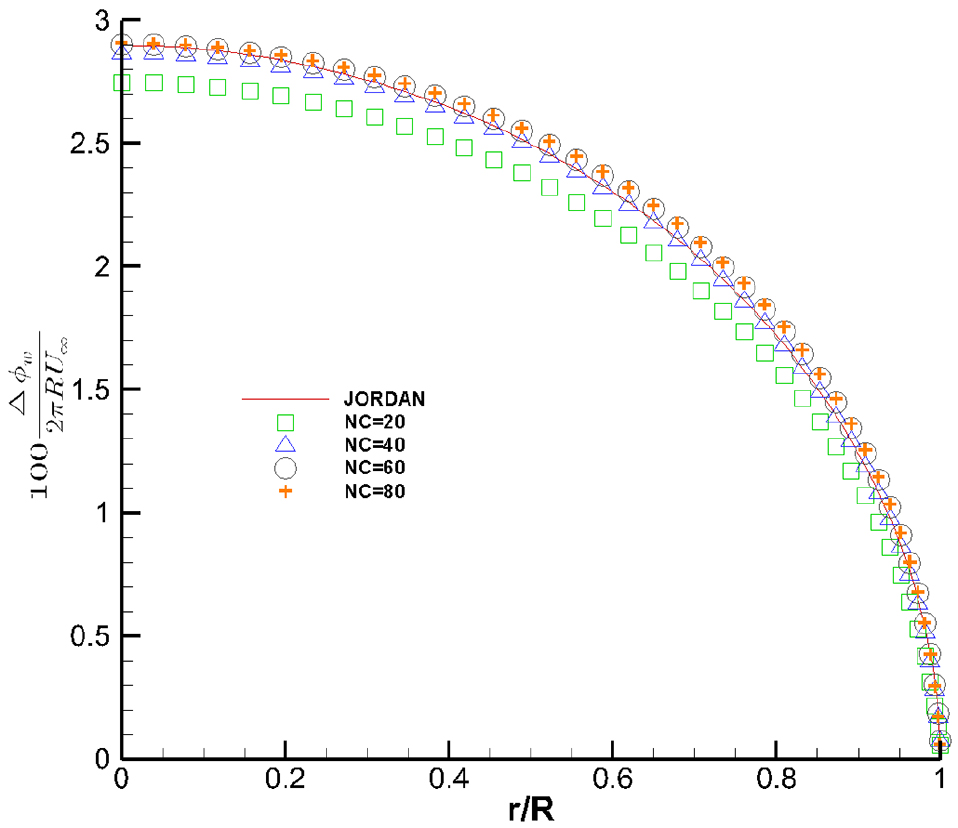
Effect of the chord-direction number of panels on the circulation distribution of the circular wing(NACA 0001, α=5.73°)
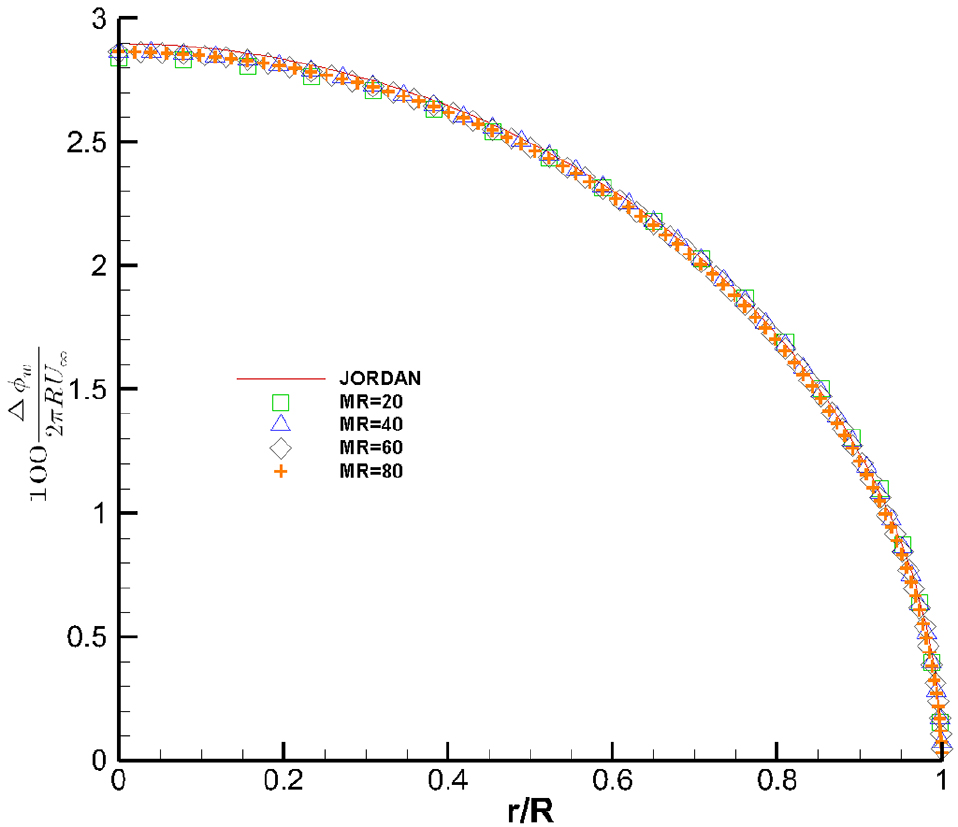
Effect of the span-direction number of panels on the circulation distribution of the circular wing(NACA 0001, α=5.73°)
원형 날개의 두께가 증가하면 날개 뒷날에서 교차 유동의 크기가 증가하고, 이로 인해 날개 뒷날에서의 하중이 증가하여 영하중 조건을 만족하지 못하게 된다 (Fig. 20). 영하중 조건을 만족시키기 위해 압력 kutta 조건을 적용 하고, 반복 계산을 통해 압력 kutta 조건을 만족시키게 된다. 반복 계산 과정에서 후류면의 다이폴 강도는 감소하게 되고, 결과적으로 두께가 증가함에 따라 순환(circulation)이 감소된다. 압력 kutta 조건의 반경별 만족 여부는 Fig. 21에 보였고, 원형 날개의 두께 증가에 따른 순환(circulation)의 반경 방향 크기는 Fig. 22에 나타내었다.
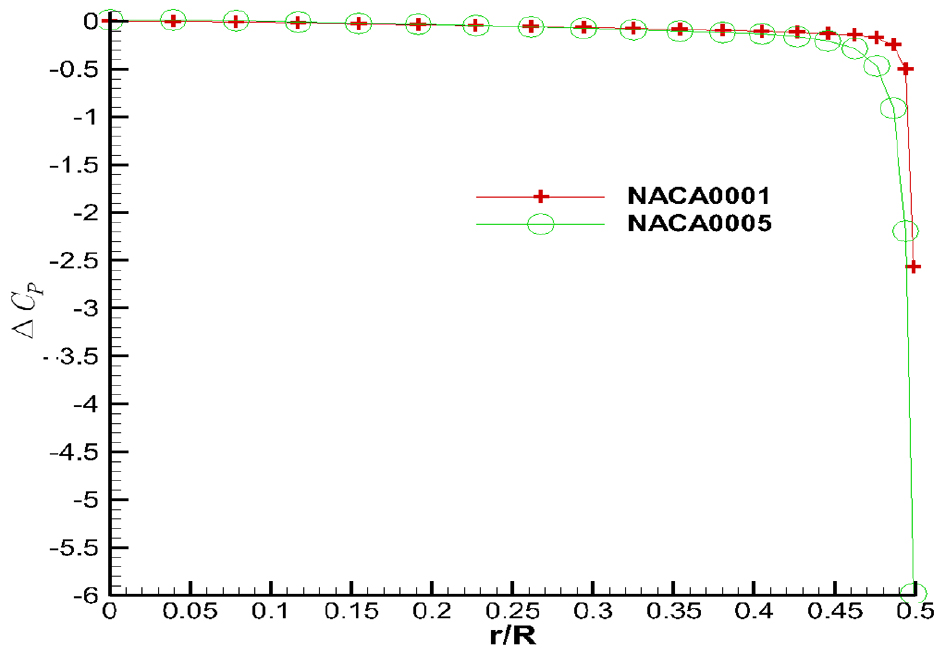
Effect of the cross flow on the span-direction ∆Cp(=CNnodeP-CP1) of the circular wing(Nnode=41, Mr=20, α=5.73°)
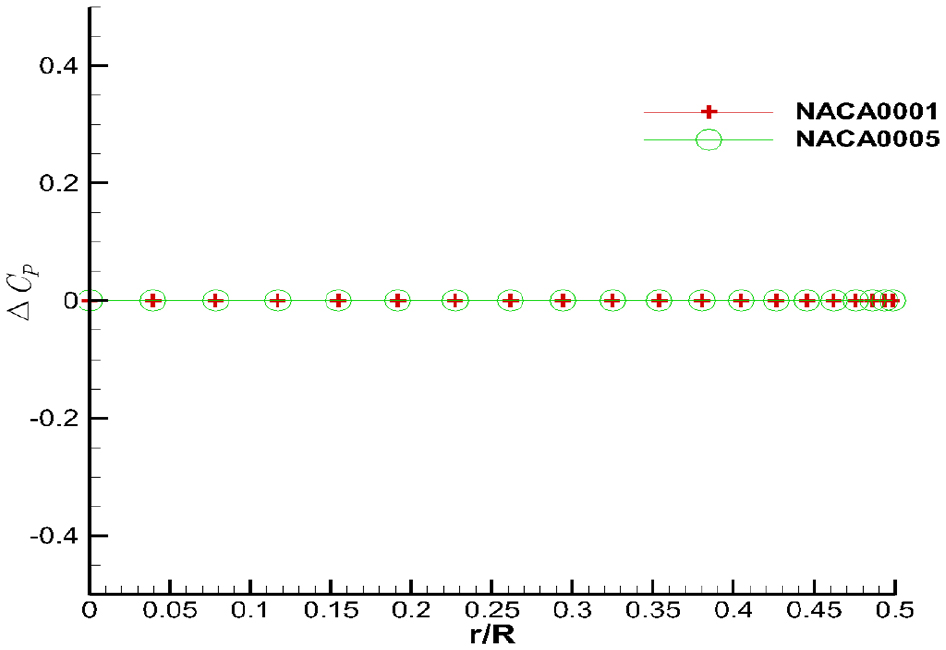
Effect of the pressure kutta condition on the span-direction ∆Cp(=CNnodeP-C1P) of the circular wing (α=5.73°)
Fig. 20에서 보면 날개 뒷날에서 교차 유동으로 인해 영하중 조건을 만족 시키지 못하고 있음을 확인 할 수 있고, 원형 날개의 두께가 증가하면 영향이 더 커짐을 확인 할 수 있다. Fig. 21에서 보면 반경 방향으로 날개 뒷날에서 압력 차가 영이 됨을 확인 할 수 있고, 압력 kutta 조건이 정상적으로 적용되었음을 확인 할 수 있다.
저차 패널법과의 비교는 두께가 코오드 길이의 1%()인 타원체에 대해 유체의 입사각이 0도 일 경우에 해석해와의 표준편차()를 이용해 비교하였고, 그 형상은 Fig. 23과 같다.
표준편차의 계산은 다음과 같다.
| (26) |
여기서, 은 전체 제어점의 개수, 는 해석해의 포덴셜 값에서 각 패널법의 포텐셜 값을 뺀 값이다.
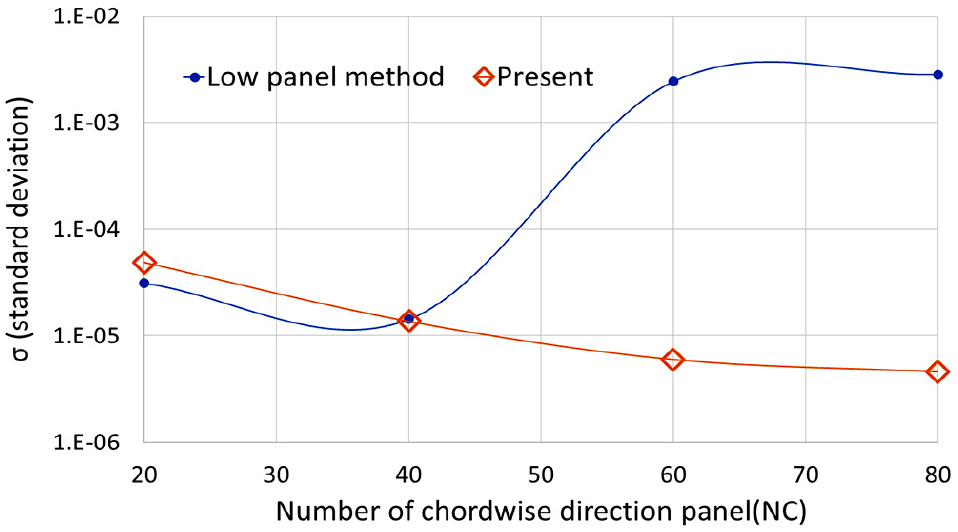
계산은 코오드 방향과 반경방향으로 패널의 개수를 각각 증가시켜가며 결과를 비교하였다. 결과의 비교는 Table 2 와 Fig. 24, Fig. 25에 나타내었다.
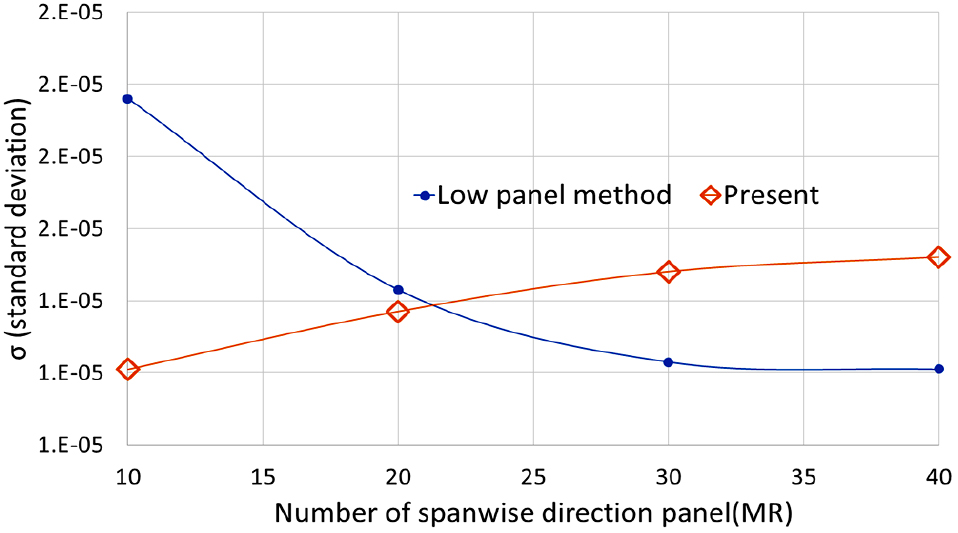
Table 2는 각 방향의 패널 개수 변화에 따른 표준편차를 나타내었다. Fig. 24의 y축은 표준편차를 log 스케일로 표현 하였고, x축은 코드방향 패널의 개수이다. Fig. 25의 y축은 표준편차의 값이고, x축은 방경방향 패널의 개수이다.
아래의 결과에서 보면 코오드 방향 패널의 개수가 증가하면 삼각형 패널의 정도가 높아짐을 확인 할 수 있다. 반면 반경방향의 패널의 개수가 증가하면 저차 패널의 정도가 높아짐을 확인 할 수 있다. 이는 패널의 왜도(skewness)에 의한 영향으로 보이며, 패널의 왜도에 대한 추가적인 연구가 필요 하다고 판단된다.
5. 결 론
본 연구에서는 삼각형 패널상에 다이폴의 강도를 선형적으로 분포 시켜 정식화 하였다. 삼각형 패널은 동일 반경상에 삼각형 패널을 서로 엇갈리게 배치하여 Green의 정리를 만족하는 밀폐된 형상을 구현하였다. 특이점은 삼각형 패널의 각 꼭짓점에 위치시켜 패널간 특이점 강도가 연속적으로 분포할 수 있게 하였다. 제어점의 위치는 특이점의 위치와 일치시키고, kutta 조건의 용이한 적용을 위해 날개 뒷날의 제어점은 패널의 변을 따라 날개의 앞날 방향으로 이동시켜 배치하였다.
정식화에 대한 검증은 해석해가 존재하는 간단한 3차원 물체에 대해 진행 하였다. 먼저 해석해가 존재하는 양력이 없는 구와 타원체에 대해 진행 하였고, 해석해와의 비교 결과 해석해와 잘 일치함을 보였다. 이어서 양력이 존재하는 원형 날개에 대해 Jordan(1973)의 결과와 비교 하였다. 비교 결과 패널의 개수가 증가함에 따라 Jordan(1973)의 결과에 수렴함을 확인 할 수 있었다.
검증 결과 본 연구에서 진행한 삼각형 패널상에 선형적으로 다이폴의 강도가 분포하는 패널법의 정식화가 성공적으로 이루어졌다고 판단된다.
저차 패널법과의 결과 비교를 통해 저차 패널법 보다 정도 높은 결과가 나옴을 확인 할 수 있었다. 다만, 반경방향으로 패널의 개수가 증가할 경우 저차 패널법에 비해 낮은 정도를 보이는데, 이는 패널의 왜도(Skewness)에 의한 영향으로 보인다. 추후 패널의 왜도(Skewness)에 대한 연구가 필요하다고 판단된다.
References
-
Jordan. P. F., 1973, Exact solution for lifting surfaces. AIAA Journal, 11, pp.1123-1129.
[https://doi.org/10.2514/3.50557]

- Kim, G.D., 2003. Application of high order panel method for improvement of prediction of marine propeller performance. Ph.D, Chungnam National University.
- Lee, C.S., & Shu, J.C., 1995. Dipole distributions on a hyperboloidal panel. Journal of the Society of Naval Architects of Korea, 32(2), pp.32-42.
- Lee, J.T., 1987, A potential based panel method for the analysis of marine propellers in steady flow. Ph.D. Department of Ocean Engineering, M.I.T.
-
Oh, J.A. & Lee, J.T., 2013, Viscous flow analysis around a blade section be a hybrid scheme combining a panel method and a CFD method. Journal of the Society of Naval Architects of Korea, 50(2), pp.355-363.
[https://doi.org/10.3744/SNAK.2013.50.5.355]

-
Park, G.D., Oh, J.A. & Lee, J.T., 2015. Flow analysis around a wing section by a piecewise linear panel method. Journal of the Society of Naval Architects of Korea, 52(5), pp.380-386.
[https://doi.org/10.3744/SNAK.2015.52.5.380]

- Suh, J.C., Lee, J.T., & Suh, S.B., 1992, A bilinear source and doublet distribution over a planar and its applications to surface panel method, 19th symposium on naval hydrodynamics office of naval research, pp.839-847.
-
van Oosterom, A. & Strackee, J., 1983, The solid angle of a panel triangle, IEEE Transactions on Biomedical Engineering, vol, BME-30, no.2, February, pp.125-126.
[https://doi.org/10.1109/TBME.1983.325207]