쇄빙연구선 ARAON호의 국부 빙하중 추정을 위한 영향계수행렬의 보완
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper focuses on the improvement of the influence coefficient matrix method for estimation of local ice load on the icebreaking research vessel ARAON. The influence coefficient matrix relates ice pressure on the hull plate to the measured/calculated hull strain/stress. Conventionally von Mises equivalent stresses representing hull stresses and ice pressure acting on the hull plate are utilized to assemble the influence coefficient matrix. Because of the three dimensional features of the ship-ice collision process, an enhanced method to assemble the influence coefficient matrix is derived considering ice loads in the X, Y, and Z direction simultaneously. Furthermore the location of ice loads acting on hull-plate may fall outside the measuring sensor area, and the enhanced influence coefficient matrix is modified to reduce the difference between the actual and the estimated ice loads by expanding the domain outward from the sensor area. The developed method for enhanced influence coefficient matrix is applied to IBRV ARAON during the 2019 Antarctic ice field test and the local ice loads in three directions are efficiently calculated compared to those by a conventional method.
Keywords:
Local ice load, Influence coefficient matrix, IBRV ARAON키워드:
국부 빙하중, 영향계수행렬, 쇄빙연구선 아라온1. 서 론
빙해역에서 운항되는 쇄빙선박에 작용하는 국부 빙하중을 산정하기 위해서는 해빙과 직접 접촉하는 선체 외부에 압력센서를 설치하여 계측하는 것이 효과적이다. 하지만 이런 종류의 센서는 얼음과 접촉 시 쉽게 손상을 입어서 지속적인 사용이 현실적으로 불가능하기 때문에 보통은 선체 내부에 변형률 게이지 등 외판의 변형량을 계측하여 이로부터 간접적으로 선체 외판에 작용하는 국부 빙하중을 추정하는 방법이 사용된다 (Ritch et al., 1999; Edgecombe et al., 1992). 국내에서도 쇄빙연구선 ARAON호에 변형률 게이지를 설치하여 빙충격에 따른 외판의 변형률을 계측하는 현장시험을 매년 수행해 온 바 있다.
직접 계측된 선체 외판의 변형률로부터 외판에 작용한 빙하중을 추정할 때 일반적으로 사용되는 방법은 빙하중이 직접 작용하는 선체구조 부위의 영향계수행렬(Influence Coefficient Matrix, ICM)을 구하는 것이다. 영향계수행렬은 특정한 영역에 단위하중을 작용했을 때, 변형률 게이지가 설치된 각각의 영역에 발생하는 변형률을 행렬의 형태로 만든 것으로서 해당 영역에 대한 유한요소 구조해석을 반복적으로 수행하여 구하게 된다.
Lee et al. (2013)은 2010년 ARAON호의 북극해 최초 실선시험에서 선수부 외판에 설치된 변형률 게이지로부터 직접 계측된 변형률을 이용하여 선체 외판에 발생한 응력으로 변환하고 여기에 영향계수행렬을 곱하여 외판에 작용한 빙압력을 계산하였다. 또한 Min et al. (2016)과 Jeon et al. (2018)은 선수미 방향의 1축 변형률 대신 3축 로제트 게이지에서 계측되는 변형률을 von Mises 등가응력 변환을 통해 영향계수행렬을 구성해 국부 빙하중을 추정한 바 있다.
이들 대부분의 선행연구에서 사용된 영향계수행렬은 ARAON호의 선체 외판에 수직한 방향으로 단위하중을 가하는 방법을 통해 도출되었다. 하지만 이런 방식으로 유도한 영향계수행렬의 경우 실제 빙하중이 선체 외판에 수직하게 작용한다면 정확한 해석이 가능하겠지만 실제 빙하중의 방향은 외판에 수직하지 않을 경우가 다반사이고 이 경우 정확한 빙하중 분석이 어려워지는 단점이 있다. 실제 빙하중의 방향과 크기를 보다 정확하게 추정하기 위해서는 영향계수행렬을 도출하는 기존의 방법을 보완할 필요가 있다.
본 연구는 쇄빙선박의 국부 빙하중을 효율적으로 추정하기 위해 보완된 영향계수행렬 산정법에 대한 것이다. 이를 위해 계측 영역에 가해지는 압력과 계측 지점에서의 von Mises 등가응력을 이용한 기존의 방법을 보완하여 실제 계측 영역에 가해지는 X, Y, Z의 3방향 하중을 동시에 추정하는 향상된 영향계수행렬 산정법을 제시하였다. 또한 구조물에 작용하는 하중의 경우 계측이 수행되는 영역에만 가해지는 것이 아니므로 구조해석 시 계산 영역의 확장을 통해 영향계수행렬을 새로 계산하여 하중 추정의 오차를 줄이는 방법도 확인하였다.
한편 이렇게 개발된 영향계수행렬 산정 방법을 이용하여 2019년 쇄빙연구선 아라온호의 남극 항해 시 계측된 변형률 데이터를 이용하여 계측 부위의 국부 빙하중을 계산하고 그 패턴을 분석하였다. 본 연구를 통해 선체의 외판에 작용하는 실제 하중의 방향을 고려할 수 있다는 점이 연구의 제일 큰 성과로 판단할 수 있으며, 특히 선체 길이 방향의 빙하중 Fx 의 경우는 선박의 빙저항(ice resistance)과의 연관시킬 수 있으며 추후 빙해수조 및 빙해역 현장에서 계측된 빙저항과의 비교 분석이 가능할 것이라 예상된다.
2. 영향계수행렬의 구성
영향계수는 구조물의 특정 지점에 단위하중이 작용했을 때, 하중이 가해진 지점에 생기는 변위 또는 응력을 비롯한 인근 영역에서 발생하는 변위 또는 응력을 말한다. 영향계수는 실제 구조물에 하중을 직접 가해 구하는 것이 가장 정확하지만, 하중을 실제로 가하기 어려운 경우 유한요소법을 이용한 구조해석을 통해 구할 수 있다. 관심 지점이 여러 곳인 경우 반복적인 구조해석을 통해 각각의 관심 지점에 대한 영향계수를 구하고 이를 영향계수행렬로 정리할 수 있다. 영향계수행렬을 이용하면 하중과 응력의 관계를 식 (1)과 같이 나타낼 수 있다.
| (1) |
여기서 {σ}는 대상 구조물에서 계측된 응력벡터, [C]는 영향계수행렬, {F}는 구조물에 가해진 하중벡터를 의미한다.
식 (1)은 역행렬을 사용하여 식 (2)와 같은 관계식을 도출할 수 있다.
| (2) |
식 (2)는 하중을 직접 계측하지 않더라도, 영향계수행렬과 계측된 변형률(여기서는 변환된 응력)만으로 구조물에 가해진 하중의 크기를 추정할 수 있음을 의미한다.
쇄빙선박의 경우 선체의 외부와 해빙과의 접촉부에 계측 센서를 설치하는 것이 매우 제한적이다. 하지만 ARAON호를 대상으로 영향계수행렬을 산정할 수 있다면 식 (2)를 통해 선체 외판에서 계측된 변형률만으로 ARAON호에 가해진 빙하중을 추정할 수 있다.
2.1 ARAON호 변형률 계측
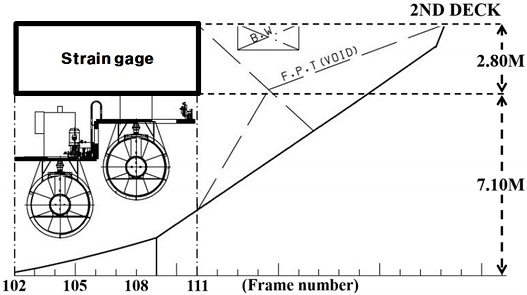
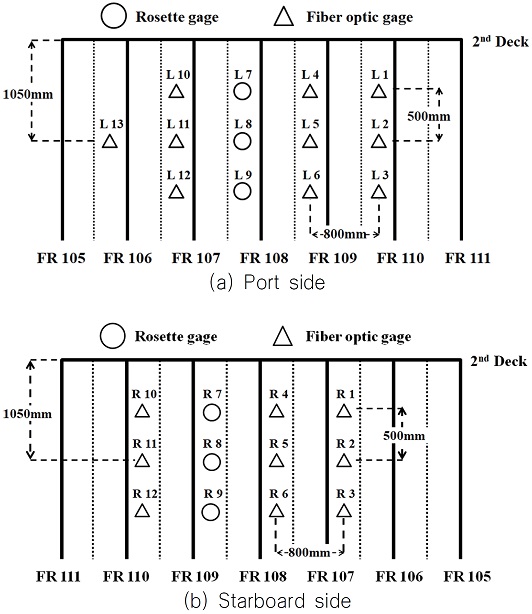
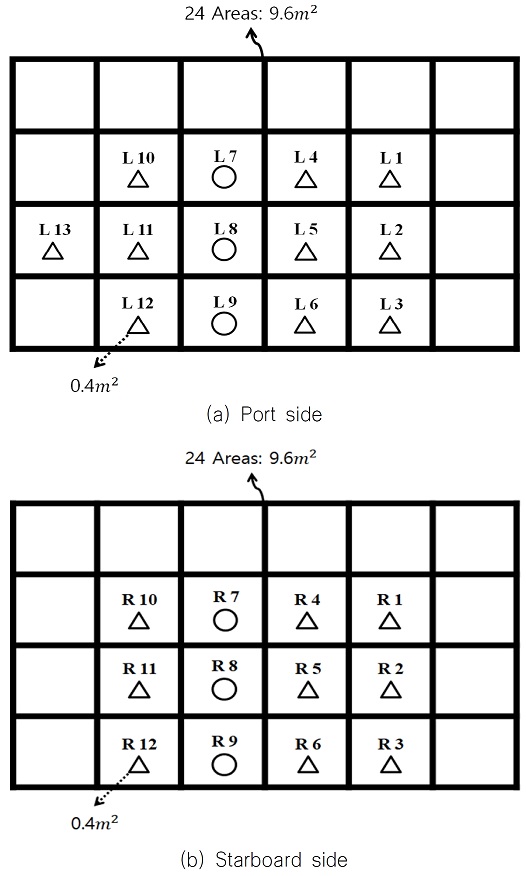
국내 최초의 쇄빙연구선 ARAON호는 2009년 건조된 이후 현재까지 매년 남극과 북극을 오가며 실선시험을 수행해 왔다. 특히 선수부에 가해지는 국부 빙하중을 간접적으로 추정하기 위해 Fig. 1과 같이 ARAON호 선수격벽 뒤 외판 안쪽 2nd deck 하부의 102번 프레임부터 110번 프레임 사이에 변형률 계측센서를 설치하여 해빙과 접촉할 때 발생하는 외판과 프레임의 변형률을 계측하였다. 센서의 부착 위치와 종류는 매년 조금씩 변경되어 왔기 때문에 본 논문에서는 가장 최근 수행된 2019년 11월 남극해 실선시험에서 설치된 변형률 계측센서 위치를 대상으로 영향계수행렬을 도출하였다. 2019년 남극해 실선시험에서는 Fig. 2와 같이 ARAON호의 내부 선체 외판 좌현에 광섬유 센서 10세트, 로제트 게이지 3개가 설치되었으며 우현에는 광섬유 센서 9세트, 로제트 게이지 3개가 설치되었다. 각 변형률 계측센서 사이 거리는 수평 방향으로 800 mm, 수직 방향으로 500 mm이며, 이를 기준으로 변형률 계측센서 하나가 대표하는 영역을 0.4 m2로 결정하였다. 또한 R1~R12, L1~L12 센서가 대표하는 영역의 전체 넓이인 4.8 m2를 국부 빙하중을 계산하는 영역으로 정의하였다. 이때 좌현의 경우 L13번 센서가 대표하는 영역은 좌현과 우현에서 정의되는 국부 빙하중 영역 크기를 동일하게 만들기 위해 제외하였다.
2.2 ARAON호의 유한요소 해석
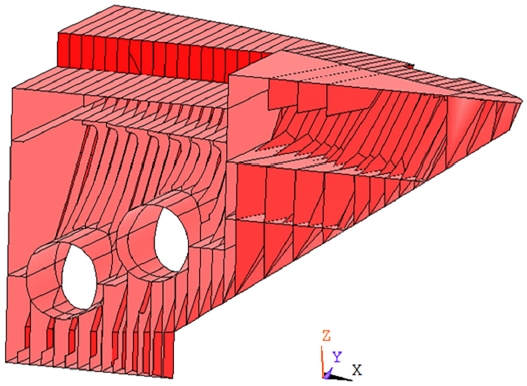
ARAON호의 영향계수행렬을 산정하기 위한 유한요소 해석을 위해 변형률 센서 설치부를 포함한 ARAON호의 선수부 좌현을 Fig. 3에 나타낸 것과 같이 모델링하였다. 이때, 선체 길이 방향을 X축, 선체 측면 방향을 Y축, 선체에 수직한 상하 방향을 Z축이라 정의하였다. 모델의 경계조건은 선체 중심선에서 대칭조건을 적용하였으며, 선미 방향으로 경계부인 횡격벽은 6자유도를 모두 구속하였다.
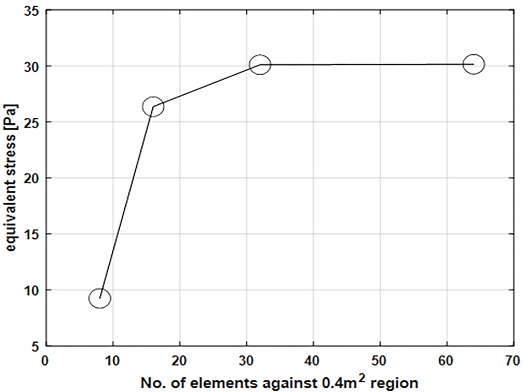
유한요소 해석결과에 대한 신뢰성을 확보하기 위해 L8번 센서가 대표하는 0.4 m2 영역을 8개, 16개, 32개, 64개의 요소로 나누었을 때, 단위압력에 의해 발생하는 등가응력의 크기를 비교하였다. Fig. 4에 의하면 계산되는 등가응력이 요소의 수가 32개 이상에서는 계산 결과가 수렴하는 것을 알 수 있는데 따라서 본 연구에서는 변형률 센서 하나가 대표하는 영역을 32개 요소로 작게 분할한 모델을 사용하여 유한요소 해석을 수행하였다.
유한요소 해석은 상용 프로그램인 ANSYS를 이용하였고 선체 외판에는 Shell 181 요소를 사용하였다. 선체 외판의 물성치로 ARAON호의 외판 소재인 EH36 강재의 항복강도 355MPa, 탄성계수 200GPa, 포아송비 0.3을 사용하였다.
2.3 ARAON호의 영향계수행렬 구성
ARAON호를 대상으로 하는 선행연구 (Lee et al., 2013; Min et al., 2016)에서 영향계수행렬 구성에 사용된 방법은 센서가 부착된 선체 계측영역에 대하여 수직한 방향으로 단위압력을 가하고 이로부터 유한요소 해석을 통해 계산되는 외판 응력 사이의 관계로부터 유도할 수 있다. 이때 외판 응력으로는 계측에 사용되는 센서의 종류에 따라 선체 길이 방향의 응력만을 계산하거나 von Mises 등가응력을 주로 계산한다. ARAON호의 경우 선체 길이 방향의 응력이 외판에 발생하는 주된 응력이긴 하지만, 2012년 남극 실선시험에서와 같이 빙하중의 크기가 북극해 실선시험에 비해 상대적으로 큰 경우는 선체 길이 방향뿐만 아니라 다른 방향의 응력도 무시할 수 없다는 것을 알게 되었고, 특히 von Mises 등가응력의 경우는 2차원 응력상태에서 항복조건을 판단하기 위해 사용하는 것으로 항상 양의 값으로 계산하기 때문에 주응력의 방향까지 고려한다면 선체 외판에 작용하는 빙하중과 외판의 거동을 선형적으로 연결시키는 지표로 사용하기에는 적합지 않다. 실제 선체에 작용하는 빙하중은 얼음과 선체의 입체적인 충돌 상황에 따라 선체의 전후 방향뿐 아니라 선체의 측면 방향, 상하 방향으로 동시에 작용하는 것으로 보아야 할 것이며 기존에 사용되어 온 영향계수행렬 구성법은 이러한 하중의 3차원 특성을 고려하여 수정되어야 한다.
이런 배경으로 본 연구에서는 실제 계측영역에 가해지는 X, Y, Z 세 방향의 하중 성분 (즉 Fx Fy Fz)을 모두 고려하여 영향계수행렬을 보완하고자 하였다. 변형률 계측센서 하나가 대표하는 영역 0.4 m2에 하중이 등분포로 작용한다고 가정하였으며, 각 방향의 단위하중에 대응하는 외판의 3가지 평면응력 성분 (σx σy τxy)을 계산하여 영향계수행렬을 구성하였다.
보완된 영향계수행렬은 식 (3)과 식 (4)로 나타낼 수 있다.
| (3) |
| (4) |
한편 ARAON호 경우처럼 유한요소 해석에 사용되는 영역과 계측이 수행되는 영역의 실제 면적에 차이가 큰 경우, 빙하중이 계측영역을 벗어난 부분에 작용하더라도 그 구조응답이 계측영역에서 측정이 되기 때문에 실제 그 부위에 하중이 작용하지 않아도 마치 하중이 작용한 것과 같은 결과를 초래할 수 있다.
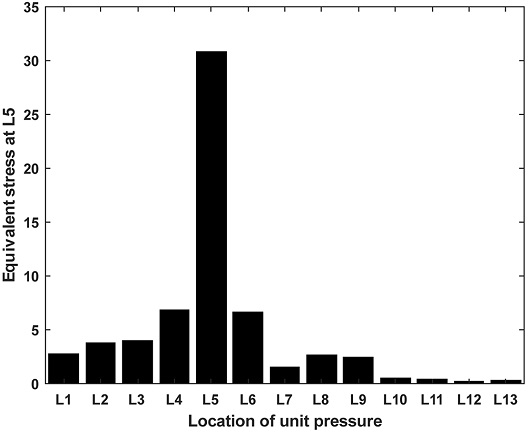
ARAON호의 외판에 설치된 변형률 계측센서에서 측정된 계측값은 센서가 부착된 영역에 가해진 하중에 의한 변형률뿐만 아니라 주변부에 가해진 하중에 의한 변형률의 중첩에 의한 것이다. 예를 들어 Fig. 5는 L1 ~ L13 센서 각각의 위치에 하중을 가했을 때, L5번 센서 위치에서 발생하는 응력을 계산한 것이다. Fig. 5에 의하면 L5번 위치를 제외한 다른 위치에 하중이 작용한 경우에도 L5번 센서 위치에서 응력이 발생하는 것을 알 수 있다.
이런 영향은 하중이 작용한 위치와 분포에 따라 차이는 있지만 영향계수행렬을 통해 하중을 정확하게 추정하기 위해서는 구조물에 가해지는 하중의 작용점을 파악해야 한다는 것을 의미한다. 하지만 ARAON호와 같이 하중의 작용점을 정확하게 파악하기 어려운 경우, 이러한 영향을 최소화하는 방법으로 영향계수행렬을 구성할 때 계측부를 포함하는 영역의 확장을 통해 어느 정도 보정할 수 있다. 본 연구에서는 계산 영역을 확장하여 영향계수행렬을 새로 구성하고 이를 통해 하중 추정의 오차를 줄이는 방법을 확인하고자 하였다.
Fig. 5를 살펴보면 L5 센서를 둘러싸고 있는 L1, L2, L3, L4, L6, L7, L8, L9 센서 위치에 가해진 하중이 L5번 센서의 위치에 응력을 발생시키는 것을 볼 수 있다. 이는 L5번 센서가 대표하는 0.4㎡ 면적에 대한 국부 빙하중을 추정하기 위해서는 최소한 L5번 센서를 둘러싸고 있는 8개 센서를 포함한 9개의 센서에 대한 영향계수행렬이 필요하다는 것을 의미한다. 이로 미루어 봤을 때, L1~L12번 센서의 계측영역으로 정의된 면적에 영향계수행렬을 구성하는 대신 L1~L12번 센서의 계측영역을 포함하는 주변부의 영역까지 확대한 9.6 m2에 대해서 영향계수행렬을 새롭게 구성할 필요가 있다. 센서 설치부의 아래 영역은 thruster hole 때문에 고려하지 않았다.
Fig. 6에 나타낸 모든 영역에 각각 X, Y, Z 방향의 단위하중을 가하는 과정을 반복적으로 수행하여, 좌현의 경우 L1~L13, 우현의 경우 R1~R12 센서가 위치한 곳에서 계산된 평면응력을 조합하여 영향계수행렬을 구성하였다. 도출된 영향계수행렬 [C]는 좌현의 경우 39x72, 우현의 경우 36x72의 크기를 가지며, 요소의 단위는 Pa/N이다. 이때, 영향계수행렬은 정방행렬이 아니므로 역행렬을 얻기 위해서 Moore-Penrose의 의사역행렬(pseudo inverse) 과정을 이용한다. 의사역행렬은 특이값 분해(singular value decomposition)를 사용하는 것으로서, 특이값 분해는 행렬을 대각화하여 특정한 구조로 분해하는 방식이며, 모든 행렬 형태에 대해 적용할 수 있다고 알려져 있다 (Klema and Laub, 1980).
3. 계산 결과 및 고찰
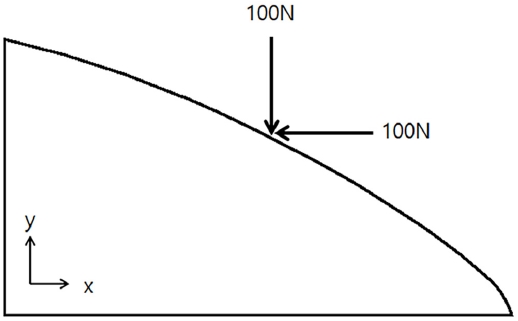
본 3장에서는 ARAON호의 유한요소 구조해석을 통해 보완된 영향계수행렬(enhanced ICM)의 유효함을 검증하고자 한다. 먼저 Fig. 7에 나타낸 것과 같이 L8번 센서가 위치한 영역 0.4 m2에 X, Y, Z 방향의 하중을 각각 –100N, -100N, -100N (합력은 173.21N) 을 가한 뒤 계산된 결과를 Table 1에 정리하였다. 각 방향의 좌표계는 X축은 선수 방향을 +로, Y축은 좌현 방향을 +로, Z축은 선체 상향을 +로 정의하였다.
Table 1은 von Mises 등가응력으로 구성한 기존의 영향계수행렬을 이용한 계산 결과와 새로 보완된 영향계수행렬의 계산 결과를 나타낸 것이다. 표를 보면 기존의 영향계수행렬을 이용했을 때와 보완된 영향계수행렬을 이용한 결과 모두 하중이 가해진 L8 위치에서 계산된 하중이 가장 크게 나타남을 알 수 있다. 하지만 기존의 영향계수행렬을 이용한 계산 결과는 실제 가해진 하중에 비해 상당히 작은 값인데 비해 보완된 영향계수행렬을 이용한 계산에서는, L8에서의 X, Y, Z 방향 하중이 실제 가해진 하중에 비해 다소 높게 계산되었다. 하지만 각 방향의 하중 및 합력의 크기는 처음 가해진 하중을 비교적 가깝게 역추정하는 것을 알 수 있다. 계산의 오차는 전체 구조 중 일부 영역에 대해서만 영향계수행렬을 구성하고 여기에 유사역행렬 처리기법을 적용한 결과로 발생하는 것으로 판단되며, 현실에서는 불가능하지만 모든 영역에서 변형률을 계측할 수 있다면, 정방행렬의 형태로 영향계수행렬을 구성할 수 있을 것이며, 이를 통해 정확한 하중을 추정할 수 있을 것이다.
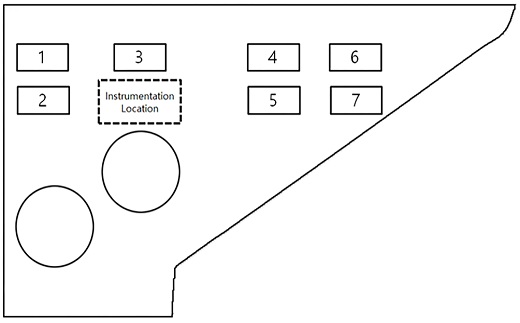
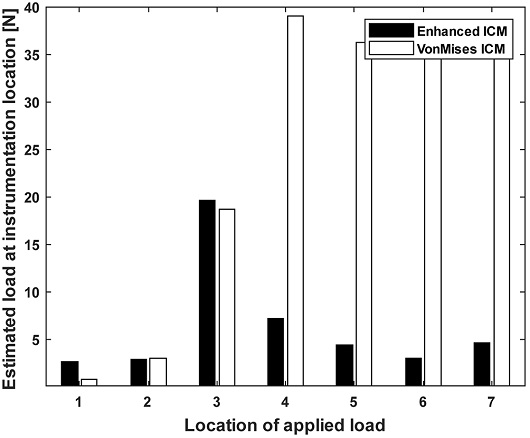
한편 계측영역이 아닌 곳에 하중이 가해졌을 때 추정된 계산 사례를 보면, 예를 들어 Fig. 8과 같이 ARAON호의 선수부 1~7번 지점에 173.21N (X 방향 –100N, Y 방향 –100N, Z 방향 –100N)의 힘이 가해졌을 때, Fig. 6에서 정의한 계측영역(3번 지점 아래)에서 발생하는 응력을 계산하였다. 계산된 응력은 기존의 von Mises 등가응력과 보완된 영향계수행렬을 통해 하중으로 다시 계산되었으며, 그 결과를 Fig. 9에 나타내었다.
그림을 보면 실제 계측영역에는 하중이 가해지지 않았음에도 모든 경우 하중을 추정한 것을 알 수 있다. 이러한 결과는 계측영역에서 멀리 떨어진 곳에 하중이 가해졌음에도 계측영역에서는 실제로 변형이 발생하고 응력도 계산되기 때문인데 그 영향은 하중이 가해진 지점이 계측지점에서 멀어질수록 작다고 볼 수 있다. 영향계수행렬을 구성할 때 계측부를 포함하는 영역의 확장이 필요한 이유이다.
4. ARAON호 실측 빙하중 데이터 분석
ARAON호의 2019년 남극항해 중 기록된 변형률 데이터와 보완된 영향계수행렬을 이용하여 ARAON호에 가해진 국부 빙하중의 크기와 패턴을 분석하였다. 2019년 남극항해에서 ARAON호는 Fig. 10과 같이 평탄빙을 비롯한 다양한 형태의 얼음 속을 운항하며 데이터를 기록하였다. 또한 선상에 설치된 통합계측시스템을 활용해 선속, 흘수, 파괴된 해빙의 단면을 촬영한 영상정보 등 다양한 데이터도 수집하였다.
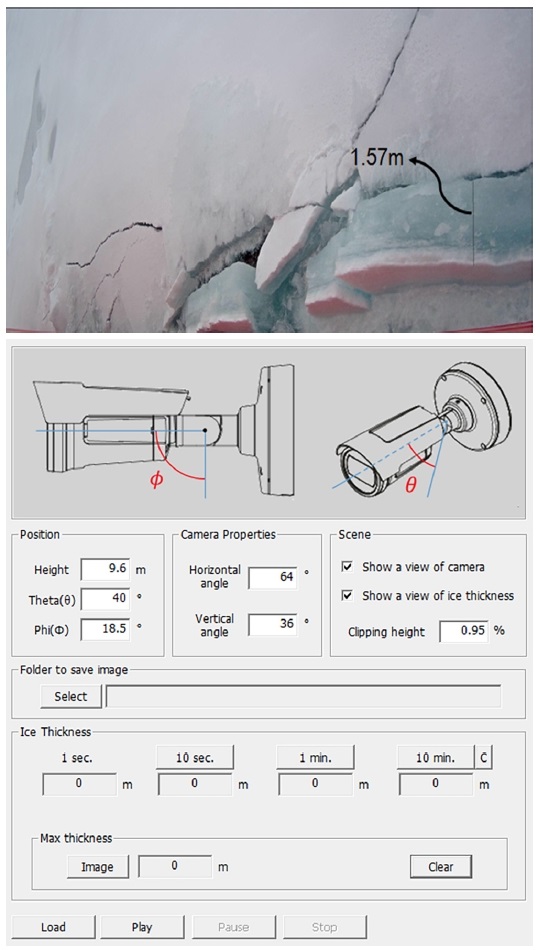
본 연구에서는 Fig. 11와 같이 pack ice 조건에서 약 80분 동안 계측된 데이터 세트를 선택하여 분석하였다. 이때 변형률 데이터는 편의상 우현에서 계측된 데이터만 분석에 사용하였다. 선속 데이터는 선체 중앙부에 설치된 GPS를 통해 수집하였다. 해빙의 두께는 선체 중앙부에서 촬영된 해빙의 단면 영상과 Fig. 12의 이미지 처리 소프트웨어를 통해 추정하였다 (Park et al., 2014). Fig. 12에서 볼 수 있듯이 이미지 처리 소프트웨어를 사용한 해빙의 두께 추정은 해빙의 단면이 드러났을 때만 가능하므로 모든 해빙의 두께를 추정하기는 어렵지만 별도의 장비를 설치하지 않고, 대략적인 해빙 두께 분포를 추정할 수 있다는 장점이 있다.
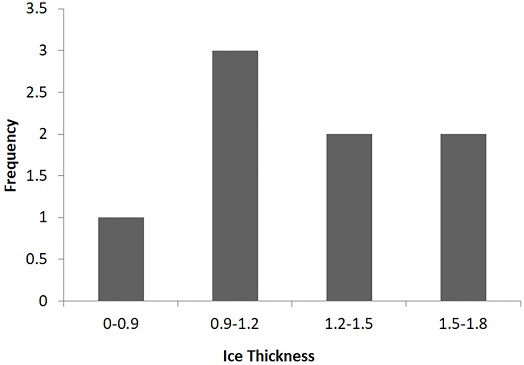
Fig. 13은 80분 간 촬영된 영상 데이터 중 단면이 드러난 데이터만을 사용하여 추정된 해빙의 두께 분포를 히스토그램으로 나타낸 것이다. 추정된 해빙의 평균 두께는 약 1.3m 이다.
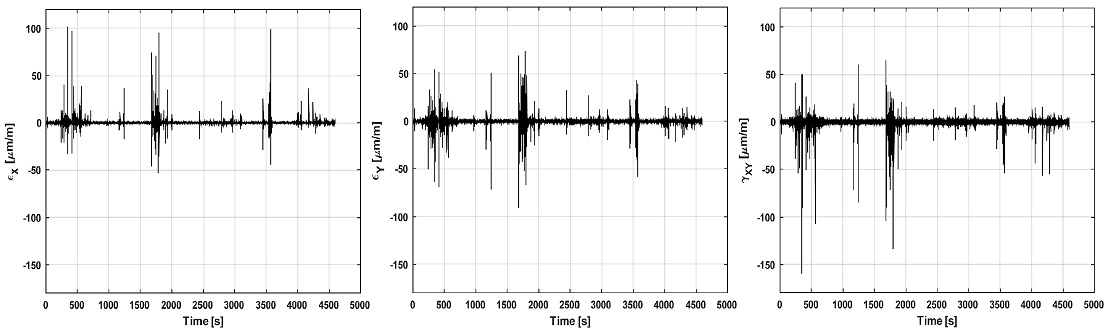
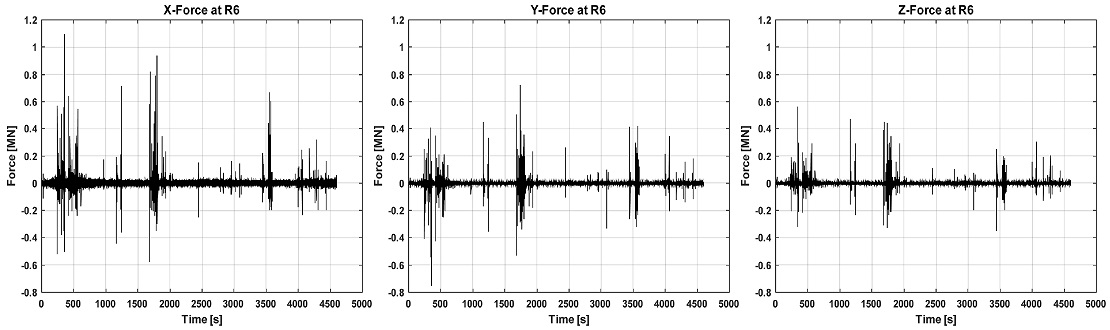
선체 외판은 2차원 평판으로 가정하였으며, ARAON호 선수부의 우현 R6 센서에서 계측된 수직변형률 εX, εY와 전단변형률 γXY을 Fig. 14에 나타내었다.
계측된 평면변형률(εX, εY, γXY)은 2차원 응력-변형률 관련 식 (5), (6), (7)을 통해 두 방향의 평면 수직응력과 전단응력으로 계산되었다. 여기서 ν는 포아송 비, E는 탄성계수, G는 전단탄성계수를 각각 의미한다.
| (5) |
| (6) |
| (7) |
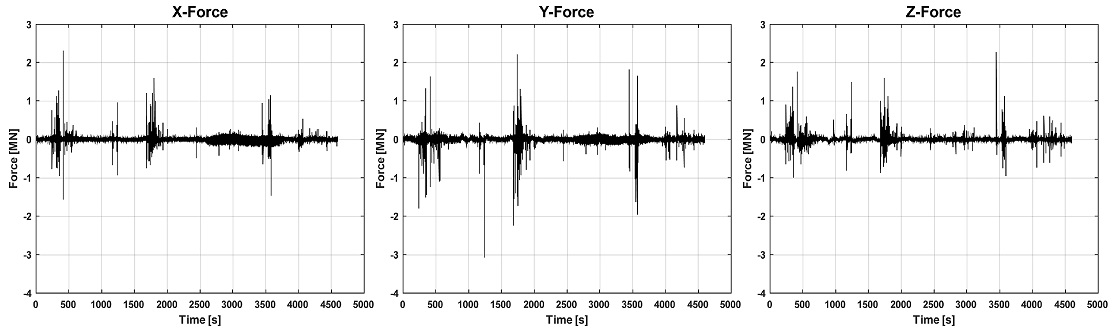
계산된 응력과 보완된 영향계수행렬(enhanced ICM)을 사용하여 R6 센서가 부착된 지점에서 계산된 각 방향의 하중을 Fig. 15에 나타내었으며, 모든 지점에서의 하중을 합친 결과를 Fig. 16에 나타내었다. 선체 외판에 가해지는 하중 성분 중 우현에서 좌현으로 가해지는 하중 (Y 방향으로 대략 외판에 수직한 하중)이 가장 크게 작용한 것을 볼 수 있으며, X 방향, Z 방향의 하중 성분도 일정량 발생하는 것을 알 수 있다.
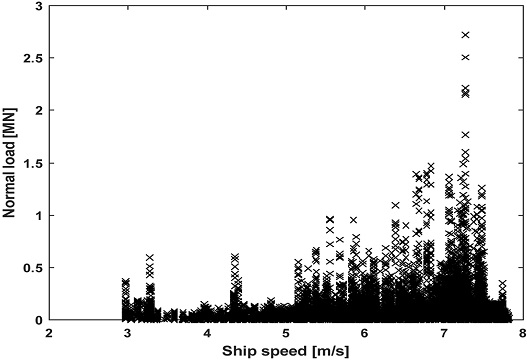
각 방향의 하중 성분을 구할 수 있으므로 선체 외판에 수직한 방향의 힘도 계산할 수 있다. Fig. 17은 선체 외판에 수직한 방향으로 작용하는 하중을 선속과 함께 나타낸 것이다.
Fig. 17을 보면 pack ice 조건에서 선속이 커지는 경우 선체 외판에 수직한 하중 또한 큰 것을 알 수 있으며, 7.27 m/s 의 선속에서 최대 빙하중 2.72 MN이 작용했음을 보여준다.
5. 결 론
본 연구는 쇄빙선박의 국부 빙하중을 효율적으로 추정하기 위해 보완된 영향계수행렬 산정법에 대한 것이다. 계측 영역에 가해지는 압력과 계측 지점에서의 von Mises 등가응력을 이용한 기존의 방법을 보완하여 실제 계측 영역에 가해지는 X, Y, Z의 3방향 하중을 동시에 추정하는 향상된 영향계수행렬 산정법을 제시하였다, 또한 구조물에 작용하는 하중의 경우 계측이 수행되는 영역에만 가해지는 것이 아니므로 구조해석 시 계산 영역의 확장을 통해 영향계수행렬을 새로 계산하여 하중 추정의 오차를 줄이는 방법도 확인하였다.
계측영역 외부에 하중이 가해졌을 경우, 실제 계측영역에 하중이 가해지지 않았음에도 기존의 영향계수행렬과 보완된 영향계수 행렬 모두 일정량의 하중이 발생했다고 추정하였는데, 3차원 하중에 대해서는 기존의 영향계수행렬을 사용한 결과보다는 보완된 영향계수행렬을 사용한 것이 좀 더 하중을 실제 상황에 가깝게 추정하는 것을 알 수 있다.
한편 이렇게 개발된 영향계수행렬 산정 방법을 이용하여 2019년 쇄빙연구선 ARAON호의 남극 항해 시 계측된 변형률 데이터를 이용하여 계측 부위의 국부 빙하중을 계산하고 그 패턴을 분석하였다. 보완된 영향계수행렬을 이용하여 2019년 pack ice 조건의 남극해에서 계측된 ARAON호의 실선데이터를 분석하였다. 분석결과 우현을 기준으로 우현에서 좌현 방향 (Y 방향) 하중이 가장 크게 발생하며, 선체 길이 방향 (X 방향)과 상하 방향 (Z 방향)으로도 일정량의 하중이 발생하는 것을 알 수 있었다. 각 하중 성분과 외판에 수직한 방향의 법선 벡터간의 내적을 통해 선체 외판에 수직한 방향으로 작용하는 빙하중 성분을 계산할 수 있었으며 선속이 커질수록 선체 외판에 작용하는 수직 빙하중 역시 크게 작용한 것을 알 수 있었다.
본 연구를 통해 선체의 외판에 작용하는 실제 하중의 방향을 고려할 수 있다는 점이 연구의 제일 큰 성과로 판단할 수 있으며, 특히 선체 길이 방향의 빙하중 Fx 의 경우는 선박의 빙저항(ice resistance)과의 연관시킬 수 있으며 추후 빙해수조 및 빙해역 현장에서 계측된 빙저항과의 비교 분석이 가능할 것이라 예상된다.
Acknowledgments
본 연구는 2021년 선박해양플랜트연구소의 주요사업인 “극한환경 중 선박성능, 추진기성능, 빙성능 평가기술 및 기계학습기반 성능예측기술 개발 (PES3911)” 과제의 위탁과제 연구비 지원 (project No.10063417)으로 수행된 결과의 일부이며, 2019년 ARAON호의 남극해 실선시험을 위한 극지연구소(KOPRI)의 협력에도 감사드립니다.
References
- Edgecombe, M., St. John, J., Liljestrom, G. & Ritch, R., 1992. Full scale measurements on hull-ice impact loads and propulsion machinery response onboard icebreaker Oden during the 1991 International Arctic Ocean Experiment, Transport Canada Report TP 11252E.
-
Jeon, M., Choi, K., Min, J.K. & Ha, J.S., 2018. Estimation of local ice load by analyzing shear strain data from the IBRV ARAON’s 2016 Arctic voyage. International Journal of Naval Architecture and Ocean Engineering, 10(3), pp.421-425.
[https://doi.org/10.1016/j.ijnaoe.2018.02.009]

-
Klema, V. & Laub, A., 1980. The singular value decomposition: Its computation and some applications. IEEE Transactions on automatic control, 25(2), pp.164-176.
[https://doi.org/10.1109/TAC.1980.1102314]

-
Lee, T.K., Kim, T.W., Rim, C.W. & Kim, S., 2013. A study on calculation of local ice pressures for ARAON based on data measured at arctic sea. Journal of Ocean Engineering and Technology, 27(5), pp.88-92.
[https://doi.org/10.5574/KSOE.2013.27.5.088]

-
Min, J.K., Choi, K., Cheon, E.J. & Kim, J.M., 2016. Ice load estimation procedures for IBRV ARAON by analyzing shear strain data measured in arctic sea. Journal of Ocean Engineering and Technology, 30(6), pp.468-473.
[https://doi.org/10.5574/KSOE.2016.30.6.468]

- Park, I., Nam, J.H., Byun, S. & Park, J., 2014. Conversion of pixel-based ice thickness to physical unit for image of broken ice patch. Proceedings of the Society of CAD/CAM Conference, pp.523-528.
- Ritch, R., St. John, J., Browne, R. & Sheinberg, R., 1999. Ice load impact measurements on the CCGS Louis S. St. Laurent during the 1994 arctic ocean crossing, 18th International Conference on Offshore Mechanics and Arctic Engineering, St. John’s Newfoundland, 11-16 July 1999.