Ship Type 해양 구조물 전선 해석 시 Topside와 Interface가 Hull에 미치는 영향 연구
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In the existing whole ship analysis, topside was modeled as mass element. However recently, the topside is modeled as beam element due to the owner’s requirement to improve the maturity of the whole ship FE model. To follow the owner’s requirement, detailed information for topside drawing and modeling, which may delay analysis schedule, is needed. However, it is hard to respond effectively to this matter due to the lack of study on the topside from the hull perspective. Therefore in this study, the effect of the topside on the hull is investigated when the topside is modeled as a mass element or beam element respectively. In addition, the interface modeling method is analyzed to verify modeling method used in the existing whole ship analysis. The results indicate that the interface and topside modeling method used in existing whole ship analysis are appropriate. This conclusion will be the technical basis for responding to owner’s requirement about the topside modeling method.
Keywords:
Whole ship analysis, Topside, Interface, Hull, Topside Module Support(TMS)키워드:
전선해석, 탑사이드, 인터페이스, 선체, 탑사이드 모듈 서포트1. 서 론
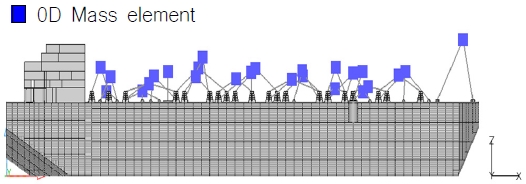
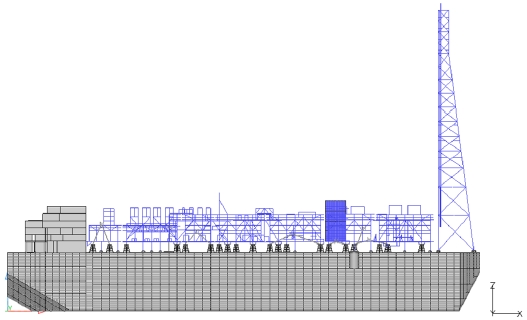
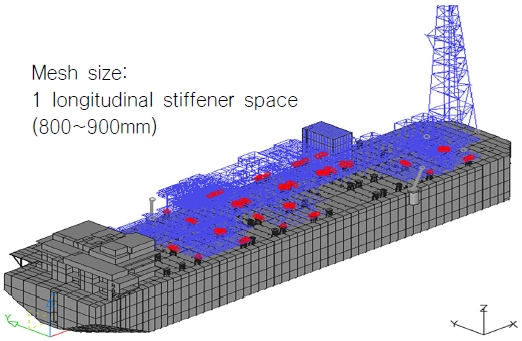
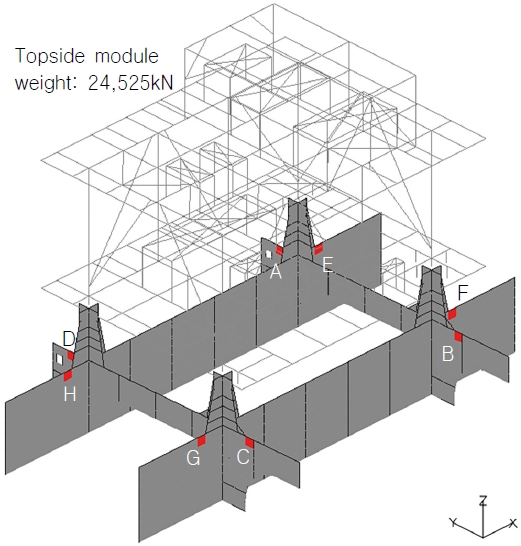
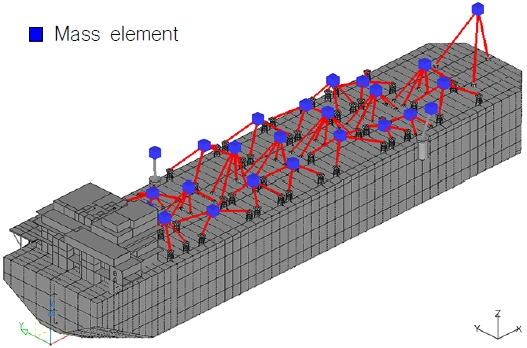
전선 해석은 구조 설계 업무 중 하나로써 발주처 요구에 의해 수행되며 Fig. 1과 같은 전선 구조 모델이 사용된다. 전선 구조 모델은 Topside와 Hull로 나눌 수 있는데 Hull은 주로 2D shell 요소와 1D beam 요소를 이용해 Modeling 된다. 이와 달리 Topside는 일반적으로 Fig. 2와 같이 0D mass 요소로 Modeling 되어왔는데 이 방법은 Topside 전체 구조를 Modeling 하지 않고 Topside와 동일한 Weight를 갖는 Mass 요소를 Topside의 무게 중심(Center Of Gravity, GOG)에 구현하는 것이다. 그러나 최근에는 Topside를 Beam 요소로 구현하는 추세인데 이 방법은 Fig. 3과 같이 전선 구조 모델의 완성도를 높이고자 Beam 요소로 Topside 구조 전체를 도면과 동일하게 구현하는 것이다.
실제로 발주처가 관성력 분배나 Deflection의 영향을 확인하기 위하여 Beam 요소를 이용한 Topside 구현을 요구한 사례가 있었다. 하지만 Topside를 Beam 요소로 구현하기 위해서는 Topside 도면과 모델 등 추가 정보가 필요하다는 단점이 있다. 이로 인해 전선 구조 모델의 용량이 증가하고 전선 해석 일정에 상당한 영향을 미치는 것에도 불구하고 Hull 관점에서의 Topside 구현 방법에 대한 연구가 거의 없기 때문에 발주처 요구에 효과적으로 대응할 수 없었다.
Topside를 주제로 한 앞선 연구를 살펴보면 Topside 설계를 위해 지지 조건을 변수로 Topside의 Stress를 비교한 연구(Jang & Ko, 2018)와 Topside leg 개수, Support의 높이에 따라 Topside의 Stress를 비교한 연구 (Joo, 2013) 등 Topside 관점에서의 연구는 수행된 적이 있지만 Hull 관점에서의 연구는 부족한 실정이다.
이에 본 연구에서는 Topside가 Beam 요소 또는 Mass 요소로 구현될 때 각각 Hull에 미치는 영향과 Topside와 Hull을 연결해 주는 인터페이스(interface) 구현 방법을 분석하였다. Hull은 유한 요소 해석(Finite Element Analysis, FEA) 모델을 만들 때 사용하는 일반적인 방법으로 모델링 하였으며, 해양 구조물에만 존재하는 TMS(Topside Module Support)는 관련된 논문 (Hong, 2018)을 참고하여 모델링 하였다. 이를 통해 Mass 요소를 사용한 기존의 전선 해석 방법을 검증하고 추후 Topside 구현에 대한 발주처 요구에 효과적으로 대응할 수 있는 기술적 자료를 확보하고자 하였다.
2. 인터페이스 구현 방법
2.1 인터페이스 이상화
인터페이스는 Topside와 Hull에 해당하는 TMS를 연결해 주는 부분으로 Topside 구현 방법에 따라 인터페이스 구현 방법도 직접적인 영향을 받게 된다. 따라서 인터페이스 구현 방법에 대한 연구를 먼저 수행한 후 이를 바탕으로 Topside 구현 방법에 의한 영향을 분석하였다.
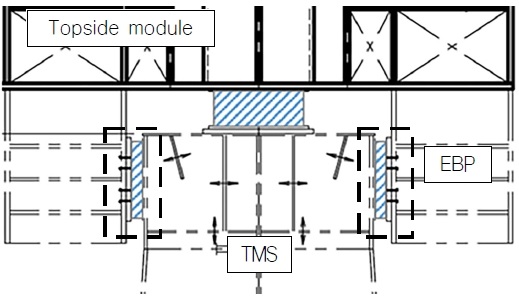
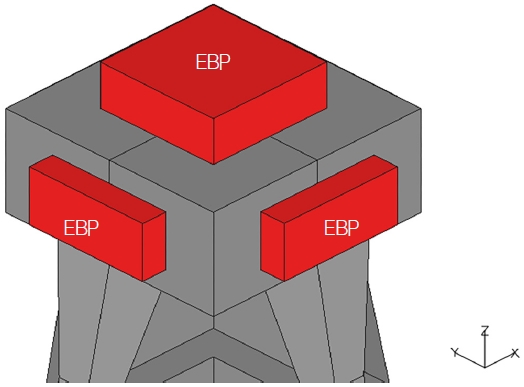
연구 대상은 Fig. 4와 같은 EBP(Elastomeric Bearing Pad)가 적용된 Sliding type의 인터페이스로 Topside module과 TMS를 연결하는데 주로 사용되는 Type이다.
올바른 해석 결과를 얻기 위해서는 인터페이스가 가지고 있는 다양한 특징을 적절하게 이상화하여 구현하는 것이 중요한데 이를 위해 Table 1에 Sliding type 인터페이스의 특징과 전선 구조 모델에 반영하기 위한 이상화 방법을 정리하였다.
EBP stiffness는 EBP가 Steel이 아닌 강성(stiffness)을 지닌 Rubber로써 Topside module과 TMS 사이에 위치해 완충 작용을 한다는 것이다. 또한 Fig. 4와 같이 Pad 형태로 Face contact를 하지만 전선 해석에서는 점 접촉으로 이상화한다. 따라서 EBP는 강성을 지닌 1D 요소로 이상화될 수 있다.
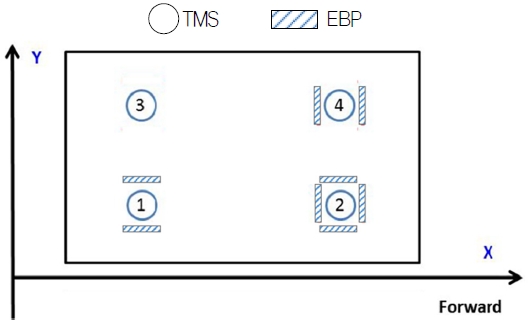
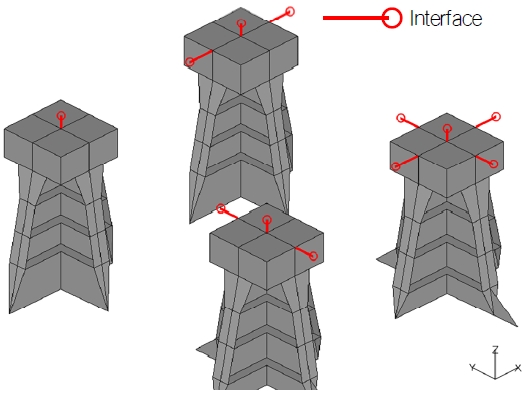
TMS별 EBP 설치 위치(EBP position by TMS)는 일반적으로 4개의 TMS가 1개의 Toside module을 지지하는데 Fig. 5와 같이 TMS 마다 EBP의 설치 위치가 다른 것이다. 이는 Topside module과 Hull 간의 Global 거동 간섭을 최소화하기 위한 것으로 이를 통해 Topside module의 기울어짐(tilting)이 Hull에 영향을 주지 않고, Hull의 거동(hogging 또는 sagging 등에 의한 deflection)이 Topside module에 영향을 주지 않는다.
마찰력(friction)은 EBP와 Topside module의 연결이 Sliding type이기 때문에 생기는 특징이다. Topside module과 TMS의 상대 운동에 의해 마찰력이 발생하게 되는데 Hull의 관점에서 볼 때 마찰력은 Topside module weight에 비해 굉장히 작으므로 무시한다.
2.2 연구 방법
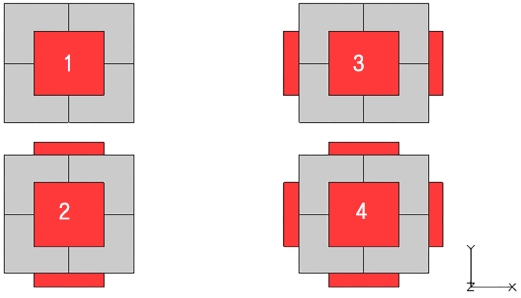
Table 1을 정리하면 인터페이스는 강성을 가지는 1D 요소로 EBP의 실제 위치에 맞게 Modeling 함으로써 구현할 수 있다. 이에 적합한 요소는 Spring이지만 기존의 전선 해석에서 사용한 RBE2 요소와 몇 가지 비교군을 추가하여 Table 2와 같이 4개의 Case를 선정하였다.
Case 1의 RBE2는 Stress 등의 결과를 구할 필요 없이 힘의 전달만을 목적으로 할 때 사용하는 요소로써 Hull의 입장에서는 인터페이스가 평가 대상이 아니므로 이 경우에 해당한다. RBE2가 강성을 가지지 않지만 이러한 이유로 기존의 전선 해석에서 인터페이스 구현에 사용되었으며 본 연구에서는 기존의 인터페이스 구현 방법을 검증하기 위한 Case로 선정하였다.
RBE2 사용 시 Table 3와 같이 EBP 위치에 따른 구속 조건을 반영하여 자유도(Degree Of Freedom, DOF)를 고려해야 한다.
Fig. 6은 EBP와 TMS를 나타낸 그림으로 Face contact의 특성을 고려했을 때 X축에 위치한 EBP는 6자유 운동 중 X축 병진 운동 / Y축 회전 운동 / Z축 회전 운동을 구속한다.
Case 2의 RBE3를 사용하면 TMS와 연결된 절점에서의 해석 결과를 구할 수 있다는 장점이 있지만 그만큼 해석 시간이 길어진다는 단점이 있다. 전선 해석에서는 TMS가 평가 대상이 아니므로 RBE3를 사용하지 않지만 RBE2와의 비교를 위해 선정된 Case이다. Case 3의 Spring은 강성을 갖는 1D 요소를 사용한 Case로서 X축과 Y축의 Spring에는 1,000 kN/mm를, Z축의 Spring에는 3,000 kN/mm를 적용하였다. Case 4의 Rod는 Spring과의 비교를 위해 선정된 Case로 Spring과 동일한 Deformation을 유발하는 Area의 Rod를 사용하였다.
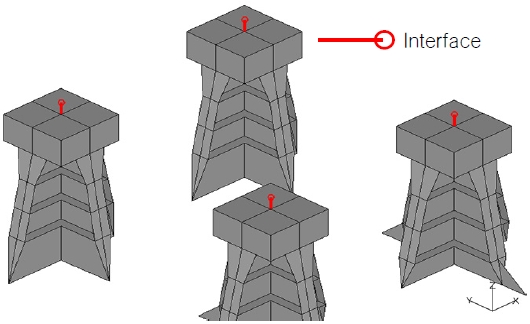
각 Case 별로 RBE2, RBE3, Spring, Rod는 Fig. 7과 같이 Modeling 되어 Topside module과 TMS를 연결한다.
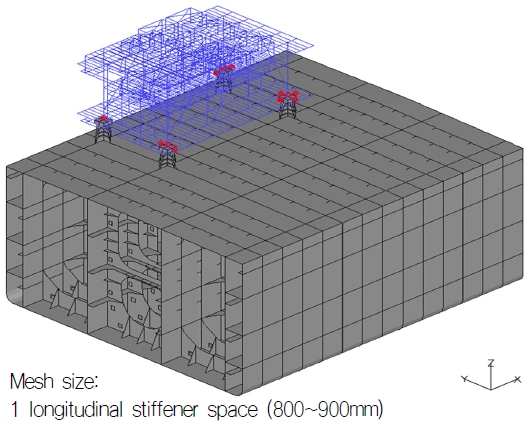
Table 2에 따라 4가지 Case로 이상화된 인터페이스를 Fig. 8의 1 Cargo hold를 포함하는 모델에 구현하였다.
유한 요소 해석을 수행하기 위해 Table 4와 같이 4가지 Case에 동일한 하중과 경계 조건을 적용하였는데 인터페이스 구현 조건만 다르고 나머지 조건은 동일하게 함으로써 인터페이스 차이에 의한 영향을 분석하였다.
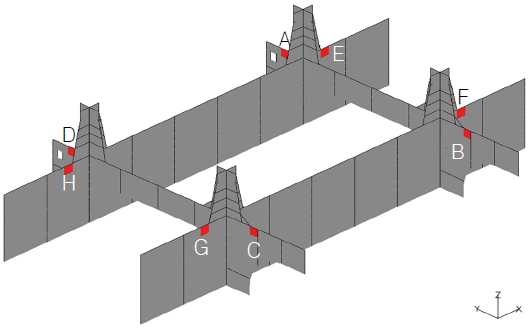
FEA 결과는 Fig. 9에 나타낸 구역을 대상으로 분석하였는데 가장 보수적인 해석 결과를 얻을 수 있도록 Global loads의 영향이 가장 큰 1 Cargo hold의 중앙부이며 Local loads의 영향이 가장 큰 Topside module 하부의 8곳(A~H)를 선정하였다.
2.3 연구 결과
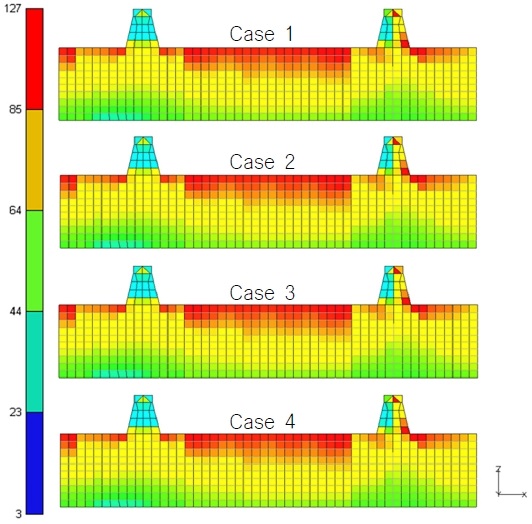
4가지 Case에 대한 FEA 결과로 von-Mises stress 분포를 Fig. 10에 나타내었다.
그리고 Fig. 9에 표시한 8개 지점에서의 von-Mises stress 값을 비교하여 Table 5에 정리하였다.
Fig. 10과 Table 5에 따르면 모든 Case에서 Stress 분포와 크기의 차이가 없다는 것을 확인할 수 있는데 이를 통해 인터페이스 구현에 중요한 것은 1D 요소의 종류가 아니라 힘을 잘 전달하기 위한 연결이라는 것을 알 수 있다.
Stress 비교와 더불어 EBP가 TMS마다 다르게 설치된다는 특징을 이용해 Deformation 결과를 통해서도 인터페이스 구현 방법을 검증하였다.
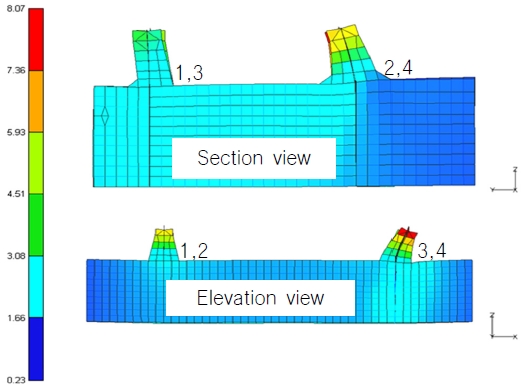
Fig. 11의 1번, 2번 TMS는 X축 EBP가 없으므로 X축 하중이 작용하지 않고 1번, 3번 TMS는 Y축 EBP가 없으므로 Y축 하중이 작용하지 않는다.
Fig. 12는 Case 1의 결과로 Table 4의 Local loads에 의한 TMS의 Deformation을 나타낸 것이다. Fig. 11에서 예상한 대로 1번, 2번 TMS에는 X축의 변형이 발생하지 않고 1번, 3번 TMS에는 Y축의 변형은 발생하지 않는 것을 확인할 수 있다.
Table 5와 Fig. 12를 종합해 보면 RBE2로 인터페이스 이상화 시 Topside module과 TMS 사이의 힘을 잘 전달하고 EBP의 실제 위치에 맞게 TMS의 Deformation을 유발하므로 인터페이스 이상화에 적합한 방법이라는 것을 알 수 있다.
뿐만 아니라 Spring 요소를 사용하기 위해서는 강성 크기 정보가 필요하고 Rod 요소를 사용하기 위해서는 Area 정보가 필요하지만 RBE2는 이러한 정보 없이도 사용 가능하며 RBE3에 비해 해석 속도가 빠르다는 장점이 있다.
또한 RBE2를 사용하면 인터페이스 구현을 효율화할 수 있다는 장점도 있는데 Fig. 13에 효율화된 인터페이스를 나타내었다. Fig. 7처럼 인터페이스를 구현하는 경우 12개의 RBE2에 각기 다른 자유도를 고려해야 한다. 또한 TMS마다 설치 위치가 다르기 때문에 Modeling 과정에서 Human error가 발생할 수 있다. 반면에 Fig. 13과 같이 Z축에만 RBE2를 구현하는 인터페이스 효율화를 통해 Human error를 줄이고 Modeling 시간도 줄일 수 있다. 기존 대비 RBE2의 개수가 줄었지만 그에 맞게 자유도를 조정해 줌으로써 동일한 해석 결과를 기대할 수 있고 3.1절에서 이를 검증하였다.
3. Topside 구현 방법
효율화된 RBE2로 이상화한 인터페이스 구현 방법을 확인한 후 Topside 구현 방법의 차이가 Hull에 어떤 영향을 미치는지 분석하고자 Topside가 Beam 또는 Mass로 구현된 2개의 전선 구조 모델을 이용해 전선 해석을 수행하였다.
3.1 인터페이스 검증
2절에서 FEA로 검증된 인터페이스 구현 방법이 전선 해석에서도 유효한지 검증하고자 Table 6과 같이 5개의 Case를 선정하여 전선 해석을 수행하였다.
Case 1부터 4까지는 Fig. 7과 같이 실제 위치와 동일하게 인터페이스를 구현하고 Case 5는 Fig. 13과 같이 효율화된 인터페이스가 구현되어 Fig. 14와 같은 길이 약 300m의 VLCC급 FPSO 전선 구조 모델에 구현되었다.
전선 해석에서는 Bending moment와 Topside loads만 적용한 것이 아니라 Table 7과 같이 Full load condition의 전선 해석 하중과 경계 조건을 적용하였으며 인터페이스 구현 조건만 다르고 나머지 조건은 동일하게 하여 인터페이스 차이에 의한 영향을 분석하였다.
전선 해석 결과는 Fig. 15에 나타낸 구역을 대상으로 분석하였는데 Global loads의 영향이 가장 큰 전선 구조 모델의 중앙부에서 Local loads의 영향을 가장 크게 받는 Topside module 하부의 8곳(A~H)를 선정하였다.
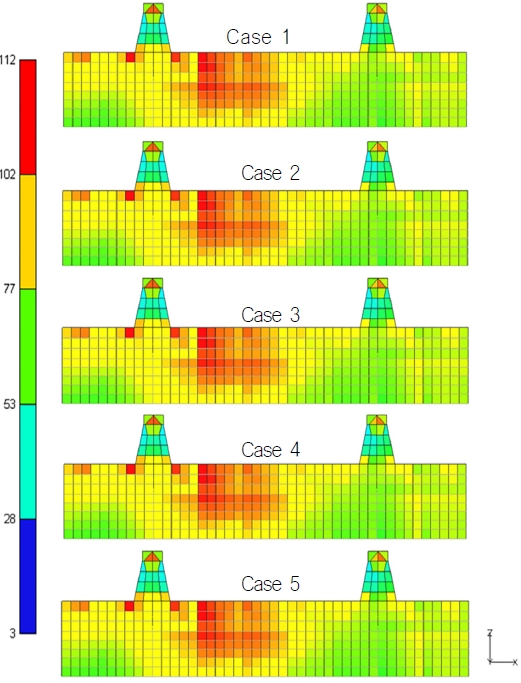
5가지 Case에 대해 전선 해석을 실시한 후 Fig. 15에 표시한 구역의 von-Mises stress 분포를 Fig. 16에 나타내었고 Stress 비교 결과는 Table 8에 정리하였다.
Fig. 16과 Table 8에 따르면 모든 Case에서 Stress 분포와 크기의 차이가 없으며 이를 통해 전선 구조 모델을 이용한 전선 해석에서도 효율화된 RBE2로 인터페이스를 구현하는 방법이 적합하다는 것을 알 수 있다.
3.2 Topside 차이에 의한 영향 분석
3.1에서 검증된 효율화된 RBE2를 이용한 인터페이스 구현 방법을 이용하여 Topside 구현 방법의 차이가 Hull에 미치는 영향을 분석하였다. 이를 위해 Table 9와 같이 Topside 구현 방법을 다르게 한 2개의 Case를 선정하여 Full load condition의 전선 해석 하중과 경계 조건을 동일하게 적용하였다. Topside 구현 조건만 다르고 나머지 조건은 동일하게 하여 Topside 구현 차이에 의한 영향을 분석하였다.
Case 1은 Fig. 14와 동일한 모델을 사용하였고 Case 2는 Fig. 17과 같이 Topside를 Mass로 변경하였다.
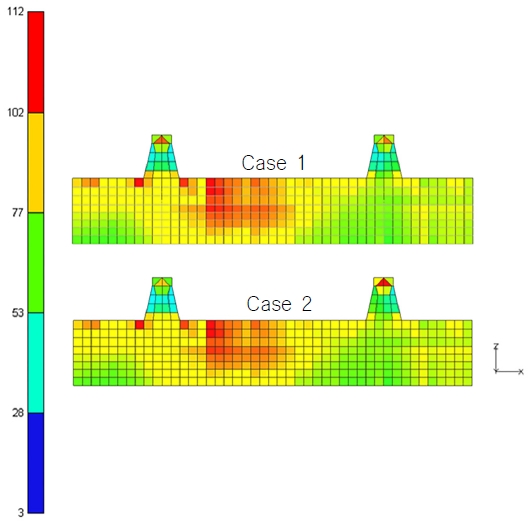
2가지 Case에 대한 해석 결과는 Fig. 15와 같은 구역에서 분석하였고 von-Mises stress 분포는 Fig. 18에 나타내었다. von-Mises stress를 Table 10에 정리하면서, 2가지 Case간 von-Mises stress 차이를 구조 설계에 사용되는 Criteria로 나눈 비율도 함께 정리하였다. 이때 사용된 Criteria는 Lloyd 선급에서 제시하는 값이며 이를 통해 해석의 유효성을 검증하고 설계 관점에서의 유의미한 판단이 가능하다.
가장 큰 차이가 A의 0.8%인 것에서 알 수 있듯이 2가지 Case에서 Stress 차이는 거의 없다.
이를 통해 전선 해석에서 Topside 구현 방법의 차이가 Hull에 미치는 영향이 없다는 것을 알 수 있다.
4. 결 론
본 연구에서는 1 Cargo hold 모델과 전선 구조 모델을 이용하여 인터페이스와 Topside를 구현하는 방법에 대해 분석하였다. 이를 통해 인터페이스 구현 방법을 정의하고 Topside 구현 방법이 Hull에 미치는 영향을 파악하였으며 결론적으로 Mass 요소와 RBE2를 사용한 기존의 전선 해석 방법이 적합하다는 것까지 확인할 수 있었다.
이는 Topside 도면과 모델 정보 없이 Topside weight와 COG 정보만으로 빠르게 전선 구조 모델을 생성할 수 있기 때문에 초기 Ship type 해양 구조물 개발 시 적용이 가능하며 EPC에서도 구조 설계의 효율을 높이고 전선 해석 공정을 준수하면서 합리적인 해석 결과까지 얻을 수 있다.
Hull 관점에서 살펴본 Topside 구현에 대한 본 연구 결과는 추후 전선 해석 시 Topside를 합리적으로 구현하기 위한 자료로써 발주처 요구에 효과적으로 대응할 수 있는 기술적 근거가 될 것으로 기대된다.
Acknowledgments
It is noted that this paper is a revised edition based on the proceedings of KAOSTS 2021 in IVCC.
References
- Hong, J.M. et al., 2018. Stool modeling using the stool builder function of FEGate for Ship. In: KAOSTS, Jeju, 24-25 May 2018.
- Jang, B.S. & Ko, D.E., 2018. A study on the structural behavior of FPSO topside module by support condition. Journal of the Korea Academia-Industrial cooperation Society, 19(11) pp.18-23.
- Joo, J.K., 2013. Floating topside module supporting system sensitivity study. In: KAOSTS, ICC, 23-25 May 2013.