부분 침수 조건에서 작동하는 프로펠러의 공기유입과 축계 기진력에 대한 실험적 연구
 ; Gyukpo Park3 ; Jongyeol Park3
; Gyukpo Park3 ; Jongyeol Park3 ; Shin Hyung Rhee3, 4
; Shin Hyung Rhee3, 4 ; Jaehoon Yoo5 ; Suyeong Park6
; Jaehoon Yoo5 ; Suyeong Park6
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License(http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Through a series of bollard pull tests of a propeller in partially submerged condition, thrust, torque, and shaft excitation force of a conventional propeller model were measured using a six-component load cell. By variation of the Weber number and Reynolds number, a consistent towing tank model test condition was derived. The effects of propeller immersion depth on the ventilation behavior and change of force and moment acting onto the propeller shaft were investigated. The decrease in thrust owing to the inception of ventilation was confirmed, and a large degree of dispersion of the thrust and torque coefficients were also observed in the transition region where the blade tip was under the water surface. The shaft excitation force was derived from the force and moment onto the propeller shaft.
Keywords:
Model test, Bollard pull test, Shaft excitation force키워드:
모형 시험, 볼라드 풀 시험, 축계 기진력1. 서 론
일반적인 선박용 스크루 프로펠러에 대한 추진 성능 연구는 완전히 물에 잠겨 자유수면을 배제할 수 있도록 충분한 깊이를 가정한 조건에서 수행되는 경우가 일반적이다(Park et al., 2011; Rijpkema et al., 2013; Seo et al., 2016). 하지만 실제 선박의 운용에서는 경하흘수(ballast) 상태나 악천후 시 과도한 피칭 등으로 인해 프로펠러가 수면에 가깝게 위치하거나 수면 위로 일부가 노출되는 상태가 종종 발생한다. 이와 같은 상황에서는 프로펠러가 설계 흘수보다 작은 흘수에서 운용되면서 불균일한 추력을 발생시켜 축계 계통과 베어링에 부하를 발생하고, 소음과 진동을 동반한 손상이나 국부적 마찰로 인한 화재가 발생할 가능성이 있다.
Paik et al. (2008)은 회류수조에서 프로펠러의 침수 조건을 변화시키면서 자유수면이 프로펠러 주위 유동에 미치는 영향을 입자영상유속계(Particle Image Velocimetry, PIV)를 이용해 계측하였고, 자유수면에 가까워짐에 따라 slipstream 내 축방향 속도 감소를 확인하였다. Paik et al. (2017)은 전산유체역학 기법을 통해 자유수면 아래 회전하는 프로펠러의 유체역학적 특성은 침수 조건 뿐만 아니라 축척비, 전진비에 영향을 받는다고 분석하였다.
이러한 자유수면-추진기 상호작용의 대표적인 물리현상은 공기유입(ventilation)이다. 추진기의 흡입면은 매우 낮은 압력이 발생하므로, 수면을 통해 공기를 빨아들일 수 있다. 이때 추진기 주위는 밀도가 낮은 공기를 밀어내는 상황이 되므로 공기유입이 발생한 날개는 추력이 크게 감소하여 축계의 힘과 모멘트의 불균형을 초래한다. 이로 인한 기진력 외에도, 불안정한 수면 요동으로 인한 높은 진동수의 기진력이 발생하기도 하는데, 이들은 설계 시 고려되지 않은 사항으로 축계의 내구성에 악영향을 미칠 수 있다.
부분 침수조건에서 추력과 토크에 치명적인 영향을 미치는 공기유입은 Kempf (1934)가 처음으로 확인한 이래로 많은 연구가 수행되었다. Koushan (2006, 2007), Koushan et al. (2011)은 단순 부분 침수 조건 뿐만 아니라 강제 heave 운동과 파랑 중에서 공기유입에 의한 추력 감소를 확인하였다. Kozlowska et al. (2009)은 부분 침수 안벽 계류시험을 통해 수면 근처에 위치한 추진기는 흡입면에 깔때기 모양으로 공기유입이 발생하는 vortex funnel 생성의 가능성이 있으며, 날개 끝이 수면에 가까워지면서 프로펠러 회전과 동시에 공기유입이 발생하는 현상을 확인하였다. 그리고 연구 결과를 이용하여 추력 손실을 추정하는 계산식을 제안하였다. Califano & Steen (2011)은 침수 깊이(h)와 추진기 반지름(R)의 비율에 대해, h/R>2.0에서는 자유수면 보텍스가, h/R<1.5에서는 팁 보텍스가 공기 유입에 지배적인 역할을 하는 것을 실험적으로 확인하였다. 또한, Lee & Paik (2018)은 프로펠러 수면 노출을 포함한 부분 침수조건에서 회전수가 높고 자유수면에 가까울수록 공기유입이 증가하여 추력과 토크가 급격히 감소하는 것을 수치해석적으로 확인하였다. 이러한 연구는 대부분 수면 관통 프로펠러(surface piercing propeller)나 덕트 프로펠러, 스러스트 바디를 갖는 특수 추진기에 대한 것이고, 일반적인 상선용 추진기가 수면 근처에서 구동될 때의 운항 조건을 체계적으로 다루지 못했다는 한계가 있다.
한편, 저수심이나 과도한 운동과 같은 프로펠러의 설계 외 조건의 운항에서는 추력 편심의 이동으로 축계에 불안정한 힘과 모멘트가 작용하여 축계 베어링이나 날개 뿌리 부분의 손상을 유발하기도 한다. Vartdal et al. (2009)은 직진 및 회두 시 프로펠러의 횡력이 선미 축계의 베어링에 미치는 영향을 확인하였다. Amini & Steen (2011)은 아지무스 프로펠러의 횡력과 굽힘모멘트 계측을 통해 권장 기준보다 더 낮은 전진비와 사항각에서 프로펠러 설계 하중의 3-4배의 힘이 베어링에 가해지는 것을 확인하여, 설계 외 조건에서 베어링에 가해지는 반력에 대한 명확한 규정의 필요성을 제기하였다. Ortolani et al. (2018)은 자유항주 시험을 통해 회두 시 쌍축 선박에 작용하는 내·외 축계 기진력을 분석하였다. Kim et al. (2020)은 설계 외 조건에서 복합소재 유연 프로펠러의 성능해석 연구를 수행하였고 낮은 전진비에서 강한 하중으로 인한 형상의 변형 정도 증가를 확인하였다.
이러한 축계, 국부 하중 분석 기법을 수면의 영향을 받는 추진기의 기진력 분석에 적용할 경우, 축계의 손상을 막기 위한 실제 운항 조건의 선정에 도움이 될 것으로 기대된다. 다만 축계 하중의 추정과 관련하여, 고전적인 축계 정렬(alignment) 분석은 아직까지 정적인 조건에서 최적의 설계를 달성하는데 중점을 두고 있는 실정이다. 한 예로, 국제수조회의(International Towing Tank Conference, ITTC)에 따르면 선미 튜브 베어링에 작용하는 횡력은 프로펠러 설계 하중의 50% 이내, 예측 산포도는 하중의 25% 이내로 권장할 뿐이며 (Molland et al., 2005) 선급에서는 부분 침수 조건에서는 속력을 줄이고 타각을 적게 사용할 것을 소극적으로 주문하고 있다 (American Bureau of Shipping, 2018). 이러한 설계 조건을 구체화하기 위해서는 부분 침수 조건에서의 축계 하중 분석에 대한 신뢰성 있는 실험이나 전산유체역학 해석을 통한 자료 확보가 시급하다.
본 연구에서는 부분 침수 조건의 모형시험을 통해 일반 상선용 프로펠러 모형의 추력과 토크, 축계 기진력을 6분력계를 이용하여 계측하였다. 계측된 결과는 수심에 따른 추진 성능, 기진력 성분, 추력편심의 이동 변화를 분석하는데 이용되었고 이를 통해 의미 있는 실험 조건과 해당 조건에서 축계 하중의 특성을 파악하는 것을 목적으로 하였다. 본 연구의 결과는 적합한 물리적 상사를 통해 실선의 문제로 확장될 수 있도록 하였다.
2. 실험 장비 및 조건
2.1 실험 시설과 장비
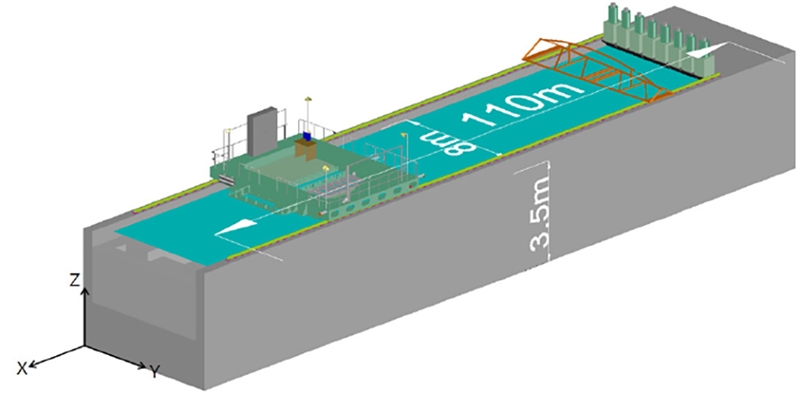
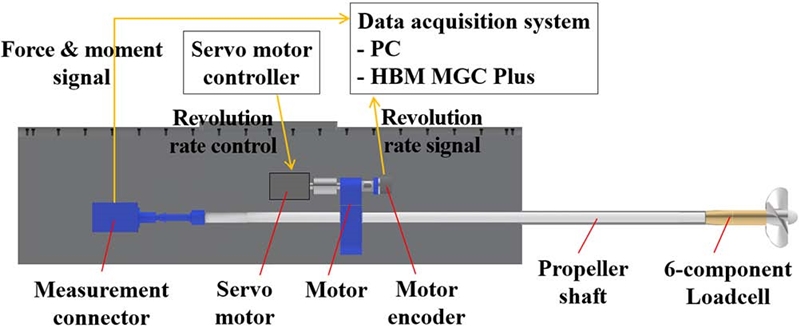
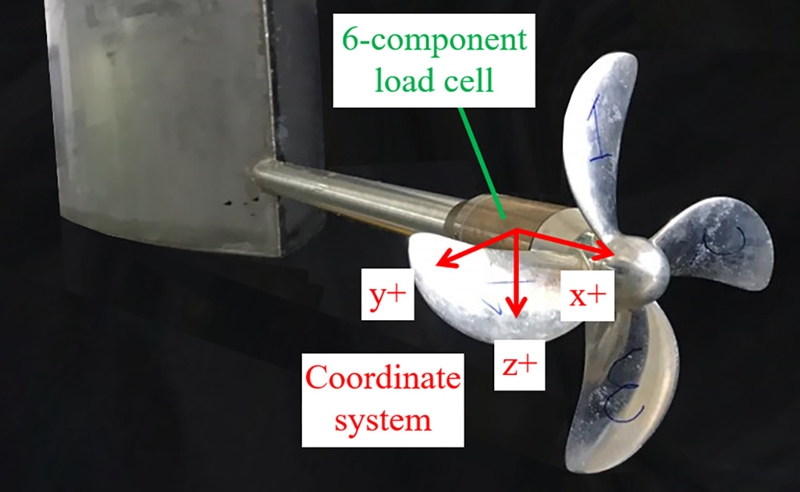
본 실험은 서울대학교 예인수조에서 수행되었다. Fig. 1은 예인수조와 예인전차의 배치 구조이며 예인전차 위에 프로펠러 단독성능 시험 장비가 설치된다. 장비의 형상 및 내부 장비 배치는 Fig. 2와 같으며 ITTC (2008) 권고사항에 따라 구동축 하우징과 프로펠러간 간격을 1.5-2.0D 이상 떨어지도록 제작하였다(D는 프로펠러 직경). 축계에는 6분력계가 설치되어 3방향 병진에 대해 최대 힘 200N, 3방향 회전에 대해 모멘트 20N·m를 계측할 수 있도록 하였다. 추진기의 회전수는 서보모터를 통해 제어되고, 힘과 모멘트, 회전수 신호는 PC와 MGC Plus 데이터 취득장비(HBM, Darmstadt, Germany)로 구성된 데이터 처리 시스템(Data Acquisition System, DAS)에서 수신하였다. 본 실험에서는 초당 600Hz의 데이터를 샘플링 하였는데 이는 최대 회전수 15rps 조건에서 4익 프로펠러 실험 시 각 날개 사이의 위상을 10등분 한 것이다. Load cell은 Fig. 3과 같이 축계와 함께 회전하는데, 축계의 각도 정보를 받아 선수방향이 +x, 우현방향이 +y, 하향이 +z인 오른손 좌표계로 변환하였다.
2.2 실험 대상
실험에 사용된 모형 프로펠러 HP1289는 공개 선형인 KVLCC2의 프로펠러 KP458을 일부 수정한 형상으로 기본 제원은 Table 1과 같다. H는 프로펠러 허브의 지름이다.
2.3 실험 조건
Table 2는 실험 조건이다. 안벽 계류조건을 상정하여 전진 속도가 없는 조건에서 부분 침수조건 h/R과 회전수(n) 조건을 설정하였다. h/R에서 h는 자유수면에서 프로펠러 축계까지 수직 거리, R은 프로펠러 반지름이다. ITTC (2008)의 권고사항에 따라 프로펠러 단독성능 시험 시 자유수면으로부터 공기유입을 피하기 위한 조건인 h/R=3.0의 실험 결과를 힘과 모멘트의 기준값으로 설정하였으며, 프로펠러 축계가 자유수면에 일치하는 h/R=0.0까지 0.2 단위로 깊이 조건을 설정하였다. 실제 운용 조건과 관련하여, HP1289 프로펠러가 선박에 장착 시 침수 깊이는 h/R=2.83이며, 경하 흘수에서는 h/R=1.15이기 때문에 본 실험 조건은 실제 실선에서 나타날 수 있는 조건을 충분히 포함하는 것으로 보았다. h/R=0.2 간격의 실험 이후에는 추력과 토크가 급격히 변하는 구간의 선형성을 분석하기 위해 h/R=1.3, 1.5 조건을 추가로 수행하였다.
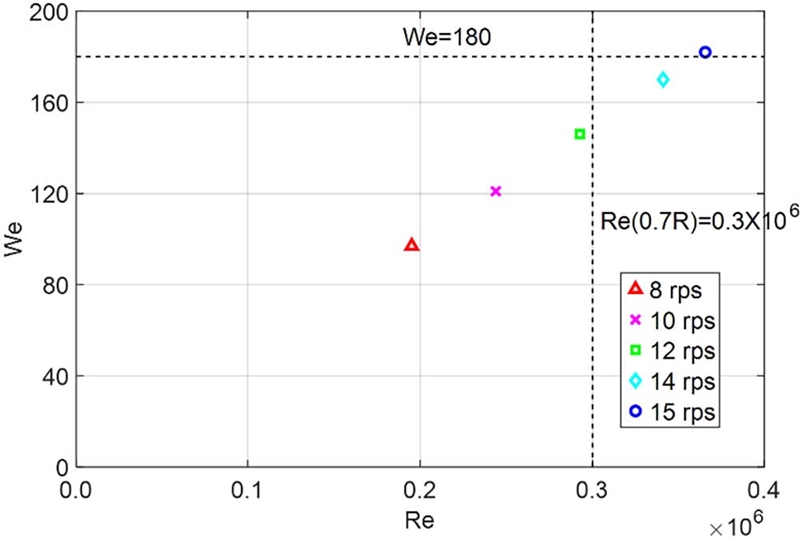
회전수의 경우 ITTC (2014)는 층류효과를 피하기 위해 프로펠러 0.7R 위치에서 코드 길이(C0.7R) 기준 레이놀즈 수(Reynolds number, Re, 식 (1)) 0.2×106 이상을 권고하나, Minsaas et al. (1975)는 자유수면 아래 회전하는 프로펠러와 심수에서 작동하는 프로펠러는 레이놀즈 수에 대한 의존성을 무시하기 위해서 최소 레이놀즈 수 0.3×106을 권고한다. 본 연구에서는 회전수 14rps 이상에서 이를 만족하나 회전수에 따른 변화 추이를 살펴보기 위해 이보다 낮은 8, 10, 12rps의 실험 또한 수행하였다. ν는 실험이 수행된 청수의 운동학적 점성계수이다.
| (1) |
한편, Shiba (1953)에 따르면 부분 침수된 물체의 경우 실선과의 상사를 위해 표면장력 효과를 무시하려면 웨버 수(Weber number, We, 식 (2))가 최소 180 이상이 권고된다. 본 연구에서는 회전수 15rps에서 웨버 수 기준을 충족할 수 있게 된다. S는 물의 표면장력(N/m)을 의미한다.
| (2) |
회전수별 웨버 수와 레이놀즈 수를 정리하면 Fig. 4와 같다. 15rps 조건에서 레이놀즈 수와 웨버 수의 권고값을 모두 만족하는 것을 확인하였다.
3. 실험 결과 및 해석
침수 깊이, 추진기 회전수에 따른 추력, 토크, 축계 기진력의 변화 추이를 확인하였다. 실험을 통해 계측된 힘(F)과 모멘트(M)는 각각 식 (3), (4)와 같이 무차원화 하였다.
| (3) |
| (4) |
3.1 6분력 계측 결과
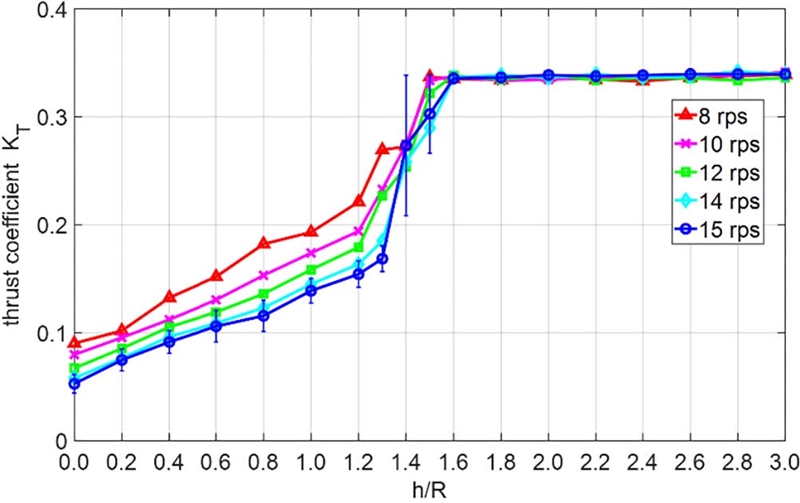
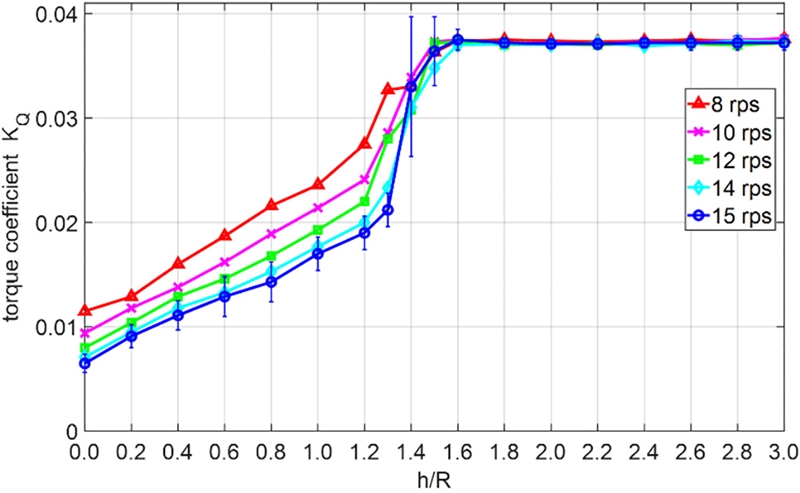
Fig. 5, 6은 침수 깊이에 따른 추력계수(KT), 토크 계수(KQ)의 변화이다. h/R=1.6-3.0까지는 추력, 토크 계수의 변화가 거의 없기 때문에 수면의 영향이 없는 완전 침수 조건으로 판별될 수 있다.
h/R =1.2보다 침수 깊이가 작아질수록, 즉 추진기가 수면에 가까워질수록 추력과 토크 계수는 비교적 선형적인 감소 추이를 보인다. 8rps 조건에서는 선형적이지 않은 결과의 요동이 보였는데, 이는 작은 추력, 토크가 걸리는데 따른 계측 정밀도의 한계로 생각된다.
Fig. 7은 침수 깊이에 따른 추진기 전면의 공기 혼입 양상을 수중카메라로 촬영한 사진이다. 자유수면에서 h/R=1.5까지는 추진기 날개를 따라 발생하는 링 모양의 공기유입이 잘 관측되었다. 작은 침수 깊이 조건에서는 프로펠러가 입수 시 공기를 끌고 들어가면서 공기유입이 발생하는 것으로 보인다. 이외에도, 수면과 추진기 영역을 잇는 vortex funnel이 h/R=1.5와 2.0에서 나타났다. Denny (1956)의 연구에서 묘사된 바와 같이 vortex funnel은 추진기의 흡입면과 수면을 잇는 수직방향으로 회전하는 강한 보오텍스를 따라 공기가 혼입되는 현상이다. h/R=1.5에서는 vortex funnel이 불규칙하게 형성되었는데, 이는 해당 영역의 추력과 토크 계수의 급격한 변화와도 연관이 있는 것으로 보인다.

Snapshots of the ventilation inception with immersion ratio variation (h/R=0.0, 0.8, 1.5, 2.0) (n=15rps)
Califano & Steen (2011)은 이러한 간헐적 구간(intermittent regime)에서는 자유수면 보텍스와 팁 보텍스가 동시에 작용하며 자유수면 보텍스의 무작위하고 불안정한 특성 때문에 추력값의 편차가 크다고 분석한 바 있다. Fig. 5, 6에서 15rps의 침수 조건별 표준편차를 오차막대로 나타냈을 때 간헐적으로 급격한 공기유입이 발생하는 h/R=1.4, 1.5에서 큰 분산도를 확인할 수 있었다.
침수 조건과 회전수에 따른 공기유입 경향을 Table 3과 같이 구분하였다. 침수 조건의 경우 공기유입이 간헐적으로 급격하게 발생하는 h/R=1.3-1.5구간을 확인할 수 있었다. 회전수에 따른 구간별 차이는 크진 않았으나 회전수가 증가할수록 웨버 수가 증가하면서 표면장력의 영향이 줄어들고, 공기가 수면을 뚫고 혼입되기가 쉬워지는 것으로 보인다.

Classification of ventilation inception at submergence ratio & propeller revolution rate variation(× : no ventilation, ○ : intermittently weak vortex funnel inception, ◐ : intermittently strong vortex funnel and ventilation inception, ● : consistent ventilation inception)
Fig. 8은 h/R=0.0, 0.8, 1.5, 2.0 조건의 날개 위상에 따른 추력 계수 주기를 나타낸 것이다. 0 rad은 수직 상방향으로 추진기날개가 놓인 상황이다. h/R=1.5에서는 한 주기 동안 추력의 변동 폭은 작으나 불안정한 공기유입으로 인해 실험의 반복에 따른 변동 폭은 크게 나타났다. 이는 Kozlowska et al. (2011)의 연구 결과와 같이 vortex funnel의 생성이 불규칙하여 추진기 주위 유동 현상이 크게 달라지기 때문이다. 이는 본 연구에서 가장 높은 웨버 수 조건에서 수행된 결과이나, 실험 결과의 일관성이 나타나지 않는 천이영역으로 확인되었다. 따라서 해당 침수 조건에 대한 연구는 더욱 높은 웨버 수 조건에서 추가로 수행되어야할 것으로 보인다. 한편, h/R이 1보다 작은 조건인 0.8에서는 추진기 날개 자체가 수면을 관통하며 입수하기 때문에 한 주기 동안의 변동 폭은 입수 충격을 포함하여 h/R=1.5보다 크게 나타났다. 다만 유동 현상은 안정적이게 되어 실험 반복에 따른 분산은 작아졌다.
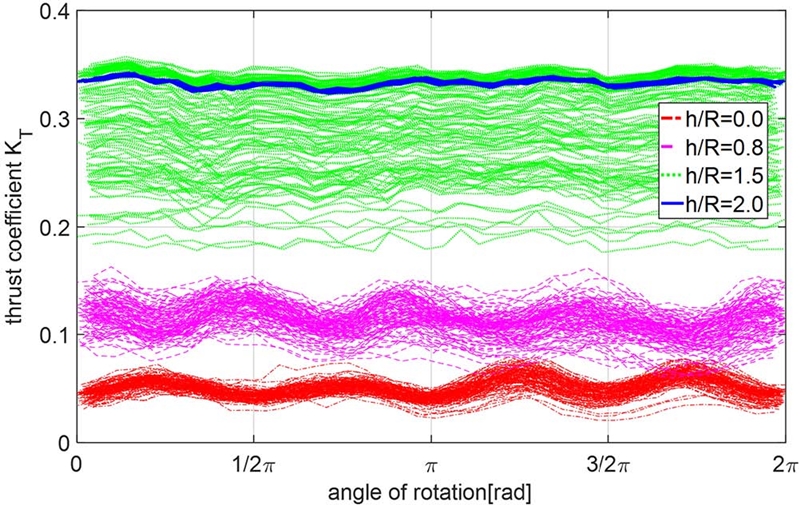
Time-history of KT in a revolution of the propeller with immersion ratio variation (h/R=0.0, 0.8, 1.5, 2.0) (n=15rps)
충분히 깊은 조건인 h/R>1.6 조건에서는 추력, 토크를 제외한 힘과 모멘트 성분이 0으로 기대되었지만, 실험 시스템의 정렬, 동력계의 force coupling 등으로 인한 불확실성으로 인해 작은 값이 기록되었다.
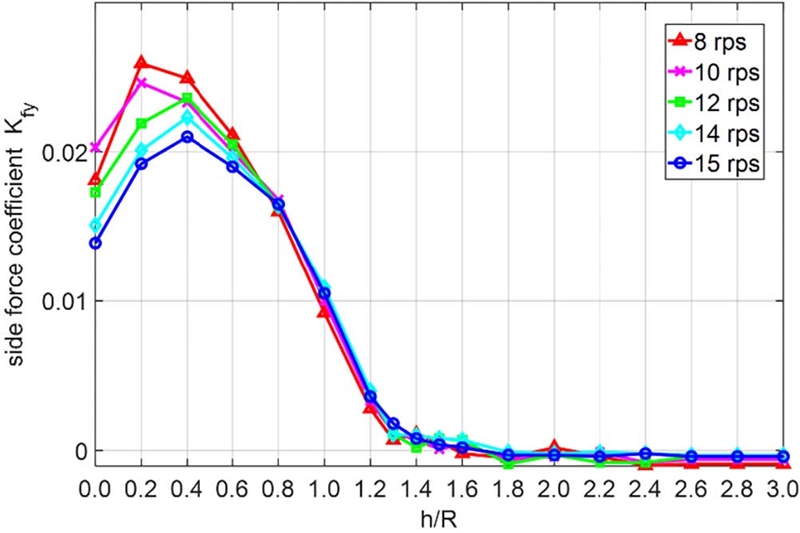
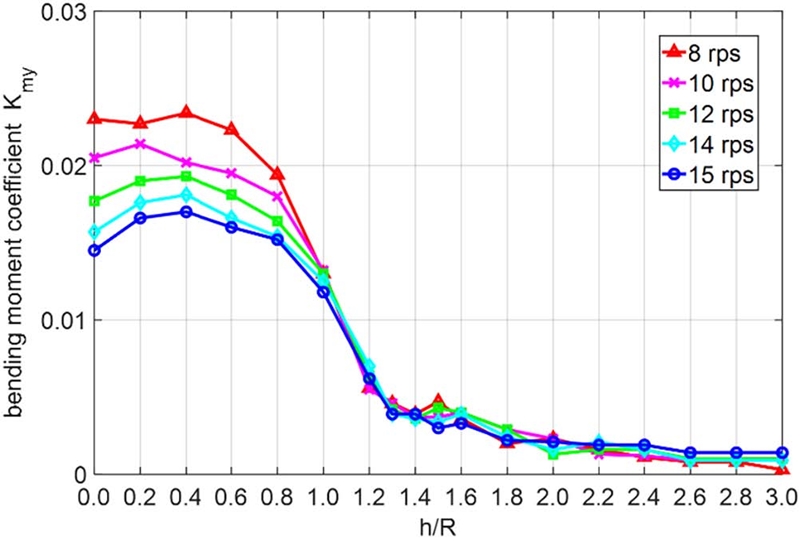
Fig. 9, 10은 각각 횡력 계수 Kfy와 y축 방향 굽힘모멘트 계수 Kmy의 시계열 평균값을 나타낸다. 즉 Kmy는 축이 위아래로 휘는 정도를 의미하는데, 공기 유입으로 인해 추진기의 상하간의 추력차이가 발생하는 것을 감안하면 공기유입의 영향을 가장 크게 받을 모멘트 성분으로 여겨진다.
추진기의 횡력을 분석하자면 각 날개에서 발생하는 횡력 성분은 심수 조건에서는 서로 상쇄되기 때문에 축계에 영향을 주지 않는다. 하지만 부분 침수나 수면에 가까운 상태에서는 날개에서 발생하는 유체력이 반대쪽 위상의 날개와 상쇄되지 않기 때문에, Kfy의 경우 수면 근처로 추진기가 위치하면서 그 크기가 커졌다. Kmy또한 같은 경향을 보였는데, 완전 침수 조건에서 수심이 얕아짐에 따라 증가하다가 h/R=0.4를 기점으로 감소하였다. 이는 프로펠러 하단까지 공기가 유입되는 h/R =0.4 조건은 추진기가 발생하는 추력 자체가 줄어들며 추진기의 날개별 추력 차이로 인한 횡력, 굽힘 모멘트가 줄어들기 때문으로 보인다.
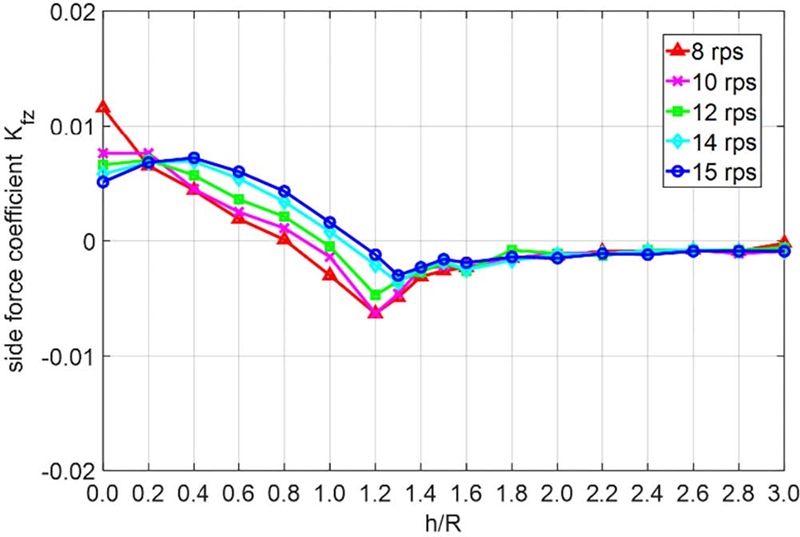
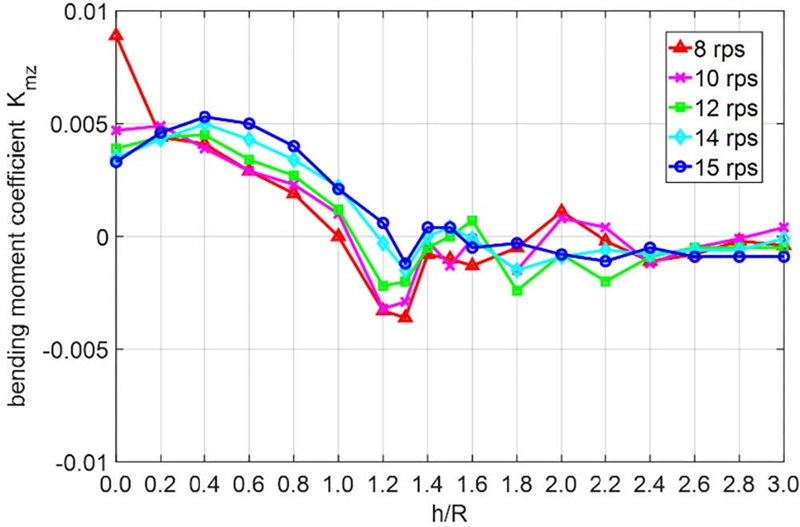
수직력 계수 Kfz와 z축 방향 굽힘모멘트 계수 Kmz의 시계열 평균값은 Fig 11, 12와 같이 8rps를 제외한 회전수에서 뚜렷한 경향성을 보였다. 하지만 그 크기는 앞의 Kfy와 Kmy에 비하면 작은 수준이다. 낮은 회전수에서 Kfz의 최소값이 h/R=1.2에서 나타나나, 웨버 수 증가에 따라 해당 조건의 값이 커지므로, 실선에서는 유의미한 수준의 국부 최소값이 발생하지 않을 것으로 생각되어, 전체적으로 h/R의 감소에 따라 양의 값이 증가할 것으로 보인다. h/R=0.4를 기점으로 힘과 모멘트가 감소하는 현상은 앞서와 동일하게 나타났다.
3.2 축계 기진력 및 베어링 반력 추정 결과
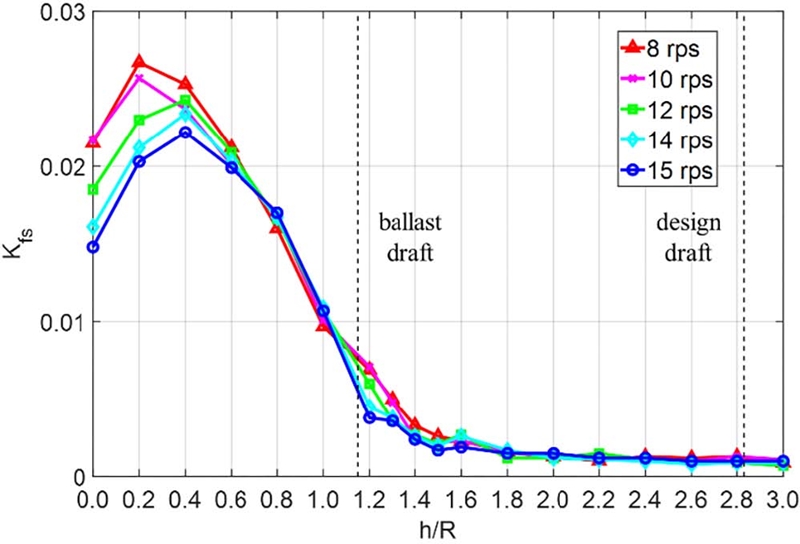
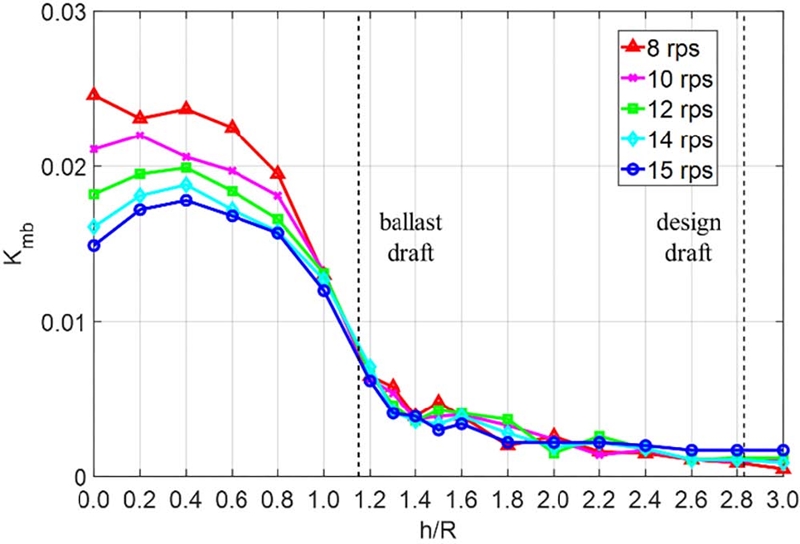
Fig. 13, 14는 축계에 작용하는 기진력 성분(힘과 모멘트)을 나타낸다. Kfs는 식 (5)와 같이 추력을 제외한 횡력과 수직력의 합력이며 Kmb는 식 (6)과 같이 토크를 제외한 모멘트의 합을 의미한다.
| (5) |
| (6) |
h/R=1.8-3.0까지는 값의 차이가 1% 이내로 유의미한 관측 결과가 나타나지 않았으나 h/R=1.6부터 기진력과 반력이 증가하여 경하 흘수에서는 설계 흘수보다 3.5배 이상 큰 기진력 성분이 작용하는 것을 확인하였다. 앞서 축계의 힘과 모멘트가 최대값을 보이던 h/R=0.4에서 가장 큰 축계 기진력 성분이 확인되었다.
실험 결과를 바탕으로 Fig. 15와 같이 일반 상선용 프로펠러의 축계 베어링 A, C의 위치를 추진기면로부터 각각 1.0DP, 0.2DP로 가정하고 베어링에 작용하는 반력을 아래와 같이 계산하였다.
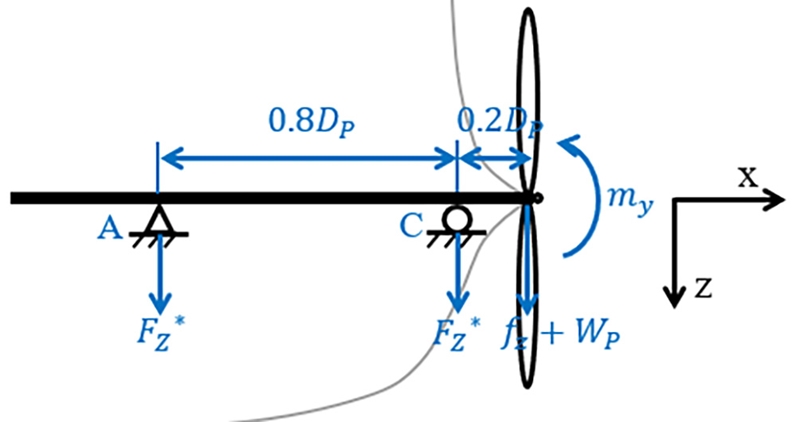
Layout of the propeller shaft bearing and hydrodynamic force and moment acting onto the shaft of a propeller (Leontopoulos, 2016)
베어링 A에 작용하는 힘은 식 (7)과 같고,
| (7) |
베어링 C에 작용하는 힘은 식 (8)과 같다.
| (8) |
따라서 베어링에 작용하는 반경 방향 힘은 식 (9)와 같다.
| (9) |
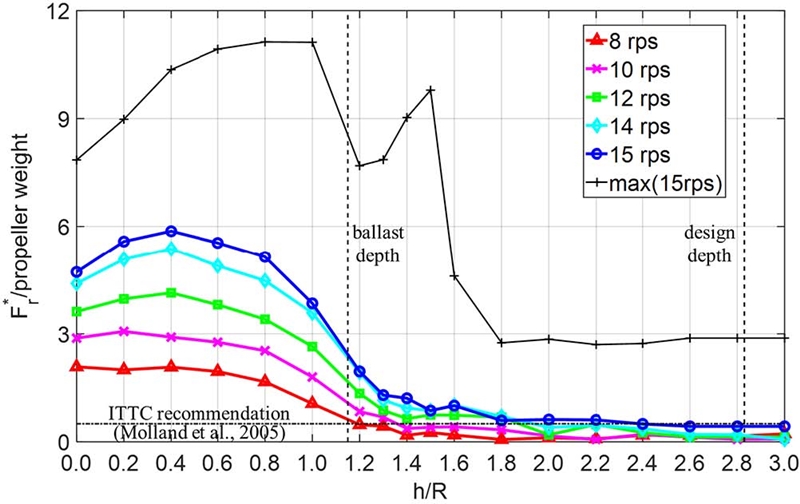
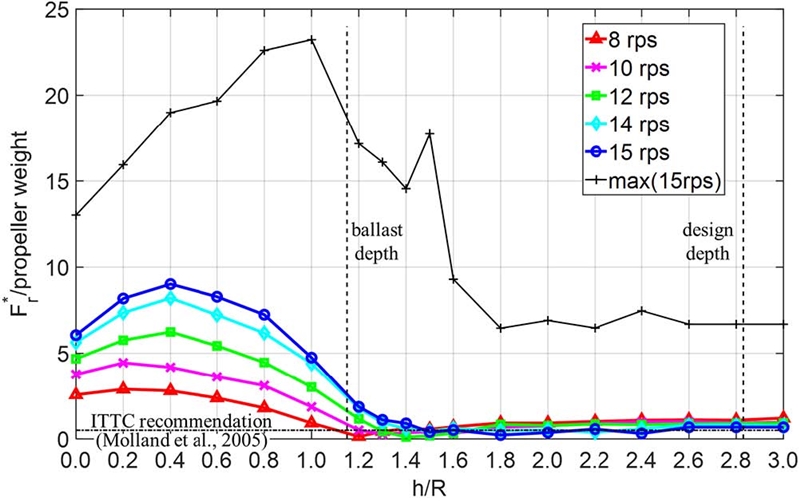
Fig 16, 17은 Fr*을 프로펠러 중량 WP로 나눈 값으로 h/R=0.4에서 평균적으로 가장 큰 하중이 작용한 것을 확인할 수 있다. 이는 ITTC 권고 기준을 훨씬 넘는 수준으로 15rps의 경하 흘수에서조차 Fr*이 프로펠러 설계 하중의 2배 이상이 작용하였다. 때문에 부분 침수 조건에서 베어링에 작용하는 반력에 대한 ITTC 권고사항의 기준을 현실적으로 개정할 필요가 있음을 알 수 있다.
한편, 순간 최대 하중(검정색 선)은 베어링 A, C 모두 프로펠러 날개 끝이 수면에 닿기 시작한 h/R=0.8-1.0에서 가장 컸으며 공기유입이 간헐적으로 가장 심하게 나타난 구간인 h/R=1.4-1.5에서는 국부 최대값을 갖는다. 즉, 간헐적 구간에서는 공기유입이 프로펠러 유체 주변의 속도장을 급변시켜 베어링 반력에도 큰 영향을 미치는 것으로 분석할 수 있다. 따라서 베어링 설계 시 선박의 운용 조건에 따라 이러한 순간 최대 하중범위를 고려할 필요가 있다.
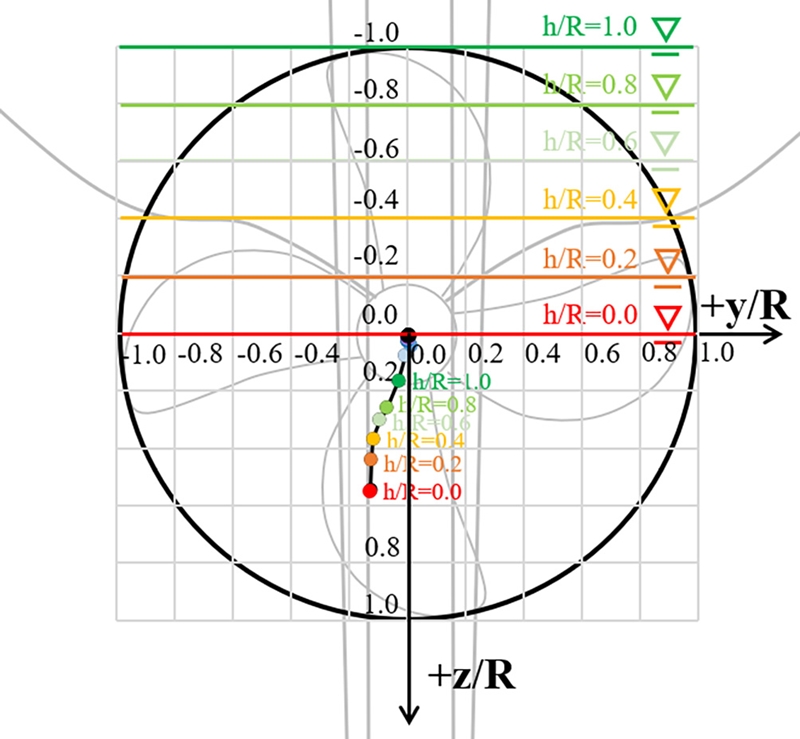
추력편심은 프로펠러 평면 상 회전축 중심에서 프로펠러 추력선이 반경 방향으로 떨어진 거리를 나타내며 식 (10)과 같이 추력과, y축 방향 모멘트, z축 방향 모멘트에 의해 정의된다.
| (10) |
Fig 18에 h/R=0.0-3.0까지 침수조건별 추력편심의 이동을 나타내었다. y축 성분은 h/R=0.4-1.3까지 수심이 얕아질수록 Mz의 증가 및 Fx의 감소로 -y축 방향으로 중심이 이동하다 이후 h/R=0.0까지 Mz의 감소로 종축으로부터 일정한 횡방향 거리를 유지한다. 다만 전체적으로 중심이 하방으로 이동하면서 축계에 큰 하중이 걸릴 것을 알 수 있다. 다만 이러한 경향은 실험이 수행된 균일 유동(uniform flow) 중의 편심 양상을 나타낸 것이다. 실제 선박 선미에서 작동하는 추진기의 경우에는 자항 상태에서 상부에 더 큰 하중이 걸리므로, 수심 변화에 따른 상부 하중 감소의 영향이 더 강해서 편심의 양상이 더 커질 것으로 예상된다.
4. Re, We의 변화
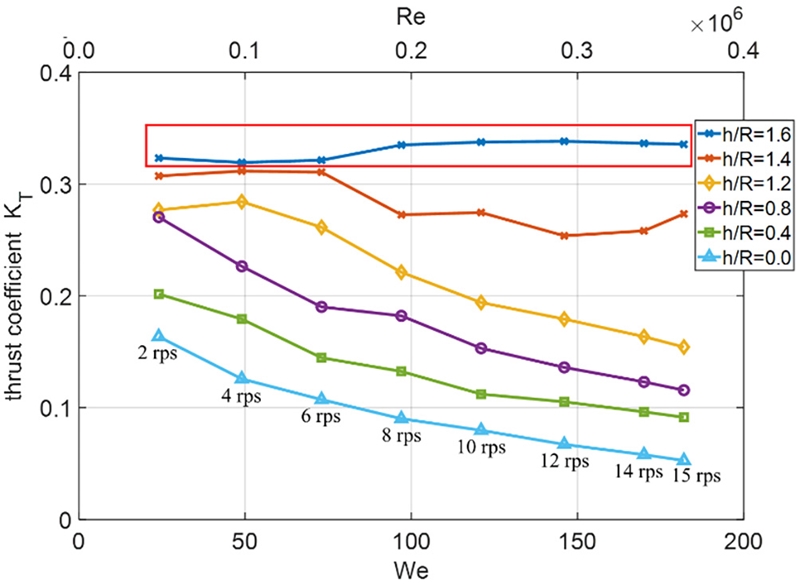
계측값에 대한 레이놀즈 수와 웨버 수의 영향을 확인하기 위해 동일 침수조건에서 회전수 2, 4, 6rps를 추가적으로 실험하였다. 레이놀즈 수의 경우 Fig. 19의 적색 상자와 같이 h/R≥1.6에서는 0.2×106 이상에서 추력 계수값이 수렴하였다. 반면 웨버 수는 h/R=1.5부터 그보다 얕은 조건까지 영향을 미치는 것으로 보였다. h/R=1.3-1.5에서는 웨버 수 증가에도 불구하고 Table 3에서 확인했던 불규칙 공기유입 현상으로 인해 값이 수렴하지 않는 천이 영역 특성을 가지며, 일관된 결과를 확인하기 위해서는 더 높은 웨버 수에서 실험을 수행할 필요가 있겠다. h/R≤1.2에서는 웨버 수에 따른 추력 계수의 완전한 수렴은 확인하지 못했지만 웨버 수의 추이를 확인할 수 있었다. 따라서 추후 시험에는 레이놀즈 수와 웨버 수를 고려한 높은 회전수에서 추력 계수 변동이 심한 h/R=1.3-1.5 구간을 면밀한 조건으로 수행할 필요가 있어 보인다.
5. 결 론
본 연구에서는 부분 침수 모형시험을 통해 일반 상선용 프로펠러에 작용하는 힘과 모멘트를 6분력계를 이용하여 계측하였고, 침수조건과 회전수에 따른 추진성능과 기진력 성분, 추력편심의 이동을 확인하였다. 침수 깊이 조건의 변화에 따른 공기유입에 의한 추력 성능의 저하를 확인하였고 천이영역에서(h/R=1.3-1.5) 추력과 토크 계수의 큰 분산도를 확인할 수 있었다.
침수조건에 대한 레이놀즈 수와 웨버 수의 영향을 확인하였는데 레이놀즈 수는 h/R≥1.6 조건에서는 0.2×106 이상에서 값이 수렴하였고 웨버 수는 h/R≤1.2 조건에서는 값이 커질수록 수렴하나 h/R=1.3-1.5는 실험 결과가 일관되지 않은 천이 영역 특성을 갖기 때문에 추후 레이놀즈 수와 웨버 수를 고려한 높은 회전수에서 실험할 필요성이 제기된다.
본 연구를 통해 얻어진 모형시험의 프로펠러 기진력 특성은 ITTC 규정 마련을 위한 기초 자료는 물론 전산유체역학 해석의 검증자료로도 활용 가능하다. 또한 본 연구의 결과는 적합한 물리적 상사를 통해 일반 상선용 프로펠러를 운용하는 실제 선박에서 침수조건별 축계 기진력 추정에 확장될 수 있다. 추후에는 부분 침수 조건에 전진속도를 적용한 시험을 추가로 수행, 전진비에 따른 기진력과 수면 거동을 분석할 수 있다. 이에 더하여 작은 흘수의 자항 중 추진기 축계 기진력 등의 연구를 통해 실선의 운용에 대해 의미 있는 시험 결과를 얻어낼 것으로 기대된다.
Acknowledgments
본 연구는 현대중공업(주) “Off-design 조건에서의 프로펠러 축기진력 특성 평가(과제번호: 0668-20190202)”의 지원으로 수행된 연구결과 중 일부임을 밝히며, 연구 수행을 위한 2020년 해군사관학교 해양연구소의 지원에 감사드립니다.
References
- American Bureau of Shipping (ABS)., 2018. Guide for enhanced shaft alignment. ABS, Houston, TX.
-
Amini, H. & Steen, S., 2011. Experimental and theoretical analysis of propeller shaft loads in oblique inflow. Journal of Ship Research, 55(4), pp.268-288.
[https://doi.org/10.5957/JOSR.55.4.100044]

-
Califano, A. & Steen, S., 2011. Identification of ventilation regimes of a marine propeller by means of dynamic-loads analysis. Ocean Engineering, 38(14-15), pp.1600-1610.
[https://doi.org/10.1016/j.oceaneng.2011.07.009]

-
Denny, D. F. (1956). An experimental study of air-entraining vortices in pump sumps. Proceedings of the Institution of Mechanical Engineers, 170(1), pp.106-125.
[https://doi.org/10.1243/PIME_PROC_1956_170_019_02]

- International Towing Tank Conference (ITTC)., 2008. Testing and extrapolation methods propulsion, propulsor open water test. ITTC-Recommended Procedures and Guidelines, 7.5-02-03-02.1. ITTC, Zurich, Switzerland.
- International Towing Tank Conference (ITTC)., 2014. Open water test. ITTC-Recommended Procedures and Guidelines, 7.5-02-03-02.1. ITTC, Zurich, Switzerland.
- Kempf, G., 1934. The influence of viscosity on thrust and torque of a propeller working near the surface. Transactions of the Institution of Naval Architects, 76, pp.321-326.
-
Kim, J., Ahn, B. & Kim, G., 2020. Design of flexible composite propellers considering fluid-structure interaction. Journal of the Society of Naval Architects of Korea, 57(2), pp.61-69.
[https://doi.org/10.3744/SNAK.2020.57.2.061]

- Koushan, K., 2006. Dynamics of ventilated propeller blade loading on thrusters. Proceedings of the World Maritime Technology Conference (WMTC’06), London, UK, 6-10 March 2006.
- Koushan, K., 2007. Dynamics of propeller blade and duct loading on ventilated thrusters in dynamic positioning mode. Proceedings of the Dynamic Positioning Conference, Houston, TX, 9-10 October 2007.
- Koushan, K., Spence, S. & Savio, L., 2011. Ventilated propeller blade loadings and spindle moment of a thruster in calm water and waves. Proceedings of the Second International Symposium on Marine Propulsors (SMP’11), Hamburg, Germany, 15-17 June 2011.
- Kozlowska, A.M., Steen, S. & Koushan, K., 2009. Classification of different type of propeller ventilation and ventilation inception mechanism. Proceedings of the 1st International Symposium on Marine Propulsors (SMP’09), Trondheim, Norway, 22-24 June 2009.
- Kozlowska, A.M., et al., 2011. Numerical and experimental study of propeller ventilation. Proceedings of the 2nd International Symposium on Marine Propulsors (SMP’11), Hamburg, Germany, 15-17 June 2011.
-
Lee, S. & Paik, K.J., 2018. URANS simulation of a partially submerged propeller operating under the bollard condition. Brodogradnja: Teorija i praksa brodogradnje i pomorske tehnike, 69(1), pp.107-121.
[https://doi.org/10.21278/brod69107]

- Leontopoulos, C., 2016. Shaft alignment challenges – The single sterntube bearing design. Proceedings of the 6th technical meeting, American Bureau of Shipping, Athens, Greece, 18 February 2016.
- Minsaas, K.J., Wermter, R. & Hansen, A.G., 1975. Scale effects on propulsion factors. Proceedings of the 14th International Towing Tank Conferences, Proceedings Volume 3, Ottawa, Canada, September 1975.
- Molland, A. et al., 2005. Report of the propulsion committee. proceedings, 24th International Towing Tank Conference (ITTC), vol. I, Edinburgh, UK, 4-10 September 2005.
-
Ortolani, F. et al., 2018. Experimental and numerical investigation of propeller loads in off-design conditions. Journal of Marine Science and Engineering, 6(2), Article No. 45.
[https://doi.org/10.3390/jmse6020045]

- Paik, B.G., Lee, J.Y. & Lee, S.J., 2008. Effect of propeller immersion depth on the flow around a marine propeller. Journal of Ship Research, 52(2), pp.102-113.
-
Paik, K.J., 2017. Numerical study on the hydrodynamic characteristics of a propeller operating beneath a free surface. International Journal of Naval Architecture and Ocean Engineering, 9(6), pp.655-667.
[https://doi.org/10.1016/j.ijnaoe.2017.02.006]

-
Park, S. et al., 2011. Numerical analysis of a tip vortex flow for propeller tip shapes. Journal of the Society of Naval Architects of Korea, 48(6), pp. 501-508.
[https://doi.org/10.3744/SNAK.2011.48.6.501]

- Rijpkema, D., Starke, B. & Bosschers, J., 2013. Numerical simulation of propeller-hull interaction and determination of the effective wake field using a hybrid RANS-BEM approach. Proceedings of the 3rd International Symposium on Marine Propulsors (SMP’13), Launceston, Australia, 5-7 May 2013.
- Shiba, H., 1953. Air-drawing of marine propellers. Report of Transportation Technical Research Institute, 9, pp.1-320.
-
Seo, J., Lee, S.J., Han, B. & Rhee, S. H., 2016. Influence of design parameter variations for propeller-boss-cap-fins on hub vortex reduction. Journal of Ship Research, 60(4), pp.203-218.
[https://doi.org/10.5957/jsr.2016.60.4.203]

- Vartdal, B.J., Gjestland, T. & Arvidsen, T.I., 2009. Lateral propeller forces and their effects on shaft bearings. 1st International Symposium on Marine Propulsors (SMP’09), Trondheim, Norway, 22-24 June 2009.