MR Tanker 실선 및 모형선 프로펠러 캐비테이션 및 변동압력 수치해석 연구

1. 서론

부하가 큰 추진기의 경우 캐비테이션 발생이 증가하여 추진기 효율의 감소는 물론 선체 변동압력을 증가시킨다. 설계 단계에서 이러한 실선 추진기 유동의 특성을 파악하기 위해 중형 및 대형캐비테이션터널을 통해 얻은 모형시험 결과를 바탕으로 실선 성능을 분석하고 있으며, 모형시험 기술의 정확도를 높이려는 연구들이 수행되고 있다(Kim et al., 2009). Kim et al.(2000)과 Choi et al.(2011)은 실선 캐비테이션 성능 추정을 위해 각각 Reynolds수 변화와 추정한 실선 반류로 모형시험들을 수행한 바 있다. 이와 함께 최근 실선 계측 및 대형 캐비테이션터널(LCT, Large Cavitation Tunnel) 모형시험 등을 기반으로 모형선-실선 상관관계 해석 기술의 고도화에 관한 연구들도 진행되고 있다(Kim et al., 2010(a); Kim et al., 2010(b); Kim et al., 2013; Ahn et al., 2016).

한편으로, 최근 수치해석 기법의 발달과 더불어 하드웨어 기술의 발달로 대용량 해석이 가능하여 모형시험과의 상호보완적으로 전산유체역학(CFD) 수치해석 기술을 많이 활용하고 있다. 또한, CFD 기술의 경우도 모형시험과 마찬가지로 모형선-실선 상관관계 분석에 유용한 도구로 사용될 수 있는 것으로 판단되고 있다. 관련 연구들을 간략히 살펴보면, Choi et al.(2003)은 상선 주위 유동에 대한 스케일 영향을 CFD해석 통해 조사한 바 있고, Yang et al.(2010)은 KVLCC, KCS 그리 KLNG의 다양한 선박의 모형과 실선 반류를 수치해석하고 그 상관관계를 분석한 연구결과를 발표하였다. Hochkirch & Mallol(2013)은 모형선과 실선 유동에 대한 스케일 영향 그리고 CFD를 이용한 실선 성능 추정의 가능성과 그 중요성에 관한 연구를 소개한 바 있다. Ji et al.(2010)은 실선 프로펠러에 대한 비정상 및 캐비테이션 유동을 해석하고 이로 인한 압력 변동을 연구하였다.

본 논문에서는 상기 서술한 연구들의 일환으로 Ahn et al. (2016)의 MR Tanker에 대한 일련의 LCT 모형시험 및 실선 프로펠러 캐비테이션 관찰 결과를 인용한다. 또한 동일한 조건으로 CFD를 이용한 수치해석을 수행하고 그 결과를 각 항목별로 비교한다. 모형선 반류와 실선 반류 수치해석 결과로 부터 반류 수축(wake contraction) 특성과 타당성을 살펴본다. 프로펠러 캐비테이션 수치추정 결과는 모형 및 실선 프로펠러 캐비테이션 관찰 결과와 각각 비교한다. 그리고 선미 변동압력에 대한 수치해석 결과는 LCT 모형시험 및 실선 계측 결과와 비교한다. 그리고 수치해석방법으로 실선과 모형선 프로펠러 날개표면의 압력분포와 프로펠러 전방에서 총 유속(total velocity)분포를 비교하여 물리적인 타당성을 살펴본다. 따라서 본 연구의 CFD 수치해석 기법이 실선 캐비테이션과 변동압력 추정 정도와 활용 가능성을 논의하였다.

2. 수치해석 방법

본 논문에서 수치해석 대상선박의 선체와 프로펠러 주위 유동장 수치해석에는 범용 유동해석 프로그램인 STAR-CCM+ (Siemens, 2018)을 활용하였다. 관련된 수치해석 기법을 간략히 소개하면 다음과 같다. 유동은 완전히 발달된 비압축성 난류유동으로 가정하며, 유동장 지배방정식은 연속방정식(continuity equation)과 운동량 보존방정식인 RANS 방정식(Reynolds averaged Navier-Stokes equations)이다. 지배방정식의 수치 해는 유한체적법(finite volume method)으로 해석되며, 방정식의 시간 적분과 공간에 대한 이산화는 2차 정확도의 수치해석 기법이 사용되었다. 이때, 비압축성 유동해석 시 요구되는 유체의 속도와 압력의 연성은 SIMPLE(Semi-Implicit Method for Pressure-Linked Equation, Patankar, 1980) 알고리즘으로 해석하였다. 사용한 난류모형은 프로펠러 면에서 훅크(hook)형 반류를 갖는 선형에 추천되는 RSM(Reynolds Stress Model)을 채택하였다(Launder et al., 1975).

선박 선미 변동압력의 주요 원인이 되는 프로펠러에 발생하는 캐비테이션 현상은 단순화된 Rayleight-Plesset방정식을 기반으로 하는 Sauer(2000)의 캐비테이션 모델을 이용하여 해석하였다. 여기서, 증기와 물에 대한 이상유동(two-phase flow)은 VOF(Volume of Fluid)법을 이용하여 처리된다.

프로펠러의 회전운동은 먼저 정상유동 상태에서 프로펠러 주위 유동을 주어진 회전수로 회전하는 방법인 MRF(Moving Reference Frame)법으로 유동을 충분히 수렴시킨 후, 프로펠러 격자를 직접 회전시키는 방법인 일명, sliding mesh법으로 비정상 유동 해석을 이어가는 방법으로 고려하였다.

3. 수치해석 결과

3.1 수치해석 조건

본 논문에서는 MR 탱커선을 대상으로 실선과 모형선 스케일에 대하여 각각 실해역 시운전 조건과 대형 캐비테이션터널(LCT)에서 모형시험 조건에서 수치해석을 수행하고 모형선 및 실선 시험 결과(Ahn et al., 2016)와 비교 검토한다. 비교 대상항목은 각각의 시험조건에서 대상선박의 공칭반류(nominal wake), 프로펠러 날개 캐비테이션 발생 및 선체표면 변동압력 특성이다. 그리고 수치해석 결과를 통하여 모형 및 실선프로펠러 작동 시 총 유속분포와 날개면 압력분포를 비교한다. 그 모형선 형상은 Fig. 1(a)과 같으며 프로펠러와 선체표면 변동압력 센서의 상대적인 위치는 Fig. 1(b)에 보는 바와 같다.

Fig. 1.

Model ship of the MR tanker and the location of hull pressure sensors above propeller

실선 실해역 시운전시 조건은 Table 1에 보는 바와 같으며 수치해석에서도 동일한 선속 14.2노트와 프로펠러 회전수 103RPM에서 수행되었다. 그리고 LCT 모형시험 조건에서의 수치해석 조건은 Table 2와 같으나 추력일치법 적용에 따라 프로펠러 회전수를 44rps로 설정되었으며 이는 모형시험 회전수와 약 0.3%의 차이를 보인다.

Table 1.

Sea trial test condition of full-scale ship (Ahn et al 2016)

Table 2.

Model test condition at LCT (Ahn et al 2016)

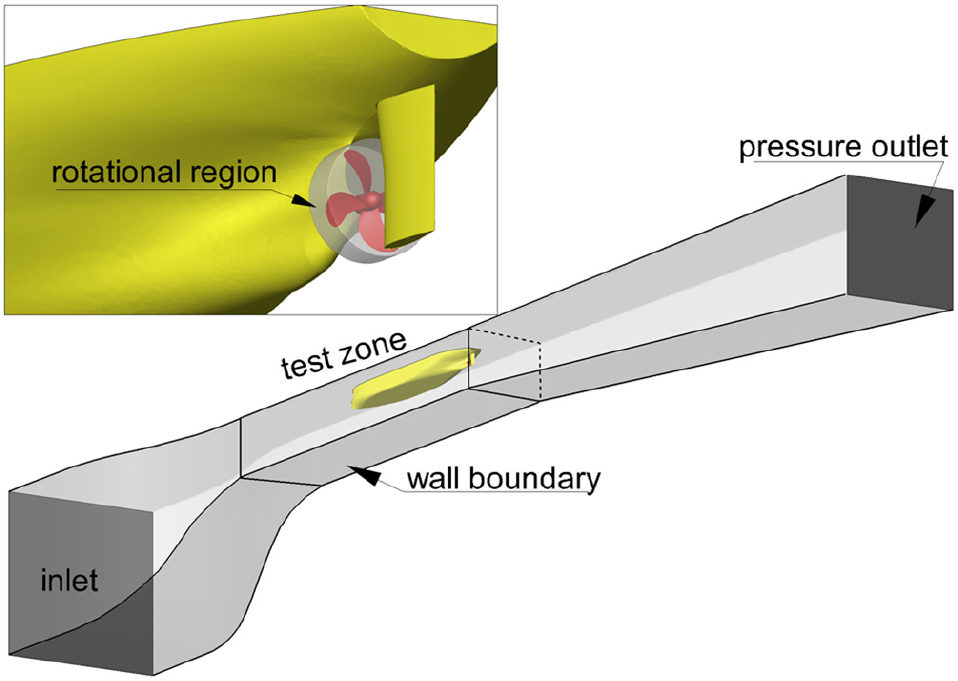
LCT 모형시험 상태 재현을 위한 수치해석 계산 영역과 사용한 경계조건은 Fig. 2에 보는 바와 같다. 수치해석 영역은 LCT의 시험부와 함께 수축부와 확산부를 포함한다. 수축부의 유입면에서는 속도 유입 조건(velocity inlet), 확산부의 출구면에서는 압력 유출 조건(pressure outlet) 그리고 터널 내부벽면에는 벽면조건(no-slip condition)을 부과하였다. 그림에는 본 논문에서 사용한 프로펠러 회전 영역을 함께 보여주고 있다.

Fig. 2.

Computational domain for LCT model test simulation

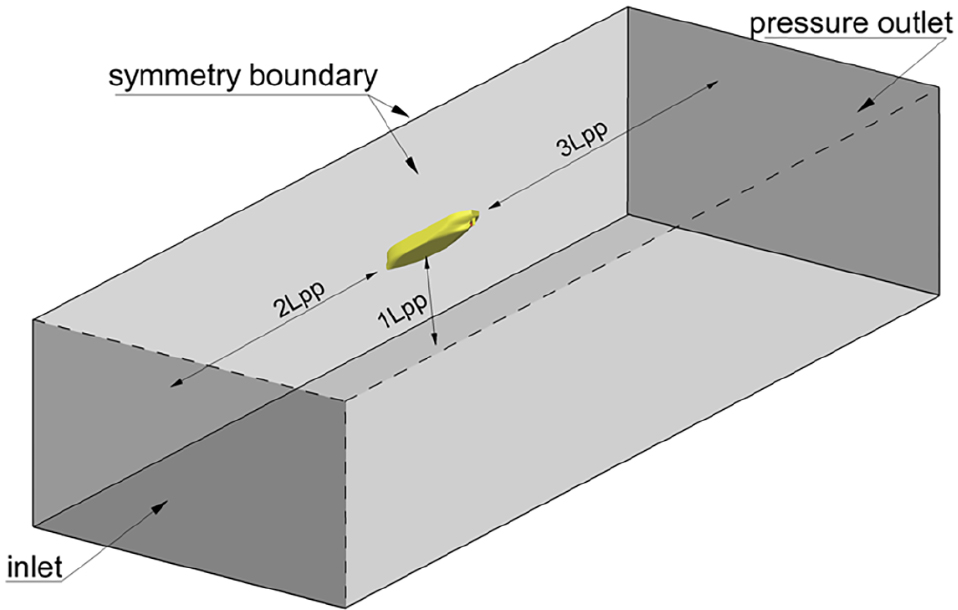
실선 공칭반류 수치해석에 사용된 계산영역과 경계조건은 Fig. 3에 보는 바와 같다. 유동장 영역은 선체의 상류로 2$$ L_{pp}$$, 하류 방향으로 3$$ L_{pp}$$, 측면과 수면아래 깊이 방향으로 약 1$$ L_{pp}$$의 거리에 경계면들이 각각 위치해 있다. 계산영역의 유입면과 출구에 각각 속도유입 경계조건과 압력유출 경계조건을 적용하고, 벽면 경계조건이 적용되는 선체와 프로펠러를 제외한 나머지 경계면은 대칭(symmetry) 경계조건을 적용하였다. 다만, 실선 캐비테이션 수치해석에서는 자유수면에 대해 대칭 경계조건을 사용하지 않고 VOF법을 사용하여 자유수면에 대한 운동역학적 경계조건과 동역학적 경계조건을 만족시켜 선체가 만드는 파를 직접 해석하였다.

Fig. 3.

Computational domain for full-scale ship simulation

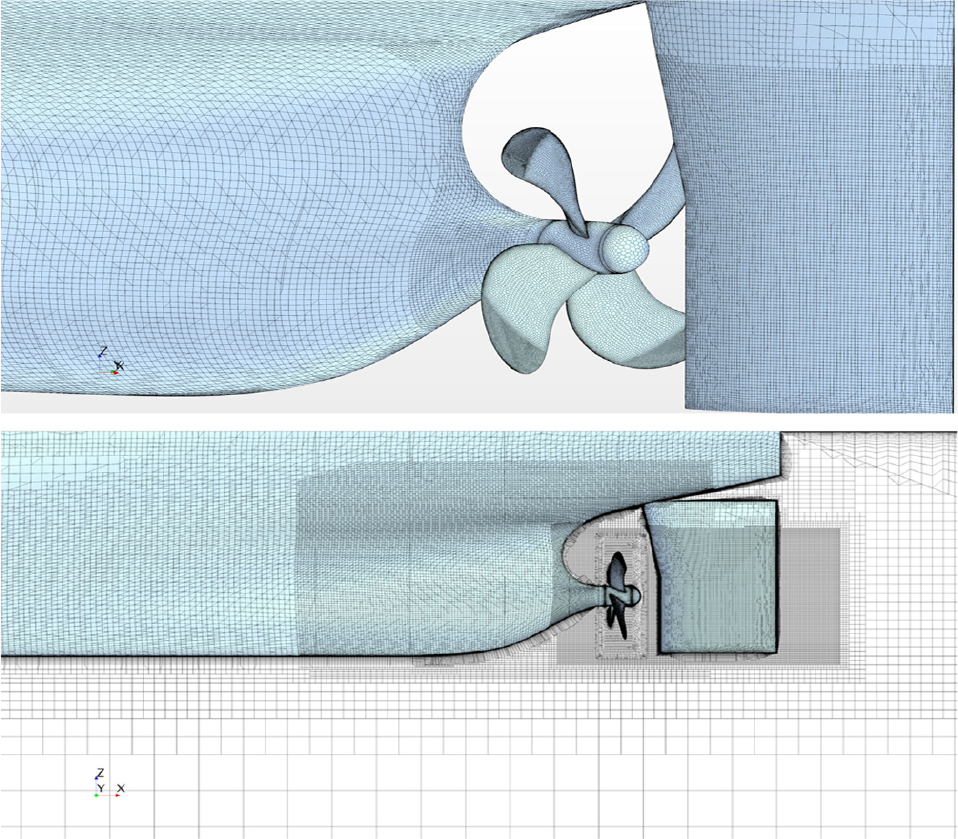
Fig. 4는 선미 선체와 프로펠러 표면 격자분포와 이들 주위 공간 격자분포를 보여주고 있다. 선체주위 비 회전 영역에서 수치해석 격자생성은 STAR-CCM+에서 제공하는 직교격자 요소 기반의 비정렬 격자계 생성법인 Trimmer라 불리는 방법을 사용한다. 프로펠러를 포함하는 회전영역은 Polyhedral 격자계 생성법으로 격자를 생성한다. 이때, 선체 영역에 6.6백만(M)개 그리고 프로펠러 영역에 1.8M개의 격자수를 사용하여 총 격자수는 약 8.8M개이다. 자유수면 파 해석을 포함하는 실선 캐비테이션 수치해석에 사용된 총 격자수는 약 20M개이다. 여기서, LCT 모형시험 캐비테이션 해석에 사용된 격자계는 $$ y^{+}$$≈1 그리고 실선 캐비테이션 해석 문제에서는 $$ y^{+}$$≈10의 분포가 되도록 설정하였다.

Fig. 4.

Surface and field grids in the stern region

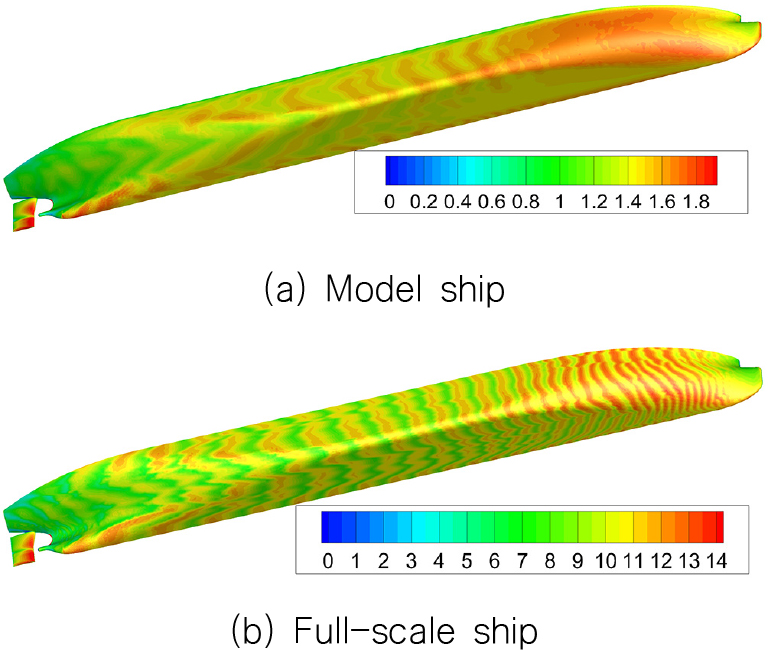
Fig. 5는 앞서 설명한 모형선과 실선의 표면에 생성된 격자계의 $$ y^{+}$$ 분포를 보여주고 있다. 모형선 격자의 경우 $$ y^{+}$$ 값의 영역이 약 1.8 이하의 값들을 가졌으며, 실선의 경우 초기에는 10을 계획했으나 선체주위 유동해석 후 확인한 결과 약 15 이하 값들로 분포하였다.

Fig. 5.

Wall y+ distribution

3.2 선체 공칭반류 척도효과 특성 비교

프로펠러 캐비테이션 및 변동압력의 정량적인 특성은 실험적 또는 수치적으로 재현되는 반류분포 특성에 따라 크게 영향을 받는다. 따라서 모형선과 실선의 선체반류 특성파악과 정량적 추정은 프로펠러 설계 및 성능해석에 매우 중요한 사항이다. 본 절에서는 수치해석에 사용된 반류분포 특성을 먼저 살펴보고자 한다. Hoekstra(1974)는 모형선 보다 실선에서 유동 경계층 두께 감소, 자유수면 영향 및 물리적 현상에 따른 경험과 고찰 등을 통하여 반류 확장(wake extrapolation) 기법을 제안한 바 있다. 그는 등가 속도분포가 3 방향으로 수축(iso-velocity contour contraction)을 가정하였다. 첫째 프로펠러 축 방향으로 수축, 둘째 12시-6시 방향 대칭면으로 수축, 셋째는 이미지 효과로 자유수면 방향으로 이동이다. 그리고 Kim et al.(2013)은 LCT에서 시험적으로 터널 유속변화에 대응하여 경계층 유동변화에 따른 반류분포 특성을 살펴보았다.

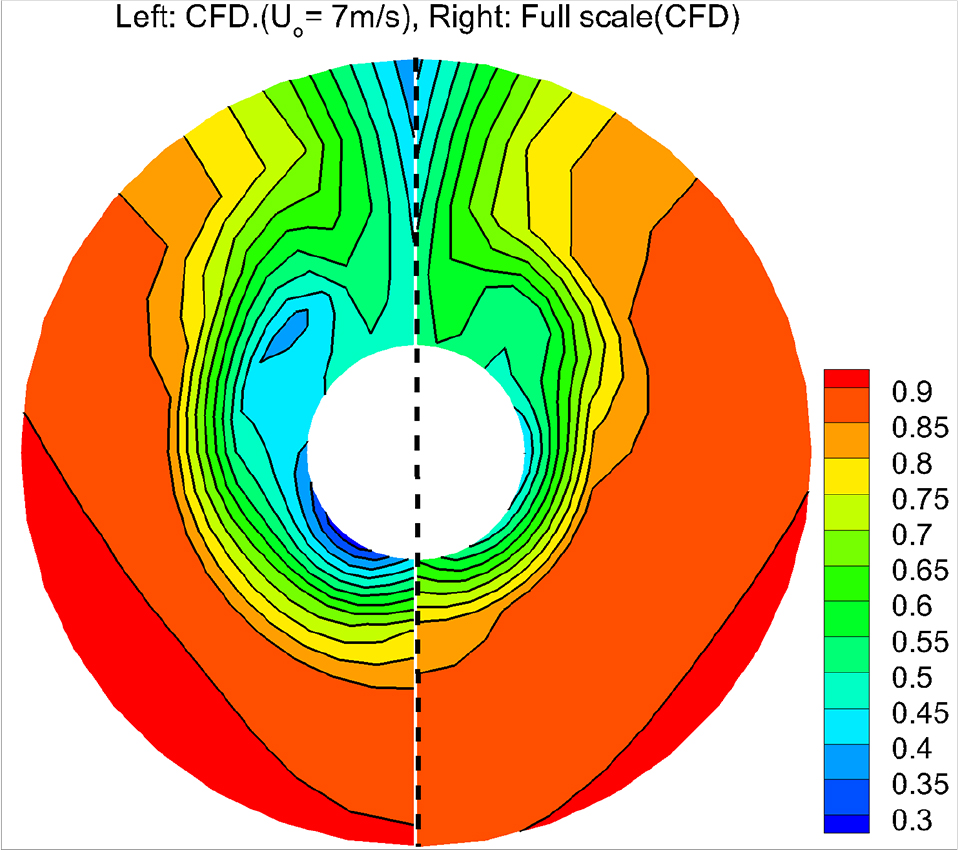
예인수조에서 모형선 자항선속과 LCT에서 캐비테이션 시험 유속에 해당하는 각각의 유입속도(U₀) 1.47m/s, 8.0m/s에 대하여 LCT에서 LDV로 계측한 모형선 공칭반류(Kim et al., 2014) Fig. 6에서 보는 바와 같다. Fig. 7은 LCT 모형시험 조건(Table 2)과 실선 프로펠러 캐비테이션 수치해석 조건(Table 1)에서 공칭반류 CFD 해석결과를 보여준다. Fig. 6과 Fig. 7 경우에 유입속도 또는 스케일이 커지면 즉 유동의 Reynolds수 증가로 인하여 전술한 바와 같이 3방향 반류수축 현상을 확인할 수 있다. 수치해석 결과도 앞서 Hoekstra 제안과 같이 정성적으로 모형선 반류가 실선 반류로 확장되는 것을 확인할 수 있다.

Fig. 6.

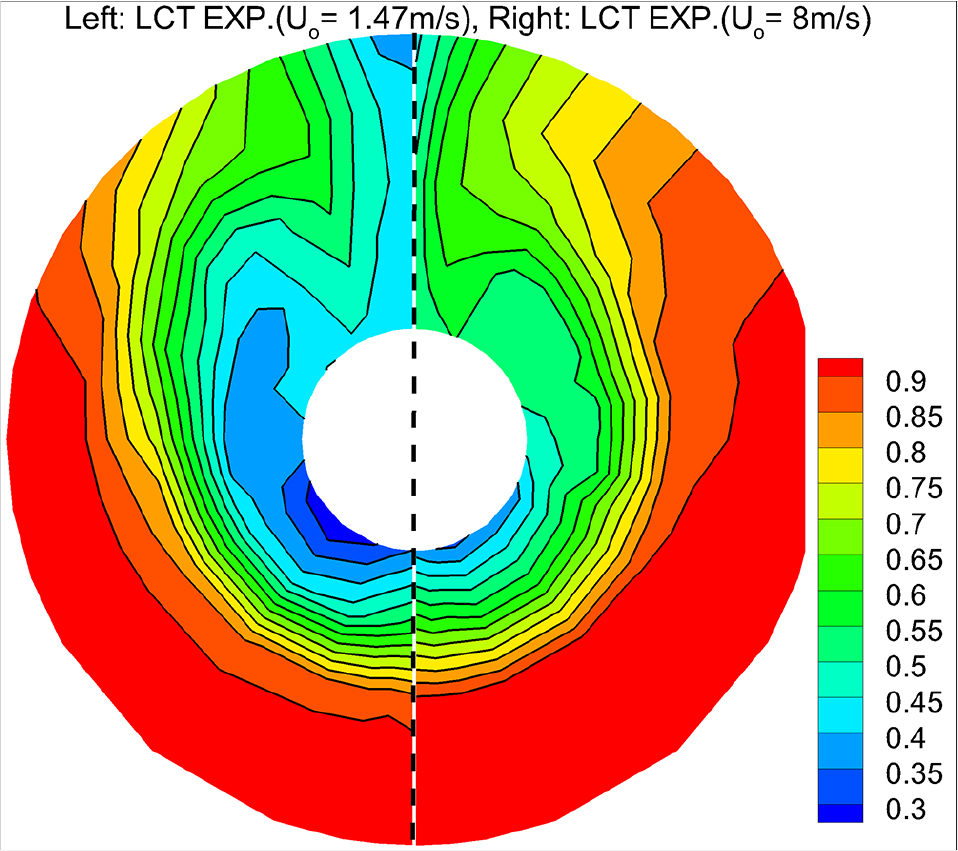
Comparison of nominal axial velocity contours at propeller plane on variation of U0 (LDV measurement at LCT)

Fig. 7.

Contraction of nominal velocity contours at propeller plane using a CFD computation

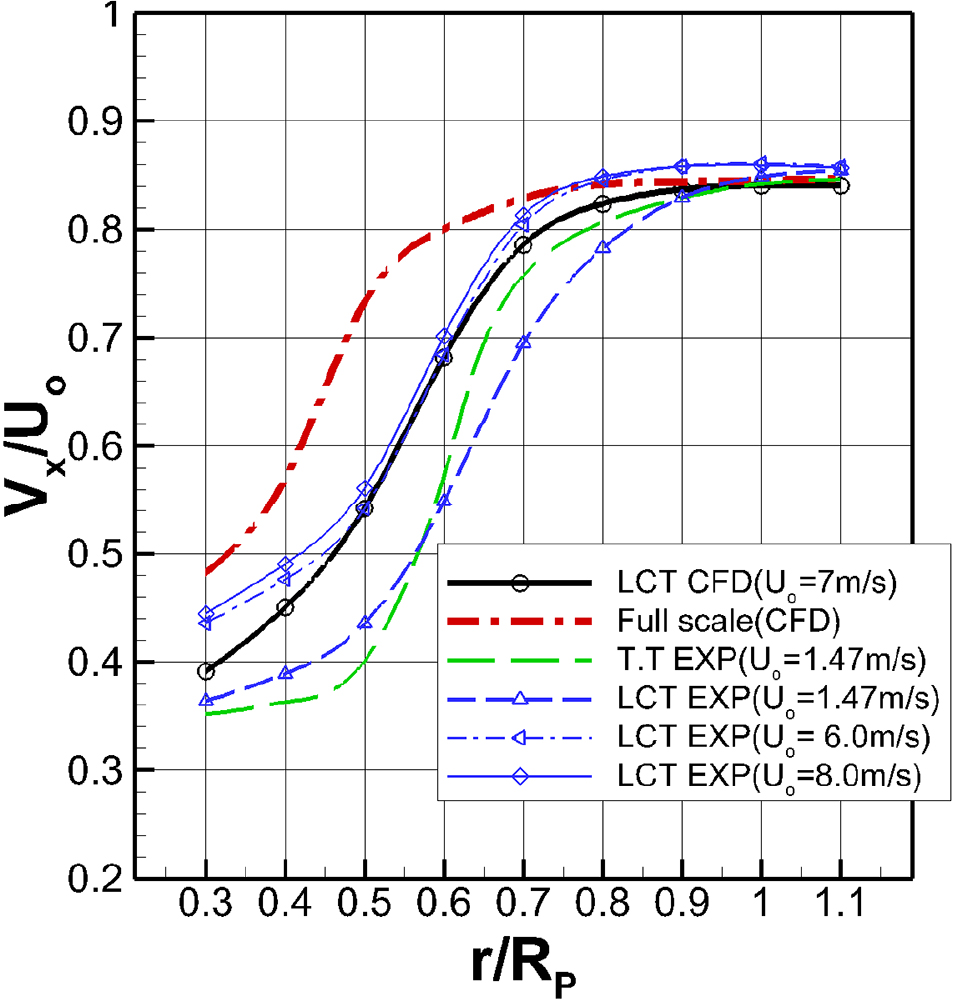
예인수조에서 자항 선속과 LCT(시험부 유속변화 3조건)에서 각각 계측한 반류 그리고 LCT 모형선 시험조건(Fig. 2)과 실선 조건(Fig. 3)에서 수행한 수치해석 결과를 원주방향의 축방향 평균유속 분포는 Fig. 8에서 반경별로 보여준다. 여기서 R_P는 프로펠러 반경을 의미한다. 이 경우에 LCT 모형선 계측결과는 Fig. 8에 보는 바와 같이 U₀가 클수록 유속이 가속되는 분포를 보이며 U₀가 6m/s 이상에 이르면 반류 유동장이 상당히 수렴된 것으로 보인다. 모형선 반류계측 결과도 모형선 시험유속에 따라 달라지는 Reynolds수 영향으로 경계층 유동 변화를 볼 수 있다. 안쪽반경에 해당하는 축 근처 유동 수치해석 결과는 다소 차이를 보인다. 또한 CFD 해석결과로 비교하면 실선조건의 원주방향 평균유속분포는 LCT 모형선 수치해석 결과보다 축 방향으로 반류 수축현상이 현저하다. 전반적으로 반경별로 축 방향으로 약 0.12R_P 만큼 수축 이동으로 보인다. CFD 해석 기반으로 LCT 모형선 조건 및 실선조건에서 반경방향으로 적분한 평균반류는 각각 0.290 및 0.208이며 실선조건에서 평균유속이 약 12% 증가하는 것을 알 수 있다. 수조 자항시험 모형선 선속 U₀=1.47m/s에서 평균 반류는 0.322 이다. 그리고 LCT 계측에서 U₀가 1.47m/s, 6.0m/s, 8.0m/s 일 때 평균반류는 각각 0.333, 0.258, 0.250으로 계산된다. 즉 Reynolds수 증가에 따라 평균유속이 증가하는 경향을 보인다.

Fig. 8.

Comparison of circumferential mean axial velocity distribution at different U0(CFD & Exp.)

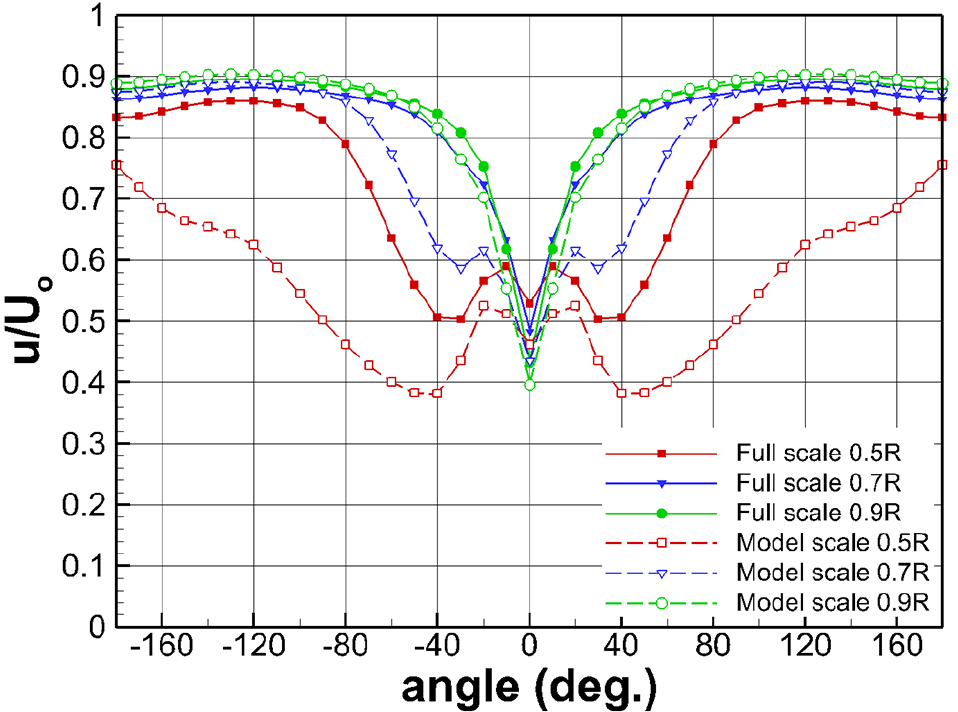
Fig. 9는 Fig. 7 수치해석 결과를 반경별로 원주방향으로 공칭반류 축방향 유속분포 및 반류수축 정도를 보여준다. 이는 Reynolds수 차이에 기인하는 선체표면의 경계층 유동변화로 인하여 바깥반경(outer radius) 보다 안쪽 반경(inner radius) 영역에서 반류 수축이 상대적으로 큰 것을 보여준다.

Fig. 9.

Comparison of circumferential axial velocities distribution by CFD for model & full-scale ship

아직까지는 현실적으로 실선에서 공칭반류 또는 총 유속 계측은 불가능하다. 따라서 모형시험 조건과 실선운항 조건에서 CFD 해석 결과로부터 국부유동 특성을 비교해 보고자 한다.

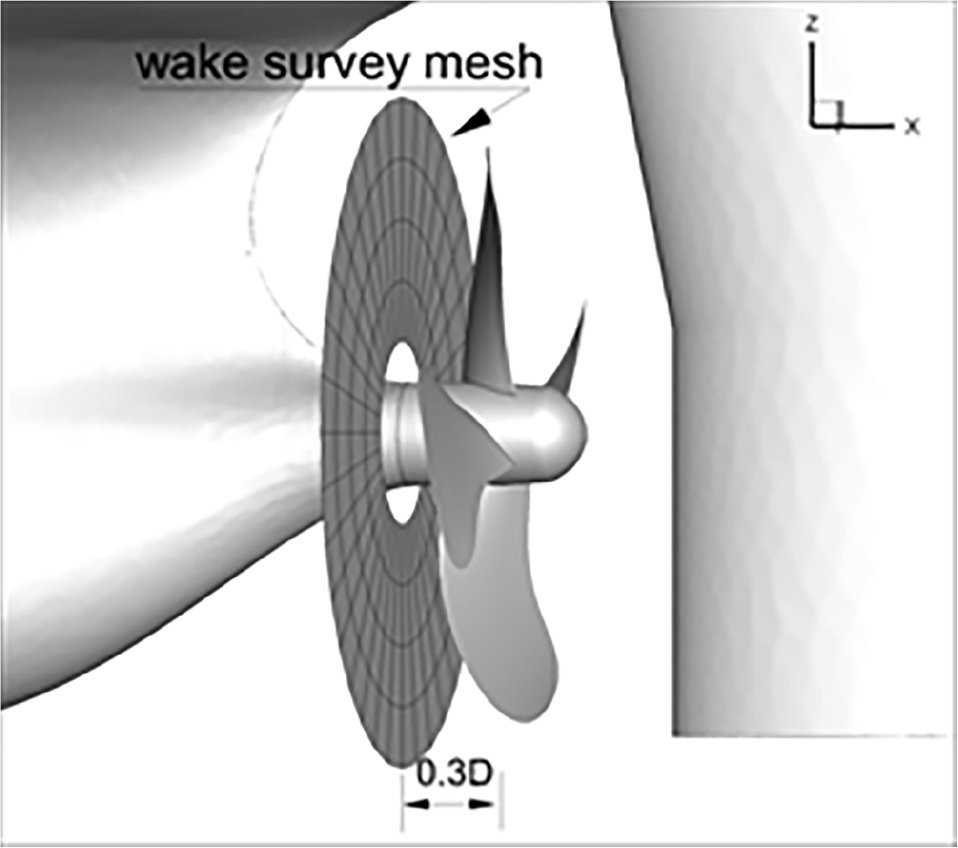
Fig. 11은 선미에서 프로펠러 작동시 프로펠러 전방으로 0.3 Dia. 위치(Fig. 10)에서 계산된 (a) 축 방향 Vx, (b) 반경방향 Vr (c) 원주방향 Vt 각각의 총 유속을 나타낸다. 반류 중에서 프로펠러 캐비테이션성능 모형시험(Table 2)은 프로펠러 추력일치법(K_T identity method)을 적용하고 실선 프로펠러 캐비테이션 성능모사는 Table 1과 같이 실제 운항상태로 설정하였다.

Fig. 10.

Calculation plane of total velocities upstream of the propeller

Fig. 11.

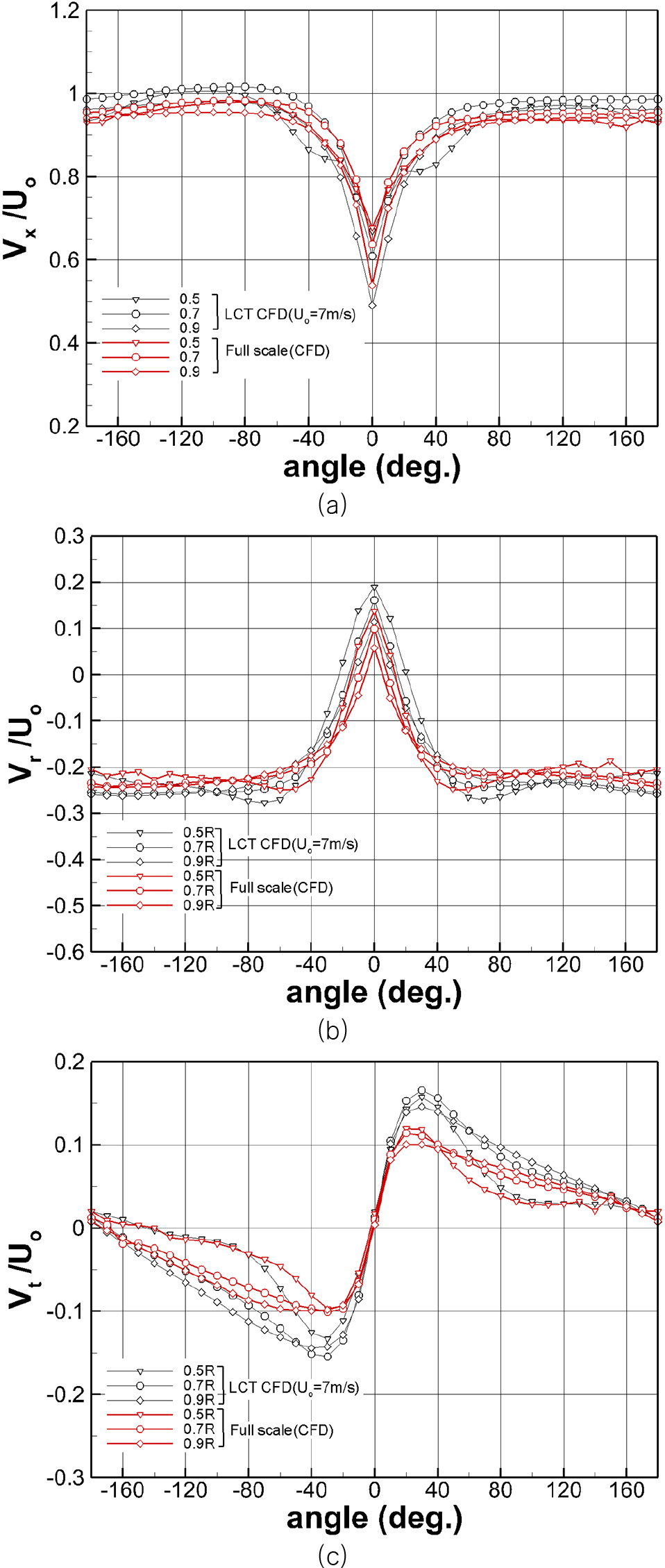
Comparison of total velocity distribution by CFD computation : (a) Axial velocity, (b) Tangential velocity, (c) Circumferential velocity

Fig. 9에서 안쪽 반경에서 모형과 실선 공칭반류 크기와 분포는 차이를 보아는 반면에 총 유속분포는 반경에 무관하게 360도 전 영역에서 상호 정성적 정량적으로 유사한 경향을 보인다. 특히 모형선의 경우에 원주방향 총 유속크기는 캐비테이션이 발생하는 날개각도 영역에서 보다 큰 경향을 보여준다. 이는 모형선 조건에서 수치해석 결과의 캐비테이션 발생량이 상대적으로 적을 것임을 예상하게 한다. 이와 같이 추력일치법 적용 시 특히 선미부 선체반류와 프로펠러 작동으로 발생하는 상호작용 유속(interaction velocity)과 공칭반류로 구성되는 프로펠러 유기속도(induced velocity)와 유효속도(effective velocity)(Carlton, 1994) 합으로 나타나는 총 유속분포가 실선과 모형선에서 반경별로 360도 영역에서 정성적 정량적으로 상호 유사한 경향을 보이고 있다.

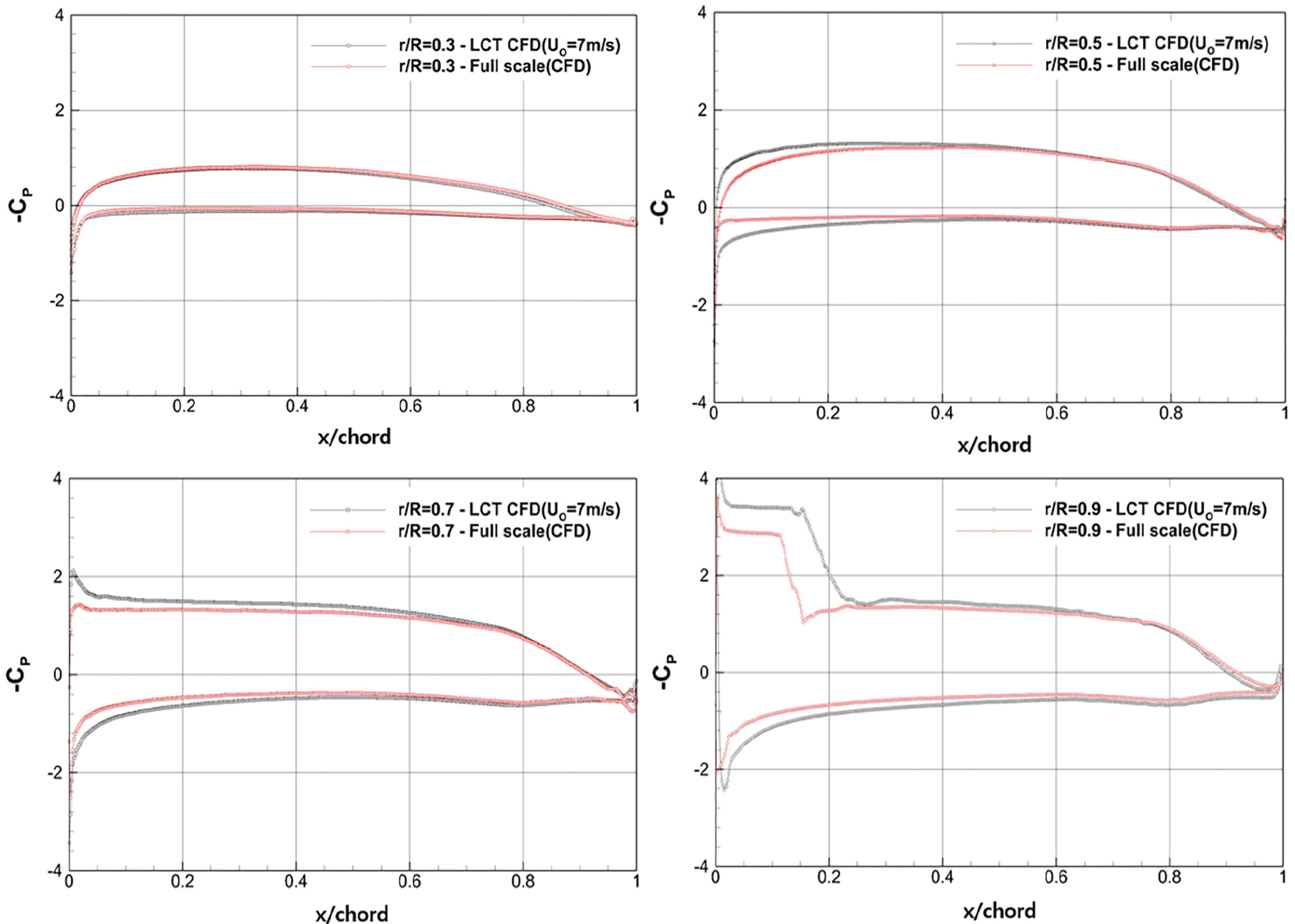
앞서 살펴본 프로펠러 날개 캐비테이션 발생 특성과 날개표면 국부유동 특성을 비교를 위하여 날개표면의 압력분포를 살펴본다. 수치해석 조건은 실선 및 모형선 경우에 대하여 각각 Table 1, Table 2에 보는 바와 같다. Fig. 12는 프로펠러 기준날개 각도가 30도인 경우를 보여준다. Fig. 12의 좌우 열은 각각 압력면 및 흡입면 압력분포, 상하 행은 각각 LCT 모형선 및 실선 프로펠러의 압력분포를 보여준다. Fig. 13는 0.3R, 0.5R, 0.7R, 0.9R 각 반경별로 모형 및 실선 프로펠러의 날개표면의 압력분포 비교를 보여준다. Fig. 12와 Fig. 13를 살펴보면 전반적으로 상호 유사한 경향을 보이며 모형선 프로펠러의 앞날(leading edge) 근처의 압력값 절대치가 실선의 경우보다 크다. 따라서 수치해석상 모형선 조건에서 프로펠러 캐비테이션 발생면적과 변동압력 수준이 실선 경우보다 크게 예측되는 것과 같은 경향을 보인다.

Fig. 12.

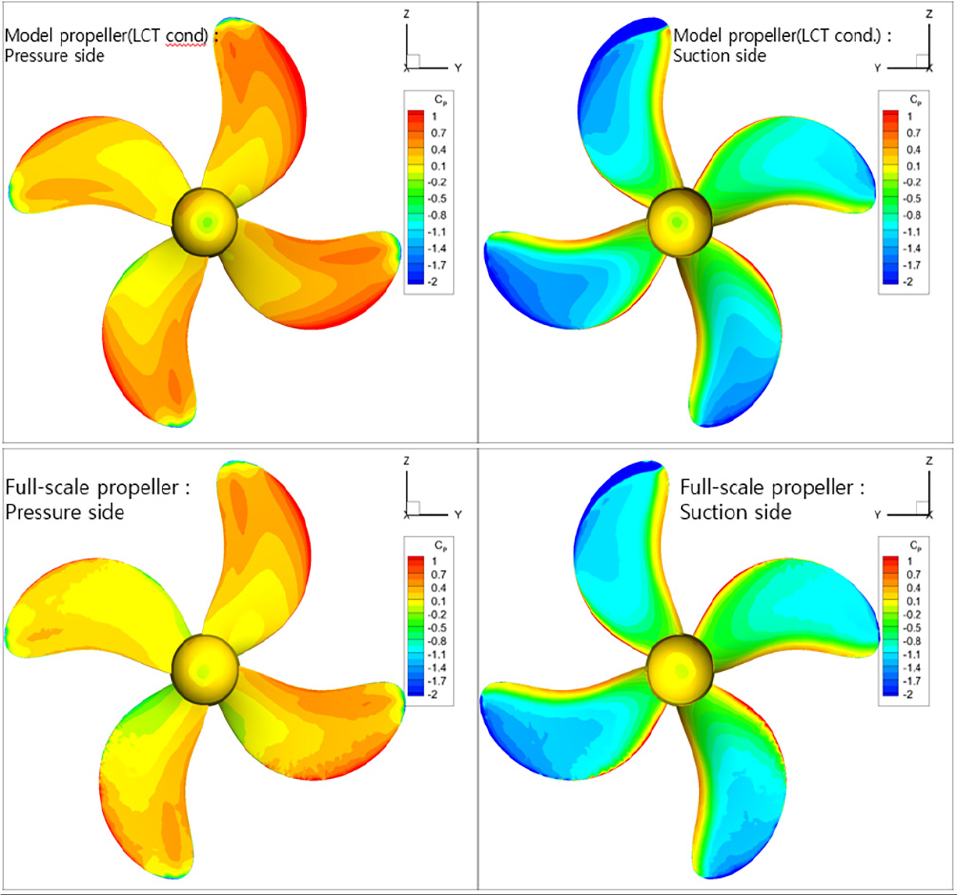
Comparison of computational pressure distribution on propeller blade surface of model propeller with full-scale ship(θ=300)

Fig. 13.

Comparison of computational pressure distribution on blade sections of model propeller with full-scale

3.3 프로펠러 캐비테이션 및 날개표면 압력분포

비정상 캐비테이션 유동 해석은 먼저, 주어진 캐비테이션수의 터널내 압력 조건 그리고 실선의 경우 정수압 조건에서 캐비테이션이 없는 상태에 대해 2°의 회전각도에 해당하는 시간간격으로 3회전 계산하여 프로펠러 주위 비정상 유동을 수렴시켰다. 이후, 캐비테이션을 포함한 해석으로 0.5°의 회전각도에 대응되는 시간간격으로 1.25회전 해석하였다. 본 수치해석에서 변동압력 해석을 위해 충분히 긴 시간의 변동압력 해석은 수행하지 않은 것은 제한된 계산영역인 LCT 조건 해석에 사용된 압력유출 경계조건에 의한 압력의 반사 영향이 해에 나타날 수 있는 수치 해석적 문제 때문이다. 제한된 계산영역에서의 경계조건으로 인한 이러한 수치 해석적 문제에 대한 논의는 향후, 별도 연구를 통해 소개할 계획이다.

대상 프로펠러에서 나타나는 주된 캐비테이션은 프로펠러의 앞날부터 발생하는 얇은 층 캐비테이션(sheet cavitation)과 날개 끝(tip)에서 발생하는 날개 끝 보오텍스 캐비테이션(tip vortex cavitation)으로 구성된다. Fig. 14는 MCR 조건에서 LCT 모형시험과 실선시험 조건에서 관찰된 프로펠러 캐비테이션들과 각각에 해당하는 수치해석 결과들을 함께 비교하고 있다. 그림에서 프로펠러의 날개각도(Ɵ)는 12시 방향을 0°로 하며 프로펠러가 회전하는 방향을 양의 날개각도로 한다. 비교하는 날개 위치각도는 30°, 40°, 50°, 60° 이다. LCT 모형선 상태에서 얇은 층 캐비테이션은 수치해석 결과가 모형시험 결과와 비교적 만족스러운 일치를 보여주고 있다. 반면에 날개 끝 보오텍스 캐비테이션은 수치적으로는 다소 적게 예측되고 있으나 정성적으로는 유사한 형상을 보여주고 있다. 이는 날개 끝 보오텍스 중심부 근처 급격한 압력변화 모사에 대한 심화 연구가 필요하다.

Fig. 14.

Comparison of Propeller cavitation patterns obtained from experimental observation and CFD computation for model & full-scale ship propeller

그리고 실선 프로펠러 캐비테이션 관찰 사진은 날개 앞날과 날개 끝 영역을 보다 확대 촬영되었으며 실선에서 촬영 각도는 모형선 시험 캐비테이션 관찰 각도와 일부 차이가 있다. 실선관찰 결과는 모형선 프로펠러 캐비테이션 관찰결과와 일부 차이는 있으나 전반적으로 유사한 경향을 보인다. 또한 실선 수치해석 결과는 모형시험, 실선시험 및 모형선 수치해석 결과보다 캐비테이션 발생량이 다소 작게 추정되었지만 정성적인 경향은 좋은 일치를 보여주고 있다. 이는 캐비테이션 발생량과 직접적인 관계가 있는 캐비테이션 변동압력의 수치해석 결과 비교에서도 유사한 경향을 보여주고 있다.

Fig. 15는 Kim et al.(2017)의 연구에서와 같이 프로펠러 날개 끝 주위에 격자를 집중한 경우와 그렇지 않은 경우에 대하여 날개각도 30°와 60°에 위치에서 날개 끝 보오텍스 캐비테이션 수치해석 결과 비교를 보여준다. 앞서 Fig. 14에서 보이는 수치해석 결과는 날개 끝 주위에 격자를 집중한 경우이다.

Fig. 15.

Tip grid refinement versus tip vortex cavitation

최근 연구결과들을 살펴볼 때 프로펠러에서 박리되는 날개 끝 보오텍스 캐비테이션의 경우 RANS 난류모형보다 DES (Detached Eddy Simulation) 또는 LES(Large Eddy Simulation)를 사용할 때 모형시험 결과에 보다 근접하는 것을 알 수 있다.(Salvatore et al. 2009). 그러나 Kim et al.(2017)의 연구 결과에서도 볼 수 있듯이, 본 연구를 통해 RANS 난류모형 조건에서 격자집중으로 캐비테이션 발생량과 변동압력 추정은 어느 정도 타당하게 해석할 수 있음을 알 수 있다.

3.4 선미 변동압력

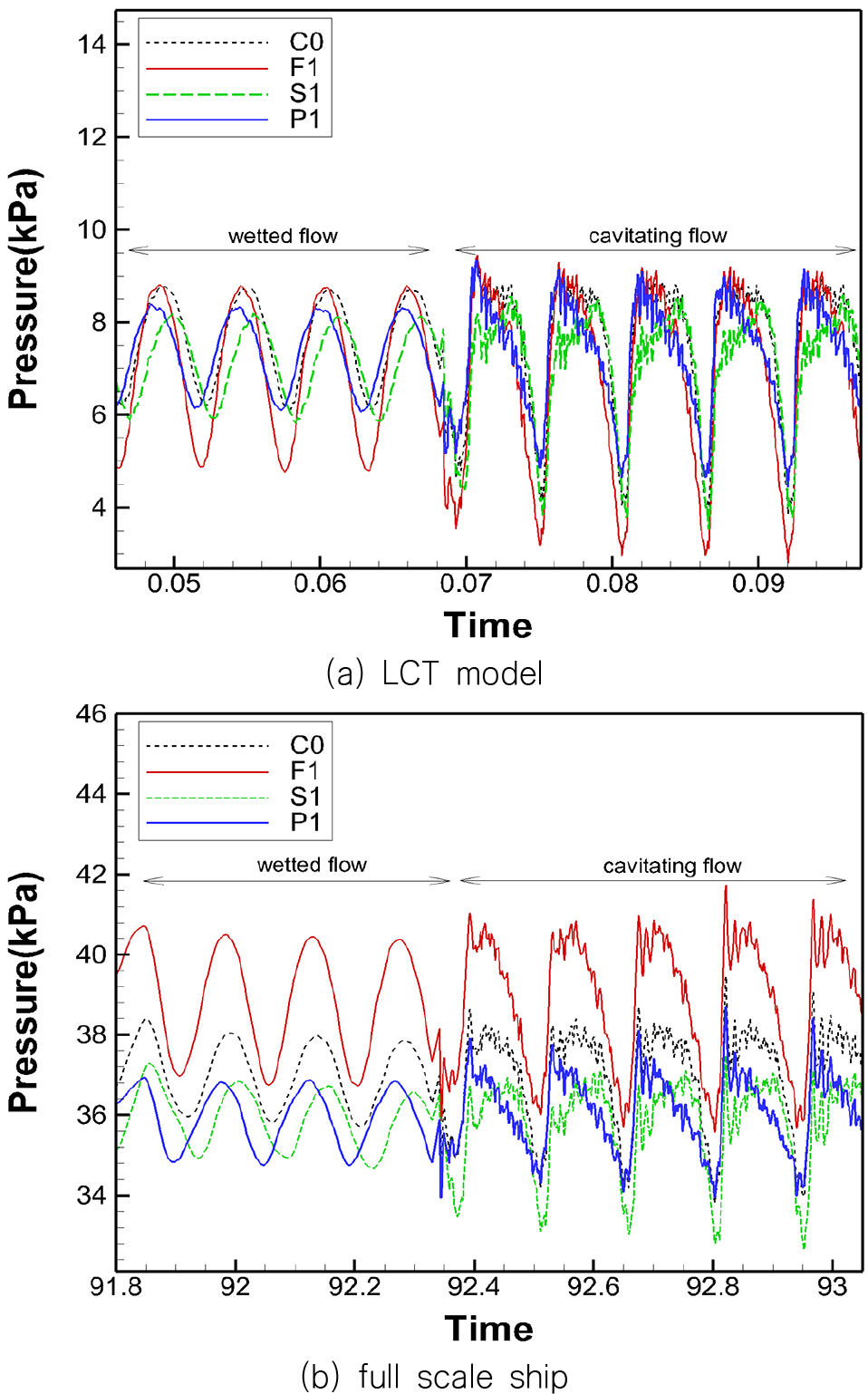
모형선 및 실선에 대한 변동압력 계측 및 수치해석은 3.2절에서 수행한 프로펠러 캐비테이션 관찰시험 및 수치해석과 동일한 조건에 수행되었다. Fig. 16은 Fig. 1에서 설명한 C0, F1, S1, P1 압력계측 위치에서 모형선 및 실선 조건에서 캐비테이션이 발생하기 전과 발생한 후의 압력변화를 보여주고 있다. 3.2절에서 설명한 바와 같이 캐비테이션 해석은 모형선과 실선 모두 1.25회전 동안 수행하고 이때의 시계열(time series) 데이터를 바탕으로 변동압력 주파수 해석을 수행하였다. 실선의 경우 정수압(hydrostatic pressure)의 차이들이 변동압력 결과에 나타나고 있으며, 캐비테이션의 영향으로 변동압력의 진폭이 커지고 고차 성분들이 압력 변화에 나타나는 것을 볼 수 있다.

Fig. 16.

Time series of the pressure fluctuations computed for the LCT model ship and Full scale ship

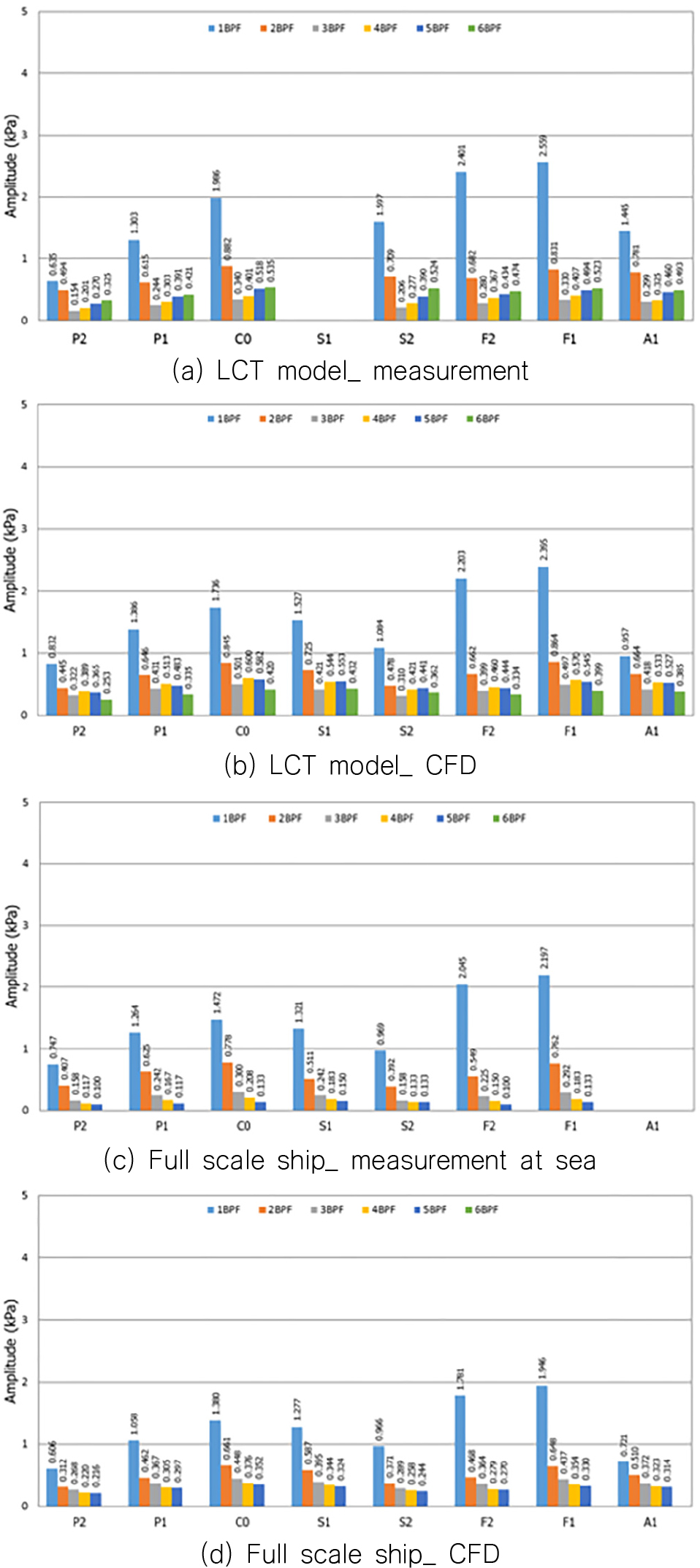
Fig. 17에 보여주는 모형선 시험과 해당하는 수치해석 결과는 실선으로 확장(ITTC, 1987)하여 각 계측점마다 날개 주파수 별로 변동압력 진폭을 보여준다.

Fig. 17.

Pressure fluctuation induced by propeller cavitation for the LCT model ship and Full scale ship

모형선과 실선 변동압력 계측치들은 각각의 경우에 해당하는 수치해석 결과보다 정량적으로는 다소 크게 나타났다. 그리고 모형선에 대한 계측과 수치해석 결과는 각각의 경우에 해당하는 실선 계측과 수치해석 결과보다 정량적으로 다소 큰 값을 보여준다. 이는 모형 및 실선에서 발생하는 복잡한 캐비테이션 현상 재현에 수치해석상 수반하는 수치감쇠 및 모델링 오차 등으로 한계가 있는 것으로 판단된다.

그러나 실선과 모형선에 대한 수치해석 결과는 정량적 차이가 작으며 정성적으로 상당히 유사한 경향을 주고 있다. 따라서 실선 프로펠러 캐비테이션 유기 변동압력 추정에 CFD 기법의 적용 가능성을 보여주며 결과의 정확도를 일부 유추할 수 있을 것으로 사료된다.

4. 결 론

본 논문에서는 실선과 모형선 프로펠러에 대한 캐비테이션 관찰과 변동압력 계측자료가 있는 MR 탱커선을 대상으로 수치해석을 수행하였다. CFD 수치해석기법으로 실선과 모형선의 반류, 프로펠러 캐비테이션 및 변동압력 수준을 예측하였다. 실선과 모형선의 프로펠러 캐비테이션 발생과 변동압력 수준 수치해석 예측치가 모형 및 실선시험 결과와 정성적으로 유사한 경향을 보여주며, 정량적으로도 활용가치가 있는 결과를 주고 있다.

이것은 실해역에서 실선 반류계측 시험은 불가능하지만 간접적으로 LCT에서 재현된 반류와 반류분포 수치해석 결과가 비교적 타당하기 때문으로 판단된다. 또한 수치해석 결과 모형 프로펠러와 실선 프로펠러 작동 시 총 유속 분포 및 날개면 압력분포도 상호 타당한 결과를 보여준다.

LCT에서 LDV로 계측한 공칭반류 자료 비교와 Reynolds수 변화에 대한 공칭반류 수치해석 결과 비교에서는 공히 Hoekstra (1974)의 반류수축 현상을 확인하였다. 대상선 실선에서는 선체표면 경계층유동 두께가 보다 얇아져서 모형선(U₀=7.0 m/s 기준) 수치해석 결과 비교에서는 평균유속이 약 12% 증가를 나타낸다.

모형선과 실선 프로펠러 날개 끝 하류 캐비테이션 길이가 다소 짧거나 해석되지 않은 경우는 수치감쇠와 수치 모델링 오차로 인한 것으로 판단된다. 향후 다른 선종에 대한 검증연구, 난류모형 및 수치해석 기법 등에 대한 지속적인 연구가 필요한 것으로 사료된다.

Acknowledgments

본 논문은 선박해양플랜트연구소(KRISO)가 수행 중인 주요사업(PES3393)과제와 민군기술개발과제(PNS3450)의 지원으로 작성 되었습니다.

References

• Ahn, J. W., Paik, B. G., Seol, H. S., Park, Y. H., Kim, G. D., Kim, K. S., Jung, B. J. & Choi, S. J., 2016. Comparative study of full-scale propeller cavitation test and LCT model test for MR tanker. Journal of the Society of Naval Architects of Korea, 53(3), pp.171-179. [https://doi.org/10.3744/SNAK.2016.53.3.171]
• Choi, G. H., Chang, B. J., Hur, J. W. & Cho, D. S., 2011. Comparison of cavitation patterns between model-scale observations using model and full-scale wakes and full-scale observations for a propeller of crude oil carrier. Journal of the Society of Naval Architects of Korea, 48(1), pp.15-22. [https://doi.org/10.3744/SNAK.2011.48.15]
• Choi, J.E. Min, K.S. Chung, S.H. & Seo, H.W., 2003. Study on the scale effects on the flow characteristics around a full slow-speed ship. Proceedings of the 8th Numerical Ship Hydrodynamics, Pusan, Republic of Korea, 22 September 2003.
• Hoekstra M. 1974. Prediction of full scale wake characteristics base on model wake survey. International Shipbuilding Progress, 22(250), pp.204-219. [https://doi.org/10.3233/ISP-1975-2225002]
• Hochkirch, K. & Mallol, B., 2013. On the importance of full-scale CFD simulations for ships. Proceedings of the 12th International Conference on Computer Applications and Information Technology in the Maritime Industries, Cortona, Italy, 15-17 April 2013.
• ITTC, 1987. Report of The Cavitation Committee, 18th International Towing Tank Commitee, Kobe, Japan, October 1987.
• Ji, B., Luo, X. W., Wu, Y. L., Liu S. H., Xu, H. Y. & Oshima A., 2010. Numerical investigation of unsteady cavitating turbulent flow around a full scale marine propeller. 9th International Conference of Hydrodynamics, Shanghai, China, 11-15 October 2010.
• Carlton, J.S., 1994. Marine Propeller and Propulsion, Butterworth-Heinemann.
• Kim, K. S., Ahn, J. W., Park, Y.H., Kim, G. D., Kim, S. P., Yu, Y. W. & Lee C. S., 2013. Correlation study on pressure fluctuation measurement at large cavitation tunnel with full-scale data for two container carriers. 12th International Symposium on Practical Design of Ships and Other Floating Structures, Changwon, Republic of Korea, 24-27 October 2013.
• Kim, J. I., Park, I. R., Kim, K. S. & Ahn, J. W., 2017. Numerical analysis of non-cavitating and cavitating performance of a SVA Potsdam propeller. Journal of the Society of Naval Architects of Korea, 54(3), pp.215-226. [https://doi.org/10.3744/SNAK.2017.54.3.215]
• Kim, K. S. Kim, K. Y. Ahn, J. W. & Lee J. T, 2000. Effect of Reynolds number, leading edge roughness and air content on the cavitation performance of model propellers. Journal of the Society of Naval Architects of Korea, 37(1), pp.10-25.
• Kim, K. S. et. al., 2009. Construction of the low noise large cavitation tunnel. KRISO Report No. UCPNS101A -2100-7.
• Kim, K. S., Park, Y.H., Ahn, J. W., Kim, G. D. & Kim, S. P., 2010. A Study of propeller cavitation of a LNG carrier in large cavitation tunnel. Proceedings of Society of Naval Architects of Korea, July 2010.
• Kim, K. S., Paik, B. G., Ahn, J. W., Park, Y. H. & Kim, G. D., 2010. A Propeller cavitation test and PIV measurements method in LCT and MCT of MOERI. Proceeding of International Propulsion Symposium IPS'10, Okayama, Japan, 19-20 April 2010.
• Kim, K. S., Ahn, J. W., Moon I. S. et al., 2014. Development of cavitation performance control technology for environment-friendly propulsion. Final report of KRISO.
• Launder, B.E., Reece, G.J. & Rodi, W., 1975. Progress in the development of a Reynolds-stress turbulence closure. Journal of Fluid Mechanics, 68(3), pp.537-566. [https://doi.org/10.1017/S0022112075001814]
• Patankar, S.V., 1980. Numerical Heat Transfer and Fluid Flow, Hemisphere, Washington D.C.
• Salvatore, F., Streckwall, H. & Terwisga, T., 2009. Propeller cavitation modelling by CFD-results from the VIRTUE 2008 Rome Workshop. First International Symposium on Marine Propulsors smp'09, Trondheim, Norway, 22-24 June 2009.
• Sauer J., 2000. Instationär kavitierende Strömungen-Ein neues Modell, basierend auf Front Capturing (VoF) und Blasendynamik. PhD. thesis, Universität Karlsruhe.
• Siemense, 2018. STAR-CCM+ 11.04 User Guide, URL: https://support.industrysoftware.automation .siemens.com/general/documentation.shtml (Accessed 1 January 2018).
• Yang, H. U., Kim, B. N., Yoo, J. H. & Kim, W. J., 2010. Wake comparison between model and full scale ships using CFD. Journal of the Society of Naval Architects of Korea, 47(2), pp.150-162. [https://doi.org/10.3744/SNAK.2010.47.2.150]