176k Bulk Carrier에 대한 신개념 타입의 Pre-Swirl Duct의 개발 및 CFD 해석
Abstract
This paper shows numerical results for the estimation of the propulsor efficiency of Pre-Swirl Duct for 176k bulk carrier as well as its design method. Reynolds averaged Navier-Stokes equations have been solved and the k-epsilon model applied for the turbulent closure. The propeller rotating motion is determined using a sliding mesh technique. The design process is divided into each part of Pre-Swirl Duct, duct and Pre-Swirl Stator. The design of duct was performed first because it is located further upstream than Pre-Swirl Stator. The distribution of velocity through the duct was analyzed and applied for the design of Pre-Swirl Stator. The design variables of duct include duct angle, diameter, and chord length. Diameter, chord length, equivalent angle are considered when designing the Pre-Swirl Stator. Furthermore, a variable pitch angle stator is applied for the final model of Pre-Swirl Duct. The largest reduction rate of the delivered power in model scale is 7.6%. Streamlines, axial and tangential velocities under the condition that the Pre-Swirl Duct is installed were reviewed to verify its performance.
Keywords:
CFD, Pre-Swirl Duct, Bulk carrier, Propulsion performance, Energy saving device키워드:
전산유체역학, 전류고정덕트, 살물선, 추진성능, 에너지 절감 장치1. 서론
최근 전 세계적으로 지구온난화 문제가 심각해짐에 따라 친환경 선박 기술에 (green ship technology)에 대한 관심이 높아지고 있다. 국제 해사기구(International Maritime Organization, IMO)에서는 에너지 효율 설계 지수(Energy Efficiency Design Index, EEDI)를 적용하여 신조 및 기존 운항 선박의 이산화탄소 배출량을 규제하고 있다. 이에 따라 전 세계적으로 EEDI를 감소시키기 위한 여러 가지 방안들이 활발히 연구되어지고 있으며, 그 중 에너지 저감 장치(energy saving device)를 부착하여 추진효율 개선을 통한 EEDI 감소 효과를 노리는 기술 연구가 활발히 진행 중에 있다.
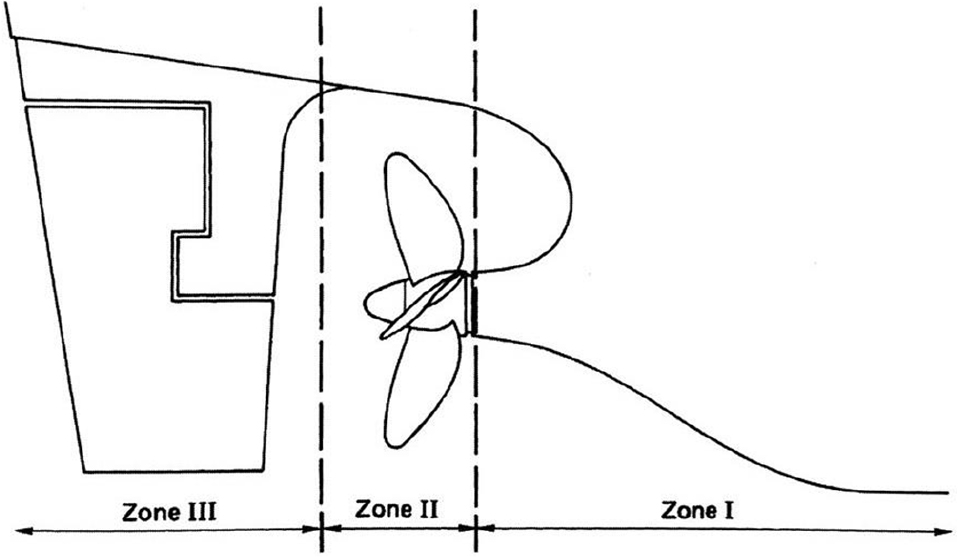
에너지 저감 장치는 장착 위치에 따라 Fig. 1과 같이 크게 3가지 영역으로 분류할 수 있다(Carlton, 1994). ZoneⅠ은 프로펠러 앞쪽에 위치하여 프로펠러의 유입류를 개선하여 효율을 증가시키는 장치로 대표적으로 전류고정날개(Pre-Swirl Stator, PSS), 전류고정덕트(Pre-Swirl Duct, PSD) 등이 해당된다. Zone Ⅱ에서는 프로펠러 자체의 형상의 변화 및 회전에너지를 회수하는 개념으로 효율을 증가시키며, 대표적으로 상반회전프로펠러(Contra-rotating Propeller, CRP), 팁 레이크 프로펠러(tip rake propeller) 등이 있다.
Zone Ⅲ는 프로펠러 후류를 개선시키거나 프로펠러 허브에 발생하는 허브 와류(Hub vortex)를 감소시킴으로써 추진 효율을 향상 시킬 수 있는 장치로, 비대칭 타 (twisted rudder), 추력날개(thrust fin), 러더 벌브(rudder bulb) 등이 있다.
본 논문은 전류고정덕트에 대한 내용을 다루고 있다. 이러한 전류고정덕트는 덕트와 전류 고정날개가 결합된 형태를 가지며, 덕트의 추력 및 반류개선 효과와 전류고정날개의 회전에너지 회수의 효과를 동시에 갖는 장치이다.
이전에는 Fig. 2와 같이 덕트가 크고, 전류고정날개가 덕트 중심축 안쪽에 위치하는 형태를 가졌으며, 이러한 전류고정덕트는 주로 저속비대선에 적용되어 약 3~8% 추진효율 개선효과를 보이는 것으로 확인된 바 있다.
그러나 최근에는 선박의 선미부 선형이 날씬해지면서 Fig.3과 같이 덕트의 크기를 줄이고 전류고정날개를 크게 하는 등 다양한 형상의 전류고정덕트가 개발되고 있다.
그러나 위 2가지 전류고정덕트는 전류고정날개가 안쪽에 있기 때문에 덕트의 가속 효과를 방해 할 수 있으며, 덕트와 고정날개가 만나는 영역에서 코너 보텍스가 발생하여 효율을 저감시킬 수 있다. 또한 현재 일정피치 전류고정날개(constant pitch angle type Pre-swirl Stator)가 적용되어 지고 있으나, 이는 제작의 용이성을 위한 것으로써 덕트의 내부와 외부의 유속 및 유동각의 차이가 큰 PSD의 경우에는 각 반경에서 적절치 못한 받음각(angle of attack)을 가질 가능성이 있다.
이에 따라 선행연구에서 Song et al. (2013)은 위 문제점을 개선시키기 위하여 Fig. 4와 같이 덕트를 상류로 위치시켜 신개념의 PSD를 설계하였다. 또한 CFD를 이용하여 기존 Type과 균일 유동장(uniform flow field)에서 안쪽에서 생기는 보텍스 크기 및 압력계수, 저항성능을 비교하였다. 그러나 이는 균일류 조건에서 진행된 연구이다.
본 연구에서는 상용코드인 Star-CCM+를 이용하여 자항상태에서 신개념 전류고정덕트의 최적화 연구를 수행하였고, 다음 3가지 과정으로 진행하였다.
첫째로 유입류를 먼저 받는 덕트의 크기 및 상하부 받음각을 변화시켜가며 설계하고, 성능 및 상하부에서의 유선을 비교하였다. 둘째로, 덕트를 지난 유속을 고려하여 일정피치 전류고정날개를 최적화 하였고, 설계 방법을 4.2절에 기재하였다.
셋째로, CFD를 이용하여 덕트의 안쪽, 바깥쪽 유입각을 분석하여, 반경별 변화피치 전류고정날개(variable pitch angle type Pre-swirl Stator)를 설계하고, 성능 및 유동특성을 분석하였다.
위의 3가지 과정을 통해 본 연구에서는 효율적인 신개념 전류고정덕트에 대한 개념설계를 제시하였다.
2. 대상 선형
대상선형은 176k bulk carrier이다. 대상선형, 프로펠러의 주요 요목은 Table 1, Table 2와 같다.
3. 수치 해석 기법
3.1 지배방정식 및 해석 기법
신개념 전류고정덕트의 추진성능 향상을 확인하기 위해 범용소프트웨어 Star-CCM+ 11.02 version을 사용하였으며, 비압축성 난류 유동의 지배방정식은 연속방정식과 Reynolds averaged Navier-Stokes equation을 사용하였으며 다음과 같이 표현된다.
| (1) |
| (2) |
지배방정식의 해는 유한체적법(Finite Volume Method, FVM)을 이용하여 구하였으며, 난류모델은 k-ɛ model을 사용하였다. 벽면에서 첫 번째 격자점까지의 무차원거리, y+는 30으로 설정하였다.
3.2 경계 조건 및 격자 구성
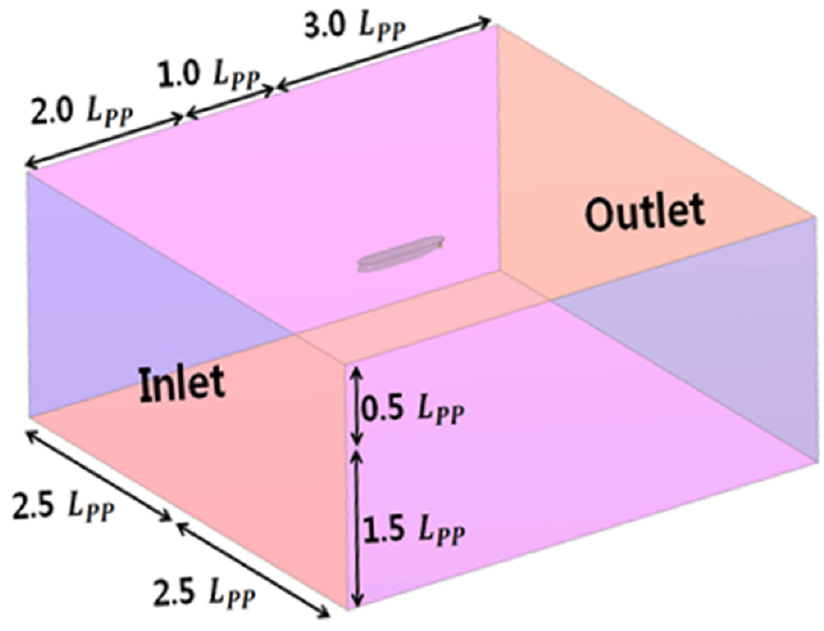
추진성능을 확인하기 위해 예인 및 자항 조건에서 계산을 수행하였으며, 모형 스케일의 설계속도인 0.917m/s에서 계산을 수행하였다. 해석영역의 크기는 Lpp를 기준으로 Fig. 5와 같이 설정하였으며, 충분한 거리를 두어 경계가 유동해석에 영향을 주지 않도록 해주었다. 고정된 모형선에 유속이 흘러 들어와 상대속도가 생성되도록 하기 위해 경계조건은 Inlet, Top, Bottom은 velocity inlet, Outlet은 pressure outlet, Side는 symmetry로 구성하였다.
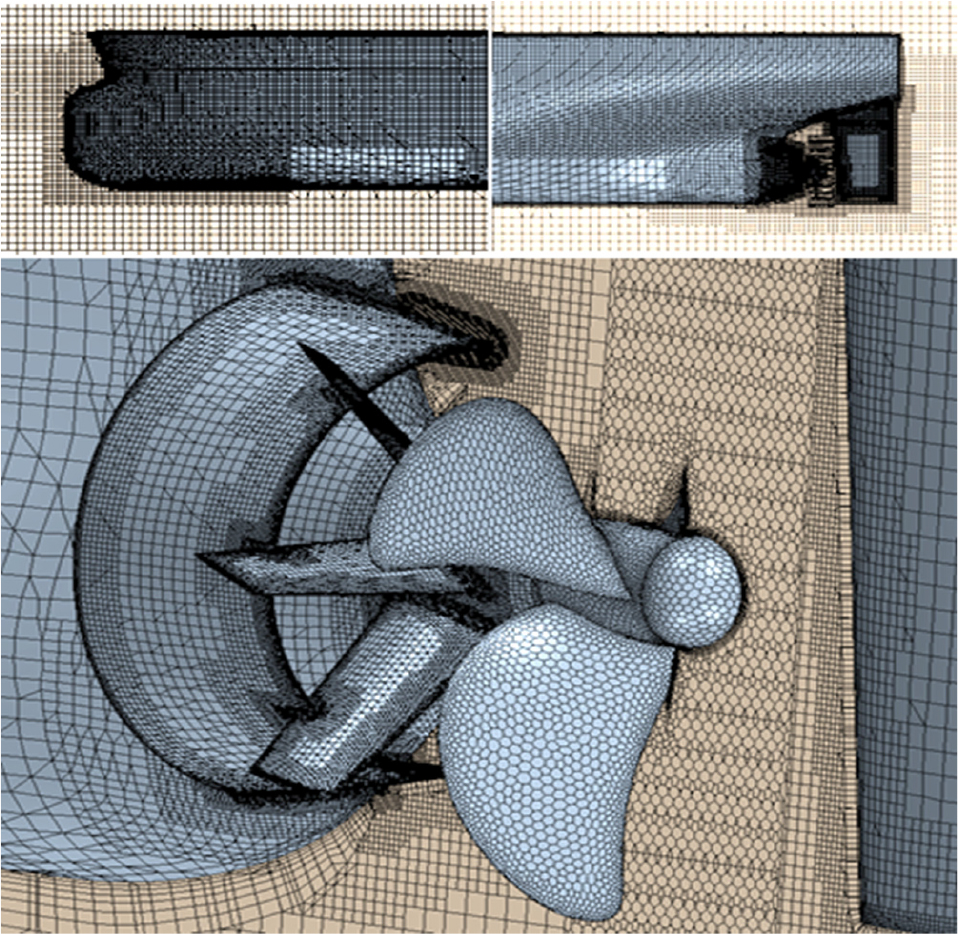
격자 구성은 Fig. 6와 같으며, 유속의 변화가 상대적으로 클 것으로 예상되는 선수부 및 선미부에 격자를 조밀하게 생성해주었다. 전체적인 격자는 트리머 격자(trimmed mesh)로 생성해주었으며, 격자의 크기가 전체 영역에서 급격하게 변화하지 않게 생성해주었다. 프로펠러 회전영역은 다각형 격자(polyhedral mesh)로 생성해줌으로써 계산의 정확도를 높이고자 하였다. 또한 유속이 급격하게 변하는 벽면 근처 유동을 정확히 해석하기 위해 Star-CCM+에서 제공하는 Prism layer를 이용하였으며 벽면으로부터 무한유동까지 유속변화가 점차 작아지는 것을 고려하여 격자의 크기가 벽면에서부터 점차 커지도록 구성해주었다. 또한, Prism layer의 적용 시 격자가 곡률을 가지는 벽면을 따라 규칙적으로 구성되기 때문에 수치해석 해의 정확도를 높이는 효과가 있을 것으로 보인다. Prism layer는 총 7개 y+는 약 60으로 설정하였다. 본 연구에서 사용된 격자구성의 검증을 위해 Song et al. (2013)에서 진행되었던 저항실험 결과와 본 연구에서 계산한 CFD 결과를 비교하였을 때 3% 미만의 차이가 나는 것을 확인하였으며 이를 바탕으로 본 연구의 격자구성이 적합하다고 판단하였다. 모형실험과 CFD의 결과는 Table 3에 나타내었다. 총 격자수는 Case별로 조금씩 다르며 약 450만개에서 500만개로 사이로 구성하였다.
4. 에너지 저감 장치의 설계 및 수치 해석 결과
본 연구에서는 덕트와 전류고정날개가 결합한 형태를 가지는 PSD를 최적화하기 위해 각 장치 별 설계를 진행하였다. 유동의 흐름순서에 맞게 상대적으로 상류에 위치한 덕트의 설계를 우선적으로 진행하였으며, 최적화 된 덕트를 지난 유동을 분석하여 전류고정날개의 설계에 이용하였다.
4.1 덕트의 설계 및 수치해석 결과
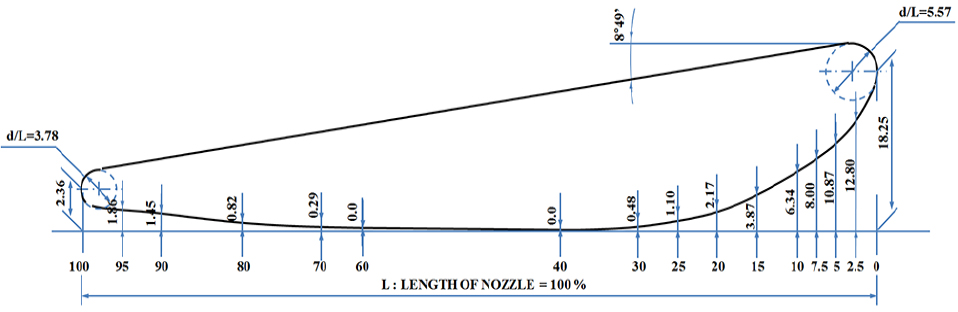
본 연구에서 사용한 덕트의 단면은 Fig. 7에 나타낸 MARIN's Nozzle No. 19A이다.
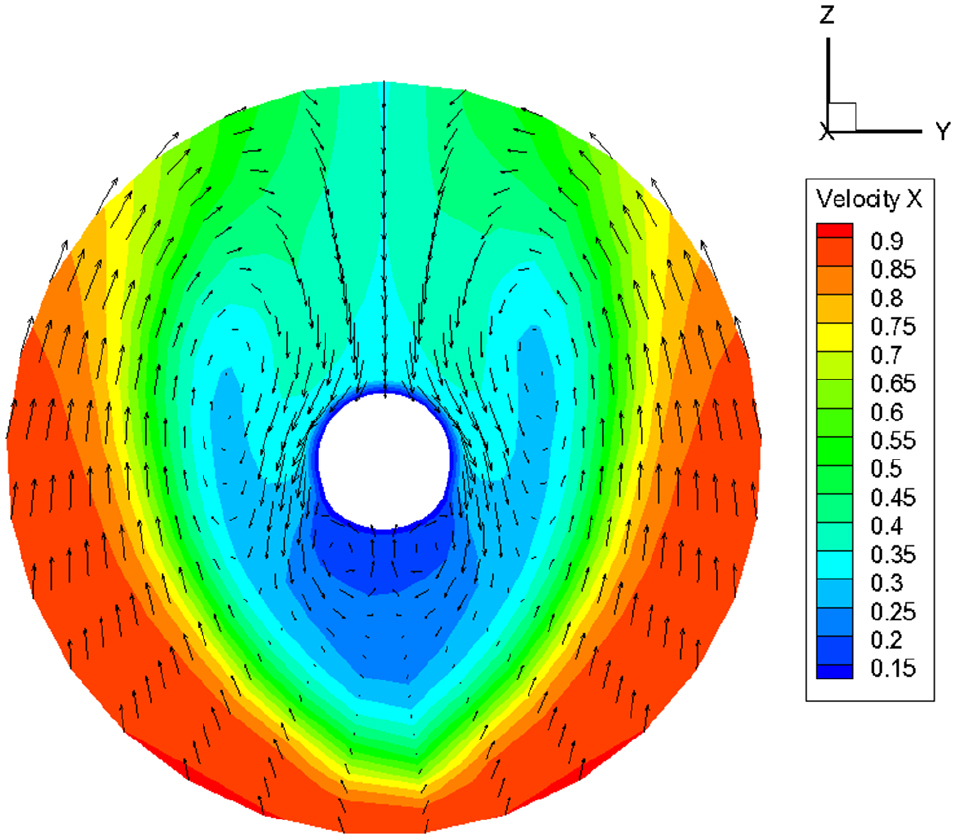
덕트의 설계변수는 덕트의 직경, 코드길이, 그리고 위 아래 단면의 경사각으로 설정하였다. 기준이 되는 덕트의 직경을 결정하기 위해 알몸선체(Barehull) 상태에서의 반류분포를 확인해보았으며, Fig. 8에 나타내었다. 본 연구에서 사용한 덕트는 가속덕트이기 때문에 덕트가 저속구간에 위치하도록 초기 직경을 결정하였으며, 덕트 상하부의 경사각은 Song et al. (2013)에서 사용하였던 값을 이용하였다. Table 4에 case 1의 덕트의 제원을 모형 스케일로 나타내었다. 경사각은 단면의 평행부와 x축 사이의 각도로 정의하였다.
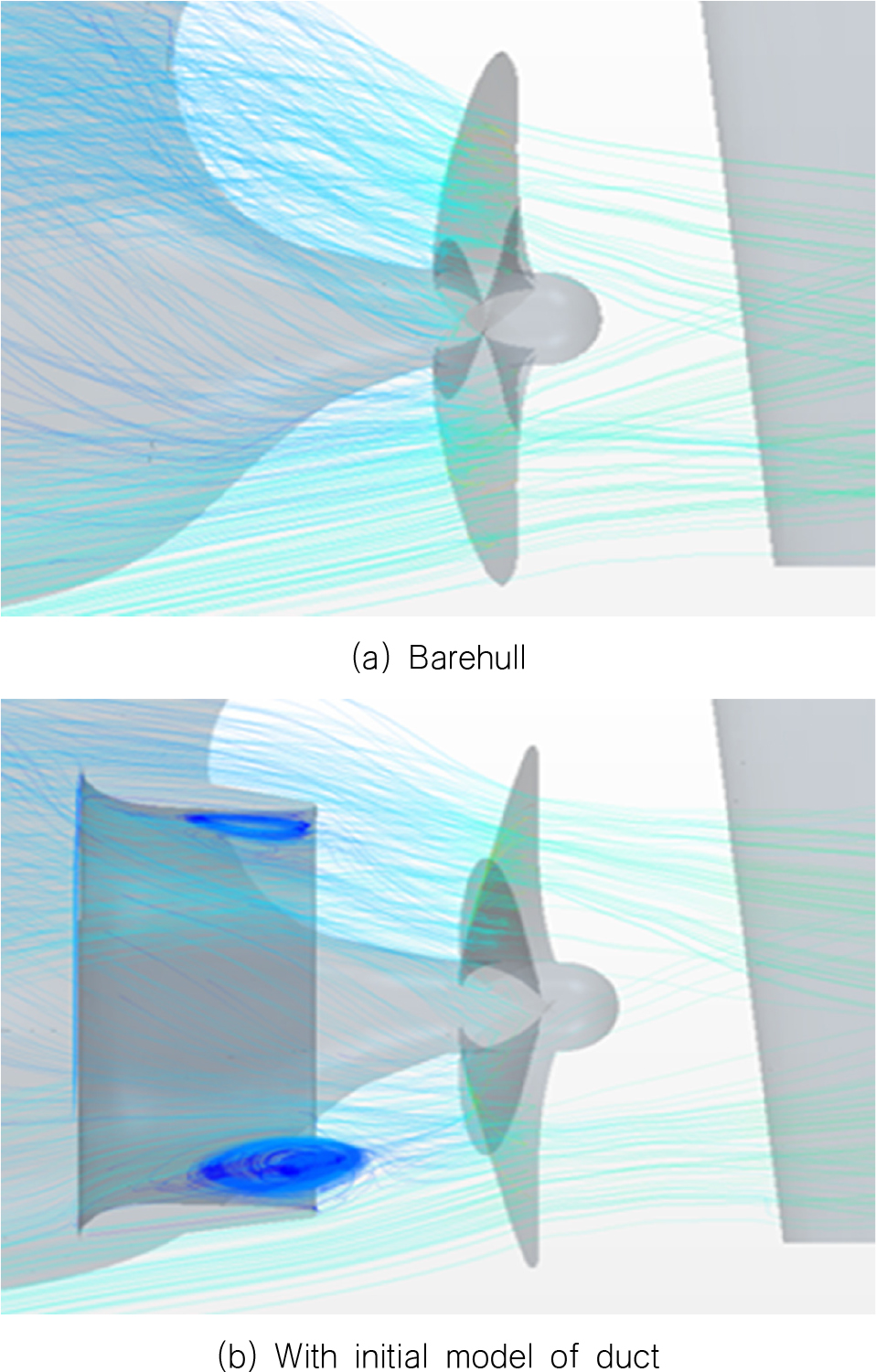
Table 5에는 CFD를 이용하여 해석한 초기모델의 자항성능 결과를 나타내었으며, 자항점을 얻기 위해 2가지 회전수를 적용하여 수행하고 내삽법을 이용하여 결정하였다. 자항해석에 사용한 Rn는 6.52e+6, Fn는 0.12, FD는 6.24N 이다. Fig. 9에는 알몸선체에서의 유선과 덕트를 부착하였을 때의 유선을 나타내었다.
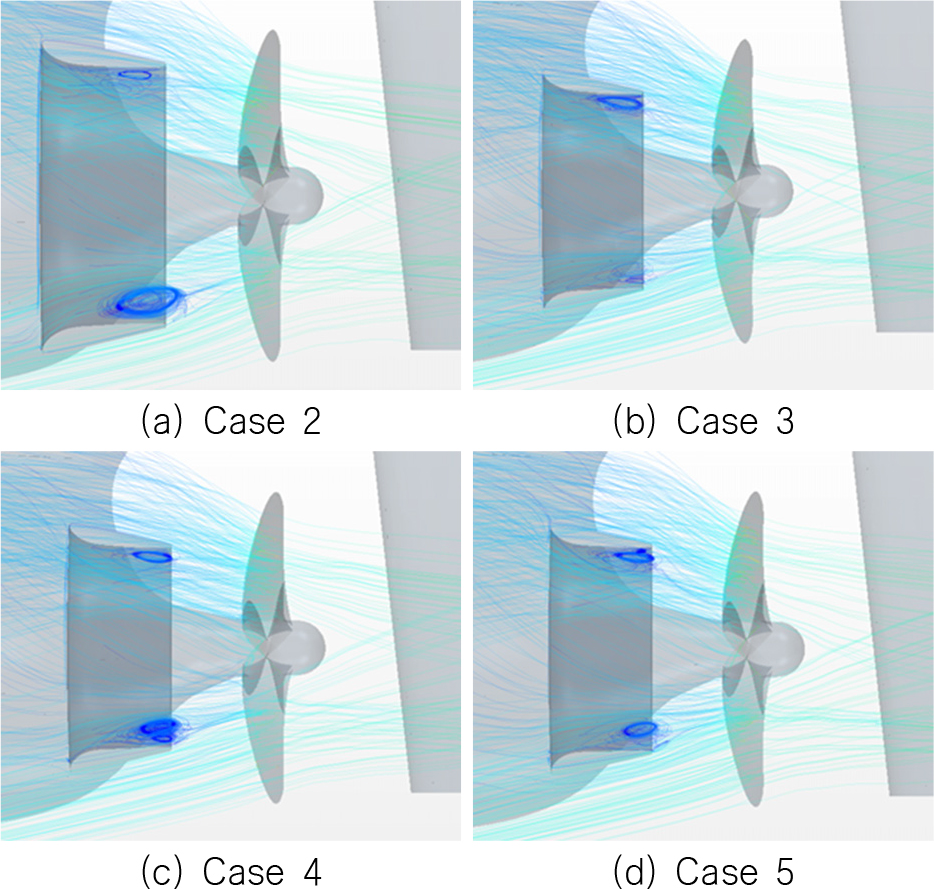
Fig. 9(b)에서 나타난 것과 같이 duct case 1을 부착한 경우, 덕트 하부에서 박리현상이 과도하게 발생하는 것을 볼 수 있으며 모형선의 전달동력 측면에서 5.2%의 추진효율 감소를 확인할 수 있었다. 이를 바탕으로 덕트의 상하부에서의 경사각은 유동각 분석을 통해 설정해야 한다고 판단하였으며, 이후 4번의 사례연구를 추가적으로 진행하였다. Case 2는 박리현상을 줄이고자 하부 경사각을 증가시켜주었으며, case 3는 제작단가 및 구조적 안정성을 고려하여 실선 스케일에서의 크기가 Mewis Duct와 유사하도록 직경과 코드길이를 줄여주었다. Case 4와 5는 case 3에 여전히 발생하는 박리현상을 없애고자 상하부 경사각을 조절하였지만 큰 차이를 보이지 않았다. 각 case에서의 제원은 Table 6에 나타내었으며, Table 7에는 각 case의 자항점에서의 추진성능을 나타내었다.
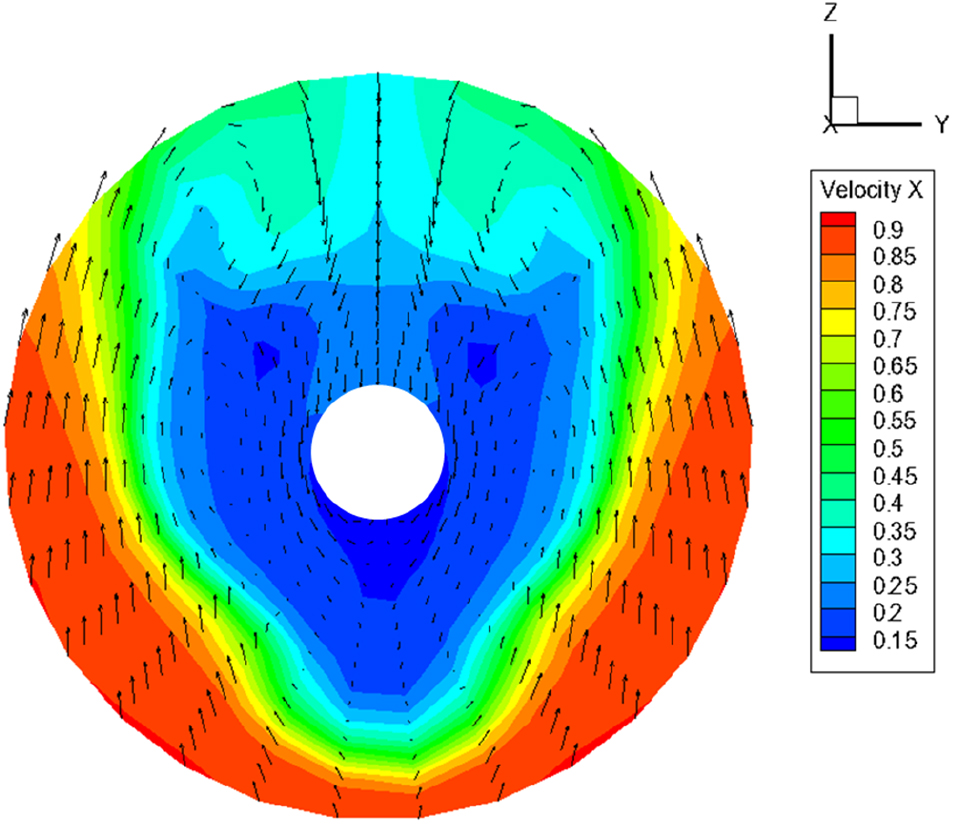
사례연구를 수행한 결과, 2.8%의 추진효율 상승을 보인 Case 3를 최적 덕트로 선정하였으며, 각 덕트 주변에서의 유선을 분석함으로써 duct 1에 비해 어떤 변화가 생겼는지 확인하였으며, Fig. 10에 나타내었다. 또한, 최적 덕트로 선정한 Case 3의 덕트를 부착하였을 시의 반류분포를 확인하였으며, Fig. 11에 나타내었다. 본 연구에서는 가속덕트를 부착하였으나 덕트로 인한 반류상승에 따라 유속은 더 느려진 것으로 보인다. 축 방향 유속의 감소로 인해 프로펠러 받음각이 커지게 되었으며, 덕트 내부 유동이 균일화 된 것으로 인해 추진효율 상승이 있었던 것으로 보인다.
4.2 전류고정날개의 설계 및 수치해석결과
전류고정날개의 설계변수는 코드직경비(c/D), 캠버코드비(c/f0), 두께직경비(t/D) 그리고 피치각으로 설정하였다. 2017년 Shin et al.은 선종 별 최적 전류고정날개의 제원 결정 방법에 관한 연구를 수행하였다. 선종 별 공칭반류를 기준으로 코드직경비, 캠버코드비, 두께직경비를 1차 보간식을 통해 결정하였는데 본 연구에서는 Case 3의 덕트를 지났을 때의 공칭반류인 0.600을 기준으로 하여 제원을 결정하였으며 Table 8에 나타내었다.
전류고정날개의 피치각을 결정하기위해 양력면 이론을 기반으로 하며 프로펠러와 전류고정날개의 상호 유기 속도를 고려하여 반복 계산을 하도록 프로그램화 되어있는 PASTA(Pre-Swirl Asymmetric Stator Analysis) 프로그램을 사용하였다. PASTA 프로그램은 반류시험을 수행하여 얻은 반류를 토대로 최적 고정날개 설계를 위한 것으로 KRISO에서 수행된 연구에 의해 개발 되어진 프로그램이다.(Lee et al., 1992) 본 연구에서는 CFD해석을 통해 얻은 반류를 이용하였으며, 역시 Case 3의 덕트를 부착하였을 때의 반류를 입력값으로 해주었다.
고정날개의 변수들을 조절하면 각 고정날개의 반경별 Γ가 달라지게 되는데, Γ는 순환세기로서 날개에 걸리는 부하를 간접적으로 표현하기 때문에 이 값을 가지고 성능을 비교할 수 있다.(Shin et al., 2016)
PASTA 프로그램은 Γ를 이에 상응하는 등가 받음각으로 표현하여 조금 더 직관적으로 분석할 수 있도록 하였다. 등각받음각의 개념은 아래와 같다.
| (3) |
| (4) |
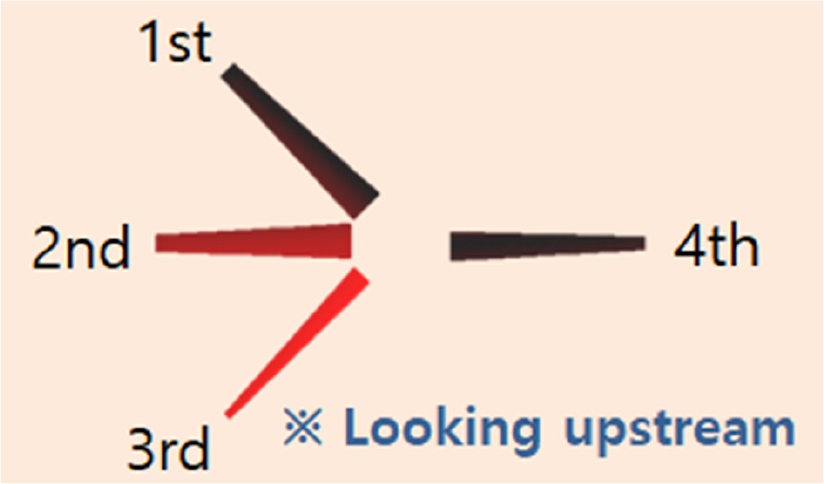
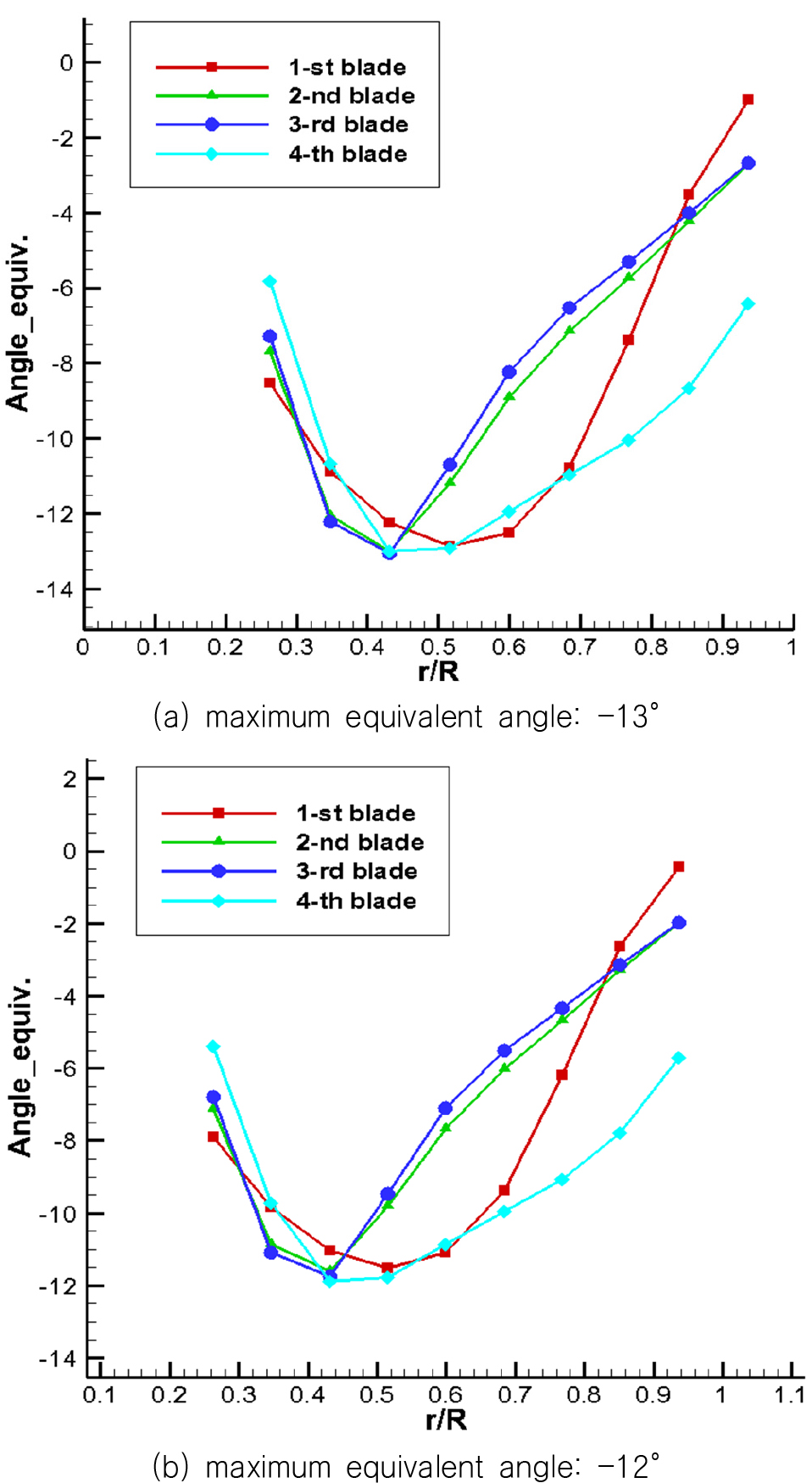
여기서 G는 무차원화 된 부하값이며, u는 국부 유입속도, c는 코드길이를 의미한다. 피치각을 변경하여 각 날개에 걸리는 최대 등가 받음각이 -13°와 -12°가 되도록 하여 각 날개에 작용하는 최대 부하량을 일치시켜주었다.(Kwon, 2013) 이에 따른 날개 별 피치각은 Table 9과 같으며, 각 날개의 번호 부여는 Fig. 12에 나타내었다. 또한, 반경 별 등가 받음각은 Fig. 13에 나타내었다.
Fig. 14에는 최적화 된 덕트와 전류고정날개를 결합한 첫 번째 case의 PNU PSD를 대상선에 부착한 형상을 나타내었다. 전류고정날개와 프로펠러간의 간격은 0.25Dp이며 전류고정날개와 덕트는 Song et al. (2013)와 같이 전류고정날개의 0.6R에서의 코드길이의 10%가 맞물리도록 위치시켰다.
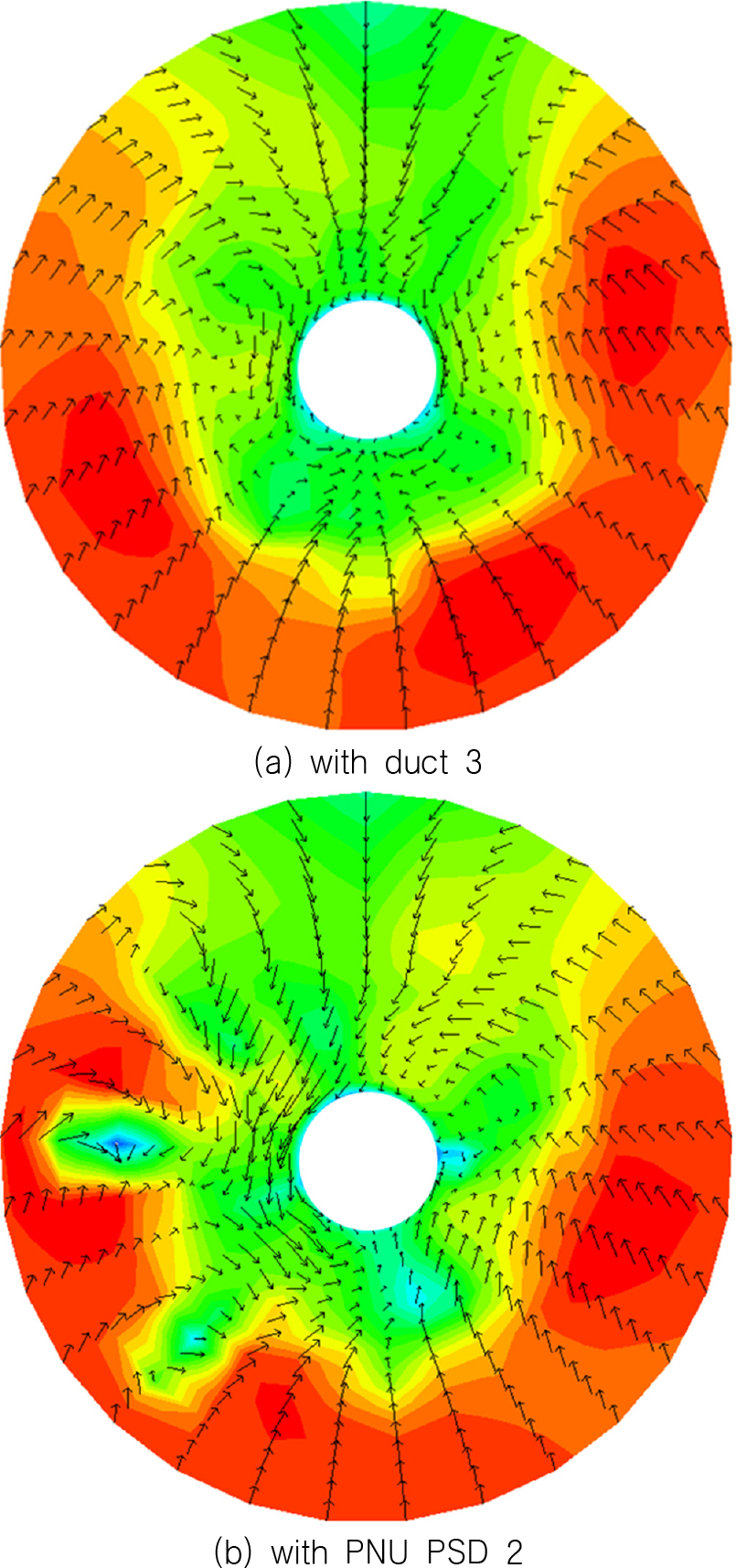
각 case 의 PNU PSD를 부착하여 자항해석을 수행하여 자항점에서의 추진성능을 확인하였으며, Table 10에 나타내었다. 알몸선체 상태와 비교하였을 때 case 2의 PNU PSD를 부착하였을 때가 전달동력 측면에서 약 5.9%의 추진효율 상승이 있었다. 최적 덕트만 부착한 경우와 비교하였을 때 약 3%의 추진효율 상승이 있었는데 이를 확인하기 위해 프로펠러면 바로 상류지점(just upstream of propeller plane)서의 유속분포를 확인해보았으며, Fig. 15에 나타내었다.
전류고정날개가 추가로 부착된 경우 덕트만 부착된 경우에 비해 고정날개의 위치에서 프로펠러의 회전방향과 반대되는 방향의 유동이 잘 형성되는 것을 확인할 수 있었으나 국부적으로 저속구간이 발생하는 점을 확인할 수 있었다. 이와 같은 문제점을 파악하기 위해 전류고정날개의 각 날개 주변의 국부유동을 확인해보았으며 Fig. 16에 나타내었다.
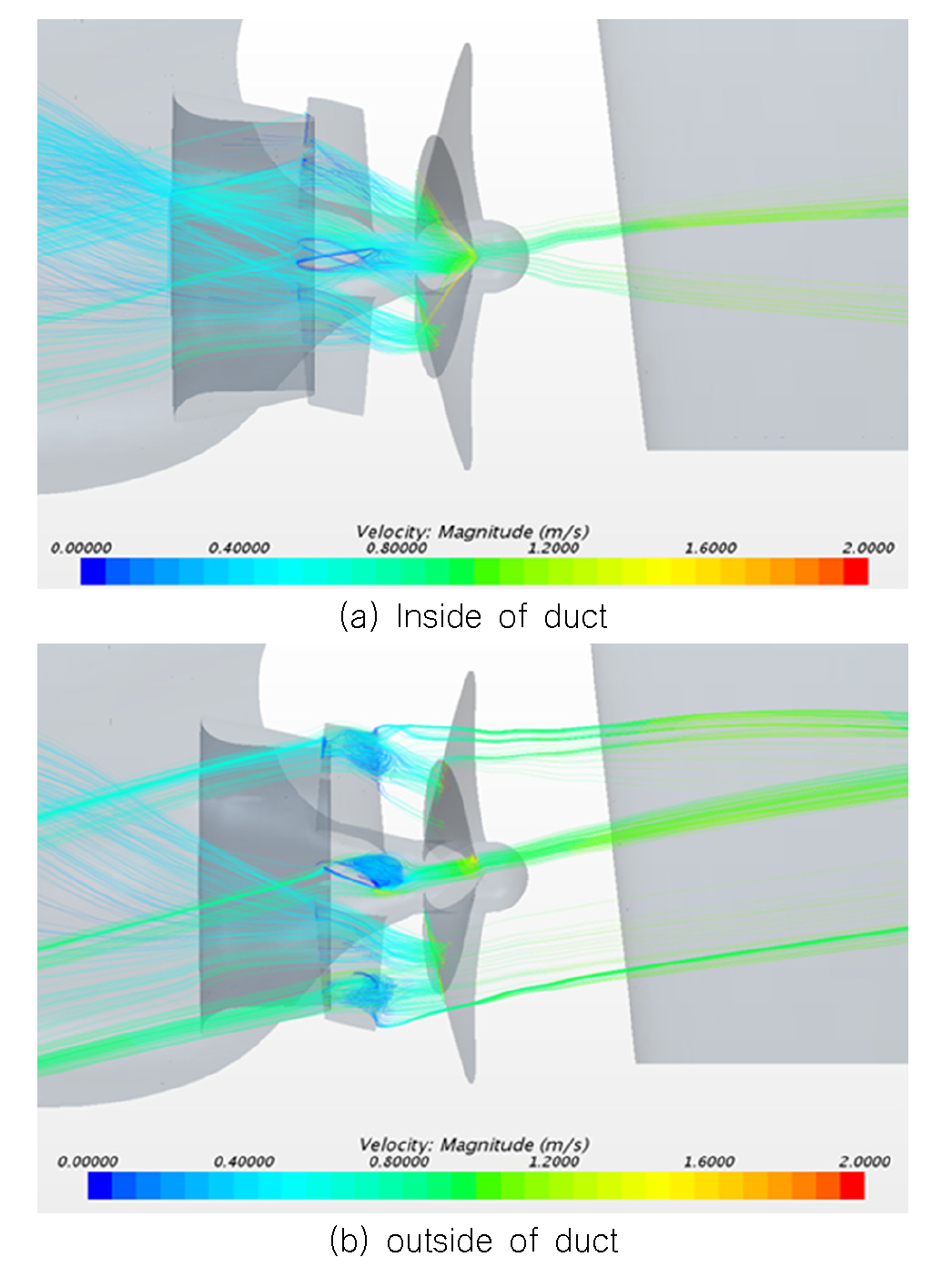
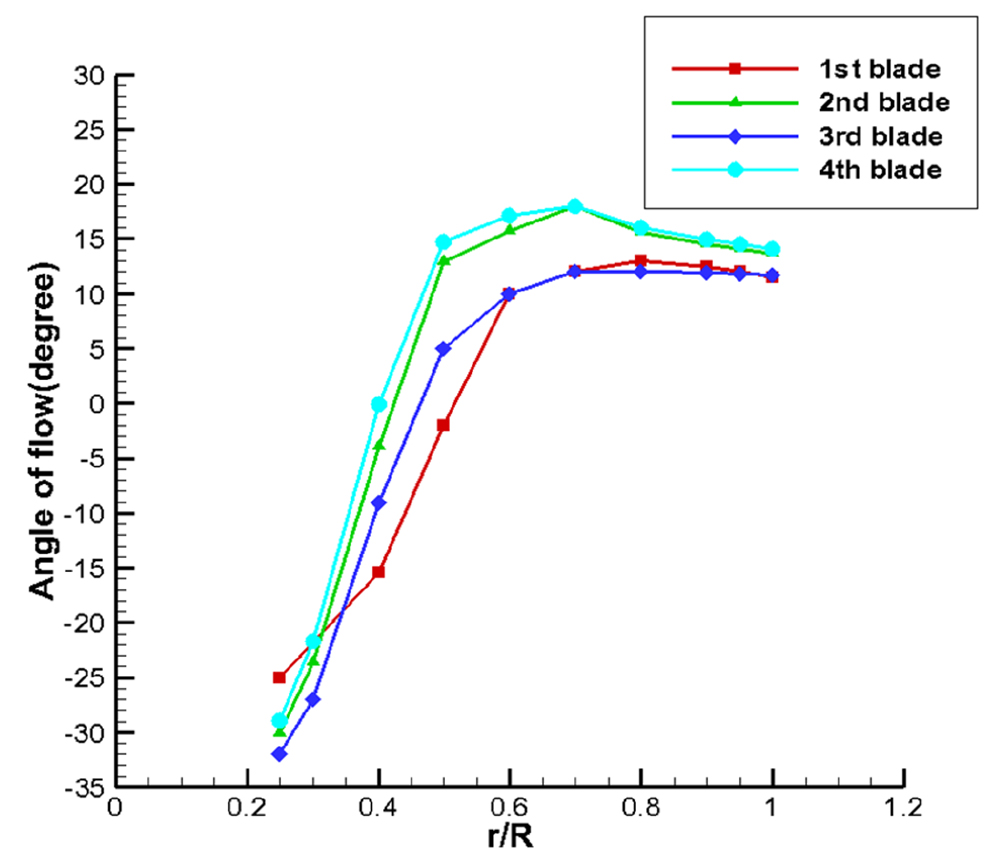
Fig. 16 (a)는 덕트 내부에 위치한 각 날개에서의 국부적인 유선을 나타내었으며, Fig. 16 (b)에는 덕트 외부에 위치한 각 날개에서의 국부적인 유선을 나타내었다. 앞서 Fig. 11에서 보았듯이 덕트 외부의 유속은 덕트 내부의 유속에 비해 상대적으로 빠르며 선미하부에서 올라오는 상향류가 그대로 유지되기 때문에 같은 피치각임에도 불구하고 Fig. 16의 (a)와 (b)처럼 다른 유동현상을 보이는 것을 확인할 수 있다. (a)의 경우 덕트를 지난 유동이 고정날개 단면을 잘 따라 흐르는 것을 확인할 수 있지만 (b)의 경우 과도한 받음각을 갖게 되어 박리현상이 발생하는 것을 확인할 수 있다. 이러한 문제점을 해결하기위해 본 연구에서는 반경 별로 다른 피치각을 설정할 수 있는 변화피치 전류고정날개를 적용하였다. 각 반경에서의 적절한 피치각을 설정하기 위해 각 날개의 부착 위치에서의 유동각을 분석해보았으며, Fig. 17에 나타내었다. 반경 별 유동각은 직교좌표계의 유속 성분을 원통좌표계로 변환하여 접선방향 속도성분(tangential velocity)과 축방향 속도성분(axial velocity)의 비(ratio)로 계산하였다.
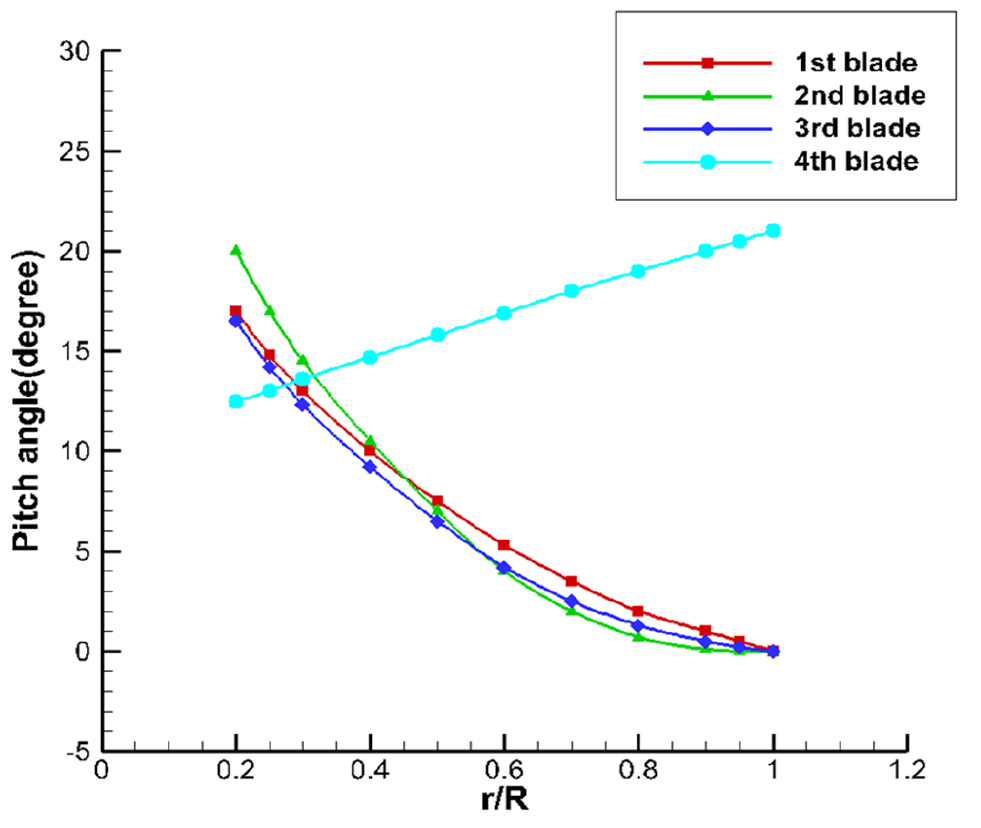
Fig. 17에서 볼 수 있듯이 덕트 내부에서는 유동각의 변화가 큰 반면에 외부에서는 유동각 변화가 작은 것을 확인할 수 있다. 또한 모든 날개의 허브에서의 유동각이 약 -30°에 달하는 것을 확인할 수 있는데 이에 맞도록 피치각을 설정할 경우 과도한 피치각으로 인해 저항측면에서 불리할 수 있다. 그렇기 때문에 허브에서의 최대 피치각은 PNU PSD 2에 적용한 피치각으로 제한하였다. 또한 모든 날개의 팁에서의 유동각은 약 10°~15°인 것을 확인할 수 있는데 이에 맞게 피치각을 설정할 경우 음의 피치각을 갖게 될 수 있다. 이는 고정날개의 주요 성능인 역회전 유동 생성에 위배되는 현상을 야기하므로 최소 피치각은 0°로 제한하였다. 각 날개의 반경 별 피치각은 Table 11과 같으며 Fig. 18에 그래프로 나타내었다. 4번 날개는 1,2,3번과 달리 유동을 위쪽으로 꺾어 올려주어야 하기 때문에 피치각 분포의 차이가 반대되는 것을 확인할 수 있다.
위와 같은 변화피치 전류고정날개를 적용하여 PNU PSD 3를 모델링하였으며 적용 결과는 Table 12에 나타내었다.
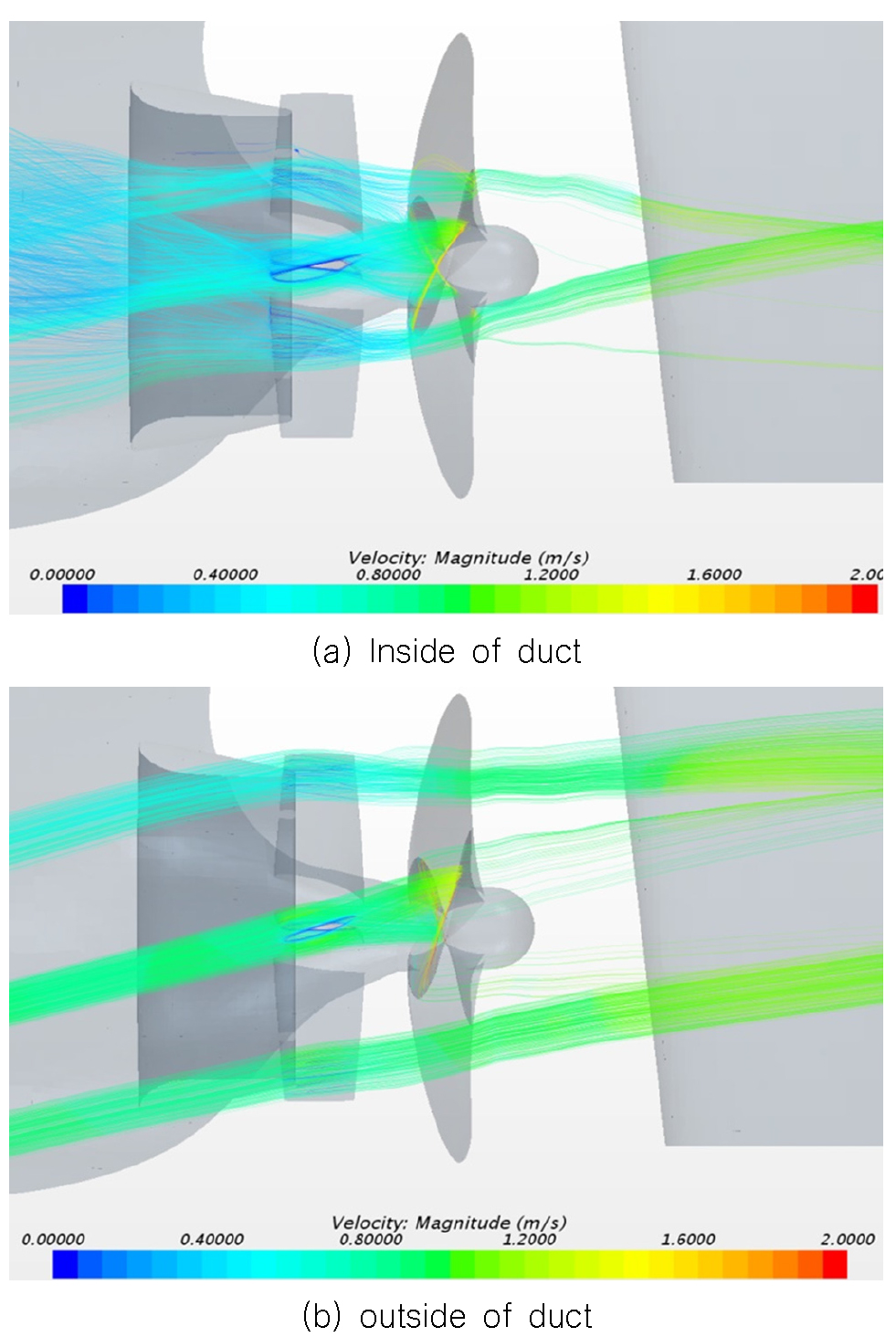
PNU PSD 3을 부착한 결과 약 7.6%의 추진효율 상승이 있었다. 개선점을 알아보기 위해 고정피치 전류고정날개에서 문제가 되었던 고정날개 주변의 유선을 확인하였으며, Fig. 19에 나타내었다.
Fig. 16의 고정피치 전류고정날개와 비교하였을 때 덕트 내부에서도 유선이 고르게 펴지는 것을 확인할 수 있었으며, 외부에서는 문제가 되었던 박리현상이 없어지는 것을 확인할 수 있었다. 이로 인해 저항 및 토크가 감소하는 효과가 있었으며, 고정피치와 비교하였을 때 1.7%의 추가적인 효율 상승이 있었던 것으로 보인다.
5. 결 론
본 연구에서는 176k Bulk Carrier의 추진효율을 상승시키기 위해 새로운 타입의 Pre-Swirl Duct를 개발하였으며, CFD해석을 통해 성능을 확인하였다. 기존의 Mewis Duct의 약점을 고려하여 덕트의 위치를 상류로 위치시켜주었으며 덕트의 뒷날과 고정날개의 앞날이 고정날개 코드길이의 10%가 맞물리도록 설정하였다.
에너지 절감장치를 설계하는 과정을 덕트와 전류고정날개로 나누었으며, 유동의 흐름순서에 맞게 덕트 설계를 우선적으로 진행하였다. 이후, 덕트를 지난 유동을 고려하여 전류고정날개를 설계하였으며, 덕트 내외부의 유속 및 유동각 차이를 고려하여 변화피치 고정날개를 적용하였다.
덕트는 직경, 코드길이, 상,하부 경사각을 설계변수로 설정하여 사례연구를 수행하였고 최적화 된 덕트를 부착한 경우, 알몸선체상태와 비교하였을 때 프로펠러면으로 들어오는 유속을 느리게 하고 특히 덕트 내부에서는 균일한 유동이 들어오게 해줌에 따라 약 2.8%의 추진효율이 상승하는 것을 확인하였다.
전류고정날개는 코드직경비, 캠버코드비, 두께직경비, 피치각을 설계변수로 설정하였으며 앞의 3가지 설계변수는 공칭반류를 기준으로 결정하였고 피치각은 등가받음각 개념을 이용하여 결정하였다. 최대등가받음각이 -12°일 때 가장 좋은 효율을 보였으며 덕트와 함께 부착하였을 때 약 5.9%의 추진효율이 상승함을 확인하였다. 고정날개는 역회전 유동을 형성하여 프로펠러 받음각을 크게 해주는 효과가 있었고 이로 인해 회전수 감소효과를 보였다. 하지만 덕트 외부에 위치한 고정날개에서 과도한 받음각으로 인해 박리현상이 발생하는 것을 확인할 수 있었으며 이를 고려하여 변화피치 고정날개를 적용하였다.
각 반경 별 유동각은 덕트 내부에서 그 변화가 상대적으로 크고 외부에서 적은 것을 확인하였으며, 이에 맞게 반경 별 피치각 분포를 결정하였다. 변화피치 고정날개를 적용한 결과 약 7.6%의 추진효율 상승을 확인하였으며, 장치 주변의 유선을 확인함으로써 덕트 내부와 외부에서 유동이 개선된 것을 확인할 수 있었다. 본 연구를 통해 전류고정덕트 설계 시 고정날개의 직경이 덕트의 직경보다 큰 경우 덕트 내부와 외부의 유속 및 유동각 차이를 고려하기 위해 변화피치 고정날개를 적용하는 것이 유리함을 확인하였다.
Acknowledgments
이 논문은 한국연구재단 선도연구센터지원사업(글로벌핵심연구센터)의 지원으로 연구되었음 (No. 2011-0030013).
References
- Carlton, J.S., 1994. Marine propellers and propulsion, Butterworth and Heinemann, London, pp.299-324.
- Kwon, J.I., 2013. A study on the based asymmetric Pre-Swirl Stator for a container ship. Master Thesis, Pusan National University.
- Lee, J.T., Kim, M.C., Suh, J.C., Kim, S.H. & Choi, J.K., 1992. Development of a Pre-Swirl stator-propeller system for improvement of propulsion efficiency : a symmetric stator propulsion system. Transactions of the Society of Naval Architects of Korea, 29(4), pp.132-145.
-
Shin, Y.J., Kim, M.C., Kang, J.G. & Lee, J.H., 2016. Study on performance of asymmetric Pre-Swirl Stator according to variations in dimensions and blade tip shape. Journal of Ocean Engineering and Technology, 30(6), pp.431-439.
[https://doi.org/10.5574/KSOE.2016.30.6.431]

- Shin, Y.J., Kim, M.C., Shin, I.R. & Kim, H.U., 2017. Study on optimization of Asymmetric PSS for each ship type. Proceedings of 2017 Joint Conference of The Korean Association of Ocean Science and Technology Societies, April 2017, Busan BEXCO.
-
Song, H.J., Kim, M.C., Lee, W.J., Lee, K.W. & Kim, J.H., 2013. Development of the new energy saving device for the reduction of fuel of 176k bulk carrier. Journal of the Society of Naval Architects of Korea, 52(6), pp.419-427.
[https://doi.org/10.3744/SNAK.2015.52.6.419]